2020重庆中考复习利用旋转法解几何最值问题应用举例

利用旋转法解几何最值问题应用举例
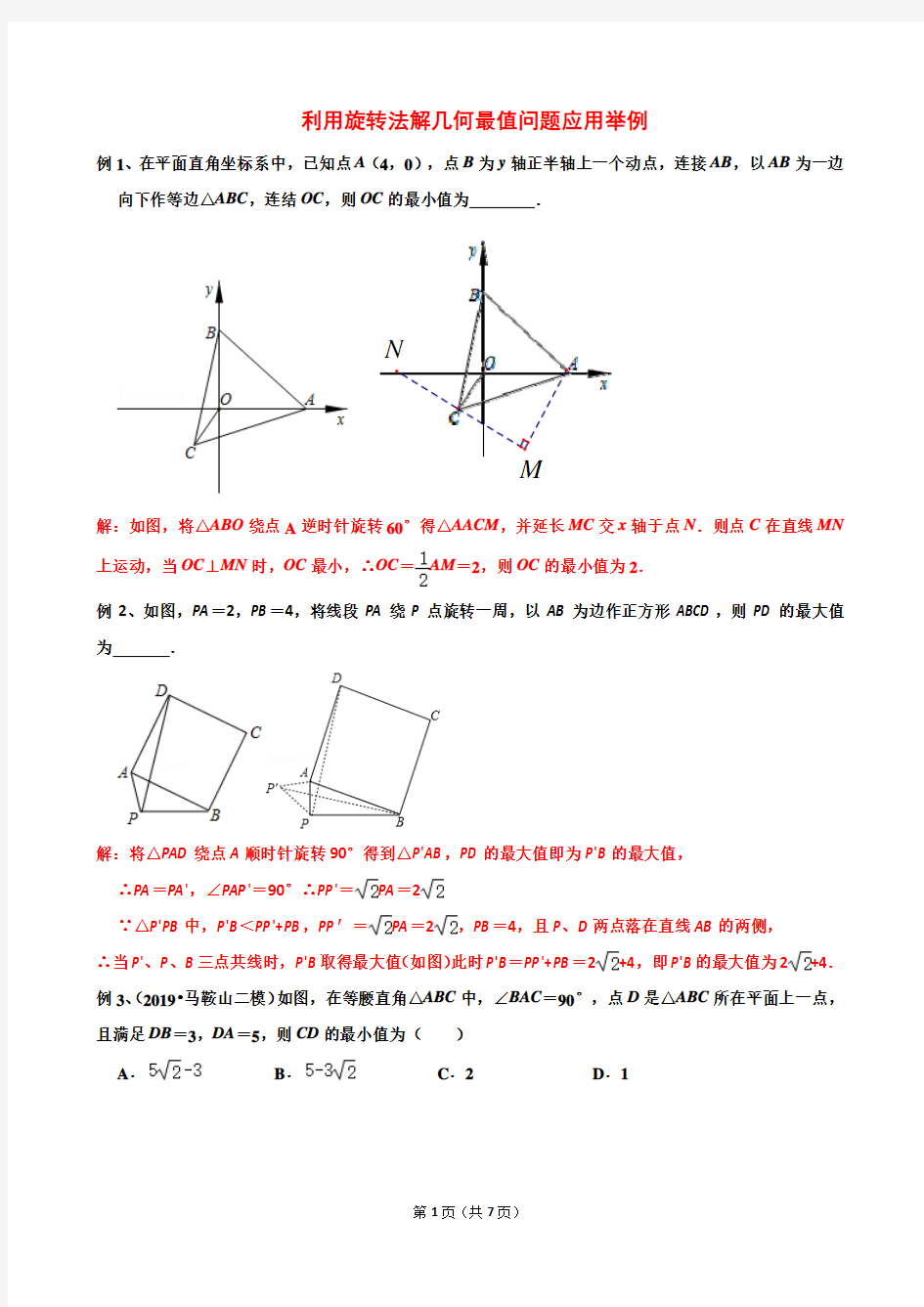
例1、在平面直角坐标系中,已知点A (4,0),点B 为y 轴正半轴上一个动点,连接AB ,以AB 为一边
向下作等边△ABC ,连结OC ,则OC 的最小值为 .
M
解:如图,将△ABO 绕点A 逆时针旋转60°得△AACM ,并延长MC 交x 轴于点N .则点C 在直线MN 上运动,当OC ⊥MN 时,OC 最小,∴OC =AM =2,则OC 的最小值为2.
例2、如图,PA =2,PB =4,将线段PA 绕P 点旋转一周,以AB 为边作正方形ABCD ,则PD 的最大值为 .
解:将△PAD 绕点A 顺时针旋转90°得到△P 'AB ,PD 的最大值即为P 'B 的最大值,
∴PA =PA ',∠PAP '=90°∴PP '=
PA =2 ∵△P 'PB 中,P 'B <PP '+PB ,PP ′=PA =2,PB =4,且P 、D 两点落在直线AB 的两侧,
∴当P '、P 、B 三点共线时,P 'B 取得最大值(如图)此时P 'B =PP '+PB =2
+4,即P 'B 的最大值为2+4. 例3、(2019?马鞍山二模)如图,在等腰直角△ABC 中,∠BAC =90°,点D 是△ABC 所在平面上一点,且满足DB =3,DA =5,则CD 的最小值为( )
A . B
. C .2 D .1
解:将△ADC绕点A顺时针旋转90°,得到△ABE.则CD=BE,△ADE是等腰直角三角形,ED=5.∵AE、AD、BD都是定值,∴当E、B、D三点共线时,BE最小,即CD最小.此时BE最小值为DE﹣BD=5﹣3.故选:A.
例4、如图,平行四边形ABCD中,∠B=60°,BC=12,AB=10,点E在AD上,且AE=4,点F是AB上一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为 .
解:将线段AE绕点E逆时针旋转120°得到EH,连接HG,过点H作HM⊥AD, ∵四边形ABCD是平行四边形,∴∠A+∠B=180°,∴∠A=120°,
∵将线段AE绕点E逆时针旋转120°得到EH,将线段EF绕点E逆时针旋转120°得到EG, ∴EF=EG=4,AE=EH,∠AEH=∠FEG=120°,
∴∠DEH=60°,∠AEF=∠HEG,且EF=EG,AE=EH,∴△AEF≌△HEG(SAS)
∴∠A=∠EHG=120°=∠AEH,∴AD∥HG,∴点G的轨迹是过点H且平行于AD的直线, ∴当DG⊥HG时,线段GD长度有最小值,∵∠HEM=60°,EH=4,HM⊥AD,
∴EM=2,MH=EM=2,∴线段GD长度的最小值为2,
例5、(2019?宿迁)如图,正方形ABCD的边长为4,E为BC上一点,且BE=1,F为AB边上的一个动点,连接EF,以EF为边向右侧作等边△EFG,连接CG,则CG的最小值为 .
解:由题意可知,点F是主动点,点G是从动点,点F在线段上运动,点G也一定在直线轨迹上运动 将△EFB绕点E旋转60°,使EF与EG重合,得到△EFB≌△EHG,从而可知△EBH为等边三角形,点G在垂直于HE的直线HN上,作CM⊥HN,则CM即为CG的最小值,作EP⊥CM,可知四边形HEPM
为矩形,则CM=MP+CP=HE+EC=1+=,故答案为.
例6、如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段EF 绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为( )
A.3 B.2 C.4 D.2+2
解:如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H. ∵四边形ABCD是菱形,∴AD=BD,∵AE=ED,AN=NB,∴AE=AN,
∵∠A=60°,∴△AEN是等边三角形,∴∠AEN=∠FEG=60°,∴∠AEF=∠NEG,
∵EA=EN,EF=EG,∴△AEF≌△NEG(SAS),∴∠ENG=∠A=60°,∵∠ANE=60°,
∴∠GNB=180°﹣60°﹣60°=60°,∴点G的运动轨迹是射线NG,易知B,E关于射线NG对称, ∴GB=GE,∴GB+GC=GE+GC≥EC,在Rt△DEH中,∵∠H=90°,DE=2,∠EDH=60°,
∴DH=DE=1,EH=,在Rt△ECH中,EC==2,∴GB+GC≥2,
∴GB+GC的最小值为2.故选:B.
例7、如图,AB=6,点M为线段AB外一个动点,且AM=2,MB=MN,∠BMN=90°,则线段AN的最大值为 .
解:如图,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP, 则△APM是等腰直角三角形,∴MA=MP=2,BP=AN,∴PA=2,
∵AB=6,∴线段AN长的最大值=线段BP长的最大值,
∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=6+2.
例8、(2019?龙岩一模)如图,△ABC中,∠ABC=30°,AB=4,BC=5,P是△ABC内部的任意一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .
解:如图,将△ABP绕着点B逆时针旋转60°,得到△DBE,连接EP,CD,∴△ABP≌△DBE
∴∠ABP=∠DBE,BD=AB=4,∠PBE=60°,BE=PE,AP=DE,∴△BPE是等边三角形
∴EP=BP∴AP+BP+PC=PC+EP+DE,∴当点D,点E,点P,点C共线时,PA+PB+PC有最小值CD ∵∠ABC=30°=∠ABP+∠PBC,∴∠DBE+∠PBC=30°,∴∠DBC=90°,∴CD==, 练习
1、(2019?常熟市二模)已知x轴上一点A(1,0),B为y轴上的一动点,连接AB,以AB为边作等边
△ABC如图所示,已知点C随着点B的运动形成的图形是一条直线,连接OC,则AC+OC的最小值是 .
解:将△ABO绕点A逆时针旋转60°得△ACD,并作直线CD,延长AD交y轴于点A'.
∵等边△ABC、等边△AOD,∴AB=AC,AO=AD,∠BAC=∠OAD=60°
∴∠BAC﹣∠OAC=∠OAD﹣∠OAC,∴∠BAO=∠CAD
在△BAO和△CAD中,∴△BAO≌△CAD(SAS),∴∠AOB=∠ADC∵∠AOB=90° ∴∠ADC=90°,∴CD⊥AD,∴点C随着点B的运动形成的图形是直线CD
∵∠AOA'=90°,∠OAD=60°∴∠AA'O=30°∴OA=AA' ∴AD=OA=AA'
∴点D是AA'的中点,∵CD⊥AD,∴CD是AA'的中垂线 ∴AC=A'C,∴AC+OC=A'C+OC
又∵点C在直线CD上运动,所以点O、C、A'三点共线时,A'C+OC的值最小,最小值为OA'的长.
在R△AOA'中,∠AOA'=90°,∠OAD=60°,OA=1,O A'=OA=,∴AC+OC的最小值为
.
2、已知:AD=2,BD=4,以AB为一边作等边三角形ABC.使C、D两点落在直线AB的两侧.
当∠ADB变化时,则CD的最大值 .
解:把△ADC绕点A顺时针旋转60°得到△AEB,则AE=AD,BE=DC,∠EAD=60°, ∴△ADE为等边三角形,∴DE=DA=2,∠ADE=60°,
当E点在直线BD上时,BE最大,最大值为2+4=6,∴CD的最大值为6.
3、如图,在等腰直角△ABC中,∠BAC=90°,点D是△ABC所在平面上一点,且满足DB=6,DA=10,则CD的最小值为
解:将△ADC绕点A顺时针旋转90°,得到△ABE.则CD=BE,△ADE是等腰直角三角形,ED=10.∵AE、AD、BD都是定值,∴当E、B、D三点共线时,BE最小,即CD最小.此时BE最小值为DE﹣BD=10﹣5.故选:A.
4、如图,平行四边形ABCD中,∠B=60°,BC=6,AB=5,点E在AD上,且AE=2,点F是AB上
一点,连接EF,将线段EF绕点E逆时针旋转120°得到EG,连接GD,则线段GD长度的最小值为 .
解:将线段AE 绕点E 逆时针旋转120°得到EH ,连接HG ,过点H 作HM ⊥AD ,
∵四边形ABCD 是平行四边形,∴∠A +∠B =180°,∴∠A =120°,
∵将线段AE 绕点E 逆时针旋转120°得到EH ,将线段EF 绕点E 逆时针旋转120°得到EG , ∴EF =EG ,AE =EH ,∠AEH =∠FEG =120°,
∴∠DEH =60°,∠AEF =∠HEG ,且EF =EG ,AE =EH ,∴△AEF ≌△HEG (SAS )
∴∠A =∠EHG =120°=∠AEH ,∴AD ∥HG ,∴点G 的轨迹是过点H 且平行于AD 的直线, ∴当DG ⊥HG 时,线段GD 长度有最小值,∵∠HEM =60°,EH =2,HM ⊥AD ,
∴EM =1,MH =,∴线段GD 长度的最小值为,
5、如图,长方形 ABCD 中,AB=3,BC=4,E 为 BC 上一点,且 BE =2,F 为 AB 边上的一个动点,连接 EF ,将 EF 绕着点 E 顺时针旋转 45?到 EG 的位置,连接 FG 和 CG ,则 CG 的最小值为 .
F
解:由题意可知,点F 是主动点,点G 是从动点,点F 在线段上运动,点G 也一定在直线轨迹上运动,
将△EFB 绕点E 旋转45°,使EF 与EG 重合,得到△EFB ≌△EHG ,从而可知△EBH 为等腰直角三角形,点G 在垂直于HE 的直线HG
上,作CM ⊥HG ,则CM
即为CG 的最小值,作EN ⊥CM ,可知四边形HENM 为矩形,则CM =MN +CN =HE =12 6、(2019秋?海曙区校级月考)如图,菱形ABCD 的边长是6,∠A =60°,E 是AD 的中点,F 是AB 边上一个动点,EG =EF 且∠GEF =60°,则GB +GC 的最小值是
A
A
解:取AB的中点H,连接HG、HE、HG、BE、CE,则△AEF≌△HEG
∴∠GHE=∠A=60°,∴HG∥AD,可知△BHG≌△EHG,∴BG=GE,∴CE的长就是GB+GC的最小值;
在Rt△EBC中,EB=3,BC=6,∴EC=3,∴GB+GC的最小值3.
7、如图,AB=8,点M为线段AB外一个动点,且AM=4,MB=MN,∠BMN=90°,则线段AN的最大值为.
解:如图,连接BN,∵将△AMN绕着点M顺时针旋转90°得到△PBM,连接AP, 则△APM是等腰直角三角形,∴MA=MP=4,BP=AN,∴PA=4,∵AB=8,
∴线段AN长的最大值=线段BP长的最大值,
∴当P在线段BA的延长线时,线段BP取得最大值最大值=AB+AP=8+4.
8、(2019秋?蔡甸区期中)如图,在△ABC中,∠ABC=60°,AB<AC,点P是△ABC内一点,AB=6,
BC=8,则PA+PB+PC的最小值是 .
解:如图,将△PBF绕点B逆时针旋转60°得到△BFE,作EH⊥CB交CB的延长线于H. ∵∠ABC=60°,∠PBF=60°,∵∠ABP=∠EBF,∴∠EBF+∠BC=60°,∴∠EBC=120°, ∵PB=BF,∠PBF=60°,∴△PBF是等边三角形,∴PB=PF,
∵PA=EF,∴PA+PB+PC=CP+PF+EF,
根据两点之间线段最短可知,当E,F,P,C共线时,PA+PB+PC的值最小,最小值=EC的长, 在Rt△EBH中,∵∠EBH=60°,EB=6,
∴BH=BE?cos60°=3,EH=EB?sin60°=3,∴CH=BH+CB=3+8=11,
∴EC===2.
重庆中考几何题分类汇编(含答案)
重庆中考几何题分类汇编(含答案) 类型1 线段的倍分:要证线段倍与半,延长缩短去实验 例1 如图Z3-1,在△ABC中,AB=AC,CM平分∠ACB交AB于M,在AC的延长线上截取CN=BM,连接MN 交BC于P,在CB的延长线截取BQ=CP,连接MQ. (1)求证:MQ=NP; (2)求证:CN=2CP. 针对训练: 1.如图Z3-2,在?ABCD中,AC⊥BC,点E、点F分别在AB、BC上,且满足AC=AE=CF,连接CE、AF、EF. (1)若∠ABC=35°,求∠EAF的度数; (2)若CE⊥EF,求证:CE=2EF.
2.已知,在△ABC 中,AB =AC ,∠BAC =90°,E 为边AC 任意一点,连接BE. (1)如图①,若∠ABE=15°,O 为BE 中点,连接AO ,且AO =1,求BC 的长; (2)如图②,F 也为AC 上一点,且满足AE =CF ,过A 作AD⊥BE 交BE 于点H ,交BC 于点D ,连接DF 交BE 于点G ,连接AG.若AG 平分∠CAD,求证:AH =1 2 AC. 3.在△ACB 中,AB =AC ,∠BAC =90°,点D 是AC 上一点,连接BD ,过点A 作AE⊥BD 于E ,交BC 于F. (1)如图①,若AB =4,CD =1,求AE 的长; (2)如图②,点G 是AE 上一点,连接CG ,若BE =AE +AG ,求证:CG =2AE.
4.在等腰直角三角形ABC 中,∠BAC =90°,AB =AC ,D 是斜边BC 的中点,连接AD. (1)如图①,E 是AC 的中点,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′,当AD =6时,求AE′的值. (2)如图②,在AC 上取一点E ,使得CE =1 3AC ,连接DE ,将△CDE 沿CD 翻折到△CDE′,连接AE′交 BC 于点F ,求证:DF =CF.
2020年重庆中考几何第26题专题训练一(含答案解析)
2020年中考几何题专题训练一答案解析 \1、已知:在△ABC中,BC=2AC,∠DBC=∠ACB,BD=BC,CD交线段AB于点E.(1)如图1,当∠ACB=90°时,则线段DE、CE之间的数量关系为; (2)如图2,当∠ACB=120°时,求证:DE=3CE; (3)如图3,在(2)的条件下,点F是BC边的中点,连接DF,DF与AB交于G,△DKG和△DBG 关于直线DG对称(点B的对称点是点K,延长DK交AB于点H.若BH=10,求CE的长.
2、(2016春?重庆校级期中)在△ABC中,AB=AC,D为射线BC上一点,DB=DA,E为射线AD上一 点,且AE=CD,连接BE. (1)如图1,若∠ADB=120°,AC=2,求DE的长; (2)如图2,若BE=2CD,连接CE并延长交AB于点F,求证:CF=3EF; (3)如图3,若BE⊥AD,垂足为点E,猜想AE,BE,BD之间的数量关系,直接写出关系式.
3、(2019秋?江岸区校级月考)在菱形ABCD中,∠ABC=60° (1)如图1,P是边BD延长线上一点,以AP为边向右作等边△APE,连接BE、CE. ①求证:CE⊥AD;②若AB=,BE=,求AE的长; (2)如图2,P是边CD上一点,点D关于AP的对称点为E,连接BE并延长交AP的延长线于点F,连接DE、DF.若BE=11,DE=5,求△ADF的面积. 4、(2016秋?南岗区校级月考)已知:如图,在等边△ABC中,点D是AC上任意一点,点E在BC延长 线上,连接DB,使得BD=DE.
(1)如图1,求证:AD=CE; (2)如图2,取BD的中点F,连接AE、AF.求证:∠CAE=∠BAF; (3)如图3,在(2)的条件下,过点F作AE的垂线,垂足为H,若AH=.求EH的长. 5、已知,在Rt△ABC中,∠C=90°,AC=BC,点D在边BC上,连接AD,作DE⊥AD,且DE=AD, 连接BE、AE,DE与AB交于点H,
用旋转法………作辅助线证明平面几何题
用旋转法………作辅助线证明平面几何题 旋转法就是在图形具有等邻边特征时,可以把图形的某部分绕等邻边的公共端点,旋转另一位置的引辅助线的方法。 1、旋转方法主要用途是把分散的元素通过旋转集中起来,从而为证题创造必要的条 件。 2、旋转时要注意旋转中心、旋转方向、旋转角度的大小(三要素:中心、方向、大小); 3、旋转方法常用于竺腰三角形、等边三角形及正方形等图形中。 例1: 例2 已知,在Rt ABC中 B=AC;∠BAC=90?; D为BC边上任意一点,求证:2AD2=BD2+CD2. 证明:把ABD绕点A逆时钍方向旋转90?,得?ACE,则ABD??ACE,∴BD=CE,∠B=∠ACE; ∠BAD=∠CAE, AD=AE。 又∠BAC=90?;∴∠DAE=90? 所以: D E2=AD2+AE2=2AD2。 因为:∠B+∠ACB=90? 所以:∠DCE=90? CD2+CE2=DE2=2AD2 即: 2AD2=BD2+CD2。 注:也可以把ADC顺时针方向旋转90?来证明。 注 E C D
已知,P 为等边ABC 内一点,PA=5,PB=4,PC=3,求 ∠BPC 的度数。 证明:把 ABP 绕点B 顺时钍方向旋转90 ?,得?CBD ,则 ABP ??CBD ,∴BP=BD AP=CD=5, ∠ABP=∠CBD ,所以 ∠BAP+∠PBC=∠CBD+∠PBC=60?,所以 BPD 为等边三角形。 ∠PBD=60? PD=PB=4所以: C D 2=PD 2+PC 2。因为: ∠DPC=90?所以: ∠BPC=∠BPD+∠DPC=60?+90?=150? 注:也可以把CAP 绕点C 逆时针方向旋转60?来证明。 D C 例3: 如图:在正方形ABCD 中,E 为AD 边上一点,BF 平分∠CBE 交CD 于F 点。求证:BE=CF+AE 证明:把ABE 绕点B 顺时针方向旋转90?得BCN 。则:ABE ?BCN ,所以: ∠ABE=∠CBN ,BE=BN ,AE=CN 。因为:四边形ABCD 是正方形,所以:CD AB ,∠NFB=NBF 因为:∠ABF=∠ABE+∠EBF ,∠NBF=∠NBC+∠CBF ,而:∠EBF=∠FBC ;∠NBF=∠NFB 所以:BN=NF=CN+CF 所以:BE=AE+CF 。注:也可以把BCF 绕点B 逆时针方向旋转90?来证明。
重庆中考第26题专题专训(教师版)
重庆中考数学第26题专题专训 1.如图1,在平面直角坐标系中,抛物线y=﹣x2﹣x﹣2与x轴交于A,B两点(点A 在点B的左侧),交y轴于点C. (1)求直线AC的解析式; (2)点P是直线AC上方抛物线上的一动点,过点P作PD⊥AC,垂足为D,当线段PD的长度最大时,点Q从点P出发,先以每秒1个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒3个单位的速度运动到点C停止,当点Q在整个运动中所用时间t最少时,求点M的坐标; (3)如图2,将△BOC沿直线BC平移,平移后B,O,C三点的对应点分别是B′,O′,C′,点S是坐标平面内一点,若以A,C,O′,S为顶点的四边形是菱形,请直接写出所有符合条件的点S的坐标. 解:(1)当y=0时,﹣x2﹣x﹣2=0, 解这个方程,得:x 1=﹣6,x 2 =﹣1, ∴点A(﹣6,0),B(﹣1,0), 当x=0时,y=﹣2, ∴C(0,﹣2), 设直线AC的解析式为:y=ax+b(a≠0), 将点A(﹣6,0),C(0,﹣2)代入得:, ∴,∴直线AC的解析式为:y=﹣x﹣2;(3分)(2)如图1,过点P作PE∥y轴交直线AC于点E, 设P(a,﹣),则点E(a,﹣﹣2), ∴PE=(﹣)﹣(﹣﹣2)=﹣﹣2a,
∵AO=6,OC=2,∴AC===2, ∵∠PDE=∠AOC=90°,∠PED=∠ACO, ∴△PDE∽△AOC,∴=, ∴PD=PE==﹣﹣, 对称轴是:a=﹣3, ∵﹣, ∴当a=﹣3时,PD的长度最大,此时点P的坐标为(﹣3,2), 如图1所示,在x轴上取点F(1,0),连接CF并延长, ∴CF===3,∴sin∠OCF==, 点M是y轴上一点,过点M作MH⊥CF于点H, 由△CHM∽△COF,可知:=, ∵t==PM+MH, 如图2,当P、M、H在同一直线上时,t的值最小, 此时,过P作PK⊥y轴于K, 由△PKM∽△COF,可知:=2,∴KM=,∴M(0,),(7分)(3)如图3,当四边形ACSO'是菱形时,过S作SG⊥y轴于G,延长O'C'交x轴于H,∵四边形ACSO'是菱形, ∴AO'=AC=SC,AO'∥SC, ∴∠AMC=∠BCS, ∴∠AO'H+∠MC'O'=∠BCO+∠OCS, ∵∠MC'O'=∠BCO, ∴∠AO'H=∠OCS, ∵∠AHO'=∠CGS, ∴△O'AH≌△CSG, ∴AH=SG,O'H=CG, Rt△OCB中,sin∠OCB==, ∴sin∠BC'H==,
解析法证明平面几何经典问题--举例
五、用解析法证明平面几何问题----极度精彩!充分展现数学之美感!何妨一试? 例1、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引两条直线分别交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二) (例1图) (例2图) 例2、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、 BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . 【部分题目解答】 例1、(难度相当于高考压轴题) ; ,、点的方程为:直线的方程为:设直线方程为:轴建立坐标系,设圆的为为原点,轴,为如图,以)(),(,AD ,,)-(2211222y x C y x B nx y mx y AB r a y x Y AO A x MN ===+ 、;则,、,C B )()(4433y x E y x D , 1 - ;12-2-)1,{)-(22 2212212222222+=+=+=++=+=m r a x x m am x x r a amx x m y r a y x mx y 由韦达定理知:得:(消去,1- ;1222 243243+=+=+n r a x x n an x x 同理得: ),-(---23 23 22x x x x y y y y CD = 方程为:直线 ,--Q 3 23 223Q y y y x y x x = 点横坐标:由此得 , --P 1 41441P y y y x y x x = 点横坐标:同理得 ,------1 41441323223P Q y y y x y x y y y x y x x x AQ AP ===;即证:,只需证明:故,要证明 N B
历年重庆中考几何题归类
历年重庆中考几何题归类 2015A 卷 6.如图,直线AB ∥CD ,直线EF 分别与直线AB,CD 相交于点G ,H 。若1=135°,则2的度数为( ) A. 65° B. 55° C. 45° D. 35° 9.如图,AB 是的直径,点C 在上,AE 是的切线,A 为切点,连接BC 并延长交AE 于点D , 若AOC=80°,则ADB 的度数为( ) A. 40° B. 50° C. 60° D. 20° 12.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与轴平行,A,B 两点的纵坐标分别为3,1,反比例函数的图像经过A,B 两点,则菱形对ABCD 的面积为( ) A. 2 B. 4 C. D. 15.如图,在等腰直角三角形ABC 中,ACB=90°,AB=,以A 为 圆心,AC 长为半径作弧,交AB 于点D ,则阴影部分的面积是 。 18.如图,矩形ABCD 中,AB=,AD=10,连接BD ,DBC 的角平分线BE 交DC 于点E ,现把△BCE 绕点B 逆时针旋转,记旋转后的△BCE 为△,当射线和射线都与线段AD 相交时,设交点分别F,G ,若△BFD 为等腰三角形,则线段DG 长为 。 ∠∠O e O e O e ∠∠x 3 y x = 2242∠4246∠BC E ''BE 'BC '6题图 9题图 12题图
20.如图,在△ABD 和△FEC 中,点B,C,D,E 在同一直线上, 且AB=FE,BC=DE,B=E 。 求证:ADB=FCE. 五、解答题: (本大题2个小题,每小题12分,共24分)解答题时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括作辅助线),请将解答过程书写在答题卡...中对应的位置上. 25.如图1,在△ABC 中,ACB=90°,BAC=60°,点E 角平分线上一点,过点E 作AE 的垂线,过点A 作AB 的线段,两垂线交于点D ,连接DB ,点F 是BD 的中点,DH ⊥AC ,垂足为H ,连接EF ,HF 。 (1)如图1,若点H 是AC 的中点,AC=,求AB ,BD 的长。 (2)如图1,求证:HF=EF 。 (3)如图2,连接CF ,CE ,猜想:△CEF 是否是等边三角形若是,请证明;若不是,请说明理由。 ∠∠∠∠∠∠2318题图 16题图 20题图
2015年重庆中考数学几何证明题__(专题练习+答案详解)
2015年重庆中考数学24题专题练习 1、如图,等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,连接BE,CE (1)求证:BE=CE; (2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD. 2、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G为CH的中点. (1)若HE=HG,求证:△EBH≌△GFC; (2)若CD=4,BH=1,求AD的长.
3、如图,梯形ABCD中,AB∥CD,AD=DC=BC,∠DAB=60°,E是对角线AC延长线上一点,F是AD延长线上的一点,且EB⊥AB,EF⊥AF. (1)当CE=1时,求△BCE的面积; (2)求证:BD=EF+CE. 4、如图.在平行四边形ABCD中,O为对角线的交点,点E为线段BC延长线上的一点,且.过点E EF∥CA, 交CD于点F,连接OF. (1)求证:OF∥BC; (2)如果梯形OBEF是等腰梯形,判断四边形ABCD的形状,并给出证明.
5、如图,梯形ABCD中,AD∥BC,∠ABC=90°,BF⊥CD于F,延长BF交AD的延长线于E,延长CD交BA 的延长线于G,且DG=DE,AB=,CF=6. (1)求线段CD的长; (2)H在边BF上,且∠HDF=∠E,连接CH,求证:∠BCH=45°﹣∠EBC. 6、如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠D=45°. (1)若AB=6cm,,求梯形ABCD的面积; (2)若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点,且满足EF=GH,∠EFH=∠FHG,求证:HD=BE+BF.
巧用旋转法解几何题
百度文库-让每个人平等地提升自我 巧用旋转法解几何题 将一个图形绕着某一点旋转一个角度的图形变换叫做旋转,由旋转的性质可知旋转前后的 图形全 等,对应点到旋转中心的连线所组成的夹角等于旋转角。旋转法是在图形具有公共端点的相 等的线段特征时,可以把图形的某部分绕相等的线段的公共端点, 旋转另一位置的引辅助线的方法, 主要用途是把分散的元素通过旋转集中起来,从而为证题创造必要的条件。旋转方法常用于等腰三 角形、等边三角形及正方形等图形中。现就旋转法在几何证题中的应用举例加以说明,供同学们参 考。 例1.如图,在Rt △ ABC 中,/ C=90°, D 是AB 的中点,E , F 分别 AC 和BC 上,且 DEL DF, 求证:EF 2=A ^+B F" 分析:从 所证的结论来看,令人联想到勾股定理,但注意到 EF , AE BF 三条线段不在同一个三角 形中,由于D 是中点,我们可以考虑以 D 为旋转中心,将 BF 旋转到和AE 相邻的位置,构造一个直 角三角形,问题便迎刃而解。 证明:延长 FD 到G 使DG=DF 连接AG EG ?/ AD=DB / ADG=/ BDF ???" ADd " BDF ( SAS ???/ DAG=/ DBF BF=AG ? AG// BC ???/ C=90°A Z EAG=90 ? EG=Ah+AG=AE+BF ?/ DEI DF ? EG=EF 2 2 2 ? EF=AE+BF 例 2,如图 2,在"ABC 中,/ ACB=90 , AC=BC P 是"ABC 内一点,且 PA=3 PB=1, PC=2 求/ BPC 的度数. 分析:题目已知条件中给出了三条线段的长度和一个直角,但已知的三条线段不在同一三角形中, 故可考虑通过旋转变换移至一个三角形中,由于" ACB 是等腰直角三角形,宜以直角顶点 C 为旋转 中心。 解:作 MC L CP,使 MC=CP 连接 PM , BM F E A
解析法在几何中的应用 -
解析法在几何中的应用 姓名:周瑞勇 学号:201001071465 专业:物理学 指导教师:何巍巍
解析法在几何的应用 周瑞勇 大庆师范学院物理与电气信息工程学院 摘要:通过分析几何问题中的各要素之间的关系,用最简练的语言或形式化的符号来表达他们的关系,得出解决问题所需的表达式,然后设计程序求解问题的方法称为解析法。 关键词:几何问题,表达关系,表达式,求解问题 一前言 几何学的历史深远悠久,欧几里得总结前人的成果,所著的《几何原本》。一直是几何学的坚固基石,至今我国中学教学的几何课本仍未脱离他的衣钵。长期的教学实践证明,采用欧式体系学习几何是培养学生逻辑思维能力的行之有效的方法。 但是,事物都有两重性。实践同样证明,过多强调它的作为也是不适当的。初等几何的构思之难,使人们为此不知耗费了多少精力,往往为寻求一条神奇、奥秘的辅助线而冥思苦索。开辟新的途径,已是势在必行。近些年来,用解析法、向量法、复数法、三角法证明几何问题,受到越来越多的数学工作者的重视。 由于平面几何的内容,只研究直线和园的问题,所以我们完全可以用解析法来研究几何问题。解析法不仅具有几何的直观性,而且也还有证明方法的一般性。综合几何叙述较简,但构思困难,而解析法思路清晰,过程简捷,可以作为证明几何问题中一种辅助方法,两者课去唱补短,想得益彰。 二解析法概述 几何数学主要是从几何图形这个侧面去研究客观事物的,其基本元素是点,代数学则主要是从数量关系这个侧面来研究客观事物,其基本元素是数。笛卡尔综合了前人的成果,创立了坐标概念,把代数学和几何学结合起来,于是产生了以研究点的位置和一对有序实数的关系、方程和曲线以及有研究连续运动而产生
重庆中考2017-2018学年上期几何证明习题一 (1)
重庆中考2017-2018学年上期几何证明习题一 1、如图,在Rt △ABC 中,∠A=30°,点D 是AB 边上的中点,斜边AB 的中点,DM ⊥DN ;连接DM,DN 分别交BC,CA 于点E,F ; (1)如图1,若CD =4,求△ABC 的周长; (2)如图2,若点E 为AC 的中点,将线段CE 绕点C 旋转60°,使点E 至点F 处,连接BF 交CD 于点M ,取DF 的中点N ,连接MN ,求证:MN=2CM (3)如图3,以点C 为旋转中心将线段CD 绕点C 顺时针旋转90°,使点D 至点E 处,连接BE 交CD 于点M ,连接DE ,取DE 的中点N ,连接MN ,试猜想线段BD 、MN 、MC 之间的关系并证明; 2.如图,∠BAC =60°,∠CDE =120°,AB =AC ,DC =DE ,连接BE ,P 为BE 的中点 (1) 如图1,若A 、C 、D 三点共线,求∠PAC 的度数 (2) 如图2,若A 、C 、D 三点不共线,求证:AP ⊥DP (3) 如图3,若点C 线段BE 上,AB =1,CD =2,请直接写出PD 的长度 E D A B C M N F E D A B C M N 图1 图3 图2 C B A D
3、如图,△ABC 中,以AC 为斜边向下作等腰Rt △ADC ,直角边AD 交BC 于点E , (1) 如图1,若∠ACB=30°, ∠B=45°, , 求线段DC 的长; (2) 如图2,若等腰Rt △ADC 的直角顶点D 恰好落在线段BC 的垂直平分线上,过点A 作AF ⊥BC 于点F ,连接DF ,求证: 4.如图,Rt △ABC 中,∠C=90°,点D 是AC 上的一点,过D 作DE ⊥AB ,垂足为点E ,连接BD ,∠ADE=∠BDE. (1)如图1,若BC=2 ,AC=4,求AE 的长; (2)如图2,AG //BD ,且AG=CD ,点F 是线段BC 的中点. 求证:∠FDC=∠DGA. 图2 图1 A B C D C B 图2 B C D 24题图 2 24题图1
重庆中考数学第18题专题1几何部分
重庆中考数学第18题专题1(几何部分) 1. 如图,在正方形ABCD和正方形DEFG中,点G在AD上,连接AC,BF交于点H,连接DH,若BC=4,DG=1,那么DH的长是. 2.如图,在正方形ABCD中, E为AD中点,AH⊥BE于点H,连接CH并延长交AD于点F, CP ⊥CF交AD的延长线于点P,若EF=1,则DP的长为_________. 3、如图,以RtABC△的斜边AB为一边在△ABC同侧作正方形ABEF.点O为AE与BF的 交点,连接CO,若CA = 2,CO=22,那么CB的长为______________. 4.如图,正方形ABCD的边长为3,延长CB至点M,使BM=1,连接AM,过点B 作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为.
5.如图,正方形ABCD的对角线AC、BD相交于点O,∠BAC的平分线交BD于点E,交BC于点F,点G是AD的中点,连接CG 交BD于点H,连接FO并延长FO交CG于点P,则PG:PC的值为_____________. 6、如图,正方形ABCD中,点E、F、G分别为AB、BC、CD边上的点,EB=3cm,GC=4cm,连接EF、FG、GE恰好构成一个等边三角形,则正方形的边长为cm。 7.如图所示,在梯形ABCD中,AB∥CD,E是BC的中点,EF⊥AD于点F,AD=4,EF=5,则梯形ABCD的面积是. 8、如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD 上,将AB、AD分别和AE、AF折叠,点B、D恰好都将在点G处, 已知BE=1,则EF的长为. 9、如图,Rt△ABC中,C= 90o,以斜边AB为边向外作正 方形ABDE,且正方形对角线交于点O,连接OC,已知 AC=5,OC=62,则另一直角边BC的长为.
2020重庆中考复习数学第26题专题训练六(含答案解析)
2020重庆中考复习数学第26题专题训练六 1、如图1,在△ABC中,∠BAC=90°,AC=2AB,D是线段AC中点,E是线段AD上一点,过点D作 DF⊥BE交BE的延长钱于点F,连接AF,过点A作AG⊥AF于点A,交BF于点G (1)若∠ABE=∠C,BC=2,求AE的长; (2)若点E为AD中点,求证:GE﹣FE=FD; (3)如图2,连接BD,点N为BD中点,连接GN,若AD=GF,请直接写出NG、GE、EA的数量关系.
4、已知△ABC中,点D为BC的中点,BD=AB,AD⊥BC. (1)如图1,求∠BAD的度数; (2)如图2,点E为BC上一点,点F为AC上一点,连接AE、BF交于点G,若∠AGF=60°,求证:BE=CF; (3)如图3,在(2)的条件下,点G为BF的中点,点H为AG上一点,延长BH交AC于点K,AK =HK,BM⊥AE交AE延长线于点M,BG=9,HM=10,求线段AG的长.
5、已知△ABC中,∠B=60°,点D是AB边上的动点,过点D作DE∥BC交AC于点E,将△ADE沿 DE折叠,点A对应点为F点. (1)如图1,当点F恰好落在BC边上,求证:△BDF是等边三角形; (2)如图2,当点F恰好落在△ABC内,且DF的延长线恰好经过点C,CF=EF,求∠A的大小; (3)如图3,当点F恰好落在△ABC外,DF交BC于点G,连接BF,若BF⊥AB,AB=9,求BG 的长.
6、如图,在△ABC中,AB=AC,∠BAC=90°,D为BC边的中点,点E在直线BC上(不与点D重合), 连接AE,过点C作直线AE的垂线,垂足为点F,交直线AD于点G,连接EG. (1)如图(1),当点E在线段BD上时,易证DE=DG,请直接写出三条线段BE,AB,EG之间的数量关系是 ; (2)如图(2),当点E在线段BC的延长线上时,请写出三条线段BE、AB、EG之间的数量关系,并证明你的结论; (3)若线段BC=2,当△AEG为等腰三角形时,请直接写出的值.
解析法巧解中考数学压轴题
解析法巧解中考压轴题 在平面几何题中,适当的建立直角坐标系,利用代数的方法解决几何问题,即解析法,有时会显得更简洁高效.现以近年中考压轴题为例,分析说明解析法之妙.例1 (2013泰州)如图1,在矩形ABCD中,点P在边CD上,且与C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连结PQ,M为PQ中点. 若AD=10,AB=a,DP=8,随着a的大小的变化,点M的位置也在变化.当点M 落在矩形ABCD外部时,求a的取值范围. 分析本题将矩形、三角形、动点、参数相结合,考察学生利用相似解决问题的综合能力,难度较大,区分度高,按照参考答案给出的解题思路,如图2所示,当点M落在矩形ABCD外部时,须满足的条件是“BE>MN”.分别求出BE与MN的表达式,列不等式求解,即可求出a的取值范围. 由△ADP∽△ABQ,解得QB=4 5 a. 由△QBE∽△QCP,同样由比例关系得出BE= () 28 225 a a a - + . 又因为MN为QCP的中位线,得出 MN=1 2 PC= 1 2 (a-8). 再由BE>MN, 即 () 28 225 a a a - + () 1 8 2 a >- 得出a> . 当点M落在矩形ABCD外部时,a的取值范围为a>. 这种解法不仅要想到添加辅助线,还两次运用了相似比,计算量大,易出错.比较稳妥而简洁的做法是将图形放进直角坐标系中,利用数形结合的方法来解决此类问题. 一如何建立合适、恰当的坐标系呢通常需要考虑以下两点: 第一,让尽可能多的点落在直角坐标系上,这些点的坐标含有数字O,可以起到简化运算的功效; 第二,考虑图形的对称性,同样,也能起到简化运算的作用. 解答如图3所示,建立以B点为原点,BC方向为x轴正半轴,BA方向为y轴正半轴的直角坐标系.
重庆中考数学最新几何证明题专题
G F E D C B A H A B C D G F E 中考复习专练 1.如图所示,在正方形ABCD 的边CB 的延长线上取点F ,连结AF ,在AF 上取点G ,使得AG=AD ,连结DG ,过点 A 作AE ⊥AF ,交DG 于点E .(1)若正方形ABCD 的边长为4,且2 1 t a n =∠FAB ,求FG 的长;(2)求证:AE+BF=AF . 2. 如图,□ABCD 中,E 是BC 边的中点,连接AE ,F 为CD 边上一点,且满足∠DF A =2∠BAE .(1)若∠D =105°,∠DAF =35°.求∠F AE 的度数;(2)求证:AF =CD +CF . 3.如图,在正方形ABCD 中,点P 是AB 的中点,连接DP ,过点B 作BE DP ⊥交DP 的延长线于点E ,连接AE ,过点A 作AF AE ⊥交DP 于点F ,连接BF 。(1)若2AE =,求EF 的长;(2)求证:PF EP EB =+ 4. 如图,正方形ABCD 中,E 为AB 边上一点,过点D 作DF DE ⊥,与BC 延长线交于点F .连接EF ,与CD 边 交于点G ,与对角线BD 交于点H .(1)若2BF BD ==,求BE 的长;(2)若2ADE BFE ∠=∠,求证: FH HE HD =+. B D 24题图 E A F C
G F P E D C B A C D E A G F B p E F G O D C B A 5. 如图,正方形ABCD 中,对角线AC 与BD 相交于O ,∠ADE=15°,过D 作D G ⊥ED 于 D,且AG=AD,过G 作GF//AC 交ED 的延长线于F.(1)若ED=64,求AG . (2)求证:2DF+ED=BD 6. 如图,P 为正方形ABCD 边BC 上一点,F 在AP 上,且AF=AD ,FE ⊥AP 交CD 于点E , G 为CB 延长线上一点,BG=DE ,(1)求证:DAP BAP PAG ∠+∠=∠2 1 (2)若DE =2, AB =4,求AP 的长 7. 在□ABCD 中,对角线BD BC ⊥,G 为BD 延长线上一点且AEG ?为等边三角形,BAD ∠、CBD ∠的平分线 相交于点E ,连接AE 交BD 于F ,连接GE .(1)若□ABCD 的面积为93,求AG 的长;(2)求证:AE BE GE =+. 8. 如图,已知正方形ABCD ,点P 为射线BA 上的一点(不和点A ,B 重合),过P 作PE ⊥CP ,且CP =PE .过E 作 EF ∥CD 交射线BD 于F .(1)若CB =6,PB =2,则EF = ;DF = ;(2)请探究BF ,DG 和CD 这三条线段之间的数量关系,写出你的结论并证明;
巧用旋转法解几何题
巧用旋转法解几何题 将一个图形绕着某一点旋转一个角度的图形变换叫做旋转,由旋转的性质可知旋转前后的 图形全 等,对应点到旋转中心的连线所组成的夹角等于旋转角。旋转法是在图形具有公共端点的相 等的线段特征时,可以把图形的某部分绕相等的线段的公共端点, 旋转另一位置的引辅助线的方法, 主要用途是把分散的元素通过旋转集中起来,从而为证题创造必要的条件。旋转方法常用于等腰三 角形、等边三角形及正方形等图形中。现就旋转法在几何证题中的应用举例加以说明,供同学们参 考。 例1.如图,在Rt △ ABC 中,/ C=90°, D 是AB 的中点,E , F 分别 AC 和BC 上,且 DEL DF, 求证:EF 2=A ^+B F" 分析:从 所证的结论来看,令人联想到勾股定理,但注意到 EF , AE BF 三条线段不在同一个三角 形中,由于D 是中点,我们可以考虑以 D 为旋转中心,将 BF 旋转到和AE 相邻的位置,构造一个直 角三角形,问题便迎刃而解。 证明:延长 FD 到G 使DG=DF 连接AG EG ?/ AD=DB / ADG=/ BDF ???" ADd " BDF ( SAS ???/ DAG=/ DBF BF=AG ? AG// BC ???/ C=90°A Z EAG=90 ? EG=Ah+AG=AE+BF ?/ DEI DF ? EG=EF 2 2 2 ? EF=AE+BF 例 2,如图 2,在"ABC 中,/ ACB=90 , AC=BC P 是"ABC 内一点,且 PA=3 PB=1, PC=2 求/ BPC 的度数. 分析:题目已知条件中给出了三条线段的长度和一个直角,但已知的三条线段不在同一三角形中, 故可考虑通过旋转变换移至一个三角形中,由于" ACB 是等腰直角三角形,宜以直角顶点 C 为旋转 中心。 解:作 MC L CP,使 MC=CP 连接 PM , BM F E A
2018重庆中考数学第26题专题训练
N M P C B A 2018年重庆市中考数学26题专题训练 1.抛物线y=﹣x 2 ﹣2x+3 的图象与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交 于点C ,点D 为抛物线的顶点. (1)求A 、B 、C 的坐标; (2)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直 线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N .若点P 在点Q 左边,当矩形PQMN 的周长最大时,求△AEM 的面积;当矩 形PMNQ 的周长最大时,连接DQ .过抛物线上一点F 作y 轴的平行线,与直线AC 交 于点G (点G 在点F 的上方).若FG=2DQ ,求点F 的坐标. 2.如图,已知抛物线223y x x =-++与x 轴交于A 、B 两点 (点A 在点B 的左边),与y 轴交于点C ,连接BC 。 (1)求A 、B 、C 三点的坐标; (2)若点P 为线段BC 上的一点(不与B 、C 重合),PM ∥y 轴, 且PM 交抛物线于点M ,交x 轴于点N ,当△BCM 的面积最大时, 求△BPN 的周长;当△BCM 的面积最大时,在抛物线的对称轴上 存在点Q ,使得△CNQ 为直角三角形,求点Q 的坐标。 3.如图,对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于 A 、 B 两点,其中A 点的坐标为(-3,0)。 (1)求点B 的坐标和抛物线的解析式。 (2)已知a 1=,C 为抛物线与y 轴的交点。 ①若点P 在抛物线上,且POC BOC S 4S ??=,求点P 的坐标; ②设点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度 的 最大值。
最新重庆中考数学第26题专题训练
N M P C B A 1.如图,抛物线y=﹣x 2﹣2x+3 的图象与x 轴交于A 、 B 两点(点A 在点B 的左边),与y 轴交于点 C ,点 D 为抛物线的顶点. (1)求A 、B 、C 的坐标; (2)点M 为线段AB 上一点(点M 不与点A 、B 重合),过点M 作x 轴的垂线,与直线AC 交于点E ,与抛物线交于点P ,过点P 作PQ ∥AB 交抛物线于点Q ,过点Q 作QN ⊥x 轴于点N .若点P 在点Q 左边,当矩形PQMN 的周长最大时,求△AEM 的面积; (3)在(2)的条件下,当矩形PMNQ 的周长最大时,连接DQ .过抛物线上一点F 作y 轴的平行线,与直线AC 交于点G (点G 在点F 的上方).若FG=2 DQ ,求点F 的坐标. 2.如图,已知抛物线2 23y x x =-++与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,连接BC 。 (1)求A 、B 、C 三点的坐标; (2)若点P 为线段BC 上的一点(不与B 、C 重合),PM ∥y 轴,且PM 交抛物线于点M ,交x 轴于点N ,当△BCM 的面积最大时,求△BPN 的周长; (3)在(2)的条件下,当BCM 的面积最大时,在抛物线的对称轴上存在点Q ,使得△CNQ 为直角三角形,求点Q 的坐标。 3.如图,对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于A 、B 两点,其中A 点的坐 标为(-3,0)。 (1)求点B 的坐标; (2)已知a 1=,C 为抛物线与y 轴的交点。 ①若点P 在抛物线上,且POC BOC S 4S ??=,求点P 的坐标; ②设点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度的最大值。 4.如图,已知抛物线y=x 2+bx+c 的图象与x 轴的一个交点为B (5,0),另一个交点为A ,且与y 轴交于点C (0,5).
高中竞赛数学讲义第56讲解析法证几何题
第56讲 解析法证 几何题 解析法是利用代数方法解决几何问题的一种常用方法.其一般的顺序是:建立坐标系,设出各点坐标及各线的方程,然后根据求解或求证要求进行代数推算.它的优点是具有一般性与程序性,几何所有的平面几何问题都可以用解析法获解,但对于有些题目演算太繁. 此外,如果建立坐标系或设点坐标时处理不当,也可能增加计算量.建系设点坐标的一般原则是使各点坐标出现尽量多的0,但也不可死搬教条,对于一些“地位平等”的点、线,建系设点坐标时,要保持其原有的“对称性”. A 类例题例1.如图,以直角三角形ABC 的斜边A B 及直角边B C 为边向三角形两侧作正方形ABDE 、CBFG . 求证:DC ⊥FA . 分析 只要证k C D ·k AF =-1,故只要求点D 的坐标. 证明 以C 为原点,CB 为x 轴正方向建立直角坐标系.设A (0,a ),B (b ,0),D (x ,y ). 则直线AB 的方程为ax +by -ab =0. 故直线BD 的方程为bx -ay -(b ·b -a ·0)=0, 即bx -ay -b 2=0. ED 方程设为ax +by +C =0. 由AB 、ED 距离等于|AB |,得 |C +ab | a 2+b 2=a 2+b 2, 解得C =±(a 2+b 2)-ab . 如图,应舍去负号. 所以直线ED 方程为ax +by +a 2+b 2-ab =0. 解得x =b -a ,y =-b .(只要作DH ⊥x 轴,由△DBH ≌△BAC 就可得到这个结果). 即D (b -a ,-b ). 因为k AF =b -a b ,k CD =-b b -a ,而k AF ·k CD =-1.所以DC ⊥FA . 例2.自ΔABC 的顶点A 引BC 的垂线,垂足为D ,在AD 上任取一点H ,直线BH 交AC 于E ,CH 交AB 于F . 试证:AD 平分ED 与DF 所成的角. 证明 建立直角坐标系,设A (0,a ),B (b ,0),C (c ,0),H (0,h ),于是 BH :x b +y h =1 AC :x c +y a =1 过BH 、AC 的交点E 的直线系为: λ(x b +y h -1)+μ(x c +y a -1)=0. 以(0,0)代入,得λ+μ=0. y x H F E D C B A y x O A B C D E F G
巧用旋转法解几何题
巧用旋转法解几何题
∵AD=DB ,∠ADG=∠BDF ∴⊿ADG ≌⊿BDF (SAS ) ∴∠DAG=∠DBF ,BF=AG ∴AG ∥BC ∵∠C=90°∴∠EAG=90° ∴EG 2 =AE 2 +AG 2 =AE 2 +BF 2 ∵DE ⊥DF ∴EG=EF ∴EF 2 =AE 2 +BF 2 例2,如图2,在⊿ABC 中,∠ACB=90°,AC=BC ,P 是⊿ABC 内一点,且PA=3,PB=1,PC=2,求∠BPC 的度数. 分析:题目已知条件中给出了三条线段的长度和一个直角,但已知的三条线段不在同一三角形中,故可考虑通过旋转变换移至一个三角形中,由于⊿ACB 是等腰直角三角形,宜以直角顶点C 为旋转中心。 解:作MC ⊥CP ,使MC=CP ,连接PM ,BM ∵∠ACB=90°,∠PCM=90°∴∠1=∠2 ∵AC=BC , ∴⊿CAP ≌⊿CBM (SAS ) ∴MB=AP=3 G F E D C B A
∵PC=MC ,∠PCM=90° ∴∠MPC=45° 由勾 股定理 PM== 2 2MC PC = 2 2PC =22, 在⊿MPB 中,PB 2 +PM 2 =(22)2 +12=9=BM 2 ∴⊿MPB 是直角三角形 ∴∠BPC=∠CPM+∠MPB=45°+90°=135° 例3,如图3,直角三角形ABC 中,AB=AC ,∠BAC=90°,∠EAF=45°,求证:EF 2=BE 2+CF 2 分析:本题求证的结论和例1十分相似,无法直接用勾股定理,可通过旋转变换将BE ,CF 转移到同一个直角三角形中,由于⊿BAC 是等腰直角三角形,不妨以A 为旋转中心,将∠BAE 和∠CAF 合在一起,取零为整。 证明:过A 作AP ⊥AE 交BC 的垂线CP 于P ,连结 PF ∵∠EAP=90°,∠EAF=45° ∴∠PAF=45° ∵∠BAC=90° ∴∠BAE=∠PAC A P M C B A
第56讲 解析法证几何题教学内容
第56讲解析法证 几何题
第56讲解析法证 几何题 解析法是利用代数方法解决几何问题的一种常用方法.其一般的顺序是:建立坐标系,设出各点坐标及各线的方程,然后根据求解或求证要求进行代数推算.它的优点是具有一般性与程序性,几何所有的平面几何问题都可以用解析法获解,但对于有些题目演算太繁. 此外,如果建立坐标系或设点坐标时处理不当,也可能增加计算量.建系设点坐标的一般原则是使各点坐标出现尽量多的0,但也不可死搬教条,对于一些“地位平等”的点、线,建系设点坐标时,要保持其原有的“对称性”. A类例题 收集于网络,如有侵权请联系管理员删除
斜边AB及直角边BC为边向三角形两 侧作正方形ABDE、CBFG. 求证:DC⊥FA. 分析只要证k CD·k AF=-1,故只要求点D的坐标. 证明以C为原点,CB为x轴正方向建立直角坐标 系.设A(0,a),B(b,0),D(x,y). 则直线AB的方程为ax+by-ab=0. 故直线BD的方程为bx-ay-(b·b-a·0)=0, 即bx-ay-b2=0. ED方程设为ax+by+C=0. 由AB、ED距离等于|AB|,得 |C+ab| =a2+b2, a2+b2 解得C=±(a2+b2)-ab. 如图,应舍去负号. 收集于网络,如有侵权请联系管理员删除
所以直线ED方程为ax+by+a2+b2-ab=0. 解得x=b-a,y=-b.(只要作DH⊥x轴,由△DBH≌△BAC就可得到这个结果). 即D(b-a,-b). 因为k AF=b-a b,k CD= -b b-a,而k AF·k CD=-1.所以 DC⊥FA. 例2.自ΔABC的顶点A引BC的垂线,垂足为D,在AD上任取一点H,直线BH交AC于E,CH交AB于F.试证:AD平分ED与DF所成的角. 证明建立直角坐标系,设A(0,a),B(b,0),C(c,0),H(0,h),于是 BH:x b+ y h=1 AC:x c+ y a=1 x
2021年重庆年中考26题三角形四边形几何综合专题练习(八中试题集)
2021年重庆年中考26题三角形四边形几何综合专题(八中试题集) 1(八中2020级初三下定时训练九)在菱形ABCD中,∠ABC=60°,点M是对角线BD上一动点,将线段CM绕点C顺时针旋转120°到CN,连接DN,连接NM并延长,分别交AB、CD于点P、Q. (1)如图1,若CM⊥BD且PQ=4,求菱形ABCD的面积; (2)如图2,求证:PM=QN.
2(八中2020级初三下定时训练五))已知:在△ABC中,∠C=90°,BC=AC. (1)如图1,若点D、E分别在BC、AC边上,且CD=CE,连接AD、BE,点O、M、N分别是AB、AD、BE 的中点.求证:△OMN是等腰直?三角形; (2)将图1中△CDE绕着点C顺时针旋转90°如图2,O、M、N分别为AB、AD、BE中点,则(1)中的结论是否成?,并说明理由; (3)如图3,将图1中△CDE绕着点C顺时针旋转,记旋转?为α(0<α<360°),O、M、N分别为AB、AD、BE中点,当MN=,请求出四边形ABED的?积.
3(八中2020级初三下定时训练八)问题提出 (1)如图①,在等腰Rt△ABC中,斜边AC=4,点D为AC上一点,连接BD,则BD的最小值为; 问题探究 (2)如图②,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,求AD的最小值; 问题解决 (3)如图③,四边形ABCD是规划中的休闲广场示意图,其中∠BAD=∠ADC=135°,∠DCB=30°,AD=2km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.
