有关函数f(x)=(ax+b)+(cx+d)的不等式及最值问题解题策略

高考有关函数())0(,≠+±+=ac d cx b ax x f 的解题策略

广西大学附属中学 潘承猛

关于函数())0(,≠+±+=ac d cx b ax x f 的不等式问题及最值问题是高考全国卷选做题中常见题型．解不等式常用的方法是“画数轴法”、“零点分段法”、“函数图象法”；求最值常用的方法是“绝对值三角不等式法”、“零点分段法”、“函数图象法”．若c a =，应优先“画数轴法”和“绝对值三角不等式法”解题，若c a ≠，则不便使用．“零点分段法”和“函数图象法”是通法，但“零点分段法”运算量大，错误率高，而“函数图象法”通过数形结合，将不等式问题转化为方程问题，增加直观性，大大降低运算量，从而降低了运算错误率．深挖函数())0(,≠+±+=ac d cx b ax x f 性质，可以更快捷、准确的解这类题．

我们先来讨论函数())0(,≠+±+=ac d cx b ax x f 的图象特征．含绝对值函

数本质上是分段函数，在

c

d

a b ≠的请情况下，其图象由三段构成，并且连在一起不断开．该为了表述方便，从左到右分别叫做第一段、 第二段、 第三段．由于在第三段，绝对值里的两个一次式都大于零，而在第一段，绝对值里的两个一次式都小于零，所以第一段的解析式等于第三段解析式乘以-1，这两段图象为变化趋势刚好相反的射线，利用这一性质可以按照以下三个步骤快速作出它的图象．

第一步：描出图象的两个分段点???? ?

???? ??--a b f a b ,，????

????? ??--c d f c d ,，连接两点

所得线段即为第二段图象．

第二步：在第三段，直接把绝对值符号当成括号，求出第三段函数解析式，根据x 系数画出第三段射线图象．

第三步：利用第一段的解析式等于第三段解析式乘以-1，写出第一段解析式，并画出第一段射线图象．

由此也可以概括出())0(,≠+±+=ac d cx b ax x f 的图象可分为三种类型：

（1）开口向上型：当第三段x 系数为正数时，此时，函数有最小值，

()?

??

?????? ??-??? ??-=c d f a b f x f ,min min ；

（2）开口向下型：当第三段x 系数为负数时，此时，函数有最大值，

()?

??

?????? ??-??? ??-=c d f a b f x f ,max max ；

（3）平行x 轴型：当第三段x 系数为零时，此时，函数既有最大值又最小

值，()????????? ??-??? ??-=c d f a b f x f ,max max ，()???

?????? ??-??? ?

?-=c d f a b f x f ,min min ．

以下我们通过例子来看怎样使用这种方法快速解题．

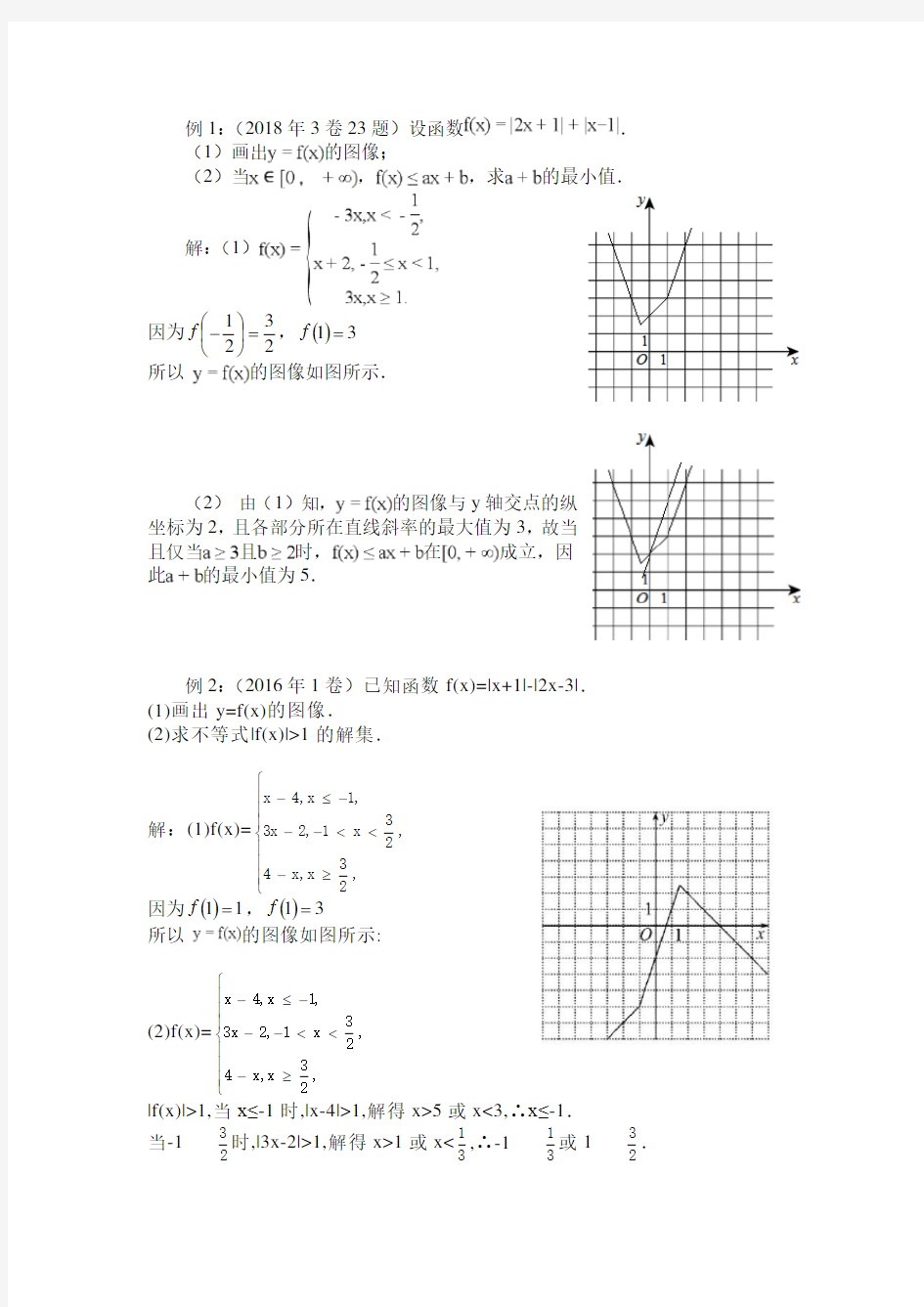
例1：（2018年3卷23题）设函数．

（1）画出的图像； （2）当，，求

的最小值．

解：（1）

因为23

21=??? ??-f ，()31=f

所以 的图像如图所示．

（2） 由（1）知，的图像与y 轴交点的纵坐标为2，且各部分所在直线斜率的最大值为3，故当且仅当且时，在成立，因此的最小值为5．

例2：（2016年1卷）已知函数f(x)=|x+1|-|2x-3|． (1)画出y=f(x)的图像．

(2)求不等式|f(x)|>1的解集．

解：(1)f(x)=x 4,x 1,33x 2,1

x ,2

34x,x ,2

?

?-≤-?

?--<

-≥??

因为()11=f ，()31=f 所以 的图像如图所示:

(2)f(x)=x 4,x 1,33x 2,1

x ,2

34x,x ,2

?

?-≤-?

?--<

-≥??

|f(x)|>1,当x≤-1时,|x-4|>1,解得x>5或x<3,∴x≤-1． 当-1

时,|3x-2|>1,解得x>1或x<13

,∴-1

或1

．

当x≥3

2时,|4-x|>1,解得x>5或x<3,∴32

≤x<3或x>5．

综上,x<13

或15,∴|f(x)|>1的解集为1∞,3??

- ??

?

∪(1,3)∪(5,+∞)．

1．（2015年1卷）已知函数错误!未找到引用源。=|x+1|-2|x-a|，a>0． （Ⅰ）当a=1时，求不等式f （x ）>1的解集；

（Ⅱ）若f （x ）的图像与x 轴围成的三角形面积大于6，求a 的取值范围． 【解析】：（Ⅰ）当a=1时，不等式f （x ）>1化为|x+1|-2|x-1|＞1，

等价于11221x x x ≤-??--+->?或111221x x x -<?或11221

x x x ≥??+-+>?，解得2

23x <<，

所以不等式f （x ）>1的解集为2

{|2}3

x x <<．

（Ⅱ）由题设可得，12,1()312,112,x a x f x x a x a x a x a --<-??

=+--≤≤??-++>?，

所以函数()f x 的图像与x 轴围成的三角形的三个顶点分别为21

(

,0)3

a A -，(21,0)B a +，(,+1)C a a ，所以△ABC 的面积为22

(1)3

a +．

由题设得22

(1)3

a +＞6，解得2a >．所以a 的取值范围为（2，+∞）．

2．（2016年3卷）已知函数f(x)=|2x-a|+a ． (1)当a=2时,求不等式f(x)≤6的解集．

(2)设函数g(x)=|2x-1|,当x ∈R 时,f(x)+g(x)≥3,求a 的取值范围．

【解析】(1)当a=2时,f(x)= |2x-2| +2,解不等式|2x-2|+2≤6得-1≤x≤3． 因此f(x)≤6的解集为{}x 1x 3-≤≤．

(2)当x ∈R 时,f(x)+g(x)=2x a - +a+12x -≥2x a 12x -+-+a=1a -+a, 所以当x ∈R 时,f(x)+g(x)≥3等价于1a -+a≥3, ① 当a 1时,①等价于 ≤1a 3,无解a -+≥

当a 1时,①等价于 a 1a 3,解得a 2.>-+≥≥所以a 的取值范围是)2,∞.?+? 3．（2016年1卷）已知函数f(x)=|x+1|-|2x-3|． (1)画出y=f(x)的图像．

(2)求不等式|f(x)|>1的解集．

【解析】(1)如图所示:

(2)f(x)=x 4,x 1,33x 2,1

x ,2

34x,x ,2

?

?-≤-?

?--<

-≥??

|f(x)|>1,当x≤-1时,|x-4|>1,解得x>5或x<3,∴x≤-1． 当-1

2

时,|3x-2|>1,解得x>1或x<13

,∴-1

或

1

当x≥32时,|4-x|>1,解得x>5或x<3,∴3

2

≤x<3或x>5．

综上,x<1

3或15,∴|f(x)|>1的解集为1∞,3??- ??

?∪(1,3)∪(5,+∞)．

4．（2017年1卷）已知函数f （x ）=–x 2+ax +4，g (x )=│x +1│+│x –1│． （1）当a =1时，求不等式f （x ）≥g （x ）的解集；

（2）若不等式f （x ）≥g （x ）的解集包含[–1，1]，求a 的取值范围．

【解析】：将函数()11g x x x =++-化简可得()2121121x

x g x x x x >??

=-≤≤??-<-?

（1） 当1a =时，作出函数图像可得()()f x g x ≥

的范围在F 和G 点中间，联立2

24y x

y x x =??=-++?

可得点171,171G ??

-- ? ?

??

， 因此可得解集为1711,2??

--????

．

（2）即()()f x g x ≥在[]1,1-内恒成立，故而可得22422x ax x ax -++≥?-≤恒成立，根据图像可得：函数y ax =必须在12,l l 之间，故而可得11a -≤≤．

5．（2017年3卷）已知函数()||||f x x x =+1--2． （1）求不等式()f x ≥1的解集；

（2）若不等式()f x x x m 2≥-+的解集非空，求m 的取值范围． 【解析】

⑴()|1||2|f x x x =+--可等价为()3,121,123,2--??

=--<

x f x x x x ≤≥．由()1f x ≥可得：

①当1-x ≤时显然不满足题意；②当12x -<<时，211-x ≥，解得1x ≥； ③当2x ≥时，()31=f x ≥恒成立．综上，()1f x ≥的解集为{}|1x x ≥． ⑵不等式()2-+f x x x m ≥等价为()2-+f x x x m ≥，

令()()2

g x f x x x =-+，则()g x m ≥解集非空只需要()max ????g x m ≥．

而()22

23,1

31,123,2?-+--?=-+--<

x x x g x x x x x x x ≤≥．①当1-x ≤时，()()max 13115g x g =-=---=-????；

②当12x -<<时，()2

max

3335312224g x g ????

==-+?-=?? ? ???????

；

③当2x ≥时，()()2

max 22231g x g ==-++=????．综上，()max

54

g x =????，故54

m ≤． 方法2是零点分段法，是通法。

例如：

方法3是函数图像法，也是通法。 例如：

根据本人教学实践，对于基础中等偏下的同学，图象法是最容易理解，运算最简

单的一种方法。解决这类问题最好的方法是数形结合，即弄清楚

典例

例1：设()212f x x x =-++ （Ⅰ）求不等式()4f x ≥的解集；

（Ⅱ）若不等式()2f x m <-的解集是非空集合，求实数m 的取值范围．

解：（Ⅰ） ()()()()3242131x x f x x x x x -<-??

=-+-≤≤??>?

，图象为:

由44=+-x ，得0=x ；由43=x ，得34

=

x 由图象知不等式()4f x ≥的解集为),3

4

[]0,(+∞-∞Y

（Ⅱ）由图知，()()31min ==f x f

由不等式()2f x m <-的解集是非空集合，得23-

解得，(,1)(5,)m ∈-∞-+∞U

点评：该图象属于“开口向上型”，用图象法的好处是把解不等式问题转化为解方程问题（结合函数图象写出解集），避免了零点分段法中繁琐的求交集、并集，提高了运算的准确率．而第（2）问中用到的最值也可以直接由函数图象得出．而其中所蕴含的数形结合思想、函数与方程思想又是要求学生要熟练掌握的．

例2：已知函数()x x x g 21--=，()522++-=x a x x f ．

（Ⅰ）解不等式()4->x g ；

（Ⅱ）若存在R x ∈1，也存在R x ∈2，使得()()21x g x f =成立，求实数a 的取值范围．

解：（Ⅰ）由题意可得10()130111x x g x x x x x +??

=-<

，≤，，，，≥，图象为:

由41-=+x ，得5-=x ；由41-=--x ，得3=x 由图象知，不等式()4g x >-的解集为()3,5-

（Ⅱ）因为存在1x ∈R ，也存在2x ∈R ，使得

12()()

f x

g x =成立，所以，{|()}{|()}y y f x x y y g x x =∈=∈≠?R R I ，，，

又()|2||25||(2)(25)||5|f x x a x x a x a =-++--+=+≥，由（Ⅰ）知，max ()1g x =， 所以|5|1a +≤，解得64a --≤≤，所以，实数a 的取值范围为[64]--，． 点评：该题图象属于“开口向下型”．

例3．设函数()|2||1|f x x x =+-- （Ⅰ）解不等式()1-≥x f ；

（Ⅱ）若关于x 的不等式()+4|12|f x m ≥-有解，求实数m 的取值范围． 解：（Ⅰ）函数()f x 可化为

3,

2()21,213,2x f x x x x -≤-??

=+-<

，图象如下：

由112-=+x ，得1-=x ；由图象知， 不等式()1-≥x f 的解集为[)+∞-,1

（Ⅱ）关于x 的不等式()+4|12|f x m ≥-有解等价于()max ()+4|12|f x m ≥-， 由（Ⅰ）可知max ()3f x =，于是 |12|7m -≤， 解得 [3,4]m ∈-

点评：该题图象属于“平行x 轴型”．有了图象，恒成立问题（或对R x ∈?，都有…）、有解问题（或对R x ∈?0，使得…）怎样转化为最值问题也就一目了然了．