高考备考立体几何的逆问题截面问题学案
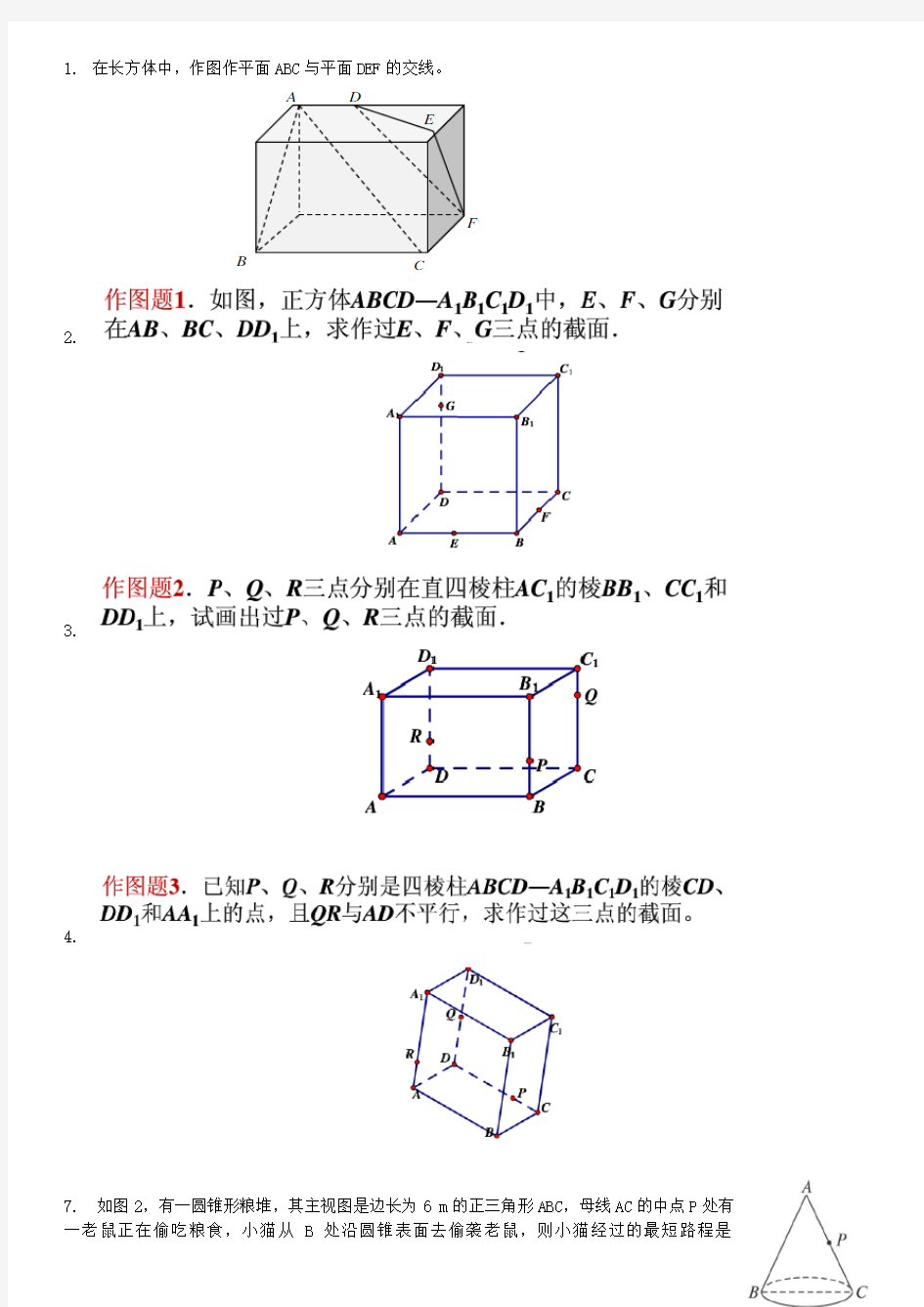

1. 在长方体中,作图作平面ABC 与平面DEF 的交线。
2.
3.
4.
7. 如图2,有一圆锥形粮堆,其主视图是边长为6 m 的正三角形ABC ,母线AC 的中点P 处有
一老鼠正在偷吃粮食,小猫从B 处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是
B A C
D F
E
F
P
D 1
C 1
B 1
A 1
D
C
B
A
m.(结果不取近似数)
8.一个圆锥形建筑物高1510米,母线PB 长40米,节日期间,计划从A 处开始绕侧面一周到母线PA 上的点C 处都挂上彩带.已知PC=10米,问需要彩带多少米(结果不取近似值。)
1.(2013昆明市市二统)如图,四棱锥P- ABCD 的底面ABCD 是矩形,侧面PAB 是正三角形,AB =2,BC =2, PC =6, (I )求证:PD ⊥AC ;
(II )已知棱PA 上有一点E ,若二面角E —BD —A
的大小为45°,试求BP 与平面EBD 所成角的正弦值。
2. (2012昆明市市二统)如图长方体1111ABCD A B C D 中,P 是线段AC
上任意一点.
(Ⅰ)判断直线1B P 与平面11AC D 的位置关系并证明;
(Ⅱ)若AB BC =,E 是AB 的中点,二面角111A DC D --的余弦值是10
,求直线1B E 与平面11AC D 所成角的正弦值.
3. (2013昆明市市二统)如图,四边形ABCD 是正方形,PD MA ∥,
MA AD ⊥,PM CDM ⊥平面, 1
2
MA PD =
. (Ⅰ)求证:平面ABCD ⊥平面AMPD ;
(Ⅱ)若BC 与PM 所成的角为45,求二面角M BP C --的余弦值.
4.(2014届昆明市市二统)四棱锥P-ABCD的底面是正方形,每条侧棱的长都等于底面边长,AC∩BD=O,E、F 、G 分别是PO 、AD 、AB 的中点。 (1)求证:PC ⊥面EFG ;
(2)求面EFG 与面PAB 所成的二面角的正弦值。
A
B
C
D
P
M
5.(河北省邯郸市第一中学2016届高三数学下学期研七考试试题)如图1,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,E为BC上一点,BE=2EC,DE=3,将梯形ABCD沿DE折成直二面角B-DE-C,如图2所示。
(1)求证:面AEC⊥面ABED;
(2)设点A关于点D的对称点为G,点M在△BCE所在平面内,且直线GM与面ACE所成的角为
3
π
,求出点M与点B的最短距离。
6.(江西省上饶市重点中学2016届高三数学第一次联考试题)长方形ABCD 中,AB =2,AD =1,M 为DC 中点,将△ADM 沿AM 折起,使面ADM ⊥面ABCM 。 (1)求证:AD ⊥BM ;
(2)若点E 是线段DB 上的一动点,问点E 在何位置时,二面角E-AM-D的大小为
4
π。
C
D
E
A B C D
A
B C D E
7. (广东省东莞一中、松山湖学校2016届高三数学上学期12月联考试卷)如图,在四棱锥P ﹣ABCD 中,AD∥BC ,AB ⊥AD ,AB ⊥PA ,BC=2AB=2AD=4BE ,平面PAB ⊥平面ABCD , (Ⅰ)求证:平面PED ⊥平面PAC ;
(Ⅱ)若直线PE 与平面PAC 所成的角的正弦值为
,求二面角A ﹣PC ﹣D 的平面角的余弦值.
8. 【2015江苏高考,22】如图,在四棱锥P ABCD -中,已知PA ⊥平面ABCD ,且
四
边
形
ABCD
为
直
角
梯
形
,
2
ABC BAD π
∠=∠=
,2,1PA AD AB BC ====
(1)求平面PAB 与平面PCD 所成二面角的余弦值;
(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成角最小时,求线段BQ 的长
P
A B
C
D
Q
9.【2015高考天津,理17】(本小题满分13分)如图,在四棱柱
1111ABCD A B C D 中,侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB ,
1
2,5AC
AA AD CD
,且点M 和N 分别为11C D B D 和的中点.
(I)求证://MN 平面ABCD ;
(II)设E 为棱11A B 上的点,若直线NE 和平面ABCD 所成角的正弦值为1
3
,求线段1A E 的长
10.【2015高考福建,文20】如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,PO 垂直于圆O 所在的平面,且1PO =OB =. (Ⅰ)若D 为线段AC 的中点,求证C A ⊥平面D P O ; (Ⅱ)若2BC =,点E 在线段PB 上,求CE OE +的最小值.
N
M
C 1
B 1
1
D
A
B
D 1
11.(2014-2015学年上学期云大附中星耀校区高二年级期末考试) 如图,在直三棱柱111C B A ABC 中,点D 是BC 的中点.请您在图中用黑色碳素笔.....作图,过点1
A 作一截面与平面D AC 1平行,并证明;
A
B
C
1A 1
B 1
C D
高中数学“立体几何初步”教学研究
专题讲座 高中数学“立体几何初步”教学研究 袁京生北京市朝阳区教育研究中心 一、“立体几何初步”教学内容的整体把握 (一)“立体几何初步”内容的背景分析 1.从立体几何发展的历程看立体几何课程 (1)不同学段几何学习的特点 一个学生从小学的数学课中就接触到了空间图形,由于知识和年龄的限制,他们对空间图形的认识方法主要是大量的观察、操作,对空间图形形成一定的感性认识. 在初中,课程安排了简单几何体的概念及体积公式,三视图的基本知识,正方体的截面、展开问题,建立了长方体模型概念,已初步具有平面几何基础知识及推理论证能力, 总体上看,初中学生对空间图形的认识主要是直观感知,操作确认,但平面几何的学习又呈现出思辨论证等理性的特征. 总之,高中以前的学生对空间图形的认识主要是对图形的整体形象的直观感知,操作确认,这种基于直观和操作的认知的优点是简便、直观,不需要更多的知识作基础,但不足也是很明显的,即不能对空间图形及其内部的元素关系进行深入的分析,不能产生对空间图形本质的认识. 当学生进入高中以后,教材对空间图形的有了专门的介绍:立体几何.从历次的立体几何教材看,无论教材怎样变化,高中立体几何的最终目标都是要从学生可接受的理论高度来认识空间图形.除了传统的综合几何外,近几年的高中《大纲》或《课程标准》还引入了空间向量,空间向量进入几何,使几何有了更多代数的味道,因此现行的高中几何不完全是欧式几何. 当我们回顾大学的几何学习时,容易发现,大学的几何学习正是沿着几何代数化的方向展开,无论《空间解析几何》、《高等几何》、《微分几何》等无不是通过代数的手段对几何进行研究,通过代数的形式呈现几何结论. (2)几何研究方法的发展
苏教必修2立体几何初步初步教案学案立体几何第10课时作业
第10课直线与平面的位置关系 分层训练 1?给出下列四个命题 ①若一条直线与一个平面内的一条直线平行,则这条直线与这个平面平行; ②若一条直线与一个平面内的两条直线平行,则这条直线与这个平面平行; ③若平面外的一条直线和这个平面内的一条 直线平行,那么这条直线和这个平面平行; ④若两条平行直线中的一条与一个平面平行, 则另一条也与这个平面平行? 其中正确命题的个数是() A. 0 B. 1 C. 2 D. 3 2?梯形ABCD 中,AB//CD, AB 1 a , CD? a ,则 CD与平面a内的直线的位置关系只能是() A.平行 B.平行或异面 C.平行或相交 D.异面或相交 3.如图aA3 =CD , ady =EF , ^门丫=AB 若AB// a,贝U CD与EF __________ ( “平行”或“不平行” ? 6?如图,E、F、G、H分别是空间四边形ABCD 的边AB、BC、CD、DA的中点,求证: (1) 四点E、F、G、H共面; (2) BD〃平面EFGH , AC// 平面EFGH . 4?如图,在三棱柱ABC-A 1B1C1中,E C BC , F C B1C1 , EF//C1C,点M C 平面AA1B1B,点M、E、F确定平面丫,试作平面丫与三棱柱 ABC-A 1B1C1 表面的交线,其画法5?如图,AB〃a , AC//BD , C Ca , D Ca ,求证: AC=BD. C E
拓展延伸 如图,在四棱锥P-ABCD中,M、N分别是AB、 PC的中点,若ABCD是平行四边形,求证: MN// 平面PAD . 节学习疑点: 学生质疑 教师释疑
考点81 空间几何体的截面问题
考点81 空间几何体的截面问题 1.(2018?新课标Ⅰ,理12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( ) A B C D 【答案】A 【解析】正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长 ,α截此正方体所得截面最大值为:26=,故选A . 2.(2015?新课标Ⅱ,理19)如图,长方体1111ABCD A B C D -中,16AB =,10BC =,18AA =,点E ,F 分别在11A B ,11D C 上,114A E D F ==,过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形. (1)在图中画出这个正方形(不必说明画法和理由); (2)求直线AF 与平面α所成角的正弦值. 【解析】(1)交线围成的正方形EFGH 如图: (2)作EM AB ⊥,垂足为M ,则:10EH EF BC ===,18EM AA ==, ∴6MH ,10AH ∴=。 以边DA ,DC ,1DD 所在直线为x ,y ,z 轴,建立如图所示空间直角坐标系,则: (10A ,0,0),(10H ,10,0),(10E ,4,8),(0F ,4,8),∴(10,0,0),(0,6,8)EF EH =-=-。 设(,,)n x y z =为平面EFGH 的法向量,则:100680n EF x n EH y z ?=-=??=-=?? ,取3z =,则(0,4,3)n =, 若设直线AF 和平面EFGH 所成的角为θ,则:45sin |cos ,|1805AF n θ=<>==,∴直线AF 与平面α .
立体几何动点问题
立体几何与平面解析几何的交汇问题 在教材中,立体几何与解析几何是互相独立的两章,彼此分离不相联系,实际上,从空间维数看,平面几何是二维的,立体几何是三维的,因此,立体几何是由平面几何升维而产生;另一方面,从立体几何与解析几何的联系看,解析几何中的直线是空间二个平面的交线,圆锥曲线(椭圆、双曲线、抛物线)是平面截圆锥面所产生的截线;从轨迹的观点看,空间中的曲面(曲线)是空间中动点运动的轨迹,正因为平面几何与立体几何有这么许多千丝万缕的联系,因此,在平面几何与立体几何的交汇点,新知识生长的土壤特别肥沃,创新型题型的生长空间也相当宽广,这一点,在高考卷中已有充分展示,应引起我们在复习中的足够重视。 一、动点轨迹问题 这类问题往往是先利用题中条件把立几问题转化为平面几何问题,再判断动点轨迹。 例1定点A 和B 都在平面α内,定点α?P ,α⊥PB , C 是α内异于A 和B 的动点,且AC PC ⊥。那么,动点C 在平面α内的轨迹是( ) A. 一条线段,但要去掉两个点 B. 一个圆,但要去掉两个点 C. 一个椭圆,但要去掉两个点 D. 半圆,但要去掉两个点 例2若三棱锥A —BCD 的侧面ABC 内一动点P 到平面BCD 距离与到棱AB 距离相等,则动点P 的轨迹与△ABC 组成的图形可能是( ) ) 解:设二面角A —BC —D 大小为θ,作PR ⊥面BCD ,R 为垂足,PQ ⊥BC 于Q ,PT ⊥AB 于T ,则∠PQR =θ, 且由条件PT=PR=PQ·sinθ,∴ 为小于1的常数,故轨迹图形应选(D )。 二、几何体的截痕
例3:球在平面上的斜射影为椭园:已知一巨型广告汽球直径6米,太阳光线与地面所成角为60°,求此广告汽球在地面上投影椭圆的离心率和面积(椭圆面积公式为S=πab ,其中a,b 为长、短半轴长)。 解:由于太阳光线可认定为平行光线,故广告球的投影 椭园等价于以广告球直径为直径的圆柱截面椭园:此时 b=R ,a= =2R ,∴离心率 , 投影面积S=πab=π·k·2R=2πR 2=18π。 三、动点与某点(面)的距离问题 , 例4.正方体1111D C B A ABCD -中,棱长为a ,E 是 1AA 的中点, 在对角面D D BB 11上找一动点M ,使AM+ME 最小.a 23. 四、常见的轨迹问题 (1) 轨迹类型识别 此类问题最为常见,求解时,关注几何体的特征,灵活选择几何法与代数法. 例5、(北京)平面α的斜线AB 交α于点B ,过定点A 的动直线l 与AB 垂直,且交 α于点C ,则动点C 的轨迹是( ) A .一条直线 B.一个圆 C.一个椭圆 D.双曲线的一支 【解析】直线l 运动后形成的轨迹刚好为线段AB 的垂面,由公理二易知点C 刚好落在平面α与线段AB 的垂面的交线上,所以动点C 的轨迹是一条直线.选择 A. 总结:空间的轨迹最简单的一直存在形式就是两个平面的交线,处理问题中注意识别即可. 例6、如图,在正方体ABCD A 1 B 1C 1D 1 中,若四边形A 1BCD 1 内一动点P 到AB 1和 BC 的距离相等,则点P 的轨迹为( ) … A .椭圆的一部分 B .圆的一部分 C .一条线段 D .抛物线的一部分 O E 例4题图 A % C D A 1 C 1 D 1 B 1 M - C D B C P O
苏教必修2立体几何初步初步教案学案立体几何第11课时
第11课时直线与平面垂直听课随笔 、【学习导航】 学习要求 1?掌握直线与平面的位置关系? 2 .掌握直线和平面平行的判定与性质定 理. .3.应用直线和平面平行的判定和性质定理证明两条直线平行等有关问题. 自学评价 1. 直线和平面垂直的定义:______________ 符号表示:______________________________ 垂线:___________________________________ 垂面:___________________________________ 垂足:___________________________________ 思考:在平面中,过一点有且仅有一条直线与已知直线垂直,那么在空间。 (1) 过一点有几条直线与已知平面垂直? 答: (2) 过一点有几条平面与已知直线垂直? 答: 2.定理:过一点有且只有一条直线与已知平面垂直,过一点有且只有一个平面与已知直线垂直 3.点到平面的距离:____________________ 4.直线与平面垂直的判定定理:已知: 求证: 证明: 6 .直线和平面的距离: 【精典范例】 例1:.求证:如果两条平行直线中的一条垂直于一个平面,那么另一条直线也垂直于这个平面. 思维点拔: 要证线面垂直,只要证明直线与平面内的两条相交直线垂直,或利用定义进行证明。 Rt△ ABC所在平面外一点S,且SA=SB=SC (1)求证:点S在斜边中点D的连线SD丄面ABC ⑵若直角边BA=BC,求证:BD丄面SAC 符号表示_________________________________ 5 .直线和平面垂直的性质定理: 追踪训练1
苏教必修2立体几何初步初步教案学案立体几何第23课时
第23课时立体几何总复习课⑵ 一、【学习导航】知识网络见上一课时间 学习要求 1?会证线线、线面、面面的平行与垂直的问题,会求简单的线线、线面、面面间的角与距离以及简单几何体的面积与体积 2、了解并能运用分割求和的思想。 A、平行 B 、相交C 、异面 D 、以上都有可能 2、在正方体ABCD AB I GD,中,下列几种说法正确的是 A AC i AD B、D1C1 AB C AC i 与DC 成45°角D、AC i与BiC 成60°角 3、若直线丨P平面,直线a,则丨与a的位置关系是 A l Pa B丨与a异面 C 、丨与a相交D丨与a没有公共点 4、下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面 平行;(3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.其中正确的个数有 A 1 B 、2 C 3 D 、4 5、在空间四边形ABCD各边AB、BC、CD、DA上分别取E、F、G、H四点,如果与 EF、GH能相交于点P,那么 A、点必P在直线AC上B点P必在直线BD上 C点P必在平面ABC内D、点P必在平面ABC外、 6.如图:直三棱柱ABC-ABC的体积为V点P、Q分别在侧棱AA和 CC上,AP=QQ则四棱锥B-APQC勺体积为 V V 2345
【精典范例】、 例 1:已知 ABC 中 ACB 90°, SA 面 ABC , AD SC ,求证:AD 面 SBC 例 2:已知△ BC [中,/ BCD 90°, BGCt =1, AB 丄平面 BCD) / ADB 60°, E 、 AD 上的动点,且 思维点拔:灵活掌握与运用立体几何中的基本知识与方法。才能有效的解决问 题。 追踪训练 1. a , b , c 表示直线,M 表示平 面,给出下列四个命题:①若 a // M b // M 则a // b ;②若 b M a / b ,则a / M ③若a 丄 c , b 丄c ,则a / b ;④若a 丄M b 丄M 则a / b .其中正确命题的 个数 有 A 、0个 B 1个 C 、2个 D 3个 2. 在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体 ,则截去8个三 棱锥后,剩下的凸多面体的体积是 2 7^4 5 A 、一 B 、一 C 、一 D 3 6 5 6 3 ?已知PA 垂直平行四边形 ABCD 所在平面,若 PC BD ,平行则四边形 ABCD 一定 是 . _______ 4、如图,在直四棱柱 A 1B 1G D 1 — ABCD^,当底面四边形 ABCD?足条件 ___________ 时,有A B 丄B D 1.(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形 AE AF (0 AC AD 1). (I)求证:不论入为何值,总有平面 BEF 丄平面ABC (H)当入为何值时,平面 BEF 丄平面ACD .)
立体几何中的截面(解析版)
专题13 立体几何中的截面 【基本知识】 1.截面定义:在立体几何中,截面是指用一个平面去截一个几何体(包括圆柱,圆锥,球,棱柱,棱锥、长方体,正方体等等),得到的平面图形,叫截面。其次,我们要清楚立体图形的截面方式,总共有三种,分别为横截、竖截、斜截。最后,我们要了解每一种立体图形通过上述三种截面方式所得到的截面图有哪些。 2、正六面体的基本斜截面: 3、圆柱体的基本截面:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形。 【基本技能】
技能1.结合线、面平行的判定定理与性质性质求截面问题; 技能2.结合线、面垂直的判定定理与性质定理求正方体中截面问题; 技能3.猜想法求最值问题:要灵活运用一些特殊图形与几何体的特征,“动中找静”:如正三角形、正六边形、正三棱锥等; 技能4.建立函数模型求最值问题:①设元②建立二次函数模型③求最值。 例1 一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能 ... 是() 分析考虑过球心的平面在转动过中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D。 例2 如图,在透明的塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,固定容器底面一边BC于地面上,再将容器倾斜,随着倾斜程度的不同,有下列四个命题: ①水的部分始终呈棱柱状; ②水面EFGH的面积不改变; ③棱A1D1始终与水面EFGH平行; ④当容器倾斜到如图5(2)时,BE·BF是定值; 其中正确的命题序号是______________ A C B D
分析 当长方体容器绕BC 边转动时,盛水部分的几何体始终满足棱柱定义,故①正确;在转动过程中EH//FG ,但EH 与FG 的距离EF 在变,所以水面EFGH 的面积在改变,故②错误;在转动过程中,始终有BC//FG//A 1D 1,所以A 1D 1//面EFGH ,③正确;当容器转动到水部分呈直三棱柱时如图5(2),因为 BC BF BE V ??= 2 1 水是定值,又BC 是定值,所以BE ·BF 是定值,即④正确。所以正确的序号为①③④. 例3 有一容积为1 立方单位的正方体容器ABCD-A 1B 1C 1D 1,在棱AB 、BB 1及对角线B 1C 的中点各有一小孔E 、F 、G ,若此容器可以任意放置,则该容器可装水的最大容积是( ) A . 21 B .87 C .12 11 D .4847 分析 本题很容易认为当水面是过E 、F 、G 三点的截面时容器可装水的容积最大图(1),最大值为 8 7 12121211=???- =V 立方单位,这是一种错误的解法,错误原因是对题中“容器是可以任意放置”的理解不够,其实,当水平面调整为图(2)△EB 1C 时容器的容积最大,最大容积为1211 112121311=????-=V , 故选C 。 例4 正四棱锥P ABCD -的底面正方形边长是3,O 是P 在底面上的射影,6, PO Q =是 AC 上的一点,过Q 且与, PA BD 都平行的截面为五边形EFGHL ,求该截面面积的最大值. C 1 A B C D A 1 D 1 B 1 E G F 图(1) C 1 A B C D A 1 D 1 B 1 E G F 图(2)
2019-2020年高中数学必修二第一章《立体几何初步》学案
2019-2020年高中数学必修二第一章《立体几何初步》学案 一、课前自学 [学习目标] 1.了解螺旋体的概念; 2.理解几何体轴截面的的概念,并解决一些简单的问题。 [预习指导] 1、螺旋体 (1)一条绕着它所在的平面内的一条定直线旋转形成的曲面叫做旋转面;的旋转面围成的几何体叫做旋转体。(平面曲线、封闭) (2)特殊的旋转体:圆柱、圆锥、圆台、球。 2、球 (1)以半圆的所在的直线为旋转轴,将半圆旋转所形成的曲面叫做球面。所围成的几何体叫做球体,简称球。半圆的叫做球心,连接球心与球面上任意一点的线段叫做半径,连接球面上两点并且过的线段叫做球的。(直径、球面、圆心、球心、直径) (2)表示:球心为O时记为球O 。 3、圆柱、圆锥、圆台 (1)概念:分别以矩形的、直角三角形的一条、直角梯形垂直于底边的 所在直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫做圆柱、圆锥、圆台。圆台也可以看作是用于圆锥的平面截这个圆锥而得到的,垂直于的边旋转而成的圆面叫做它们的底面;旋转轴的边旋转而成的曲面叫做它们的侧面,无论转到什么位置这条边都叫做侧面的(一边、直角边、腰、底面、旋转轴、不垂直于母线) (2)表示:圆柱OO’,圆锥SO ,圆台OO’(如上图) 二、课堂练习 [精讲点拨] 1、如何理解简单旋转体的有关概念? (1)对于定义应该注意以下几点: ①旋转轴是一条直线;②旋转面是曲面;③旋转体为实体。 (2)几种简单旋转体的比较:
想一想:以上旋转体还可以由怎样的平面图形旋转而成? 提示:球,圆柱、圆锥、圆台还可以分别由圆,矩形、等腰三角形、等腰梯形绕其 ..对称轴 ...旋转半周而成。
立体几何轨迹与截面问题
轨迹与截面(二) 1.如图,在正方体中,是的中点,为底面内一动点,设 与底面所成的角分别为均不为.若,则动点的轨迹为() A. 直线的一部分 B. 圆的一部分 C. 椭圆的一部分 D. 抛物线的一部分 2.正方体棱长为4,,分别是棱,的中点,则过三点的平面截正方体所得截面的面积为() A. B. C. D. 3.已知球O的半径为2,圆M和圆N是球的互相垂直的两个截面,圆M和圆N的面 MN=() 积分别为2π和π,则|| A.1 B3.2 D5 4.如图,在四棱锥P﹣ABCD中,侧面PAD为正三角形,底面ABCD为正方形,侧面PAD ⊥底面ABCD,M为底面ABCD内的一个动点,且满足MP=MC,则点M在正方形ABCD内的
轨迹为( ) A . B . C . D . 5.如图,记长方体1111ABCD A B C D -被平行于棱11C B 的平面EFGH 截去右上部分后剩下的几何体为Ω,则下列结论中不正确... 的是( ) A .EH ∥FG B .四边形EFGH 是平行四边形 C .Ω是棱柱 D .Ω是棱台 6.如图,在正方体1111ABCD A B C D -中,P 是侧面11BB C C 内一动点,若P 到直线BC 与直线11C D 的距离相等,则动点P 的轨迹所在的曲线是( ) 11 A 1 B 1 P D C A.直线 B.圆 C.双曲线 D.抛物线
7.如图,在棱长为1的正方体1111ABCD A B C D -中,P 为棱11A B 中点,点Q 在侧面 11DCC D 内运动,若1PBQ PBD ∠=∠,则动点Q 的轨迹所在曲线为( ) A.直线 B.圆 C.双曲线 D.抛物线 8.如图所示,最左边的几何体由一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得,现用一个竖直的平面去截这个几何体,则截面图形可能是( ) A .①② B .②③ C .③④ D .①⑤ 9.如图,正方体1111ABCD A B C D -的棱长为3,以顶点A 为球心,2为半径作一个球,则图中球面与正方体的表面相交所得到的两段弧长之和等于( ) A . 56π B .23π C .π D .76 π 10.(2015秋?河南期末)如图,在平行六面体ABCD ﹣A 1B 1C 1D 1中,底面是边长为2的正方形,若∠A 1AB=∠A 1AD=60°,且A 1A=3,则A 1C 的长为( )
立体几何截面问题
立体几何中的截面问题剖析 用平面去截一个几何体,截面的情况可以帮助我们更好地认识几何体,对于一个几何体不同切截方式,所以得截面可能出现不同的情况. 以正方体为例:平面截正方体的截面图形 三角形: 四边形 五边形 六边形 类型一:与截面有关的求值问题 1、在棱长为2的正方体1111ABCD A B C D -中,M 是棱11A D 的中点,过1C ,B ,M 作正方体的截面,则这个截面的面积为( ) A .35 B .35 C .92 D .98 2、 体积为216的正方体1111ABCD A B C D -中,点M 是线段11D C 的中点,点N 在线段11B C 上,//MN BD ,则正方体1111ABCD A B C D -被平面AMN 所截得的截面面积为( ) A. 2717 B .2117 C .1517 D .1317
正三棱柱111ABC A B C -中,所有棱长均为2,点,E F 分别为棱111,BB A C 的中点,若过点,,A E F 作一截面,则截面的周长为( ) A .425133+ B .225133 + C .2513+ D .13252 + 反馈练习: 1、在棱长为2的正方体1111D C B A ABCD -中,E 是正方形C C BB 11的中心,M 为11D C 的中点,过M A 1的平面α与直线DE 垂直,则平面α截正方体1111D C B A ABCD -所得的截面面积为( ) A .23 B .26 C .225 D .3 2、如图,在正方体````ABCD A B C D -中,平面垂直于对角线AC ,且平面截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S ,周长为l ,则( ) A .S 为定值,l 不为定值 B .S 不为定值,l 为定值 C .S 与l 均为定值 D .S 与l 均不为定值 类型二:与截面有关的最值问题 1、已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( ) A .433 B .332 C .423 D .2 3
高中数学第一章教案《立体几何初步》
第一章立体几何初步 示范教案 整体设计 教学分析 本节课是对第一章的基本知识和方法的总结与归纳,从整体上来把握本章内容,使学生的基本知识系统化和网络化,基本方法条理化.值得注意的是对于本章知识结构,学生比较陌生,教师要帮助学生完成,并加以引导. 三维目标 通过总结和归纳立体几何的知识,能够使学生综合运用知识解决有关问题,培养学生分析、探究和思考问题的能力,激发学生学习数学的兴趣,培养其分类讨论的思想和提高其抽象思维能力. 重点难点 教学重点:①空间几何体的结构特征. ②由三视图还原为实物图. ③面积和体积的计算. ④平行与垂直的判定与性质. 教学难点:形成知识网络. 课时安排 1课时 教学过程 导入新课 设计 1.第一章是整个立体几何的基础,为了系统地掌握本章的知识和方法,本节对第一章进行复习.教师点出课题. 设计2.大家都知道,农民伯伯在春天忙着耕地、播种、浇水、施肥、治虫,非常辛劳,到了秋天,他们便忙着收获.到了收获的季节,他们既高兴又紧张,因为收获比前面的工作更重要,收获的多少决定着一年的收成.我们前面的学习就像播种,今天的小结就像收获,希望大家重视今天的小结学习.教师点出课题. 推进新课 新知探究 提出问题 请同学们自己梳理本章知识结构. 对比直线与平面、平面与平面的平行关系与垂直关系. 对比面积、体积各自之间的关系. 讨论结果: (1)本章知识结构:
(2)平行关系与垂直关系的对比: (3)①柱、锥、台的侧面积关系:
其中c′、c 分别为上、下底面周长,h′为斜高或母线长,h 为正棱柱或圆柱的高. ②柱、锥、台的体积关系: 其中S 上、S 下分别为台体的上、下底面积,h 为高,S 为柱体或锥体的底面积. ③球的表面积和体积:S 球面=4πR 2,V 球=43 πR 3 . 应用示例 思路1 例1 下列几何体是台体的是( ) 解析:A 中的“侧棱”没有相交于一点,所以A 不是台体;B 中的几何体没有两个平行的面,所以B 不是台体;很明显C 是棱锥,D 是圆台. 答案:D 点评:本题主要考查台体的结构特征.像这样的概念辨析题,主要是依靠对简单几何体的结构特征的准确把握. 变式训练 1.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括( ) A .一个圆台、两个圆锥 B .两个圆台、一个圆柱
高中数学 第一章《立体几何初步》1-2课时教学案 苏教版必修2
1.1.1 第1课时棱柱、棱锥、棱台 学习目标:1.认识棱柱、棱锥和棱台的结构特征,并能运用这些特征描述现实生活中简单物体的结构; 2.了解棱柱、棱锥和棱台的概念; 3.初步培养学生的空间想象能力和抽象括能力. 学习重点:让学生感受大量空间实物及模型、概括出棱柱、棱锥和棱台的结构特征. 学习难点:棱柱、棱锥和棱台的结构特征的概括. 学习过程: 一、课前准备:自学课本P4~7 1.基本概念: ①棱柱:由的空间几何体叫 做棱柱.叫做棱柱的底面, 叫做棱柱的侧面. 棱柱的特点:两个底面是,且,侧面都是. ②棱锥:当时,得到的几何体叫做棱锥. 棱锥的特点:底面是,侧面是. ③棱台:用,另 一个叫做棱台.即. 棱台的特点:两个底面是,侧面是,侧棱. ④多面体:由的几何体叫做多面体. 2.由平面六边形沿某一方向平移形成的空间几何体是. 3.下列说法中,正确的有. ①棱柱的侧面可以是三角形②正方体的各条棱都相等 ③棱柱的各条侧棱都相等④正方体和长方体都是特殊的四棱柱 ⑤用一个平面去截一个长方体, 截面一定是长方形 4.已知一长方体,根据图中三种状态所显示的数字,可推出“?”处的数字是. 5.有两个面互相平行, 其余各面都是梯形的多面体是. ①棱柱②棱锥③棱台④可能是棱台, 一定不是棱柱或棱锥 6.构成多面体的面最少是个,该多面体称为或. 二、合作探究: 例1.棱柱的特点是:⑴两个底面是全等的多边形,⑵多边形的对应边互相平行,⑶棱柱的侧面都是平行四边形.反过来,若一个几何体具备上述三点,能构成棱柱吗?或者说,上面三点能作为棱柱的定义吗? 例2.三棱柱有个面,个顶点,条棱,可以称为五面体;还有其他五面体吗?
人教版高中数学必修二教学案-《立体几何初步》全章复习
人教版高中数学必修一教学讲义 年级:上课次数: 学员姓名:辅导科目:数学学科教师: 课题《立体几何初步》全章复习 课型□预习课□同步课■复习课□习题课 授课日期及时段 教学内容 《立体几何初步》全章复习 【知识网络】 【要点梳理】 知识点一:空间几何体的结构与特征 本章出现的几何体有:①棱柱与圆柱统称为柱体;②棱锥与圆锥统称为锥体;③棱台与圆台统称为台体;④球体. 柱体常以直三棱柱、正三棱柱、正四棱柱、正六棱柱、圆柱等为载体,锥体一般以正三棱锥、正四棱锥、正六棱锥、圆锥等为载体,计算高、斜高、边心距、底面半径、侧面积和体积等.在研究正棱锥和圆锥、正棱台和圆台时要充分利用其中的直角三角形:高线,边心距,斜高组成的直角三角形;高线,侧棱(母线),外接圆半径(底面半径)组成的直角三角形. 空间几何体的三视图:主视图:它能反映物体的高度和长度;左视图:它能反映物体的高度和宽度;俯视图:
【典型例题】 类型一:空间几何体的三视图 例1.某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图. (1)请画出该安全标识墩的侧(左)视图 (2)求该安全标识墩的体积 (3)证明:直线BD 平面PEG 【思路点拨】(1)由于墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH,故其正视图与侧视图全等. (2)由三视图我们易得,底面为边长为40cm的正方形,长方体的高为20cm,棱锥高为60cm,代入棱柱和棱锥体积公式,易得结果. 【解析】(1)侧视图同正视图,如下图所示.
立体几何中的最值
立体几何最值问题 姓名 立体几何主要研究空间中点、线、面之间的位置关系,与空间图形有关的线段、角、体积等最值问题常常在试题中出现。下面举例说明解决这类问题的常用方法。 一、运用变量的相对性求最值 例1. 在正四棱锥S-ABCD 中,SO ⊥平面ABCD 于O ,SO=2,底面边长为2,点P 、Q 分别在线段BD 、SC 上移动,则P 、Q 两点的最短距离为( ) A. 5 5 B. 5 5 2 C. 2 D. 1 二、定性分析法求最值 例2. 已知平面α//平面β,AB 和CD 是夹在平面α、β之间的两条线段。AB ⊥CD ,AB=3,直线AB 与平面α成30°角,则线段CD 的长的最小值为______。 三、展成平面求最值 例 3. 如图3-1,四面体A-BCD 的各面都是锐角三角形,且AB=CD=a ,AC=BD=b ,AD=BC=c 。平面α分别截棱AB 、BC 、CD 、DA 于点P 、Q 、R 、S ,则四边形PQRS 的周长的最小值是( ) A. 2a B. 2b C. 2c D. a+b+c 图3-1 四、利用向量求最值 例4. 在棱长为1的正方体ABCD-EFGH 中,P 是AF 上的动点,则GP+PB 的 最小值为_______。
