常用数学公式表

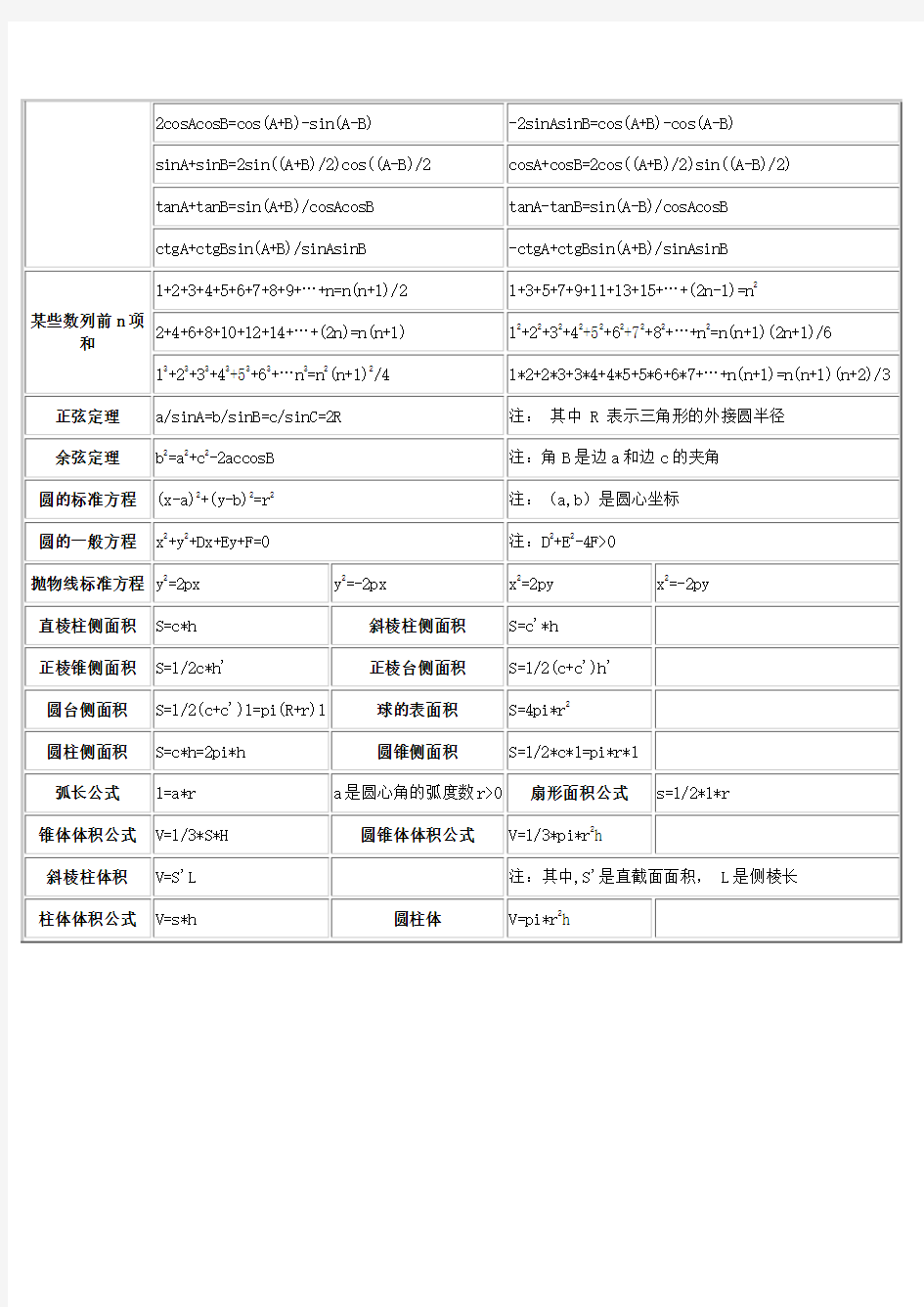
常用数学公式表
常用数学公式表
公式分类公式表达式
乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)
三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b||a|≤b<=>-b≤a≤b
|a-b|≥|a|-|b| -|a|≤a≤|a|
一元二次方程的解 -b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a
根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理
判别式 b2-4a=0 注:方程有相等的两实根
b2-4ac>0 注:方程有一个实根
b2-4ac<0 注:方程有共轭复数根
三角函数公式
两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA
cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB
tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)
ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)
倍角公式 tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga
cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a
半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)
cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)
tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))
ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))
和差化积 2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)
2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)
sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2)
tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB
ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB
某些数列前n项
和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n2
2+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2 )/3
正弦定理 a/sinA=b/sinB=c/sinC=2R 注:其中 R 表示三角形的外接圆半径
余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角
圆的标准方程 (x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标
圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0
抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py
直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c'*h
正棱锥侧面积 S=1/2c*h' 正棱台侧面积 S=1/2(c+c')h'
圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi*r2
圆柱侧面积 S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l
弧长公式 l=a*r a是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r 锥体体积公式 V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h
斜棱柱体积 V=S'L 注:其中,S'是直截面面积, L是侧棱长
柱体体积公式 V=s*h 圆柱体 V=pi*r2h
公式分类公式表达式
cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a
半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)
cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)
tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))
ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))
和差化积 2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)
2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)
sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2)
tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB
ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB
某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n2 2+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6
13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理 a/sinA=b/sinB=c/sinC=2R 注:其中 R 表示三角形的外接圆半径
余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角
圆的标准方程 (x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标
圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0
抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py
直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c'*h
正棱锥侧面积 S=1/2c*h' 正棱台侧面积 S=1/2(c+c')h'
圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi*r2
圆柱侧面积 S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l
弧长公式 l=a*r a是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r
锥体体积公式 V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h
斜棱柱体积 V=S'L 注:其中,S'是直截面面积, L是侧棱长
柱体体积公式 V=s*h 圆柱体 V=pi*r2h
同角三角函数的基本关系式
同角三角函数的基本关系式
倒数关系: 商的关系:平方关系:
tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 sinα/cosα=tanα=
secα/cscα
cosα/sinα=cotα=
cscα/secα
sin2α+cos2α=1
1+tan2α=sec2α
1+cot2α=csc2α
(六边形记忆法:图形结构
“上弦中切下割,左正右余中
间1”;记忆方法“对角线上
两个函数的积为1;阴影三角
形上两顶点的三角函数值的
平方和等于下顶点的三角函
数值的平方;任意一顶点的三
角函数值等于相邻两个顶点
的三角函数值的乘积。”)
诱导公式(口诀:奇变偶不变,符号看象限。)
sin(-α)=-sinαcos(-α)=cosαtan(-α)=
-tanα
cot(-α)=
-cotα
sin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα
sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-
α)=-cosα
cos(3π/2-
α)=-sinα
tan(3π/2-
α)=cotα
cot(3π/2-
α)=tanα
sin(3π/2+
α)=-cosα
cos(3π/2+
α)=sinα
tan(3π/2+
α)=-cotα
cot(3π/2+
α)=-tanα
sin(2π-α)
=-sinα
cos(2π-α)
=cosα
tan(2π-α)
=-tanα
cot(2π-α)
=-cotα
sin(2kπ+
α)=sinα
cos(2kπ+
α)=cosα
tan(2kπ+
α)=tanα
cot(2kπ+
α)=cotα
(其中k∈Z)
两角和与差的三角函数公式万能公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
tanα+tanβtan(α+β)=——————
1-tanα ·tanβ
tanα-tanβtan(α-β)=——————
1+tanα ·tanβ
2tan(α/2) sinα=——————
1+
tan2(α/2)
1-
tan2(α/2)
cosα=——————
1+
tan2(α/2)
2tan(α/2) tanα=——————
1-tan2(α/2)
半角的正弦、余弦和正切公式三角函数的降幂公式
二倍角的正弦、余弦和正切公式三倍角的正弦、余弦和正切
公式
sin2α=2sinαcosα
cos2α=cos2α-sin2α=2cos2α-1=1-2sin2α
2tanα
tan2α=—————
1-tan2αsin3α=3sinα-4sin3αcos3α=4cos3α-3cosα
3tanα-tan3α
tan3α=——————
1-3tan2α
三角函数的和差化积公式三角函数的积化和差公式
α+βα-β
sinα+sinβ=2sin———·cos———
2 2
α+
1 sinα·cosβ=-[sin(α+β)+sin(α-β)]
2
1 cosα·sinβ=-[sin(α+
βα-β
sinα-sinβ=2cos———·sin———
2 2
α+
βα-β
cosα+cosβ=2cos———·cos———
2 2
α+βα-β
cosα-cosβ=-2sin———·sin———
2 2 β)-sin(α-β)]
2
1 cosα·cosβ=-[cos(α+β)+cos(α-β)]
2
1
sinα·sinβ=—-[cos(α+β)-cos(α-β)]
2
化asinα ±bcosα为一个角的一个三角函数的形式(辅助角的三角函数的公式)
基本几何图形的面积和体积
基本几何图形的面积和体积
高等数学常用公式大全
高数常用公式 平方立方: 22222222 332233223223332233222(1)()()(2)2()(3)2()(4)()()(5)()()(6)33()(7)33()(8)222(a b a b a b a ab b a b a ab b a b a b a b a ab b a b a b a ab b a a b ab b a b a a b ab b a b a b c ab bc ca -=+-++=+-+=-+=+-+-=-+++++=+-+-=-+++++= 21221)(9)()(),(2) n n n n n n a b c a b a b a a b ab b n ----++-=-++++≥ 三角函数公式大全 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1 -cotAcotB + cot(A-B) =cotA cotB 1 cotAcotB -+ 倍角公式 tan2A =A tan 12tanA 2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3 π -a) 半角公式 sin( 2A )=2cos 1A - cos( 2A )=2cos 1A + tan( 2A )=A A cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan( 2 A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2 b a -
小学数学中的计算公式大全{完整
小学数学中的计算公式大全 1、每份数×份数=总数总数÷每份数=份数 总数÷份数=每份数 2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数 3、速度×时间=路程路程÷速度=时间 路程÷时间=速度 4、单价×数量=总价总价÷单价=数量 总价÷数量=单价 5、工作效率×工作时间=工作总量 工作总量÷工作效率=工作时间 工作总量÷工作时间=工作效率 6、加数+加数=和和-一个加数=另一个加数 7、被减数-减数=差被减数-差=减数 差+减数=被减数 8、因数×因数=积积÷一个因数=另一个因数 9、被除数÷除数=商被除数÷商=除数 商×除数=被除数 小学数学图形计算公式 1、正方形:C周长S面积a边长 周长=边长×4C=4a 面积=边长×边长S=a×a
2、正方体:V:体积a:棱长 表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a 3、长方形:C周长S面积a边长 周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab 4、长方体:V:体积s:面积a:长b: 宽h:高 (1)表面积(长×宽+长×高+宽高)×2 S=2(ab+ah+bh) (2)体积=长×宽×高V=abh 5、三角形s面积a底h高 面积=底×高÷2 s=ah÷2 三角形高=面积×2÷底 三角形底=面积×2÷高 6、平行四边形:s面积a底h高 面积=底×高s=ah 7、梯形:s面积a上底b下底h高 面积=(上底+下底)×高÷2 s=(a+b)×h÷2 8 、圆形:S面C周长∏d=直径r=半径 (1)周长=直径×∏=2×∏×半径C=∏d=2∏r (2)面积=半径×半径×∏ 9、圆柱体:v:体积h:高s:底面积r:底面半径
公务员考试常用数学公式汇总(完整打印版)
公务员考试常用数学公式汇总(完整版) 一、基础代数公式 1. 平方差公式:(a +b )×(a -b )=a 2-b 2 2. 完全平方公式:(a±b)2=a 2±2ab +b 2 完全立方公式:(a ±b )3=(a±b)(a 2 ab+b 2) 3. 同底数幂相乘: a m ×a n =a m +n (m 、n 为正整数,a≠0) 同底数幂相除:a m ÷a n =a m -n (m 、n 为正整数,a≠0) a 0=1(a≠0) a -p = p a 1 (a≠0,p 为正整数) 4. 等差数列: (1)s n = 2)(1n a a n ?+=na 1+21 n(n-1)d ; (2)a n =a 1+(n -1)d ; (3)n = d a a n 1 -+1; (4)若a,A,b 成等差数列,则:2A =a+b ; (5)若m+n=k+i ,则:a m +a n =a k +a i ; (其中:n 为项数,a 1为首项,a n 为末项,d 为公差,s n 为等差数列前n 项的和) 5. 等比数列: (1)a n =a 1q -1; (2)s n =q q a n -11 ·1) -((q ≠1) (3)若a,G,b 成等比数列,则:G 2=ab ; (4)若m+n=k+i ,则:a m ·a n =a k ·a i ; (5)a m -a n =(m-n)d (6)n m a a =q (m-n) (其中:n 为项数,a 1为首项,a n 为末项,q 为公比,s n 为等比数列前n 项的和) 6.一元二次方程求根公式:ax 2+bx+c=a(x-x 1)(x-x 2) 其中:x 1=a ac b b 242-+-;x 2=a ac b b 242---(b 2-4a c ≥0) 根与系数的关系:x 1+x 2=-a b ,x 1·x 2=a c 二、基础几何公式 1. 三角形:不在同一直线上的三点可以构成一个三角形;三角形内角和等于180°;三角形中任两 边之和大于第三边、任两边之差小于第三边; (1)角平分线:三角形一个的角的平分线和这个角的对边相交,这个角的顶点和交点之间的线段,叫做三角形的角的平分线。 (2)三角形的中线:连结三角形一个顶点和它对边中点的线段叫做三角形的中线。 (3)三角形的高:三角形一个顶点到它的对边所在直线的垂线段,叫做三角形的高。 (4)三角形的中位线:连结三角形两边中点的线段,叫做三角形的中位线。 (5)内心:角平分线的交点叫做内心;内心到三角形三边的距离相等。 重心:中线的交点叫做重心;重心到每边中点的距离等于这边中线的三分之一。 垂线:高线的交点叫做垂线;三角形的一个顶点与垂心连线必垂直于对边。 外心:三角形三边的垂直平分线的交点,叫做三角形的
小学数学常用公式大全(单位换算表)
小学数学常用图形周长面积体积计算公式: 1,正方形 C周长S面积a边长 周长=边长×4 面积=边长×边长 C=4a S=a×a S=a2 2,正方体 V体积a棱长 表面积=棱长×棱长×6体积=棱长×棱长×棱长S表=a×a×6 表=6a2 V=a×a×a V= a3 3,长方形 C周长S面积a边长 周长=(长+宽)×2 C=2(a+b) 面积=长×宽 S=ab 4,长方体 V体积S面积a长b宽h高 (1)表面积=(长×宽+长×高+宽×高)×2 (2)体积=长×宽×高 S=2(ab+ah+bh) V=abh 5,三角形 S面积a底h高 面积=底×高÷2 S=ah÷2 三角形高=面积×2÷底 三角形底=面积×2÷高 6,平行四边形 S面积a底h高 面积=底×高S=ah 7,梯形 S面积a上底b下底h高 面积=(上底+下底)×高÷2 S=(a+b)× h÷2 8,圆形
S面积C周长π圆周率 d直径r半径 周长=直径×π 周长=2×π×半径 面积=半径×半径×π C=πd C=2πr S=πr2 d=C÷π d=2r r=d÷2 r=C÷2÷πS环=π(R2-r2) 9,圆柱体 V体积h高S底面积r底面半径C底面周长 侧面积=底面周长×高 (2)表面积=侧面积+底面积×2 (3)体积=底面积×高 S侧=Ch S侧=πdh V=Sh V=πr2h 圆柱体积=侧面积÷2×半径 10,圆锥体 V体积h高 S底面积r底面半径 体积=底面积×高÷3 V=Sh÷3 长度单位换算 1千米=1000米;1米=10分米 1分米=10厘米;1米=100厘米 1厘米=10毫米 面积单位换算 1平方千米=100公顷;1公顷=10000平方米;1平方米=100平方分米1平方分米=100平方厘米;1平方厘米=100平方毫米 1平方米=0.0015亩;1万平方米=15亩 1公顷=15亩=100公亩=10000平方米 1公亩等于100平方米 1(市)亩等于666.66平方米 体(容)积单位换算 1立方米=1000立方分米;1立方分米=1000立方厘米;1立方分米=1升1立方厘米=1毫升;1立方米=1000升 重量单位换算
(完整版)小学数学常用公式大全(单位换算表)
小学数学常用公式(单位换算表) 长度单位换算 1千米=1000米 1米=10分米 1分米=10厘米 1米=100厘米 1厘米=10毫米 面积单位换算 1平方千米=100公顷 1公顷=10000平方米 1平方米=100平方分米 1平方分米=100平方厘米 1平方厘米=100平方毫米 体(容)积单位换算 1立方米=1000立方分米 1立方分米=1000立方厘米 1立方分米=1升 1立方厘米=1毫升 1立方米=1000升 重量单位换算 1吨=1000千克 1千克=1000克 1千克=1公斤 人民币单位换算 1元=10角 1角=10分 1元=100分 时间单位换算 1世纪=100年 1年=12月 大月(31天)有:1\3\5\7\8\10\12月 小月(30天)的有:4\6\9\11月 平年2月28天,闰年2月29天 平年全年365天,闰年全年366天 1日=24小时 1时=60分 1分=60秒 1时=3600秒 一、长度 (一) 什么是长度 长度是一维空间的度量。 (二) 长度常用单位 * 公里(km) * 米(m) * 分米(dm) * 厘米(cm) * 毫米(mm) (三) 单位之间的换算 1厘米=10 毫米 * 1分米=10 厘米 * 1米=1000 毫米 * 1千米=1000 米 二、面积 (一)什么是面积 面积,就是物体所占平面的大小。对立体物体的表面的多少的测量一般称表面积。 (二)常用的面积单位 平方毫米 * 平方厘米 * 平方分米 * 平方米 * 平方千米 (三)面积单位的换算 * 1平方厘米=100 平方毫米 * 1平方分米=100平方厘米 * 1平方米=100 平方分米* 1公倾=10000 平方米 * 1平方公里=100 公顷 三、体积和容积 (一)什么是体积、容积 体积,就是物体所占空间的大小。 容积,箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。 (二)常用单位 1 体积单位 * 立方米 * 立方分米 * 立方厘米 2 容积单位 * 升 * 毫升 (三)单位换算 1 体积单位 * 1立方米=1000立方分米;* 1立方分米=1000立方厘米 2 容积单位 * 1升=1000毫升;* 1升=1立方米;* 1毫升=1立方厘米 四、质量 (一)什么是质量 质量,就是表示物体有多重。 (二)常用单位 * 吨 t * 千克 kg * 克 g (三)常用换算 * 一吨=1000千克; * 1千克=1000克 五、时间 (一)什么是时间 是指有起点和终点的一段时间 (二)常用单位 世纪、年、月、日、时、分、秒(三)单位换算 * 1世纪=100年;*平年1年=365天;*闰年一年=366天 * 一、三、五、七、八、十、十二是大月大月有31 天 * 四、六、九、十一是小月小月有30天 * 平年2月有28天闰年2月有29天 * 1天= 24小时 * 1小时=60分 * 一分=60秒 - 1 -
中小学数学常用公式大全
中小学数学常用公式大全 体(容)积单位换算 1立方分米=1升 1立方厘米=1毫升1立方米=1000升重量单位换算1吨=1000千克 1千克=1000克 1千克=1公斤 长度单位换算1千米=1000米 1米=10分米 1分米=10厘米 1厘米=10毫米 利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成 本-1)×100% 涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1) 利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%) 浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量流水问题 顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度 静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2 追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差 速度差=追及距离÷追及时间 相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和 速度和=相遇路程÷相遇时间 图形计算公式 1、小正方形:C周长 S面积 a边长周长=边长×4C=4a面积=边长×边长 2、正方体:V:体积 a:棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长 3、长方形:C周长 S面积 a边长周长=(长+宽)×2 C=2(a+b) S=ab 4、长方体:V:体积 s:面积 a:长 b:宽 h:高 (1)表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh) (2)体积=长×宽×高V=abh 5、三角形:s面积 a底 h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底 三角形底=面积×2÷高 6、平行四边形:s面积 a底 h高面积=底×高 s=ah 7、梯形:s面积 a上底 b下底 h高面积=(上底+下底)×高÷2 s=(a+b)×h÷2 8、圆形:S面C周长∏d=直径r=半径 (1)周长=直径×∏=2×∏×半径C=∏d=2∏r (2)面积=半径×半径×∏ 9、圆柱体:v体积 h:高 s:底面积 r:底面半径 c:底面周长 (1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2 (3)体积=底面积×高 (4)体积=侧面积÷2×半径 10、圆锥体:v体积 h高 s底面积 r底面半径体积=底面积×高÷3 1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数 2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数 3、速度×时间=路程路程÷速度=时间路程÷时间=速度 4、单价×数量=总价总价÷单价=数量总价÷数量=单价 5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间 工作总量÷工作时间=工作效率 6、加数+加数=和和-加数=另一个加数 7、被减数-减数=差被减数-差=减数差+减数=被减数 8、因数×因数=积积÷一个因数=另一个因数 9、被除数÷除数=商被除数÷商=除数商×除数=被除数
小学常用数学公式汇总
数量关系计算公式 1、单价×数量=总价 2、单产量×数量=总产量 3、速度×时间=路程 4、工效×时间=工作总量 5、加数+加数=和 6、一个加数=和-另一个加数 7、被减数-减数=差 8、减数=被减数-差 9、被减数=减数+差 10、因数×因数=积 11、一个因数=积÷另一个因数 12、被除数÷除数=商 13、除数=被除数÷商 14、被除数=商×除数 15、有余数的除法:被除数=商×除数+余数 一个数连续用两个数除,可以先把后两个数相乘,再用它们的积去除这个数,结果不变。例:90÷5÷6=90÷(5×6) 1公里=1千米 1千米=1000米 1米=10分米 1分米=10厘米 1厘米=10毫米
1平方米=100平方分米 1平方分米=100平方厘米 几何公式 1.正方形 正方形的周长=边长×4 公式:C=4a 正方形的面积=边长×边长公式:S=a×a 正方体的体积=边长×边长×边长公式:V=a×a×a 2.长方形 长方形的周长=(长+宽)×2 公式:C=(a+b)×2 长方形的面积=长×宽公式:S=a×b 长方体的体积=长×宽×高公式:V=a×b×h 3.三角形 三角形的面积=底×高÷2 公式:S= a×h÷2 4.平行四边形 平行四边形的面积=底×高公式:S= a×h 5.梯形 梯形的面积=(上底+下底)×高÷2 公式:S=(a+b)h÷2
6.圆 直径=半径×2 公式:d=2r 半径=直径÷2 公式:r= d÷2 圆的周长=圆周率×直径公式:c=πd =2πr 圆的面积=半径×半径×π 公式:S=πrr 7.圆柱 圆柱的侧面积=底面的周长×高公式:S=ch=πdh=2πrh 圆柱的表面积=底面的周长×高+两头的圆的面积公式:S=ch+2s=ch+2πr2圆柱的总体积=底面积×高公式:V=Sh 8.圆锥 圆锥的总体积=底面积×高×1/3 公式:V=1/3Sh 9.三角形内角和=180度
数学常用公式精致版
MBA 数学常用公式 初等数学 一、初等代数 1. 乘法公式与因式分解: (1) 222 )2a b a ab b ±=±+( (2) 2222)222a b c a b c ab ac bc ++=+++++( (3)22()()a b a b a b -=-+ (4) 33223)33a b a a b ab b ±=±+±( (5)3322()()a b a b a ab b ±=±+ 2. 指数 (1)m n m n a a a +?= (2)m n m n a a a -÷= (3)()m n mn a a = (4)()m m m ab a b = (5)()m m m a a b b = (6)1m m a a -= 3. 对数(log ,0,1a N a a >≠) (1)对数恒等式 log a N N a =,更常用ln N N e = (2)log ()log log a a a MN M N =+ (3)log ()log log a a a M M N N =- (4)log ()log n a a M n M = (5 )1log log a a M n = (6)换底公式log log log b a b M M a = (7)log 10a =,log 1a a = 4.排列、组合与二项式定理 (1)排列 (1)(2)[(1)]m n P n n n n m =--???-- (2)全排列 (1)(2)321! n n P n n n n =--?????=
l O b b a A C (3)组合 (1)(2)[(1)] ! !!()!m n n n n n m n C m m n m --???--==- 组合的性质: (1)m n m n n C C -= (2)1 11m m m n n n C C C ---=+ (3)二项式定理 01111n n n n n n n n n n C a C a b L C ab C b ---=++++n (a+b) ● 展开式特征: 1)11,0,1,...,k n k k k n k T C a b k n -++==通项公式:第项为 2)1n +项数:展开总共项 3)指数: 1100;a n b n ???→???→逐渐减逐渐加的指数:由; 的指数:由各项a 与b 的指数之和为n 4)展开式的最大系数: 212132n n n n C n C +++n 当n 为偶数时,则中间项(第项)系数最大 2n+1当n 为奇数时,则中间两项(第和项)系数最大。 2 ● 展开式系数之间的关系 1)n r n C -=r n C ,即与首末等距的两相系数相等。 1 2.2n n n n n C C C ++=),即展开式各项系数之和为2n 0241 35 132,n n n n n n n C C C C C C -++=++=)即奇数项系数和等于偶数项系数和 二、平面几何 1. 图形面积 (1)任意三角形 11sin 22S bh ab C == (2)平行四边形:sin S bh ab ?== (3)梯形:S =中位线×高=1 2(上底+下底)×高 (4)扇形: 21 1 22S rl r θ== 弧长 l r θ=
常用数学公式大全
常用数学公式大全 1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数 2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数 3、速度×时间=路程路程÷速度=时间路程÷时间=速度 4、单价×数量=总价总价÷单价=数量总价÷数量=单价 5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率 6、加数+加数=和和-一个加数=另一个加数 7、被减数-减数=差被减数-差=减数差+减数=被减数 8、因数×因数=积积÷一个因数=另一个因数 9、被除数÷除数=商被除数÷商=除数商×除数=被除数 小学数学图形计算公式 1、正方形C周长S面积a边长周长=边长×4C=4a面积=边长×边长S=a×a 2、正方体V:体积a:棱长表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长V=a×a×a 3、长方形 C周长S面积a边长 周长=(长+宽)×2C=2(a+b) 面积=长×宽S=ab 4、长方体 V:体积s:面积a:长b:宽h:高 (1)表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh) (2)体积=长×宽×高V=abh 5三角形 s面积a底h高 面积=底×高÷2s=ah÷2 三角形高=面积×2÷底 三角形底=面积×2÷高 6平行四边形 s面积a底h高 面积=底×高s=ah 7梯形 s面积a上底b下底h高 面积=(上底+下底)×高÷2s=(a+b)×h÷2 8圆形 S面积C周长∏d=直径r=半径 (1)周长=直径×∏=2×∏×半径C=∏d=2∏r (2)面积=半径×半径×∏ 9圆柱体 v:体积h:高s;底面积r:底面半径c:底面周长 (1)侧面积=底面周长×高 (2)表面积=侧面积+底面积×2 (3)体积=底面积×高 (4)体积=侧面积÷2×半径
1~6年级数学公式大全
1~6年级数学公式大全 1、单价×数量=总价 2、单产量×数量=总产量 3、速度×时间=路程 4、工效×时间=工作总量 5、加数+加数=和一个加数=和+另一个加数 被减数-减数=差减数=被减数-差被减数=减数+差 因数×因数=积一个因数=积÷另一个因数 被除数÷除数=商除数=被除数÷商被除数=商×除数 有余数的除法:被除数=商×除数+余数 一个数连续用两个数除,可以先把后两个数相乘,再用它们的积去除这个数,结果不变。例:90÷5÷6=90÷(5×6) 6、1公里=1千米 1千米=1000米 1米=10分米 1分米=10厘米 1厘米=10毫米 1平方米=100平方分米 1平方分米=100平方厘米 1平方厘米=100平方毫米 1立方米=1000立方分米 1立方分米=1000立方厘米 1立方厘米=1000立方毫米 1吨=1000千克 1千克= 1000克= 1公斤= 1市斤 1公顷=10000平方米。 1亩=666.666平方米。 1升=1立方分米=1000毫升 1毫升=1立方厘米 7、什么叫比:两个数相除就叫做两个数的比。如:2÷5或3:6或1/3 比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。 8、什么叫比例:表示两个比相等的式子叫做比例。如3:6=9:18 9、比例的基本性质:在比例里,两外项之积等于两内项之积。 10、解比例:求比例中的未知项,叫做解比例。如3:χ=9:18 11、正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。如:y/x=k( k一定)或kx=y 12、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关 系。如:x×y = k( k一定)或k / x = y 百分数:表示一个数是另一个数的百分之几的数,叫做百分数。百分数也叫做百分率或百分比。
小学数学常用公式大全数量关系计算公式
小学数学常用公式大全(数量关系计算公式) 1、单价×数量=总价 2、单产量×数量=总产量 3、速度×时间=路程 4、工效×时间=工作总量 5、加数+加数=和一个加数=和+另一个加数 被减数-减数=差减数=被减数-差被减数=减数+差 因数×因数=积一个因数=积÷另一个因数 被除数÷除数=商除数=被除数÷商被除数=商×除数 有余数的除法:被除数=商×除数+余数 一个数连续用两个数除,可以先把后两个数相乘,再用它们的积去除这个数,结果不变。例:90÷5÷6=90÷(5×6) 6、1公里=1千米 1千米=1000米 1米=10分米 1分米=10厘米 1厘米=10毫米 1平方米=100平方分米 1平方分米=100平方厘米 1平方厘米=100平方毫米 1立方米=1000立方分米 1立方分米=1000立方厘米 1立方厘米=1000立方毫米 1吨=1000千克 1千克= 1000克= 1公斤= 1市斤 1公顷=10000平方米。 1亩=平方米。 1升=1立方分米=1000毫升 1毫升=1立方厘米 7、什么叫比:两个数相除就叫做两个数的比。如:2÷5或3:6或1/3 比的前项和后项同时乘以或除以一个相同的数(0除外),比值不变。 8、什么叫比例:表示两个比相等的式子叫做比例。如3:6=9:18 9、比例的基本性质:在比例里,两外项之积等于两内项之积。 10、解比例:求比例中的未知项,叫做解比例。如3:χ=9:18 11、正比例:两种相关联的量,一种量变化,另一种量也随着化,如果这两种量中相对应的的比值(也就是商k)一定,这两种量就叫做成正比例的量,它们的关系就叫做正比例关系。如:y/x=k( k一定)或kx=y 12、反比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系就叫做反比例关系。如:x×y = k( k一定)或k / x = y 百分数:表示一个数是另一个数的百分之几的数,叫做百分数。百分数也叫做百分率或百分比。
公务员考试常用数学公式汇总
常用数学公式汇总 一、基础代数公式 1.平方差公式:(a+b)×(a-b)=a2-b2 2.完全平方公式:(a±b)2=a2±2ab+b2 完全立方公式:(a±b)3=(a±b)(a2ab+b2) 3.同底数幂相乘:am×an=am+n(m、n为正整数,a≠0) 同底数幂相除:am÷an=am-n(m、n为正整数,a≠0) a0=1(a≠0) a-p=(a≠0,p为正整数) 4.等差数列: (1)sn==na1+n(n-1)d; (2)an=a1+(n-1)d; (3)n=+1; (4)若a,A,b成等差数列,则:2A=a+b; (5)若m+n=k+i,则:am+an=ak+ai; (其中:n为项数,a1为首项,an为末项,d为公差,sn为等差数列前n项的和) 5.等比数列: (1)an=a1q-1; (2)sn=(q1) (3)若a,G,b成等比数列,则:G2=ab; (4)若m+n=k+i,则:am·an=ak·ai; (5)am-an=(m-n)d (6)=q(m-n) (其中:n为项数,a1为首项,an为末项,q为公比,sn为等比数列前n项的和) 6.一元二次方程求根公式:ax2+bx+c=a(x-x1)(x-x2) 其中:x1=;x2=(b2-4ac0) 根与系数的关系:x1+x2=-,x1·x2= 二、基础几何公式 1.三角形:不在同一直线上的三点可以构成一个三角形;三角形内角和等于180°;三角形中任两 边之和大于第三边、任两边之差小于第三边; (1)角平分线:三角形一个的角的平分线和这个角的对边相交,这个角的顶点和交点之间的线段,叫做三角形的角的平分线。 (2)三角形的中线:连结三角形一个顶点和它对边中点的线段叫做三角形的中线。 (3)三角形的高:三角形一个顶点到它的对边所在直线的垂线段,叫做三角形的高。(4)三角形的中位线:连结三角形两边中点的线段,叫做三角形的中位线。 (5)内心:角平分线的交点叫做内心;内心到三角形三边的距离相等。 重心:中线的交点叫做重心;重心到每边中点的距离等于这边中线的三分之一。 垂线:高线的交点叫做垂线;三角形的一个顶点与垂心连线必垂直于对边。 外心:三角形三边的垂直平分线的交点,叫做三角形的外心。外心到三角形的三个顶点的距离相等。 直角三角形:有一个角为90度的三角形,就是直角三角形。直角三角形的性质: (1)直角三角形两个锐角互余; (2)直角三角形斜边上的中线等于斜边的一半;(3)直角三角形中,如果有一个锐角等
初中三年数学常用公式定理大全
初中数学定理、公式汇编 第一篇数与代数 第一节数与式 一、实数 1.实数的分类:整数(包括:正整数、0、负整数)和分数(包括:有限小数和无限环循小数)都是有理数.如:-3,,0.231,0.737373…,,等;无限不环循小数叫做无理数. 如:π,,0.1010010001…(两个1之间依次多1个0)等.有理数和无理数统称为实数. 2.数轴:规定了原点、正方向和单位长度的直线叫数轴。实数 和数轴上的点一一对应。 3.绝对值:在数轴上表示数a的点到原点的距离叫数a的绝对值, 记作∣a∣。正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0。如:丨-_丨=;丨3.14-π丨=π- 3.1 4. 4.相反数:符号不同、绝对值相等的两个数,叫做互为相反数。 a的相反数是-a,0的相反数是0。 5.有效数字:一个近似数,从左边笫一个不是0的数字起,到最末 一个数字止,所有的数字,都叫做这个近似数的有效数字. 如:0.05972精确到0.001得0.060,结果有两个有效数字6,0. 6.科学记数法:把一个数写成a×10n的形式(其中1≤a<10,n是整 数),这种记数法叫做科学记数法. 如:407000=4.07× 105,0.000043=4.3×10-5. 7.大小比较:正数大于0,负数小于0,两个负数,绝对值大的 反而小。
8.数的乘方:求相同因数的积的运算叫乘方,乘方运算的结果 叫幂。 9.平方根:一般地,如果一个数x的平方等于a,即x2=a那么这 个数a就叫做x的平方根(也叫做二次方根式)。一个正数有两个平方根,它们互为相反数;0只有一个平方根,它是0本身; 负数没有平方根. 10.开平方:求一个数a的平方根的运算,叫做开平方. 11.算术平方根:一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x就叫做a的算术平方根,0的算术平方根是0.12.立方根:一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根(也叫做三次方根),正数的立方根是正数;负数的立方根是负数;0的立方根是0. 13.开立方:求一个数a的立方根的运算叫做开立方. 14.平方根易错点:(1)平方根与算术平方根不分,如 64的平方根为士8,易丢掉-8,而求为64的算术平方根;(2)4的平方根是士2,误认为4平方根为士 2,知道4=2. 15.二次根式: (1)定义:形如a(a≥0)的式子叫做二次根式. 16.二次根式的化简: 17.最简二次根式应满足的条件:(1)被开方数的因式是整式或整数;(2)被开方数中不含有能开得尽的因数或因式. 18.同类二次根式:几个二次根式化成最简二次根式以后,如果被
高等数学一常用公式表
常用公式表(一) 1。乘法公式 ()()22212a b a ab b +=++ ()()2 2222a b a ab b -=-+ ()()()223a b a b a b -=+- ()()()33224a b a b a ab b +=+-+ ()()()33225a b a b a ab b -=-++ 2、指数公式: ()()0 110a a =≠ ()12p p a a -= ()3m n a = ()4m n m n a a a += ()5m m n m n n a a a a a -÷= = ()() 6n m m n a a = ()() 7n n n ab a b = ()8n n n a a b b ?? = ??? ()2 9a = (10a = () 1 111a a -= (1 2 12a = 3、指数与对数关系: (1)若N a b =,则 N b a log = (2)若N b =10 ,则N b lg = (3)若N e b =,则N b ln = 4、对数公式: (1) b a b a =log , ln b e b = (2)log 10,ln 10a == (3)N a aN =log ,ln N e N = ()ln 4log ln a N N a = (5)a b b e a ln = (6)N M MN ln ln ln += ()7ln ln ln M M N N =- (8) M n M n ln ln = ()1 9ln ln M n = 5、三角恒等式: (1)22sin cos 1α α+= (2)2 2 1tan sec αα += (3)221cot csc αα+= () sin 4tan cos αα α = () cos 5cot sin αα α = ()1 6cot tan α α = ()17csc sin α α = ()18sec cos αα = 6.倍角公式: (1)α ααcos sin 22sin = ()2 2tan 2tan 21tan αα α = - (3)α αααα2 2 2 2 sin 211cos 2sin cos 2cos -=-=-= 7.半角公式(降幂公式): ()2 1cos 1sin 22 α α -= ()2 1cos 2cos 2 2 α α += ()1cos sin 3tan 2 sin 1cos α ααα α -= = +
小学数学常用公式84261知识讲解
小学数学常用公式 84261
小学数学常用公式 小学数学公式:和差倍及平均数问题 什么是和差问题?已知大小两个数的和,以及了们的差,求这两个数各是多少的应用题叫做和差问题。 什么是和倍问题?已知两个数的和及它们之间的倍数关系,求两个数各是多少的应用题叫做和倍问题。 什么是差倍问题?已知两个数的差,及两个数的倍数关系,求两个数各是多少的应用题叫做差倍问题。 什么是平均数?平均数是指在一组数据中所有数据之和再除以数据的个数。和差问题的公式 (和+差)÷2=大数 (和-差)÷2=小数 和倍问题 和÷(倍数-1)=小数 小数×倍数=大数 (或者和-小数=大数) 差倍问题 差÷(倍数+1)=大数 小数×倍数=大数 (或小数+差=大数) 平均数问题公式 总数量÷总份数=平均数。
相遇问题公式: 相遇路程=速度和×相遇时间 相遇时间=相遇路程÷速度和 速度和=相遇路程÷相遇时间 浓度问题公式: 溶质的重量+溶剂的重量=溶液的重量 溶质的重量÷溶液的重量×100%=浓度 溶液的重量×浓度=溶质的重量 溶质的重量÷浓度=溶液的重量 小学数学公式:植树问题公式 什么是植树问题?这类应用题是以“植树”为内容。凡是研究总路程、株距、段数、棵树四种数量关系的应用题,叫做植树问题。 植树问题公式: 1、非封闭线路上的植树问题主要可分为以下三种情形: ⑴如果在非封闭线路的两端都要植树,那么: 株数=段数+1= 全长÷株距+1 全长=株距×(株数-1) 株距=全长÷(株数-1) ⑵如果在非封闭线路的一端要植树,另一端不要植树,那么: 株数=段数=全长÷株距 全长=株距×株数 株距=全长÷株数
高中数学常用公式大全
高中数学常用公式大全 1. 元素与集合的关系 U x A x C A ∈??,U x C A x A ∈??. 2.德摩根公式 ();()U U U U U U C A B C A C B C A B C A C B ==I U U I . 3.集合12{,,,}n a a a L 的子集个数共有2n 个;真子集有2n –1个;非空子集有2n –1个;非空的真子集有2n –2个. 4.二次函数的解析式的三种形式 (1)一般式2 ()(0)f x ax bx c a =++≠; (2)顶点式2 ()()(0)f x a x h k a =-+≠; (3)零点式12()()()(0)f x a x x x x a =--≠. 5.方程0)(=x f 在),(21k k 上有且只有一个实根,与0)()(21
高考数学备考常用公式大全
高考数学备考:常用公式大全 141. 面积射影定理 ' cos S S θ=. (平面多边形及其射影的面积分别是S 、'S ,它们所在平面所成锐二面角的为θ). 142. 斜棱柱的直截面 已知斜棱柱的侧棱长是l ,侧面积和体积分别是 S 斜棱柱侧和V 斜棱柱,它的直截面的周长和面积分别是 1c 和1S ,则 ① 1S c l =斜棱柱侧. ②1V S l =斜棱柱. 143.作截面的依据 三个平面两两相交,有三条交线,则这三条交线交于一点或互相平行. 144.棱锥的平行截面的性质 如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点到截面距离与棱锥高的平方比(对应角相等,对应边对应成比例的多边形是相似多边形,相似多边形面积的比等于对应边的比的平方);相应小棱锥与小棱锥的侧面积的比等于顶点到截面距离与棱锥高的平方比. 145.欧拉定理(欧拉公式) 2V F E +-=(简单多面体的顶点数V 、棱数E 和面数F). (1)E =各面多边形边数和的一半.特别地,若每个面的边数为n 的多边形,则面数F 与棱数E 的关系: 12E nF = ;
(2)若每个顶点引出的棱数为m ,则顶点数V 与棱数E 的关系: 12E mV =. 146.球的半径是R ,则 其体积3 43V R π=, 其表面积2 4S R π=. 147.球的组合体 (1)球与长方体的组合体: 长方体的外接球的直径是长方体的体对角线长. (2)球与正方体的组合体: 正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长. (3) 球与正四面体的组合体: 棱长为a 的正四面体的内切球的半径为, 外接球的半径为. 148.柱体、锥体的体积 13V Sh =柱体(S 是柱体的底面积、h 是柱体的高). 13V Sh =锥体(S 是锥体的底面积、h 是锥体的高). 149.分类计数原理(加法原理) 12n N m m m =+++. 150.分步计数原理(乘法原理) 12n N m m m =???.
小学数学常用公式大全
. 小学数学常用公式大全(单位换算表)长度单位换算 1千米=1000米1米=10分米 1分米=10厘米1米=100厘米 1厘米=10毫米 面积单位换算 1平方千米=100公顷 1公顷=10000平方米 1平方米=100平方分米 1平方分米=100平方厘米 1平方厘米=100平方毫米 体(容)积单位换算 1立方米=1000立方分米 1立方分米=1000立方厘米 1立方分米=1升
. 1立方厘米=1毫升 1立方米=1000升 重量单位换算 1吨=1000千克 1千克=1000克 1千克=1公斤 人民币单位换算 1元=10角 1角=10分 1元=100分 时间单位换算 1世纪=100年1年=12月 大月(31天)有:1\3\5\7\8\10\12月 小月(30天)的有:4\6\9\11月 平年2月28天,闰年2月29天
平年全年365天,闰年全年366天 1日=24小时1时=60分 1分=60秒1时=3600秒 * 1世纪=100年;* 1年=365天平年;* 一年=366天闰年* 一、三、五、七、八、十、十二是大月大月有31 天 * 四、六、九、十一是小月小月小月有30天 * 平年2月有28天闰年2月有29天 * 1天= 24小时* 1小时=60分* 一分=60秒 小学数学常用公式大全(几何体计算公式) 小学数学几何形体周长面积体积计算公式 1、长方形的周长=(长+宽)×2C=(a+b)×2 2、正方形的周长=边长×4C=4a 3、长方形的面积=长×宽S=ab 4、正方形的面积=边长×边长S=a.a=a 5、三角形的面积=底×高÷2S=ah÷2
6、平行四边形的面积=底×高S=ah 7、梯形的面积=(上底+下底)×高÷2S=(a+b)h÷2 8、直径=半径×2d=2r半径=直径÷2r=d÷2 9、圆的周长=圆周率×直径=圆周率×半径×2c=πd=2πr 10、圆的面积=圆周率×半径×半径 小学数学常用公式大全(数量关系计算公式) 1、单价×数量=总价 2、单产量×数量=总产量 3、速度×时间=路程 4、工效×时间=工作总量 5、加数+加数=和一个加数=和+另一个加数 被减数-减数=差减数=被减数-差被减数=减数+差 因数×因数=积一个因数=积÷另一个因数 被除数÷除数=商除数=被除数÷商被除数=商×除数 有余数的除法:被除数=商×除数+余数 一个数连续用两个数除,可以先把后两个数相乘,再用它们的积去除这个数,结果不变。例:90÷5÷6=90÷(5×6) 6、1公里=1千米1千米=1000米
小学数学所有公式大全-人教版
人教版小学数学公式大全 一、小学数学几何形体周长面积体积计算公式 长方形的周长=(长+宽)×2 C=(a+b)×2 长方形的面积=长×宽S=ab 正方形的周长=边长×4 C=4a 正方形的面积=边长×边长S= a×a 三角形的面积=底×高÷2.S= a×h÷2 平行四边形的面积=底×高S= a×h 梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷2 直径=半径×2 d=2r半径=直径÷2 r= d÷2 圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr 圆的面积=圆周率×半径×半径 内角和:三角形的内角和=180度. 长方体的体积=长×宽×高公式:V=abh 长方体(或正方体)的体积=底面积×高公式:V=abh 正方体的体积=棱长×棱长×棱长公式:V=aaa 圆的周长=直径×π公式:L=πd=2πr 圆的面积=半径×半径×π公式:S=πr2 圆柱的表(侧)面积:圆柱的表(侧)面积等于底面的周长乘高.公式:S=ch=πdh=2πrh
圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积.公式:S=ch+2s=ch+2πr2 圆柱的体积:圆柱的体积等于底面积乘高.公式:V=Sh 圆锥的体积=底面×积高.公式: 分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减. 分数的乘法则:用分子的积做分子,用分母的积做分母. 分数的除法则:除以一个数等于乘以这个数的倒数. 二、单位换算 (1)1公里=1千米1千米=1000米1米=10分米1分米=10厘米1厘米=10毫米 (2)1平方米=100平方分米1平方分米=100平方厘米1平方厘米=100平方毫米 (3)1立方米=1000立方分米1立方分米=1000立方厘米1立方厘米=1000立方毫米 (4)1吨=1000千克1千克= 1000克= 1公斤= 2市斤(5)1公顷=10000平方米1亩=666.666平方米 (6)1升=1立方分米=1000毫升1毫升=1立方厘米 (7)1元=10角1角=10分1元=100分 (8)1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月 平年2月28天,闰年2月29天平年全年365天,闰年全年366天1日=24小时1时=60分
