(完整版)常微分方程组(边值)

常微分方程组边值问题解法
打靶法Shooting Method (shooting.m ) %打靶法求常微分方程的边值问题
function [x,a,b,n]=shooting(fun,x0,xn,eps) if nargin<3 eps=1e-3; end
x1=x0+rand;
[a,b]=ode45(fun,[0,10],[0,x0]'); c0=b(length(b),1);
[a,b]=ode45(fun,[0,10],[0,x1]'); c1=b(length(b),1);
x2=x1-(c1-xn)*(x1-x0)/(c1-c0); n=1;
while (norm(c1-xn)>=eps & norm(x2-x1)>=eps) x0=x1;x1=x2;
[a,b]=ode45(fun,[0,10],[0,x0]'); c0=b(length(b),1);
[a,b]=ode45(fun,[0,10],[0,x1]'); c1=b(length(b),1)
x2=x1-(c1-xn)*(x1-x0)/(c1-c0); n=n+1; end x=x2;
应用打靶法求解下列边值问题:
()()???
????==-
=010004822y y y dx
y d 解:将其转化为常微分方程组的初值问题
()?????
?
?????==-==t dx dy
y y y dx
dy y dx dy x 0011221
048
命令:
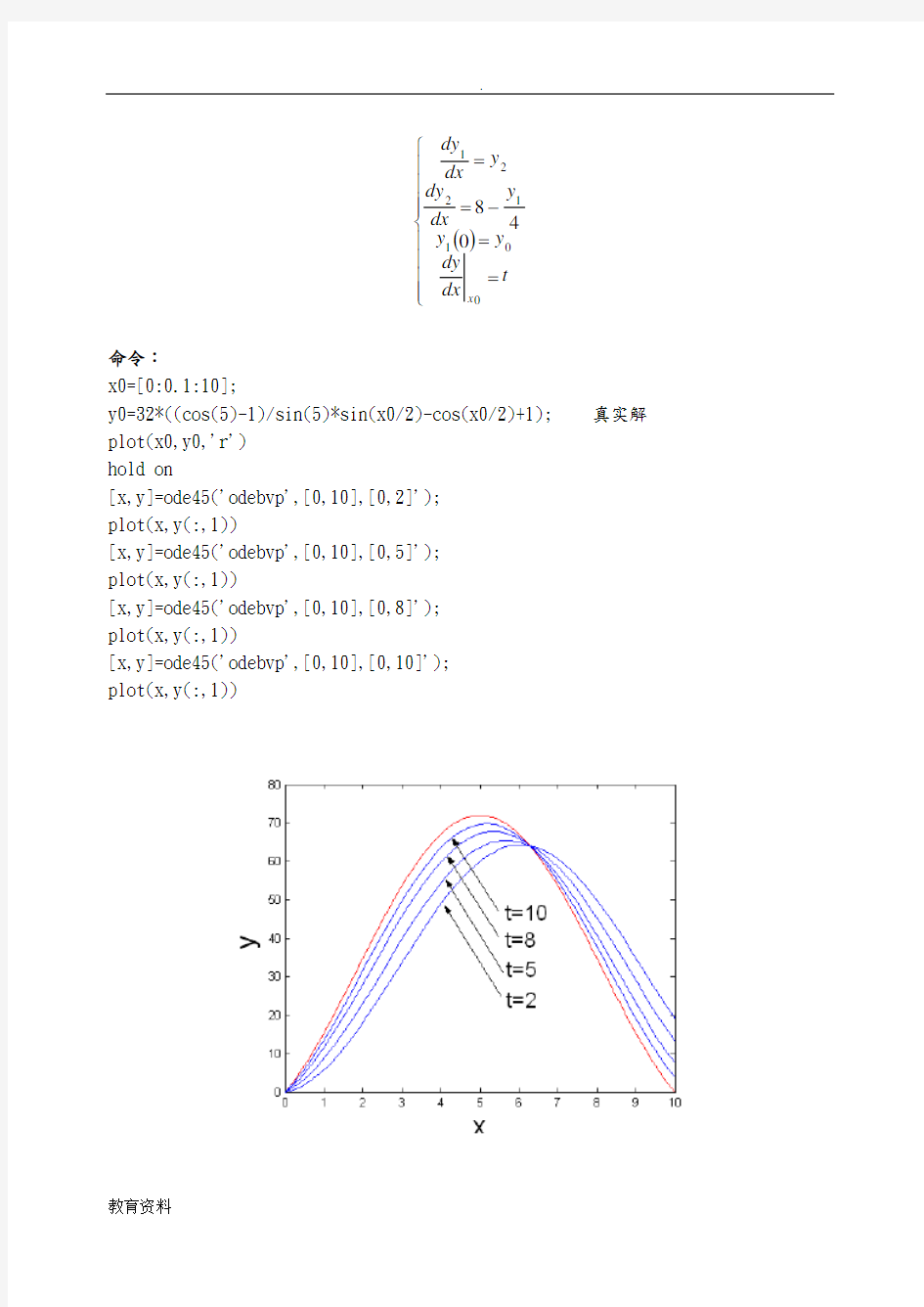
x0=[0:0.1:10];
y0=32*((cos(5)-1)/sin(5)*sin(x0/2)-cos(x0/2)+1); 真实解 plot(x0,y0,'r') hold on
[x,y]=ode45('odebvp',[0,10],[0,2]'); plot(x,y(:,1))
[x,y]=ode45('odebvp',[0,10],[0,5]'); plot(x,y(:,1))
[x,y]=ode45('odebvp',[0,10],[0,8]'); plot(x,y(:,1))
[x,y]=ode45('odebvp',[0,10],[0,10]'); plot(x,y(:,1))
函数:(odebvp.m)
%边值常微分方程(组)函数
function f=odebvp(x,y)
f(1)=y(2);
f(2)=8-y(1)/4;
f=[f(1);f(2)];
命令:
[t,x,y,n]=shooting('odebvp',10,0,1e-3)
计算结果:(eps=0.001)
t=11.9524
plot(x,y(:,1))
x0=[0:1:10];
y0=32*((cos(5)-1)/sin(5)*sin(x0/2)-cos(x0/2)+1); hold on
plot(x0,y0,’o’)
有限差分法Finite Difference Methods FDM (difference.m ) 同上例:
4822y dx y d -=?4822
11i i i i y h y y y -=+--+ 2121
842h y y h y i i i =+???
?
??--+- 若划分为10个区间,则:
????????????--=???????????????????????????
????????????
????? ??--???? ??--???
?
??--???? ??----08880842114211421142222212212
2
22h h h h y y y y h h h h n n M M O O O
函数:(difference.m )
%有限差分法求常微分方程的边值问题
function [x,y]=difference(x0,xn,y0,yn,n) h=(xn-x0)/n;
a=eye(n-1)*(-(2-h^2/4)); for i=1:n-2 a(i,i+1)=1; a(i+1,i)=1; end
b=ones(n-1,1)*8*h^2; b(1)=b(1)-0; b(n-1)=b(n-1)-0; yy=a\b;
x(1)=x0;y(1)=y0; for i=2:n
x(i)=x0+(i-1)*h;
y(i)=yy(i-1);
end
x(n)=xn;y(n)=yn;
命令:
[x,y]=difference(0,10,0,0,100);
计算结果:
x0=[0:0.1:10];
y0=32*((cos(5)-1)/sin(5)*sin(x0/2)-cos(x0/2)+1); 真实解plot(x0,y0,'r')
hold on
[x,y]=difference(0,10,0,0,5);
plot(x,y,’.’)
[x,y]=difference(0,10,0,0,10);
plot(x,y,’--’)
[x,y]=difference(0,10,0,0,50);
plot(x,y,’-.’)
正交配置法Orthogonal Collocatioin Methods CM
构造正交矩阵函数(collmatrix.m)
%正交配置矩阵(均用矩阵法求对称性与非对称性正交配置矩阵)
function [am,bm,wm,an,bn,wn]=collmatrix(a,m,fm,n,fn)
x0=symm(a,m,fm); %a为形状因子;m为零点数;fm为对称的权函数(0为权函数1,非0为权函数1-x^2)
for i=1:m
xm(i)=x0(m+1-i);
end
xm(m+1)=1;
for j=1:m+1
for i=1:m+1
qm(j,i)=xm(j)^(2*i-2);
cm(j,i)=(2*i-2)*xm(j)^(2*i-3);
dm(j,i)=(2*i-2)*(2*i-3+(a-1))*xm(j)^(2*i-3+(a-1)-1-(a-1));
end
fmm(j)=1/(2*j-2+a);
end
am=cm*inv(qm);
bm=dm*inv(qm);
wm=fmm*inv(qm);
x1=unsymm(n,fn); %n为零点数;fn为非对称的权函数(0为权函数1,非0为权函数1-x) xn(1)=0;
for i=2:n+1
xn(i)=x1(n+2-i);
end
xn(n+2)=1;
for j=1:n+2
for i=1:n+2
qn(j,i)=xn(j)^(i-1);
if j==0 | i==1
cn(j,i)=0;
else
cn(j,i)=(i-1)*xn(j)^(i-2);
end
if j==0 | i==1 | i==2
dn(j,i)=0;
else
dn(j,i)=(i-2)*(i-1)*xn(j)^(i-3);
end
end
fnn(j)=1/j;
end
an=cn*inv(qn);
bn=dn*inv(qn);
wn=fnn*inv(qn);
%正交多项式求根(适用于对称问题)
function p=symm(a,m,fm) %a为形状因子,m为配置点数,fm为权函数for i=1:m
c1=1;
c2=1;
c3=1;
c4=1;
for j=0:i-1
c1=c1*(-m+j);
if fm==0
c2=c2*(m+a/2+j);%权函数为1
else
c2=c2*(m+a/2+j+1);%权函数为1-x^2
end
c3=c3*(a/2+j);
c4=c4*(1+j);
end
p(m+1-i)=c1*c2/c4/c3;
end
p(m+1)=1;%为多项式系数向量,求出根后对对称问题还应开方才是零点p=sqrt(roots(p));
%正交多项式求根(适用于非对称性问题)
function p=unsymm(n,fn) if fn==0
r(1)=(-1)^n*n*(n+1);%权函数为1 else
r(1)=(-1)^n*n*(n+2);%权函数为1-x end
for i=1:n-1 if fn==0
r(i+1)=(n-i)*(i+n+1)*r(i)/(i+1)/(i+1);%权函数为1 else
r(i+1)=(n-i)*(i+n+2)*r(i)/(i+1)/(i+1);%权函数为1-x end end
for j=1:n
p(n+1-j)=(-1)^(j+1)*r(j); end
p(n+1)=(-1)^(n+1); p=roots(p);
应用正交配置法求解以下等温球形催化剂颗粒内反应物浓度分布,其浓度分布的数学模型为:
???
?
?
???
?=====??? ??S
C C r dr dC r R C dr dC r dr d r
,10,03612
22 解:
(1)标准化
令R r x /=,S C C y /=代入微分方程及边界条件得:
???
?
?
???
?=====???
??1,10,036122y x dx dy x y
dx dy x dx d x
(2)离散化
0361
1
=-∑+=j N i i ji
y y B
1,2,1+=N j Λ
(3)转化为代数方程组(以3=N 为例)
???
???????=????????????????????----000036363636
432144434241
343332312423222114131211y y y y B B B B B B B B B B B B B B B B 因为141==+y y N ,所以整理上式得:
?
??
??
?????+----=????????????
??????---3636363644342414321434241333231232221131211B B B B y y y B B B B B B B B B B B B 本例中的代数方程组为线性方程组,可采用线性方程组的求解方法;若为非线性方程组则
采用相应的方法求解。
命令:N=3,权函数为1-x
2
[am,bm,wm,an,bn,wn]=collmatrix(3,3,1,3,1);(只用对称性配置矩阵) b1=bm; for i=1:4
b1(i,i)=bm(i,i)-36; end
a0=b1(1:4,1:3); b0=-b1(1:4,4); y=a0\b0; y(4)=1;
p=exam31(3,3);(注意要对文件修改权函数为1-x 2
) x=[0.3631,0.6772,0.8998,1]; %零点 plot(x,y,'o') hold on
x0=0:0.1:1; %真实解 y0=sinh(6*x0)./x0/sinh(6); plot(x0,y0,'r')
若权函数改为1,则以下语句修改,其他不变
[am,bm,wm,an,bn,wn]=collmatrix(3,3,0,3,1);(只用对称性配置矩阵)
p=exam31(3,3);(注意要对文件修改权函数为1)x=[0.4058,0.7415,0.9491,1]; %零点
计算结果:
权函数为1- x2
权函数为1
y 正交配置法真实解
边值问题的MatLab 解法
()()???==<<=''21,10104e y y x y y ? ()()???
??==='='2111221
1,104e
y y y y y y 精确解:
x e y 2=
函数:(collfun1.m )
function f=collfun1(x,y) f(1)=y(2); f(2)=4*y(1); f=[f(1);f(2)]; (collbc1.m )
function f=collbc1(a,b) f=[a(1)-1;b(1)-exp(2)];
命令:
solinit=bvpinit([0:0.1:1],[1,1])
sol=bvp4c(@collfun1,@collbc1,solinit) plot(sol.x,sol.y) hold on
plot(sol.x,exp(2*sol.x),'*') 真实解
()()
()()??
?='='<<-=-'++''-e y y x e x y y x y x /11,20101212 ? ()
()()()??
?
??
='='+-+-='='-e y y y x y e x y y y x /11,2012111
212221 精确解:
()x e x y --=1
函数:(collfun2.m )
function f=collfun2(x,y) f(1)=y(2);
f(2)=(1-x.^2).*exp(-x)+2*y(1)-(x+1).*y(2); f=[f(1);f(2)]; (collbc2.m )
function f=collbc2(a,b) f=[a(2)-2;b(2)-exp(-1)];
命令:
solinit=bvpinit([0:0.1:1],[1,1]);
sol=bvp4c(@collfun2,@collbc2,solinit); plot(sol.x,sol.y) hold on
plot(sol.x,(sol.x-1).*exp(-sol.x),'*') 真实解
()()()()?????='='-<<-=-'+''2/32,011221ln 212y y y x x x
x y y y ? ()()()()???????
==--+-='='2
/32,0112ln 212212
21221y y y y x y x x y y y 精确解:
x x y ln +=
函数:(collfun3.m )
function f=collfun3(x,y) f(1)=y(2);
f(2)=(2-log(x))./x+y(1)./x-y(2).^2; f=[f(1);f(2)]; (collbc3.m )
function f=collbc3(a,b) f=[2*a(1)-a(2);b(2)-1.5];
命令:
solinit=bvpinit([1:0.1:2],[1,1]);
sol=bvp4c(@collfun3,@collbc3,solinit); plot(sol.x,sol.y) hold on
plot(sol.x,sol.x+log(sol.x),'*') 真实解
在260C ?的基础面上,为促进传热在此表面上增加纯铝的圆柱形肋片,其直径为25mm ,高为150mm ;该柱表面受到16C ?气流的冷却,气流与肋片表面的对流传热系数为15K m W ?2/,肋端绝热;
肋片的导热系数为236K m W ?/,假设肋片的导热热阻与肋片表面的对流传热热阻相比可以忽略;试求肋片中的温度分布,及单个肋片的散热量为多
少?
解:根据以上条件可知:导热热阻与对流热阻相比可以忽略,则在肋片径向上没有温度分布,在轴向上存在温度分布,外界气流与肋片的对流传热则可转化为内热源;故该问题为导热系数为常数的一维稳定热传导,其导热微分方程为:
()C A t t hp dx
t d λλ∞-=Φ=&2
2 边界条件为:0=x 时,C 2600?=t (肋根);H x =时,
0==H
x dx
dt
(肋端绝热)。
分析解:()
()[]()
mH ch H x m ch t t t t --+=∞∞0,C A hp m λ=;传热量:0
=-=x C
dx dt
A Q λ
这是两点边值的常微分方程求解问题,故可转化为如下形式:
()()()??
??
??
?≤≤==-='='∞H
x H y y A y y hp y y y C 0,0,260021221
λ
260?
函数:(leipianfun.m leipianbc.m)
%圆柱形肋片(常微分方程组)
function f=leipianfun(x,y)
f(1)=y(2);
f(2)=15*pi*0.025/236/pi/0.025^2*4*(y(1)-16);
f=[f(1);f(2)];
%圆柱形肋片(边界条件)
function f=leipianbc(a,b)
f=[a(1)-260;b(2)];
命令:
solinit=bvpinit([0:0.01:0.150],[1,1]);
sol=bvp4c(@leipianfun,@leipianbc,solinit); %sol.y中每行对应sol.x节点的因变量值即:第一行为y1,第二行为y2值,依此类推;故第一行为函数值,第二行对应的一阶导数。
plot(sol.x,sol.y(1,:))
%以下为分析解
m=sqrt(15*pi*0.025/236/(pi/4*0.025^2))
c1=(exp(m*(sol.x-0.15))+exp(-m*(sol.x-0.15)))/2;
c2=(exp(m*(0.15))+exp(-m*(0.15)))/2;
t=16+(260-16)*c1/c2;
hold on
plot(sol.x,t,'*')
%计算传热量
q=-236*pi*0.025^2/4*sol.y(2,1);
计算结果:
q=40.1052W
在直径为20mm 的圆管外安装环形肋片,其表面温度为260C ?,肋片导热系数为45K W/m ?,置于16C ?、对流传热系数为150K W/m 2?的气流中;试根据单个环肋的传热量大小确定适宜的肋片高度和肋片厚度;并给出肋高为0.01m ,肋厚为0.0003m 环肋的温度分布。
解:近似为:导热系数为常数的一维稳定热传导,其导热微分方程为:
()()λδ
λλ∞∞-=-=
Φ
=??? ??t t h A t t hp dr dt r dr d r C 21& 边界条件为:1r r =时,C 2600?=t (肋根);H r r r +==12时,
02
==r r dr
dt
(肋端绝热)。
这是两点边值的常微分方程求解问题,故可转化为如下形式:
()()()??
??
??
?
≤≤==--='='∞2
122112221,0,2602r x r r y r y x y y y h y y y λδ
函数:(huanleifun.m huanleibc.m ) %环形肋片(常微分方程组)
function f=huanleifun(x,y,h,nada,delta,t0,tf) f(1)=y(2);
f(2)=2*h/nada/delta*(y(1)-tf)-y(2)./x;
f=[f(1);f(2)];
%环形肋片(边界条件)
function f=huanleibc(a,b,h,nada,delta,t0,tf)
f=[a(1)-t0;b(2)];
命令:(hq.m)
%环肋不同肋高对散热量的影响
function [q,sol]=hq
h=150;
nada=45;
delta=0.0003;
t0=260;
tf=16;
r=0.01;
H=[0.001,0.002,0.003,0.004,0.005,0.006,0.007,0.008,0.009,0.01,0.012,0.014,0.0 16,0.018,0.02,0.03];
x=r+H;
for i=1:length(x)
solinit=bvpinit([r:0.001:x(i)],[1,1]);
sol=bvp4c(@huanleifun,@huanleibc,solinit,[],h,nada,delta,t0,tf);
q(i)=-nada*2*pi*r*delta*sol.y(2,1);
end
H=[0.001,0.002,0.003,0.004,0.005,0.006,0.007,0.008,0.009,0.01,0.012,0.014,0.0 16,0.018,0.02,0.03];
[q,sol]=hq;
plot(H,q)
计算结果:(肋厚为0.3mm)
由图可知,适宜的肋高可取0.005~0.015m。
命令:(dq.m)
%环肋不同肋厚对散热量的影响
function [q,sol]=dq
h=150;
nada=45;
delta=[0.0001,0.0002,0.0003,0.0004,0.0005,0.0006,0.0008,0.0009,0.001,0.0015,0 .002,0.0025,0.003,0.0035,0.004,0.005];
t0=260;
tf=16;
r=0.01;
x=r+0.01;
for i=1:length(delta)
solinit=bvpinit([r:0.001:x],[1,1]);
sol=bvp4c(@huanleifun,@huanleibc,solinit,[],h,nada,delta(i),t0,tf);
q(i)=-nada*2*pi*r*delta(i)*sol.y(2,1);
end
delta=[0.0001,0.0002,0.0003,0.0004,0.0005,0.0006,0.0008,0.0009,0.001,0.0015,0 .002,0.0025,0.
003,0.0035,0.004,0.005];
[q,sol]=dq;
plot(delta,q)
计算结果:(肋高为10mm)
由图可知,适宜的肋厚可取0.0005~0.002m,而在同一基础面上肋厚越大,则肋片数目越少,虽然肋厚增加散热量增大,但肋片数目减少导致的散热量减少幅度更大,所以适宜的肋厚综合考虑应取0.0005左右。
命令:(肋高为10mm,肋厚为0.3mm)
solinit=bvpinit([0.01:0.001:0.02],[1,1]);
sol=bvp4c(@huanleifun,@huanleibc,solinit,[],150,45,0.0003,260,16); plot(sol.x-0.01,sol.y(1,:))
计算片状催化剂中等温一级不可逆反应的有效因子(等温内部效率因子)。已知数学模型为:
)(2
2
2c f dx
c d φ=,10< 00 ==x dx dc ,()11=c 其中c 为浓度;x 为催化剂的厚度;φ为Thiele 模数,6=φ;()c c f =;对片状催化剂,等温效率因子为: ()()()()()?=??=??=1 0101 0101 01dx c f dx c dx c f dx c f dx c f S η 解:本题为二阶ODE-BVP 方程,转化为一阶ODEs : ()???='='12 2 21 y f y y y φ B.C. ()002=y ,()111=y 目录 引言 (1) 1预备知识 (2) 定义1.1(奇异Sturm-Liouville边值问题的正解) (2) 引理1.1.1 (2) 定义1.2(凸集的概念) (3) 定义1.3锥的定义 (3) 定义1.4(全连续算子的概念) (3) 1.5 (常微分边值问题的定义) (4) 定义1.6混合单调算子得定义) (4) 2 常微分方程边值问题正解得存在性 (5) 2.1 奇异Sturm-Liouville常微分边值问题的正解存在在 (5) 子 (8) 2.2 一类二阶边值问题的存在性 (9) 3一类混合单调算子应用 (11) 3.1一类混合单调算子的存在唯一性?........................ 错误!未定义书签。 3.2 求常微分边值问题的例题 (13) 结束语 (15) 参考文献 (15) 致 (16) 常微分方程边值问题与不动点定 (数学与统计学院 11级数学与应用数学2班)指导教师:攀峰 引言 从历史上看在有了微积分这个概念以后,紧接着出现了常微分方程。发展初期是属于“求通解”得时代,当人们从初期的热潮中结束要从维尔证明了卡帝方程中是一定不会存在一般性的初等解的时候开始的,并且柯西紧接着又提出了初值问题,常微分方程开始从重视“求通解”转向重视“求定解”的历史时代。 大学我们都学习了常微分方程这门学科,如果要研究它的定解问题,我们首先就会知道是常微分方程的初值问题。然而,在科学技术、生产实际问题中,我们还是提出了另一类定解问题-边值问题。对于常微分方程边值问题,伟大的科学家最早在解决二阶线性微分方程时,提出了分离变量法。[]1.在牛顿时期,科学家们已经提出过常微分的边值问题,牛顿也对常微分边值问题进行过研究,并且在1666年10月牛顿已经在这个领域取得了很大的成就,但是由于种种原因当时并没有整理成论文,所以没有及时出版。但在1687年他终于把在常微分方程上研究的成果发表了,虽然不是在数学著作中,却是他的一本力学著作中(《自然哲学的数学原理》)。 在微积分刚创立时期,雅克.伯努利来自瑞士的科学家提出了远著文明的问题-悬链线问题,紧着的地二年著名数学家莱布尼兹就给出了正确的解答,通过对绳子上个点受力分析,建立了以下方程 这个方程满足的定解条件是y(a)=α;y(b)=β.这是一个典型的常微分方程的边值问题。从这开始,常微分边值问题已经是科学家研究微分方程是不可或缺的工具,我就简单列举几个例子:(比如种族的生态系统;梁的非线性震动)等。对于怎么研究它, 微分方程公式运用表 一、 一阶微分方程 判断特征: (,)dy f x y dx = 类型一:()()dy g x h y dx =(可分离变量的方程) 解法(分离变量法): ()()dy g x dx h y =,然后两边同时积分。 类型二:()()dy P x y Q x dx +=(一阶线性方程) 解法(常数变易法):()()(())P x dx P x dx y e C Q x e dx -??=+? 类型三: (,)(,)dy f x y f tx ty dx ==(一阶齐次性方程) 解法(换元法):y u x =?令类型一 类型四:P()y=Q(x)y n dy x dx +(伯努利方程) 解法(同除法):1()()n n dy y P x y Q x dx --+=?类型二 二、 可降阶的高阶微分方程 类型一:()()n y f x = 解法(多次积分法):(1)()()n du u y f x f x dx -=? =?令多次积分求 类型二:''(,')y f x y = 解法:'(,)dp p y f x p dx =?=?令一阶微分方程 类型三:''(,')y f y y = 解法:'(,)dp dp dy dp p y p f y p dx dy dx dy =?==??令类型二 三、线性微分方程 类型一:''()'()0y P x y Q x y ++=(二阶线性齐次微分方程) 解法:找出方程的两个任意线性不相关特解:12(),()y x y x 则:1122()()()y x c y x c y x =+ 类型二:''()'()()y P x y Q x y f x ++=(二阶线性非齐次微分方程) 解法:先找出对应的齐次微分方程的通解:31122()()()y x c y x c y x =+ 再找出非齐次方程的任意特解()p y x ,则:1122()()()()p y x y x c y x c y x =++ 类型三:'''0y py q ++=(二阶线性常系数齐次微分方程) 解法(特征方程法):2 1,20p q λλλ++=?= (一)122121240x x p q y c e c e λλλλ?=->?≠?=+ (二)12120()x y c c x e λλλλ?=?==?=+ (三)12120,(cos sin )x i i y e c x c x αλαβλαβββ? 《常微分方程》课程教学大纲 课程代码: 090131009 课程英文名称:Ordinary Differential Equations 课程总学时:48 讲课:48 实验:0 上机:0 适用专业:信息与计算科学 大纲编写(修订)时间:2017.11 一、大纲使用说明 (一)课程的地位及教学目标 本课程是信息与计算科学专业的一门专业基础课,通过本课程的学习,可以使学生获得关于常微分方程的基本理论知识,掌握普通的线性微分方程的求解办法,为对非线性微分方程的求解打下一定的基础,同时,使学生能够简单地利用数学手段去研究自然现象和社会现象,或解决工程技术问题, 是进一步学习偏微分方程、微分几何、泛函分析等后继课程的基础。 通过本课程的学习,学生将达到以下要求: 1. 掌握一阶线性微分方程的初等解法及理论、高阶线性微分方程的解法及理论,线性微分方程组理论,着重培养学生解决问题的基本技能。 2. 熟悉和掌握本课程所涉及的现代数学中的重要思想方法,提高其抽象思维、逻辑推理和代数运算的能力。 (二)知识、能力及技能方面的基本要求 1.基本知识:要求学生掌握一阶微分方程的初等解法;一阶微分方程解的存在唯一性定理、解对初值的连续性和可微性定理及解的延拓;高阶微分方程理论、常系数线性微分方程的解法、以及高阶微分方程的降阶和幂级数解法;求矩阵指数,求解常系数线性微分方程组;非线性微分方程的稳定性、V函数方法。 2.基本理论和方法:掌握一阶和高阶线性微分方程以及方程组的求解方法,理解解的存在唯一性定理及解的延拓、解对初值的连续依赖定理等理论,并能应用到具体的证明题中。了解非线性微分方程的基本理论,会对稳定性等做出讨论。培养学生逻辑推理能力和抽象思维能力;对微分方程的建模、求解的分析能力;利用微分方程理论解决实际问题的能力。 3.基本技能:使学生获得求解一阶和高阶微分方程、线性微分方程组的运算技能。 (三)实施说明 1.教学方法:课堂讲授中要重点对基本概念、基本方法和解题思路的讲解;采用启发式教学,培养学生思考问题、分析问题和解决问题的能力;引导和鼓励学生通过实践和自学获取知识,培养学生的自学能力;讲课要联系实际并注重培养学生的创新能力。 2.教学手段:本课程属于专业基础课,在教学中采用多媒体教学系统等先进教学手段,以确保在有限的学时内,全面、高质量地完成课程教学任务。 (四)对先修课的要求 本课程的教学必须在完成先修课程之后进行。本课程主要的先修课程有数学分析3、高等代数2。 (五)对习题课、实践环节的要求 1. 至少两章安排一次习题课,总学时在6学时左右。 2. 习题课的教学内容要配合主讲课程的教学进度,由老师和同学在课堂上通过讲、练结合的方式进行。主讲教师通过批改学生的作业,将作业情况反馈给学生,要补充有一定难度和综合度的练习题,以拓宽同学们的思路。 利用MATLAB求解常微分方程数值解 目录 1. 内容简介 (1) 2. Euler Method(欧拉法)求解 (1) 2.1. 显式Euler法和隐式Euler法 (2) 2.2. 梯形公式和改进Euler法 (3) 2.3. Euler法实用性 (4) 3. Runge-Kutta Method(龙格库塔法)求解 (5) 3.1. Runge-Kutta基本原理 (5) 3.2. MATLAB中使用Runge-Kutta法的函数 (7) 4. 使用MATLAB求解常微分方程 (7) 4.1. 使用ode45函数求解非刚性常微分方程 (8) 4.2. 刚性常微分方程 (9) 5. 总结 (9) 参考文献 (11) 附录 (12) 1. 显式Euler法数值求解 (12) 2. 改进Euler法数值求解 (12) 3. 四阶四级Runge-Kutta法数值求解 (13) 4.使用ode45求解 (14) 1.内容简介 把《高等工程数学》看了一遍,增加对数学内容的了解,对其中数值解法比较感兴趣,这大概是因为在其它各方面的学习和研究中经常会遇到数值解法的问题。理解模型然后列出微分方程,却对着方程无从下手,无法得出精确结果实在是让人难受的一件事情。 实际问题中更多遇到的是利用数值法求解偏微分方程问题,但考虑到先从常微分方程下手更为简单有效率,所以本文只研究常微分方程的数值解法。把一个工程实际问题弄出精确结果远比弄清楚各种细枝末节更有意思,因此文章中不追求非常严格地证明,而是偏向如何利用工具实际求解出常微分方程的数值解,力求将课程上所学的知识真正地运用到实际方程的求解中去,在以后遇到微分方程的时候能够熟练运用MATLAB得到能够在工程上运用的结果。 文中求解过程中用到MATLAB进行数值求解,主要目的是弄清楚各个函数本质上是如何对常微分方程进行求解的,对各种方法进行MATLAB编程求解,并将求得的数值解与精确解对比,其中源程序在附录中。最后考察MATLAB中各个函数的适用范围,当遇到实际工程问题时能够正确地得到问题的数值解。 2.Euler Method(欧拉法)求解 Euler法求解常微分方程主要包括3种形式,即显式Euler法、隐式Euler法、梯形公式法,本节内容分别介绍这3种方法的具体内容,并在最后对3种方法精度进行对比,讨论Euler法的实用性。 本节考虑实际初值问题 使用解析法,对方程两边同乘以得到下式 第8章 常微分方程边值问题的数值解法 引 言 第7章介绍了求解常微分方程初值问题的常用的数值方法;本章将介绍常微分方程的边值问题的数值方法。 只含边界条件(boundary-value condition)作为定解条件的常微分方程求解问题称为常微分方程的边值问题(boundary-value problem). 为简明起见,我们以二阶边值问题为 则边值问题(8.1.1)有唯一解。 推论 若线性边值问题 ()()()()()(),, (),()y x p x y x q x y x f x a x b y a y b αβ'''=++≤≤?? ==? (8.1.2) 满足 (1) (),()p x q x 和()f x 在[,]a b 上连续; (2) 在[,]a b 上, ()0q x >, 则边值问题(8.1.1)有唯一解。 求边值问题的近似解,有三类基本方法: (1) 差分法(difference method),也就是用差商代替微分方程及边界条件中的导数,最终化为代数方程求解; (2) 有限元法(finite element method); (3) 把边值问题转化为初值问题,然后用求初值问题的方法求解。 差分法 8.2.1 一类特殊类型二阶线性常微分方程的边值问题的差分法 设二阶线性常微分方程的边值问题为 (8.2.1)(8.2.2) ()()()(),,(),(), y x q x y x f x a x b y a y b αβ''-=< 常微分方程教学设计 第一讲基本概念定义1如果在一个(或者一组m(有限个))方程中,未知的(unknown)量是一个(或一组m有限个))函数,并且在方程中含有未知函数只关于某一个自变量(independentvariable)的导数或微分,则称这方程为常微分方程(ordinarydifferentialequation)(或者常微分方程组(ODE’s)),简称常微分方程(组)为微分方程(DE)(组(DE’s))或方程(组).(提示)常微分方程之例:若x是自变量t的未知函数,其他的量都是已知的,则下列方程(一阶线性齐次方程)(正规形式),(一阶线性非齐次方程)(正规形式),(二阶线性齐次方程),(二阶线性非齐次方程),(Riccati 方程)(一阶非线性方程)都是常微分方程,微分方程中可以不出现未知函数x本身,但必须实质上含有未知函数x的导数.注意,在本教程中不讨论延迟(retarded)常微分方程:常微分方程组之例:记vector),是自变量t的函数,用个变量为m维列矢量(column,其中,,简记的已知函数,(以后都这样表示,不要误解为矢量x的是常微分方程组.函数),则矢量(vector)方程n阶微分方程可以通过变换组:定义2微分方程中实质上含有的未知函数x的最高阶导数的阶数称为这微分方程关于x的阶.微分方程组中各个未知函数的最高阶导数的阶数之和称为微分方程组的阶(计算阶数时把未知函数本身认为是未知函数的零阶导数).(提示)方程组的 阶:例中的方程组是n阶方程组.注意:但是如果我们把例2中的方程组看成是一个矢量x的方程,而且其中关于x的每个分量的阶都是一阶的,因此也可称它(关于x是一阶的).n 阶微分方程的一般形式为:,其中函数F在其变量的某一区域(domain)中有定义,并且一定含有未知函数x对自变量t 的n阶导数.定义3假设有在区间I上有直到n阶的连续导数的函数:以是由隐式或参数形式决定的)在区间I上满足恒等式,(可我们就说该函数是在区间I上方程的解(solution).称区间I是解的定义区间.微分方程的解根据函数的形式可分为显式(explicit)解,隐式(implicit)解和参数形式解.(提示)n阶微分方程的解可由对方程逐次进行n 次积分得到:,其中是的n次累次积分.为n个任意独立的实常数,2例:一阶方程义区间是:当时为的通解可以写成;当时为,其中c是非零实常数.定.严格而言不能写成的形式,因为后者的定义域不是一个区间.但是可以写成在不同区间上的两个通解:,和和.如果把这些解写成形式.则称为隐式解,这种隐式解也称为方程的积分.定义4微分方程的解,或隐式解在t-x平面上的几何图形是一条曲线,称为微分方程的积分曲线(integralcurve).如果在积分曲线上函数积分(integral)定义5已就最高阶导数解出的微分方程等于常数,则也称为微分方程的一个常微分方程之例:若x 是自变量t的未知函数,其他的量都是已知的,则下列方程 第四章常微分方程数值解 [课时安排]6学时 [教学课型]理论课 [教学目的和要求] 了解常微分方程初值问题数值解法的一些基本概念,如单步法和多步法,显式和隐式,方法的阶数,整体截断误差和局部截断误差的区别和关系等;掌握一阶常微分方程初值问题的一些常用的数值计算方法,例如欧拉(Euler)方法、改进的欧拉方法、龙贝-库塔(Runge-Kutta)方法、阿达姆斯(Adams)方法等,要注意各方法的特点及有关的理论分析;掌握构造常微分方程数值解的数值积分的构造方法和泰勒展开的构造方法的基本思想,并能具体应用它们导出一些常用的数值计算公式及评估截断误差;熟练掌握龙格-库塔(R-K)方法的基本思想,公式的推导,R-K公式中系数的确定,特别是能应用“标准四阶R-K公式”解题;掌握数值方法的收敛性和稳定性的概念,并能确定给定方法的绝对稳定性区域。[教学重点与难点] 重点:欧拉方法,改进的欧拉方法,龙贝-库塔方法。 难点:R—K方法,预估-校正公式。 [教学内容与过程] 4.1 引言 本章讨论常微分方程初值问题 (4.1.1) 的数值解法,这也是科学与工程计算经常遇到的问题,由于只有很特殊的方程能用解析方法求解,而用计算机求解常微分方程的初值问题都要采用数值方法.通常我们假定(4.1.1)中 f(x,y)对y满足Lipschitz条件,即存在常数L>0,使对,有 (4.1.2) 则初值问题(4.1.1)的解存在唯一. 假定(4.1.1)的精确解为,求它的数值解就是要在区间上的一组离散点 上求的近似.通常取 ,h称为步长,求(4.1.1)的数值解是按节点的顺序逐步 推进求得.首先,要对方程做离散逼近,求出数值解的公式,再研究公式的局部截 常微分方程课程教学 大纲 常微分方程课程教学大纲 英文名称:Ordinary differential equation 课程类 型: 专业基础课 理论学时:64实验学 时: 学分: 4 开课学 期: 第3学期 适用对象:数学与应用数学专业本科生考核方 式: 考试 先修课 程: 数学分析、高等代数与解析几何 一、课程简介 常微分方程是数学系本科生的必修课.通过本课程的学习,利用数学分析、高等代数的一些工具,牢固掌握微分方程学科最基本的内容,如一阶常微分方程、高阶微分方程与线性微分方程组的基本理论与解法,初步掌握其在实际问题中的应用及微分方程定性和稳定性理论的基本概念和重要结果,一般了解一阶线性偏微分方程. 二、课程教学目标 本门课程的主要任务是:通过各个教学环节逐步培养学生的抽象思维能力、逻辑推理能力、空间想象能力和自学能力,还要特别注意培养学生的熟练运算能力和综合运用所学知识去分析解决问题的能力;使学生掌握常微分方程的基本概念、基本理论和基本运算技能,为学习后继课程和进一步获得数学知识奠定必要的数学基础. 三、教学内容及要求 第一章绪论 主要内容: 1、常微分方程基本概念; 2、导出微分方程的实例; 3、微分方程的几何意义。 基本要求和教学重点: 1、了解常微分方程的基本概念; 2、领会常微分方程所讨论问题的基本内容; 3、了解常微分方程的实际背景及应用。 第二章初等积分法 主要内容: 1、变量分离方程; 2、齐次方程; 3、一阶线性方程与常数变易法; 4、全微分方程与积分因子; 5、一阶隐式微分方程。 基本要求和教学重点: 1、熟练地掌握一阶方程各种类型的初等解法. 2、学会根据所给方程的特点,引进适当的变换,增强解题能力; 3、能够合理的处理某些一阶微分方程的求解问题。 第三章一阶微分方程的解的存在定理主要内容: 1、解的存在性与唯一性定理 2、解的延拓 3、解对初值和参数的连续依赖性 4、解对初值和参数的可微性 基本要求和教学重点: 1、熟悉和理解定理证明方法; 2、掌握逐步逼近法。 第四章高阶线性微分方程 主要内容: 1、高阶线性微分方程的一般理论; 2、高阶常系数线性齐次方程的解法; 3、高阶常系数线性非齐次方程的解法; 4、变系数线性微分方程。 5、幂级数解法 基本要求和教学重点: 1、理解和掌握关于线性方程解的基本性质; 常微分方程组边值问题解法 打靶法Shooting Method (shooting.m ) %打靶法求常微分方程的边值问题 function [x,a,b,n]=shooting(fun,x0,xn,eps) if nargin<3 eps=1e-3; end x1=x0+rand; [a,b]=ode45(fun,[0,10],[0,x0]'); c0=b(length(b),1); [a,b]=ode45(fun,[0,10],[0,x1]'); c1=b(length(b),1); x2=x1-(c1-xn)*(x1-x0)/(c1-c0); n=1; while (norm(c1-xn)>=eps & norm(x2-x1)>=eps) x0=x1;x1=x2; [a,b]=ode45(fun,[0,10],[0,x0]'); c0=b(length(b),1); [a,b]=ode45(fun,[0,10],[0,x1]'); c1=b(length(b),1) x2=x1-(c1-xn)*(x1-x0)/(c1-c0); n=n+1; end x=x2; 应用打靶法求解下列边值问题: ()()??? ????==- =010004822y y y dx y d 解:将其转化为常微分方程组的初值问题 ()????? ? ?????==-==t dx dy y y y dx dy y dx dy x 0011221 048 命令: x0=[0:0.1:10]; y0=32*((cos(5)-1)/sin(5)*sin(x0/2)-cos(x0/2)+1); 真实解 plot(x0,y0,'r') hold on [x,y]=ode45('odebvp',[0,10],[0,2]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,5]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,8]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,10]'); plot(x,y(:,1)) 第九章 微分方程 一、教学目标及基本要求 (1) 了解微分方程及其解、通解、初始条件和特解的概念。 (2) 掌握变量可分离的方程和一阶线性方程的解法,会解齐次方程。 (3) 会用降阶法解下列方程:),(),,(),()(y y f y y x f y x f y n '='''=''=。 (4) 理解二阶线性微分方程解的性质以及解的结构定理。 (5) 掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程。 (6) 会求自由项多项式、指数函数、正弦函数、余弦函数,以及它们的和与二阶常系数非齐次线性微分方程的 特解和通解。 (7) 会用微分方程解决一些简单的应用问题。 二、本章教学内容的重点和难点 1、理解和熟悉微分方程的一些基本概念; 2、掌握一阶和高阶微分方程的各种初等积分法; 3、熟悉线性方程的基础理论,掌握常系数二阶线性齐次与非齐次方程的解法; 4、会列微分方程及其始值问题去解决实际问题。 三、本章教学内容的深化和拓宽: 1、分离变量法的理论根据; 2、常用的变量代换; 3、怎样列微分方程解应用题; 4、黎卡提方程; 5、全微分方程的推广; 6、二阶齐次方程; 7、高阶微分方程的补充; 8、求线性齐次方程的另一个线性无关的解; 9、求线性非齐次方程的一个特解; 10、常数变易法。 本章的思考题和习题 解下列方程(第1-6题) 1、2)0(,)1(==+'+y x y y x 2、()[]f dx x f e e x f x x x ,)(02?+=可微 3、212 22sin 22sin 1X e y x y y x ++='?+ 4、0)3(24=+-xydx dy x y 5、21)0(,1)0(,022- ='=='+''y y y x y 6、2y y y x y '-'+'= 7、已知可微函数)(x f 满足 ?-=+x x f f x f x x f dx x f 12)()1(,1)()()(和求; 8、已知)(,,1)(2 1)(10x f f x f da ax f 求可微+= ?; 9、求与曲线族C y x =+2232相交成ο45角的曲线; 10、一容器的容积为100L ,盛满盐水,含10kg 的盐,现以每分钟3L 的速度向容器内注入淡水冲淡盐水,又以同样的速度将盐水抽入原先盛满淡水的同样大小的另一容器内,多余的水便从容器内流出,问经过多少时间,两容器内的含盐量相等? 第十一章 常微分方程边值问题的数值解法 工程技术与科学实验中提出的大量问题是常微分方程边值问题.本章将研究常微分方程边值问题的数值求解方法.主要介绍三种边界条件下的定解问题和两大类求解边值问题的数值方法,打靶法算法和有限差分方法. 11.1 引言 在很多实际问题中都会遇到求解常微分方程边值问题. 考虑如下形式的二阶常微分方程 ),,(y y x f y '='', b x a <<, (11.1.1) 在如下三种边界条件下的定解问题: 第一种边界条件: α=)(a y , β=)(b y (11.1.2) 第二种边界条件: α=')(a y , β=')(b y (11.1.2) 第三种边界条件: ? ? ?=-'=-'101 0)()()()(b b y b y a a y a y βα, (11.1.13) 其中0 0, ,00000>+≥≥b a b a . 常微分方程边值问题有很多不同解法, 本书仅介绍打靶方法和有限差分方法. 11.2 打靶法 对于二阶非线性边值问题 ()()().,,βα==≤≤'=''b y a y b x a y y x f y ,,, (11.2.1) 打靶法近似于使用初值求解的情况. 我们需要利用一个如下形式问题初值解的序列: ()()v a w a w b x a w w x f w ='=≤≤'='')(,,,,,α, (11.2.2) 引进参数v 以近似原边界值问题的解.选择参数k v v =,以使: ()()β==∞ →b y v b w k k ,lim , (11.2.3) 其中),(k v x w 定义为初值问题(11.2.2)在k v v =时的解,同时()x y 定义为边值问题(11.2.1)的解. 首先定义参数0v ,沿着如下初值问题解的曲线,可以求出点),(αa 对应的初始正视图 ()()v a w a w b x a w w x f w ='=≤≤'='')(,,,,,α. (11.2.4) 如果),(0v b w 不严格收敛于β,那么我们选择1v 等值以修正近似值,直到),(0v b w 严格逼近β. 为了取得合适的参数k v ,现在假定边值问题(11.2.1)有唯一解,如果),(v x w 定义为初始问题(11.2.2)的解,那么v 可由下式确定: 0),(=-βv b w . (11.2.5) 由于这是一个非线性方程,我们可以利用Newton 法求解.首先选择初始值0v ,然后由下式生成序列 ),)(()),((111----- =k k k k v b dv dw v b w v v β,此处),(),)(( 11--=k k v b dv dw v b dv dw , (11.2.6) 同时要求求得),)(( 1-k v b dv dw ,因为),(v b w 的表达式未知,所以求解这个有一点难度;我们只能得到这么一系列的值。 ,,,),(),(),(),(1210-??k v b w v b w v b w v b w 假如我们如下改写初值问题(11.2.2),使其强调解对x 和v 的依赖性 ()()v v a w v a w b x a v x w v x w x f w ='=≤≤'=''),(,),(),,(,,,,α,(11.2.7) 保留初始记号以显式与x 的微分相关.既然要求当k v v =时),)((v b dv dw 的值,那么我们需要求出表达式(11.2.7)关于v 的偏导数.过程如下: )),(),,(,(),(v x w v x w x v f v x v w '??=?''? ),()),(),,(,()),(),,(,(v x v w v x w v x w x w f v x v x w v x w x x f ??'??+??'??= ) ,()),(),,(,(v x v w v x w v x w x w f ?'?''??+ 又因为x 跟v 相互独立,所以当b x a ≤≤上式如下; 常微分方程第三版答 案 习题1.2 1. dx dy =2xy,并满足初始条件:x=0,y=1的特解。 解: y dy =2xdx 两边积分有:ln|y|=x 2+c y=e 2 x +e c =cex 2另外y=0也是原方程的解,c=0时,y=0 原方程的通解为y= cex 2,x=0 y=1时 c=1 特解为y= e 2 x . 2. y 2dx+(x+1)dy=0 并求满足初始条件:x=0,y=1的特解。 解:y 2dx=-(x+1)dy 2y dy dy=-1 1+x dx 两边积分: - y 1 =-ln|x+1|+ln|c| y=|)1(|ln 1+x c 另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e 特解:y= | )1(|ln 1 +x c 3.dx dy =y x xy y 321++ 解:原方程为:dx dy =y y 21+3 1 x x + y y 21+dy=3 1 x x +dx 两边积分:x(1+x 2)(1+y 2)=cx 2 4. (1+x)ydx+(1-y)xdy=0 解:原方程为: y y -1dy=-x x 1 +dx 两边积分:ln|xy|+x-y=c 另外 x=0,y=0也是原方程的解。 5.(y+x )dy+(x-y)dx=0 解:原方程为: dx dy =-y x y x +- 令 x y =u 则dx dy =u+x dx du 代入有: -1 12++u u du=x 1dx ln(u 2+1)x 2=c-2arctgu 即 ln(y 2+x 2)=c-2arctg 2 x y . 6. x dx dy -y+22y x -=0 解:原方程为: dx dy =x y +x x | |-2)(1x y - 则令 x y =u dx dy =u+ x dx du 2 11u - du=sgnx x 1 dx arcsin x y =sgnx ln|x|+c 7. tgydx-ctgxdy=0 解:原方程为: tgy dy =ctgx dx 两边积分:ln|siny|=-ln|cosx|-ln|c| siny= x c cos 1=x c cos 另外y=0也是原方程的解,而c=0时,y=0. 所以原方程的通解为sinycosx=c. 8 dx dy +y e x y 32 +=0 解:原方程为:dx dy =y e y 2 e x 3 2 e x 3-3e 2 y -=c. 实验八 常微分初值问题的数值解法 8.1实验目的 ① 掌握常微分方程数值解的常用算法; ② 培养编程与上机调试能力. 8.2算法描述 8.2.1改进欧拉法 求解 '0 ()(,)()()y x f x y a x b y a y ?=≤≤?=? 对给定的(,)f x y ,用改进的欧拉公式 1111()[()()]2 n n n n n n n n n n y y hf x y h y y f x y f x y ++++=++???=++++??求解常微分方程初值问题的解. 8.2.2四阶龙格-库塔法 对上述给定的(,)f x y ,用四阶龙格-库塔法求解常微分方程初值问题 112341213243(22)6(,) 11(,)2211(,)22(,)n n n n n n n n n n h y y k k k k k f x y k f x h y hk k f x h y hk k f x h y hk +?=++++??=???=++???=++??=++?? 8.3实验题目 (1) 用改进的欧拉公式,求解常微分方程初值问题的解 20.10.4(0)1 dy y x dx y ?=?≤≤??=? (2) 用四阶龙格-库塔公式解初值问题: / 2.0 2.6,0.2(2.0)1dy x y x h dx y ?=?≤≤=??=? 8.4实验要求 (1)选择一种计算机语言设计出改进欧拉法和四阶龙格-库塔法方法求解常微分方程初值问题的程序,观察运行结果. (2)利用Matlab求解常微分方程初值问题 函数dsolve()用于求解微分方程.Dy表示:dy/dt(t 为缺省的自变量),Dny表示y对t 的n阶导数. Matlab6.1环境下操作如下: >> y=dsolve('Dy=y*y','y(0)=1') %求解题目1 >> y=dsolve('Dy=y/t','y(2.0)=1') %求解题目2 (3)利用最小二乘法拟合通过改进欧拉法求出微分方程的一系列数值解的近似函数方程.并利用Matlab的绘图功能画出函数的曲线 8.5思考 一阶微分方程初值问题有哪些数值解法?比较各种方法的优缺点并举具体例子说明之? 常微分方程组边值问题解法 打靶法Shooti ng Method (shoot in g.m ) % 丁靶法求常微分方程的边值问题 function [x,a,b ,n]=shooti ng(fu n, xO,x n, eps) if nargin<3 eps=1e-3; end x1=x0+ra nd; [a,b]=ode45(fu n, [0,10],[0,x0]'); c0=b(le ngth(b),1); [a,b]=ode45(fu n, [0,10],[0,x1]'); c1=b(le ngth(b),1); x2=x1-(c1-x n)*(x1-x0)/(c1-c0); n=1; while (no rm(c1-x n)>=eps & no rm(x2-x1)>=eps) x0=x1;x 仁x2; [a,b]=ode45(fu n,[ 0,10],[0,x0]'); cO=b(le ngth(b),1); [a,b]=ode45(fu n,[ 0,10],[0,x1]'); c1= b(le ngth(b),1) x2=x1-(c1-x n)*(x1-x0)/(c1-c0); n=n+1; end x=x2; 应用打靶法求解下列边值问题: y 10 0 解:将其转化为常微分方程组的初值问题 命令: xO=[O:O.1:1O]; y0=32*((cos(5)-1)/si n( 5)*si n(x0/2)-cos(x0/2)+1); plot(xO,yO,'r') hold on [x,y]=ode45('odebvp',[0,10],[0,2]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,5]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,8]'); plot(x,y(:,1)) [x,y]=ode45('odebvp',[0,10],[0,10]'); plot(x,y(:,1)) dy i dx y 2 dy 2 dx y i 0 y 4 y o dy dx X0 真实解 30 ' 12^4567^9 10 《常微分方程》课程大纲 一、课程简介 课程名称:常微分方程学时/学分:3/54 先修课程:数学分析,高等代数,空间解析几何,或线性代数(行列式,矩阵与线性方程组,线性空间F n,欧氏空间R n,特征值与矩阵的对角化), 高等数学(多元微积分,无穷级数)。 面向对象:本科二年级或以上学生 教学目标:围绕基本概念与基本理论、具体求解和实际应用三条主线开展教学活动,通过该课程的教学,希望学生正确理解常微分方程的基本概念,掌握基本理论和主要方法,具有一定的解题能力和处理相关应用问题的思维方式,如定性分析解的性态和定量近似求解等思想,并希望学生初步了解常微分方程的近代发展,为学习动力系统学科的近代内容和后续课程打下基础。 二、教学内容和要求 常微分方程的教学内容分为七部分,对不同的内容提出不同的教学要求。(数字表示供参考的相应的学时数,第一个数为课堂教学时数,第二个数为习题课时数) 第一章基本概念(2,0) (一)本章教学目的与要求: 要求学生正确掌握微分方程,通解,线性与非线性,积分曲线,线素场(方 向场),定解问题等基本概念。本章教学重点解释常微分方程解的几何意义。 (二)教学内容: 1.由实际问题:质点运动即距离与时间关系(牛顿第二运动定律),放射性元素衰变过程,人口总数发展趋势估计等,通过建立数学模型,导出微分方程。 2.基本概念(常微分方程,偏微分方程,阶,线性,非线性,解,定解问题,特解,通解等)。 3.一阶微分方程组的几何定义,线素场(方向场),积分曲线。 4.常微分方程所讨论的基本问题。 第二章初等积分法(4,2) (一)本章教学目的与要求: 要求学生熟练掌握分离变量法,常数变易法,初等变换法,积分因子法等初等解法。 本章教学重点对经典的几类方程介绍基本解法,勾通初等积分法与微积分学基本定理的关系。并通过习题课进行初步解题训练,提高解题技巧。 (二)教学内容: 1. 恰当方程(积分因子法); 2. 分离变量法 3. 一阶线性微分方程(常数变易法) 4. 初等变换法(齐次方程,伯努利方程,黎卡提方程) 常微分方程课程教学大纲 英文名称:Ordinary differential equation 课程类型:专业基础课 理论学时:64实验学时:0 学分: 4 开课学期:第3学期 适用对象:数学与应用数学专业本科生考核方式:考试 先修课程:数学分析、高等代数与解析几何 一、课程简介 常微分方程是数学系本科生的必修课.通过本课程的学习,利用数学分析、高等代数的一些工具,牢固掌握微分方程学科最基本的内容,如一阶常微分方程、高阶微分方程与线性微分方程组的基本理论与解法,初步掌握其在实际问题中的应用及微分方程定性和稳定性理论的基本概念和重要结果,一般了解一阶线性偏微分方程. 二、课程教学目标 本门课程的主要任务是:通过各个教学环节逐步培养学生的抽象思维能力、逻辑推理能力、空间想象能力和自学能力,还要特别注意培养学生的熟练运算能力和综合运用所学知识去分析解决问题的能力;使学生掌握常微分方程的基本概念、基本理论和基本运算技能,为学习后继课程和进一步获得数学知识奠定必要的数学基础. 三、教学内容及要求 第一章绪论 主要内容: 1、常微分方程基本概念; 2、导出微分方程的实例; 3、微分方程的几何意义。 基本要求和教学重点: 1、了解常微分方程的基本概念; 2、领会常微分方程所讨论问题的基本内容; 3、了解常微分方程的实际背景及应用。 第二章初等积分法 主要内容: 1、变量分离方程; 2、齐次方程; 3、一阶线性方程与常数变易法; 4、全微分方程与积分因子; 5、一阶隐式微分方程。 基本要求和教学重点: 1、熟练地掌握一阶方程各种类型的初等解法. 2、学会根据所给方程的特点,引进适当的变换,增强解题能力; 3、能够合理的处理某些一阶微分方程的求解问题。 第三章一阶微分方程的解的存在定理主要内容: 1、解的存在性与唯一性定理 2、解的延拓 3、解对初值和参数的连续依赖性 4、解对初值和参数的可微性 基本要求和教学重点: 1、熟悉和理解定理证明方法; 2、掌握逐步逼近法。 教学大纲 一、教学目的、任务 常微分方程历来是综合性大学数学系各专业的核心基础课程,不仅是进一步学习泛函分析、数理方程、微分几何的必要准备,本身也在工程力学、流体力学、天体力学、电路振荡分析、工业自动控制以及化学、生物、经济等领域有广泛的应用. 通过本课程学习,不仅为后行课程打下基础,而且以穿插其中的在历史上成功利用微分方程解释实际现象的著名范例来培养学生用数学理论解决实际问题的意识和初步能力. 实行中英双语教学,适时穿插工程实践背景的应用分析,培养学生的动手能力和创新意识. 二、教学内容的结构 分为六章内容讲解,具体地: 1.微分方程建模(8学时); 2.初等积分法(12学时); 3.线性系统(8学时); 4.常系数线性系统(12学时,包括若干振动问题4学时); 5.一般理论(12学时); 6.定性理论初步(12学时). 三、单元教学目标与任务 第一章绪论 1、基本内容 (1) 常微分方程模型(含Duffing机械振动、Van de Pol电磁震荡、天 文二体问题、生态种群竞争系统、物理化学系统); (2) 微分方程求解思想(解的定义、高阶方程与一阶方程组的互化, 微分方程的几何解释,包括等倾线与方向场分析等); (3) 微分方程的基本问题(通解的概念,“线性”与“非线性”微分方程). 2、基本要求 (1) 了解微分方程的背景和建模过程; (2) 理解微分方程的定解条件,尤其是初值条件; (3) 掌握高阶方程与一阶方程组的互化; (4) 理解等倾线与方向场与解的关系. 3、建议课时(8学时) (1) 常微分方程模型(2学时); (2) 微分方程求解思想(4学时); (3) 基本问题(1学时); (4) 习题课(1学时). 第二章初等积分法 1、基本内容 (1) 变量分离形式(含初等变换应用、一阶线性方程、伯努里方程、 齐次方程和线性分式方程求解); (2) 恰当方程形式(对恰当方程求通积分,以及积分因子法); (3) 隐式方程(微分法与参数法); (4) 初等积分法的一些应用(奇解与包络并引伸出解的存在唯一性问 题,Clairaut方程,高阶微分方程,平面保守系统,Riccati方程). 2、基本要求 (1) 掌握分离变量法和积分因子法; (2) 理解恰当方程的条件; (3) 掌握一阶线性方程和伯努里方程求解,掌握求解隐式微分方程微 分法与参数法; (4) 了解奇解与包络. 3、建议课时(12学时) (1) 变量分离形式及习题课(4学时); (2) 恰当方程形式及习题课(3学时); (3) 隐式方程(2学时); (4) 初等积分法的一些应用及习题课(3学时). 第三章线性方程 1、基本内容 (1) 存在性与唯一性; (2) 齐次线性方程组的通解结构(含叠加原理、Wronsky行列式及 Liouville定理);常微分方程边值问题与不动点定论文
微分方程公式运用表
常微分方程教学大纲
MATLAB求解常微分方程数值解
常微分方程边值问题的数值解法
常微分方程教学设计
常微分方程数值解
常微分方程课程教学大纲知识分享
常微分方程组(边值)
常微分方程教材
第十一章 常微分方程边值问题的数值解法汇总
常微分方程第三版答案教学文稿
常微分方程计算
常微分方程组(边值)
《常微分方程》课程大纲
常微分方程课程教学大纲
《常微分方程》教学大纲
