高一第12讲 三角函数定义及运用(教师版)

第12讲三角函数定义及运用(教师版)一.学习目标:
1.理解任意角三角函数(正弦、余弦、正切)的定义.
2.三角函数线及运用。
二.重点难点:
1.重点:三角函数的定义及应用。
2.难点:三角函数值符号的确定.三角函数线的应用。
三.知识梳理:
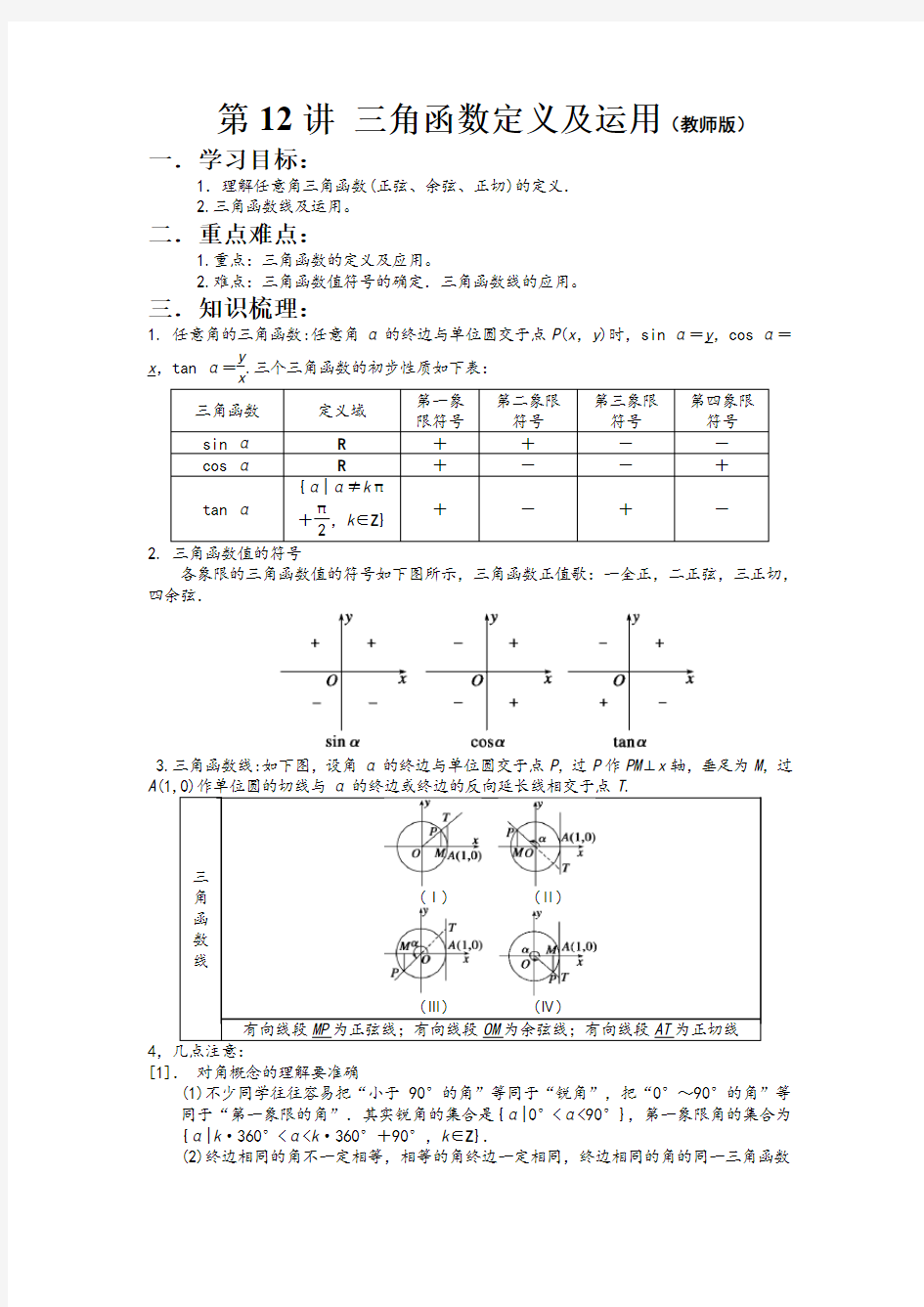
1. 任意角的三角函数:任意角α的终边与单位圆交于点P(x,y)时,sin α=y,cos α=x,tan α=
y
.三个三角函数的初步性质如下表:
各象限的三角函数值的符号如下图所示,三角函数正值歌:一全正,二正弦,三正切,四余弦.
3.三角函数线:如下图,设角α的终边与单位圆交于点P,过P作PM⊥x轴,垂足为M,过A
(Ⅰ)(Ⅱ)
(Ⅲ)(Ⅳ)
有向线段MP为正弦线;有向线段OM为余弦线;有向线段AT为正切线
4
[1].对角概念的理解要准确
(1)不少同学往往容易把“小于90°的角”等同于“锐角”,把“0°~90°的角”等
同于“第一象限的角”.其实锐角的集合是{α|0°<α<90°},第一象限角的集合为{α|k·360°<α (2)终边相同的角不一定相等,相等的角终边一定相同,终边相同的角的同一三角函数 值相等. [2]. 对三角函数的理解要透彻 三角函数也是一种函数,它可以看成是从一个角(弧度制)的集合到一个比值的集合的函数,也可以看成是以实数为自变量的函数,定义域为使比值有意义的角的范围. 如tan α=y x 有意义的条件是角α终边上任一点P (x ,y )的横坐标不等于零,也就是角 α的终边不能与y 轴重合,故正切函数的定义域为? ?? ? ?? α|α≠k π+π2 ,k ∈Z . [3] 三角函数线是三角函数的几何表示 (1)正弦线、正切线的方向同纵轴一致,向上为正,向下为负. (2)余弦线的方向同横轴一致,向右为正,向左为负. (3)当角α的终边在x 轴上时,点T 与点A 重合,此时正切线变成了一个点,当角α的终边在y 轴上时,点T 不存在,即正切线不存在. (4)在“数”的角度认识任意角的三角函数的基础上,还可以从图形角度考察任意角的三角函数,即用有向线段表示三角函数值,这是三角函数与其他基本初等函数不同的地方. 四.典例剖析: 题型一 任意角三角函数的定义 例1判断题:(1)已知sin α≥0,cos α≥0,则α是第一象限角.( ) (2)角α终边上点P 的坐标为? ?? ??-1 2,32,那么sin α=32,cos α=-12;同理角α 终边上点Q 的坐标为(x 0,y 0),那么sin α=y 0,cos α=x 0.( ) (3)若点P 在角2 3 π的终边上,且|OP |=2,则点P 的坐标为(-1,-3).( ) [答案] (1)× (2)× (3)× 解析] (1)由sin α≥0知,α终边在第一象限或第二象限,或x 轴,或y 轴的非负半轴上;由cos α≥0知,α终边在第一象限或第四象限,或y 轴,或x 轴的非负半轴上.故α终边在第一象限,或x 轴的非负半轴上,或y 轴的非负半轴上. (2)点P ? ?? ??-1 2,32在单位圆上,所以sin α=32,cos α=-12;而Q (x 0,y 0)不一定在 单位圆上,所以sin α=y 0,cos α=x 0不一定成立. (3)根据三角函数的定义,x =|OP |cos 23π=2×? ????-12=-1.y =|OP |sin 23π=2×32=3,∴P 点的坐标为(-1,3). 例2(1)已知角α的终边经过点P(m ,-3),且cosα=-4 5 ,则m 等于 A .-114 B.11 4 C .-4 D .4 [自主解答] 由题意可知,cos α=m m 2+9=-4 5,又m<0,解得m =-4. (2)角θ的终边上有一点(a ,a),a ∈R 且a≠0, 则sin θ的值是 .A.22 B .-22 C.22或-2 2 D .1 解析:由已知得r =a 2 +a 2 =2|a|, sin θ=a r = a 2|a|=????? 22a>0,-2 2a<0 所以sin θ的值是 22或-2 2 . (3)[2011年高考江西卷] 已知角θ的顶点为坐标原点,始边为x 轴的正半轴,若 P (4,y )是角θ终边上一点,且sin θ=-25 5,则y =________. 解:若角α终边上任意一点P (x ,y ),|OP |=r ,则sin α=y r ,cos α=x r ,tan α=y x . P (4,y )是角θ终边上一点,由三角函数的定义知sin θ= y 16+y 2 ,又sin θ=-25 5, ∴ y 16+y 2 =-25 5,解得y =-8. 例3(1) 已知角α的终边在直线3x +4y =0上,求sin α,cos α,tan α的值. 解:∵角α的终边在直线3x +4y =0上, ∴在角α的终边上任取一点P (4t ,-3t )(t ≠0),则x =4t ,y =-3t . r =x 2+y 2=22 (4)(3)t t +-=5|t |, 当t >0时,r =5t ,sin α=y r =-3t 5t =-35,cos α=x r =4t 5t =45,tan α=y x =-3t 4t =-3 4; 当t <0时,r =-5t ,sin α=y r =-3t -5t =35,cos α=x r =4t -5t =-45,tan α=y x =-3t 4t =-3 4 . (2)设90°≤α<180°,角α的终边上一点为P (x ,5),且cos α=2 4 x ,求sin α与tan α的值; 解析:(1)∵r =x 2 +5,∴cos α= x x 2+5,从而24x =x x 2+5 ,解得x =0或x =± 3. ∵90°≤α<180°,∴当x =-3时r =22,sin α=522 =10 4, tan α=5-3 =-15 3.当0x = 时,sin α=5 ,tan α不存在。 例4 角α终边上的点P 与A (a,2a )关于x 轴对称(a >0),角β终边上的点Q 与A 关于直线y =x 对称,求sin α·cos α+sin β·cos β+tan α·tan β的值. 解析 由题意得,点P 的坐标为(a ,-2a ),点Q 的坐标为(2a ,a ). 所以,sin α=-2a a 2+-2a 2=-25,cos α=a a 2+-2a 2=1 5 , tan α=-2a a =-2,sin β=a 2a 2+a 2=15,cos β=2a 2a 2+a 2 =2 5, tan β=a 2a =1 2,故有sin α·cos α+sin β·cos β+tan α·tan β =-25×15+15×25+(-2)×1 2=-1. 课堂小结:任意角的三角函数值与终边所在的位置有关,与点在终边上的位置无关,故要首 先判定P 点所在的象限,确定r ,最后根据定义求解. 课堂练习1:(1)点P 从(1,0)出发,沿单位圆x 2+y 2 =1逆时针方向运动2π3 弧长到达Q 点, 则Q 点的坐标为( ). A.? ????-12,32 B.? ? ???-32 ,-12 C.? ????-12,-32 D.? ? ? ??-32,12 解析 设α=∠POQ ,由三角函数定义可知,Q 点的坐标(x ,y )满足x =cos α, y =sin α,∴x =-12,y =32,∴Q 点的坐标为? ?? ??-1 2,32.答案 A (2) 已知角θ的终边上有一点P (x ,-1)(x ≠0),且tan θ=-x ,求sin θ,cos θ. 答:∵θ的终边过点(x ,-1)(x ≠0),∴tan θ=-1 x ,又tan θ=-x , ∴x 2 =1,∴x =±1.当x =1时,sin θ=-22,cos θ=22 ; 当x =-1时,sin θ=- 22,cos θ=-2 2 . (3)已知角α的顶点在原点,始边为x 轴非负半轴,终边在直线y =kx 上,若sin α=25, 且cos α<0,求实数k . 解:由sin α= 25 >0,cos α<0,知α位于第二象限,故k <0,设P (x ,kx )(x <0)是 终边上一点,则sin α= kx k 2x 2+x 2=-k 1+k 2 =2 5 ?k =-2. 题型二 三角函数符号 例5(1) 已知cos θ·tan θ<0,那么角θ是 ( ) A .第一或第二象限角 B .第二或第三象限角 C .第三或第四象限角 D .第一或第四象限角 答案 C 解析 若cos θ>0,tan θ<0,则θ在第四象限; 若cos θ<0,tan θ>0,则θ在第三象限,∴选C. (2) 已知点P (tan α,cos α)在第三象限,则角α的终边在( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 解:点P 在第三象限,tan α<0,且cos α<0;推理:由tan α<0,知α的终边在第二或第四象限,由cos α<0,知α的终边在第二或第三象限,或x 轴的非正半轴上;结论:α的终边在第二象限.选B 。 (3)sin 2cos 3tan 4的值( ). A .小于0 B .大于0 C .等于0 D .不存在 解析 ∵sin 2>0,cos 3<0,tan 4>0,∴sin 2cos 3tan 4<0.答案 A (4)若α是第三象限角,则下列各式中不成立的是 ( ) A .sin α+cos α<0 B .tan α-sin α<0 C .cos α-tan α<0 D .tan αsin α<0 答案 B 解析 在第三象限,sin α<0,cos α<0,tan α>0,则可排除A 、C 、D , (5)若θ是第二象限角,试判断 sin(cos ) cos(sin 2) θθ的符号; ∵2k π+π 2<θ<2k π+π (k ∈Z ),∴-1 -1≤sin 2θ<0,∴sin(cos θ)<0,cos(sin 2θ)>0,sin(cos )cos(sin 2)θθ<0.∴sin(cos ) cos(sin 2) θθ 的符号是负号. 课堂练习2:(1)给出下列命题: ①第二象限角大于第一象限角; ②三角形的内角是第一象限角或第二象限角; ③不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关; ④若sin α=sin β,则α与β的终边相同; ⑤若cos θ<0,则θ是第二或第三象限的角. 其中正确命题的个数是 ( ) A .1 B .2 C .3 D .4 答案 A 解析 由于第一象限角370°不小于第二象限角100°,故①错;当三角形的内角为90° 时,其既不是第一象限角,也不是第二象限角,故②错;③正确;由于sin π6=sin 5π 6 , 但π6与5π 6 的终边不相同,故④错;当cos θ=-1,θ=π时既不是第二象限角,又不是第三象限角,故⑤错.综上可知只有③正确. (2)如果点P (sin θ·cos θ,2cos θ)位于第三象限,试判断角θ的终边所在的象限; 解:(1)因为点P 在第三象限,∴sin θ·cos θ<0且2cos θ<0, 因此必有sin θ>0,cos θ<0,故θ的终边在第二象限. 题型三 三角函数线及运用 例6 判断题:(1)α∈? ????0,π2,则tan α>α>sin α.( ) (2)α为第一象限角,则sin α+cos α>1.( ) [答案] (1)√ (2)√ [解析] (1)设角α与单位圆交于P ,则MP =sin α,AT =tan α,如图所示,PA 的长l =α.连接AP ,△POA 的面积=12OA ·MP =1 2 sin α.,扇形OAP 的面积 =12l ·OA =12α,△OAT 的面积=12OA ·AT =1 2tan α.∵S △POA 2 tan α,∴sin α<α 例7(1)若0 2 同时成立的x 的取值范围是 ( ) A .π3 B .π3 C .π6 D .π3 答:B (2)已知θ∈? ?? ??-π2,π2且sin θ+cos θ=a ,其中a ∈(0,1),则关于tan θ的值,以下四个答案中,可能正确的是 ( ) A .-3 B .3或13 C .-13 D .-3或-1 3 答:C 例8 (1)求函数y =lg(3-4sin 2 x )的定义域; (2)设θ是第二象限角,试比较sin θ2,cos θ2,tan θ 2的大小. 解 (1)∵3-4sin 2x >0,∴sin 2 x <34,∴-32 .[2分] 利用三角函数线画出x 满足条件的终边范围(如图阴影部分所示), ∴x ∈? ????k π-π3,k π+π3(k ∈Z ).[4分] (2)∵θ是第二象限角,∴π 2 +2k π<θ<π+2k π,k ∈Z , ∴π4+k π<θ2<π2+k π,k ∈Z ,∴θ 2 是第一或第三象限的角. (如图阴影部分),结合单位圆上的三角函数线可得: ①当θ2是第一象限角时,sin θ2=AB ,cos θ2=OA ,tan θ2=CT ,,cos θ2 2; ②当θ 2是第三象限角时,sin θ2=EF ,cos θ2=OE ,tan θ2=CT ,得sin θ2 2在第三象限时,sin θ 2 θ 2 2 . 课堂小结:第(1)小题的实质是解一个简单的三角不等式,可以用三角函数图象,也可以用三角函数线.用三角函数线更方便.2.第(2)小题比较大小,由于没有给出具体的角度,所以用图形可以更直观的表示.3.本题易错点:①不能确定θ 2 所在的象限;②想不到应用三角函 数线.原因在于概念理解不透,方法不够灵活. 五.品味高考(家庭作业): 1.(2011年高考题山东文)若点(a ,9)在函数y =3x 的图象上,则tan 6 απ 的值为 …( ) A .0 B C .1 D . 答案为:D 2.(2009年高考题全国文).已知△ABC 中,12 cot 5 A =- ,则cosA= ( ) A. 1213 B. 513 C. 513- D. 1213 - 答案为:D 3. (2008年高考题全国文)若sin 0α<且tan 0α> 是,则是( ) A .第一象限角 B . 第二象限角 C . 第三象限角 D . 第四象限角 答案为:C 由sinα<0得α在三,四象限.,tanα>0得α在一,三象限. 4. (2008年高考题浙江理)若cos 2sin αα+=tan α= (A )12 (B )2 (C )1 2 - (D )2- 答案为:B 解析:22 cos 2sin sin cos 1 αααα?+=??+=??2 sin (2sin )1αα?+=∴ sin 5cos αα?=-??? ?=?? ∴tanα=2. 5. (2008年高考题四川理)设0≤a <2π.若sin a α的取值范围是 (A )(,)32ππ (B )(,)3ππ (C )4(,)33ππ (D )3(,)32 ππ 答:C. 6.(2012年高考(辽宁理))已知,(0,π),则= ( ) A . 1 B . C . D .1 答:A.用答案验证法。 7.(2011年高考题重庆文)若 3cos 5α=- ,且3(,)2π απ∈,则tanα=__________. 答案为:4 3, 8.(2010年高考题全国文)已知α是第二象限的角,tanα=1 2,则cosα=________. 答案为:- 9. (2011年高考题福建文)设函数()cos f θθθ=+,其中,角θ的顶点与坐标原点重合,始边与x 轴非负半轴重合,终边经过点P(x ,y),且0≤θ≤π. (1)若点P 的坐标为1(,22,求f(θ)的值; 答案为:解:(1)由点P 的坐标和三角函数的定义可得 sin cos αα-= α∈tan α-2 - 2 sin 21cos 2θθ?=??? ?=?? ,于是1()cos 2 2f θθθ=+=+= 三角函数公式 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1 -cotAcotB + cot(A-B) =cotA cotB 1 cotAcotB -+ 倍角公式 tan2A =A tan 12tanA 2 - Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3π -a) 半角公式 sin( 2 A )=2cos 1A - cos( 2 A )=2cos 1A + tan( 2 A )=A A cos 1cos 1+- cot( 2 A )=A A cos 1cos 1-+ tan( 2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a - sina-sinb=2cos 2 b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2 b a - tana+tanb=b a b a cos cos ) sin(+ 积化和差 sinasinb = -21 [cos(a+b)-cos(a-b)] cosacosb = 21 [cos(a+b)+cos(a-b)] sinacosb = 21 [sin(a+b)+sin(a-b)] cosasinb = 21 [sin(a+b)-sin(a-b)] 诱导公式 sin(-a) = -sina cos(-a) = cosa sin(2π -a) = cosa cos(2π -a) = sina sin(2π +a) = cosa cos(2 π +a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =a a cos sin 万能公式 高中数学三角函数教案 一、教学目标 1.掌握任意角的正弦、余弦、正切函数的定义包括定义域、正负符号判断;了解任意 角的余切、正割、余割函数的定义. 2.经历从锐角三角函数定义过度到任意角三角函数定义的推广过程,体验三角函数概 念的产生、发展过程. 领悟直角坐标系的工具功能,丰富数形结合的经验. 3.培养学生通过现象看本质的唯物主义认识论观点,渗透事物相互联系、相互转化的 辩证唯物主义世界观. 4.培养学生求真务实、实事求是的科学态度. 二、重点、难点、关键 重点:任意角的正弦、余弦、正切函数的定义、定义域、正负符号判断法. 难点:把三角函数理解为以实数为自变量的函数. 关键:如何想到建立直角坐标系;六个比值的确定性α确定,比值也随之确定与依赖性比值随着α的变化而变化. 三、教学理念和方法 教学中注意用新课程理念处理传统教材,学生的数学学习活动不仅要接受、记忆、模 仿和练习,而且要自主探索、动手实践、合作交流、阅读自学,师生互动,教师发挥组织者、引导者、合作者的作用,引导学生主体参与、揭示本质、经历过程. 根据本节课内容、高一学生认知特点和我自己的教学风格,本节课采用“启发探索、 讲练结合”的方法组织教学. 四、教学过程 [执教线索: 回想再认:函数的概念、锐角三角函数定义锐角三角形边角关系——问题情境:能推广 到任意角吗?——它山之石:建立直角坐标系为何?——优化认知:用直角坐标系研究锐角三 角函数——探索发展:对任意角研究六个比值与角之间的关系:确定性、依赖性,满足函数 定义吗?——自主定义:任意角三角函数定义——登高望远:三角函数的要素分析对应法则、定义域、值域与正负符号判定——例题与练习——回顾小结——布置作业] 三角函数题型总结-教师版 111111 cos sin sin 2224 S x y = =?=ααα, …… …………7分 2221112||[cos()]sin()sin(2)223343 S x y πππ = =-+?+=-+ααα. … …………9分 依题意得 2sin 22sin(2)3π=-+αα, 整 理得 cos20 =α. ………………11分 因为 62 ππ<<α, 所以 23π <<πα, 所 以 22 π= α, 即 4 π = α. …… …………13分 2、三角形中求值 〖例〗(2013年高考北京卷(理))在△ABC 中,a =3,b 6,∠B =2∠A . (I)求cosA 的值; (II)求c 的值. 【答案】 解:(I)因为a =3,b =2 ,∠B =2∠A . 所以在△ABC 中,由正弦定理得3sin sin 2A A =.所以2sin cos sin 3A A A =.故cos 3 A =. (II)由(I)知 cos A = ,所以 sin A == .又因为 ∠B=2∠A,所以2 1cos 2cos 13 B A =-= .所以2sin 1cos B B = -= . 在△ABC 中,53sin sin()sin cos cos sin C A B A B A B =+=+=所以sin 5sin a C c A ==. 【举一反三】 (2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对)) 设ABC ?的内角 ,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=. (I)求B (II)若31 sin sin 4 A C = ,求C . 【答案】 ③三角不等式 高中数学公式:三角函数公式大全三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及本质也是学好三角函数的关键所在,下面是三角函数公式大全: 锐角三角函数公式 sin α=∠α的对边 / 斜边 cos α=∠α的邻边 / 斜边 tan α=∠α的对边 / ∠α的邻边 cot α=∠α的邻边 / ∠α的对边 倍角公式 Sin2A=2SinA?CosA Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=(2tanA)/(1-tanA^2) (注:SinA^2 是sinA的平方 sin2(A)) 三倍角公式 sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a) 三倍角公式推导 sin3a =sin(2a+a) 页 1 第 =sin2acosa+cos2asina 辅助角公式 Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中 sint=B/(A^2+B^2)^(1/2) cost=A/(A^2+B^2)^(1/2) tant=B/A Asinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B 降幂公式 cos(2α))/2=versin(2α)/2sin^2(α)=(1- cos^2(α)=(1+cos(2α))/2=covers(2α)/2 -cos(2α))/(1+cos(2α))tan^2(α)=(1 推导公式 tanα+cotα=2/sin2α 2cot2α-cotα=-tanα s2α=2cos^2α1+co 1-cos2α=2sin^2α 1+sinα=(sinα/2+cosα /2)^2=2sina(1-sin2a)+(1-2sin2a)sina =3sina-4sin3a cos3a =cos(2a+a) =cos2acosa-sin2asina 页 2 第 =(2cos2a-1)cosa-2(1-sin2a)cosa =4cos3a-3cosa 导数与三角函数压轴题归纳总结 近几年的高考数学试题中频频出现含导数与三角函数零点问题,内容主要包括函数零点个数的确定、根据函数零点个数求参数范围、隐零点问题及零点存在性赋值理论.其形式逐渐多样化、综合化. 一、零点存在定理 例1.【2019全国Ⅰ理20】函数,为的导数.证明: (1)在区间 存在唯一极大值点; (2)有且仅有2个零点. 【解析】(1)设()()g x f x '=,则()()() 2 11 cos ,sin 11g x x g x x x x '=- =-+++. 当1,2x π??∈- ???时,单调递减,而()00,02g g π?? ''>< ??? , 可得在1,2π?? - ?? ?有唯一零点,设为. 则当()1,x α∈-时,()0g x '>;当,2x πα?? ∈ ??? 时,. 所以在()1,α-单调递增,在,2πα?? ???单调递减,故在1,2π?? - ???存在唯一极大 值点,即()f x '在1,2π?? - ?? ?存在唯一极大值点. (2)()f x 的定义域为. (i )由(1)知, ()f x '在()1,0-单调递增,而()00f '=,所以当时, ,故()f x 在单调递减,又,从而是()f x 在的唯 一零点. ()sin ln(1)f x x x =-+()f x '()f x ()f x '(1,)2 π-()f x ()g'x ()g'x α()0g'x <()g x ()g x (1,)-+∞(1,0)x ∈-()0f 'x <(1,0)-(0)=0f 0x =(1,0]- (ii )当0,2x π?? ∈ ??? 时,由(1)知,在单调递增,在单调递减,而 ,02f π??'< ???,所以存在,2πβα?? ∈ ???,使得,且当时, ;当,2x πβ??∈ ???时,.故在单调递增,在,2πβ?? ???单调递 减.又,1ln 1022f ππ???? =-+> ? ???? ?,所以当时,. 从而()f x 在0,2π?? ??? 没有零点. (iii )当,2x ππ??∈ ???时,()0f x '<,所以()f x 在,2ππ?? ???单调递减.而 ()0,02f f ππ??>< ??? ,所以()f x 在,2ππ?? ??? 有唯一零点. (iv )当时,()l n 11x +>,所以<0,从而()f x 在没有零点. 综上, ()f x 有且仅有2个零点. 【变式训练1】【2020·天津南开中学月考】已知函数3()sin (),2 f x ax x a R =-∈且 在,0,2π?? ????上的最大值为32π-, (1)求函数f (x )的解析式; (2)判断函数f (x )在(0,π)内的零点个数,并加以证明 【解析】(1)由已知得()(sin cos )f x a x x x =+对于任意的x∈(0, 2 π), 有sin cos 0x x x +>,当a=0时,f(x)=? 3 2 ,不合题意; 当a<0时,x∈(0, 2π),f′(x)<0,从而f(x)在(0, 2 π )单调递减, 又函数3 ()sin 2f x ax x =- (a∈R)在[0, 2 π]上图象是连续不断的, 故函数在[0, 2 π ]上的最大值为f(0),不合题意; ()f 'x (0,)α,2απ?? ???(0)=0f '()0f 'β=(0,)x β∈()0f 'x >()0f 'x <()f x (0,)β(0)=0f 0,2x ?π?∈ ???()0f x >(,)x ∈π+∞()f x (,)π+∞ 三角函数公式 1.正弦定理: A a sin = B b sin =C c sin = 2R (R 为三角形外接圆半径) 2.余弦定理:a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cos bc a c b A 2cos 2 22-+= 3.S ⊿= 21a a h ?=21ab C sin =21bc A sin =21ac B sin =R abc 4=2R 2A sin B sin C sin =A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=C B A c sin 2sin sin 2=pr=))()((c p b p a p p --- (其中)(2 1 c b a p ++=, r 为三角形内切圆半径) 4.诱导公试 注:奇变偶不变,符号看象限。 注:三角函数值等于α的同名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名不变,符号看象限 注:三角函数值等于α的 异名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即: 函数名改变,符号看象限 5.和差角公式 ①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =± ③β αβ αβαtg tg tg tg tg ?±= ± 1)( ④)1)((βαβαβαtg tg tg tg tg ?±=± 6.二倍角公式:(含万能公式) ①θ θ θθθ2 12cos sin 22sin tg tg += = ②θ θ θθθθθ2 22 2 2 2 11sin 211cos 2sin cos 2cos tg tg +-=-=-=-= ③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2 θθ+= 7.半角公式:(符号的选择由 2 θ 所在的象限确定) ①2cos 12 sin θθ -± = ②2 cos 12sin 2θ θ-= ③2cos 12cos θθ+±= ④2cos 12 cos 2 θθ += ⑤2sin 2cos 12θθ=- ⑥2 cos 2cos 12θθ=+ ⑦2 sin 2 cos )2 sin 2 (cos sin 12θ θθθθ±=±=± ⑧θ θ θθθθθ sin cos 1cos 1sin cos 1cos 12 -=+=+-± =tg 8.积化和差公式: [])sin()sin(21cos sin βαβαβα-++=[] )sin()sin(21 sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++= ()[]βαβαβα--+-=cos )cos(2 1 sin sin 9.和差化积公式: 高一数学三角函数教案 高一数学《三角函数》教案如下: 已知三角函数值求角反正弦,反余弦函数 目的:要求学生初步了解理解反正弦、反余弦函数的意义,会由已知角的正弦值、余弦值求出范围内的角,并能用反正弦,反余弦的符号表示角或角的集合。 过程: 一、简单理解反正弦,反余弦函数的意义。 由 1在R上无反函数。 2在上, x与y是一一对应的,且区间比较简单 在上,的反函数称作反正弦函数, 记作,奇函数。 同理,由 在上,的反函数称作反余弦函数, 记作 二、已知三角函数求角 首先应弄清:已知角求三角函数值是单值的。 已知三角函数值求角是多值的。 例一、1、已知,求x 解:在上正弦函数是单调递增的,且符合条件的角只有一个 ∴ 即 2、已知 解:,是第一或第二象限角。 即。 3、已知 解: x是第三或第四象限角。 即或 这里用到是奇函数。 例二、1、已知,求 解:在上余弦函数是单调递减的, 且符合条件的角只有一个 2、已知,且,求x的值。 解:, x是第二或第三象限角。 3、已知,求x的值。 解:由上题:。 介绍:∵ ∴上题 例三、见课本P74-P75略。 三、小结:求角的多值性 法则:1、先决定角的象限。 2、如果函数值是正值,则先求出对应的锐角x; 如果函数值是负值,则先求出与其绝对值对应的锐角x, 3、由诱导公式,求出符合条件的其它象限的角。 四、作业:P76-77 练习 3 习题4.11 1,2,3,4中有关部分。 高一数学《三角函数的周期性》教案如下: 一、学习目标与自我评估 1 掌握利用单位圆的几何方法作函数的图象 2 结合的图象及函数周期性的定义了解三角函数的周期性,及最小正周期 3 会用代数方法求等函数的周期 角的概念、定义 一、知识清单 1. 终边相同的角 ①与α(0°≤α<360°)终边相同的角的集合(角α与角β的终边重合): {} Z k k ∈+?=,360 |αββο ; ②终边在x 轴上的角的集合:{}Z k k ∈?=,180|οββ; ③终边在y 轴上的角的集合:{}Z k k ∈+?=,90180|οοββ; ④终边在坐标轴上的角的集合:{}Z k k ∈?=,90|οββ. 2. 角度与弧度的互换关系:360°=2π 180°=π 1°=0.01745 1=57.30°=57°18′ 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零, 熟记特殊角的弧度制. 3.弧度制下的公式 扇形弧长公式r =l α,扇形面积公式211 ||22 S R R α==l ,其中α为弧所对圆心 角的弧度数。 4.三角函数定义: 利用直角坐标系,可以把直角三角形中的三角函数推广到任意角的三角数.在α终边上任取一点(,)P x y (与原点不重合),记22||r OP x y ==+, 则sin y r α=,cos x r α=,tan y x α=,cot x y α=。 注: ⑴三角函数值只与角α的终边的位置有关,由角α的大小唯一确定,∴三角函数是以角为自变量,以比值为函数值的函数. ⑵根据三角函数定义可以推出一些三角公式: ①诱导公式:即 2 k π αα±→或902k αα±→o 之间函数值关系()k Z ∈,其规律是“奇变偶不变,符号看象限” ;如sin(270)α-=o cos α- ②同角三角函数关系式:平方关系,倒数关系,商数关系. ⑶重视用定义解题. 高中三角函数公式大全[图] 1 三角函数的定义1.1 三角形中的定义 图1 在直角三角形中定义三角函数的示意图在直角三角形ABC,如下定义六个三角函数: ?正弦函数 ?余弦函数 ?正切函数 ?余切函数 ?正割函数 ?余割函数 1.2 直角坐标系中的定义 图2 在直角坐标系中定义三角函数示意图在直角坐标系中,如下定义六个三角函数: ?正弦函数 ?余弦函数 r ?正切函数 ?余切函数 ?正割函数 ?余割函数 2 转化关系2.1 倒数关系 2.2 平方关系 2 和角公式 3.1 倍角公式 3.3 万能公式 4 积化和差、和差化积 4.1 积化和差公式 证明过程 首先,sin(α+β)=sinαcosβ+sinβcosα(已证。证明过程见《和角公式与差角公式的证明》)因为sin(α+β)=sinαcosβ+sinβcosα(正弦和角公式) 则 sin(α-β) =sin[α+(-β)] =sinαcos(-β)+sin(-β)cosα =sinαcosβ-sinβcosα 于是 sin(α-β)=sinαcosβ-sinβcosα(正弦差角公式) 将正弦的和角、差角公式相加,得到 sin(α+β)+sin(α-β)=2sinαcosβ 则 sinαcosβ=sin(α+β)/2+sin(α-β)/2(“积化和差公式”之一) 同样地,运用诱导公式cosα=sin(π/2-α),有 cos(α+β)= sin[π/2-(α+β)] =sin(π/2-α-β) =sin[(π/2-α)+(-β)] =sin(π/2-α)cos(-β)+sin(-β)cos(π/2-α) =cosαcosβ-sinαsinβ 于是 高一数学三角函数公式大全 sinα=∠α的对边/斜边 cosα=∠α的邻边/斜边 tanα=∠α的对边/∠α的邻边 cotα=∠α的邻边/∠α的对边 倍角公式 Sin2A=2SinA?CosA Cos2A=CosA2-SinA2=1-2SinA2=2CosA2-1 tan2A=(2tanA)/(1-tanA2) (注:SinA2是sinA的平方sin2(A)) 三倍角公式 sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a=tana·tan(π/3+a)·tan(π/3-a) 三倍角公式推导 sin3a=sin(2a+a)=sin2acosa+cos2asina 三角函数辅助角公式 Asinα+Bcosα=(A2+B2)’(1/2)sin(α+t),其中sint=B/(A2+B2)’(1/2) cost=A/(A2+B2)’(1/2) tant=B/A Asinα+Bcosα=(A2+B2)’(1/2)cos(α-t),tant=A/B 降幂公式 sin2(α)=(1-cos(2α))/2=versin(2α)/2 cos2(α)=(1+cos(2α))/2=covers(2α)/2 tan2(α)=(1-cos(2α))/(1+cos(2α)) 三角函数推导公式 tanα+cotα=2/sin2α tanα-cotα=-2cot2α 1+cos2α=2cos2α 1-cos2α=2sin2α 1+sinα=(sinα/2+cosα/2)2=2sina(1-sin2a)+(1- 2sin2a)sina=3sina-4sin3a cos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosa sin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2- sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°- a)/2]cos[(60°-a)/2]=4s inasin(60°+a)sin(60°-a) cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a- (√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{- 2sin[(a+30°)/2]sin[(a-30°)/2]}=-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=- 4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a) 上述两式相比可得 tan3a=tanatan(60°-a)tan(60°+a) 高中数学必修4知识点总结 第一章 三角函数(初等函数二) ?? ?? ?正角:按逆时针方向旋转形成的角1、任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角 2、角α的顶点与原点重合,角的始边与x 轴的非负半轴重合,终边落在第几象限,则称α为第几象限角. 第一象限角的集合为{} 36036090,k k k αα?<, 则sin y r α= ,cos x r α= ,()tan 0y x x α= ≠. 10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正. 11、三角函数线:sin α=M P ,cos α=O M ,tan α=AT . 12、同角三角函数的基本关系:()2 2 1sin cos 1αα+= 第一讲 任意角与三角函数诱导公式 1. 知识要点 角的概念的推广: 平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。 象限角的概念: 在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。 终边相同的角的表示: α终边与θ终边相同(α的终边在θ终边所在射线上)?2()k k αθπ=+∈Z 。 注意:相等的角的终边一定相同,终边相同的角不一定相等. α终边在x 轴上的角可表示为:,k k Z απ=∈; α终边在y 轴上的角可表示为:,2 k k Z π απ=+∈; α终边在坐标轴上的角可表示为:,2 k k Z π α= ∈. 角度与弧度的互换关系:360°=2π 180°=π 1°= 1=°=57°18′ 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零. α与2 α的终边关系: 任意角的三角函数的定义: 设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点), 它与原点的距离是0r =>,那么sin ,cos y x r r αα==, ()tan ,0y x x α= ≠,cot x y α=(0)y ≠,sec r x α=()0x ≠,()csc 0r y y α=≠。 三角函数值只与角的大小有关,而与终边上点P 的位置无关。 三角函数线的特征:正弦线MP“站在x 轴上(起点在x 轴上)”、余弦线OM“躺在x 轴上(起点是原点)”、正切线AT“站在点(1,0)A 处(起点是A )” 同角三角函数的基本关系式: 1. 平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= 2. 倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1, 3. 商数关系:sin cos tan ,cot cos sin αα αααα = = 注意:1.角α的任意性。 2.同角才可使用。 3.熟悉公式的变 形形式。 三角函数诱导公式:“ (2 k πα+)”记忆口诀: “奇变偶不变,符号看象限” 典型例题 例1.求下列三角函数值: (1)cos210o; (2)sin 4 5π 例2.求下列各式的值: (1)sin(-3 4π ); (2)cos(-60o)-sin(-210o) 例3.化简 ) 180sin()180cos() 1080cos()1440sin(?--?-?-?-?+?αααα 常用的诱导公式有以下几组: 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα (k∈Z) cos(2kπ+α)=cosα (k∈Z) tan(2kπ+α)=tanα (k∈Z) cot(2kπ+α)=cotα (k∈Z) 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα公式六: π/2±α及3π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα sin(3π/2+α)=-cosα cos(3π/2+α)=sinα tan(3π/2+α)=-cotα cot(3π/2+α)=-tanα sin(3π/2-α)=-cosα cos(3π/2-α)=-sinα tan(3π/2-α)=cotα cot(3π/2-α)=tanα (以上k∈Z) 注意:在做题时,将a看成锐角来做会比较好做。 诱导公式记忆口诀 规律总结 上面这些诱导公式可以概括为: 对于π/2*k ±α(k∈Z)的三角函数值, ①当k是偶数时,得到α的同名函数值,即函数名不改变; ②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan. (奇变偶不变) 然后在前面加上把α看成锐角时原函数值的符号。(符号看象限) 例如: sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。 当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。 所以sin(2π-α)=-sinα 上述的记忆口诀是: 奇变偶不变,符号看象限。 公式右边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α 所在象限的原三角函数值的符号可记忆 水平诱导名不变;符号看象限。 各种三角函数在四个象限的符号如何判断,也可以记住口诀“一全正;二正弦(余割);三两切;四余弦(正割)”. 这十二字口诀的意思就是说: 第一象限内任何一个角的四种三角函数值都是“+”; 第二象限内只有正弦是“+”,其余全部是“-”; 第三象限内切函数是“+”,弦函数是“-”; 第四象限内只有余弦是“+”,其余全部是“-”. 1 .1 图 7.3图7 .2图7三角函数及其有关概念 [知识清单] 一、角的概念 1. 角 角是以一点为公共端点的两条射线组成的图形.公共端点叫做角的顶点, 两条射线叫做 角的边。 2.正角、负角、零角 正角与负角是由旋转的方向决定的,我们把按逆时针方向旋转所形成的角 叫做正角,把按顺时针方向旋转所形成的角叫做负角形成一个数值为0的角,我们把这个角叫做零角。 3.终边相同的角 具有相同的终边的角叫做终边相同的角,如图7.1中的边相同的角。 ①终边相同的角不一定相等,但相等的角,终边一定相同; ②终边相同的角有无数多个,它们相差360°的整数倍,如: α与360()k k Z α+∈ ,β与360()k k Z β+∈ ,β与360()k k α+∈ Z 都是终边相同的角。 例 设176π α=- ,则与α终边相同的最小正角是多少? 解 1717777236066666 πππππα=-=--+=-?+ 所以,与176 πα=-终边相同的最小正角是76π 。 例 设203π α=,则与α终边相同的绝对值最小的负角是多少? 解 2020444 436033333 πππππα==+-=?- 所以,所求之角是43 π-。 4. 象限角 在第几象限,我们就说这个角是第几象限的角,如αβ与个象限,我们称其为界限角。 例 900- 是第几象限的角? 解 9002360-=-? , 所以900- 是第二象限的角。 例:-572。是( )象限的角。 5、角的度量 1). 角度制 当射线绕端点逆时针方向旋转使终边与始边第一次重 合时所形成的角叫做周角,规定1周角为360o。1周角的1 360 为1度, 2). 弧度制 等于半径长的圆弧所对的圆心角称为1弧度的角。用弧 度作单位来测量角的制度叫做弧度制。1弧度也记为1rad 定义式 ) ct 函数关系 倒数关系:;; 商数关系:;. 平方关系:;;.诱导公式 公式一:设为任意角,终边相同的角的同一三角函数的值相等: 公式二:设为任意角,与的三角函数值之间的关系: 公式三:任意角与的三角函数值之间的关系: 公式四:与的三角函数值之间的关系: 公式五:与的三角函数值之间的关系: 公式六:及与的三角函数值之间的关系: 记背诀窍:奇变偶不变,符号看象限.即形如(2k+1)90°±α,则函数名称变为余名函数,正弦变余弦,余弦变正弦,正切变余切,余切变正切。形如2k×90°±α,则函数名称不变。 诱导公式口诀“奇变偶不变,符号看象限”意义: k×π/2±a(k∈z)的三角函数值.(1)当k为偶数时,等于α的同名三角函数值,前面加上一个把α看作 锐角时原三角函数值的符号; (2)当k为奇数时,等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号。 记忆方法一:奇变偶不变,符号看象限: 记忆方法二:无论α是多大的角,都将α看成锐角. 以诱导公式二为例: 若将α看成锐角(终边在第一象限),则π十α是第三象限的角(终边在第三象限),正弦函数的函数值在第三象限是负值,余弦函数的函数值在第三象限是负值,正切函数的函数值在第三象限是正值.这样,就得到了诱导公式二. 以诱导公式四为例: 若将α看成锐角(终边在第一象限),则π-α是第二象限的角(终边在第二象限),正弦函数的三角函数值在第二象限是正值,余弦函数的三角函数值在第二象限是负值,正切函数的三角函数值在第二象限是负值.这样,就得到了诱导公式四. 诱导公式的应用: 运用诱导公式转化三角函数的一般步骤: 特别提醒:三角函数化简与求值时需要的知识储备:①熟记特殊角的三角函数值;②注意诱导公式的灵活运用;③三角函数化简的要求是项数要最少,次数要最低,函数名最少,分母能最简,易求值最好。 高中数学三角函数公式整理下面是高中数学三角函数公式大全: 1.两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA) 2.倍角公式 tan2A = 2tanA/(1-tan^2 A) Sin2A=2SinA?CosA Cos2A = Cos^2 A--Sin^2 A =2Cos^2 A—1 =1—2sin^2 A 3.三倍角公式 sin3A = 3sinA-4(sinA)^3; cos3A = 4(cosA)^3 -3cosA tan3a = tan a ? tan(π/3+a)? tan(π/3-a) 4.半角公式 sin(A/2) = √{(1--cosA)/2} cos(A/2) = √{(1+cosA)/2} tan(A/2) = √{(1--cosA)/(1+cosA)} cot(A/2) = √{(1+cosA)/(1-cosA)} tan(A/2) = (1--cosA)/sinA=sinA/(1+cosA) 5.和差化积 sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosB 6.积化和差 sin(a)sin(b) = -1/2*[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2*[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2*[sin(a+b)+sin(a-b)] cos(a)sin(b) = 1/2*[sin(a+b)-sin(a-b)] 7.诱导公式 sin(-a) = -sin(a) cos(-a) = cos(a) sin(π/2-a) = cos(a) cos(π/2-a) = sin(a) sin(π/2+a) = cos(a) cos(π/2+a) = -sin(a) sin(π-a) = sin(a) cos(π-a) = -cos(a) sin(π+a) = -sin(a) cos(π+a) = -cos(a) tgA=tanA = sinA/cosA 8.万能公式 sin(a) = [2tan(a/2)] / {1+[tan(a/2)]^2} cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]^2} tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2} 《521三角函数的概念(第一课时)》 教学设计 教学目标 1.了解三角函数的背景,体会三角函数与现实世界的密切联系: 2.经历三角函数概念的抽象过程,借助单位圆理解任意角三角函数(正弦、余弦、正 切)的左义,发展数学抽象素养. 教学重难点 教学重点:正弦函数、余弦函数、正切函数的立义. 教学难点:理解三角函数的对应关系,包括影响单位圆上点的坐标变化的因素分析,以及三角函数的宦义方式的理解;对符号Slna, COS◎和tana的认识. 课前准备 PPT课件 教学过程 (一)创设情境 引导语:我们知道,现实世界中存在着各种各样的“周而复始”变化现象,圆周运动是这类现象的代表.如图1, G)O上的点P以ZI为起点做逆时针方向的旋转?在把角的范圉推广到 任意角后,我们可以借助角a的大小厂 变化刻画点P的位置变化.又根据弧度制的左义 00的半径无关,因此,不失一般性,我们可以先研究单位圆上点的运动?现在的任务是: 如图1,单位圆OO上的点P以J为起点做逆时针方向旋转, 建立一个函数模型,刻画点P的位置变化情况. 问题1:根据已有的研究函数的经验,你认为我们可以按怎样的路径研究上述问题? 预设的师生活动;学生在独立思考的基础上进行交流、讨论. 预设答案:明确研究背景一对应关系的特点分析一下左义一研究性质. 设计意图:明确研究的内容、过程和基本方法,为具体研究指明方向. (二)新知探究 引导语:下而我们利用直角坐标系来研究上述问题?如图2,以单位圆的圆心O为原点, 以射线CU为X轴的非负半轴,建立直角坐标系,点ZI的坐标为(1, 0), 点P的坐标为(X, 0.射线OA从X轴的非负半轴开始,绕点O按逆时针方向 旋转角α,终I匕位置为OR 问题2:当α=-时,点P的坐标是什么?当―壬或迹时,点P 6 2 3 的坐标又是什么?它们是唯一确泄的吗? 一般地,任意给定一个角久它的终边OP与单位圆交点P的坐标能唯一确定吗? 预设的师生活动:在学生求出O=Z时点P的坐标后追问以下问题. 6 追问:(1)求点P的坐标要用到什么知识? (2)求点P的坐标的步骤是什么?点P的坐标唯一确泄吗? (3)如何利用上述经验求O=还时点P的坐标? 3 (4)利用信息技术,任意画一个角α,观察它的终边OP与单位圆交点P的坐标,你有什么发现?你能用函数的语言刻画这种对应关系吗? 预设答案:(I)直角三角形的性质; 高三文科数学专题复习 三角函数、解三角形 专题一 三角函数的概念、同角三角函数的关系式及诱导公式 A 组 三年高考真题(2016~2014年) 1.(2015·福建,6)若sin α=- 5 13 ,且α为第四象限角,则tan α的值等于( ) A.125 B.-125 C.512 D.-512 1.解析 ∵sin α=-513,且α为第四象限角, ∴cos α=1213,∴tan α=sin αcos α=-5 12,故选D. 答案 D 2.(2014·大纲全国,2)已知角α的终边经过点(-4,3),则cos α=( ) A.45 B.35 C.-35 D.-45 2.解析 记P (-4,3),则x =-4,y =3,r =|OP |=(-4)2+32=5, 故cos α=x r =-45=-4 5,故选D. 3.(2014·新课标全国Ⅰ,2)若tan α>0,则( ) A.sin α>0 B.cos α>0 C.sin 2α>0 D.cos 2α>0 3.解析 由tan α>0,可得α的终边在第一象限或第三象限,此时sin α与cos α同号, 故sin 2α=2sin αcos α>0,故选C. 答案 C 4.(2016·新课标全国Ⅰ,14)已知θ是第四象限角,且sin ????θ+π4=35,则tan ????θ-π 4=________. 4.解析 由题意,得cos ????θ+π4=45,∴tan ????θ+π4=34.∴tan ????θ-π4=tan ????θ+π4-π 2=-1 tan ??? ?θ+π4=-43. 答案 -4 3 5.(2016·四川,11)sin 750°=________. 5.解析 ∵sin θ=sin(k ·360°+θ),(k ∈Z ), ∴sin 750°=sin(2×360°+30°)=sin 30°=12. 答案 1 2 6.(2015·四川,13)已知sin α+2cos α=0,则2sin αcos α-cos 2α的值是________. 6.解析 ∵sin α+2cos α=0, ∴sin α=-2cos α,∴tan α=-2, 又∵2sin αcos α-cos 2α= 2sin α·cos α-cos 2αsin 2α+cos 2α=2tan α-1tan 2α+1, ∴原式=2×(-2)-1 (-2)2+1 =-1. 答案 -1 B 组 两年模拟精选(2016~2015年) 1.(2016·济南一中高三期中)若点(4,a )在12 y x =图象上,则tan a 6π的值为( ) A.0 B. 3 3 C.1 D. 3 1.解析 ∵a =412=2, ∴tan a 6 π= 3. 答案 D 2.(2016·贵州4月适应性考试)若sin ????π2+α=-3 5,且α∈????π2,π,则sin ()π-2α=( ) A.2425 B.1225 C.-1225 D.-24 25 2.解析 由sin ????π2+α=-35得cos α=-35, 又α∈????π2,π, 则sin α=4 5 ,高中三角函数公式大全必背知识点
高中数学三角函数教案
三角函数题型总结-教师版
高中数学公式三角函数公式大全
高考数学导数与三角函数压轴题综合归纳总结教师版
高中数学三角函数公式大全全解
高一数学三角函数教案
三角函数概念x教师版
三角函数公式大全(很详细)
高一数学三角函数公式大全
人教版 高中数学必修4 三角函数知识点
人教版数学必修四三角函数复习讲义
最新三角函数-高中数学诱导公式大全
三角函数(课时一)教师版
最全高中数学三角函数公式
高中数学三角函数公式总结
高中数学人教A版(2019)必修第一册第五章三角函数的概念教案
高三文科数学专题复习 三角函数、解三角形 (教师版)
