三角不等式

定义域: 解sinxa )。以sinx0时在在y 轴正半轴取有向线段Op 。(a<0时在在y 轴负半轴取有向线段Op 。)②过P 点做与x 轴平行的虚线,交单位圆与12p p 、两点,
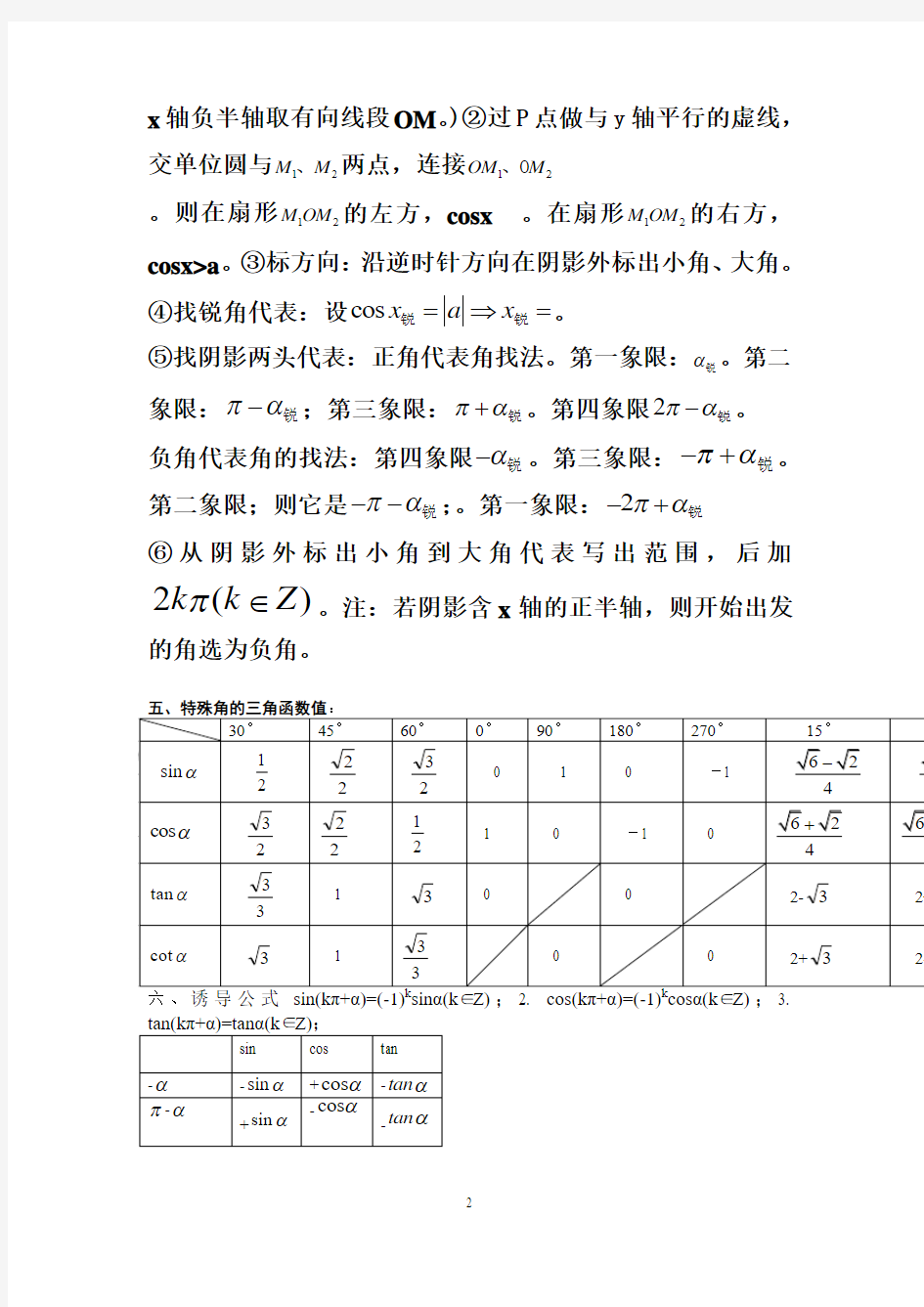
连接12op p 、o 。则在扇形12p op 的下方,sinx 形 12p op 的上方,sinx>a 。 ③标方向:沿逆时针方向在阴影外标出小角、大角。 ④找锐角代表:设sin x a x =?=锐锐。 ⑤找阴影两头代表:正角代表角找法。第一象限:α锐。第二象限:πα-锐;第三象限:π α+锐。第四象限2πα-锐。 负角代表角的找法:第四象限α-锐。第三象限:πα-+锐。第二象限;则它是πα--锐;。第一象限:2πα-+锐 ⑥从阴影外标出小角到大角代表写出范围,后加 2()k k Z π∈。注:若阴影含 x 轴的正半轴,则开始出 发的角选为负角。 y =如求函数 (∵)122120 --?? ? ? ?=-≥cos sin πx x ∴,如图:sin x ≤ 2 2 ()∴,25424 012k x k k Z y ππππ - ≤≤+∈≤≤+ 解cosxa )①在x 轴上取有向线段OM,使得OM=a.(a>0时在在x 轴正半轴取有向线段OM 。(a<0时在在 x 轴负半轴取有向线段OM 。)②过P 点做与y 轴平行的虚线,交单位圆与12M M 、两点,连接12OM M 、O 。则在扇形12M OM 的左方,cosxa 。③标方向:沿逆时针方向在阴影外标出小角、大角。④找锐角代表:设cos x a x =?=锐锐。 ⑤找阴影两头代表:正角代表角找法。第一象限:α锐。第二象限:πα-锐;第三象限:πα+锐。第四象限2πα-锐。 负角代表角的找法:第四象限α-锐。第三象限:πα-+锐。第二象限;则它是πα--锐;。第一象限:2πα-+锐 ⑥从阴影外标出小角到大角代表写出范围,后加 2()k k Z π∈。注:若阴影含x 轴的正半轴,则开始出发 的角选为负角。 六、 三角函数值等于α的同名三角函数值,前面加 上一个把α看作锐角时,原三角函数值的符号;即:函数名不变,符号看左边角的象限 三角函数值等于α的异名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名改变,正变余,余变正,符号看左边角的象限 结合公式转化为特殊角并且消除非特殊角的三角函数而得解. 若是角度一般步骤:1?用“- α”公式化为正角的三角函数;2?用“2k π + α”公式化为[0,2π]角的三角函数;3?用“π±α”或“2π - α”公式化为锐角的三角函数.口诀:负化正,大化小,化到锐角再查表。 若是弧度。则用sin ..(sin()........tan()tan sin ..(cos ..(cos()s ..(k k k k k k co k απαπαα ααπαα?+=+=?-??+=? -?是偶数) 是奇数) 是偶数) 是奇数) 一般三角函数的图像与性质. 用“五点法”作下列函数在长度为一个周期的闭区间上的简图 指导:y =sin x 的图象在[0,2π]上的五个关键点的坐标为:(0,0),????π2,1,(π,0),????3π 2,-1,(2π,0). y =cos x 的图象在[0,2π]上的五个关键点的坐标为:(0,1),????π2,0,(π,-1),? ????3π2,0,(2π,1). R R ,2x x k k ππ??≠+∈Z ???? 函数B x A y ++=)sin(?ω),(其中00>>ωA 的最大值是B A +,最小值是A B -,周 期是ω π 2= T ,频率是π ω 2= f ,相位是?ω+x ,初相是?;其图象的对称轴是直线)(2 Z k k x ∈+ =+π π?ω,凡是该图象与直线B y =的交点都是该图象的对称中心。 一、正弦型函数sin()y A x k ω?=++ 的性质:周期为2π ω min max min max ....=2K 2X ,0..()....=2K 2 ....=2K +2X ,0..()....=2K 2 y A K x R A K Z y A K x y A K x R A K Z y A K x πω?ππω?ππω?ππω?π? =-++-??∈>∈? ?=+++??? =++??∈<∈? ?=-++-??此时当若此时此时当若此时 时在在y 轴正半轴取有向线段Op 。(a<0时在在y 轴负半轴取有向线段Op 。)②过P 点做与x 轴平行的虚线,交单位圆与12p p 、两点,连接12op p 、o 。则在扇形12p op 的下方,sinxa 。 ③标方向:沿逆时针方向在阴影外标出小角、大角。 ④找锐角代表:设sin x a x =?=锐锐。 ⑤找阴影两头代表:正角代表角找法。第一象限:α锐。第二象限:πα-锐;第三象限: πα+锐。第四象限2πα-锐。 负角代表角的找法:第四象限α-锐。第三象限:πα-+锐。第二象限;则它是πα--锐;。第一象限:2πα-+锐 ⑥从阴影外标出小角到大角代表写出范围,后加2()k k Z π∈。注:若阴影含x 轴的正半轴,则开始出发的角选为负角。 y =如求函数 (∵)122120--?? ? ??=-≥cos sin πx x ∴,如图:sin x ≤ 22 ()∴,25424 012k x k k Z y ππππ - ≤≤+∈≤≤+ 解cosxa )①在x 轴上取有向线段OM,使得OM=a.(a>0时在在x 轴正半轴取有 向线段OM 。(a<0时在在x 轴负半轴取有向线段OM 。)②过P 点做与y 轴平行的虚线,交单位圆与12M M 、两点,连接12OM M 、O 。则在扇形12M OM 的左方,cosxa 。③标方向:沿逆时 针方向在阴影外标出小角、大角。④找锐角代表:设cos x a x =?=锐锐。 ⑤找阴影两头代表:正角代表角找法。第一象限:α锐。第二象限:πα-锐;第三象限: πα+锐。第四象限2πα-锐。 负角代表角的找法:第四象限α-锐。第三象限:πα-+锐。第二象限;则它是πα--锐;。第一象限:2πα-+锐 ⑥从阴影外标出小角到大角代表写出范围,后加2()k k Z π∈。注:若阴影含x 轴的正半轴,则开始出发的角选为负角。 练习:解不等式:cos 2 x <- 注:正切不等式:利用y=tanx 的在,22ππ?? - ??? 的图像。 tan 1x <例:解 tan x << 例:解 两类题型:角集与角集的交并补:利用直角坐标系。 例:求2log (tan 1)y x +的定义域。 角集与数集的交并补:利用数轴,需对k 取值。 例:求y = 练习:(1)已知函数()f x 的定义域为[0,1],求函数(cos )f x 的定义域 (2)函数tan( )4 y x π =-的定义域为___________,值域为___________ (3)求函数y =lg sin 2x +9-x 2的定义域 (4)求函数y =sin x -cos x 的定义域 8大性质:函数B x A y ++=)sin(?ω),(其中00>>ωA 的最大值是B A +,最小值是 A B -,周期是ω π 2= T ,频率是π ω 2= f ,相位是?ω+x ,初相是?;其图象的对称轴 是直线)(2 Z k k x ∈+ =+π π?ω,凡是该图象与直线B y =的交点都是该图象的对称中心。 例1:求下列函数的周期,最大值、最小值以及使函数达到最大、最小值的x : (1)y =2sin(2x + 3 π )+1;(2)y =-3sin(3x - 4 π ). 解 (1 当2x +3 π = 2 π +2k π,即当x = 12 π +k π,(k ∈z )时,函数达到最大值y max =3,; 当2x + 3 π =- 2 π +2k π,即当x =- 12π +k π,(k ∈z )时,函数达到最小值y min =-1;. (2)A =-3, ω=3,周期T =ω π2=32π;最大值y max =3,最小值y min =-3; 当3x -4π=2π+2k π,即当x =4 π+32πk ,(k ∈z )时,函数达到最大值; 当3x -4π=-2 π+2k π,即x =-12π+32πk ,(k ∈z )时,函数达到最小值. X ,=sin ---R x y θω?θθθ?+=当则令,并求出的范围,后画出的图象,从图中找出在的范围中图象的最高点和最低点的纵坐标,从而求出函数的值域。即:换元范围画图找最高、最低点 例2:y =2sin(2x + 3 π )+1,X 0,,6π?? ∈????当求值域。 二、配方法:)0(sin sin 2≠++=a c x b x a y 型。此类型可化为)0(2≠++=a c bt at y 在 区间]1,1[-上的最值问题。 []22 25153311211124828133133 261224 1682168 min max y sin x sin x ,.y t t ,t ,x k ,k z, y t x k ,k z,y ππππ=-++??∈-=--+-≤≤∴=-=-∈ ??? =-?+=-=∴=+∈=-?+=求的最值。 解:令t=sinx,则t 求函数2 23cos 4cos 1,[,]33 y x x x ππ =-+∈的最大值和最小值 2224y cos x sin x cos x =+-北京:求的最值。 三 引入参数法(换元法)含有x x x x cos sin cos sin ?±与的最值问题。解此类型最值问题通 常令x x t cos sin ±=,x x t cos sin 212 ?±=,22≤≤-t ,再进一步转化为二次函数在区间 上的最值问题。 例6 求函数y=sinx+cosx+sinxcosx 的最大值。 解 : ().c o s s i n 21c o s s i n 2 x x x x +=+令sinx+cosx=t ,则 []() t t y t t x x +-=∴-∈-=2 1 ,2,221cos sin 22,其中 [] 2 ,2-∈t 当 .221,14sin ,2max +=∴=??? ? ? +=y x t π 2,函数x x x x x f cos sin 1cos sin )(++= 的值域 四、 利用三角函数的有界性此为d x c b x a y -+= co s co s 型的三角函数类型一:利用 1co s 1s i n ,≤≤x x 这一有界性求最值。 例1:求函数x x y sin 21 sin --= 的值域。 解:由x x y sin 21sin --=变形为(1)sin 21y x y +=+,知1y ≠-,则有21 sin 1 y x y +=+, 21|sin |||11y x y +=≤+2 2221||1(21)(1)1 y y y y +?≤?+≤++20 3y ?-≤≤,则此函数的值域是2 [,0]3 y ∈- 五、关于正余弦一类二次齐次式的求最值。方向:化同角。 要用到:①降幂升角公式:2 1cos 2cos 2αα+=,2 1cos 2sin 2 αα-= ②sin α·cos α= α2sin 2 1 ③、辅助角:sin cos a b αα+)α?+(?所在象 限由点(,)a b 的象限决定,tan b a ?= ). 如sin cos )4A A A +=+π; s i n c o s 2s i n (3x x x = +πcos 2sin()6 x x x +=+π 注:(1)一般a>0,b>0.若为负,提取符号“﹣”。一般正弦”sin ”写前面,此时,前后前后符号 一致。 (2)前后 角度一致。如:asin2x-bcos2x= (3)常见形式 : 1sin 2x x = 1 2cos 22 x x ±= cos 22 x x ±= 二、单调区间:研究函数sin()y A x ω?=+性质的方法:类比于研究sin y x =的性质,只需将sin()y A x ω?=+中的x ω?+看成sin y x =中的x ,但在求sin()y A x ω?=+的单调区间时, 注:①结果写成区间的形式,标明k Z ∈。②不同的单调区间,中间用逗号“,”隔开。③0ω<时,通过诱导公式先将ω化正。如(1)函数23 y sin(x )π =-+ 的递减区间是__ ;(答: 151212 [k ,k ](k Z )π πππ- +∈ ④小范围[],x m n ∈时求单调区间,须对k 取值。 例:求[]2cos( 2)0,23 y x x π π=-∈在的单调递增区间。 和差角公式 1、sin()sin cos cos sin αβαβαβ±=±; c o s ()c o s c o s s i n αβαβαβ±=; tan tan tan()1tan tan αβ αβαβ ±±= 2 、 二 倍 角 公 式 sin 22sin cos ααα =. 22tan tan 21tan ααα = -. 2222cos 2cos sin 2cos 112sin ααααα =-=-=-. 推论:降幂升角公式:2 1cos 2cos 2αα+= ,2 1cos 2sin 2 αα-= 升幂降角公式:2 1cos 22cos αα+=,2 1cos 22sin αα-= 1±sin α=(2 cos 2 sin α α ±)2 2 2 |cos sin |θθ =± 3、半角公式:2cos 12 sin αα -± = 2c o s 12c o s αα+±= 4 、 . 三 倍 角公式 (主要用于连乘积) 3sin 33sin 4sin 4sin sin()sin()33ππ θθθθθθ=-=-+. 3cos34cos 3cos 4cos cos()cos()33 ππ θθθθθθ=-=-+ 0000()sin()() 2 ()s()() 2()sin()2 (,)()cos()(2 k f x A x k Z k k f x Aco x k Z k x k x f x A x k x k x k x k x f x A x k x k x ?πω?π?ππ?πω??π πω?πω?ω?πω?πω?π ω?π?=?? =+∈??=+??? ?=+ ?=+∈???=?? +=+?=? =++???+=?? +=?==++?+=+?为奇函数为偶函数为奇函数为偶函数对称轴对称中心对称轴对称中心,)k ?? ???α ααααααsin cos 1cos 1sin cos 1cos 12tan -=+=+-±= .323tan tan tan 3tan tan()tan()13tan 33 θθππ θθθθθ-= =-+- 5、公式的变形:①、辅助角:sin cos a b αα+)α?+(?所在象限由点(,)a b 的象限决定,tan b a ?= ). 如,如sin cos )4 A A A += +π ; s i n c o s 2s i n () 3 x x x = +π , cos 2sin()6 x x x +=+π 注:(1)一般a>0,b>0.若为负,提取符号“﹣”。一般正弦”sin ”写前面,此时,前后前后符号一致。 (2)前后 角度一致。如:asin2x-bcos2x= (3)常见形式 : 1sin 2x x = 1 2cos 22 x x ±= cos 22 x x ±= ②、1s i n c o s s i n 22 ααα= tan tan αβ±()()tan 1tan tan αβαβ=± 22cos sin cos 2ααα-= _______________tan 1tan 1=-+αα; ______________tan 1tan 1=+-αα ; tan tan αβ±()()tan 1tan tan αβαβ=± ___________tan tan 1=-βα;tan α+ cot α= α αα2sin 2 cos sin 1= ? tan α- cot α= -2cot2α 三角函数方程练习题 1.求下列方程的解集 (1)2 3sin -=x (2) 2 1cos - =x (3) 6tan 36-=x (4) 3sin 2-=x (5) 1cos -=x (6) 32tan 3=x (7) 32)3 2sin(4=-πx (8) 2 1)3 cos(- =+ π x (9) 1)6 tan(3-=- π x 2.根据下列条件,求下列方程的解集 (1) 4)4cos(8-=-x π )2,0(π∈x (2) 1)4 32sin(2-=+ πx ),(ππ-∈x (3) 32)26 tan(2-=-x π )6 5,3( )3 ,6(π ππ π?- ∈x (4) 3 3tan -=x ]4,2[ππ-∈x (5) 2 2)6 sin(= - π x ],0[π∈x 3.求方程内的所有实根之和在]2,0[01sin sin 62 π=--x x . 4. 若的值求其中的解是方程απααπ ),2,0(,1)cos(23 ∈=+=x x 5.若的值求其中的解是方程απααπ ),2,0(,1)sin(26 ∈=+=x x 三角函数不等式练习题 1.写出终边在下列直线上的角的集合 (1)0,3≥=x x y (2) x y 3 3- = (3) ||x y = 2.写出下列阴影部分(包括边界)表示的角的集合. (1) (2) (3) 2.求下列不等式的解集.并在坐标系中用阴影部分画出解集 (1)2 1sin ≥x (2) 2 1cos ≥ x (3) 1sin 2-≤x 3.求下列不等式的解集 (1) 2 3sin 2 1≤ ≤x (2) 2 1sin 2 1≤ ≤- x (3) 2 1cos 0≤ ≤x 基本不等式与余弦定理综合求解三角形面积的最值探究 建水县第二中学: 贾雪光 从最近几年高考试题的考查情况看,解三角形部分的考查中主要是对用正、余弦定理来求解三角形、实际应用问题, 这两种常见考法中,灵活应用正余弦定理并结合三角形中的内角和定理,大边对大角,等在三角形中进行边角之间的相互转化,以及与诱导公式特别是C B A sin )sin(=+、 C B A sin 2 cos =+的联系是关键。 于是多数教师在复习备考过程中,往往都会将大量的时间和精力花在对正余弦定理的变形,转化,变式应用上,当然这也无可厚非,但是我在高考备考复习教学中发现了这样一类题目,如: 1、在锐角△ABC 中,a, b, c 分别为内角A, B, C 的对边,且A A 2 2sin 21cos =+ ,7 = a 求△ABC 的面 积的最大值;2、已知向量)2 1,(sin A M =与)cos 3sin ,3(A A N +=共线,其中A 是△ABC 的内角,(1)求角A 的大小;(2)若BC=2,求△ABC 的面积S 的最大值。3、△ABC 中,a, b, c 分别为内角A, B, C 的对边,向量)2cos ,2 (cos ),1,4(2 A A N M =-=,2 7= ?N M ,(1)求角A 的大小;(2)若3=a 是判 断当c b ?取得最大值时△ABC 的形状。面对这样的问题,我们如何来引导学生很自然的过度,用一种近乎水到渠成的方法来求解呢? 实际上我们在教学和学习的过程中往往会忽略一个很明显的问题,那就是余弦定理与基本不等式的综合,如果我们在讲授正余弦定理的时候能在引入正课时多下一点功夫,我们就会有意外的收获哦。 我在教学中是这样处理的:实际上在余弦定理中我们总有这样一组公式: A bc c b a cos 222 2 ?-+=, B ac c a b cos 2222?-+=, C ab b a c cos 2222?-+= 同时在基本不等式中我们总有这样一组公式:bc c b 222≥+,ac c a 222≥+ ,ab a b 222≥+在三角形中各边都是正数,所以上面三个式子在a 、 b 是三角形的三边时总是成立的,如果我们将两组公式综合后会发现这样的一组公式即:)cos 1(22A bc a -?≥,)cos 1(22C ac b -?≥ )c o s 1(22c ab c -?≥于是我们就有方程等式,得到了一组不等式,而在涉及到最值得求解时,我们常用的处理方法是,一求函数值域;二、导函数;三、基本不等式即均值定理;但是前两种方法显然都不可能用于求解上面两个题目类型的求解,于是在涉及到与解三角形有关的三角形的面积的最大值时我们就只能考虑用均值定理了,自然也就要用到上面我们推导得出的这一组公式罗。 于是我没有: 例1:在锐角△ABC 中,a, b, c 分别为内角A, B, C 的对边,且A A 2 2sin 21cos =+ ,7 = a 求 1.4 绝对值三角不等式 教案1 (新人教选修4-5) 教学目标: 1:了解绝对值三角不等式的含义,理解绝对值三角不等式公式及推导方法, 会进行简 单的应用。 2:充分运用观察、类比、猜想、分析证明的数学思维方法,体会转化和数形结合的数 学 思想,并能运用绝对值三角不等式公式进行推理和证明。 教学重点:绝对值三角不等式的含义,绝对值三角不等式的理解和运用。 教学难点:绝对值三角不等式的发现和推导、取等条件。 教学过程: 一、复习引入: 关于含有绝对值的不等式的问题,主要包括两类:一类是解不等式,另一类是证明不等式。本节课探讨不等式证明这类问题。 1.请同学们回忆一下绝对值的意义。 ?? ? ??<-=>=0000x x x x x x ,如果,如果,如果。 几何意义:在数轴上,一个点到原点的距离称为这个点所表示的数的绝对值。 2.证明一个含有绝对值的不等式成立,除了要应用一般不等式的基本性质之外,经常还要用到关于绝对值的和、差、积、商的性质: (1)a a ≥,当且仅当0≥a 时等号成立,.a a -≥当且仅当0≤a 时等号成立。 (2)2 a a =, (3) b a b a ?=?, (4) )0(≠= b b a b a 那么? b a b a +=+?b a b a +=- 二、讲解新课: 结论:a b a b ++≤(当且仅当0ab ≥时,等号成立.) 已知,a b 是实数,试证明:a b a b ++≤(当且仅当0ab ≥时,等号成立.) 方法一:证明:10 .当ab ≥0时, 20. 当ab <0时, 探究: ,,a b a b +, 之间的什么关系? b a - 向量、解三角形、数列、不等式测试卷 一、选择题(本大题共12小题,每小题5分,共60分) 1.由11a =,3d =确定的等差数列{}n a , 当298n a =时,n 等于 ( ) A.99 B.100 C.96 D.101 2.ABC ?中,若?===60,2,1B c a ,则ABC ?的面积为 ( ) A . 2 1 B .23 C.1 D.3 3.如图,在△ABC 中,1 ,3,,,2 BD DC AE ED AB a AC b BE = ===若则= ( ) A .1133a b + B .11 24a b -+ C .1124a b + D .11 33 a b -+ 4.已知3≥x ,函数1 1 -+=x x y 的最小值是 ( ) A .2 7 B .4 C .8 D .6 5.设a 、b 、c 是单位向量,且a ·b =0,则()()a c b c -?-的最小值为 ( ) A 、2- ( B )22- ( C )1- (D)12- 6.在各项均为正数的等比数列 {}n b 中,若783b b ?=,则 3132log log b b ++……314log b +等于 ( ) (A) 5 (B) 6 (C)7 (D)8 7.设,x y 满足约束条件1 2x y y x y +≤?? ≤??≥-? ,则3z x y =+的最大值为 ( ) A . 5 B. 3 C. 7 D. -8 8.在ABC ?中,80,100,45a b A ?===,则此三角形解的情况是 ( ) A.一解 B.两解 C.一解或两解 D.无解 9.已知b a ,满足:a =3,b =2,b a +=4,则b a -=( ) A .3 B .5 C .3 D 10 10.一个等比数列}{n a 的前n 项和为48,前2n 项和为60,则前3n 项和为( ) 不等式的解法 绝对值不等式 例1 解绝对值不等式|x+3|>|x-5|. {x |x>1}. 例2 对任意实数x ,若不等式|x+1|-|x-2|>k 恒成立,则实数k 的取值范围是( ) A .k<3 B .k<-3 C .k≤3 D .k≤-3 选B . 例3 解不等式|3x-1|>x+3. {x | x<- ,或x>2}. 例4 解不等式 |x-5|-|2x+3|<1 {x |x<-7或 x> } |x+3|+|x-3|>8. 例5 解不等式1≤|2x-1|<5. {x |-2 指数不等式 例1、解不等式 (1)12>x (2) ) 1(332)21(22--- 高中数学解三角形题型目录一.正弦定理 1.角角边 2.边边角 3.与三角公式结合 4.正弦定理与三角形增解的应对措施 5.边化角 6.正弦角化边 二.余弦定理 1.边边边 2.边角边 3.边边角 4.与三角公式结合 5.比例问题 6.余弦角化边 7.边化余弦角 三.三角形的面积公式 1.面积公式的选用 2.面积的计算 3.正、余弦定理与三角形面积的综合应用 四.射影定理 五.正弦定理与余弦定理综合应用 1.边角互化与三角公式结合 2.与平面向量结合 3.利用正弦或余弦定理判断三角形形状 4.三角形中的最值问题 (1)最大(小)角 (2)最长(短)边 (3)边长或周长的最值 (4)面积的最值 (5)有关正弦或余弦或正切角等的最值 (6)基本不等式与余弦定理交汇 (7)与二次函数交汇 六.图形问题 1.三角形内角之和和外角问题 2.三角形角平分线问题 3.三角形中线问题 4.三角形中多次使用正、余弦定理 5.四边形对角互补与余弦定理的多次使用 6.四边形与正、余弦定理 六.解三角形的实际应用 1.利用正弦定理求解实际应用问题 2.利用余弦定理求解实际应用问题 3.利用正弦和余弦定理求解实际应用问题 一.正弦定理 1.角角边 ?=?=?= 例.在中,解三角形 ABC A B a 30,45,2,. ?=?=?== 练习1.在中则 ABC A B a c ,30,45, . 练习2.在中,已知45,,求 ?=?=?= 30. ABC C A a b 2.边边角 例中,解这个三角形?===? ABC a .45,. 练习1中,则 ?==+== . 1,2,sin ABC a b A C B C 练习2.中则 ?===?= ,3,60,_____ ABC c b C A 第23讲 三角不等式 竞赛热点 含有未知数的三角函数的不等式叫做三角不等式。 在高中数学竞赛内容中,涉及三角不等式的问题有三类:一是三角不等式的证明,二是解三角不等式,三是应用三角不等式求最值。 处理三角不等式的问题一方面要有扎实的三角变形能力,另一方面还需要有三角函数的图象和性质的认识。同时,对不等式的有关性质和证明方法要能灵活运用。 解题示范 例1:已知N n ∈,2≥n ,求证: .3 21cos 31cos 21cos >n Λ 思路分析:本题从三角变形入手不易,不可考虑利用x x 三角形不等式的应用 根据两点之间线段最短导出了三角形任意两边之和大于第三边,我们把这个关系叫做三角形不等式.这一定理在证明一些结构特别的不等式中有广泛应用.下面我们举几个例子来说明这个定理的应用,并探究命题者是如何编拟这些题目的. 类型一类型一::证明形如a b c +>型的不等式 例1、已知x y z 、、 +> 证明:作角∠120AOB = ,∠120BOC = ,则∠120AOC = , 设x y z OA OB OC ===、、,由余弦定理: == 又OA OB OC,+>所以原不等式成立. 例2、已知x y z 、、 > 证明:在空间直角坐标系中,取A(,0,0)B 0,0)C 00)x y z 、(,、(,,, 则C A == 又AB BC C,A +>所以原不等式成立. 类型二类型二::证明形如a b c d ++>型的不等式 例3、已知x y z 、、为正数,求证: y z).+>++ 证明:如右图,以x y z ++为边作正方形, 则 ).BC CD AB x y z =++≥++ D x y z x y z 类型三类型三::证明形如a b c d e +++>型的不等式 例4、设01,01x y <<<<求证: ++≥ 证明:左边即表示动点(,)P x y 到四个定点(0,0),(1,0),(1,1),(0,1)O A B C 的距离之和. 另由题设知,P 在边长为1的正方形OABC 的内部. 由()()OP BP CP AP OB AC +++≥+=知原不等式成立. 应当注意,有些不等式从表面上看很难用三角形不等式来证明,似乎只能用代数方法证明,但是如果仔细分析,也可能用上三角形不等式,一般说来,用三角形不等式证明要比代数方法简单的多,但是其构造的难度也很大,需要一些很技巧的变形,例如配方变形法,凑两点间距离公式等. 例5、已知正数x y 、满足1x y += , 2.+≥ 分析分析::用代数法可以使用分析法,并随时利用1x y += 这个条件进行化简. 证明证明::2,+≥ 只要证22224,x y y ++++≥x 即证22224,x y y ++++≥x 即证22224,x y y ++++≥x 即证22[()2]x y xy x y +?+++ 注意到1x y +=,即证2[12]14,xy ?++≥ 即证14,xy ≥+ 即证224(4()52)1816(),xy xy xy xy ?+≥++ 即证287,xy ?≥?1,4xy ≤ 而21(,24x y xy +≤=故14 xy ≤成立.所以原不等式成立. 高中数学必修5解三角形、数列、不等式测试题 (考试时间120分钟,总分150分) 一.选择题 (本大题共12小题 ,每小题5分,共60分,请把正确答案填在答题卡上) 1.已知a ,b 为非零实数,且a 1 b 2.sin15°cos45°+cos15°sin45°等于( ) A .0 B . 2 1 C . 2 3 D .1 3.ABC ?中,若?===60,2,1B c a ,则ABC ?的面积为 ( ) A .21 B .2 3 C.1 D.3 4.在数列{}n a 中,1a =1,12n n a a +-=,则51a 的值为 ( ) A .99 B .49 C .102 D . 101 5.已知0x >,函数4 y x x = +的最小值是 ( ) A .5 B .4 C .8 D .6 6.在等比数列中,112a =,12q =,132 n a =,则项数n 为 ( ) A. 3 B. 4 C. 5 D. 6 7.不等式20(0)ax bx c a ++<≠的解集为R ,那么( ) A. 0,0a ?≥ D. 0,0a >?> 8.设,x y 满足约束条件12x y y x y +≤?? ≤??≥-? ,则3z x y =+的最大值为 ( ) A . 5 B. 3 C. 7 D. -8 9.若)4 π tan( α-=3,则tan α 等于( ) A .-2 B .2 1- C . 2 1 D .2 10.在等差数列{a n }中,若a 3+a 9+a 15+a 21=8,则a 12等于( ) A .1 B .-1 C .2 D .-2 11.下列各式中,值为 2 3 的是( ) A .2sin15°-cos15° B .cos 215°-sin 215° C .2sin 215°-1 D .sin 215°+cos 215° 12.关于x 的方程2 210ax x +-=至少有一个正的实根,则a 的取值范围是( ) A .a ≥0 B .-1≤a <0 C .a >0或-1<a <0 D .a ≥-1 二.填空题(共4小题,每题5分,共20分,请把正确答案填在答题卡上) 13.在△ABC 中,若∠A =60°,∠B =45°,BC =32,则AC = 14. 不等式组260302x y x y y +-≥?? +-≤??≤? 表示的平面区域的面积为 15.不等式 21 131 x x ->+的解集是 . 16. 已知数列{}n a 满足23123222241n n n a a a a ++++=-,则{}n a 的通项公式 三.解答题(本大题共6小题,满分70分.解答须写出文字说明、证明过程和演算步骤, 并把正确解答过程写在答题卡上) 17. (10分)(1) 解不等式0542<++-x x ,(2) 求函数的定义域:5y = 1、如图(1),在等腰三角形ACB 中,5AC BC ==,8AB =,D 为底边AB 上一动点(不与点A B ,重合),DE AC ⊥,DF BC ⊥,垂足分别为E F ,,则D E D F += . 2、阅读下列内容后,解答下列各题: 几个不等于0的数相乘,积的符号由负因数的个数决定. 例如:考查代数式(1)(2)x x --的值与0的大小 当1x <时,10x -<,20x -<,(1)(2)0x x ∴--> 当12x <<时,10x ->,20x -<,(1)(2)0x x ∴--< 当2x >时,10x ->,20x ->,(1)(2)0x x ∴--> 综上:当12x <<时,(1)(2)0x x --< 当1x <或2x >时,(1)(2)0x x --> 满足 时,(3)运用你发现的规律,直接写出当x 满足 时,(7)(8)(9)0x x x -+-<. 3、.已知Rt ABC △的周长是4+2,则ABC S =△ . 4、如图,在ABC △中,AB AC =,点E F 、分别在AB 和AC 上,CE 与BF 相交于点D ,若AE CF D =,为BF 的中点,AE AF :的值为___________. 5、 有两个分数A=4444333,B=555554444 ,问:A 与B 哪个大? 6、|2a -24|+(3a -b -k )2 =0,那么k 取什么值时,b 为负数. 7、一堆有红、白两种颜色的球若干个,已知白球的个数比红球少,但白球的2倍比红球多.若把每一个白球都记作“2”,每一个红球都记作“3”,则总数为“60”,那么这两种球各有多少个? 8、是否存在整数m ,使关于x 的不等式 m x 31+ >m m x 9+ 与1+x >32m x +-是同解不等 式?若存在,求出整数m 9、如图,一次函数y 1=k 1x +b 1与y 2=k 2x +b 2的图象相交 于A(3,2),则不等式(k 2-k 1)x +b 2-b 1>0的解集为 10、如果x ,y 满足不等式组3050 x x y x y ≤?? +≥??-+≥?,那么你能画出 点(x ,y)所在的平面区域吗? 11、如图,已知函数y =3x +b 和y =ax -3的图象交于点 P(-2,-5),则根据图象可得不等式3x +b >ax -3的解 集是_______________. 图(1) ax -3 11题 数列、简单逻辑、解三角形、基本不等式、圆锥 曲线综合练习 (后附详细答案与解析) 1.“x=-1“是“x2+x=0“() A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 2.已知椭圆上一点P到椭圆一个焦点的距离为4,则它到 另一个焦点的距离() A. 6 B. 5 C. 4 D. 2 3.命题“若△ABC不是等腰三角形,则它的任何两个内角不相 等”的逆否命题是() A. 若△ABC有两个内角相等,则它是等腰三角形 B. 若△ABC任何两个内角不相等,则它不是等腰三角形 C. 若△ABC是等腰三角形,则它的任何两个内角相等 D. 若△ABC任何两个角相等,则它不是等腰三角形 4.设S n为等比数列{a n}的前n项和,a2-8a5=0,则=() A. B. C. 2 D. 17 5.在△ABC中,角A,B,C的对边分别为a,b,c,且B=,b2=ac, 则△ABC一定是() A. 直角三角形 B. 钝角三角形 C. 等边三角形 D. 等腰直角三角形 6.在△ABC中,内角A,B,C的对边分别是a,b,c,若=2, b2-a2=ac,则cos B等于() A. B. C. D. 7.设F1,F2分别是双曲线的左右焦点,点M (a,b).若∠MF1F2=30°,则双曲线C的离心率为() A. B. C. 2 D. 8.设F1,F2为曲线C1:的焦点,P是曲线C2:-y2=1与 C1的一个交点,则cos∠F1PF2的值是() A. B. C. D. 9.若函数f(x)在R上可导,且f(x)=x2+2f'(2)x-3,则() A. f(0)<f(4) B. f(0)=f(4) C. f(0)>f(4) D. 以上都不对 10.已知双曲线C:=1(a>0,b>0),以C的右焦点F(c, 0)为圆心,以a为半径的圆与C的一条渐近线交于A,B两点, 若|AB|=c,则双曲线C的离心率为() A. B. C. D. 11.已知关于x的不等式x2-ax-b<0的解集是(2,3),则a+b的 值是() A. -11 B. 11 C. -1 D. 1 12.已知抛物线y2=4x,过焦点且倾斜角为60°的直线与抛物线交于 A、B两点,则△AOB的面积为() A. B. C. D. 13.公差不为0的等差数列{a n}的前n项和为S n,若a2,a5,a14成 等比数列,,则a10=______. 14.命题“?x∈R,x2+1<0”的否定是______. 2013-2014学年度第二学期解三角形和不等式的大题 注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上 第I卷(选择题) 请点击修改第I卷的文字说明 一、选择题(题型注释) 第II 卷(非选择题) 请点击修改第II 卷的文字说明 二、填空题(题型注释) (1,求)(x f 的取值范围; (2)设△ABC 的内角A 、B 、C 所对的边分别为a 、b 、c ,已知A 为锐角,2=b ,3=c ,求)cos(B A -的值. 【答案】21m n =?-. (1(2,求b 的大小. 【答案】(1)()f x 递减区间是2 3.已知函数f(x)x ∈[1,+∞). (1)当a =4时,求函数f(x)的最小值; (2)若对任意x ∈[1,+∞),f(x)>0恒成立,试求实数a 的取值范围. 【答案】(1)6(2)()3,-+∞ 4.(1)已知y =4x -2 (2)已知x>0,y>01,求x +y 的最小值. 【答案】(1)y max =1.(2)最小值为16 5.某营养师要为某个儿童预订午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物、6个单位的蛋白质和6个单位的维生素C ;一个单位的晚餐含8个单位的碳水化合物、6个单位的蛋白质和10个单位的维生素C.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物、42个单位的蛋白质和54个单位的维生素C. 如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐? 【答案】4个单位的午餐和3个单位的晚餐, 6.设z =2x +y ,式中变量满足下列条件:4335251x y x y x ≤?? ≤??≥? --,+,,求z 的最大值和最小值. 【答案】12 3 7.在△ABC 中,a =3,b = B =2∠A. (1)求cosA 的值; (2)求c 的值. 【答案】(1 2)5. 8.在△ABC 中,内角C B A 、、的对边分别为c b a 、、,已知cos sin a b C c B =+.(Ⅰ) 求B ; (Ⅱ)若2= b ,求△ABC 面积的最大值. 【答案】 9.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c, 且 (1 的值; ( 2)若 求bc 的最大值. 【答案】(1(2 10.△ABC 中,BC =7,AB =3 (1)求AC ; (2)求∠A . 【答案】(1)5 (2) 120-=∠A 三个内角,他们的对边分别为a 、b 、c ,且 (1)求 A; (2 的值,并求ABC ?的面积。 【答案】(1212.在ABC ?中,(1)求sin A 的值; 解三角不等式 (1)cos x ≥ [2,2],66k k k Z ππππ-+∈ (2)cos x ≤ 11[2,2],66k k k Z ππππ++ ∈ (3)sin x ≥ 2[2,2],33k k k Z ππππ++ ∈ (4)sin 2 x ≤ 4[2,2],33k k k Z ππππ-+∈ (5)tan x ≥ [,),32k k k Z π π ππ++∈ (6)tan x ≤ (,],23 k k k Z ππ ππ-+∈ 求定义域 (1)()f x = {|222,}2 x k x k x k k Z π ππππ≤<+=+∈或 (2)()f x = {|22}2 x k x k k Z π ππ≤<+ ∈ (3)()lg(cos )f x x = {|22,}26x k x k k Z ππππ-<≤+∈ (4) ()lg(sin )f x x = {|22,}3x k x k k Z ππππ+≤<+∈ (5) ()f x = 53{|22,}42x k x k k Z ππππ+<<+∈ (6)()f x = 43(2,2)(2,2),3232k k k k k Z ππππππππ++?+ +∈ (7) lg(tan ()x f x = 73(2,2)(2,2),3262k k k k k Z ππππππππ++?++∈ (8) ()f x = (,),42 k k k Z π π ππ+ +∈ (9) ()f x = 33(2,2)(2,2),3242k k k k k Z ππππππππ++?+ +∈ (10) lg(tan ()x f x = 73(2,2)(2,2),3262k k k k k Z ππππππππ++?++∈ 求单调区间 (1)()lg(sin )f x x = 增:(2,2],2 k k k Z π ππ+∈ 减:[2,2),2 k k k Z π πππ+ +∈ (2)12 ()log (sin )f x x = 增:[2,2),2k k k Z π πππ+ +∈ 减:(2,2],2 k k k Z π ππ+∈ (3)()lg(sin 2)f x x = 增:(,],4 k k k Z π ππ+ ∈ 减:[,),42 k k k Z π π ππ+ +∈ (4)12 ()log (sin 2)f x x = 增:[,),42k k k Z π πππ+ +∈ 减:(,],4 k k k Z π ππ+∈ (5)()lg(cos )f x x = 增:(2,2],2k k k Z πππ- ∈ 减:[2,2),2 k k k Z π ππ+∈ (6) 12 ()log (cos )f x x = 增:[2,2),2 k k k Z π ππ+∈ 减:(2,2],2 k k k Z π ππ- ∈ (7) ()lg(tan )f x x = 增:(,),2 k k k Z π ππ+ ∈ 无减区间 第一章 解三角形 例1 某地出土一块类似三角形刀状的古代玉佩,其一角已破损,现测得如下数据: BC=2.57cm,CE=3.57cm,BD=4.38cm,B=450,C=1200.为了复原,请计算原玉佩两边的长(结果精确到0.01cm ) 例2台风中心位于某市正东方向300km 处,正以40km/h 的 速度向西北方向移动,距离台风中心250km 范围内将会受到其影响。如果台风速度不变,那么该市从何时起要遭受台风影响?这种影响持续多长时间(结果精确到0.1h )? 例3如图 在△ABC 中,=(x,y ),AC =(u,v),求证:△ABC 的面积S= 2 1︱xv-yu ︱. 例4 如图所示,有两条直线AB 和CD 相交成800角,交点是O,甲、乙两人同时从点O 分别沿OA,OC 方向出发,速度分别是4km/h,4.5km/h,3时后两人相距多远(结 例5 如图 是公元前约400年古希腊数学家泰特托斯用来构造无理数2,3,5,、、、的图形,试计算图中线段BD 的长度及∠DA B 的大小(长度精确到0.1,角度精确到10)。 例6如图,在梯形ABCD 中,A D ∥BC,AB=5,AC=9, ∠BCA=300,∠ADB=450 ,求BD 的长。 例7 一次机器人足球比赛中,甲队1号机器人由点A 开始作匀速直线运动,到达点B 时,发现足球在点D 处正以2倍于自己的速度向点A 作匀速直线滚动。如图,已知AB=42dm,AD=17dm, ∠BAC=450 .若忽略机器人原地旋转所需的时间,则该机器人最快可在何处截住足球? 例8 如图所示,已知⊙O 的半径是1,点C 在直径AB 解三角形与不等式 一、选择题 1.锐角三角形ABC 中,sin A 和cos B 的大小关系是( ) A . sin A =cos B B . sin A <cos B C . sin A >cos B D . 不能确定 2.在△ABC 中,已知a =2b cos C ,那么△ABC 的内角B 、C 之间的关系是( ) A .B >C B .B =C C .B 解三角不等式专题 1、利用单位圆或观察正弦曲线,写出满足下列条件的区间: 0sin )1(>x 0s i n )2(≤x 21 sin )3(≥x 21s i n )4(- 2、利用单位圆或观察余弦曲线,写出满足下列条件的区间: 0cos )1(≥x 0c o s )2( 6、利用单位圆或根据正切函数的图象,写出满足下列条件的区间: 0tan )1(>x 0t a n )2(≤x 33 tan )3(≥x 33t a n )4(- 1、利用单位圆解不等式3tan α+3>0 解:要使3tan α+3>0,即要tan α>- 33 如图14,由正切线可知 k π-6π<α< k π+2 π ,k ∈Z ∴ 不等式的解集为(k π-6π,k π+2 π),k ∈Z 2、求函数y=21cos sin - +x x 的定义域。 解:由?????≥-≥021cos 0sin x x 得?? ???≥≥21cos 0sin x x 如图15,则图中阴影部分(Ⅰ)和(Ⅱ)的公共部分即为不等式组的解. ∴函数的定义域为{x | 2 k π≤x ≤2 k π+3 π, k ∈Z }. 小提示:首先要把不等式变为基本型(最简单的三角不等式),对于三角不等式组应分别确定区域,取其公共部分。 3、求函数 y=+lg(2sinx+)的定义域. 分析:定义域即为使函数有意义的x 的值所组成的集合. 解:要使函数y 有意义,必须 根据上面说明的步骤在单位圆中画出符合条件的x 的范围,据阴影部分写出: +2k π 高考数学大题狂练 第二篇 三角函数与三角形 专题03 解三角形与不等式,最值和范围问题的结合 1.在ABC ?中,角,,A B C 的对边分别为,,a b c ,且 cos cos 23sin A B C a b +=. (1)求角B 的大小; (2)若ABC ?的面积为3, B 是钝角,求b 的最小值. 【答案】(1)3B π =或23 π. (2)6. 由正弦定理得23sin cos cos sin sin B A B A B C +=, ∴()23sin sin A B B C +=, 又在ABC ?中, ()sin sin 0A B C +=≠,∴3sin B = 3B π=或23π. (2)由13sin 2ac B =, 3sin B =2ac =, 又23 B π=, 2222cos b a c ac B =+- 222226a c ac =++≥+=, 当且仅当a c =时取等号,∴b 6. 2.已知ABC ?三个内角 ,,A B C 的对边分别为,,a b c , ABC ?的面积S 满足2223S a b c =+-. (1)求角C 的值; (2)求()cos2cos A A B +-的取值范围. 【答案】(1)23π;(2)(3 )222 33cos 1sin 42 a b c ab C S ab C +-=-== tan 3C =0C π<<, 23 C π∴=. (2)()33cos2cos =cos2cos 2cos2sin2322 A A B A A A A π? ?+-+-=+ ??? =3sin 23A π??+ ?? ? 0,2333A A π π π π<<∴<+ 三角形不等式的应用举例 根据两点之间线段最短导出了三角形任意两边之和大于第三边,我们把这个关系叫做三角形不等式.这一定理在证明一些结构特别的不等式中有广泛应用.下面我们举几个例子来说明这个定理的应用. 类型一:证明形如a b c +>型的不等式 例1、已知x y z 、、 > 证明:作角∠120AOB = ,∠120BOC = ,则∠120AOC = , 设x y z OA OB OC ===、、,由余弦定理: == 又OA OB OC,+>所以原不等式成立. 例2、已知x y z 、、 > 证明:在空间直角坐标系中,取A(,0,0)B 0,0)C 00)x y z 、(,、(,,, 则BC C A == 又AB BC C,A +>所以原不等式成立. 类型二:证明形如a b c d ++>型的不等式 例3、已知x y z 、、 y z).>++ 证明:以x y z ++为边作正方形, ).BC CD AB x y z =++≥++ D A x y z x y z 类型三:证明形如a b c d e +++>型的不等式 例4、设01,01x y <<<<求证: ≥ 证明:左边即表示动点(,)P x y 到四个定点(0,0),(1,0),(1,1),(0,1)O A B C 的距离之和. 另由题设知,P 在边长为1的正方形OABC 的内部. 由()()OP BP CP AP OB AC +++≥+=知原不等式成立. 应当注意,有些不等式从表面上看很难用三角形不等式来证明,似乎只能用代数方法证明,但是如果仔细分析,也可能用上三角形不等式,一般说来,用三角形不等式证明要比代数方法简单的多,但是其构造的难度也很大,需要一些很技巧的变形,例如配方变形法,凑两点间距离公式等. 例5、已知正数x y 、满足1x y +=, 2.≥ 分析:用代数法可以使用分析法,并随时利用1x y += 这个条件进行化简. 证明:2, 只要证22224,x y y ++++≥x 即证22224,x y y ++++≥x 即证22224,x y y ++++x 即证22[()2]x y xy x y +-+++ 注意到1x y +=,即证2[12]14,xy -++ 即证14,xy ≥+ 即证224(4()52)1816(),xy xy xy xy -+≥++ 即证287,xy -≥-1,4 xy ≤ 而21(),24x y xy +≤=故14 xy ≤成立. 所以原不等式成立. 如果用几何法,开始要用消元法,中间利用两点间距离公式配凑,最后也用到了三角形不等式: 证明:左边== 太原北辰双语学校高二年级第二学期数学学科作业题 课题:绝对值三角不等式 班级: 姓名: 命题日期: 3 月 13日 1.绝对值的意义. 在数轴上,一个点到原点的距离称为这个点所表示的数的绝对值. 即|x |=???? ?x ,x >0,0,x =0,-x ,x <0. 2.绝对值三角不等式 定理1:如果a ,b 是实数,则|a +b |≤|a |+|b |,当且仅当ab ≥0时,等号成立.关于定理1的几点说明: (1)定理1的证明:|a +b |≤|a |+|b |?(a +b )2≤(|a |+|b |)2?a 2 +b 2+2ab ≤a 2+b 2+2|a ||b |?ab ≤|a ||b |?ab ≤|ab |,由已知知识可知 ab ≤|ab |一定成立,因而不等式|a +b |≤|a |+|b |成立.又由于上面每 一步都是恒等变形及ab =|ab |?ab ≥0可知,当且仅当ab ≥0时,等号成立. (2)对定理的几何说明,实际上是利用了绝对值的几何意义,证明 了不等式|a +b |≤|a |+|b |. (3)定理1还可以变形为|a -b |≤|a |+|b |,等号成立的充要条件是ab ≤0. (4)由定理1还可以得出许多正确的结论,例如:如果a ,b 是实数,那么|a |-|b |≤|a +b |≤|a |+|b |;|a |-|b |≤|a -b |≤|a |+|b |. 思考2 说出下列不等式等号成立的条件: (1)|a |+|b |≥|a +b |; (2)|a |-|b |≤|a +b |; (3)|a -c |≤|a -b |+|b -c |. 3.含有绝对值的不等式的证明中,常常利用|a |≥a ,|a |≥-a 及绝对值的和的性质. 思考3 当|a |>a 时,a ∈________;当|a |>-a 时,a ∈(0,+∞). 一层练习 1.若|x -a |三角方程与三角不等式练习题
基本不等式与余弦定理综合求解三角形面积的最值探究
(完整版)绝对值三角不等式
向量解三角形数列不等式测试卷
绝对值指数对数三角不等式的解法
高中数学解三角形题型完整归纳
(完整版)三角不等式
高中数学复习指导:三角形不等式的应用
高中数学必修5解三角形、数列、不等式测试题
三角形与不等式
解三角形、数列、基本不等式、简单逻辑、圆锥曲线综合训练
不等式与解三角形大题
解三角不等式,复合函数单调区间练习
必修5 解三角形、数列、不等式
解三角形和不等式
解三角不等式专题
专题2.3+解三角形与不等式最值和范围问题的结合-高考数学备考之百强校大题狂练
三角形不等式的应用举例(含练习题)
绝对值三角不等式
