全等三角形中重要几何模型专题讲解(手拉手模型、截长补短、中线倍长)

全等三角形中重要几何模型专题讲解
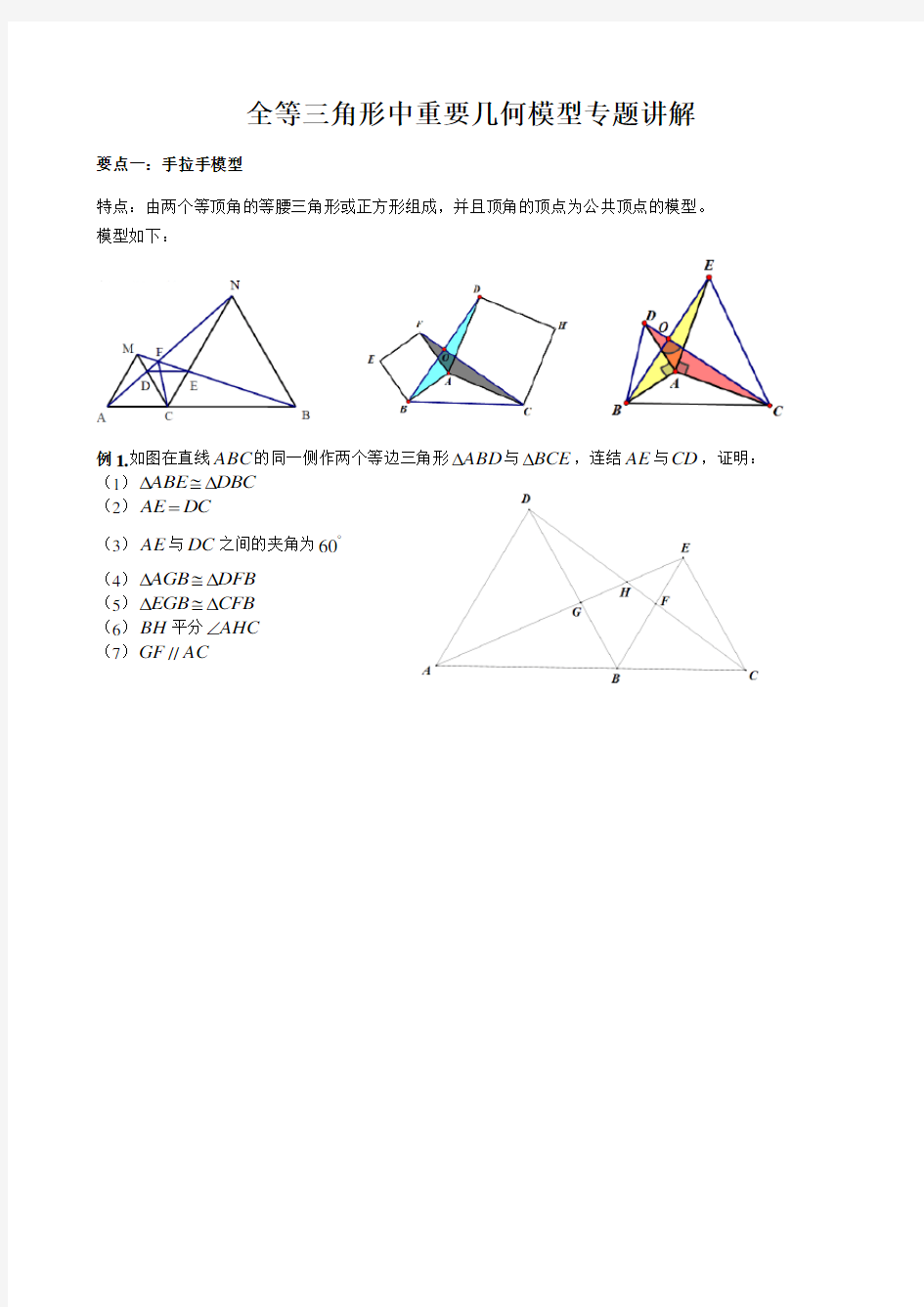
要点一:手拉手模型
特点:由两个等顶角的等腰三角形或正方形组成,并且顶角的顶点为公共顶点的模型。 模型如下:
例1.如图在直线ABC 的同一侧作两个等边三角形ABD ?与BCE ?,连结AE 与CD ,证明:
(1)DBC ABE ???
(2)DC AE =
(3)AE 与DC 之间的夹角为?60
(4)DFB AGB ???
(5)CFB EGB ???
(6)BH 平分AHC ∠
(7)AC GF //
全等几何模型讲解7
常见的几何模型 一、旋转主要分四大类:绕点、空翻、弦图、半角。 这四类旋转的分类似于平行四边形、矩形、菱形、正方形的分类。 1.绕点型(手拉手模型) (1)自旋转: ? ? ? ? ? ? ? ,造中心对称 遇中点旋 全等 遇等腰旋顶角,造旋转 ,造等腰直角 旋 遇 ,造等边三角形 旋 遇 自旋转构造方法 180 90 90 60 60
例题讲解: 1. 如图所示,P是等边三角形ABC的一个点,PA=2,PB=3 2,PC=4,求△ABC的边长。 C A B P 2. 如图,O是等边三角形ABC一点,已知:∠AOB=115°,∠BOC=125°,则以线段OA、OB、OC为边构成三角形的各角度数是多少? https://www.360docs.net/doc/b36287845.html,/Services/BlogAttachment.ashx?AttachmentID=1924 3.如图,P是正方形ABCD一点,且满足PA:PD:PC=1:2:3,则∠APD= . 4.如图(2-1):P是正方形ABCD一点,点P到正方形的三个顶点A、B、C的距离分别为PA=1,PB=2,PC=3。求此正方形ABCD面积。 A B C O
(2)共旋转(典型的手拉手模型) 模型变形: 等边三角形共顶点 共顶点等腰直角三角形 共顶点等腰三角形 共顶点等腰三角形
例题讲解: 1. 已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与B,C 重合),以AD 为边作菱形ADEF(按A,D,E,F 逆时针排列),使∠DAF=60°,连接CF. (1) 如图1,当点D 在边BC 上时,求证:① BD=CF ? ②AC=CF+CD. (2)如图2,当点D 在边BC 的延长线上且其他条件不变时,结论AC=CF+CD 是否成立?若不成立,请写出AC 、CF 、CD 之间存在的数量关系,并说明理由; (3)如图3,当点D 在边BC 的延长线上且其他条件不变时,补全图形,并直接写出AC 、CF 、 CD 之间存在的数量关系。 2.(13中考) 在△ABC 中,AB=AC ,∠BAC=α(?<
全等三角形辅助线之截长补短和倍长中线(原题+解析)
全等三角形辅助线之截长补短与倍长中线 一.填空题(共1小题) 1.(2015秋?宿迁校级月考)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC 交BC于D.若BD:DC=3:2,点D到AB的距离为6,则BC的长是.二.解答题(共10小题) 2.(2010秋?涵江区期末)如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD. 3.如图,AD是△ABC中BC边上的中线,求证:AD<(AB+AC).4.(2013秋?藁城市校级期末)在△ABC中,∠ACB=90°,AC=BC,直线,MN 经过点C,且AD⊥MN于点D,BE⊥MN于点E. (1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE; (2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE; (3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系请你直接写出这个数量关系,不要证明. 5.已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC的数量关系,并说明理由. 6.(2012秋?西城区校级期中)已知:如图,△ABC中,点D,E分别在AB,AC边上,F是CD中点,连BF交AC于点E,∠ABE+∠CEB=180°,判断BD与CE 的数量关系,并证明你的结论. 7.(2010秋?丰台区期末)已知:如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC,点D是△ABC内的一点,且AD=AC,若∠DAC=30°,试探究BD与CD的数量关系并加以证明. 8.已知点M是等边△ABD中边AB上任意一点(不与A、B重合),作∠DMN=60°,交∠DBA外角平分线于点N. (1)求证:DM=MN; (2)若点M在AB的延长线上,其余条件不变,结论“DM=MN”是否依然成立请你画出图形并证明你的结论. 9.(2015春?闵行区期末)如图所示,在正方形ABCD中,M是CD的中点,E 是CD上一点,且∠BAE=2∠DAM.求证:AE=BC+CE. 10.已知:如图,ABCD是正方形,∠FAD=∠FAE.求证:BE+DF=AE.11.(2010秋?巢湖期中)如图,CE、CB分别是△ABC、△ADC的中线,且AB=AC.求证:CD=2CE.
高中数学解析几何中的基本公式
解析几何中的基本公式 1、 两点间距离:若)y ,x (B ),y ,x (A 2211,则212212)()(y y x x AB -+-= 特别地:x //AB 轴, 则=AB 。 y //AB 轴, 则=AB 。 2、 平行线间距离:若0C By Ax :l ,0C By Ax :l 2211=++=++ 则:2 221B A C C d +-= 注意点:x ,y 对应项系数应相等。 3、 点到直线的距离:0C By Ax :l ),y ,x (P =++ 则P 到l 的距离为:2 2 B A C By Ax d +++= 4、 直线与圆锥曲线相交的弦长公式:?? ?=+=0 )y ,x (F b kx y 消y :02 =++c bx ax ,务必注意.0>? 若l 与曲线交于A ),(),,(2211y x B y x 则:2122))(1(x x k AB -+= 5、 若A ),(),,(2211y x B y x ,P (x ,y )。P 在直线AB 上,且P 分有向线段AB 所成的比 为λ, 则??? ????λ+λ+=λ+λ+=112121y y y x x x ,特别地:λ=1时,P 为AB 中点且??????? +=+=222 121y y y x x x 变形后:y y y y x x x x --= λ--= λ21 21或 6、 若直线l 1的斜率为k 1,直线l 2的斜率为k 2,则l 1到l 2的角为),0(,π∈αα 适用范围:k 1,k 2都存在且k 1k 2≠-1 , 2 11 21tan k k k k +-= α 若l 1与l 2的夹角为θ,则= θtan 21211k k k k +-,]2 ,0(π ∈θ 注意:(1)l 1到l 2的角,指从l 1按逆时针方向旋转到l 2所成的角,范围),0(π l 1到l 2的夹角:指 l 1、l 2相交所成的锐角或直角。 (2)l 1⊥l 2时,夹角、到角= 2 π 。 (3)当l 1与l 2中有一条不存在斜率时,画图,求到角或夹角。
初中数学全等三角形截长补短
全等三角形——截长补短法 一、知识梳理: 截长补短法 截长补短法是几何证明题中十分重要的方法。通常来证明几条线段的数量关系。 截长法: (1)过某一点作长边的垂线 (2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 补短法 (1)延长短边。 (2)通过旋转等方式使两短边拼合到一起。…… 二、典型例题: 例1、如图,在ABC ?中,60BAC ∠=?,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数. 及时练习: 如图所示,在Rt △ABC 中,∠C=90°,BC=AC ,AD 平分∠BAC 交BC 于D ,求证:AB=AC+CD . 例2、已知ABC ?中,60A ∠ =,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明. D O E C B A
M D C B A P C B A 及时练习: 如图,已知在ABC 内,0 60BAC ∠=,0 40C ∠=,P ,Q 分别在BC ,CA 上,并且AP , BQ 分别是BAC ∠,ABC ∠的角平分线。求证:BQ+AQ=AB+BP 例3、如图.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM . 求证:AE =BC +CE . 及时练习: 如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k , ∠AMD =75°,∠BMC =45°,则AB 的长为 ( ) A . a B . k C . 2 k h + D . h 例4、以ABC ?的AB 、AC 为边向三角形外作等边ABD ?、ACE ?,连结CD 、BE 相交于点O . 求证:OA 平分DOE ∠.
解析几何中的基本公式
解析几何中的基本公式 解析几何学(analytic geometry )是借助坐标系,用代数方法研究几何对象之间的关系和性质的一门几何学分支,亦叫坐标几何。由法国数学家笛卡儿和费马等人创建,其思想来源可上溯到公元前两千年。 两点间距离:若)y ,x (B ),y ,x (A 2211,则2 12212)()(y y x x AB -+-= 平行线间距离:若0C By Ax :l , 0C By Ax :l 2211=++=++ 则:2221B A C C d +-= 注意点:x ,y 对应项系数应相等。 点到直线的距离:0C By Ax :l ),y ,x (P =++οο 则P 到l 的距离为: 2 2B A C By Ax d +++= οο 直线与圆锥曲线相交的弦长公式:? ? ?=+=0)y ,x (F b kx y 消y :02 =++c bx ax ,务必注意.0>? 若l 与曲线交于A ),(),,(2211y x B y x 则: 2 122))(1(x x k AB -+= 若A ),(),,(2211y x B y x ,P (x ,y )。P 在直线AB 上,且P 分有向线段AB 所成的比为λ, 则??? ????λ+λ+=λ+λ+=112121y y y x x x ,特别地:λ=1时,P 为AB 中点且??????? +=+=222121y y y x x x 变形后: y y y y x x x x --=λ--= λ21 21或
若直线l1的斜率为k1,直线l2的斜率为k2,则l1到l2的角为),0(,π∈αα 适用范围:k1,k2都存在且k1k2≠-1 , 21121tan k k k k +-= α 若l1与l2的夹角为θ,则=θtan 2 12 11k k k k +-,]2,0(π∈θ 注意:(1)l1到l2的角,指从l1按逆时针方向旋转到l2所成的角,范围),0(π l1到l2的夹角:指 l1、l2相交所成的锐角或直角。 (2)l1⊥l2时,夹角、到角=2π 。 (3)当l1与l2中有一条不存在斜率时,画图,求到角或夹角。 (1)倾斜角α,),0(π∈α; (2)]0[,π∈θθ→ →,,夹角b a ; (3)直线l 与平面 ] 20[π ∈ββα,,的夹角; (4)l1与l2的夹角为θ,∈ θ] 20[π ,,其中l1//l2时夹角θ=0; (5)二面角,θ],0(π∈α; (6)l1到l2的角)0(π∈θθ,, 直线的倾斜角α与斜率k 的关系 每一条直线都有倾斜角α,但不一定有斜率。 若直线存在斜率k ,而倾斜角为α,则k=tan α。 直线l1与直线l2的的平行与垂直
a全等三角形之手拉手模型倍长中线截长补短法
手拉手模型 要点一:手拉手模型 特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点 结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA平分∠BOC 变形: 例1.如图在直线ABC的同一侧作两个等边三角形ABD ?,连结AE与CD,?与BCE 证明 (1)DBC ? ? ABE? (2)AE与DC之间的夹角为? 60 (3)BH平分AHC ∠ 变式精练1:如图两个等边三角形ABD ?,连结 ?与BCE AE与CD, 证明(1)DBC ? ABE? ? (2)AE与DC之间的夹角为? 60
(3)AE 与DC 的交点设为H ,BH 平分AHC ∠ 变式精练2:如图两个等边三角形ABD ?与BCE ?,连结AE 与CD , 证明(1)DBC ABE ??? (2)AE 与DC 之间的夹角为?60 (3)AE 与DC 的交点设为H ,BH 平分AHC ∠ 例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ???是否成立 (2)AG 是否与CE 相等 (3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠ 例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ???是否成立 (2)AG 是否与CE 相等 (3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠ 例4:两个等腰三角形ABD ?与BCE ?,其中 BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,
解析几何公式大全
平行线间距离:若l i : Ax By C i 0, 12 : Ax By C20 则:d C i C2I J A2B2 注意点:x, y对应项系数应相等。 点到直线的距离:P(x , y ),I:Ax By C 0 则P到1的距离为: |Ax d By C 解析几何中的基本公式 .A2B2 直线与圆锥曲线相交的弦长公式:y kx b F(x,y) 0 2 消y:ax bx c 0,务必注意0. 若I与曲线交于A(x1, y1), B(x2, y2) 则:AB v'(1 k2)(X2 X i)2 若A(x i, y i), B(X2, y2),P(x,y)。P在直线AB上,且P分有向线段AB所成的比为 i y i y2 i ,特别 地: x =1时,P为AB中点且 y x-i x2 2 y i y2 2 变形后:—i或」 X2 x y2 y 若直线l i的斜率为k i,直线|2的斜率为k2,则l i到|2的角为, (0, ) 适用范围:k i,k2都存在且k i k2 —i , tan k2 k i i k i k2
I i 到I 2的夹角:指 11、 12相交所成的锐角或直角。 (2) l 1 I 2时,夹角、到角=—。 2 (3) 当11与I 2中有一条不存在斜率时,画图,求到角或夹角。 直线的倾斜角 与斜率k 的关系 每一条直线都有倾斜角 ,但不一定有斜率。 若直线存在斜率k ,而倾斜角为 ,则k=tan 。 直线I 1与直线I 2的的平行与垂直 (1)若I 1, I 2均存在斜率且不重合:①I 1//I 2 k 1=k 2 ② I 1 I 2 k 1k 2=— 1 (2)若 I 1 : A 1x B 1 y C 1 0, I 2 : A 2X B 2y C 2 若A 1、A 2、B 1、B 2都不为零 I 1//I 2 △邑 C !; A 2 B 2 C 2 若i i 与12的夹角为,则tan 注意:(1 ) I i 到12的角,指从 k i k 2 1 kk 11按逆时针方向旋转到 I 2所成的 角, (0,) (1) 倾斜角 , (0,); (2) a, b 夹角, [0, ]; (3) 直线I 与平面 的夹角 ,[0,,] (4) I 1与I 2的夹角为 [0,—],其 中 2 (5) 二面角, (0,]; (6) I 1到I 2的角, (0, ) I 1//I 2时夹角 =0; I 1 I 2 A 1A 2+B 1B 2=0;
全等三角形作辅助线专题一重点截长补短法可
D C B A E D F C B A 全等三角形作辅助线经典例题 常见辅助线的作法有以下几种: 1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”. 2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全 等变换中的“旋转”. 3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中 的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻 转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形) 5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是 之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、倍长中线(线段)造全等 1:已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________. 2:如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小. 3:如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE. E D C B A 中考应用: 以ABC ?的两边AB、AC为腰分别向外作等腰Rt ABD ?和等腰Rt ACE ?,90, BAD CAE ∠=∠=? 连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC ?为直角三角形时,AM与DE的位置关系是,线段AM与DE的数量关系是; (2)将图①中的等腰Rt ABD ?绕点A沿逆时针方向旋转?θ(0<θ<90)后,如图②所示,(1)
全等三角形截长补短拔高练习(含答案)
八年级数学全等三角形辅助线添加之截长补短 (全等三角形)拔高练习 试卷简介:本讲测试题共两个大题,第一题是证明题,共7个小题,每小题10分;第二题解答题,2个小题,每小题15分。 学习建议:本讲内容是三角形全等的判定——辅助线添加之截长补短,其中通过截长补短来添加辅助线是重点,也是难点。希望同学们能学会熟练通过截长补短来做辅助线,进而构造出全等的三角形。 一、解答题(共1道,每道20分) 1.如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=(AD+AB).问:∠1和∠2有何关系? 答案: 解:∠1+∠2=180° 证明:过点C作CF⊥AN于点F,由于AC平分∠NAM,所以CF=CE,则在Rt△ACF和Rt△ACE 中 ∴△ACF≌△ACE(HL),∴AF=AE,由于2AE=AD+AB,所以AB-AE=AF-AD ∴DF=BE,在△CFD和△CEB中所以△CFD≌△CEB(SAS),∴∠2=∠FDC,又∠1+∠FDC=180°,∴∠1+∠2=180°。 解题思路:见到角平分线就要想到作垂直,找到全等关系是解决此类问题的关键 易错点:找到三角形全等的所有条件
试题难度:四颗星知识点:三角形 二、证明题(共8道,每道10分) 1.如图,已知△ABC中,∠A=90°,AB=AC,BE平分∠ABC,CE⊥BD于E,求证:CE=BD. 答案: 延长CE交BA的延长线于点H,由BE平分ABC,BE CE,得CE=EH=CH。 又1+H=90°,,2+H=90° 1= 2 在△ACH和△ABD中 HAC=DAB=90° AC=AB 1= 2 △ACH≌△ABD(ASA) CH=BD CE=CH=BD 解题思路: 根据题意,要证明CE=BD,延长CE与BA,由题意的垂直平分线可得CE的两倍长CH,只需证明CH=BD即可,很显然有全等可以证明出结论 易错点:不能正确利用题中已知条件BF平分∠ABC,CE⊥BD于E,做出辅助线,进而解答。试题难度:三颗星知识点:全等三角形的判定与性质 2. 如图,已知正方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE=DF.
解析几何公式大全
解析几何中的基本公式 1、 两点间距离:若)y ,x (B ),y ,x (A 2211,则212212)()(y y x x AB -+-= 2、 平行线间距离:若0C By Ax :l ,0C By Ax :l 2211=++=++ 则:2 2 21B A C C d +-= 注意点:x ,y 对应项系数应相等。 3、 点到直线的距离:0C By Ax :l ),y ,x (P =++ 则P 到l 的距离为:2 2 B A C By Ax d +++= 4、 直线与圆锥曲线相交的弦长公式:? ? ?=+=0)y ,x (F b kx y 消y :02 =++c bx ax ,务必注意.0>? 若l 与曲线交于A ),(),,(2211y x B y x 则:2122))(1(x x k AB -+= 5、 若A ),(),,(2211y x B y x ,P (x ,y )。P 在直线AB 上,且P 分有向线段AB 所成的比为λ, 则??? ????λ+λ+=λ+λ+=112121y y y x x x ,特别地:λ=1时,P 为AB 中点且??????? +=+=2221 21y y y x x x 变形后:y y y y x x x x --=λ--= λ21 21或 6、 若直线l 1的斜率为k 1,直线l 2的斜率为k 2,则l 1到l 2的角为),0(,π∈αα 适用范围:k 1,k 2都存在且k 1k 2≠-1 , 2 11 21tan k k k k +-= α 若l 1与l 2的夹角为θ,则= θtan 2 1211k k k k +-,]2,0(π ∈θ 注意:(1)l 1到l 2的角,指从l 1按逆时针方向旋转到l 2所成的角,范围),0(π l 1到l 2的夹角:指 l 1、l 2相交所成的锐角或直角。 (2)l 1⊥l 2时,夹角、到角= 2 π 。
八年级数学 全等三角形截长补短法专题
A D B C E 图2-1 截长补短法 人教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例. 例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC . 求证:∠BAD +∠BCD =180°. 分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现. 证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2 ∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中, ?? ?==CD AD DF DE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180° 例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB . 求证:CD =AD +BC . 分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的. 证明:在CD 上截取CF =BC ,如图2-2 在△FCE 与△BCE 中, ?? ? ??=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1. A B C D 图1-1 F E D C B A 图1-2 A D B C E F 1 234 图2-2
全等三角形常见的几何模型
1、绕点型(手拉手模型) (1)自旋转:?????? ?,造中心对称遇中点旋 全等遇等腰旋顶角,造旋转 ,造等腰直角 旋遇,造等边三角形旋遇自旋转构造方法00 00018090906060 (2 )共旋转(典型的手拉手模型) 例1、在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) AE=DC ( 3) AE 与DC 的夹角为60。 (4) △AGB ≌△DFB (5) △ EGB ≌△CFB (6) BH 平分∠AHC (7) GF ∥AC 变式练习1、如果两个等边三角形△ABD 和△BCE ,连接 AE 与CD ,证明: (1) △ABE ≌△DBC (2) AE=DC (3) AE 与DC 的夹角为60。 (4) AE 与DC 的交点设为H,BH 平分∠AHC 变式练习2、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1)△ABE ≌△DBC (2)AE=DC (3)AE 与DC 的夹角为60。 (4)AE 与DC 的交点设为H,BH 平分∠AHC
3、(1)如图1,点C 是线段AB 上一点,分别以AC ,BC 为边在AB 的同侧作等边△ACM 和△CBN ,连接AN ,BM .分别取BM ,AN 的中点E ,F ,连接CE ,CF ,EF .观察并猜想△CEF 的形状,并说明理由. (2)若将(1)中的“以AC ,BC 为边作等边△ACM 和△CBN ”改为“以AC ,BC 为腰在AB 的同侧作等腰△ACM 和△CBN ,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由. 例4、例题讲解: 1. 已知△ABC 为等边三角形,点D 为直线BC 上的一动点(点D 不与B,C 重合),以AD 为边作菱形ADEF(按A,D,E,F 逆时针排列),使∠DAF=60°,连接CF. (1) 如图1,当点D 在边BC 上时,求证:① BD=CF ? ②AC=CF+CD. (2)如图2,当点D 在边BC 的延长线上且其他条件不变时,结论AC=CF+CD 是否成立?若不成立,请写出AC 、CF 、CD 之间存在的数量关系,并说明理由; (3)如图3,当点D 在边BC 的延长线上且其他条件不变时,补全图形,并直接写出AC 、CF 、CD 之间存在的数量关系。 2、半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 例1、如图,正方形ABCD 的边长为1,AB,AD 上各存在一点P 、Q ,若△APQ 的周长为2, 求PCQ 的度数。 Q
全等三角形~截长补短
1 2 截长补短 截长补短”是几何证明题中十分重要的方法, 通常用来证明几条线段的数量关系, 即若 题目条件或结论中含有 a b c ”的条件,需要添加辅助线时可以考虑 截长补短”的方法。 另外的较短线段。 补短法: ①延长较短线段中的一条,使延长出来的线段等于另外的较短线段,然后证明两线段之和等 于较长线段。即延长a ,得到b ,证:a b ①延长较短线段中的一条, 使延长后的线段等于较长线段, 一条较短线段。 即延长a ,得到c ,证:b c-a 。 例1.已知:如图,在 △ ABC 中,△仁△Z, △ B=2AC .求证: 1.补短法: 证明:如图,延长 AB 到E ,使BE=BD ,连接DE . △ △ABD 是 △BDE 的一个外角 △ △ABDME + △BDE ABE=BD △ △EMBDE △ △ABD=2 △E △ △ABD=2 △C △ △EMC 在 AADE 和 AADC 中 △ △ADE △△ADC (AAS )截长法:在较长的线段上截取一条线段等于较短线段, 再设法证明较长线段的剩余线段等于 然后证明延长出来的部分等于另 AC=AB+BD . AD AD
1 2 证明:如图,在 CD 上截取CF=CB . △CE 平分△CBD 在△CFE 和 △CBE 中 △AE=AC △AC=AB + BE=AB + BD 2.截长法: 证明:如图,在 AC 上截取AF=AB ,连接DF . 在△ABD 和△AFD 中 AB AF AD AD △ △ABD △△AFD ( SAS ) △ ABMAFD , BD=FD △ △B=2 △C △ △AFD =2 △C △ △AFD 是^DFC 的一个外角 △ △AFD me + 舉DC △ AFDCmC ADF=FC ABD=FC △AC=AF+FC=AB+BD 例2.如图,在四边形 ABCD 中,△ A=AB=90,点 E 为AB 边上一点,且 DE 平分△ ADC , CE 平分△ BCD .求证:CD=AD+BC . CF CB CE CE
解析几何公式大全
解析几何中的基本公 式 1、两点间距离:若)y ,x (B ),y ,x (A 2211,则212212)()(y y x x AB -+-= 2、平行线间距离:若0C By Ax :l , 0C By Ax :l 2211=++=++ 则:2 2 21B A C C d +-= 注意点:x ,y 对应项系数应相等。 3、点到直线的距离:0C By Ax :l ),y ,x (P =++οο 则P 到l 的距离为:2 2 B A C By Ax d +++= οο 4、直线与圆锥曲线相交的弦长公式:???=+=0 )y ,x (F b kx y 消y :02=++c bx ax ,务必注意.0>? 若l 与曲线交于A ),(),,(2211y x B y x 则:2122))(1(x x k AB -+= 5、若A ),(),,(2211y x B y x ,P (x ,y )。P 在直线AB 上,且P 分有向线段AB 所成的比为λ, 则??? ????λ+λ+=λ+λ+=112121y y y x x x ,特别地:λ=1时,P 为AB 中点且??????? +=+=2221 21y y y x x x
变形后:y y y y x x x x --=λ--= λ21 21或 6、若直线l 1的斜率为k 1,直线l 2的斜率为k 2,则l 1到l 2的角为),0(,π∈αα 适用范围:k 1,k 2都存在且k 1k 2≠-1 , 2 11 21tan k k k k +-= α 若l 1与l 2的夹角为θ,则= θtan 2 1211k k k k +-,]2,0(π ∈θ 注意:(1)l 1到l 2的角,指从l 1按逆时针方向旋转到l 2所成的角,范围),0(π l 1到l 2的夹角:指 l 1、l 2相交所成的锐角或直角。 (2)l 1⊥l 2时,夹角、到角= 2 π 。 (3)当l 1与l 2中有一条不存在斜率时,画图,求到角或夹角。 7、(1)倾斜角α,),0(π∈α; (2)]0[,π∈θθ→ →,,夹角b a ; (3)直线l 与平面]2 0[π ∈ββα,,的夹角; (4)l 1与l 2的夹角为θ,∈θ]2 0[π ,,其中l 1//l 2时夹角θ=0; (5)二面角,θ],0(π∈α; (6)l 1到l 2的角)0(π∈θθ,, 8、直线的倾斜角α与斜率k 的关系
全等三角形常见的几何模型
全等三角形常见的几何 模型 集团文件版本号:(M928-T898-M248-WU2669-I2896-DQ586-M1988)
1、绕点型(手拉手模型) (1)自旋转:???????,造中心对称遇中点旋全等 遇等腰旋顶角,造旋转,造等腰直角 旋遇,造等边三角形 旋遇自旋转构造方法0000 018090906060 (2)共旋转(典型的手拉手模型) 例1、在直线ABC 的同一侧作两个等边三角形△ABD 和 △ BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) A E=DC (3) A E 与DC 的夹角为60。 (4) △AGB ≌△DFB (5) △EGB ≌△CFB (6) B H 平分∠AHC (7) G F ∥AC 变式练习1、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1) △ABE ≌△DBC (2) A E=DC (3) A E 与DC 的夹角为60。 (4) A E 与DC 的交点设为H,BH 平分∠AHC 变式练习2、如果两个等边三角形△ABD 和△BCE ,连接AE 与CD ,证明: (1)△ABE ≌△DBC (2)AE=DC (3)AE 与DC 的夹角为60。 (4)AE 与DC 的交点设为H,BH 平分∠AHC
3、(1)如图1,点C是线段AB上一点,分别以AC,BC为边在AB的同侧作等边△ACM和△CB N,连接AN,BM.分别取BM,AN的中点E,F,连接CE,CF,EF.观察并猜想△CEF的形状,并说明理由. (2)若将(1)中的“以AC,BC为边作等边△ACM和△CBN”改为“以AC,BC为腰在AB的同侧作等腰△ACM和△CBN,”如图2,其他条件不变,那么(1)中的结论还成立吗?若成立,加以证明;若不成立,请说明理由. 例4、例题讲解: 1. 已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B,C重合),以AD为边作菱形ADEF(按A,D,E,F逆时针排列),使∠DAF=60°,连接CF. (1)?如图1,当点D在边BC上时,求证:①?BD=CF???②AC=CF+CD. (2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由; ? (3)如图3,当点D在边BC的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD 之间存在的数量关系。 2、半角模型 说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。 例1、如图,正方形ABCD的边长为1,AB,AD上各存在一点P、Q,若△APQ的周长为2, 求PCQ 的度数。
全等三角形之截长补短法
例题1 如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD. 考点:全等三角形的判定与性质. 专题:证明题. 分析:利用已知条件,求得∠B=∠E,∠2=∠1,AD=AD,得出△ABD≌△AED(AAS),∴AE=AB.∵AE=AC+CE=AC+CD,∴AB=AC+CD. 解答:证法一:如答图所示,延长AC,到E使CE=CD,连接DE. ∵∠ACB=90°,AC=BC,CE=CD, ∴∠B=∠CAB=45°,∠E=∠CDE=45°, ∴∠B=∠E. ∵AD平分∠BAC, ∴∠1=∠2 在△ABD和△AED中, ∠B=∠E,∠2=∠1,AD=AD, ∴△ABD≌△AED(AAS). ∴AE=AB. ∵AE=AC+CE=AC+CD, ∴AB=AC+CD. 证法二:如答图所示,在AB上 截取AE=AC,连接DE, ∵AD平分∠BAC, ∴∠1=∠2. 在△ACD和△AED中, AC=AE,∠1=∠2,AD=AD, ∴△ACD≌△AED(SAS). ∴∠AED=∠C=90,CD=ED, 又∵AC=BC,
∴∠B=45°. ∴∠EDB=∠B=45°. ∴DE=BE, ∴CD=BE. ∵AB=AE+BE, ∴AB=AC+CD. 点评:本题考查了全等三角形的判定和性质;通过SAS的条件证明三角形全等,利用三角形全等得出的结论来求得三角形各边之间的关系. 例题2 图,AD是△ABC中BC边上的中线,求证:AD<(AB+AC). 考点:全等三角形的判定与性质;三角形三边关系. 专题:计算题. 分析:可延长AD到E,使AD=DE,连BE,则△ACD≌△EBD得BE=AC,进而在△ABE中利用三角形三边关系,证之. 解答:证明:如图延长AD至E,使AD=DE,连接BE. ∵BD=DC,AD=DE,∠ADC=∠EDB ∴△ACD≌△EBD∴AC=BE 在△ABE中,AE<AB+BE,即2AD<AB+AC∴AD<(AB+AC) 点评:本题主要考查全等三角形的判定及性质以及三角形的三边关系问题,能够熟练掌握.
解析几何常用公式
1. AB →,A 为AB →的起点,B 为AB →的终点。线段AB 的长度称作AB →的长度,记作|AB → |.数轴上同向且 相等的向量叫做相等的向量.....。零向量的方向任意。..........在数轴上任意三点A 、B 、C ,向量AB →、BC → 、AC →的坐标都具有关系:AC =AB +BC . .. AC →=AB →+ 2.设 AB → 是数轴上的任一个向量,则AB =OB -OA =x 2-x 1,d (A ,B )=|AB |=|x 2-x 1|. 4.. A (x 1,y 1),B (x 2,y 2),则两点A 、B 的距离公式d (A ,B )=?x 2-x 1?2+?y 2-y 1?2 若B 点为原点,则d (A ,B )=d (O ,A )=x 21+y 21; 5. A (x 1,y 1),B (x 2,y 2),中点M( x 1+x 22, y 1+y 2 2 ). A (x ,y )关于M (a ,b )的对称点B(2x 0-x ,2y 0-y ). 6. 直线倾斜角::x 轴正向与直线向上的方向所成的角叫做这条直线的倾斜角,规定,与x 轴 平行或重合的直线的倾斜角为0°. 7.直线的位置与斜率、倾斜角的关系 ①k =0时,倾斜角为0°,直线平行于x 轴或与x 轴重合. ②k >0时,直线的倾斜角为锐角,k 值增大,直线的倾斜角也增大,此时直线过第一、三象限. ③k <0时,直线的倾斜角为钝角,k 值增大,直线的倾斜角也增大,此时直线过第二、四象限. ④垂直于x 轴的直线的斜率不存在,它的倾斜角为90°. 8. 若直线l 上任意两点A (x 1,y 1),B (x 2,y 2)且x 1≠x 2,则直线l 的斜率k =y 2-y 1 x 2-x 1 . 9.直线方程的五种形式 (1)点斜式:经过点P 0(x 0,y 0)的直线有无数条,可分为两类:斜率存在时,直线方程为 y -y 0=k (x -x 0);斜率不存在时,直线方程为x =x 0. (2)斜截式:已知点(0,b ),斜率为k 的直线y =kx +b 中,截距b 可为正数、零、负数. (3)两点式: y -y 1y 2-y 1=x -x 1 x 2-x 1(x 1≠x 2,y 1≠y 2 ) (4) 截距式:当直线过(a,0)和(0,b )(a ≠0,b ≠0)时,直线方程可以写为x a +y b =1,当直线斜率 不 存在(a =0)或斜率为0(b =0)时或直线过原点时,不能用截距式方程表示直线. (5)一般式:Ax +By +C =0的形式.(220A B +≠)
(精品)全等三角形——截长补短法
D C B A 全等三角形——截长补短法 一、知识梳理: 截长补短法 截长补短法是几何证明题中十分重要的方法。通常来证明几条线段的数量关系。 截长法: (1)过某一点作长边的垂线 (2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 补短法 (1)延长短边。 (2)通过旋转等方式使两短边拼合到一起。…… 二、典型例题: 例1、如图,在ABC ?中,60BAC ∠=?,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数. 及时练习: 如图所示,在Rt △ABC 中,∠C=90°,BC=AC ,AD 平分∠BAC 交BC 于D ,求证:AB=AC+CD . 例2、已知ABC ?中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.
N E B M A D M D C B A D O E C B A 及时练习: 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=?,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系? 例3、如图.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM . 求证:AE =BC +CE . 及时练习: 如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k , ∠AMD =75°,∠BMC =45°,则AB 的长为 ( ) A . a B . k C . 2 k h + D . h 例4、以ABC ?的AB 、AC 为边向三角形外作等边ABD ?、ACE ?,连结CD 、BE 相交于点O . 求证:OA 平分DOE ∠.
高中解析几何秒杀公式及解题套路
高中解析几何秒杀公式及解题套路 高中解析几何秒杀公式是什幺,解析几何解题套路有哪些,怎幺能 用一套完整的思路做所有类似的题目?把所有类型题都搞定?下面是高中解 析几何秒杀公式及解题套路,希望你看完能上岸。 1高考解析几何的统一解题套路以高考解析几何为例1、问题都是以平 面上的点、直线、曲线如圆、椭圆、抛物线、双曲线这三大类几何元素为基础构成的图形的问题2、演绎规则就是代数的演绎规则,或者说就是列方 程、解方程的规则。当然,能用代数规则处理的问题必须是代数形式的,比如,平面上的点、直线、曲线构成的图形能用代数方法来处理,前提是构成 这些图形的点、直线、曲线必须是代数形式的。有了以上两点认识,我们可 以毫不犹豫地下这幺一个结论,那就是解决高考解析几何问题无外乎做两项 工作1、几何问题代数化。2、用代数规则对代数化后的问题进行处理。至此,我们可以发掘出一套规整的高考解析几何的统一解题套路步骤1:把题目中 的点、直线、曲线这三大类基础几何元素用代数形式表示出来(一化)步骤 2:把题目中的点与直线、曲线的从属关系用代数形式表示出来(二代)说明:这里的“从属关系”指的是什幺?实际上,在解析几何中,“点”是比直线、曲线 更基础的几何元素——任何几何图形,包括直线和曲线,都被视为是由一个 个的“点”构成的(用数学语言来表达:任何几何图形,包括直线和曲线,都 是由点构成的集合)。但为了使我们的解题套路各步骤之间条例更分明。 我们把点、直线、曲线视为构成任何其它几何图形的基础。所以,这里的“从属关系”是点与直线、曲线的属于关系问题——如果某个点在某条直线或 曲线上,那幺这个点的坐标就可代入这条直线或曲线的方程。步骤3:图形
全等三角形专题——截长补短练习
全等三角形专题 ——截长补短 角的平分线具有其特有的性质,这一性质在许多问题里都有着广泛的应用,而“截长补短法”又是解决这一类问题的一种特殊的方法,利用此种方法常可使思路豁然开朗。 1、 如图, AD BC //,点E 在线段AB 上,ADE CDE ∠=∠,DCE ECB ∠=∠, 求证:CD=AD+BC 2、已知如图,1=2∠∠,P 为BN 上一点,且PD BC ⊥于点D,且0 180 BAP BCP ∠+∠=, 求证:AB+BC=2BD 2、 已知,如图在ABC 中,2 C B ∠ = ∠,12∠=∠, 求证:AB=AC+CD 4、已知ABC 中,0 60A ∠=,BD ,CE 分别评分ABC ∠和ACB ∠,BD,CE 交于点O ,试判断BE,CD,BC 的数量关系,并加以证明。 5、如图所示,ABC 是边长为1的等边三角形,BDC 是顶角为0 120的等腰三角形,以D 为顶点的一个 060的MDN ∠,点M ,N 分别在AB,AC 上,求AMN 的周长。 6、如图,在ABC 中,0 60BAC ∠=,AD 是BAC ∠的平分线,且AC=AB+BD,求ABC ∠的度数。 7、已知如图,ABCD 是正方形,FAD FAE ∠=,求证:BE+DF=AF 8、在ABC 中,2B C ∠=∠,且AD BC ⊥于D ,求证:CD=AB+BD
全等三角形在中考中必考题型 1、已知,在中ABC ,0C=90∠,AC=BC ,直线l绕点A旋转,过点B,C分别向直线l做垂线,垂足 分别是点D、点E。 (1)如图1,求证:BD+CE=AE; (2)当直线l绕点A顺时针转到如图2,则BD、CE 、AE 之间满足的数量关系 是 2、已知ABCD ,连接AC,AC=AB,E为线段BC上的一动点,F为直线DC上一动点,且EAF B ∠=∠。 (1)如图(1) ,当060B ∠=时,求证:CE+CF=CA 。 3、已知ABC ,有一个以P 为顶点的角,且1 2 APE ACD ∠=∠,将此角的顶点放在边BC 上,角的一边始 终经过点A ,另一边与ACB ∠的外角的平分线交于点E 。 (1)如图1,当ABC 三角形为等边三角形时,求证:CP+CE=CA 。 4、在中Rt ABC 中,090ACB ∠=,AC=BC ,点P 为BC 所在直线上一点,分别过点B 、C 作直线AP 的垂线,垂足分别为点D ,X 。 (1)当点P 在线段BC 上时,如图1,求证:2AD BD CE -= (2)当点P 在CB 的反向延长线上时,如图2,线段AD 、BD 、CE 三者之间满足的数量关系是 B
