二次函数图像性质总结

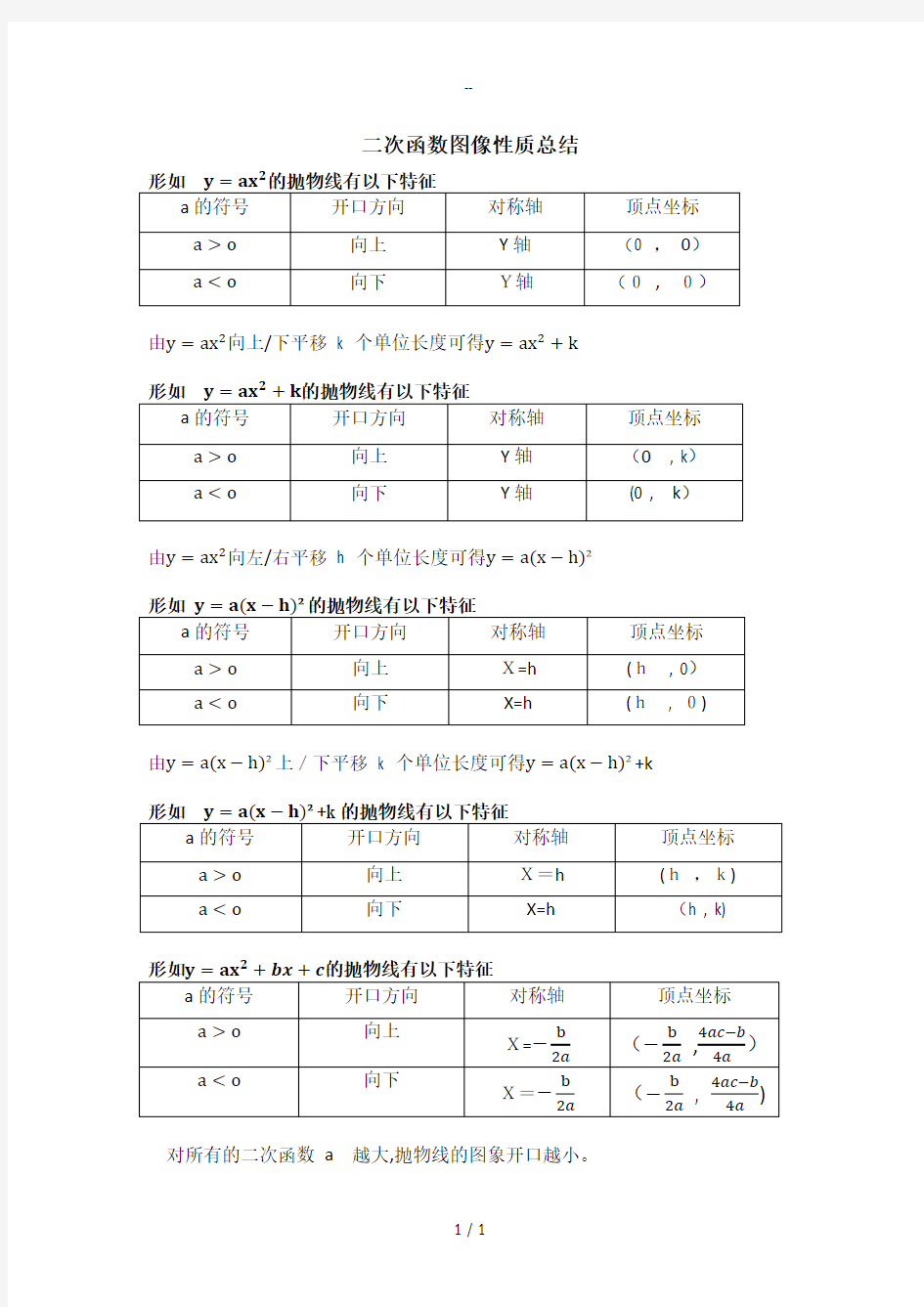
由y=ax2向上/下平移k 个单位长度可得y=ax2+k

由y=ax2向左/右平移h 个单位长度可得y=a(x?h)2

由y=a(x?h)2上／下平移k 个单位长度可得y=a(x?h)2+k

对所有的二次函数a越大,抛物线的图象开口越小。

对所有的二次函数，其性质如下图：

如何求函数解析式：

（1）形如y=ax2:图像上任意一点(ｘ ,y）带入求ａ的值。可得函数解析式。

（2）形如y=ax2+k: 需知两点，顶点(0，k）和任意一点（x ,y) 带入,将k、ａ求出。可得函数解析式。

（3）形如y=a(x?h)2：需知两点,顶点（h，０）和任意一点(x ,y）带入，将h、a求出。可得函数解析式。

（4）y=a(x?h)2+k : 需知两点,顶点(h,k)和任意一点(x ,y）带入,将ｈ、ｋ、a求出。可得函数解析式。

（5）形如y=ax2+bx+c: 需知三点,将三个点的x、y值带入,建立三元一次方程组，将a、b、c求出。可得函数解析式。

初中数学二次函数知识点总结

初中数学二次函数知识点总结 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN

初中数学二次函数知识点总结原文阅读 I.定义与定义表达式一般地，自变量x和因变量y之间存在如下关系：y=ax^2+bx+c （a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下,IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大.）则称y为x的二次函数。二次函数表达式的右边通常为二次三项式。 II.二次函数的三种表达式一般式：y=ax^2+bx+c（a，b，c为常数，a≠0）顶点式：y=a(x-h)^2+k [抛物线的顶点P（h，k）] 交点式：y=a(x-x?)(x-x ?) [仅限于与x轴有交点A（x?，0）和 B（x ?，0）的抛物线] 注：在3种形式的互相转化中，有如下关系: h=-b/2a k=(4ac-b^2)/4a x?,x?=(-b±√b^2-4ac)/2a III.二次函数的图像在平面直角坐标系中作出二次函数y=x^2的图像，可以看出，二次函数的图像是一条抛物线。

IV.抛物线的性质 1.抛物线是轴对称图形。对称轴为直线 x = -b/2a。对称轴与抛物线唯一的交点为抛物线的顶点P。特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0） 2.抛物线有一个顶点P，坐标为：P ( -b/2a ，(4ac-b^2)/4a )当-b/2a=0时，P 在y轴上；当Δ= b^2-4ac=0时，P在x轴上。 3.二次项系数a决定抛物线的开口方向和大小。当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口。|a|越大，则抛物线的开口越小。 4.一次项系数b和二次项系数a共同决定对称轴的位置。当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右。 5.常数项c决定抛物线与y轴交点。抛物线与y轴交于（0，c） 6.抛物线与x轴交点个数 Δ= b^2-4ac＞0时，抛物线与x轴有2个交点。 Δ= b^2-4ac=0时，抛物线与x轴有1个交点。

二次函数的图像与性质知识点及练习

第二节二次函数的图像与性质 1．能够利用描点法做出函数y ＝ax 2，y=a(x-h)2 ，y ＝a(x-h)2 +k 和c bx ax y ++=2图象，能根据图象认识和理解二次函数的性质； 2．理解二次函数c bx ax y ++=2中a 、b 、c 对函数图象的影响。一、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点. 例1. 在同一平面坐标系中分别画出二次函数y ＝x 2 ，y ＝-x 2 ，y ＝2x 2 ，y ＝-2x 2 ，y ＝2（x-1）2 的图像。一、二次函数的基本形式 1. y ＝ax 2 的性质：

2. y＝ax2＋k的性质：（k上加下减） 3. y＝a（x-h）2的性质：（h左加右减） 4. y＝a (x－h)2＋k的性质： 5. y＝ax2+bx+c的性质：

二、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下： 2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二： ⑴c bx ax y ++=2 沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2 变成 m c bx ax y +++=2（或m c bx ax y -++=2） ⑵c bx ax y ++=2 沿x 轴平移：向左（右）平移m 个单位，c bx ax y ++=2 变成 c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即2 2424b ac b y a x a a -? ?=++ ??? ，其中2424b ac b h k a a -=-= ，．六、二次函数图象的对称二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1. 关于x 轴对称【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位

中考数学二次函数知识点总结

中考数学二次函数知识点总结 I. 定义与定义表达式一般地，自变量x和因变量y之间存有如下关系：y=ax^2+bx+c (a, b, c为常数，a z0,且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下，lal还能够决定开口大小，lal越大开口就越小,IaI 越小开口就越大. )则称y 为x 的二次函数。二次函数表达式的右边通常为二次三项式。 II. 二次函数的三种表达式一般式：y=ax A2+bx+c (a, b, c 为常数，a z0) 顶点式：y=a(x-hF2+k[抛物线的顶点P (h, k)] 交点式：y=a(x-x)(x-x)[ 仅限于与x 轴有交点A(x, 0)和B( x, 0) 的抛物线] 注：在 3 种形式的互相转化中,有如下关系： h=-b/2a k=(4ac-bA2)/4a x,x=(- b±V bA2-4ac)/2a III. 二次函数的图像在平面直角坐标系中作出二次函数y=xA2 的图像,能够看出,二次函数的图像是一条抛物线。 IV. 抛物线的性质 1. 抛物线是轴对称图形。对称轴为直线x=-b/2a 。对称轴与抛物线的交点为抛物线的顶点P。特别地，当b=0时，抛物线的对称轴是y 轴(即直线x=0)

2. 抛物线有一个顶点P,坐标为：P（-b/2a , （4ac-"2）/4a）当-b/2a=0 时，P在y轴上；当△二b^2-4ac=0时，P在x轴上。 3. 二次项系数a 决定抛物线的开口方向和大小。当a>0时，抛物线向上开口；当a v0时，抛物线向下开口。|a|越大，则抛物线的开口越小。 4. 一次项系数b 和二次项系数a 共同决定对称轴的位置。当a与b同号时（即ab> 0）,对称轴在y轴左；当a与b异号时（即ab v 0）,对称轴在y轴右。 5. 常数项c 决定抛物线与y 轴交点。抛物线与y 轴交于（0, c） 6. 抛物线与x 轴交点个数 △=b A2-4ac >0时，抛物线与x轴有2个交点。 △=bA2-4ac=0时，抛物线与x轴有1个交点。 △=bA2-4ac v 0时，抛物线与x轴没有交点。 X的取值是虚数（x=-b±V bA2 —4ac的值的相反数，乘上虚数i，整个式子除以2a） V. 二次函数与一元二次方程特别地,二次函数（以下称函数）y=axA2+bx+c, 当y=0 时,二次函数为关于x 的一元二次方程（以下称方程）,即 axA2+bx+c=0 此时，函数图像与x轴有无交点即方程有无实数根。函数与x轴交点的横坐标即为方程的根。

二次函数知识点汇总(全)

二次函数知识点(第一讲) 一、二次函数概念： 1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征： ⑴ 等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． ⑵ a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数的基本形式 1. 二次函数基本形式：2y ax =的性质： a 的绝对值越大，抛物线的开口越小。 2. 2y ax c =+的性质：（上加下减）

3. ()2 y a x h =-的性质：（左加右减） 4. ()2 y a x h k =-+的性质：三、二次函数图象的平移 1. 平移步骤：方法一：⑴ 将抛物线解析式转化成顶点式()2 y a x h k =-+，确定其顶点坐标()h k ，； ⑵ 保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：

【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2. 平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．概括成八个字“左加右减，上加下减”．方法二： ⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成 m c bx ax y +++=2（或m c bx ax y -++=2） ⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成 c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）四、二次函数() 2 y a x h k =-+与2 y ax bx c =++的比较从解析式上看，()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即2 2424b ac b y a x a a -? ?=++ ??? ，其中2424b ac b h k a a -=-= ，．五、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点. 六、二次函数2y ax bx c =++的性质 1. 当0a >时，抛物线开口向上，对称轴为2b x a =-，顶点坐标为2424b ac b a a ??-- ??? ，．当2b x a <- 时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2b x a =-时，y 有

二次函数的图像及性质

《二次函数的图像及性质》教学案例及反思教师：同学们，我们上一节课一起研究了二次函数的表达式，那么我们一起来回忆一下表达式是什么？学生齐答：y=ax2+bx+c(a,b,c是常数，a不为0) 教师：好，那么请同学们在黑板上写出一些常数较简单的二次函数表达式. （学生表现很踊跃，一下写出了十多个）教师：黑板上这些二次函数大致有几个类型？学生：（讨论了3分钟）四大类!有y=ax2+bx+c;y=ax2+bx;y=ax2+c;y=ax2! 教师：太棒了！同学们归纳的很好，今天我们就一起来研究比较简单的一种y=ax2的图像及性质！教师在学生板书的函数中选了四个，并把复杂的系数换成简单的常数，找到如下函数：y=x2;y=-x2;y=2x2;y=-2x2.(教师在这里让学生自己准备素材！) 教师启发学生利用函数中的“列表，描点，连线”的方法，把画上述四个函数的任务分配给A,B,C,D小组，一组一个在已画好的坐标系的小黑板上动手操作.生在自己提供的素材上进行再“加工”，兴趣很大，合作交流充分，课堂气氛活跃.教师到每组巡视、指导，在确认画图全部正确的情况下，提出了要求，开始了探究之旅. 教师：请同学们小组之间比较一下，你们画的图象位置一样吗？学生；不一样. 教师：有什么不一样？（开始聚焦矛盾）学生:开口不一样. 学生A：走向不一样. 学生B：经过的象限不一样. 学生C：我们的图象在原点的上方，他们的图象在原点的下方. 教师：看来是有些不一样，那么它们位置的不一样是由什么要素决定的？（教师指明了探究方向，但未指明具体的探究之路，这是明智的）学生：是由二次项系数的取值确定的. 教师：好了，根据同学们的回答，能得到图象或函数的那些结论？（顺水推舟，放手让学生一搏）热烈讨论后，学生D回答并板书，当a>0时，图象在原点的上方，当a<0时，图象在原点的下方。学生E:当a>0时，图象开口向上；当a<0时，图象开口向下. 学生A站起来补充:还有顶点,顶点坐标(0,0),对称轴为y轴! （这个过程约用了十多分时间，学生体会非常充分，从学生的神情看，绝大多数学生已接受了这几个学生的板书，但教师未对结论进行优化。怎么没有一个学生说出二次函数的性质呢？短暂停顿后，教师确定了思路）教师：刚才你们是研究图象的性质，你们能否由图象性质得出相应的函数的性质？看着学生茫然的目光,我在思考是不是我的问题---- 教师：请看同学们的板书，能揣摩图象“走向”的意思吗？学生：（七嘴八舌）当a>0时，图象从左上向下走到原点后在向右上爬；当a<0时，图象从左下向上爬到原点后在向右下走（未出现教师所预期的结论）教师：好，你们从图象的直观形象来理解的图象性质，很贴切，你们能从自变量与函数值之间的变化角度来说明“向上爬”和“向下走”吗？

二次函数的性质

20.4二次函数的性质教学目标： 1.从具体函数的图象中认识二次函数的基本性质. 2.了解二次函数与二次方程的相互关系. 3.探索二次函数的变化规律,掌握函数的最大值(或最小值)及函数的增减性的概念,会求二次函数的最值,并能根据性质判断函数在某一范围内的增减性教学重点：二次函数的最大值,最小值及增减性的理解和求法. 教学难点：二次函数的性质的应用. 教学过程：一、复习引入二次函数: y=ax2 +bx + c (a 1 0)的图象是一条抛物线,它的开口由什么决定呢? 补充: 当a的绝对值相等时,其形状完全相同,当a的绝对值越大,则开口越小,反之成立. 二、新课教学: 1.探索填空: 根据下边已画好抛物线y= -2x2的顶点坐标是, 对称轴是，在侧，即x_____0时, y随着x的增大而增大；在侧，即x_____0时, y随着x的增大而减小. 当x= 时，函数y最大值是____. 当x____0时,y<0. 2. 探索填空:：据上边已画好的函数图象填空：抛物线y= 2x2的顶点坐标是, 对称轴是，在侧，即x_____0时, y随着x的增大而减少；在侧，即x_____0时, y随着x的增大而增大. 当x= 时，函数y最小值是____. 当x____0时,y>0

3.归纳: 二次函数y=ax2+bx+c(a≠0)的图象和性质 (1).顶点坐标与对称轴 (2).位置与开口方向 (3).增减性与最值当a ﹥0时，在对称轴的左侧，y随着x的增大而减小；在对称轴的右侧，y随着x的增大而增大；当时，函数y有最小值。当a ﹤0时，在对称轴的左侧，y随着x的增大而增大；在对称轴的右侧，y随着x的增大而减小。当时，函数y有最大值 4.探索二次函数与一元二次方程二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图所示. (1).每个图象与x轴有几个交点？ (2).一元二次方程x2+2x=0,x2-2x+1=0有几个根?验证一下一元二次方程x2-2x+2=0有根吗? (3).二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系? 归纳: (3).二次函数y=ax2+bx+c的图象和x轴交点有三种情况: ①有两个交点, ②有一个交点, ③没有交点. 当二次函数y=ax2+bx+c的图象和x轴有交点时, 交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax2+bx+c=0的根.

二次函数知识点总结大全

1. 二次函数的定义: 2、二次函数的解析式三种形式与y 轴交点坐标（0，c ）（1）二次函数y=ax 2 （a z 0）的图象是一条抛物线，其顶点是原点，对称轴是 y 轴；当a >0时，抛物线开口向上，顶点是最低点；当 a v 0时，抛物线开口向下，顶点是取咼点； 2 ⑵二次函数?' 1 :二' b_ h_ 当a >0时，抛物线开口向上，图象有最低点，且 x >-二：，y 随x 的增大而增大，x v -二：， y 随x 的增大而减小；当a v 0时，抛物线开口向下，图象有最高点 Aac-b 1 b — X 二— I ;当a v 0时，当二时，函数有最大值 4ac-b 2 4盘 4.二次函数 y=ax2+bx+c （a 丰0）的各项系数 a 、b 、c 对其图象的影响（1） a 决定抛物线的开口方向和开口大小： a >0,开口向上；a v 0，开口向下.|a 的越大，开口越小. b X ----- （2） a 与 b 决定抛物线对称轴的位置： a 、 b 同号，抛物线的对称轴（即直线）或顶点在y 轴左侧; i x ----- a 、 b 异号，抛物线的对称轴（即直线一二）或顶点在y 轴右侧；（左同右异）； b=0时，抛物线的对称轴是 y 轴. （3） c 决定抛物线与y 轴交点（0, c ）的位置：c >0,抛物线与y 轴交于正半轴；c v 0,抛物线与y 轴交于负半轴；c=0,抛物二次函数 2 形如r ' - ■'0, a, b , c 为常数）的函数为二次函数般式 y=ax 2 +bx+c( a 丰 0) -------------- 1 2 顶点式| y = a(x - h) + k b 2 4a c — b 2 两根式 y = a(x -x j (x -x 2 ) 3、二次函数对称轴: b 2a 顶点坐标： (b 4ac-b 2) 2a' 4a 增减性：当a>0时，对称轴左边, 当a<0时，对称轴左边, y 随x 增大而减小；对称轴右边, y 随x 增大而增大；对称轴右边, y 随x 增大而增大 y 随x 增大而减小 b 71 — -- ⑶当a >0时，当丄；时，函数有最小值

二次函数图像与性质总结

二次函数的图像与性质一、二次函数的基本形式 1.二次函数基本形式：2 =的性质： y ax 2.2 =+的性质： y ax c 上加下减。 =-的性质： y a x h 左加右减。

4.()2 y a x h k =-+的性质： 1.平移步骤：方法一：⑴将抛物线解析式转化成顶点式()2 y a x h k =-+，确定其顶点坐标 ()h k ，； ⑵保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位 2.平移规律在原有函数的基础上“h 值正右移，负左移；k 值正上移，负下移”．

概括成八个字“左加右减，上加下减”．方法二： ⑴c bx ax y ++=2沿y 轴平移:向上（下）平移m 个单位，c bx ax y ++=2变成 m c bx ax y +++=2（或m c bx ax y -++=2） ⑵c bx ax y ++=2沿轴平移：向左（右）平移m 个单位，c bx ax y ++=2变成 c m x b m x a y ++++=)()(2（或c m x b m x a y +-+-=)()(2）三、二次函数()2 y a x h k =-+与2y ax bx c =++的比较从解析式上看，()2 y a x h k =-+与2y ax bx c =++是两种不同的表达形式，后者通过配方可以得到前者，即2 2424b ac b y a x a a -? ?=++ ?? ?，其中2424b ac b h k a a -=-= ，．四、二次函数2y ax bx c =++图象的画法五点绘图法：利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点. 五、二次函数2y ax bx c =++的性质 1.当0a >时，抛物线开口向上，对称轴为2b x a =-，顶点坐标为2424b ac b a a ??-- ??? ，．当2b x a <- 时，y 随x 的增大而减小；当2b x a >-时，y 随x 的增大而增大；当2b x a =-时，y 有最小值244ac b a -． 2.当0a <时，抛物线开口向下，对称轴为2b x a =-，顶点坐标为2424b ac b a a ??-- ??? ，．当2b x a <- 时，y 随x 的增大而增大；当2b x a >-时，y 随x 的增大而减小；当2b x a =-时，y 有最大值2 44ac b a -．六、二次函数解析式的表示方法 1.一般式：2y ax bx c =++（a ，b ，c 为常数，0a ≠）； 2.顶点式：2()y a x h k =-+（a ，h ，k 为常数，0a ≠）；

二次函数总结及相关典型题目

二次函数知识点总结及相关典型题目第一部分基础知识 1.定义：一般地，如果c b a c bx ax y ,,(2 ++=是常数，)0≠a ，那么y 叫做x 的二次函数. 2.二次函数2 ax y =的性质（1）抛物线2 ax y =的顶点是坐标原点，对称轴是y 轴. （2）函数2 ax y =的图像与a 的符号关系. ①当0>a 时?抛物线开口向上?顶点为其最低点； ②当0

①a 的符号决定抛物线的开口方向：当0>a 时，开口向上；当0