5.数理统计实验

工程数学

Gxxxxxxxxxxxx xxxxxx

E-mail: xxxxxxxxxxxxxx Tel: xxxxxxxxxxx

5数理统计实验：

5.1.实验目的与要求

●学会对数据的参数进行评估和作相应的假设检验

●学会对分布进行检验和数据的秩检验

●建立相应的统计模型，并用R软件求解

●对计算结果进行分析和讨论

5.2.基本实验

5.2.1.区间估计

已知某种灯泡寿命服从正态分布，在某星期所生产的该灯泡中随机抽取10只，测得其寿命（单位：小时）为

1067 919 1196 785 1126 936 918 1156 920 948

（1）试问这批灯泡中大约95%的灯泡至少使用多少小时；

（2）求这批灯泡能够使用1000小时以上的概率。略。

解：

(1)由点估计与参数估计未知参数和σ^2,可以求出均值与方差；

输入程序：

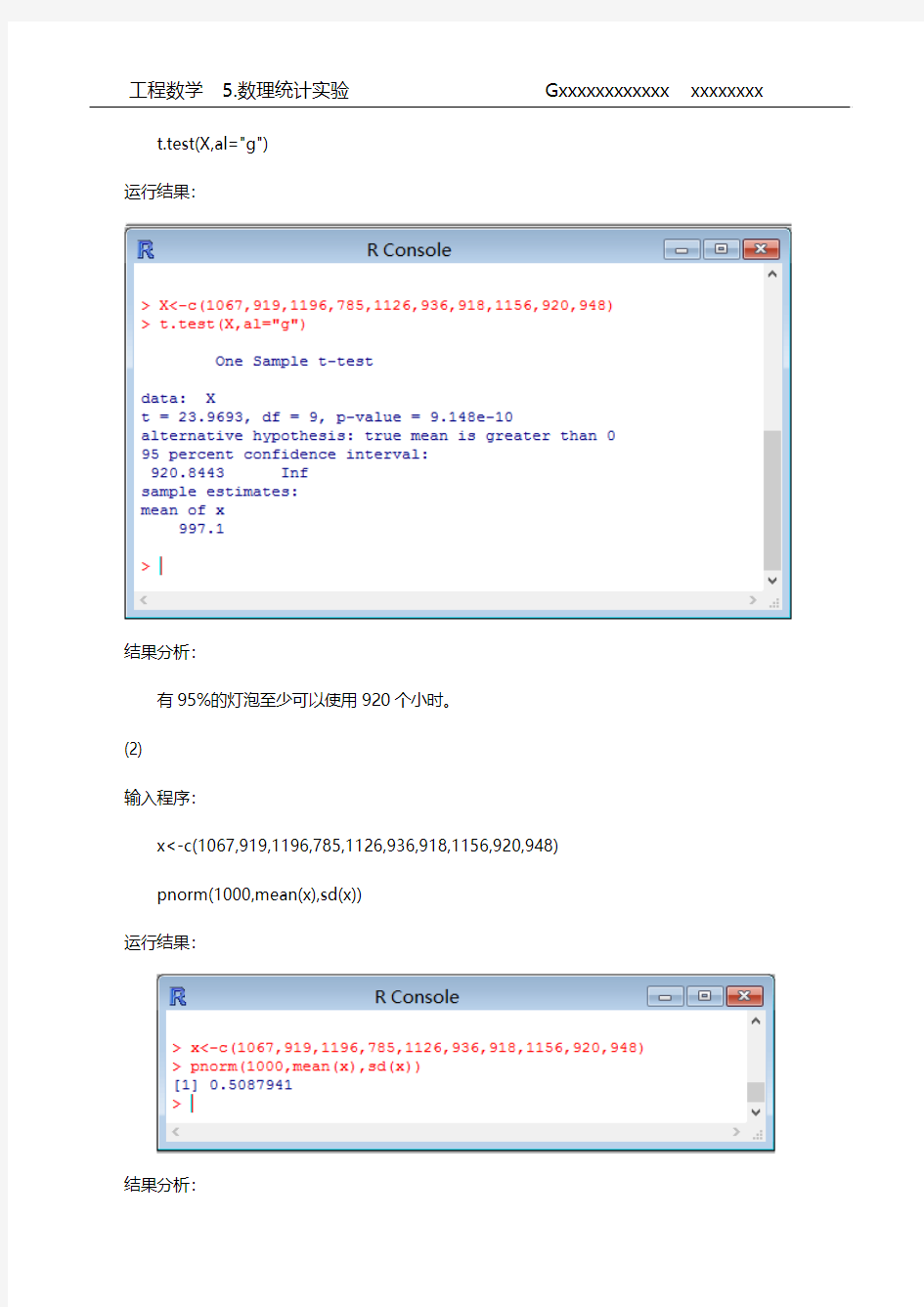
X<-c(1067,919,1196,785,1126,936,918,1156,920,948)

t.test(X,al="g")

运行结果：

结果分析：

有95%的灯泡至少可以使用920个小时。

(2)

输入程序：

x<-c(1067,919,1196,785,1126,936,918,1156,920,948) pnorm(1000,mean(x),sd(x))

运行结果：

结果分析：

灯泡能够使用1000小时以上的概率为1-0.5087941=0.4912059，即49.12%

5.2.2.假设检验I

正常男子血小板计数均值为225 x 109/L，今测得20名男性油漆作业工人的血小板计数值（单位：109/ L）

220 188 162 230 145 160 238 188 247 113

126 245 164 231 256 183 190 158 224 175

问油漆工人的血小板计数与正常成年男子有无差异，并说明油漆作业对人体血小板计数是否有影响。

解：

对于自然状态下的男子血小板的数目可以假设服从于正态分布，由点估计与参数估计未知参数和σ^2,可以求出均值、均值区间与方差；设原假设为H0:225，对立假设H1:225

输入程序：

X<-c(220,188,162,230,145,160,238,188,247,113,

126,245,164,231,256,183,190,158,224,175)

t.test(X,mu=225)

运行结果：

结果分析：

可以得出均值为= 192.15，方差σ^2=1694.728；

均值区间为（172.3827,211.9173）由此可以得出对于油漆工人而言正常男子血小板数为225单位，油漆工人明显低于正常的数量，则可以得知结论油漆作业对人体血小板数量有严重影响。5.2.3.假设检验II

为研究国产四类新药阿卡波糖胶囊效果，某医院用40名II型糖尿病病人进行同期随机对照实验。试验者将这些病人随机等分到试验组（阿卡波糖胶囊组）和对照组（拜唐苹胶囊组），分别测得试验开始前和8周后空腹血糖，算得空腹血糖下降值如表下：

试验组-0.70 -5.60 2.00 2.80 0.70 3.50 4.00 5.80 7.10 -0.50

2.50 -1.60 1.70

3.00 0.40

4.50 4.60 2.50 6.00 -1.40

对照组 3.70 6.50 5.00 5.20 0.80 0.20 0.60 3.40 6.60 -1.10

6.0 .80 2.00 1.60 2.00 2.20 1.20 3.10 1.70 -2.00

（1）假设数据服从正态分布，试用t检验（讨论方差相同和方差不同两种情况）和成对t检验来判断：国产四类新药阿卡波糖胶囊与拜唐苹胶囊对空腹血糖的降糖效果是否相同？并分析三种检验方法各自的优

越性。

（2）检验试验组和对照组的数据的方差是否相同？

解：

(1)方差相同，方差不同，成对检验3种情况

输入程序：

X<-c(-0.70, -5.60, 2.00, 2.80, 0.70, 3.50, 4.00, 5.80, 7.10, -0.50,

2.50,-1.60, 1.70,

3.00, 0.40,

4.50, 4.60, 2.50, 6.00, -1.40)

Y<-c(3.70, 6.50, 5.00, 5.20, 0.80, 0.20, 0.60, 3.40, 6.60, -1.10,

6.00, 3.80, 2.00, 1.60, 2.00, 2.20, 1.20, 3.10, 1.70, -2.00)

t.test(X, Y, var.equal=TRUE)

t.test(X, Y)

t.test(X, Y, paired=TRUE)！

运行结果：

结果分析：

方差相同结果

X<-c(-0.70, -5.60, 2.00, 2.80, 0.70, 3.50, 4.00, 5.80, 7.10, -0.50,2.50,-1.60, 1.70, 3.00, 0.40,

4.50, 4.60, 2.50, 6.00, -1.40)

Y<-c(3.70, 6.50, 5.00, 5.20, 0.80, 0.20, 0.60, 3.40, 6.60, -1.10, 6.00, 3.80, 2.00, 1.60, 2.00,

2.20, 1.20,

3.10, 1.70, -2.00)

t.test(X, Y, var.equal=TRUE)

方差不同结果

t.test(X, Y)

成对检验结果

t.test(X, Y,paired=TRUE)

结果分析：

由此可得：效果相同，统计区别不明显，三种检验方式的优越性，方差相同的情况区间最小。

(2)X,Y组单独检验运行程序

输入程序：

t.test(X)

运行结果：

输入程序：

t.test(Y)

运行结果：

结果分析：

由此可得，X组P值为0.007077，Y组为0.0001112

5.2.4.假设检验III

某医院研究乳腺癌家族史对于乳腺癌发病率的影响。假设调查了10000名50-54岁的妇女，她们的母亲曾有乳腺癌。发现她们在那个生存期的某个时刻有400例乳腺癌，而全国在该年龄段的妇女乳腺癌的患病率为2%，这组数据能否说明乳腺癌的患病率与家庭遗传有关。

解：

根据题意，假设检验采用二项分布总体，调用binom.test函数。

输入程序：

binom.test(400, 10000, 0.02)

运行结果：

结果分析：

由此可得，p-value <2.2e-16<0.05，所以拒绝接受原假设，认为这些数据说明乳腺癌的患病率与家族史有关。

5.2.5.分布检验I

Mendel用豌豆的两对相对性状进行杂交实验，黄色圆滑种子与绿色皱缩种子的豌豆杂交后，第二代根据自由组合规律，理论分离比为

黄圆：黄皱：绿圆：绿皱=9/16：3/16：3/16：1/16

实际实验值为：黄圆315粒，黄皱101粒，绿圆108粒，绿皱32粒，共556粒，问此结果是否符合自由组合规律？

解：

由题黄圆：黄皱：绿圆：绿皱= ：：：

此问题可以用Pearson拟合优度2 检验，令：09331

H: P1=,P2=,P3=,P4=

16161616输入程序：

chisq.test(c(315,101,108,32),p=c(9,3,3,1)/16)

运行结果：

结果分析：

程序运行结果表明，p-value = 0.9254>0.05，可以认为此结果是符合自由组合规律的。

5.2.

6.分布检验II

观察每分钟进入某商店的人数X，任取200分钟，所得数据表5.1所示。试分析，能否认为每分钟顾客数X服从Poisson分布（α= 0.1）。

表5.1每分钟进人商店顾客人数的频数

解：

输入程序：

1)

X<-0:5;Y<-c(92,68,28,11,1,0);

q<-ppois(X, mean(rep(X,Y)));

n<-length(Y)

p<-numeric(n);

p[1]<-q[1];

p[n]<-1-q[n-1];

for (i in 2:(n-1)) p[i]<-q[i]-q[i-1];

chisq.test(Y,p=p);

2)

Z<-c(92,68,28,12);

n<-length(Z);

p<-p[1:n-1];

p[n]<-1-q[n-1];

chisq.test(Z,p=p)

运行结果：

1)

2)

结果分析：

因为2

Pearson 检验要求在分组后，每组中的频数至少要大于等于5，而后两组中出现的频数是1，0，均小于5。由此可以得知p-value = 0.8227>>0.1，因此，能认为每分钟顾客人数X服从Poisson分布。

5.2.7.列联表检验I

向120名女性和120名男性做调查，了解他们关于给谁买节日礼物最难的看法，调查结果如表5.2所示，试分析：女性和男性在关于给谁买节日礼物最难的看法上有没有显著差异。

解：

根据题意，输入数据，用chisq.test（）函数检验：

输入程序：

x<-scan()

28 34 23 7 13 15 42 13 9 11 7 20

X<-matrix(x, nc=4, byrow=T)

chisq.test(X)

运行结果：

结果分析：

从计算结果得，p-value = 2.311e-08小于0.05，所以女性和男性在关于给谁买节日礼物最难的看法上有显著差异

5.2.8.列联表检验II

为研究人脑的左右半球恶性肿瘤的发病率是否有显著差异，对人脑恶性肿瘤和良性肿瘤的发育情况做了调查，调查结果如表5.3所示，试进行分析。

解：

输入数据，用chisq.test（）函数检验：

输入程序：

x <- matrix(c(9, 1, 3, 3), nc = 2)

chisq.test(x,correct = FALSE)

运行结果：

用fisher.test（）作独立精准检验，R程序：

x<-c(9,1,3,3)

dim(x)<-c(2,2)

fisher.test(x)

结果分析：

P的平均值，p-value = 0.1181，平且估计区间包含有1，可得出结论，说明两个变量是独立的，左右半球恶性肿瘤的发病率没有显著差异。

5.2.9.Wilcoxon秩和检验I

（1）为了了解新的数学教学方法的效果是否比原来方法的效果有所提高，从水平相当的10名学生中随机地各选5名接受新方法和原方法的教学试验。充分长一段时间后，由专家通过各种方式（如考试提问等）对10名学生的数学能力予以综合评估（为公正起见，假定专家对各个学生属于哪一组并不知道），并按其数学能力由弱到强排序，结果如表5.4所示。对α= 0.05，检验新方法是否比原方法显著地提高了教学效果。

表5.4学生数学能力排序结果

（2）若新方法与原方法得到排序结果改为表5.6所示的情形，能否说明新方法比原方法显著提高了教学效果?

表5.5学生数学能力排序结果

解：

(1)由题可以得出如下的wilcox.test()函数R程序

输入程序：

x<-c(3, 5, 7, 9, 10)

y<-c(1, 2, 4, 6, 8)

wilcox.test(x, y, alternative="greater")

运行结果：

结果分析：

由p-value = 0.1111>=0.05所以无法确定新方法有提高新效果

(2)由新的表格可以得到新的R程序

输入程序：

x<-c(4, 6, 7, 9, 10)

y<-c(1, 2, 3, 5, 8)

wilcox.test(x, y, alternative="greater")

运行结果：

结果分析：

p-value = 0.04762<0.05则可以得出新方法有一定程度的提高效果

5.2.10.Wilcoxon秩和检验II

为比较一种新疗法对某种疾病的治疗效果，将40名患者随机地分为两组，每组20人，一组采用新疗法，另一组用原标准疗法.经过一段时间的治疗后，对每个患者的疗效作仔细的评估，并划分为差、较差、一般、较好和好五个等级。两组中处于不同等级的患者人数如表5.6所示。试分析，由此结果能否认为新方法的疗效显著地优于原疗法（α=0.05）。

表5.6不同方法治疗后的结果

解：

由此调用wilcox.test()函数可以得出R程序

输入程序：

x<-c(0, 1, 9, 7, 3)

y<-c(2, 2, 11, 4, 1)

wilcox.test(x, y, alternative="greater",paired=TRUE)

运行结果：

结果分析：

p-value = 0.05则可以得出新疗法组有明显的度的提高效果

5.3.加分实验（产品装箱问题）

A厂把加工好的螺母封装成盒，标准为200个/盒。封装好的产品卖给用户。如果盒中的个数少于200，会造成用户的生产线停顿，用户会因此向该厂索赔。

（l）封装生产线采用称重计数的方式:已知螺母的重量X~N( X100, 4）（单位:克），封装时电脑自动称量盒中螺母的重量，并由此估计螺母的个数，显示在屏幕上.控制人员通过终端设定每盒中应该装填的螺母数，就可以开动由电脑控制的封装线了.为了尽量避免出现不足的情况，控制人员设定的装填个数一般比200