等腰直角三角形旋转

旋转的等腰直角三角形

【变式典型题】

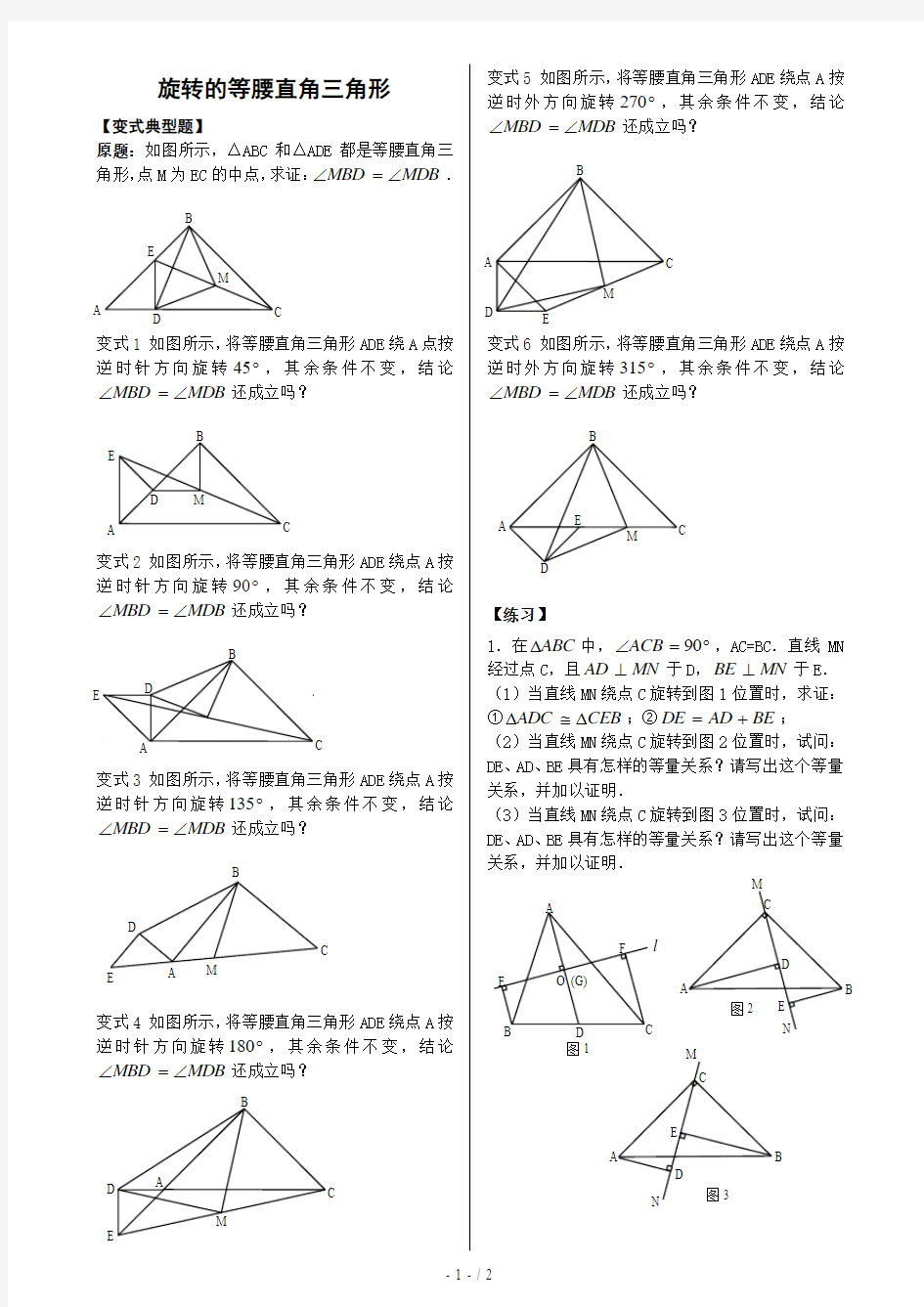
原题：如图所示，△ABC 和△ADE 都是等腰直角三

角形，点M 为EC 的中点，求证：MDB MBD ∠=∠．

变式1 如图所示，将等腰直角三角形ADE 绕A 点按逆时针方向旋转

?45，其余条件不变，结论MDB MBD

∠=∠还成立吗？

变式2

如图所示，将等腰直角三角形ADE 绕点A 按逆时针方向旋

转?90，其余条件不变，结论

MDB MBD ∠=∠还成立吗？

变式

3 如图所示，将等腰直角三角形ADE 绕点A 按逆时针方向

旋转?135，其余条件不变，结论MDB MBD ∠=∠还成立吗？

变式4 如图所示，将等腰直角三角形ADE 绕点A 按逆时针方向旋转?180，其余条件

不变，结论MDB MBD ∠=∠还成立吗？

变式5 如图所示，将等腰直角三角形ADE 绕点A 按

逆时外方向旋转?270，其余条件不变，结论MDB MBD ∠=∠还成立吗？

变式6 如图所示，将等腰直角三角形ADE 绕点A 按逆时外方向旋转?315，其余条件不变，结论MDB MBD ∠=∠还成立吗？

【练习】

1．在ABC ?中，?=∠90ACB ，AC=BC ．直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E ．（1）当直线MN 绕点C 旋转到图1位置时，求证：①CEB ADC ???；②BE AD DE +=；

（2）当直线MN 绕点C 旋转到图2位置时，试问：DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．

（3）当直线MN 绕点C 旋转到图3位置时，试问：DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．

C l

图1

2．（1）如图1，若点P为正方形ABCD边上一点，以PA为一边作正方形AEFP，连BE、DP，并延长DP 交BE于点H．求证：BE

DH⊥．

（2）如图2，将正方形AEFP逆时针旋转，使点P落在正方形ABCD内，其余条件不变，（1）的结论是否成立？若成立，请给出证明；若不成立，请说明理由．

3．在ABC

?中，AD是中线，O为

AD的中点，直

线l过O点，过A、B、C三点分别作直线l的垂线，

垂足分别为G、E、F，当直线l绕O点旋转到与AD

垂直时（如图1）易证：BE+CF=2AG．

当直线l绕O点旋转到与AD不垂直时，在图2、

图

3两种情况下，线段BE、CF、AG又是怎样的数

量关系？请写出你的猜想，并以图3的猜想给予证

明

．

思考题：

把两个全等的等腰直角三角板

ABC和

EFG（其直角

边长均为

4）叠放在一起（如图1），且使三角板

EFG的直角顶点G与三角形ABC的斜边中点O重

合．现将三角板EFG绕O点按顺时针方向旋转（旋

转角α满足条件：?

?90

0α），四边形CHGK

是旋转过程中两三角板的重叠部分（如图2）．

（1）在上述旋转过程中，BH与CK有怎样的数量关

系？四边形CHGK的面积有何变化？证明你发现的

结论；

（2）连接HK，在上述旋转过程中，设x

BH=，

GKH

?的面积为y，求y与x之间的函数关系式，

并写出自变量x的取值范围；

（3）在（2）的前提下，是否存在某一位置，使

GKH

?的面积恰好等于ABC

?面积的

？若存

在，求出此时x的值；若不存在，说明理由．

作业

完成时间：30分钟

1、如图所示，在密度均匀的铁片中挖去一圆形铁

片，现要将这一铁片分成重量相等的两块，请问你

有怎样的分法？并说明作图的道理．

2、现有如图所示的方角铁片，工人师傅想用一条

直线将其分割成面积相等的两部分，请你帮助工人

师傅设计三种不同的分割方案．

3、如图所示，请将一直角梯形形状的地块，分成

面积相等的两地，问如何分．

4、如图所示的一块空地，?

∠

∠90

A，AE∥

BC，AB∥CD，现要在这一空地上砌一堵墙（要求墙

长最短），将这块地分成面积相等的两块．

思考题：如何把任意四边形面积两等分？

图1

图1 图2

图2

专题18 解直角三角形问题(解析版)

专题18 解直角三角形问题一、勾股定理 1．勾股定理：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2=c2。 2．勾股定理逆定理：如果三角形三边长a,b,c满足a2＋b2=c2。，那么这个三角形是直角三角形。 3.定理：经过证明被确认正确的命题叫做定理。 4.我们把题设、结论正好相反的两个命题叫做互逆命题。如果把其中一个叫做原命题，那么另一个叫做它的逆命题。（例：勾股定理与勾股定理逆定理） 5. 直角三角形的性质： (1)直角三角形的两锐角互余； (2)直角三角形的两条直角边的平方和等于斜边的平方； (3)直角三角形中30°角所对直角边等于斜边的一半； (4)直角三角形斜边上的中线等于斜边的一半。 6.直角三角形的判定： (1)有一个角等于90°的三角形是直角三角形 (2) 两锐角互余的三角形是直角三角形 (3)两条边的平方和等于另一边的平方的三角形是直角三角形 (4)有一边上的中线等于这边的一半的三角形是直角三角形二、锐角三角函数 1.各种锐角三角函数的定义（1）正弦：在△ABC中，∠C=90°把锐角A的对边与斜边的比值叫做∠A的正弦，记作sinA＝∠A的对边斜边（2）余弦：在△ABC中，∠C=90°，把锐角A的邻边与斜边比值的叫做∠A的余弦，记作cosA＝∠A的邻边斜边（3）正切：在△ABC中，∠C=90°，把锐角A的对边与邻边的比值叫做∠A的正切，记作tanA＝∠A的对边∠A的邻边 2.特殊值的三角函数：专题知识回顾

三、仰角、俯角、坡度概念 1．仰角：视线在水平线上方的角； 2．俯角：视线在水平线下方的角。 3．坡度(坡比)：坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。用字母i 表示，即h i l =。把坡面与水平面的夹角记作α(叫做坡角)，那么tan h i l α==。四、各锐角三角函数之间的关系（1）互余关系 sinA=cos(90°—A)，cosA=sin(90°—A) tanA=cot(90°—A)，cotA=tan(90°—A) （2）平方关系 1cos sin 2 2=+A A （3）倒数关系 tanA ?tan(90°—A)=1 （4）弦切关系 tanA= A A cos sin :i h l =h l α

等腰三角形中的旋转题

https://www.360docs.net/doc/cb13092374.html, 彰显数学魅力！演绎网站传奇！学数学用专页第 1 页共 1 页搜资源上网站等腰三角形中的旋转题 □ 江苏徐伯良等腰三角形的性质和判定,有助于解决与之相关的若干问题.请看,它们在解决旋转问题中的应用: 例1如图1，等边△ABC 中，有一点P,连结PA 、PB ，把△ABP 顺时针旋转 60°，使边AB 与边BC 得重合，连结CQ ．，试判断△BPQ 的形状，并说明理由．析解: △BPQ 是等边三角形.理由如下: 由题意可知,BP=BQ ,∠PBQ=60°，所以△BPQ 是等边三角形. 例2 如图2，在等边△ABC 中，AC ＝9，点O 在AC 上，且AO ＝3，点P 是AB 上一动点，连结OP ，将线段OP 绕点O 逆时针旋转60°得到线段OD ．要使点D 恰好落在BC 上，则AP 的长是( ) A ．4 B ．5 C ．6 D ．8 析解:如图3所示,当线段OP 绕点O 逆时针旋转60°得到线段OD ．且使点D 恰好落在BC 上时，OP=OD, ∠DOP=60°，在△COD 中, ∠C+∠COD +∠CDO=180?,∠C=60°，而∠COD+∠DOP +∠AOP=180?,∠DOP=60°，所以∠ CDO =∠AOP , 又在△COD 中, ∠A=∠C=60°，可得△COD ≌△APO, 则AP=CO=AC-AO=6.故,选C. 例3 如图4，△ABC 中，∠ACB ＝90°，AC ＝BC ，CD 为中线．现将一直角三角板的直角顶点放在点O 上并绕点O 旋转，若三角板的两直角边分别交AC ，CB 的延长线于点G ，H ．（1）试写出图中除AC ＝BC ，OA ＝OB ＝OC 外其他所有相等的线段；（2）请从你所写的所有相等线段中任选的一组,说明相等的理由．我选择的相等线段是:_________=_________．析解:（1）根据等腰三角形的轴对称性以及三角形全等方面的知识, 可以推测,图中除AC ＝BC ，DA ＝DB ＝DC 外其他所有相等的线段有:CG=BH,AG=CH, D G=D H. （2）在△ABC 中，由∠ACB ＝90°，AC ＝BC ，AD=DB 可知, CO=OB,C O ⊥AB, ∠ABC ＝45°．而∠COG+∠GOB ＝90°，∠BOH+∠GOB ＝90°，所以∠COG ＝∠BOH ，又∠ABC ＝∠OCB=45°，所以∠OBH ＝180?-45°=135?,∠GOC ＝90?+45°=135?. 于是, ∠GCO=∠OBH ,所以△GCO ≌△HBO, 则CG=BH. 图 4 图 3 图 2 图1

辅助线构造等腰和直角三角形

构造等腰、直角三角形一、构造等腰（边）三角形：当问题中出现一点发出的二条相等线段时往往要补完整等腰（边）三角形；出现角平分线与平行线组合时可延长平行线与角的二边相交得等腰（边）三角形。通过构造等腰（边）三角形，应用等腰（边）三角形的性质得到一些边角相等关系，达到求证（解）的目的。典型例题：例1.如图，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分线与AB 的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是．例2.如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB=60°，DC=EF．（1）求证：四边形EFCD是平行四边形；（2）若BF=EF，求证：AE=AD．例3.如图，在梯形ABCD中，AD//BC，AB＝DC，过点D作DE⊥BC，垂足为E，并延长DE 至F，使EF＝DE．联结BF、CD、AC．（1）求证：四边形ABFC是平行四边形；（2）如果DE2＝BE·CE，求证四边形ABFC是矩形．二、构造直角三角形：通过构造直角三角形，应用直角三角形的性质得到一些边角关系（勾股定理，两锐角互余，锐角三角函数），达到求证（解）的目的。典型例题：例2.已知：在△ABC中，AC=a，AB与BC所在直线成45°角，AC与BC所在直线形成的 2 5 5（即cosC= 2 5 5 ，则AC边上的中线长是．例3.如图，在矩形ABCD中，AD＞AB，将矩形ABCD折叠，使点C与点A重合，折痕为MN，连结CN．若△CDN的面积与△CMN的面积比为1︰4，则MN BM 的值为【】

A．2 B．4 C．25D．26 例4.如图，在四边形ABCD中，对角线AC，BD交于点E，∠BAC=900，∠CED=450，∠DCE=900，DE=2，BE=22．求CD的长和四边形ABCD的面积．例5.某市规划局计划在一坡角为16o的斜坡AB上安装一球形雕塑，其横截面示意图如图所示．已知支架AC与斜坡AB的夹角为28o，支架BD⊥AB于点B，且AC、BD的延长线均过⊙O的圆心，AB＝12m，⊙O的半径为1.5m，求雕塑最顶端到水平地面的垂直距离(结果精确到0.01m，参考数据：cos28o≈0.9，sin62o≈0.9，sin44o≈0.7，cos46o≈0.7)．例6.周末，小亮一家在东昌湖游玩，妈妈在湖心岛岸边P处观看小亮与爸爸在湖中划船（如图）．小船从P处出发，沿北偏东60°划行200米到达A处，接着向正南方向划行一段时间到达B处．在B处小亮观测妈妈所在的P处在北偏西37°方向上，这时小亮与妈妈相距多少米（精确到米）？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，≈1.41，≈1.73）例7.如图，在扇形OAB中，∠AOB=90°，半径OA=6．将扇形OAB沿过点B的直线折叠，点O恰好落在AB上点D处，折痕交OA于点C，求整个阴影部分的周长和面积．

(完整版)解直角三角形超经典例题讲解

课题解直角三角形授课时间：备课时间：教学目标 1. 了解勾股定理 2. 了解三角函数的概念 3. 学会解直角三角形重点、难点三角函数的应用及解直角三角形考点及考试要求各考点教学方法：讲授法教学内容（一）知识点（概念）梳理考点一、直角三角形的性质 1、直角三角形的两个锐角互余可表示如下：∠C=90°?∠A+∠B=90° 2、在直角三角形中，30°角所对的直角边等于斜边的一半。 ∠A=30° 可表示如下： ?BC= 2 1AB ∠C=90° 3、直角三角形斜边上的中线等于斜边的一半 ∠ACB=90° 可表示如下： ?CD=2 1 AB=BD=AD D 为AB 的中点 4、勾股定理直角三角形两直角边a ，b 的平方和等于斜边c 的平方，即2 2 2 c b a =+ 5、摄影定理在直角三角形中，斜边上的高线是两直角边在斜边上的摄影的比例中项，每条直角边是它们在斜边上的摄影和斜边的比例中项 ∠ACB=90° BD AD CD ?=2 ? AB AD AC ?=2 CD ⊥AB AB BD BC ?=2 6、常用关系式由三角形面积公式可得： AB ?CD=AC ?BC 7.图中角α可以看作是点A 的角也可看作是点B 的角；（1）

9、（1）坡度（或坡比）是坡面的铅直高度（h ）和水平长度（l ）的比。记作i,即i = l h ；（2）坡角——坡面与水平面的夹角。记作α，有i ＝l h =tan α （3）坡度与坡角的关系：坡度越大，坡角α就越大，坡面就越陡考点二、直角三角形的判定 1、有一个角是直角的三角形是直角三角形。 2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。 3、勾股定理的逆定理如果三角形的三边长a ，b ，c 有关系2 2 2 c b a =+，那么这个三角形是直角三角形。考点三、锐角三角函数的概念 1、如图，在△ABC 中，∠C=90° ①锐角A 的对边与斜边的比叫做∠A 的正弦，记为sinA ，即 c a sin =∠= 斜边的对边A A ②锐角A 的邻边与斜边的比叫做∠A 的余弦，记为cosA ，即 c b cos =∠= 斜边的邻边A A ③锐角A 的对边与邻边的比叫做∠A 的正切，记为tanA ，即 b a tan =∠∠= 的邻边的对边A A A ④锐角A 的邻边与对边的比叫做∠A 的余切，记为cotA ，即a b cot =∠∠=的对边的邻边A A A 2、锐角三角函数的概念锐角A 的正弦、余弦、正切、余切都叫做∠A 的锐角三角函数 3、一些特殊角的三角函数值三角函数 0° 30° 45° 60° 90° sinα 21 22 23 1 cos α 1 23 2 2 21 0 tan α 0 33 1 3 不存在 cot α 不存在 3 1 3 3 0 4、各锐角三角函数之间的关系（1）互余关系 sinA=cos(90°—A)，cosA=sin(90°—A) tanA=cot(90°—A)，cotA=tan(90°—A) （2）平方关系 1cos sin 22=+A A （3）倒数关系 tanA ?tan(90°—A)=1

等边三角形、等腰直角三角形之间的旋转问题(精华)

等边三角形、等腰直角三角形之间的旋转问题（精华） 1、图（1）中，C点为线段AB上一点，△ACM，△CBN是等边三角形，AN与BM相等吗？说明理由；如图（2）C点为线段AB上一点，等边三角形ACM和等边三角形CBN在AB的异侧，此时AN与BM 相等吗？说明理由；如图（3）C点为线段AB外一点，△ACM，△CBN是等边三角形，AN与BM相等吗？说明理由． 2、如图（1）所示，点C为线段AB上一点，△ACM、△CBN是等边三角形，直线AN、MC交于点E，直线BM、CN交于点F．（1）求证：AN=MB；（2）将△ACM绕点C按逆时针方向旋转90°，其他条件不变，在图（2）中补出符合要求的图形，并判断（1）题中的结论是否依然成立，说明理由．

3、如图，已知△ABC是等边三角形，E是AC延长线上一点，选择一点D，使得△CDE是等边三角形，如果M是线段AD的中点，N是线段BE的中点，求证：△CMN是等边三角形．（根据△ACD≌△BCE，得出AD=BE，AM=BN；又△AMC≌△BNC，可得CM=CN，∠ACM=∠BCN，证明∠NCM=∠ACB=60°即可证明△CMN是等边三角形；） 1、（锦州）如图A，△ABC和△CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF 和BE．（1）线段AF和BE有怎样的大小关系?请证明你的结论；（2）将图A中的△CEF绕点C旋转一定的角度，得到图B，（1）中的结论还成立吗?作出判断并说明理由；（3）若将图A中的△ABC 绕点C旋转一定的角度，请你画山一个变换后的图形C（草图即可），（1）中的结论还成立吗?作出判断不必说明理由；（4）根据以上证明、说理、画图，归纳你的发现．（3）此小题图形不惟一，如图第（1）中的结论仍成立．（4）根据以上证明、说理、画图，归纳如下：如图A，大小不等的等边三角形ABC和等边三角形CEF有且仅有一个公共顶点C，则以点C 为旋转中心，任意旋转其中一个三角形，都有AF=BE．

(完整版)等腰直角三角形中的常用模型

等腰直角三角形中的常用模型模型一：一条直线（不与三角形的边重合）过等腰直角三角形的直角顶点（1）以原等腰直角三角形的两直角边为对应斜边，必定可以构造一对全等的直角三角形：例1．如图：Rt ΔABC 中，∠BAC =90o，AB =AC ，点D 是BC 上任意一点，过B 作 BE ⊥AD 于点E ，过C 作CF ⊥AD 于点F 。（1）求证：BE-CF=EF ；（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗？若不成立，请写出新的结论并证明。 1.如图1，等腰Rt △ABC 中，AB=CB ，∠ABC =90o，点P 在线段BC 上（不与B 、C 重合），以AP 为腰长作等腰直角△P AQ ，QE ⊥AB 于E ，连CQ 交AB 于M 。（1）求证：M 为BE 的中点（2）若PC=2PB ，求 MB PC 的值（2）以原等腰直角三角形的两直角边为对应直角边，必定可以构造一对全等的直角三角形： 3、如图：Rt ΔABC 中，∠BAC =90o，AB =AC ，点D 是BC 上任意一点，过B 作BE ⊥AD 于点E ，交AC 于点G ，过C 作CF ⊥AC 交AD 的延长线与于点F 。（1）求证：BG=AF ；（2）若D 在BC 的延长线上（如图（2）），（1）中的结论还成立吗？若不成立，请写出新的结论并证明。变式1：如图，在R t △ABC 中，∠ACB =45o，∠BAC =90o，AB=AC ，点D 是AB 的中点，AF ⊥CD 于H 交BC 于F ，BE ∥AC 交AF 的延长线于E ，求证：BC 垂直且平分DE . G G B A C D E F (2)(1)F E D C B A F D A A (2)F E D C A A B C D E F (1)(2)(3)(1)D D E E C E A A A B

专题_等腰三角形(含答案)

9、等腰三角形【知识精读】（－）等腰三角形的性质 1. 有关定理及其推论定理：等腰三角形有两边相等；定理：等腰三角形的两个底角相等（简写成“等边对等角”）。推论1：等腰三角形顶角的平分线平分底边并且垂直于底边，这就是说，等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。推论2：等边三角形的各角都相等，并且每一个角都等于60°。等腰三角形是以底边的垂直平分线为对称轴的轴对称图形； 2. 定理及其推论的作用等腰三角形的性质定理揭示了三角形中边相等与角相等之间的关系，由两边相等推出两角相等，是今后证明两角相等常用的依据之一。等腰三角形底边上的中线、底边上的高、顶角的平分线“三线合一”的性质是今后证明两条线段相等，两个角相等以及两条直线互相垂直的重要依据。（二）等腰三角形的判定 1. 有关的定理及其推论定理：如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”。）推论1：三个角都相等的三角形是等边三角形。推论2：有一个角等于60°的等腰三角形是等边三角形。推论3：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。 2. 定理及其推论的作用。等腰三角形的判定定理揭示了三角形中角与边的转化关系，它是证明线段相等的重要定理，也是把三角形中角的相等关系转化为边的相等关系的重要依据，是本节的重点。 3. 等腰三角形中常用的辅助线等腰三角形顶角平分线、底边上的高、底边上的中线常常作为解决有关等腰三角形问题的辅助线，由于这条线可以把顶角和底边折半，所以常通过它来证明线段或角的倍分问题，在等腰三角形中，虽然顶角的平分线、底边上的高、底边上的中线互相重合，添加辅助线时，有时作哪条线都可以，有时需要作顶角的平分线，有时则需要作高或中线，这要视具体情况来定。【分类解析】例1. 如图，已知在等边三角形ABC中，D是AC的中点，E为BC延长线上一点，且CE＝CD，DM⊥BC，垂足为M。求证：M是

等腰直角三角形的旋转

（图1）（图2）（图3）等腰直角三角形的旋转 1.如图，△ABC 中，AB=5，AC=3，以BC 为边作等腰Rt △BCD ，连接AD ，把△ACD 绕D 点，逆时针方向旋转900 ，得到△EBD 。（1）画出△EBD ；（2）当BC=4时，连接AE ，求△ABE 的面积；（3）当BC 的长度发生变化时，请直接写出AD 长的取值范围。 ( 备用图） 2.(1)如图1， △ACB 和△DCE 均为等腰直角三角形，∠ACB=∠DCE=90°，求证：△ACD ≌△BCE. (2) 如图2，将图1中△DCE 绕点C 逆时针旋转n °(0＜n ＜45)，使∠BED=90°，又作△DCE 中DE 边上的高CM ，请完成图2，并判断线段CM ，AE ，BE 之间的数量关系，并说明理由．（3）如图3，在正方形ABCD 中，CD=5，若点P 满足PD=1，且∠BPD=90°，请直接写出点A 到BP 的距离．

3.如图(1)，在Rt △ABC 中，∠A =90°，AC =AB =4， D ，E 分别是AB ，AC 的中点．若等腰Rt △ADE 绕点A 逆时针旋转，得到等腰Rt△AD 1E 1，如图(2)，设旋转角为α（0<α≤180°），记直线BD 1与CE 1的交点为P ．（1）求证：BD 1= CE 1；（2）当∠=1CPD 2∠1CAD 时，求1CE 的长；（3）连接PA,PAB ?面积的最大值为．（直接填写结果） 4.在等腰Rt △ABC 和等腰Rt △A 1B 1C 1中,斜边B 1C 1中点O 也是BC 的中点。 (1)如图1，则AA 1与CC 1的数量关系是；位置关系是。 (2)如图2，将△A 1B 1C 1绕点O 顺时针旋转一定角度，上述结论是否仍然成立，请证明你的结论。 (3)如图3，在（2）的基础上，直线AA 1、CC 1交于点P ，设AB=4，则PB 长的最小值是。 B P E 1B C E D D 1A 1 11 1图1

解直角三角形题型带解析

解直角三角形题型－带解析

————————————————————————————————作者: ————————————————————————————————日期:

１、（2０1７?河南）如图所示,我国两艘海监船Ａ，B在南海海域巡航，某一时刻，两船同时收到指令,立即前往救援遇险抛锚的渔船C，此时,B船在Ａ船的正南方向5海里处，A船测得渔船C在其南偏东４5°方向,B船测得渔船C在其南偏东53°方向，已知A船的航速为30海里/小时，B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援？（参考数据：sin53°≈,cos53°≈，tａn53°≈，≈1.４1）【分析】如图作ＣE⊥AB于Ｅ．设AE=ＥC=ｘ,则BE=x﹣5,在Rｔ△ＢCＥ中，根据tan５3°=,可得=,求出x，再求出BＣ、ＡC,分别求出A、B两船到C的时间，即可解决问题. 【解答】解：如图作CＥ⊥AB于Ｅ. 在Rt△ACE中,∵∠A=45°, ∴ＡE＝EC,设AE=ＥＣ＝ｘ，则ＢE=x﹣5, 在Rｔ△BCE中, ∵tan53°=, ∴＝, 解得x=2０, ∴AE=EC＝20,

∴AC=2０=28.２，ＢC==25, ∴A船到C的时间≈=０.９4小时,Ｂ船到C的时间==1小时, ∴C船至少要等待0.94小时才能得到救援． 2、(２016?河南)如图,小东在教学楼距地面９米高的窗口Ｃ处,测得正前方旗杆顶部A点的仰角为３7°,旗杆底部Ｂ点的俯角为4５°，升旗时,国旗上端悬挂在距地面2.２5米处，若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？（参考数据：ｓiｎ37°≈０.６0,ｃｏs３7°≈0.80,taｎ37°≈0．75) 【分析】通过解直角△BCD和直角△AＣD分别求得BＤ、CD以及ＡD的长度,则易得AB的长度，则根据题意得到整个过程中旗子上升高度,由“速度=”进行解答即可．【解答】解:在Rｔ△ＢＣＤ中，BＤ＝9米，∠BＣD=４5°,则BD=ＣD=9米. 在Rt△ＡＣD中,ＣD=９米，∠ＡＣＤ=37°，则AD=ＣD?tan37°≈9×0．75=6.７５（米）．所以，ＡB=ＡD+BD＝15.75米，整个过程中旗子上升高度是：15.75﹣２.２5＝13．5（米), 因为耗时45s,

等腰直角三角形中考题详解

等腰直角三角形中考题详解一、选择题（共13小题） 1、（2008?枣庄）如图，点A的坐标为（1，0），点B在直线y=﹣x上运动，当线段AB最短时，点B的坐标为（） A、（0，0） B、（，﹣） C、（，﹣） D、（﹣，） 2、（2003?烟台）如图，△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，则∠ABC的大小是（） A、40° B、45° C、50° D、60° 3、（2006?吉林）如图，在把易拉罐中的水倒入一个圆水杯的过程中，若水杯中的水在点P与易拉罐刚好接触，则此时水杯中的水深为（） A、2cm B、4cm C、6cm D、8cm 4、（2011?黑龙江）在△ABC中，BC：AC：AB=1：1：，则△ABC是（） A、等腰三角形 B、钝角三角形 C、直角三角形 D、等腰直角三角形 5、（2009?宁波）等腰直角三角形的一个底角的度数是（） A、30° B、45° C、60° D、90° 6、（2006?青海）用两个全等的等腰直角三角形拼下列图形：①等腰三角形；②等边三角形；③正方形；④等腰梯形．一定可以拼成的图形有（） A、①③ B、②④ C、②③ D、①④ 7、（2006?长春）如图，将圆桶中的水倒入一个直径为40cm，高为55cm的圆口容器中，圆桶放置的角度与水平线深圳市菁优网络科技有限公司

的夹角为45度．若使容器中的水面与圆桶相接触，则容器中水的深度至少应为（） A、10cm B、20cm C、30cm D、35cm 8、（2001?广州）已知点A和点B（如图），以点A和点B为其中两个顶点作位置不同的等腰直角三角形，一共可作出（） A、2个 B、4个 C、6个 D、8个 9、（2010?攀枝花）如图：等腰直角三角形ABC位于第一象限，AB=AC=2，直角顶点A在直线y=x上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若双曲线y=（k≠0）与△ABC有交点，则k的取值范围是（） A、1＜k＜2 B、1≤k≤3 C、1≤k≤4 D、1≤k＜4 10、△ABC和△AEF均为等腰直角三角形，其初始位置如图所示，若△AEF绕A点顺时针旋转，则BE与CF大小关系为（） A、BE＞CF B、BE=CF C、BE＜CF D、无法确定 11、如图，△ABC中，∠C=Rt∠，AC=BC，AD是∠BAC的平分线，DE⊥AB，垂足为E，若AB=10cm，则△DBE的周长等于（） A、10cm B、8cm C、12cm D、9cm 12、如下图，△ABC中，∠C=90°，∠B=45°，AD是角平分线，DE⊥AB于E，则下列结论不正确的是（）

2018中考解直角三角形真题

解直角三角形参考答案与试题解析一．选择题（共9小题） 1．（2018?孝感）如图，在Rt△ABC中，∠C=90°，AB=10，AC=8，则sinA等于（） A．B．C．D．【分析】先根据勾股定理求得BC=6，再由正弦函数的定义求解可得．【解答】解：在Rt△ABC中，∵AB=10、AC=8， ∴BC===6， ∴sinA===，故选：A． 2．（2018?绵阳）一艘在南北航线上的测量船，于A点处测得海岛B在点A的南偏东30°方向，继续向南航行30海里到达C点时，测得海岛B在C点的北偏东15°方向，那么海岛B离此航线的最近距离是（）（结果保留小数点后两位）（参考数据：≈1.732，≈1.414）A．4.64海里B．5.49海里C．6.12海里D．6.21海里【分析】根据题意画出图形，结合图形知∠BAC=30°、∠ACB=15°，作BD⊥AC于点D，以点B 为顶点、BC为边，在△ABC内部作∠CBE=∠ACB=15°，设BD=x，则AB=BE=CE=2x、AD=DE=x，据此得出AC=2x+2x，根据题意列出方程，求解可得．【解答】解：如图所示，由题意知，∠BAC=30°、∠ACB=15°，作BD⊥AC于点D，以点B为顶点、BC为边，在△ABC内部作∠CBE=∠ACB=15°，则∠BED=30°，BE=CE，设BD=x，则AB=BE=CE=2x，AD=DE=x，

∴AC=AD+DE+CE=2x+2x， ∵AC=30， ∴2x+2x=30，解得：x=≈5.49，故选：B． 3．（2018?重庆）如图，旗杆及升旗台的剖面和教学楼的剖面在同一平面上，旗杆与地面垂直，在教学楼底部E点处测得旗杆顶端的仰角∠AED=58°，升旗台底部到教学楼底部的距离DE=7米，升旗台坡面CD的坡度i=1：0.75，坡长CD=2米，若旗杆底部到坡面CD的水平距离BC=1米，则旗杆AB的高度约为（）（参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.6） A．12.6米B．13.1米C．14.7米D．16.3米【分析】如图延长AB交ED的延长线于M，作CJ⊥DM于J．则四边形BMJC是矩形．在Rt△CDJ中求出CJ、DJ，再根据，tan∠AEM=构建方程即可解决问题；【解答】解：如图延长AB交ED的延长线于M，作CJ⊥DM于J．则四边形BMJC是矩形．在Rt△CJD中，==，设CJ=4k，DJ=3k，则有9k2+16k2=4， ∴k=， ∴BM=CJ=，BC=MJ=1，DJ=，EM=MJ+DJ+DE=，在Rt△AEM中，tan∠AEM=，

直角三角形等腰直角三角形斜边直线专题

直角三角形、斜边中线、等腰直角三角形专题一、直角三角形的性质 1．一块直角三角板放在两平行直线上，如图，∠1+∠2=度． 2．如图，△ABC中，∠BAC=90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG 平分∠DAC，求证：①∠BAD=∠C；②∠AEF=∠AFE；③AG⊥EF． 3．如图所示，在△ABC中，CD，BE是两条高，那么图中与∠A相等的角有 4．如图，已知△ABC中，AB＞AC，BE、CF都是△ABC的高，P是BE上一点且BP=AC，Q是CF延长线上一点且CQ=AB，连接AP、AQ、QP，求证：△APQ是等腰直角三角形．二、含30°角的直角三角形的性质 5．在Rt△ABC中，∠ACB=60°，DE是斜边AC的中垂线，分别交AB、AC于D、E 两点．若BD=2，求AD的长

6．如图，∠AOP=∠BOP=15°，PC∥OA交OB于C，PD⊥OA于D，若PC=6，求PD的长 7．如图所示，矩形ABCD中，AB=AD，E为BC上的一点，且AE=AD，求∠EDC的度数 8．如图，△ABC为等边三角形，点D为BC边上的中点，DF⊥AB于点F，点E 在BA的延长线上，且ED=EC，若AE=2，求AF的长 9．如图所示，已知∠1=∠2，AD=BD=4，CE⊥AD，2CE=AC，求CD的长 10．如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠BAC，DE⊥AB于E，求证：（1）CD=DE；（2）AC=BE；（3）BD=2CD；

三、直角三角形斜边中线问题 11．如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，求证：△PMN为等边三角形； 12．已知锐角△ABC中，CD，BE分别是AB，AC边上的高，M是线段BC的中点，连接DM，EM．（1）若DE=3，BC=8，求△DME的周长；（2）若∠A=60°，求证：∠DME=60°；（3）若BC2=2DE2，求∠A的度数． 13．如图，在△ABC中，D是BC上一点，AB=AD，E、F分别是AC、BD的中点，EF=2，求AC的长

等腰直角三角形题型

有关等腰Rt三角形的题形在初二几何中，有几组等腰直角三角形题形非常典型。现介绍如下：一．多垂直、锐角相等例1: △ABC中, ∠BAC=90°, AB=AC, D为BC A 上一点,过B，C做BE⊥AD, CF⊥AD 求证: BE=EF+CF 证：∵BE⊥AD,∠BAC=90° E ∴∠EBA=∠CAF B D C 易证: △EBA≌△FAC ∴AE=FC, BE=AF F ∴BE=EF+CF A 例2: △ABC中, ∠B=22.5°, AB的垂直平分线交BC于D, 过D作DE⊥AC于E, AF⊥BC于F交DE于G , G E 求证: GF=FC. 证：∵∠B=22.5°∴∠ADF=45° ∵AF⊥DC ∴AF=DF B D F C ∵DE⊥AC, AF⊥DC ∴∠FDG=∠CAF. 易证△CAF≌△GDF ∴GF=FC A 思考题:1.△ABC中, ∠BAC=90°,AB=AC, AD⊥BC 于D, E为AC上一点, BE交AD于H, AF⊥BE于G. G E 求证:DH=DF H B D F C 2.△ABC中, ∠BAC=90°, AB=AC, A AD⊥BC于D, E为AD延长线上一点, AG⊥BE于G.. 求证: BE=AF, DE=DF F D B C G E 二.通过三线合一构造全等

例1：△ABC中，∠BAC=90°，AB=AC， A AB是BC边上中线，∠ABF=∠CAE，求证：EF∥AC 证：Rt△ABC中，AD为中线 ∴BD=AD，∠ABD=∠DAC=45° F 又∵∠ABF=∠CAE ∴∠DBF=∠DAE ∴易证：△DBF≌△DAE B D E C ∴DE=DF，∴∠FED=∠C=45° ∴EF∥AC 例2：等腰Rt△ABC中，∠A=90°，P为BC延长线上一点，PE⊥AB，PF⊥AC，M为BC 中点连ME、MF E 求证：ME=MF，ME⊥MF A 证：由题意知矩形AFPE ∴PF==AE，∠MAC=∠FPC=45° ∴∠MAE=∠FCM=135° ∴易证△AME≌△CMF ∴ME=MF，∠AME=∠PMF C P 又∵∠AME+∠EMC=90° B M F ∴∠EMC=∠PMF=90° ∴ME⊥MKF 思考题： 1．△ABC中，∠A=90°，AB=AC， A AD⊥BC过D作DE⊥DF 求证：DE=DF E F B D C 2．△ABC中，∠A=90°，AB=AC， A AD⊥BC，H为BC上一点， HE⊥AB，HF⊥AC连DE、DF E 求证：DE=DF，ED⊥DF F B D H C 三．利用垂直与等腰构造全等

人教版九年级数学下册-解直角三角形及其应用--知识讲解(包含典型例题讲解)

解直角三角形及其应用—知识讲解（包含典型例题讲解）【学习目标】 1．了解解直角三角形的含义，会综合运用平面几何中有关直角三角形的知识和锐角三角函数的定义解直角三角形； 2．会运用有关解直角三角形的知识解决实际生活中存在的解直角三角形问题．【要点梳理】要点一、解直角三角形在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形. 在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角. 设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有： ①三边之间的关系：a2+b2=c2(勾股定理). ②锐角之间的关系：∠A+∠B=90°. ③边角之间的关系：，，，

，，. ④，h为斜边上的高. 要点诠释： (1)直角三角形中有一个元素为定值(直角为90°)，是已知值.

(2)这里讲的直角三角形的边角关系指的是等式，没有包括其他关系(如不等关系). (3)对这些式子的理解和记忆要结合图形，可以更加清楚、直观地理解. 要点二、解直角三角形的常见类型及解法

要点诠释： 1．在遇到解直角三角形的实际问题时，最好是先画出一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的，然后按先确定锐角、再确定它的对边和邻边的顺序进行计算. 2．若题中无特殊说明，“解直角三角形”即要求出所有的未知元素，已知条件中至少有一个条件为边. 要点三、解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键. 解这类问题的一般过程是： (1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型. (2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题. (3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形. (4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解. 拓展：在用直角三角形知识解决实际问题时，经常会用到以下概念： (1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.

旋转第二篇：两个等腰直角三角形

旋转试题篇：抓基本图形，看变化接着上一篇旋转，这篇选取其中一个特例---等腰直角三角形进行讲解。如图，△ABC和三角形ADE为等腰直角三角形，△ABC固定不动，△ADE绕顶点A顺时针旋转。不难想象，△ADE的顶点旋转轨迹如图乙所示：D、E始终在在以点A为圆心、AD长为半径的圆上，且长度不变。图甲图乙在旋转的过程中，我们发现，△ADE的位置可以大致分为三种情况：情况①：一边在△ABC内一边在△ABC外，如图1所示：情况②：一边在△ABC上，如图2所示：情况③：两边都在△ABC外，如图3所示：图1图2图3 这三种情况，几何题中，是很常见的，且贯穿整个初中。请看题：一、对接情况①的常考题。【题1】⑴问题发现：如图⑴，△ACB和△DCE均为等边三角形，点A,D,E在同一直线上，连接BE。填空，∠AEB的度数为；线段AD,BE之间的数量关系为； ⑵拓展探究如图⑵，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A,D,E在同一直线上，CM为△DCE中DE边上的高，连接BE。请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由。

【题2】如图，已知等腰直角三角形ABC，点P是斜边BC上一点（不与B，C重合），PE是△ABP的外接圆⊙O的直径．（1）求证：△APE是等腰直角三角形；（2）若⊙O的直径为2，求PC2+PB2的值．二、对接情况②的常考题。【题3】在△ABC中，AB=BC，∠ABC=90°，F为AB延长线上的一点，点E在BC上，且AE=CF； ⑴求证：Rt△ABE≌Rt△CBF; ⑵若∠CAE=30°，求∠ACF的度数。【题4】如图所示，H是△ABC的高AD,BE的交点，且DH=DC，则下列结论：①BD=AD；②BC=AC； ③BH=AC；④CE=CD中，正确的有。三、对接情况③的常考题。【题5】如图①，已知△ABC，以△ABC的边AB、AC为边，分别向外作等腰直角△ABD和等腰直角△ACE，连接CD、BE、DE。（1）试说明：△ADC≌△ABE；（2）判断CD与BE有怎样的位置关系；（3）试判断△ABC与△ADE面积之间的关系，并说明理由。

八年级数学上册难点突破17一次函数中的构造等腰直角三角形法试题北师大版

专题17 一次函数中的构造等腰直角三角形法 1、如图1,等腰直角三角形ABC中,∠ACB＝90°,CB＝CA,直线ED经过点C,过A作AD⊥ED于点D,过B作 BE⊥ED于点E．求证：△BEC≌△CDA；解：（1）由题意可知：△BEO≌△AOD（K型全等）, ∴OE＝AD, ∵k＝﹣1, ∴y＝﹣x+4, ∴B（0,4）, ∴OB＝4, ∵BE＝3, ∴OE＝, ∴AD＝；（2）k＝﹣时,y＝﹣x+4, ∴A（3,0）, ①当BM⊥AB,且BM＝AB时, 过点M作MN⊥y轴, ∴△BMN≌△ABO（AAS）, ∴MN＝OB,BN＝OA, ∴MN＝4,BN＝3, ∴M（4,7）； ②当AB⊥AM,且AM＝AB时, 过点M作x轴垂线MK,

∴△ABO≌△AMK（AAS）, ∴OB＝AK,OA＝MK, ∴AK＝4,MK＝3, ∴M（7,3）； ③当AM⊥BM,且AM＝BM时, 过点M作MH⊥x轴,MG⊥y轴, ∴△BMG≌△AHM（AAS）, ∴BG＝AH,GM＝MH, ∴GM＝MH, ∴4﹣MH＝MH﹣3, ∴MH＝, ∴M（,）；综上所述：M（7,3）或M（4,7）或M（,）；（3）当k＞0时,AO＝, 过点Q作QS⊥y轴, ∴△ABO≌△BQS（AAS）, ∴BS＝OA,SQ＝OB, ∴Q（4,4﹣）, ∴OQ＝, ∴当k＝1时,QO最小值为4；当k＜0时,Q（4,4﹣）, ∴OQ＝, ∴当k＝1时,QO最小值为4,与k＜0矛盾, ∴OQ的最小值为4．

2、已如,在平面直角坐标系中,点A的坐标为（6,0）、点B的坐标为（0,8）,点C在y轴上,作直线AC．点 B关于直线AC的对称点B′刚好在x轴上,连接CB′．（1）写出点B′的坐标,并求出直线AC对应的函数表达式；（2）点D在线段AC上,连接DB、DB′、BB′,当△DBB′是等腰直角三角形时,求点D坐标；（3）如图2,在（2）的条件下,点P从点B出发以每秒2个单位长度的速度向原点O运动,到达点O时停止运动,连接PD,过D作DP的垂线,交x轴于点Q,问点P运动几秒时△ADQ是等腰三角形．解：（1）∵A的坐标为（6,0）、点B的坐标为（0,8）,

专题55 一次函数中的构造等腰直角三角形(原卷版)

专题55 一次函数中的构造等腰直角三角形 1、如图1，等腰直角三角形ABC中，∠ACB＝90°，CB＝CA，直线ED经过点C，过A作AD⊥ED于点 D，过B作BE⊥ED于点E．求证：△BEC≌△CDA； 2、已如，在平面直角坐标系中，点A的坐标为（6，0）、点B的坐标为（0，8），点C在y轴上，作直线 AC．点B关于直线AC的对称点B′刚好在x轴上，连接CB′．（1）写出点B′的坐标，并求出直线AC对应的函数表达式；（2）点D在线段AC上，连接DB、DB′、BB′，当△DBB′是等腰直角三角形时，求点D坐标；（3）如图2，在（2）的条件下，点P从点B出发以每秒2个单位长度的速度向原点O运动，到达点O

时停止运动，连接PD，过D作DP的垂线，交x轴于点Q，问点P运动几秒时△ADQ是等腰三角形． 3、定义：在平面直角坐标系中，对于任意P（x1，y1），Q（x2，y2），若点M（x，y）满足x＝3（x1+x2），y ＝3（y1+y2），则称点M是点P，Q的“美妙点”．例如：点P（1，2），Q（﹣2，1），当点M（x，y）满足x＝3×（1﹣2）＝﹣3，y＝3×（2+1）＝9时，则点M（﹣3，9）是点P，Q的“美妙点”．（1）已知点A（﹣1，3），B（3，3），C（2，﹣2），请说明其中一点是另外两点的“美妙点”；（2）如图，已知点D是直线y＝+2上的一点．点E（3，0），点M（x，y）是点D、E的“美妙点”． ①求y与x的函数关系式； ①若直线DM与x轴相交于点F，当①MEF为直角三角形时，求点D的坐标． 4、如图，过点A（1，3）的一次函数y＝kx+6（k≠0）的图象分别与x轴，y轴相交于B，C两点．（1）求k的值；（2）直线l与y轴相交于点D（0，2），与线段BC相交于点E．（i）若直线l把①BOC分成面积比为1：2的两部分，求直线l的函数表达式；（①）连接AD，若①ADE是以AE为腰的等腰三角形，求满足条件的点E的坐标．

构造等腰三角形解题的常见途径(新)

构造等腰三角形解题的常见途径等腰三角形是研究几何图形的基础，因此在许多几何问题中，常常需要构造等腰三角形才能使问题获解，那么如何构造等腰三角形呢？一般说来有以下几种途径：一、利用角平分线+平行线，构造等腰三角形当一个三角形中出现角平分线和平行线时，我们就可以寻找到等腰三角形．如图1①中，若AD 平分∠BAC ，AD ∥EC ，则△ACE 是等腰三角形；如图1②中，AD 平分∠BAC ，DE ∥AC ，则△ADE 是等腰三角形；如图1③中，AD 平分∠BAC ，CE ∥AB ，则△ACE 是等腰三角形；如图1④中，AD 平分∠BAC ，EF ∥AD ，则△AGE 是等腰三角形．例1 如图2，△ABC 中，AB ＝AC ，在AC 上取点P ，过点P 作EF ⊥BC ，交BA 的延长线于点E ，垂足为点F ．求证：．AE ＝AP ．简析要证．AE ＝AP ，可寻找一条角平分线与EF 平行，于是想到AB ＝AC ，则可以作AD 平分∠BAC ，所以AD ⊥BC ，而EF ⊥BC ，所以AD ∥EF ，所以可得到△AEP 是等腰三角形，故AE ＝AP ．例2 如图3 ，在△ABC 中，∠BAC 、∠BCA 的平分线相交于点O ，过点O 作DE ∥AC ，分别交AB 、BC 于点 D 、 E ．试猜想线段AD 、CE 、DE 的数量关系，并说明你的猜想 C A B E D O 图3 图4 F C D E B A M 图2 F B A C D P E 图1 ① D ② C D C ④ F C D

理由．简析猜想：AD +CE ＝DE ．理由如下：由于OA 、OC 分别是∠BAC 、∠BCA 的平分线，DE ∥AC ，所以△ADO 和△CEO 均是等腰三角形，则DO ＝DA ，EC ＝EO ，故AD +CE ＝DE ．例3 如图4，△ABC 中，AD 平分∠BAC ，E 、F 分别在BD 、AD 上，且DE ＝CD ，EF ＝AC ．求证：EF ∥AB ．简析由于这里要证明的是EF ∥AB ，而AD 平分∠BAC ，所以必须通过辅助线构造出平行线，这样就可以得到等腰三角形了，于是DE ＝CD 的提示下，相当于倍长中线，即延长AD 至M ，使DM ＝AD ，连结EM ，则可证得△MDE ≌△ADC ，所以ME ＝AC ，又EF ＝AC ，∠M ＝∠CAD ，所以∠M ＝∠EFM ，即∠CAD ＝∠EFM ，又因为AD 平分∠BAC ，所以∠BAD ＝∠EFD ＝∠CAD ，所以EF ∥AB ．二、利用角平分线+垂线，构造等腰三角形当一个三角形中出现角平分线和垂线时，我们就可以寻找到等腰三角形．如图5中，若AD 平分∠BAC ，AD ⊥DC ，则△AEC 是等腰三角形．例4 如图6，已知等腰R ｔ△ABC 中，AB ＝AC ，∠BAC ＝90°，BF 平分∠ABC ，CD ⊥BD 交BF 的延长线于D ．求证：BF ＝2CD ．简析由BF 平分∠ABC ，CD ⊥BD ，并在图5的揭示之下，延长线BA 、CD 交于点E ，于是△BCE 是等腰三角形，并有ED ＝CD ，余下来的问题只需证明BF ＝CE ，而事实上，由∠BAC ＝90°，CD ⊥BD ，∠AFB ＝∠DFC ，得∠ABF ＝∠DCF ，而AB ＝AC ，所以△ABF ≌△ACE ，则BF ＝CE ，故BF ＝2CD ．三、利用转化倍角，构造等腰三角形 E 图5 A B C D 图6 B F D E C A