二次函数十大基本问题

第九讲：二次函数十大基本问题

知识模块与方法

知识模块一：二次函数的定义问题

1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。 这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． 2. 二次函数2y ax bx c =++的结构特征：

（1）等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2． （2）a b c ，，是常数，a 是二次项系数，b 是一次项系数，c 是常数项．

知识、题型、方法

例1：若x m m m y 232

)3(+--=是二次函数，则=m 。

变式练习： 已知x m

m m m y 19

92

2

)972

(+---=，试讨论m 分别为何值时为正比例函数、反比例函数、

二次函数？

课堂演练一：

1. 二次函数62)

3(2

+-=-x y 的二次项系数是，一次项系数是，常数项是。

2. 若y ＝(m ＋1)x m

m -2－3x ＋1是二次函数，则m 的值为__________．

3. 已知函数4

31

2

--+=

x x y x

，则自变量x 的取值围是。

4. 某广告公司欲设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000米，设 矩形的一边长为x 米，所花费用为y 元。则y 与x 之间的函数关系式为。

5. 已知函数x

m m y 23

2

)

12(--=，当m 为何值时：

（1）y 是x 的正比例函数，且y 随着x 增大而增大。 （2）函数图象是位于第二、四象限的双曲线。 （3）函数图象是开口向上的抛物线。

知识模块二：二次函数的图象及其性质

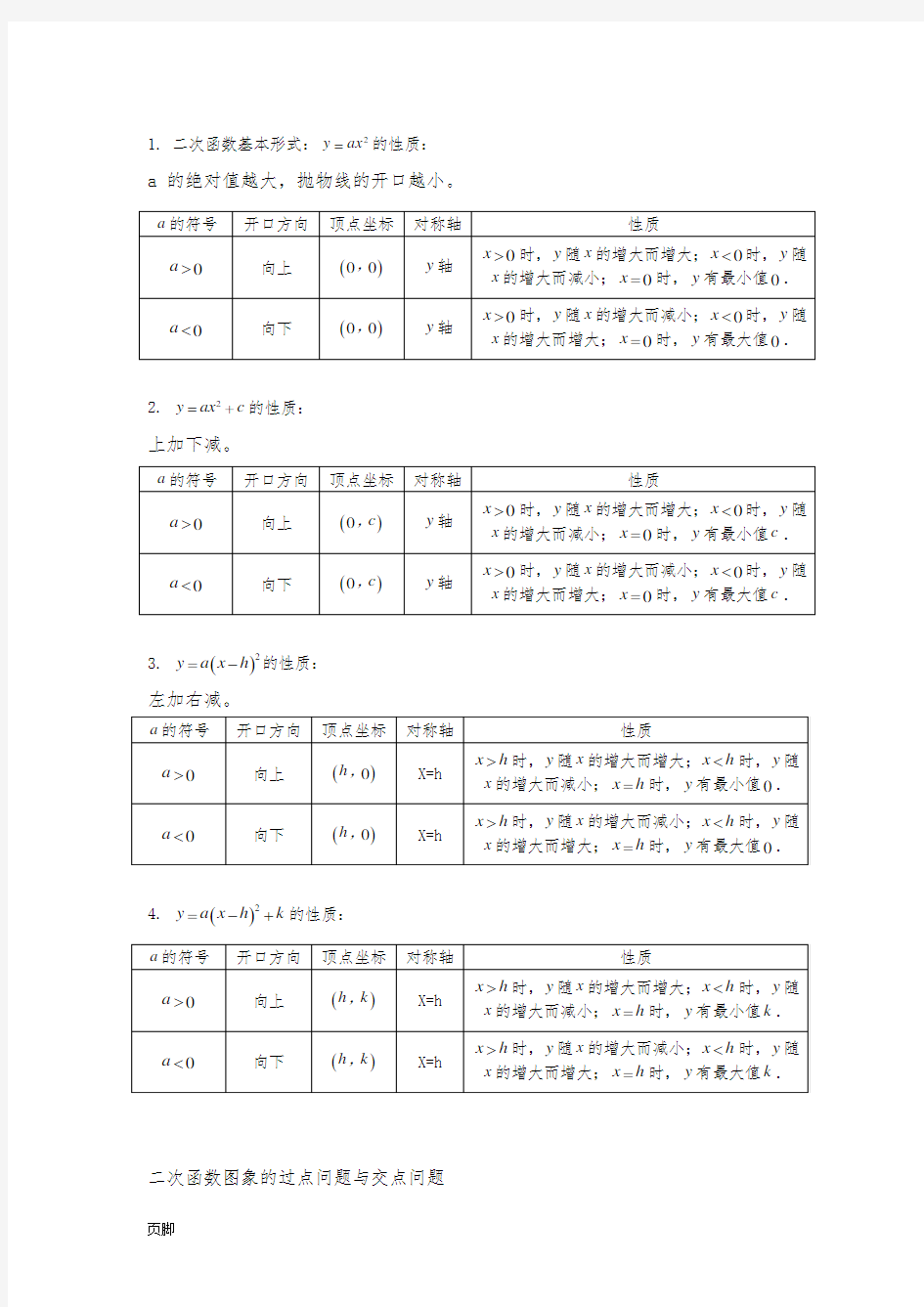
1. 二次函数基本形式：2y ax =的性质：

a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：

上加下减。

3. ()2

y a x h =-的性质：

左加右减。

4. ()2

y a x h k =-+的性质：

二次函数图象的过点问题与交点问题

中考方法点拨：二次函数图象的过点问题与交点问题实际上就是方程问题、代入求值问题

的综合，只要紧紧抓住函数图象经过的点或交点的横坐标与纵坐标都满足 函数解析式，然后代入解析式可得方程（组），从而求解。

知识、题型、方法

例2：已知抛物线x y 2

-

=和直线m x y +=3都经过点（2-，n ）

。 （1）求m ，n 的值。

（2）是否存在另一个交点？若存在，请求出。

变式练习：

1．（2008，）已知，如图，直线l 经过)0,4(A 和)4,0(B 两点，它与抛物线2

ax y =在第一象

限相交于点P ，又知AOP ?的面积为4，求a 的值。

第1题图 第2题图

2．（2008，）如图10，直线m x y +=和抛物线c bx x y ++=2

都经过点A (1，0)，B (3，2)．

（1）求m 的值和抛物线的解析式；

（2）求不等式m x c bx x +>++2

的解集(直接写出答案)。

课堂演练二：

1．二次函数22

-=x a y 的图象经过两点A （4-，2）

，B （m ，2），则=m 。 2．若抛物线c x a

y x

++=2

与x 轴的交点坐标是（1-，0）则

=+c a 。

3. 已知函数)0(2

≠=a a

y x 的图象与直线32-=x y 交于点（1，b ）

， 则求=a 。

4. 如图，是二次函数y ＝ax 2－x ＋a 2

－1的图象，则a ＝____________． 第4题图

二次函数图象的单调性问题：

A

O B P

y

O y

x

B

A

中考方法点拨：判断二次函数的单调性要紧紧抓住抛物线的开口方向和对称轴2b

x a

=-

， 对称轴2b

x a

=-

是二次函数单调性的分界点，即： 1.当0a >时，抛物线开口向上： 在2b x a <-

围，y 随x 的增大而减小；在2b x a >-围，y 随x 的增大而增大；当2b x a

=-时，y 有最小值2

44ac b a

-。

2. 当0a <时，抛物线开口向下：

在2b x a <-

围，y 随x 的增大而增大；在2b

x a

>-围，y 随x 的增大而减小； 当2b

x a

=-时，y 有最大值244ac b a -。

知识、题型、方法

例3：（2011，）如图，已知二次函数c bx x y ++=2的图象经过点（－1，0），

（1，－2），当y 随x 的增大而增大时，x 的取值围是。

变式练习第2题图 例4：（2008，东营）若A （1,413y -

）

，B （2,4

5y -），C （3,41y ）为二次函数2

45y x x =+-的图象上的三点，则1,y 2,y 3y 的大小关系是 （ ） A ．123y y y <

1．（2011，）若二次函数2()1y x m =--．当x ≤l 时，y 随x 的增大而减小，则m 的取值围是（ ）

A ．m =l

B ．m >l

C ．m ≥l

D ．m ≤l 2．（2011，）已知二次函数的图象(0≤x ≤3)如第9题图所示。关于该函数在所给自变量取值围，下列说确的是( )

A ．有最小值0，有最大值3

B ．有最小值－1，有最大值0

C ．有最小值－1，有最大值3

D ．有最小值－1，无最大值

课堂演练三：

x

y

例3图

O

1

1（1,-2）

c

bx x y ++=2-1

1．当22≤≤-x 时，二次函数x y 2

-

=的最小值是，最大值是。

2．（2011，）下列函数中,当x >0时y 值随x 值增大而减小的是（ ）． A ．y = x 2

B ．y = x －１

C ． y = 34x

D ．y = 1x

3．（2011，聊城）下列四个函数图象中，当x<0时，函数值y 随自变量x 的增大而减小的是

（ ）

4. 若A （－134，y 1），B （－1，y 2），C （53，y 3）为二次函数y ＝－x 2

－4x ＋5图象上的三

点，则y 1、y 2、y 3的大小关系是。

5. 已知x m

m m y +=2

，当=m 时，它的图象是开口向下的抛物线，这时，当

x 时，y 随x 的增大而增大。

二次函数图象的对称性问题： 知识、题型、方法

例5：（平面直角坐标系中点的对称问题）平面直角坐标系中的点P （3,-5），关于x 轴对称

的点1P 的坐标为；关于y 轴对称的点2P 的坐标为 ；关于原点对称的点3P 的坐标为。 变式练习：

在平面直角坐标系中，点（a ，b ）关于x 轴对称的点的坐标为；关于y 轴对称 的点的坐标为 ；关于原点对称的点的坐标为。

例6：（2011，）已知二次函数2

y ax bx c =++中，其函数y 与自变量x 之间的部分对应值

如下表所示：

x …… 0 1 2 3 4 …… y

……

4 1 0 1 4 ……

点A （1x ，1y ）、B （2x ，2y ）在函数的图象上，则当112,x <<234x <<时，1y 与2y 的大小关系正确的是（ ）

A ．12y y >

B ．12y y <

C ．12y y ≥

D ．12y y ≤

变式练习： 1。已知抛物线c a

y x +=-)

1(2

的图象如图7所示，该抛物线与x 轴交于A 、B 两点，B

点坐标为（2，0），则A 点坐标为。

y

O A B x 图7

2.（2011，）如图8，已知二次函数c bx x y ++=2的图象经过点（-1，0），（1，-2），该图

象与x 轴的另一个交点为C ，则AC 长为。

课堂演练四第4题图

课堂演练四：

1．已知点M ()y x ,与点N ()3,2--关于x 轴对称，则x + y = 。

2.（－3，4）关于x 轴对称的点的坐标为________，关于y 轴对称的点的坐标为________， 关于原点对称的坐标为__________。

3．（2011，枣庄）抛物线2

y ax bx c =++上部分点的横坐标x ，纵坐标y 的对应值如下表：

x

… －2 －1 0 1 2 … y

…

4

6

6

4

…

从上表可知，下列说法中正确的是。（填写序号）

①抛物线与x 轴的一个交点为（3,0）； ②函数2

y ax bx c =++的最大值为6； ③抛物线的对称轴是1

2

x =

； ④在对称轴左侧，y 随x 增大而增大． 4．（2010，日照）如图，是二次函数y=ax 2

+bx+c 图象的一部分，其对称轴为直线x =1，若其与x 轴一交点为A （3，0），则由图象可知，不等式ax 2

+bx+c ＜0的解集是.

5．（2011，）若二次函数y=ax 2

+bx+c 的x 与y 的部分对应值如下表：

X

-7

-6

-5

-4

-3

-2

x

y

图8

O

1

1

（1,-2） c

bx x y ++=2-1 A

B

C

y -27 -13 -3 3 5 3

则当x =1时，y 的值为

A 。5

B 。-3

C 。-13

D 。-27 6.（2009，襄樊）抛物线2

y x bx c =-++的图象如图9

所示， 则一元二次方程02

=++-c bx x

的两个根为。

二次函数的图象与系数a 、b 、c 之间的关系问题

中考方法点拨：（1）由抛物线开口方向确定a 的正负；（2）由对称轴02>-

=a

b

x （或0<） 确定b 的正负；（3）抛物线与y 轴交点纵坐标确定c 的正负；（4）由对称轴

12<-

=a

b

x （或1>）确定b a +2的正负；（5）令1=x 观察图象可得c b a ++的正负；同理可令1-=x ，可得c b a +-的正负；

（6）取2=x 可得c b a ++24的正负；取2-=x 可得c b a +-24的正负。 注意：以上6条性质可以相互推导，也可以用推导出来的结论去推导另外的正确结论。

知识、题型、方法

例7：（2009，）已知二次函数2

y ax bx c =++的图象如图所示，有以下结论：

①0a b c ++<；②1a b c -+>；③0abc >；④420a b c -+<；⑤1c a ->其中所有正

确结论的序号是（ ） A ．①②B ．①③④

C ．①②③⑤

D ．①②③④⑤

课堂演练五：

1。（2011，）已知抛物线y ＝ax 2

＋bx ＋c (a ≠0)在平面直角坐标系中的位置如图所示，则下列结论中正确的是( )

A ． a >0

B ． b ＜0

C ． c ＜0

D ． a ＋b ＋c >0

2。（2010，）如图，二次函数2

y ax bx c =++的图象与y 轴正半轴相交，其顶点坐标为1,12??

???

，下列结论：①ac ＜0；②a+b=0；③4ac －b 2

=4a ；④a+b+c ＜0。其中正确的个数是（ ）

y

x

O 3

x =1

图9

1 1

1- O x y

A.1

B.2

C.3

D.4

第2题图 第3题图 第4题图

3。（2011，）如图所示的二次函数2

y ax bx c =++的图象中，星同学 观

察得出了下面四条信息： （1）2

40b ac ->；（2）c >1；（3）2a －b <0；（4）a +b +c <0。 你认为其中错误．．

的有（ ） A ．2个 B ．3个C ．4个 D ．1个

4。（2011，日照）如图，是二次函数y ＝ax 2

＋bx ＋c （a ≠0）的图象的一部分， 给出

下列命题 ：①a+b+c=0；②b ＞2a ；③ax 2

+bx +c =0的两根分别为3-和1；④a -2b +c ＞0。

其中正确的命题是。（只要求填写正确命题的序号） 5。（2009，）已知二次函数2

y ax bx c =++（0a ≠）的图象如图4所示，有下列四个结论：

20040b c b ac <>->①②③④0a b c -+<，其中正确的个数有（ ）

A ．1个

B ．2个

C ．3个

D ．4个

6。（2008）已知二次函数2

y ax bx c =++（0a ≠）的图象如图5所示，有下列

四个结论：①0abc >； ②b a c <+；③420a b c ++>；④2

40b ac ->。

其中正确的结论有（）

A ．1个

B ．2个

C ．3个

D ．4个

7。（2007，）已知二次函数)0(2

≠++=a c bx ax y 的 图象如右图所示， 有下列5个结论：①0>abc ； ②c a b +<；③024>++c b a ；④b c 32<；

-1

O x =1

y

x 图5

x

y - 1

O

1 1

图4

O x

y

3

⑤)(b am m b a +>+，（1≠m 的实数）其中正确的 结论有（ ）

A 。2个

B 。3个

C 。4个

D 。5个

8。（2007，）如右图是二次函数y ＝ax 2

＋bx ＋c 图象的一部分， 图象过点A （－3，0），对称轴为x ＝－1．给出四个结论： ①b 2

＞4ac ；②2a ＋b =0；③a －b ＋c =0；④5a ＜b 。 其中正确结论是（ ）。

（A ）②④ （B ）①④ （C ）②③ （D ）①③

二次函数的平移问题 中考方法点拨：抛物线的平移只改变它的位置，不改变其形状和开口方向，即a 的值不变。

解决这类问题的关键是利用好平移特征，在图形的平移中，一个点的位置 变化和一个图形的位置变化是一致的，只须抓住抛物线的顶点需要进行怎 样的平移即可。

解答思路：先求出抛物线的顶点坐标，然后将顶点坐标进行平移改变，再利用顶点式求出

平移后的抛物线解析式。（平移前先把二次函数的解析式化成顶点式）

知识、题型、方法

例8：（1）（2011，滨州）抛物线()2

23y x =+-可以由抛物线2y x =平移得到，则下列平

移过程正确的是( )

A 。先向左平移2个单位,再向上平移3个单位

B 。先向左平移2个单位,再向下平移3个单位

C 。先向右平移2个单位,再向下平移3个单位

D 。先向右平移2个单位,再向上平移3个单位

（2）（2010，）把抛物线c bx y x

++=

2

的图象向右平移3个单位，再向下平移2个单

位，所得图象的解析式为532

+-=

x y x

，则（ ）

A 。3=b ，7=c

B 。6=b ，3=c

C 。9-=b ，5-=c

D 。9-=b ，21=c

课堂演练六：

1。（ 2011，江津）将抛物线x y x

22

-=向上平移3个单位,再向右平移4个单位等到的抛

物线是。

2。（2009，）在平面直角坐标系中，将二次函数2

2x y =的图象向上平移2个单位，所得图

象的解析式为（ ）

A ．222-=x y

B ．222

+=x y C ．2)2(2-=x y D ．2

)2(2+=x y

3。（2009，）把抛物线2

y x =-向左平移1个单位，然后向上平移3个单位，则平移后抛物

线的解析式为（ ）

A ．2(1)3y x =---

B ．2

(1)3y x =-+- C ．2(1)3y x =--+ D ．2

(1)3y x =-++

4.（2008，资阳市） 在平面直角坐标系中，如果抛物线y ＝2x 2

不动，而把x 轴、y 轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是 ( ) A ．y ＝2(x －2)2

+ 2B ．y ＝2(x + 2)2

－2 C ．y ＝2(x －2)2

－2D ．y ＝2(x + 2)2

+ 2

5。要得到二次函数2

22y x x =-+-的图象，需将2

y x =-的图象（ ）。 A ．向左平移2个单位，再向下平移2个单位 B ．向右平移2个单位，再向上平移2个单位 C ．向左平移1个单位，再向上平移1个单位 D ．向右平移1个单位，再向下平移1个单位

6。（2008，省）抛物线5422

---=x x y 经过平移得到2

2x y -=，平移方法是（ ）

A ．向左平移1个单位，再向下平移3个单位

B ．向左平移1个单位，再向上平移3个单位

C ．向右平移1个单位，再向下平移3个单位

D ．向右平移1个单位，再向上平移3个单位 7。如果将抛物线c bx y x

++=

2

沿直角坐标平面向左平移2个单位长度，再向上平移3个

单位长度得到抛物线122

+-=x y x

。你能确定b 、c 的值吗？试试看。

二次函数图象与一次函数或反比例函数图象在同一坐标系的问题 中考方法点拨：（假设法与数型结合思想） 知识、题型、方法

例9：（1）（2011，凉山州）二次函数

2

y ax bx c =++的图1像如图所示，反比列函数

x

a

y =与正比列函数y bx

=在同一坐标系的大致图像是（）

（2）（2009，）在同一直角坐标系中，函数y mx m

=+和函数222

y mx x

=-++

（m是常数，且0

m≠）的图象可能

．．是（）

课堂演练七：

1。（2011，）已知函数)

)(

(b

x

a

x

y-

-

=（其中a b

>）的图象

如下图所示，则函数b

ax

y+

=的图象可能正确的是（）

2。（2011，）二次函数2

y ax bx c

=++的图象如图2所示，则反比例函数

a

y

x

=

与一次函数y bx c

=+在同一坐标系中的大致图象是（）。

3。（2009，）二次函数2

y ax bx c

=++的图象如图3所示，则一次函数24

y bx b ac

=+-与反比例函数

a b c

y

x

++

=在同一坐标系的图象大致为（）

O x

y

O

y

x

A

O

y

x

B

O

y

x

D

O

y

x

C

y

x

1

1

O

y

x

1

-1 O

y

x

-1

-1

O

1

-1

x

y

O

（D）

1-x

y

4。（2008，省市）已知反比例函数x

k y =的图象如下图4所示，则二次函数2

22k x kx y +-=的图象大致为（ ）

图4 5。（2011，）在同一坐标系中，一次函数1+=ax y 与二次函数a x y +=2

的图像可能是

（ ）

6。（2009，）函数y =ax ＋1与y =ax 2

＋bx ＋1（a ≠0）的图象可能是（ ）

7。（2007，双柏县）在同一坐标系中一次函数y ax b =+和二次函数2y ax bx =+的图象 可能为（ ）

二次函数的解析式问题： 知识、题型、方法

用待定系数法求二次函数的解析式常用三种方法：

1．已知抛物线过三点，设一般式y ＝ax 2

＋bx ＋c ．

y

x

O y

x

O y

x

O y

O A ． B ．

C ．

D ．

y O

x

y O

x

y

O x y

O x

y

O

x

A ．

B ．

C ．

D ． 1

1

1

1

x

o y

y

o x y

o x

x

o

y

O x y O

x

y O

x

y

O

x

y

A B

C

D

2．已知抛物线顶点坐标及一点，设顶点式y ＝a(x －h)2

＋k ．

3．已知抛物线与x 轴有两个交点（或已知抛物线与x 轴交点的横坐标）， 设两根式：y ＝a(x －x 1)(x －x 2) ．（其中x 1、x 2是抛物线与x 轴交点的横坐标） 例10：（1）已知二次函数c bx a

y x

++=2

过（1-，0）

，（3，0），（0，2

3

），求此抛物线 的解析式。

（2）二次函数图象经过（3，8-），对称轴2=x ，抛物线与x 轴两交点间的距离为6， 求二次函数的解析式。

变式练习：

1. 已知二次函数过点（2，0），（4，0），顶点到x 轴的距离为1，求此函数的解析式。

2.（2011，节选）如图，直线33+=x y 交x 轴于A 点，交y 轴于B 点，过A 、B 两点的抛物线交x 轴于另一点C （3,0）。求抛物线的解析式。

课堂演练八：

1. 已知二次函数当2=x 时有最小值3，且过（1，5），则二次函数的解析式为。

2. 已知二次函数的图象经过点A （1-，0），B （3，0）且顶点的纵坐标为8-，则这个二次函数的解析式为。

3. 若抛物线c bx a

y x

++=2

的顶点坐标为（1，3）

，且与x y 2

2=的开口大小相同，方向相反，则二次函数的解析式为。

4．已知一个二次函数的图象过（0，1）、（2，4）、（3，10）三点，求这个二次函数的表达式。

5.（2011，）如图，抛物线y

=

2

1x 2

+bx －2与x 轴交于A 、B 两点，与y 轴交于C 点， 且A （一1，0）。

（1）求抛物线的解析式及顶点D 的坐标； （2）判断△ABC 的形状，证明你的结论；

（3）点M

(m ，0)是x 轴上的一个动点，当CM +DM 的值最小时，求m 的值。

6.（2011，）如图所示，二次函数y =-x 2

+2x +m 的图象与x 轴的一个交点为A （3，0）， 另一个交点为B ，且与y 轴交于点C 。 （1）求抛物线的解析式；

（2）求点B 的坐标； （3）该二次函数图象上有一点D （x ，y ）（其中x ＞0，y ＞0），使S △ABD =S △ABC ，。求点D 的坐标。

二次函数与配方法问题： 知识、题型、方法

例11：（1）（2011，）将二次函数2

45y x x =-+化为2

()y x h k =-+的形式，则y =。

（2）（2009，）抛物线1822

-+-=x x y 的顶点坐标为（ ）

（A ）（-2，7） （B ）（-2，-25） （C ）（2，7） （D ）（2，-9）

例12：（2011，）二次函数522

-+=x x y 有（ ）

A ．最大值5-

B ．最小值5-

C ．最大值6-

D ．最小值6-

变式练习：

分别在下列围求函数322

--=

x y x

的最大值或最小值。

（1）20<

课堂演练九：

1．（2011，）抛物线y ＝－(x ＋2)2

－3的顶点坐标是（ ）

(A)（2，－3）； (B)（－2，3）； (C)（2，3）； (D)（－2，－3） 2．（2011，永州）由二次函数1)3(22+-=x y ，可知（）

A ．其图象的开口向下

B ．其图象的对称轴为直线3-=x

C ．其最小值为1

D ．当3

3．(2009，)抛物线2

2()y x m n =++（m n ，是常数）的顶点坐标是（ ）

A ．()m n ，

B ．()m n -，

C ．()m n -，

D ．()m n --，

4．（2009年市）若把代数式223x x --化为()2

x m k -+的形式，其中,m k 为常数，则

m k +=。

5．若一次函数m x m y ++=)1(的图象过第一、三、四象限，则二次函数mx m y x

-=2

有（ ） A ．最大值4m B ．最大值4m - C ．最小值4m D ．最小值4

m

-

二次函数与一元二次方程问题：

知识与方法：

1. 二次函数与一元二次方程的关系（二次函数与x 轴的交点情况）：

一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况。 图象与x 轴的交点个数由一元二次方程20ax bx c ++=的判别式来决定，具体如下：

（1）当240b ac ?=->时，图象与x 轴交于两点()()1200A x B x ，，，12()x x ≠，其中的12x x ，

是一元二次方程()2

00ax bx c a ++=≠

的两根。这两点间的距21AB x x =-

（2）当0?=时，图象与x 轴只有一个交点； （3）当0?<时，图象与x 轴没有交点。

1'当0a >时，图象落在x 轴的上方，无论x 为任何实数，都有0y >； 2'当0a <时，图象落在x 轴的下方，无论x 为任何实数，都有0y <。 2. 抛物线2y ax bx c =++的图象与y 轴一定相交，交点坐标为(0，)c 。

知识、题型、方法

例13：已知抛物线)27(2

m mx y x

-++-

=（m 为常数）

。 （1）证明：不论m 何值，抛物线与x 轴恒有两个不同的交点。 （2）若抛物线与x 轴的交点A （

x 1

，0）

，B （x 2

，0）的距离AB =4（A 在B 的左边），且抛物线交y 轴正半轴于C ，求抛物线的解析式。

变式练习：

（2009，）已知抛物线2

23

4

y x kx k =+-

（k 为常数，且k ＞0）。

（1）证明：此抛物线与x 轴总有两个交点；

（2）设抛物线与x 轴交于M 、N 两点，若这两点到原点的距离分别为OM 、ON ，且

1123

ON OM -=，求k 的值。

例14：（2007，省）已知二次函数2

2y x x m =-++的部分图象如下图所示，则关于x 的一元二次方程220x x m -++=的解为。

变式练习：

（2010，日照）如图，是二次函数y=ax 2

+bx+c 图象的一部分，其对称轴为直线x =1，若其与

x 轴一交点为A （3，0），则由图象可知，不等式ax 2

+bx+c

＜0的解集是.

课堂演练十：

1．（2011，威海）二次函数2

23y x x =--的图象如图所示．当y ＜0时，自变量x 的取值围是（ ）．

A ．－1＜x ＜3

B ．x ＜－1

C ． x ＞3

D ．x ＜－1或x ＞3

2．（2009，）抛物线2

y x bx c =-++的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论：，．（对称轴方程，图象与x 正半轴、y 轴交点坐标除外）

3．（2011，襄阳）已知函数12)3(2++-=x x k y 的图象与x 轴有交点，则k 的取值围是（ ）

A.4

B.4≤k

C.4

D.4≤k 且3≠k

4．（2009，）已知二次函数c bx ax y ++=2

的y 与x 的部分对应值如下表：

x

… 1- 0 1 3 … y

…

3-

1

3

1

…

A ．抛物线开口向上

B ．抛物线与y 轴交于负半轴

C ．当x ＝4时，y ＞0

D ．方程02

=++c bx ax 的正根在3与4之间 5．（2011，宿迁）已知二次函数y ＝ax 2

＋bx ＋c （a ≠0）的图象如图，则下列结论中正确的是（ ）

A ．a ＞0

B ．当x ＞1时，y 随x 的增大而增大

C ．c ＜0

D ．3是方程ax 2

＋bx ＋c ＝0的一个根

6．抛物线)8)(2(-+=x x a y 与x 轴交于A ，B 两点，与y 轴交于点C ，若∠ACB ?=90，则

a 的值为。

7．若抛物线82

++=

bx y x

的顶点在x 轴的负半轴上，则b 的的值是。

8．已知二次函数1)2(2

++-+-

=m x m y x

。

（1）求证：无论m 取任何实数，这个二次函数的图象必与x 轴有两个交点 （2）m 为何值时，这两个交点都在原点左侧？（直接写出答案）

（3）m 为何值时，这个二次函数的图象的对称轴是y 轴？（直接写出答案）

9．若二次函数m x

m x m y 2

2

2)1(2-+-+-

=的图象关于y 轴对称，其图象顶点为A ，

与x 轴的交点为B 、C ，求△ABC 的面积。