专题3:空间向量法求角基础知识与典型例题(原卷版)

专题3:空间向量法求角基础知识与典型例题(原卷版)
⑴求异面直线所成的角
已知,a b 为两异面直线,A ,C 与B ,D 分别是,a b 上的任意两点,,a b 所成的角为θ,则cos .AC BD
AC BD θ?=
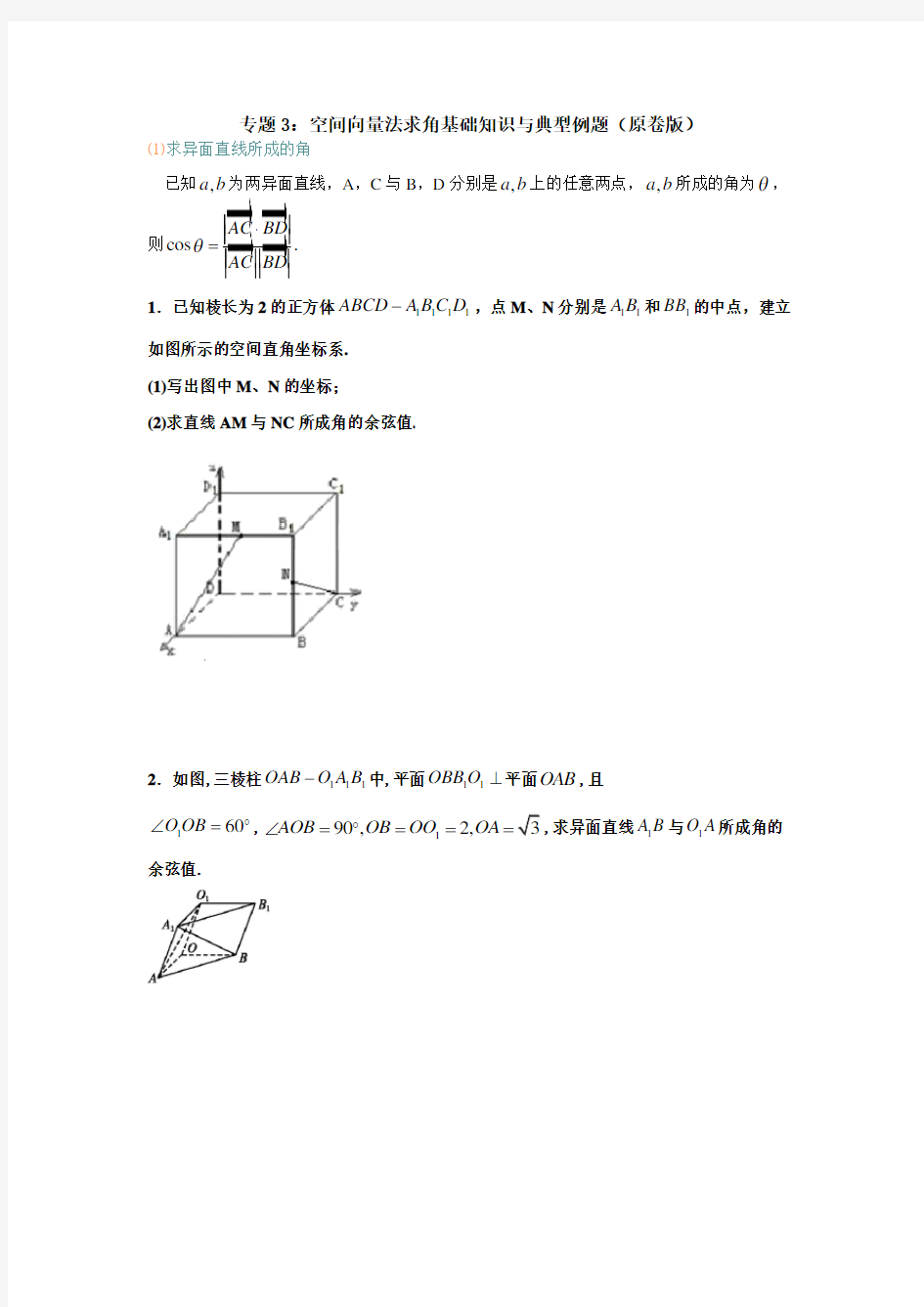
1.已知棱长为2的正方体1111ABCD A B C D -,点M 、N 分别是11A B 和1BB 的中点,建立如图所示的空间直角坐标系.
(1)写出图中M 、N 的坐标;
(2)求直线AM 与NC 所成角的余弦值.
2.如图,三棱柱111OAB O A B -中,平面11OBB O ⊥平面OAB ,且
160O OB ∠=?,190,2,3AOB OB OO OA ∠=?===,求异面直线1A B 与1O A 所成角的余弦值.
⑵求直线和平面所成的角
求法:设直线l 的方向向量为a ,平面α的法向量为u ,直线与平面所成的角为θ,a 与u 的夹角为?, 则θ为?的余角或?的补角
的余角.即有:cos s .in a u a u ?θ?=
=
3.如图,正方体1111ABCD A B C D -中,E 是1CC 的中点,求BE 与平面1B BD 所成角的正弦值.
4.如图,在三棱锥A BCD -中,ABC 是等边三角形,90BAD BCD ∠=∠=?,点P 是AC 的中点,连接,BP DP .
(1)证明:平面ACD ⊥平面BDP ;
(2)若6BD =,且二面角A BD C --为120?,求直线AD 与平面BCD 所成角的正弦值.
⑶求二面角
二面角的平面角是指在二面角βα--l 的棱上任取一点O ,分别在两个半平面内作射
线
l BO l AO ⊥⊥,,则AOB ∠为二面角βα--l 的平面角.
如图:
求法:设二面角l αβ--的两个半平面的法向量分别为m n 、
,再设m n 、的夹角为?,二面角l αβ--的平面角为θ,则二面角θ为m n 、
的夹角?或其补角.π?- 根据具体图形确定θ是锐角或是钝角:
如果θ是锐角,则cos cos m n
m n θ??==, 即arccos m n
m n θ?=;
如果θ是钝角,则cos cos m n
m n θ??=-=-, 即arccos m n m n θ??? ?=- ???. 5.如图所示,AE ⊥平面ABCD ,四边形AEFB 为矩形,//BC AD ,BA AD ⊥,224AE AD AB BC ====.
(1)求证://CF 平面ADE ;
(2)求平面CDF 与平面AEFB 所成锐二面角的余弦值.
O A
B O A B l
6.如图ABC ?和ABD ?均为等腰直角三角形,AD BD ⊥,AC BC ⊥,平面ABC ⊥平面ABD ,EC ⊥平面ABC ,1EC =,22AD =
(1)证明:DE AB ⊥;
(2)求二面角D BE A --的余弦值.
利用空间向量求空间角教案设计
利用空间向量求空间角 一、高考考纲要求: 能用向量方法解决异面直线的夹角、线面角、面面角问题.体会向量法在立体几何中的应用. 二、命题趋势: 在高考中,本部分知识是考查的重点内容之一,主要考查异面直线所成角、线面角、面面角的计算,属中档题,综合性较强,与平行垂直联系较多. 三、教学目标 知识与技能:能用向量法熟练解决异面直线的夹角、线面角、面面角的计算问题,了解向量法在研究立体几何问题中的应用; 过程与方法:通过向量这个载体,实现“几何问题代数化”的思想,进一步发展学生的空间想象能力和几何直观能力; 情感态度价值观:通过数形结合的思想和方法的应用,进一步让学生感受和体会空间直角坐标系,方向向量,法向量的魅力. 四、教学重难点 重点:用向量法求空间角——线线角、线面角、二面角; 难点:将立体几何问题转化为向量问题. 五、教学过程 (一)空间角公式 1、异面直线所成角公式:如图,设异面直线l ,m 的方向向量分别为a r ,b r ,异面直线l ,m
2、线面角公式:设直线l 为平面α的斜线,a r 为l 的方向向量,n r 为平面α的法向量,θ为 l 与α所成的角,则sin cos ,a n θ==r r a n a n ?r r r r . 3、面面角公式:设1n r ,2n r 分别为平面α、β的法向量,二面角为θ,则12,n n θ=r r 或 12,n n θπ=-r r (需要根据具体情况判断相等或互补) ,其中121212 cos ,n n n n n n ?=r r r r r r . α θ O n r a
(二)典例分析 如图,已知:在直角梯形OABC 中,//OA BC ,90AOC ∠=o ,SO ⊥面OABC ,且 1,2OS OC BC OA ====.求: (1)异面直线SA 和OB 所成的角的余弦值; (2)OS 与面SAB 所成角α的正弦值; (3)二面角B AS O --的余弦值. 解:如图建立空间直角坐标系,则(0,0,0)O , (2,0,0)A ,(1,1,0)B ,(0,1,0)C ,(0,0,1)S , 于是我们有(2,0,1)SA =-u u r ,(1,1,0)AB =-u u u r ,(1,1,0)OB =u u u r ,(0,0,1)OS =u u u r , (1)cos ,5SA OB SA OB SA OB ?== =u u r u u u r u u r u u u r u u r u u u r , 所以异面直线SA 和OB 所成的角的余弦值为5 . (2)设平面SAB 的法向量(,,)n x y z =r , 则0,0, n AB n SA ??=???=??r u u u r r u u r ,即0,20.x y x z -+=??-=? 取1x =,则1y =,2z =,所以(1,1,2)n =r , sin cos ,3OS n OS n OS n α?∴=== =u u u r r u u u r r u u u r r . (3)由(2)知平面SAB 的法向量1(1,1,2)n =u r , 又OC ⊥Q 平面AOS ,OC ∴u u u r 是平面AOS 的法向量, 令2(0,1,0)n OC ==u u r u u u r ,则有121212 cos ,n n n n n n ?== =u r u u r u r u u r u r u u r . ∴二面角B AS O --O A B C S
探索空间平面法向量的求法与方向的判定
“ 量无论无论是 和具有规具有规律性。 时有时会显得特别探索空间平面法向量的求法与方向的判定 问题,都离不开平面的 成角 ” ” 距离 “ 问题,还是 杨玉春 (铜仁市第二中学,贵州铜仁 554300) 向量具有一套完整的运算体系,可以把几何图形的性质 转化为向量运算,变抽象的逻辑推理为具体的向量运算,实 现了“数”与“形”的结合。因此用量知识解决某些立体几 何问题,有时会显得特别简洁和具有规律性。但用向量无论 是解决“成角”问题,还是“距离”问题,都离不开平面的 法向量,可以说平面的法向量是用向量来解决立几问题的瓶 颈,平面法向量的正确求出是关键。而用向量来求二面角的 大小时,往往还需判断法向量的方向,是指向二面角内还是 指向二面角外。本文介绍空间平面法向量的求法与方向的判 定。 一、平面法向量的求法 1、几何法:如图(1),若λ⊥α,在λ上任取两点A、B, 则或即为平面α的一个法向量。 2、待定系数法(两种设法):
(1)设n=(1,λ,μ)或n=(λ,1,μ)或n=(λ, μ,1)是平面α的一个法向量。a ,b 是平面α内任一两个不共线向量,由 n ·a=0 n ·b=0求出λ,μ即可。 (2)或设n=(x ,y ,z )是平面a=0 ·b=0 得出关于x 、y 、z 的三元一次方程组的一个解即为平面α的一个法向量。 3、利用空间平面方程:Ax+By+Cz+D=0(其中:A 、B 、C 不同时为零),则n=(A ,B ,C )为平面的一个法向量。 4利用向量的向量积:如图(1),设a=(111,,x y z ),b=(223,,x y z ) 则a ×b= =( ,| |,|) =(122121121221,,y z y z x z x z x y x y ---) 取n=(a ×b )(λ∈R 且λ≠0)是平面α的法向量。 二、空间平面法向量方向的判定 1、由几何法求出的法向量,此时方向看图即可。 2、由向量的向量积求出的法向量,用“右手定则”可确定a ×b 的方向,取n=λ(a ×b),当>0时,则n 方向与向
用向量法求二面角的平面角教案
第三讲:立体几何中的向量方法——利用空间向量求二面角的平面角 大家知道,立体几何是高中数学学习的一个难点,以往学生学习立体几何时,主要采取“形到形”的综合推理方法,即根据题设条件,将空间图形转化为平面图形,再由线线,线面等关系确定结果,这种方法没有一般规律可循,对人的智力形成极大的挑战,技巧性较强,致使大多数学生都感到束手无策。 高中新教材中,向量知识的引入,为学生解决立体几何问题提供了一个有效的工具。它能利用代数方法解决立体几何问题,体现了数形结合的思想。并且引入向量,对于某些立体几何问题提供通法,避免了传统立体几何中的技巧性问题,因此降低了学生学习的难度,减轻了学生学习的负担,体现了新课程理念。 为适应高中数学教材改革的需要,需要研究用向量法解决立体几何的各种问题。本文举例说明如何用向量法解决立体几何的空间角问题。以此强化向量的应用价值,激发学生学习向量的兴趣,从而达到提高学生解题能力的目的。 利用向量法求空间角,不需要繁杂的推理,只需要将几何问题转化为向量的代数运算,方便快捷。空间角主要包括线线角、线面角和二面角,下面对二面角的求法进行总结。 教学目标 1.使学生会求平面的法向量; 2.使学生学会求二面角的平面角的向量方法; 3.使学生能够应用向量方法解决一些简单的立体几何问题; 4.使学生的分析与推理能力和空间想象能力得到提高. 教学重点
求平面的法向量; 求解二面角的平面角的向量法. 教学难点 求解二面角的平面角的向量法. 教学过程 Ⅰ、复习回顾 一、回顾相关公式: 1、二面角的平面角:(范围:],0[πθ∈) 向量夹角的补角. 3、用空间向量解决立体几何问题的“三步曲”: (1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(化为向量问题) (2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(进行向量运算) (3)把向量的运算结果“翻译”成相应的几何意义。(回到图形) Ⅱ、典例分析与练习 例1、如图,ABCD 是一直角梯形,?=∠90ABC ,⊥SA 面ABCD ,1===BC AB SA ,
高中数学--空间向量之法向量求法及应用方法
高中数学空间向量之--平面法向量的求法及其应用 平面的法向量 仁定义:如果a _ :,那么向量a 叫做平面二的法向量。平面.:> 的法向量共有两大类(从方向上分) ,无 数条。 2、平面法向量的求法 斗 ■ 4 方法一(内积法):在给定的空间直角坐标系中, 设平面「的法向量n =(x,y,1)[或n =(x,1,z),或n =(1yZ ], 在平面:内任找两个不共线的向量 a,b 。由n _ :?,得n a = 0且n b = 0,由此得到关于 x, y 的方程组,解此 i 方程组即可得到n 。 方法二:任何一个 x, y, z 的一次次方程的图形是平面;反之,任何一个平面的方程是 Ax By Cz ^0 (代B,C 不同时为0),称为平面的一般方程。其法向量 n -(A, B,C);若平面与3个坐 标轴的交点为R(a,0,0), P 2(0,b,0), P 3(0,0, c),如图所示,则平面方程为?上 ]--1,称此方程为平面的截距 a b c 式方程,把它化为一般式即可求出它的法向量。 方法三(外积法):设 ,.为空间中两个不平行的非零向量,其外积 a b 为一长度等于|a||b|sinr , ( 9为 ..,.两者交角,且Ou :::二),而与..,.皆垂直的向量。通常我们采取「右手定则」,也就是右手四指由 .. 例 1、 已知,al(2,1,0),b'(-1,2,1), T T —f —f 试求(1): a^b ; (2): b 汉a. T T T T Key: (1) a b =(1,-2,5);⑵ b a =(-1,2,5) 例2、如图1-1,在棱长为2的正方体 ABCD -A 1B 1C 1D 1中, 7 T T T 的方向转为 匸的方向时,大拇指所指的方向规定为a b 的方向 ^( x i ,y i ,z i ),^(x 2, r 「 T T 丫2二2),则:a b = Z 2 X 1乙 X 2 Z 2 X 1 X 2 y 1 y 2 (注:1、二阶行列式 =ad —cb ; d 2、适合右手定 则。 x, y, z 的一次方程。
向量法求空间角(高二数学,立体几何)
A B C D P Q 向量法求空间角 1.(本小题满分10分)在如图所示的多面体中,四边形ABCD 为正方形,四边形ADPQ 是直角梯形,DP AD ⊥,⊥CD 平面ADPQ ,DP AQ AB 2 1==. (1)求证:⊥PQ 平面DCQ ; (2)求平面BCQ 与平面ADPQ 所成的锐二面角的大小. 2.(满分13分)如图所示,正四棱锥P -ABCD 中,O 为底面正方形的中心,侧棱PA 与底面ABCD 所成的角的正切值为 2 6. (1)求侧面PAD 与底面ABCD 所成的二面角的大小; (2)若E 是PB 的中点,求异面直线PD 与AE 所成角的正切值; (3)问在棱AD 上是否存在一点F ,使EF ⊥侧面PBC ,若存在,试确定点F 的位置;若不存在,说明理由. B
3.(本小题只理科做,满分14分)如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点. (1)求证:AF//平面BCE; (2)求证:平面BCE⊥平面CDE; (3)求平面BCE与平面ACD所成锐二面角的大小. P-中,PD⊥底面ABCD,且底面4.(本小题满分12分)如图,在四棱锥ABCD ABCD为正方形,G PD =分别为CB PC, ,的中点. = PD F ,2 E AD, , AP平面EFG; (1)求证:// (2)求平面GEF和平面DEF的夹角.
H P G F E D C B 5.如图,在直三棱柱111AB C A B C -中,平面1A BC ⊥ 侧面11A ABB 且12AA AB ==. (Ⅰ)求证:AB BC ⊥; (Ⅱ)若直线AC 与平面1A BC 所成的角为6 π,求锐二面角1A A C B --的大小. 6.如图,四边形ABCD 是正方形,EA ⊥平面ABCD ,EA PD ,2AD PD EA ==,F ,G , H 分别为PB ,EB ,PC 的中点. (1)求证:FG 平面PED ; (2)求平面FGH 与平面PBC 所成锐二面角的大小.
用空间向量解决空间中“夹角”问题
利用空间向量解决空间中的“夹角”问题 学习目标 : 1.学会求异面直线所成的角、直线与平面所成的角、二面角的向量方法; 2.能够应用向量方法解决一些简单的立体几何问题; 3.提高分析与推理能力和空间想象能力。 重点 : 利用空间向量解决空间中的“夹角” 难点 : 向量夹角与空间中的“夹角”的关系 一、复习引入 1.用空间向量解决立体几何问题的“三步曲” (1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;(化为向量问题) (2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(进行向量运算) (3)把向量的运算结果“翻译”成相应的几何意义。(回到图形) 2.向量的有关知识: (1)两向量数量积的定义:><=?,cos |||| (2)两向量夹角公式:| |||,cos b a >= < (3)平面的法向量:与平面垂直的向量 二、知识讲解与典例分析 知识点1:异面直线所成的角(范围:]2 , 0(π θ∈) (1)定义:过空间任意一点o 分别作异面直线a 与b 的平行线a′与b′,那么直线a′与b′ 所成的锐角或直角,叫做异面直线a 与b 所成的角. (2)用向量法求异面直线所成角 设两异面直线a 、b 的方向向量分别为和, 问题1: 当与的夹角不大于90 的角θ与 和 的夹角的关系?问题 2:a 与b 的夹角大于90°时,,异面直线a θ与a 和b 的夹角的关系? 结论:异面直线a 、b 所成的角的余弦值为| ||||,cos |cos n m = ><=θ a
例1如图,正三棱柱111C B A ABC -的底面边长为a ,侧棱长为a 2,求1AC 和1CB 所成的角. 解法步骤:1.写出异面直线的方向向量的坐标。 2.利用空间两个向量的夹角公式求出夹角。 解:如图建立空间直角坐标系xyz A -,则 )2,,0(),0,21,23(),2,21,23(),0,0,0(11a a B a a C a a a C A -- ∴ )2,21,23(1a a a AC -=,)2,21 ,23(1a a a CB = 即21 323||||,cos 22 111111==>=<,与θ的关系? 例2、如图,正三棱柱111C B A ABC -的底面边长为a ,侧棱长为a 2,求1AC 和B B AA 11面所成角的正弦值. 分析:直线与平面所成的角步骤: 1. 求出平面的法向量 2. 求出直线的方向向量 3. 求以上两个向量的夹角,(锐角)其余角为所求角 解:如图建立空间直角坐标系xyz A -,则),0,,0(),2,0,0(1a a AA ==)2,21 ,23(1a a a AC -= 设平面B B AA 11的法向量为),,(z y x n = x y
