人教中考数学复习平行四边形专项易错题及答案

一、平行四边形真题与模拟题分类汇编(难题易错题)
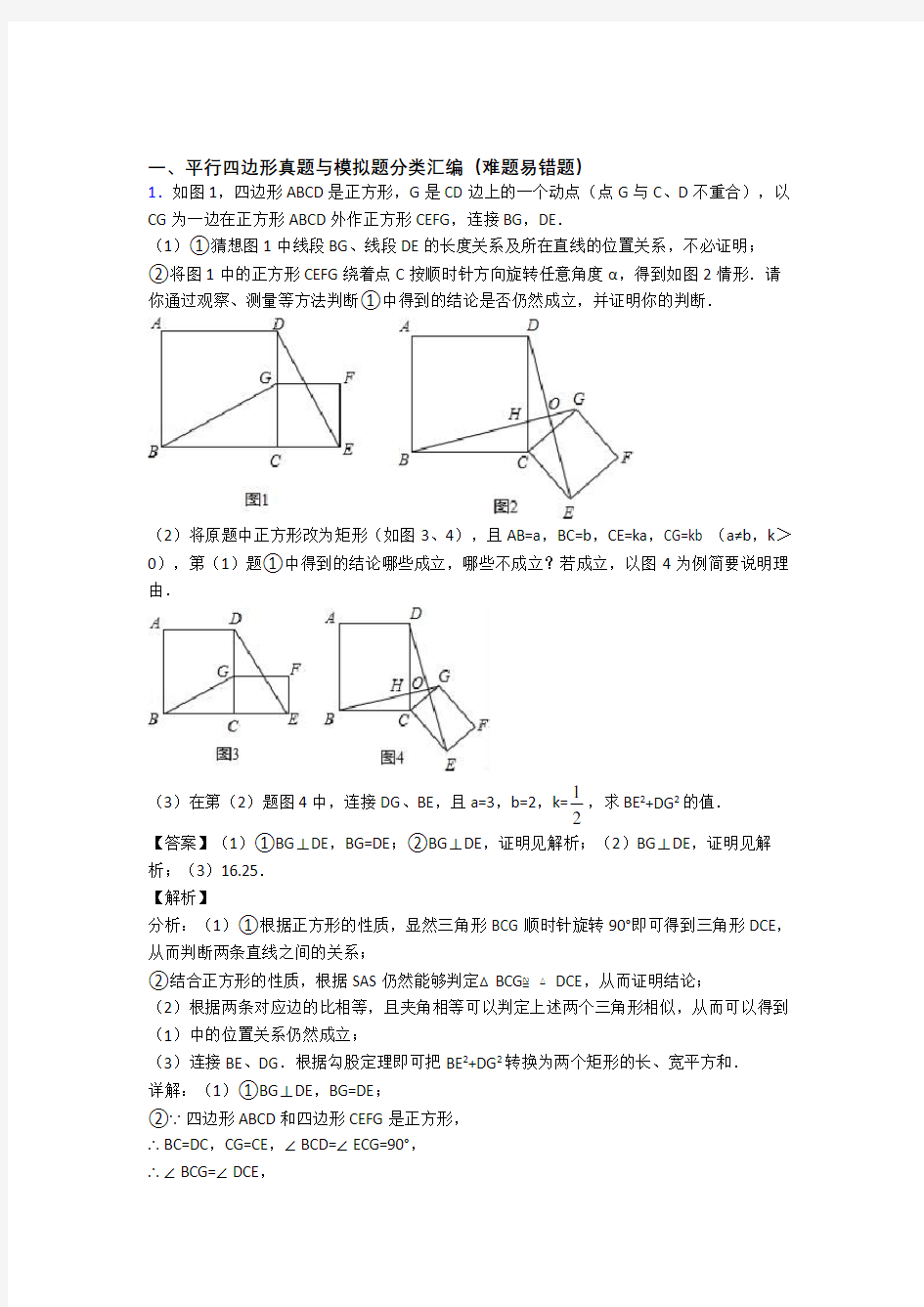
1.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.
(1)①猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;
②将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并证明你的判断.
(2)将原题中正方形改为矩形(如图3、4),且AB=a,BC=b,CE=ka,CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图4为例简要说明理由.
(3)在第(2)题图4中,连接DG、BE,且a=3,b=2,k=1
2
,求BE2+DG2的值.
【答案】(1)①BG⊥DE,BG=DE;②BG⊥DE,证明见解析;(2)BG⊥DE,证明见解析;(3)16.25.
【解析】
分析:(1)①根据正方形的性质,显然三角形BCG顺时针旋转90°即可得到三角形DCE,从而判断两条直线之间的关系;
②结合正方形的性质,根据SAS仍然能够判定△BCG≌△DCE,从而证明结论;
(2)根据两条对应边的比相等,且夹角相等可以判定上述两个三角形相似,从而可以得到(1)中的位置关系仍然成立;
(3)连接BE、DG.根据勾股定理即可把BE2+DG2转换为两个矩形的长、宽平方和.
详解:(1)①BG⊥DE,BG=DE;
②∵四边形ABCD和四边形CEFG是正方形,
∴BC=DC,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
∴△BCG≌△DCE,
∴BG=DE,∠CBG=∠CDE,
又∵∠CBG+∠BHC=90°,
∴∠CDE+∠DHG=90°,
∴BG⊥DE.
(2)∵AB=a,BC=b,CE=ka,CG=kb,
∴BC CG b
==,
DC CE a
又∵∠BCG=∠DCE,
∴△BCG∽△DCE,
∴∠CBG=∠CDE,
又∵∠CBG+∠BHC=90°,
∴∠CDE+∠DHG=90°,
∴BG⊥DE.
(3)连接BE、DG.
根据题意,得AB=3,BC=2,CE=1.5,CG=1,
∵BG⊥DE,∠BCD=∠ECG=90°
∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+4+2.25+1=16.25.
点睛:此题综合运用了全等三角形的判定和性质、相似三角形的判定和性质以及勾股定理.
2.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
【答案】(1)证明见解析;(2)当∠DOE=90°时,四边形BFED为菱形,理由见解析.【解析】
试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF (ASA);
(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.
试题解析:(1)∵在?ABCD中,O为对角线BD的中点,
∴BO=DO,∠EDB=∠FBO,
在△EOD和△FOB中
,
∴△DOE≌△BOF(ASA);
(2)当∠DOE=90°时,四边形BFDE为菱形,
理由:∵△DOE≌△BOF,∴OE=OF,又∵OB=OD,∴四边形EBFD是平行四边形,
∵∠EOD=90°,∴EF⊥BD,∴四边形BFDE为菱形.
考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.
3.如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以
4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t 秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.
【答案】(1)见解析;(2)能,t=10;(3)t=15
2
或12.
【解析】
【分析】
(1)利用t表示出CD以及AE的长,然后在直角△CDF中,利用直角三角形的性质求得DF的长,即可证明;
(2)易证四边形AEFD是平行四边形,当AD=AE时,四边形AEFD是菱形,据此即可列方程求得t的值;
(3)△DEF为直角三角形,分∠EDF=90°和∠DEF=90°两种情况讨论.【详解】
解:(1)证明:∵在Rt△ABC中,∠C=90°﹣∠A=30°,
∴AB=1
2AC=
1
2
×60=30cm,
∵CD=4t,AE=2t,
又∵在Rt△CDF中,∠C=30°,
∴DF=1
2
CD=2t,∴DF=AE;
(2)能,
∵DF∥AB,DF=AE,
∴四边形AEFD是平行四边形,
当AD=AE时,四边形AEFD是菱形,即60﹣4t=2t,解得:t=10,∴当t=10时,AEFD是菱形;
(3)若△DEF为直角三角形,有两种情况:
①如图1,∠EDF=90°,DE∥BC,
则AD=2AE,即60﹣4t=2×2t,解得:t=15
2
,
②如图2,∠DEF=90°,DE⊥AC,
则AE=2AD,即2t2(604t)
=-,解得:t=12,
综上所述,当t=15
2
或12时,△DEF为直角三角形.
4.如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
【答案】(1)见解析;(2)43;(3)见解析
【解析】
试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形
AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;
(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
试题解析:(1)证明:连接AC,
∵∠1+∠2=60°,∠3+∠2=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=∠ADC=60°
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴△ABC、△ACD为等边三角形
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
,
∴△ABE≌△ACF.(ASA)
∴BE=CF.
(2)解:由(1)得△ABE≌△ACF,
则S △ABE =S △ACF .
故S 四边形AECF =S △AEC +S △ACF =S △AEC +S △ABE =S △ABC ,
是定值.
作AH ⊥BC 于H 点,
则BH=2,
S 四边形AECF =S △ABC =
=
=; (3)解:由“垂线段最短”可知,
当正三角形AEF 的边AE 与BC 垂直时,边AE 最短.
故△AEF 的面积会随着AE 的变化而变化,且当AE 最短时,
正三角形AEF 的面积会最小,
又S △CEF =S 四边形AECF ﹣S △AEF ,则△CEF 的面积就会最大.
由(2)得,S △CEF =S 四边形AECF ﹣S △AEF =﹣=.
点睛:本题考查了菱形每一条对角线平分一组对角的性质,考查了全等三角形的证明和全等三角形对应边相等的性质,考查了三角形面积的计算,本题中求证△ABE ≌△ACF 是解题的关键.
5.已知90AOB ∠=?,点C 是AOB ∠的角平分线OP 上的任意一点,现有一个直角MCN ∠绕点C 旋转,两直角边CM ,CN 分别与直线OA ,OB 相交于点D ,点E .
(1)如图1,若CD OA ⊥,猜想线段OD ,OE ,OC 之间的数量关系,并说明理由. (2)如图2,若点D 在射线OA 上,且CD 与OA 不垂直,则(1)中的数量关系是否仍成立?如成立,请说明理由;如不成立,请写出线段OD ,OE ,OC 之间的数量关系,并加以证明.
(3)如图3,若点D 在射线OA 的反向延长线上,且2OD =,8OE =,请直接写出线段CE 的长度.
【答案】(1)详见解析;(2)详见解析;(334【解析】
【分析】
(1)先证四边形ODCE 为矩形,再证矩形ODCE 为正方形,由正方形性质可得;(2)过点C 作CG OA ⊥于点G ,CH OB ⊥于点H ,证四边形OGCH 为正方形,再证()CGD CHE ASA ???,可得;(3)根据()CGD CHE ASA ???,可得
2OE OD OH OG OC -=+=.
【详解】
解:(1)∵90AOB ∠=?,90MCN ∠=?,CD OA ⊥,
∴四边形ODCE 为矩形.
∵OP 是AOB ∠的角平分线,
∴45DOC EOC ∠=∠=?,
∴OD CD =,
∴矩形ODCE 为正方形, ∴2OC OD =,2OC OE =.
∴2OD OE OC +=.
(2)如图,过点C 作CG OA ⊥于点G ,CH OB ⊥于点H ,
∵OP 平分AOB ∠,90AOB ∠=?,
∴四边形OGCH 为正方形,
由(1)得:2OG OH OC +=
,
在CGD ?和CHE ?中, 90CGD CHE CG CH
DCG ECH ?
?∠=∠=?=??∠=∠?
, ∴()CGD CHE ASA ???,
∴GD HE =,
∴2OD OE OC +=.
(3)2OG OH OC +=
, ()CGD CHE ASA ???,
∴GD HE =. ∵OD GD OG =-,OE OH EH =+,
∴2OE OD OH OG OC -=+=
, ∴32OC =,
∴34CE =,
CE 的长度为34.
【点睛】
考核知识点:矩形,正方形的判定和性质.熟练运用特殊四边形的性质和判定是关键.
6.现有一张矩形纸片ABCD (如图),其中AB =4cm ,BC =6cm ,点E 是BC 的中点.将纸片沿直线AE 折叠,点B 落在四边形AECD 内,记为点B ′,过E 作EF 垂直B ′C ,交B ′C 于F .
(1)求AE 、EF 的位置关系;
(2)求线段B ′C 的长,并求△B ′EC 的面积.
【答案】(1)见解析;(2)S△B′EC=108 25
.
【解析】
【分析】
(1)由折线法及点E是BC的中点,可证得△B'EC是等腰三角形,再有条件证明∠AEF=90°即可得到AE⊥EF;
(2)连接BB′,通过折叠,可知∠EBB′=∠EB′B,由E是BC的中点,可得EB′=EC,
∠ECB′=∠EB′C,从而可证△BB′C为直角三角形,在Rt△AOB和Rt△BOE中,可将OB,BB′的长求出,在Rt△BB′C中,根据勾股定理可将B′C的值求出.
【详解】
(1)由折线法及点E是BC的中点,
∴EB=EB′=EC,∠AEB=∠AEB′,
∴△B'EC是等腰三角形,
又∵EF⊥B′C
∴EF为∠B'EC的角平分线,即∠B′EF=∠FEC,
∴∠AEF=180°﹣(∠AEB+∠CEF)=90°,即∠AEF=90°,
即AE⊥EF;
(2)连接BB'交AE于点O,由折线法及点E是BC的中点,
∴EB=EB′=EC,
∴∠EBB′=∠EB′B,∠ECB′=∠EB′C;
又∵△BB'C三内角之和为180°,
∴∠BB'C=90°;
∵点B′是点B关于直线AE的对称点,
∴AE垂直平分BB′;
在Rt△AOB和Rt△BOE中,BO2=AB2﹣AO2=BE2﹣(AE﹣AO)2
将AB=4cm,BE=3cm,AE=5cm,
∴AO=16
5
cm,
∴BO22
AB AO
12
5
cm,
∴BB′=2BO=24
5
cm,
∴在Rt △BB 'C 中,B ′C =22BC BB '-=
518cm , 由题意可知四边形OEFB ′是矩形,
∴EF =OB ′=
125, ∴S △B ′EC =*111812108225525
B C EF '
?=??=.
【点睛】
考查图形的折叠变化及三角形的内角和定理勾股定理的和矩形的性质综合运用.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
7.如图1,在正方形ABCD 中,点E ,F 分别是边BC ,AB 上的点,且CE=BF .连接DE ,过点E 作EG ⊥DE ,使EG=DE ,连接FG ,FC .
(1)请判断:FG 与CE 的关系是___;
(2)如图2,若点E ,F 分别是边CB ,BA 延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E ,F 分别是边BC ,AB 延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
【答案】(1)FG=CE ,FG ∥CE ;(2)成立;(3)成立.
【解析】
试题分析:(1)只要证明四边形CDGF 是平行四边形即可得出FG =CE ,FG ∥CE ;
(2)构造辅助线后证明△HGE ≌△CED ,利用对应边相等求证四边形GHBF 是矩形后,利用等量代换即可求出FG =C ,FG ∥CE ;
(3)证明△CBF ≌△DCE 后,即可证明四边形CEGF 是平行四边形.
试题解析:解:(1)FG =CE ,FG ∥CE ;
(2)过点G作GH⊥CB的延长线于点H.∵EG⊥DE,
∴∠GEH+∠DEC=90°.∵∠GEH+∠HGE=90°,∴∠DEC=∠HE.在△HGE与△CED中,
∵∠GHE=∠DCE,∠HGE=∠DEC,EG=DE,∴△HGE≌△CED(AAS),∴GH=CE,
HE=CD.∵CE=BF,∴GH=BF.∵GH∥BF,∴四边形GHBF是矩形,∴GF=BH,FG∥CH,∴FG∥CE.∵四边形ABCD是正方形,∴CD=BC,∴HE=BC,∴HE+EB=BC+EB,∴BH=EC,∴FG=EC;
(3)∵四边形ABCD是正方形,∴BC=CD,∠FBC=∠ECD=90°.在△CBF与△DCE中,
∵BF=CE,∠FBC=∠ECD,BC=DC,∴△CBF≌△DCE(SAS),∴∠BCF=∠CDE,
CF=DE.∵EG=DE,∴CF=EG.∵DE⊥EG,∴∠DEC+∠CEG=90°.∵∠CDE+∠DEC=90°,
∴∠CDE=∠CEG,∴∠BCF=∠CEG,∴CF∥EG,∴四边形CEGF平行四边形,∴FG∥CE,FG=CE.
8.在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图①,当点E自D向C,点F自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的位置关系,并说明理由;
(2)如图②,当E,F分别移动到边DC,CB的延长线上时,连接AE和DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不须证明)
(3)如图③,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?请说明理由;
(4)如图④,当E,F分别在边DC,CB上移动时,连接AE和DF交于点P,由于点E,F 的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP 的最小值.
【答案】(1)AE=DF,AE⊥DF;
(2)是;
(3)成立,理由见解析;
(4)CP=QC﹣QP=.
【解析】
试题分析:(1)AE=DF,AE⊥DF.先证得△ADE≌△DCF.由全等三角形的性质得AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;
(2)是.四边形ABCD是正方形,所以AD=DC,∠ADE=∠DCF=90°,DE=CF,所以
△ADE≌△DCF,于是AE=DF,∠DAE=∠CDF,因为∠CDF+∠ADF=90°,∠DAE+∠ADF=90°,所以AE⊥DF;
(3)成立.由(1)同理可证AE=DF,∠DAE=∠CDF,延长FD交AE于点G,再由等角的余角相等可得AE⊥DF;
(4)由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD 的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.
试题解析:(1)AE=DF,AE⊥DF.
理由:∵四边形ABCD是正方形,∴AD=DC,∠ADC=∠C=90°.
在△ADE和△DCF中,,∴△ADE≌△DCF(SAS).
∴AE=DF,∠DAE=∠CDF,由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.∴AE⊥DF;(2)是;
(3)成立.
理由:由(1)同理可证AE=DF,∠DAE=∠CDF
延长FD交AE于点G,
则∠CDF+∠ADG=90°,
∴∠ADG+∠DAE=90°.
∴AE⊥DF;
(4)如图:
由于点P在运动中保持∠APD=90°,∴点P的路径是一段以AD为直径的弧,
设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,
在Rt△QDC中,QC=,
∴CP=QC﹣QP=.
考点:四边形的综合知识.
9.已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形 AMCN是菱形,证明你的结论.【答案】(1)证明见解析;(2)当AB=AF时,四边形AMCN是菱形.证明见解析;【解析】
试题分析:(1)由已知条件可得四边形AMCN是平行四边形,从而可得AM=CN,再由AB=CD,∠B=∠D=90°,利用HL即可证明;
(2)若四边形AMCN为菱形,则有AM=AN,从已知可得∠BAM=∠FAN,又∠B=∠F=90°,所以有△ABM≌△AFN,从而得AB=AF,因此当AB=AF时,四边形AMCN是菱形.
试题解析:(1)∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD∥BC.
∵四边形AECF是矩形,∴AE∥CF.∴四边形AMCN是平行四边形.∴AM=CN.在
Rt△ABM和Rt△CDN中,AB=CD,AM=CN,∴Rt△ABM≌Rt△CDN.
(2)当AB=AF时,四边形AMCN是菱形.
∵四边形ABCD、AECF是矩形,∴∠B=∠BAD=∠EAF=∠F=90°.∴∠BAD-∠NAM=∠EAF-∠NAM,即∠BAM=∠FAN.又∵AB=AF,∴△ABM≌△AFN.∴AM=AN.由(1)知四边形AMCN是平行四边形,∴平行四边形AMCN是菱形.
考点:1.矩形的性质;2.三角形全等的判定与性质;3.菱形的判定.
10.(本题满分10分)如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.
(1)求矩形ABCD的边AD的长.
(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.
(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;
②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式
【答案】(1)AD=3;(2)y=-其中,0<x<3;(3)x=;(4)
S=.
【解析】
试题分析:(1)根据折叠图形的性质和勾股定理求出AD的长度;(2)根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式;(3)过点N作NQ⊥CD,根据Rt△NPQ 的勾股定理进行求解;(4)根据Rt△ADM的勾股定理求出MP与x的函数关系式,然后得出函数关系式.
试题解析:(1)根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得:AD=3.
(2)由折叠可知AM=MP,在Rt△MPD中,
∴∴y=-其中,0<x<3.
(3)当点N在AB上,x≥3,∴PC≤3,而PN≥3,NC≥3.
∴△PCN为等腰三角形,只可能NC=NP.
过N点作NQ⊥CD,垂足为Q,在Rt△NPQ中,
∴解得x=.
(4)当点M在CD上时,N在AB上,可得四边形ANPM为菱形.
设MP=y,在Rt△ADM中,,即∴ y=.
∴ S=
考点:函数的性质、勾股定理.
