高数下册总复习知识点归纳

高数下册总复习知识点
归纳
IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】
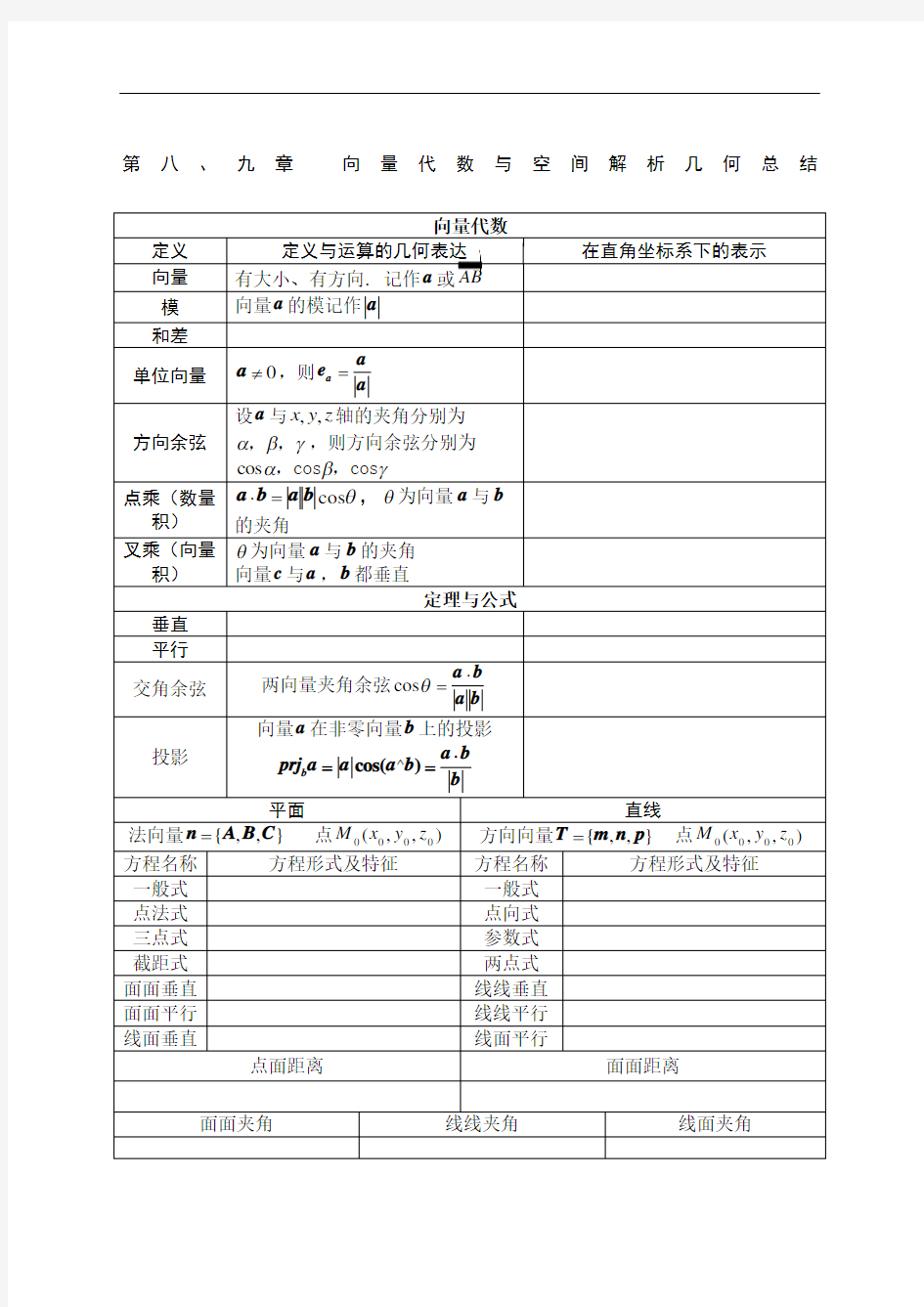
第八、九章向量代数与空间解析几何总结定义与运算的几何表达
○1定义:四步法——分割、代替、求和、取极限;
○2性质:对积分的范围具有可加性,具有线性性;
○3对坐标的积分,积分区域对称与被积函数的奇偶性。
第十二章总结
无穷级数常
数
项
级
数
傅
立
叶
级
数
幂
级
数
一
般
项
级
数
正
项
级
数
用收敛定义,
n
n
s
∞
→
lim存
常数项级数的基本性质
常数项级数的基本性质
○若级数收敛,各项同乘同一常数仍收敛
○两个收敛级数的和差仍收敛
注:一敛、一散之和必发散;两散和、差必发散.
○去掉、加上或改变级数有限项不改变其收敛性
○若级数收敛则对这级数的项任意加括号后所成的
级数仍收敛,且其和不变。
推论如果加括号后所成的级数发散则原来级数也
发散注:收敛级数去括号后未必收敛.
○(必要条件)如果级数收敛则
莱布尼茨判别法若1+
≥
n
n
u
u且0
lim=
∞
→
n
n
u,则∑∞
=
-
-
1
1
)1
(
n
n
n u收敛
n
u
∑和
n
v
∑都是正项级数,且
n
n
v
u≤.若
n
v
∑收敛,则
n
u
∑也收敛;若
n
u
∑发散,则
n
v
∑也发散.
比较判别法
比较判别法
的极限形式
n
u
∑和
n
v
∑都是正项级数,且l
v
u
n
n
n
=
∞
→
lim,则○1若
+∞
<
0, n u ∑与 n v ∑同敛或同散;○2若0 = l, n v ∑收 敛, n u ∑也收敛;○3如果+∞ = l, n v ∑发散, n u ∑也发 比值判别法 根值判别法 n u ∑是正项级数,ρ = + ∞ → n n n u u 1 lim,ρ = ∞ → n n n u lim,则1 < ρ时 收敛;1 > ρ(ρ=+∞)时发散;1 = ρ时可能收敛也可能发收 敛 性 和 函 数 展 成 幂 级 数 n n n x a ∑∞ =0 , ρ = + ∞ → n n n a a 1 lim ,1,0;,0;0,. R R R ρρρ ρ =≠=+∞===+∞缺项级数用比值审敛法求收敛半径 ) (x s的性质○在收敛域I上连续;○在收敛域) , (R R -内可导,且可逐项求导;○和函数)(x s在收敛域I上可积分,且可逐项积分.(R不变,收敛域可能变化). 直接展开:泰勒级数间接展开:六个常用展开式 ?- =π π π nxdx x f a n cos ) ( 1 ?- =π π π nxdx x f b n sin ) ( 1收敛定理 x是连续点,收敛于) (x f;x是间断点,收敛于 )] ( ) ( [ 2 1 + -+x f x f 周期 延拓 ) (x f为奇函数,正弦级数,奇延拓;) (x f为偶函数,余弦级数、偶延拓. 交 错 第八章 1、向量在轴上的投影: 性质:?cos )(a a u =(即Prj u ?cos a a =),其中?为向量a 与u 轴的夹角; u u u b a b a )()()( +=+(即Prj u =+)(b a Prj u a + Prj u b ); u u a a )()( λλ=(即Prj u λλ=)(a Prj u a ). 2、两个向量的向量积:设k a j a i a a z y x ++=,k b j b i b b z y x ++=,则 =?b a x x b a i y y b a j z z b a k =1 1) 1(+-y y b a z z b a i +21)1(+-x x b a z z b a j +3 1) 1(+- x x b a y y b a k =k b a b a j b a b a i b a b a x y y x z x x z y z z y )()()(-+-+- 注:a b b a ?-=? 3、二次曲面 (1) 椭圆锥面:222 22z b y a x =+; (2) 椭圆抛物面:z b y a x =+22 22; (旋转抛物面:z a y x =+2 22(把把xOz 面上的抛物线z a x =22 绕z 轴旋转)) (3) 椭球面:1222222=++c z b y a x ; (旋转椭球面:122 2 22=++c z a y x (把xOz 面上的椭圆122 22=+c z a x 绕z 轴旋转)) (4) 单叶双曲面:1222222=-+c z b y a x ; (旋转单叶双曲面:122 222=-+c z a y x (把 xOz 面上的双曲线122 22=-c z a x 绕z 轴旋转)) 高等数学(下)知识点 主要公式总结 第八章 空间解析几何与向量代数 1、 二次曲面 1) 椭圆锥面:2 2 222z b y a x =+ 2) 椭球面:122 222 2=++c z b y a x 旋转椭球面:1222222=++c z a y a x 3) 单叶双曲面:122 222 2=-+c z b y a x 双叶双曲面:1222222=--c z b y a x 4) 椭圆抛物面:z b y a x =+2222 双曲抛物面(马鞍面):z b y a x =-22 22 5) 椭圆柱面:1222 2=+b y a x 双曲柱面:122 22=-b y a x 6) 抛物柱面: ay x =2 (二) 平面及其方程 1、 点法式方程: 0)()()(000=-+-+-z z C y y B x x A 法向量:),,(C B A n =ρ ,过点),,(000z y x 2、 一般式方程: 0=+++D Cz By Ax 截距式方程: 1=++c z b y a x 3、 两平面的夹角:),,(1111C B A n =ρ,),,(2222C B A n =ρ, ?∏⊥∏21 0212121=++C C B B A A ;?∏∏21// 2 1 2121C C B B A A == 4、 点 ),,(0000z y x P 到平面0=+++D Cz By Ax 的距离: (三) 空间直线及其方程 1、 一般式方程:?????=+++=+++0 022221111D z C y B x A D z C y B x A 2、 对称式(点向式)方程: p z z n y y m x x 0 00-=-=- 《高等数学》(下册)复习提纲 复 习 题 1.求与平面230x +y +z +=1π:及2310x +y z +=-2π:都平行且过点(1,0,1)P -的直线方程。 2.求与直线240,:2320. x +y z +=l x +y +z =-?? -?垂直,且过点P(-1,0,1)的平面方程。 3.函数) 1ln(4)2arcsin(2 2 2 y x y x x z ---+ =的定义域为 。 4.求极限:xy xy y x 42lim +- →→。 5.证明极限 2 (,)(0,) lim x y x y x →- 0不存在。 6.计算偏导数:(1)x y z arcsin =,求 2 2 z x ??; (2)设 ),(2 x y x f y z =,求 z z x y ????,。 7.求x y e z =在点(1,2)的全微分。 8.设y z z x ln =,求 , z z x y ????。 9.求曲面3=+-xy z e z 在点)0,1,2(处的切平面及法线方程。 10.求曲线22230, 23540.x y z x x y z ?++-=?-+-=? 在点)1,1,1(处的切线和法平面方程。 11.求函数222u x y z =++在曲线32 , ,t z t y t x ===点)1,1,1(处沿曲线在该点的切线正向的 方向导数。 12.求(,,)sin()f x y z xyz xyz =的梯度。 13.求椭圆2225160x xy y y ++-=到直线80x y +-=的最短距离。 14.交换积分次序:? ?-2 2 1 0 ),(y y dx y x f dy 。 15.计算积分:(1)sin D x dxdy x ?? ,其中D 是由直线y x =及抛物线2 y x =所围成的区域; (2)dxdy y x D ?? +2 2,D :}2|),{(2 2 y y x y x ≤+; (3)???Ω +dv z x )(, Ω:球面2224x y z ++=与抛物面22 3x y z +=所围成的区域。 16.设)(x f 连续,2)(10 =?dx x f ,求??10 1 )()(x dy y f x f dx 。 17 .求曲面2z =-2 2 y x z +=所围的立体体积。 18.计算积分:(1)?+L ds y x )(2 2 ,L 为下半圆周21x y --=; (2)dy y x dx y xy L )()(2 2++-?,L 为抛物线2 x y =从(0,0)到(1,1)的一段有向弧; (3)dy x y e dx y x y e x L x )cos ()sin (-+--?,其中L 是在圆周2 2x x y -= 上由点 (2,0)到(0,0)的一段弧。 高等数学下册习题常见类型 题型1 求向量的坐标、模、方向角、方向余弦、数量积、向量积 题型2 由已知条件求平面与直线方程 题型3 计算一阶偏导数及高阶偏导数 题型4 求多元复合函数的偏导数 题型5 求方程所确定的隐函数的偏导数 题型6 求方向导数、梯度、曲线的切线、曲面的切平面 题型7 求极值、利用拉格郎日乘数法求最值 题型8 利用直角坐标计算二重积分 题型9 利用极坐标计算二重积分 题型10 计算带绝对值的二重积分 题型11 利用二重积分证明恒等式 题型12 利用对称性质计算二重积分 题型13 只有一种积分次序可计算的积分 例1、 求 2 421 2x dx dx +? ? 解:(将二次积分交换顺序) 12 212 2421 22211sin sin sin sin (1)sin cos1sin1 x D D y y D D y y dx dx dxdy dxdy y y y y dxdy dy dx y ydy y y πππππ+=+===-=-???????????U 题型14 利用投影法计算三重积分 题型15 利用柱坐标计算三重积分 题型16 利用球坐标计算三重积分 题型17 利用切片法计算三重积分 题型18 利用三重积分计算立体的体积 题型19 计算对弧长的曲线积分 题型20 计算对面积的曲面积分 题型21 计算对坐标的曲线积分 题型22 利用格林公式计算对坐标的曲线积分 题型23 曲线积分与路径无关及全微分求积 题型24 计算对坐标的曲面积分 题型25 利用高斯公式计算对坐标的曲面积分 题型26 可分离变量的微分方程、齐次方程 题型27一阶线性微分方程 题型29 可降阶方程 题型30二阶常系数非齐次线性方程 第八章 向量与解析几何 向量代数 定义 定义与运算的几何表达 在直角坐标系下的表示 向量 有大小、有方向. 记作a 或AB u u u r a (,,)x y z x y z a i a j a k a a a =++= ,,x x y y z z a prj a a prj a a prj a ===r r r 模 向量a 的模记作a a 222x y z a a a =++ 和差 c a b =+ c a b =- =+c a b {},,=±±±x x y y z z a b a b a b 单位向量 0a ≠,则a a e a = a e 2 2 2 (,,)= ++x y z x y z a a a a a a 方向余弦 设a 与,,x y z 轴的夹角分别为αβγ,,,则方向余弦分别为cos αβγ,cos ,cos cos y x z a a a a a a αβγ===r r r ,cos ,cos cos a e αβγ=(,cos ,cos ) 222cos 1αβγ+=+cos cos 点乘(数量积) θcos b a b a =?, θ为向量a 与b 的夹 角 z z y y x x b a b a b a ++=?b a 叉乘(向量积) b a c ?= θsin b a c = θ为向量a 与b 的夹角 向量c 与a ,b 都垂直 z y x z y x b b b a a a k j i b a =? 定理与公式 垂直 0a b a b ⊥??= 0x x y y z z a b a b a b a b ⊥?++= 平行 //0a b a b ??= //y z x x y z a a a a b b b b ?== 交角余弦 两向量夹角余弦b a b a ?= θcos 2 2 2 2 2 2 cos x x y y z z x y z x y z a b a b a b a a a b b b θ++= ++?++ 投影 向量a 在非零向量b 上的投影 cos()b a b prj a a a b b ∧ ?== 2 2 2 x x y y z z b x y z a b a b a b prj a b b b ++= ++ 高数重点知识总结 1、基本初等函数:反函数(y=arctanx),对数函数(y=lnx),幂函数(y=x),指数函数(x a y =),三角函数(y=sinx),常数函数(y=c) 2、分段函数不是初等函数。 3、无穷小:高阶+低阶=低阶 例如:1lim lim 020==+→→x x x x x x x 4、两个重要极限:()e x e x x x x x x x x =?? ? ??+=+=∞ →→→11lim 1lim )2(1 sin lim )1(1 0 经验公式:当∞→→→)(,0)(,0x g x f x x ,[] ) ()(lim ) (0 )(1lim x g x f x g x x x x e x f →=+→ 例如:()33lim 10 031lim -? ? ? ? ?-→==-→e e x x x x x x 5、可导必定连续,连续未必可导。例如:||x y =连续但不可导。 6、导数的定义:()00 00 ') ()(lim ) (') ()(lim x f x x x f x f x f x x f x x f x x x =--=?-?+→→? 7、复合函数求导: [][])(')(')(x g x g f dx x g df ?= 例如:x x x x x x x y x x y ++=++ = +=2412221 1', 8、隐函数求导:(1)直接求导法;(2)方程两边同时微分,再求出dy/dx 例如:y x dx dy ydy xdx y x y yy x y x - =?+- =?=+=+22,),2('0'22,),1(1 22左右两边同时微分法左右两边同时求导解:法 9、由参数方程所确定的函数求导:若?? ?==) ()(t h x t g y ,则)(')('//t h t g dt dx dt dy dx dy ==,其二阶导数:()[] ) (')('/)('/)/(/22 t h dt t h t g d dt dx dt dx dy d dx dx dy d dx y d === 10、微分的近似计算:)(')()(000x f x x f x x f ??=-?+ 例如:计算 ?31sin 高等数学下册知识点 《高等数学C2》考试大纲 一、考试内容与重点分布 1、向量代数与空间解析几何 (1) 空间向量的数量积与向量积计算方法(☆); (判断题2分, 计算题6分) ,,cos 是一个数量z z y y x x b a b a b a b a b a ++=?=?θ ,是个向量 注意:两者的运算律要会。 (2) 空间曲面方程的识别; (选择题3分) 几种常见的二次曲面 (3) 平面与直线方程及其求法(☆). (判断2分, 填空题3分, 计算题6分) Ⅰ、平面的几种方程形式: (1)点法式:过点),,(000z y x ,法向量为}C B,A,{=n 的平面方程: k j i x a y a z a x b y b z b =?b a -+-y B x x A ()(00)()00=-+z z C y ; (2) 一般式:0=+++D Cz By Ax ,其中},,{C B A =n ; (3) 截距式: 1=++c z b y a x ,其中平面与坐标轴交点),0,0(),0,,0(),0,0,(c b a ; (4) 三点式:002020 2010 101000 =---------z z y y x x z z y y x x z z y y x x , 其中),,(000z y x ,),,(111z y x ,),,(222z y x 为平面上不在一条直线上的三点. Ⅱ 、 直线的几种方程形式: (1) 点向式:p z z n y y m x x 000-=-=-,其中),,(000z y x 为 直线上定点,},,{p n m =s 为直线的方向向量; (2) 参数式:?? ???+=+=+=;pt z z nt y y m t x x 000,, (3) 两点式:1 21121121z z z z y y y y x x x x --=--=--, 其中),,(111z y x ,),,(222z y x 为直线上不重合的两点; (4) 一般式:???=+++=+++,0, 02222 1111D z C y B x A D z C y B x A 其中此二平面不平行. 注:线与线、线与面、面与面垂直或平行时直线的方向向量和平面的法向量之间的关系。 2、多元函数的微分学 (1) 二元函数极限求法(☆); (选择题3分, 计算题6分) 大一高数知识点总结 &初等函数 一、函数的概念 1、函数的定义 函数是从量的角度对运动变化的抽象表述,是一种刻画运动变化中变化量相依关系的数学模型。 设有两个变量x与y,如果对于变量x在实数集合D内的每一个值,变量y按照一定的法则都有唯一的值与之对应,那么就称x是自变量,y是x的函数,记作y=f,其中自变量x取值的集合D叫函数的定义域,函数值的集合叫做函数的值域。 2、函数的表示方法解析法 即用解析式表示函数。如y=2x+1, y=︱x︱,y=lg,y=sin3x等。便于对函数进行精确地计算和深入分析。列表法 即用表格形式给出两个变量之间函数关系的方法。便于差的某一处的函数值。图像法 即用图像来表示函数关系的方法 非常形象直观,能从图像上看出函数的某些特性。 分段函数——即当自变量取不同值时,函数的表达式不一样,如 1??2x?1, x?0?xsin, f?x???y??x ?2x?1,x?0???0 x?0 x?0 隐函数——相对于显函数而言的一种函数形式。所谓显函数,即直接用含自变量的式子表示的函数,如y=x2+2x+3,这是常见的函数形式。而隐函数是指变量x、y之间的函数关系式是由一个含x,y的方程F=0给出的,如2x+y-3=0,e 可得y=3-2x,即该隐函数可化为显函数。 参数式函数——若变量x,y之间的函数关系是通过参数式方程? x?y 而由2x+y-3=0?x?y?0等。 ?x???t?, ?t?T?给出的,??y??t? 这样的函数称为由参数方程确定的函数,简称参数式方程,t称为参数。 反函数——如果在已给的函数y=f中,把y看作自变量,x也是y的函数,则所确定的函数x=∮叫做y=f的反函数,记作x=fˉ1或y= fˉ1. 二、函数常见的性质 1、单调性 2、奇偶性=f;奇:关于y轴对称,f=-f.) 3、周期性 第八章 1、 向量在轴上的投影: 性质:?cos )(a a u =(即Prj u ?cos a a =),其中?为向量a 与u 轴的夹角; u u u b a b a )()()( +=+(即Prj u =+)(b a Prj u a + Prj u b ); u u a a )()( λλ=(即Prj u λλ=)(a Prj u a ). 2、 两个向量的向量积:设k a j a i a a z y x ++=,k b j b i b b z y x ++=,则 =?b a x x b a i y y b a j z z b a k =1 1) 1(+-y y b a z z b a i +21)1(+-x x b a z z b a j +3 1)1(+- x x b a y y b a k ) =k b a b a j b a b a i b a b a x y y x z x x z y z z y )()()(-+-+- 注:a b b a ?-=? 3、 二次曲面 (1) 椭圆锥面:222 22z b y a x =+; (2) 椭圆抛物面:z b y a x =+2222; (旋转抛物面: z a y x =+2 2 2(把把xOz 面上的抛物线z a x =22 绕z 轴旋转)) (3) 椭球面:1222222=++c z b y a x ; (旋转椭球面: 122 222=++c z a y x (把xOz 面上的椭圆122 22=+c z a x 绕z 轴旋转)) (4) 单叶双曲面:1222222=-+c z b y a x ; (旋转单叶双曲面:122 222=-+c z a y x (把 xOz 面上的双曲线122 22=-c z a x 绕z 轴旋转) ) 大学高等数学知识点整理 公式,用法合集 极限与连续 一. 数列函数: 1. 类型: (1)数列: *()n a f n =; *1()n n a f a += (2)初等函数: (3)分段函数: *0102()(),()x x f x F x x x f x ≤?=?>?; *0 ()(), x x f x F x x x a ≠?=?=?;* (4)复合(含f )函数: (),()y f u u x ?== (5)隐式(方程): (,)0F x y = (6)参式(数一,二): () ()x x t y y t =??=? (7)变限积分函数: ()(,)x a F x f x t dt = ? (8)级数和函数(数一,三): 0 (),n n n S x a x x ∞ ==∈Ω∑ 2. 特征(几何): (1)单调性与有界性(判别); (()f x 单调000,()(()())x x x f x f x ??--定号) (2)奇偶性与周期性(应用). 3. 反函数与直接函数: 1 1()()()y f x x f y y f x --=?=?= 二. 极限性质: 1. 类型: *lim n n a →∞; *lim ()x f x →∞ (含x →±∞); *0 lim ()x x f x →(含0x x ± →) 2. 无穷小与无穷大(注: 无穷量): 3. 未定型: 000,,1,,0,0,0∞ ∞∞-∞?∞∞∞ 4. 性质: *有界性, *保号性, *归并性 三. 常用结论: 11n n →, 1(0)1n a a >→, 1()max(,,)n n n n a b c a b c ++→, ()00! n a a n >→ 第一讲: 极限与连续 一. 数列函数: 1. 类型: (1)数列: *()n a f n =; *1()n n a f a += (2)初等函数: (3)分段函数: *010 2()(), ()x x f x F x x x f x ≤?=? >?; *0 0()(),x x f x F x x x a ≠?=?=?;* (4)复合(含f )函数: (),()y f u u x ?== (5)隐式(方程): (,)0F x y = (6)参式(数一,二): () () x x t y y t =?? =? (7)变限积分函数: ()(,)x a F x f x t dt = ? (8)级数和函数(数一,三): 0 (),n n n S x a x x ∞ ==∈Ω∑ 2. 特征(几何): (1)单调性与有界性(判别); (()f x 单调000,()(()())x x x f x f x ??--定号) (2)奇偶性与周期性(应用). 3. 反函数与直接函数: 1 1()()()y f x x f y y f x --=?=?= 二. 极限性质: 1. 类型: *lim n n a →∞ ; *lim ()x f x →∞ (含x →±∞); *0 lim ()x x f x →(含0x x ±→) 2. 无穷小与无穷大(注: 无穷量): 3. 未定型: 000,,1,,0,0,0∞ ∞∞-∞?∞∞∞ 4. 性质: *有界性, *保号性, *归并性 三. 常用结论: 11n n →, 1(0)1n a a >→, 1()m a x (,,)n n n n a b c a b c ++→, ()00! n a a n >→ 1(0)x x →→∞, 0lim 1x x x + →=, l i m 0n x x x e →+∞=, ln lim 0n x x x →+∞=, 高等数学下册知识点 第七章 空间解析几何与向量代数 一、填空与选择 1、已知点A (,,)321-和点B (,,)723-,取点M 使MB AM 2=,则向量OM =。 2 已知点A (,,)012和点B =-(,,)110,则AB = 。 3、设向量与三个坐标面的夹角分别为ξηζ,,,则cos cos cos 2 2 2 ξηζ++= 。 4、设向量a 的方向角απ β= 3 ,为锐角,γπβ=-4=,则a = 。 5、向量)5,2,7(-=a 在向量)1,2,2(=b 上的投影等于。 6、过点()121 -,,P 且与直线1432-=-=+-=t z t y t x ,,, 垂直的平面方程为_____________________________. 7、已知两直线方程是13021 1: 1--=-=-z y x L ,11122:2 z y x L =-=+,则过1L 且平行2L 的平面方程为____________________ 8、设直线182511:1+=--=-z y x L ,???=-+=--0320 6:2z y y x L ,则1L 与2L 的夹角为( ) (A ). 6π (B ).4π (C ).3π (D )2 π . 9、平面Ax By Cz D +++=0过x 轴,则( ) (A )A D ==0 (B )B C =≠00, (C )B C ≠=00, (D )B C ==0 10、平面3510x z -+=( ) (A )平行于zox 平面 (B )平行于y 轴(C )垂直于y 轴 (D )垂直于x 轴 11、点M (,,)121到平面x y z ++-=22100的距离为( ) (A )1 (B )±1 (C )-1 (D )1 3 12、与xoy 坐标平面垂直的平面的一般方程为 。 13、过点(,,)121与向量k j S k j i S --=--=21,32平行的平面方程为 。 14、平面0218419=++-z y x 和0428419=++-z y x 之间的距离等于?????? 。 15、过点(,,)024且与平面x z +=21及y z -=32都平行的直线方程为。 16、过点(,,)203-并与x y z x y z -+-=+-+=??? 2470 35210垂直的平面的方程为???????????? 。 二、完成下列各题 1、设)(,82,13-=-=-=λ与 b 是不平行的非零向量,求λ的值,使C B A 、、三点在 同一直线上。 2、已知不平行的两向量a 和b ,求它们的夹角平分线上的单位向量。 3、设点)1,0,1(-A 为矢量,10=与x 轴、y 轴的夹角分别为 45,60==βα,试求: (1)AB 与z 轴的夹角v ;(2)点B 的坐标。 4、求与向量k j i a 22+-=共线且满足18-=?x a 的向量x 。 5、若平面过x 轴,且与xoy 平面成 30的角,求它的方程。 第八章 空间解析几何与向量代数 (一) 向量及其线性运算 1、 向量,向量相等,单位向量,零向量,向量平行、共线、共面; 主要公式总结 第八章空间解析几何与向量代数 1、 二次曲面 1) 椭圆锥面:2 2222z b y a x =+ 2) 椭球面:122 222 2=++c z b y a x 旋转椭球面:1222222=++c z a y a x 3) 单叶双曲面:122 222 2=-+c z b y a x 双叶双曲面:1222222=--c z b y a x 4) 椭圆抛物面:z b y a x =+2222双曲抛物面(马鞍面):z b y a x =-22 22 5) 椭圆柱面:1222 2=+b y a x 双曲柱面:122 22=-b y a x 6) 抛物柱面: ay x =2 (二) 平面及其方程 1、 点法式方程: 0)()()(000=-+-+-z z C y y B x x A 法向量:),,(C B A n =ρ ,过点),,(000z y x 2、 一般式方程: 0=+++D Cz By Ax 截距式方程: 1=++c z b y a x 3、 两平面的夹角:),,(1111 C B A n =ρ ,),,(2222C B A n =ρ , 22 22 22 21 21 21 2 12121cos C B A C B A C C B B A A ++?++++= θ ?∏⊥∏210212121=++C C B B A A ;? ∏∏21//2 1 2121C C B B A A == 4、 点 ),,(0000z y x P 到平面0=+++D Cz By Ax 的距离: 2 2 2 000C B A D Cz By Ax d +++++= (三) 空间直线及其方程 专升本高等数学知识点汇总 常用知识点: 一、常见函数的定义域总结如下: (1) c bx ax y b kx y ++=+=2 一般形式的定义域:x ∈R (2)x k y = 分式形式的定义域:x ≠0 (3)x y = 根式的形式定义域:x ≥0 (4)x y a log = 对数形式的定义域:x >0 二、函数的性质 1、函数的单调性 当21x x <时,恒有)()(21x f x f <,)(x f 在21x x ,所在的区间上是增加的。 当21x x <时,恒有)()(21x f x f >,)(x f 在21x x ,所在的区间上是减少的。 2、 函数的奇偶性 定义:设函数)(x f y =的定义区间D 关于坐标原点对称(即若D x ∈,则有D x ∈-) (1) 偶函数)(x f ——D x ∈?,恒有)()(x f x f =-。 (2) 奇函数)(x f ——D x ∈?,恒有)()(x f x f -=-。 三、基本初等函数 1、常数函数:c y =,定义域是),(+∞-∞,图形是一条平行于x 轴的直线。 2、幂函数:u x y =, (u 是常数)。它的定义域随着u 的不同而不同。图形过原点。 3、指数函数 定义: x a x f y ==)(, (a 是常数且0>a ,1≠a ).图形过(0,1)点。 4、对数函数 定义: x x f y a log )(==, (a 是常数且0>a ,1≠a )。图形过(1,0)点。 5、三角函数 (1) 正弦函数: x y sin = π2=T , ),()(+∞-∞=f D , ]1,1[)(-=D f 。 (2) 余弦函数: x y cos =. π2=T , ),()(+∞-∞=f D , ]1,1[)(-=D f 。 (3) 正切函数: x y tan =. π=T , },2 )12(,|{)(Z R ∈+≠∈=k k x x x f D π , ),()(+∞-∞=D f . (4) 余切函数: x y cot =. π=T , },,|{)(Z R ∈≠∈=k k x x x f D π, ),()(+∞-∞=D f . 5、反三角函数 (1) 反正弦函数: x y sin arc =,]1,1[)(-=f D ,]2 ,2[)(π π- =D f 。 (2) 反余弦函数: x y arccos =,]1,1[)(-=f D ,],0[)(π=D f 。 (3) 反正切函数: x y arctan =,),()(+∞-∞=f D ,)2 ,2()(π π- =D f 。 (4) 反余切函数: x y arccot =,),()(+∞-∞=f D ,),0()(π=D f 。 极限 一、求极限的方法 1、代入法 代入法主要是利用了“初等函数在某点的极限,等于该点的函数值。”因此遇到大部分简单题目的时候,可以直接代入进行极限的求解。 2、传统求极限的方法 (1)利用极限的四则运算法则求极限。 (2)利用等价无穷小量代换求极限。 (3)利用两个重要极限求极限。 (4)利用罗比达法则就极限。 大一下高数下册知识 点 高等数学下册知识点 第八章 空间解析几何与向量代数 (一) 向量线性运算 定理1:设向量a ≠0,则向量b 平行于a 的充要条件是存在唯一的实数λ,使 b =λa 1、 线性运算:加减法、数乘; 2、 空间直角坐标系:坐标轴、坐标面、卦限,向量的坐标分解式; 3、 利用坐标做向量的运算:设),,(z y x a a a a = ,),,(z y x b b b b = ; 则 ),,(z z y y x x b a b a b a b a ±±±=± , ),,(z y x a a a a λλλλ= ; 4、 向量的模、方向角、投影: 1) 向量的模: 222z y x r ++= ; 2) 两点间的距离公式:2 12212212)()()(z z y y x x B A -+-+-= 3) 方向角:非零向量与三个坐标轴的正向的夹角γβα,, 4) 方向余弦:r z r y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα 5) 投影:?cos Pr a a j u =,其中?为向量a 与u 的夹角。 (二) 数量积,向量积 1、 数量积:θcos b a b a =? 1)2a a a =? 2)?⊥b a 0=?b a z z y y x x b a b a b a b a ++=? 2、 向量积:b a c ?= 大小:θsin b a ,方向:c b a ,,符合右手规则 1)0 =?a a 2)b a //?0 =?b a z y x z y x b b b a a a k j i b a =? 运算律:反交换律 b a a b ?-=? (三) 曲面及其方程 1、 曲面方程的概念:0),,(:=z y x f S 2、 旋转曲面: yoz 面上曲线0),(:=z y f C , 绕y 轴旋转一周:0),(22=+±z x y f 绕 z 轴旋转一周: 0),(22=+±z y x f 3、 柱面: 0),(=y x F 表示母线平行于z 轴,准线为?????==0 0),(z y x F 的柱面 4、 二次曲面 高等数学(下)知识点 高等数学下册知识点 第八章 空间解析几何与向量代数 (一) 向量及其线性运算 1、 向量,向量相等,单位向量,零向量,向量平行、共线、共面; 2、 线性运算:加减法、数乘; 3、 空间直角坐标系:坐标轴、坐标面、卦限,向量的坐标分解式; 4、 利用坐标做向量的运算:设),,(z y x a a a a = , ),,(z y x b b b b = , 则 ),,(z z y y x x b a b a b a b a ±±±=± , ),,(z y x a a a a λλλλ= ; 5、 向量的模、方向角、投影: 1) 向量的模: 2 22z y x r ++= ; 2) 两 点 间 的 距 离 公式: 212212212)()()(z z y y x x B A -+-+-= 3) 方向角:非零向量与三个坐标轴的正向的夹角 γβα,, 4) 方 向 余 弦 : r z r y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα 高等数学(下)知识点 5) 投影:?cos Pr a a j u =,其中?为向量a 与u 的夹角。 (二) 数量积,向量积 1、 数量积:θ cos b a b a =? 1)2a a a =? 2)?⊥b a 0=?b a z z y y x x b a b a b a b a ++=? 2、 向量积:b a c ?= 大小:θsin b a ,方向:c b a ,,符合右手规 则 1)0 =?a a 2)b a //?0 =?b a z y x z y x b b b a a a k j i b a =? 运算律:反交换律 b a a b ?-=? (三) 曲面及其方程 1、 曲面方程的概念:0),,(:=z y x f S 2、 旋转曲面: 第1章 函数与极限总结 1、极限的概念 (1)数列极限的定义 给定数列{x n },若存在常数a ,对于任意给定的正数ε (不论它多么小), 总存在正整数N , 使得对于n >N 时的一切n , 恒有 |x n-a |<ε 则称a 是数列{x n }的极限, 或者称数列{x n }收敛于a , 记为 a x n n =∞ →lim 或xn →a (n→∞). (2)函数极限的定义 设函数f (x)在点x 0的某一去心邻域内(或当0x M >>)有定义,如果存在常数A , 对于任意给定的正数ε (不论它多么小), 总存在正数δ,(或存在X ) 使得当x满足不等式0<|x -x0|<δ 时,(或当x X >时) 恒有 |f (x)-A |<ε , 那么常数A就叫做函数f (x)当0x x →(或x →∞)时的极限, 记为 A x f x x =→)(lim 0 或f (x )→A (当x →x0).( 或lim ()x f x A →∞ =) 类似的有:如果存在常数A ,对0,0,εδ?>?>当00:x x x x δ-<<(00x x x δ<<-)时,恒有()f x A ε-<,则称A 为()f x 当0x x →时的左极限(或右极限)记作 00 lim ()(lim ())x x x x f x A f x A - +→→==或 显然有0 lim ()lim ()lim ())x x x x x x f x A f x f x A -+→→→=?== 如果存在常数A ,对0,0,X ε?>?>当()x X x X <->或时,恒有()f x A ε-<,则称A 为()f x 当x →-∞(或当x →+∞)时的极限 记作lim ()(lim ())x x f x A f x A →-∞ →+∞ ==或 显然有lim ()lim ()lim ())x x x f x A f x f x A →∞ →-∞ →+∞ =?== 2、极限的性质 (1)唯一性 若a x n n =∞ →lim ,lim n n x b →∞ =,则a b = 若0() lim ()x x x f x A →∞→=0() lim ()x x x f x B →∞→=,则A B = (2)有界性 (i)若a x n n =∞ →lim ,则0M ?>使得对,n N + ?∈恒有n x M ≤ 高等数学知识点总结 导数公式: 基本积分表: 三角函数的有理式积分: 222 2 12211cos 12sin u du dx x tg u u u x u u x +==+-=+= , , , a x x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(2 2 = '='?-='?='-='='2 2 22 11)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +- ='+= '--='-='? ?????????+±+ =±+=+=+= +-=?+=?+-== +==C a x x a x dx C shx chxdx C chx shxdx C a a dx a C x ctgxdx x C x dx tgx x C ctgx xdx x dx C tgx xdx x dx x x )ln(ln csc csc sec sec csc sin sec cos 2 2 2 2 2 2 2 2 C a x x a dx C x a x a a x a dx C a x a x a a x dx C a x arctg a x a dx C ctgx x xdx C tgx x xdx C x ctgxdx C x tgxdx +=-+-+= -++-=-+=++-=++=+=+-=? ???????arcsin ln 21ln 21 1csc ln csc sec ln sec sin ln cos ln 2 2 2 22 22 2 ? ????++ -= -+-+--=-+++++=+-= == -C a x a x a x dx x a C a x x a a x x dx a x C a x x a a x x dx a x I n n xdx xdx I n n n n arcsin 2 2 ln 2 2)ln(2 21cos sin 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0π π 高等数学下册知识点 第八章 空间解析几何与向量代数 (一) 向量及其线性运算 1、 向量,向量相等,单位向量,零向量,向量平行、共线、共面; 2、 线性运算:加减法、数乘; 3、 空间直角坐标系:坐标轴、坐标面、卦限,向量的坐标分解式; 4、 利用坐标做向量的运算:设),,(z y x a a a a = ,) ,,(z y x b b b b = , 则 ),,(z z y y x x b a b a b a b a ±±±=± , ),,(z y x a a a a λλλλ= ; 5、 向量的模、方向角、投影: 1) 向量的模: 2 22z y x r ++= ; 2) 两点间的距离公式: 212212212)()()(z z y y x x B A -+-+-= 3) 方向角:非零向量与三个坐标轴的正向的夹角γβα,, 4) 方向余弦: r z r y r x ===γβαcos ,cos ,cos 1cos cos cos 222=++γβα 5) 投影:?cos Pr a a j u =,其中?为向量a 与u 的夹角。 (二) 数量积,向量积 1、 数量积:θ cos b a b a =? 1)2a a a =? 2)?⊥b a 0=?b a z z y y x x b a b a b a b a ++=? 2、 向量积:b a c ?= 大小: θ sin b a ,方向:c b a ,,符合右手规则 1)0 =?a a 2)b a //?0 =?b a z y x z y x b b b a a a k j i b a =? 运算律:反交换律 b a a b ?-=? 一、多元函数的极限与连续 1、n 维空间 2R 为二元数组),(y x 的全体,称为二维空间。3R 为三元数组),,(z y x 的全体,称为三 维空间。 n R 为n 元数组),,,(21n x x x 的全体,称为n 维空间。 n 维空间中两点1212(,,,),(,,,)n n P x x x Q y y y L L 间的距离: ||PQ 邻域: 设0P 是n R 的一个点, 是某一正数, 与点0P 距离小于 的点P 的全体称为点0P 的 邻域,记为),(0 P U ,即00(,){R |||}n U P P PP 空心邻域: 0P 的 邻域去掉中心点0P 就成为0P 的 空心邻域,记为 0(,)U P o =0{0||}P PP 。 内点与边界点:设E 为n 维空间中的点集,n P R 是一个点。如果存在点P 的某个邻域 ),( P U ,使得E P U ),( ,则称点P 为集合E 的内点。 如果点P 的任何邻域内都既有 属于E 的点又有不属于E 的点,则称P 为集合E 的边界点, E 的边界点的全体称为E 的边界. 聚点:设E 为n 维空间中的点集,n P R 是一个点。如果点P 的任何空心邻域内都包含E 中的无穷多个点,则称P 为集合E 的聚点。 开集与闭集: 若点集E 的点都是内点,则称E 是开集。设点集n E R , 如果E 的补集 n E R 是开集,则称E 为闭集。 区域与闭区域:设D 为开集,如果对于D 内任意两点,都可以用D 内的折线(其上的点都属于D )连接起来, 则称开集D 是连通的.连通的开集称为区域或开区域.开区域与其边界的并集称为闭区域. 有界集与无界集: 对于点集E ,若存在0 M ,使得(,)E U O M ,即E 中所有点到原点的距离都不超过M ,则称点集E 为有界集,否则称为无界集. 如果D 是区域而且有界,则称D 为有界区域. 有界闭区域的直径:设D 是n R 中的有界闭区域,则称1212,()max{||}P P D d D PP 为D 的直径。同济六版高等数学(下)知识点整理
高等数学知识点总结 (1)
_《高等数学》(下)复习提纲(本科)
高数下(同济六)知识点知识分享
高数知识点总结
高等数学下册知识点
大一高数知识点总结
同济六版高等数学(下)知识点整理
大学全册高等数学知识点(全)
高等数学知识点归纳
高等数学下册知识点
高等数学(下)知识点总结
专升本高等数学知识点汇总
大一下高数下册知识点资料
高数下册知识点
《高等数学》-各章知识点总结——第1章
考研高等数学知识点总结
高数下册知识点
高等数学 各章知识点总结——第9章
