正弦和余弦表

正弦余弦表
A 0ˊ 6ˊ12ˊ 18ˊ 24ˊ 32ˊ 36ˊ 42ˊ 48ˊ 54ˊ 60ˊcosA 1ˊ 2ˊ 3ˊ
sinA 0.0000 90°0.0003 0.0006 0.0009 0° 0.0000 0017 0035 0052 0070 0087 0105 0122 0140 0157 0175 89° 3 6 9
1° 0715 0192 0209 0227 0244 0262 0279 0297 0314 0332 0349 88° 3 6 9
2° 0349 0366 0364 0401 0419 0436 0545 0471 0448 0506 0523 87° 3 6 9
3° 0523 0541 0558 0576 0593 0610 0628 0645 0663 0680 0698 86° 3 6 9
4° 0689 0715 0732 0750 0767 0785 0802 0819 0837 0854 0872 85° 3 6 9
5° 0.0872 0889 0906 0924 0941 0958 0976 0993 1011 1028 1045 84° 3 6 9
6° 1045 1063 1080 1097 1115 1132 1139 1167 1184 1201 1219 83° 3 6 9
7° 1219 1236 1253 1271 1288 1305 1323 1340 1357 1374 1392 82° 3 6 9
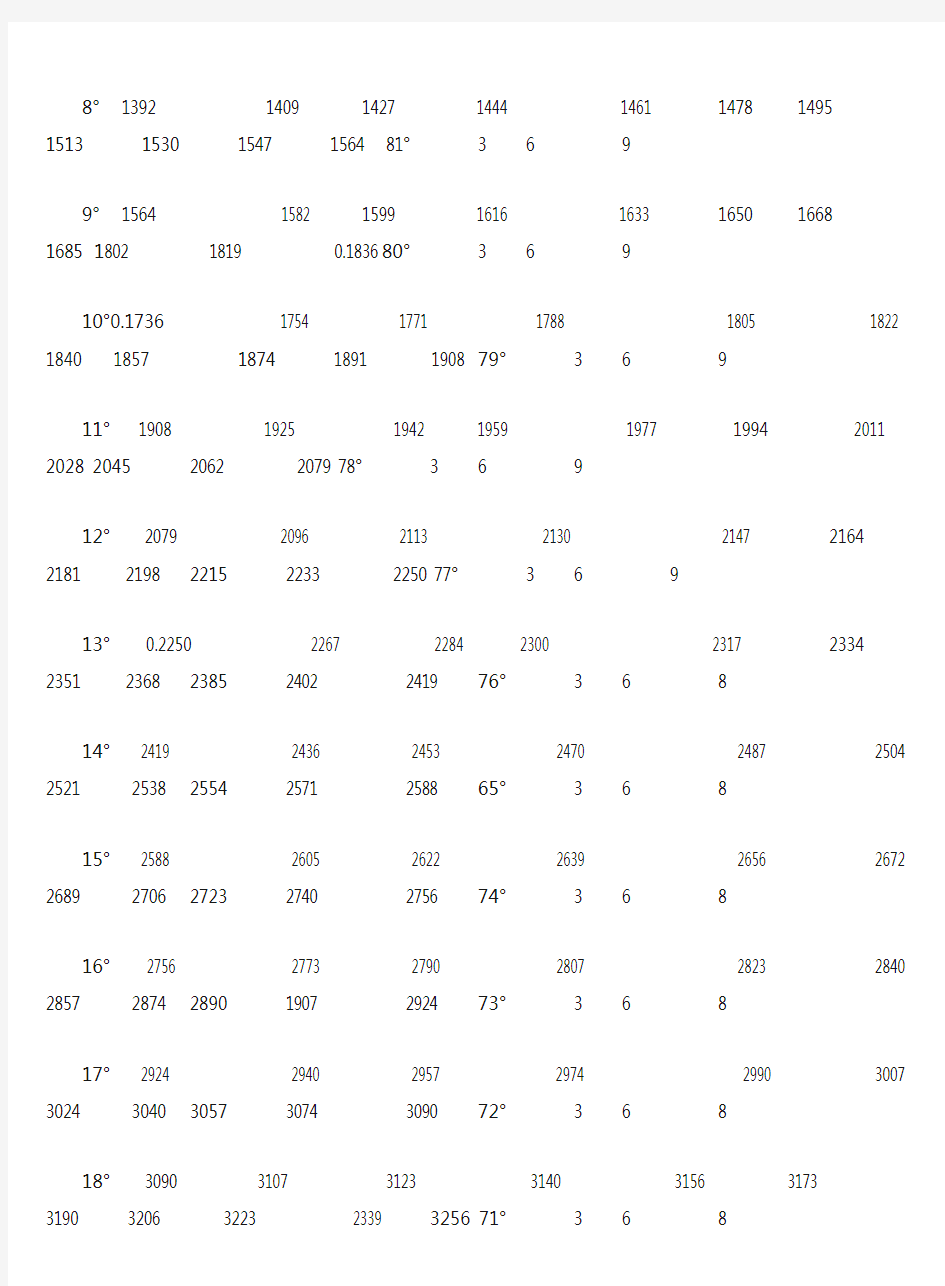
8° 1392 1409 1427 1444 1461 1478 1495 1513 1530 1547 1564 81° 3 6 9
9° 1564 1582 1599 1616 1633 1650 1668 1685 1802 1819 0.1836 80° 3 6 9
10°0.1736 1754 1771 1788 1805 1822 1840 1857 1874 1891 1908 79° 3 6 9
11° 1908 1925 1942 1959 1977 1994 2011 2028 2045 2062 2079 78° 3 6 9
12° 2079 2096 2113 2130 2147 2164 2181 2198 2215 2233 2250 77° 3 6 9
13° 0.2250 2267 2284 2300 2317 2334 2351 2368 2385 2402 2419 76° 3 6 8
14° 2419 2436 2453 2470 2487 2504 2521 2538 2554 2571 2588 65° 3 6 8
15° 2588 2605 2622 2639 2656 2672 2689 2706 2723 2740 2756 74° 3 6 8
16° 2756 2773 2790 2807 2823 2840 2857 2874 2890 1907 2924 73° 3 6 8
17° 2924 2940 2957 2974 2990 3007 3024 3040 3057 3074 3090 72° 3 6 8
18° 3090 3107 3123 3140 3156 3173 3190 3206 3223 2339 3256 71° 3 6 8
19° 3256 3272 3289 3305 3322 3338 3355 3371 3387 3404 3420 70° 3 5 8
20° 3420 3437 3453 3469 3486 3502 3518 3535 3551 3567 3584 69° 3 5 8
21° 0.3584 3600 3616 3633 3649 3665 3681 3697 3714 3730 3746 68° 3 5 8 22° 3746 3762 3778 3795 3811 3827 3843 3859 3875 3891 3907 67° 3 5 8 23° 3907 3923 3939 3955 3971 3987 4003 4019 4035 4051 4067 66° 3 5 8 25° 4226 4242 4258 4274 4289 4305 4321 4337 4352 4368 4384 64° 3 5 8 26° 4384 4399 4415 4431 4446 4462 4478 4493 4509 4524 4540 63° 3 5 8 27° 4540 4555 4571 4586 4602 4617 4633 4648 4664 4679 4695 62° 3 5 8 28°4695 4710 4726 4741 4756 4772 4787 4802 4818 4833 4848 61° 3 5 8 29°4848 4863 4879 4894 4909 4924 4939 2955 4970 4985 5000 60° 3 5 8 30°5000 5015 5030 5045 5060 5075 5090 5105 5120 5135 5150 59° 3 5 8 31°5150 5165 5180 5195 5210 5225 5240 5255 5270 5284 5299 58° 2 5 7 32°5299 5314 5329 5344 5358 5373 5388 5402 5417 5432 5446 57° 2 5 7 33°5446 5461 5476 5490 5505 5519 5534 5548 5563 5577 5592 56° 2 5 7 34°5592 5605 5621 5635 5650 5664 5678 5693 5707 5721 5736 55° 2 5 7 35°5736 5750 5764 5779 5793 5807 5821 5835 5850 5864 5878 54° 2 5 7 36°5878 5892 5906 5920 5934 5948 5962 5976 5990 6004 6018 53° 2 5 7 37°0.6018 6032 6046 6060 6074 6088 6101 6115 6129 6143 6157 52° 2 5 7 38°6157 6170 6184 6198 6211 6225 6239 6252 6266 6280 6293 51° 2 5 7 39°6293 6307 6320 6334 6347 6361 6374 6388 6401 6414 6428 50° 4 4 7 40°6428 6441 6455 6468 6481 6494 6508 6521 6534 6547 6561 49° 2 4 7 41°6561 6574 6587 6600 6613 6626 6639 6652 6665 6678 6691 48° 2 4 7 °6691 6704 6717 6730 6743 6756 6769 6782 6794 6807 6820 47° 2 4 6 43°6827 6833 6845 6868 6871 6884 6896 6909 6921 6934 6947 46 2 4 6 44°6947 6959 6972 6984 6997 7009 7022 7034 7046 7059 7071 45° 2 4 6 45°7071 7083 7096 7108 7120 7133 7145 7157 7169 7181 0.7193 44° 2 4 6
46°0.7193 7206 7218 7230 7242 7254 7266 7278 7290 7302 7314 43° 2 4 6 47°7314 7325 7337 7349 7361 7373 7385 7396 7408 7420 7431 42° 2 4 6 48°7431 7443 7455 7466 7478 7490 7501 7513 7524 7536 7547 41° 2 4 6 49°7547 7559 7570 7581 7593 7604 7615 7627 7638 7649 7660 40° 2 4 6 50°7660 7672 7683 7694 7705 7716 7727 7738 7749 7760 7771 39° 2 4 6 51°7771 7782 7793 7804 7815 7826 7837 7848 7859 7869 7880 38° 2 4 5 52°7880 7891 7902 7912 7923 7934 7944 7955 7965 7976 7986 37° 2 4 5 53°7986 7997 8007 8018 8028 8039 8049 8059 8070 8080 8090 36° 2 3 5 54°8090 8100 8111 8121 8131 8141 8151 8161 8171 8181 8192 35° 2 3 5 55°8192 8202 8211 8221 8231 8241 8251 8261 8171 8281 8290 34° 2 3 5 56°8290 8300 8210 8320 8329 8339 8348 8358 8368 8377 8387 33° 2 3 5 57°8387 8396 8406 8415 8425 8434 8443 8453 8462 8471 0.8480 32° 2 3 5 58°8480 8490 8499 8508 8517 8526 8536 8545 8554 8563 8572 31° 2 3 5 59°8572 8581 8590 8599 8607 8616 8625 8634 8643 8652 8660 30° 1 3 4 60°8660 8669 8678 8686 8695 8704 8712 8721 8729 8738 8746 29° 1 3 4 61°8746 8755 8763 8771 8780 8788 8796 8805 8813 8821 8829 28° 1 3 4 63°0.8829 8838 8846 8854 8862 8870 8878 8886 8894 8902 8910 27° 1 3 4 64°8988 8996 9003 9011 9018 9026 9033 9041 9048 9056 9063 25° 1 2 4 65°9063 9070 9078 9085 9092 9100 9107 9114 9121 9128 9135 24° 1 2 4 66°9135 9143 9150 9157 9164 9171 9178 9184 9191 9198 9272 23° 1 2 3 67°9205 9212 9219 9225 9232 9239 9245 9252 9259 9265 9272 22° 1 2 3 68°9272 9278 9285 9291 9298 9204 9311 9317 9323 9330 9226 21° 1 2 3 69°9336 9342 9348 9354 9361 9367 9373 9379 9385 9391 9397 20° 1 2 3 70°9397 9403 9409 9415 9421 9425 9432 9438 9444 9449 0.9455 19° 1 2 3
71°9455 9461 9466 9472 9478 9483 9489 9494 9500 9505 9511 18° 1 2 3 72°9511 9516 9521 9527 9532 9537 9542 9548 9552 9558 9563 17° 1 2 3 73°9563 9568 9573 9578 9583 9588 9593 9598 9603 9608 9613 16 1 2 2 74°9613 9617 9622 9627 9632 9636 9641 9646 9650 9655 9659 15° 1 2 2 75°9659 9664 9668 9673 9677 9681 9686 9690 9694 9699 9703 14° 1 1 2 76°0.9703 9707 9711 9715 9720 9724 9728 9732 9736 9740 9744 13° 1 1 2 77°9744 9748 9751 9755 9759 9763 9767 9770 9774 9778 9781 12° 1 1 2 78°9781 9785 9789 9792 9795 9799 9803 9806 9810 9813 9816 11° 1 1 2 79°9816 9820 9823 9826 9829 9833 9836 9839 9842 9845 9848 10° 1 1 2 80°9848 9851 9854 9857 9860 9863 9866 9869 9871 9874 9877 9°0 1 1 81°9877 9880 9882 9885 9888 9890 9893 9895 9898 9900 9903 8°0 1 1 82°9903 9905 9907 9910 9912 9914 9917 9919 9921 9923 9925 7°0 1 1 83°9925 9928 9930 9932 9934 9936 9938 9940 9942 9943 0.9945 6°0 1 1 84°9945 9947 9949 9951 9952 9924 9956 9957 9959 9960 9962 5°0 1 1 85°9962 9963 9965 9966 9968 9969 9971 9972 9973 9974 9976 4°0 0 1 86°0.9976 9977 9978 9979 9980 9981 9982 9983 9984 9985 9986 3°0 0 0 87°9986 9987 9988 9989 9990 9990 9991 9992 9993 9993 9994 2°0 0 0 88°9994 9995 9995 9996 9996 9997 9997 9979 9989 9989 9998 1°0 0 0 89°9998 9999 9999 9999 9999 0000 0000 0000 0000 0000 1.0000 0°
90° 1.0000
60ˊ54ˊ 48ˊ 42ˊ36ˊ 30ˊ24ˋ18ˊ 12ˊ 6ˊ 0ˊ A°1ˊ2ˊ3ˊ
.
正弦函数余弦函数的图像(附答案)
正弦函数、余弦函数的图象 [学习目标] 1.了解利用单位圆中的正弦线画正弦曲线的方法.2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.3.理解正弦曲线与余弦曲线之间的联系. 知识点一 正弦曲线 正弦函数y =sin x (x ∈R )的图象叫正弦曲线. 利用几何法作正弦函数y =sin x ,x ∈[0,2π]的图象的过程如下: ①作直角坐标系,并在直角坐标系y 轴的左侧画单位圆,如图所示. ②把单位圆分成12等份(等份越多,画出的图象越精确).过单位圆上的各分点作x 轴的垂线,可以得到对应于0,π6,π3,π 2,…,2π等角的正弦线. ③找横坐标:把x 轴上从0到2π(2π≈6.28)这一段分成12等份. ④平移:把角x 的正弦线向右平移,使它的起点与x 轴上的点x 重合. ⑤连线:用光滑的曲线将这些正弦线的终点依次从左到右连接起来,即得y =sin x ,x ∈[0,2π]的图象. 在精度要求不太高时,y =sin x ,x ∈[0,2π]可以通过找出(0,0),(π2,1),(π,0),(3π 2,-1), (2π,0)五个关键点,再用光滑曲线将它们连接起来,就可得正弦函数的简图. 思考 在所给的坐标系中如何画出y =sin x ,x ∈[0,2π]的图象?如何得到y =sin x ,x ∈R 的图象? 答案 y =sin x ,x ∈[0,2π]的图象(借助五点法得)如下: 只要将函数y =sin x ,x ∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到正弦函数y =sin x ,x ∈R 的图象. 知识点二 余弦曲线 余弦函数y =cos x (x ∈R )的图象叫余弦曲线.
正弦和余弦
正弦和余弦 导读:本文正弦和余弦,仅供参考,如果觉得很不错,欢迎点评和分享。 教学建议1.知识结构:本小节主要学习正弦、余弦的概念,30°、45°、60°角的正弦、余弦值,一个锐角的正弦(余弦)值与它的余角的余弦(正弦)值之间的关系,以及应用上述知识解决一些简单问题(包括引言中的问题)等. 2.重点、难点分析 (1)正弦、余弦函数的定义是本节的重点,因为它是全章乃至整个三角学的预备知识.有了正弦、余弦函数的定义,再学习正切和余切、解直角三角形、引入任意角三角函数便都有了基础. (2)正弦、余弦的概念隐含着角度与数值之间有一一对应关系的函数思想,并且用含有几个字母的符号组sinA,cosA来表示,学生过去未接触过,所以正弦、余弦的概念是难点. 3.理解一个锐角的正弦、余弦值的唯一性,是理解三角函数的核心. 锐角的正弦、余弦值是这样规定的:当一个锐角确定了,那么这个锐角所在的直角三角形虽然有无穷多个,但它们都是彼此相似的.如上图,当确定时,包含的直角三角形有无穷多个,但它们彼此相似:
∽ ∽ ∽ ……因此,由于相似三角形的对应边成比例,所以这些三角形的对应边的比都是相等的. 这就是说,每当一个锐角确定了,包含这个角的直角三角形的上述2种比值也就唯一确定了,它们有确定不变的对应关系.为了简单地表达这些对应关系,我们引入了正(余)弦的说法,创造了sin 和cos这样的符号. 应当注意:单独写出三角函数的符号或cos等是没有意义的.因为它们离开了确定的锐角是无法显示出它的含义;另一方面,这些符号和角写在一起时(如),它表示的就不再是角,而是一个特定的三角形的两条边的比值了(如).真正理解并掌握这些,才真正掌握了这些符号的含义,才能正确地运用它们. 4.我们应当学会认识任何位置的直角三角形中的一个锐角的正弦、余弦的表达式. 我们不仅应当熟练掌握如图那样的标准位置的直角三角形的正弦、余弦的表达式,而且能熟练地写出无论怎样放置的直角三角形的正弦、余弦的表达式.如,如图所示,若,则有 有的直角三角形隐藏在更复杂的图形中,我们也应能正确地写出所需要的三角函数表达式,如图中,ABCD是梯形,,作,我们应正确地写出如下的三角函数关系式:
正弦函数值表
0.0{0.0000} 0.1{0.0017} 0.2{0.0035} 0.3{0.0052} 0.4{0.0070} 0.5{0.0087} 0.6{0.0105} 0.7{0.0122} 0.8{0.0140} 0.9{0.0157} 1.0{0.0175} 1.1{0.0192} 1.2{0.0209} 1.3{0.0227} 1.4{0.0244} 1.5{0.0262} 1.6{0.0279} 1.7{0.0297} 1.8{0.0314} 1.9{0.0332} 2.0{0.0349} 2.1{0.0366} 2.2{0.0384} 2.3{0.0401} 2.4{0.0419} 2.5{0.0436} 2.6{0.0454} 2.7{0.0471} 2.8{0.0488} 2.9{0.0506} 3.0{0.0523} 3.1{0.0541} 3.2{0.0558} 3.3{0.0576} 3.4{0.0593} 3.5{0.0610} 3.6{0.0628} 3.7{0.0645} 3.8{0.0663} 3.9{0.0680} 4.0{0.0698} 4.1{0.0715} 4.2{0.0732} 4.3{0.0750} 4.4{0.0767} 4.5{0.0785} 4.6{0.0802} 4.7{0.0819} 4.8{0.0837} 4.9{0.0854} 5.0{0.0872} 5.1{0.0889} 5.2{0.0906} 5.3{0.0924} 5.4{0.0941} 5.5{0.0958} 5.6{0.0976} 5.7{0.0993} 5.8{0.1011} 5.9{0.1028} 6.0{0.1045} 6.1{0.1063} 6.2{0.1080} 6.3{0.1097} 6.4{0.1115} 6.5{0.1132} 6.6{0.1149} 6.7{0.1167} 6.8{0.1184} 6.9{0.1201} 7.0{0.1219} 7.1{0.1236} 7.2{0.1253} 7.3{0.1271} 7.4{0.1288} 7.5{0.1305} 7.6{0.1323} 7.7{0.1340} 7.8{0.1357} 7.9{0.1374} 8.0{0.1392} 8.1{0.1409} 8.2{0.1426} 8.3{0.1444} 8.4{0.1461} 8.5{0.1478} 8.6{0.1495} 8.7{0.1513} 8.8{0.1530} 8.9{0.1547} 9.0{0.1564} 9.1{0.1582} 9.2{0.1599} 9.3{0.1616} 9.4{0.1633} 9.5{0.1650} 9.6{0.1668} 9.7{0.1685} 9.8{0.1702} 9.9{0.1719} 10.0{0.1736} 10.1{0.1754} 10.2{0.1771} 10.3{0.1788} 10.4{0.1805} 10.5{0.1822} 10.6{0.1840} 10.7{0.1857} 10.8{0.1874} 10.9{0.1891} 11.0{0.1908} 11.1{0.1925} 11.2{0.1942} 11.3{0.1959} 11.4{0.1977} 11.5{0.1994} 11.6{0.2011} 11.7{0.2028} 11.8{0.2045} 11.9{0.2062} 12.0{0.2079} 12.1{0.2096} 12.2{0.2113} 12.3{0.2130} 12.4{0.2147} 12.5{0.2164} 12.6{0.2181} 12.7{0.2198} 12.8{0.2215} 12.9{0.2233} 13.0{0.2250} 13.1{0.2267} 13.2{0.2284} 13.3{0.2300} 13.4{0.2317} 13.5{0.2334} 13.6{0.2351} 13.7{0.2368} 13.8{0.2385} 13.9{0.2402} 14.0{0.2419} 14.1{0.2436} 14.2{0.2453} 14.3{0.2470} 14.4{0.2487} 14.5{0.2504} 14.6{0.2521} 14.7{0.2538} 14.8{0.2554} 14.9{0.2571} 15.0{0.2588} 15.1{0.2605} 15.2{0.2622} 15.3{0.2639} 15.4{0.2656} 15.5{0.2672} 15.6{0.2689} 15.7{0.2706} 15.8{0.2723} 15.9{0.2740} 16.0{0.2756} 16.1{0.2773} 16.2{0.2790} 16.3{0.2807} 16.4{0.2823} 16.5{0.2840} 16.6{0.2857} 16.7{0.2874} 16.8{0.2890} 16.9{0.2907} 17.0{0.2924} 17.1{0.2940} 17.2{0.2957} 17.3{0.2974} 17.4{0.2990} 17.5{0.3007} 17.6{0.3024} 17.7{0.3040} 17.8{0.3057} 17.9{0.3074} 18.0{0.3090} 18.1{0.3107} 18.2{0.3123} 18.3{0.3140} 18.4{0.3156} 18.5{0.3173} 18.6{0.3190} 18.7{0.3206} 18.8{0.3223} 18.9{0.3239} 19.0{0.3256} 19.1{0.3272} 19.2{0.3289} 19.3{0.3305} 19.4{0.3322} 19.5{0.3338} 19.6{0.3355} 19.7{0.3371} 19.8{0.3387} 19.9{0.3404} 20.0{0.3420} 20.1{0.3437} 20.2{0.3453} 20.3{0.3469} 20.4{0.3486} 20.5{0.3502} 20.6{0.3518} 20.7{0.3535} 20.8{0.3551} 20.9{0.3567} 21.0{0.3584} 21.1{0.3600} 21.2{0.3616} 21.3{0.3633} 21.4{0.3649} 21.5{0.3665} 21.6{0.3681} 21.7{0.3697} 21.8{0.3714} 21.9{0.3730} 22.0{0.3746} 22.1{0.3762} 22.2{0.3778} 22.3{0.3795} 22.4{0.3811} 22.5{0.3827} 22.6{0.3843} 22.7{0.3859} 22.8{0.3875} 22.9{0.3891} 23.0{0.3907} 23.1{0.3923} 23.2{0.3939} 23.3{0.3955} 23.4{0.3971} 23.5{0.3987} 23.6{0.4003} 23.7{0.4019} 23.8{0.4035} 23.9{0.4051} 24.0{0.4067} 24.1{0.4083} 24.2{0.4099} 24.3{0.4115} 24.4{0.4131} 24.5{0.4147} 24.6{0.4163} 24.7{0.4179} 24.8{0.4195} 24.9{0.4210} 25.0{0.4226} 25.1{0.4242} 25.2{0.4258} 25.3{0.4274} 25.4{0.4289} 25.5{0.4305} 25.6{0.4321} 25.7{0.4337} 25.8{0.4352} 25.9{0.4368} 26.0{0.4384} 26.1{0.4399} 26.2{0.4415} 26.3{0.4431}
正弦和余弦转换
正弦和余弦转换 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)=sinα cos(2kπ+α)=cosα tan(2kπ+α)=tanα cot(2kπ+α)=cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五: 利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα cos(2π-α)=cosα
tan(2π-α)=-tanα cot(2π-α)=-cotα 公式六: π/2±α与α的三角函数值之间的关系: sin(π/2+α)=cosα cos(π/2+α)=-sinα tan(π/2+α)=-cotα cot(π/2+α)=-tanα sin(π/2-α)=cosα cos(π/2-α)=sinα tan(π/2-α)=cotα cot(π/2-α)=tanα 诱导公式记忆口诀 ※规律总结※ 上面这些诱导公式可以概括为: 对于k·π/2±α(k∈Z)的个三角函数值, ①当k是偶数时,得到α的同名函数值,即函数名不改变; ②当k是奇数时,得到α相应的余函数值,即sin→cos;cos→sin;tan→cot,cot→tan. (奇变偶不变) 然后在前面加上把α看成锐角时原函数值的符号。 (符号看象限) 例如: sin(2π-α)=sin(4·π/2-α),k=4为偶数,所以取sinα。 当α是锐角时,2π-α∈(270°,360°),sin(2π-α)<0,符号为“-”。 所以sin(2π-α)=-sinα 上述的记忆口诀是: 奇变偶不变,符号看象限。 公式右边的符号为把α视为锐角时,角k·360°+α(k∈Z),-α、180°±α,360°-α 所在象限的原三角函数值的符号可记忆
正弦函数和余弦函数图像与性质
6、1正弦函数与余弦函数的图像与性质 一、复习引入 1、复习 (1)函数的概念 在某个变化过程中有两个变量x 、y ,若对于x 在某个实数集合D 内的每一个确定的值,按照某个对应法则f ,y 都有唯一确定的实数值与它对应,则y 就就是x 的函数,记作 ()x f y =,D x ∈。 (2)三角函数线 设任意角α的顶点在原点O ,始边与x 轴的非负半轴重合,终边与单位圆相交于点(,)P x y ,过P 作x 轴的垂线,垂足为M ;过点(1,0)A 作单位圆的切线,设它与角α的终边(当α在第一、四象限角时)或其反向延长线(当α为第二、三象限角时)相交于T 、 规定:当OM 与x 轴同向时为正值,当OM 与x 轴反向时为负值; 当MP 与y 轴同向时为正值,当MP 与y 轴反向时为负值; 当AT 与y 轴同向时为正值,当AT 与y 轴反向时为负值; 根据上面规定,则,OM x MP y ==, 由正弦、余弦、正切三角比的定义有: sin 1 y y y MP r α====; cos 1 x x x OM r α= ===; tan y MP AT AT x OM OA α= ===; 这几条与单位圆有关的有向线段,,MP OM AT 叫做角α的正弦线、余弦线、正切线。 二、讲授新课 【问题驱动1】——结合我们刚学过的三角比,就以正弦(或余弦)为例,对于每一个给定的 角与它的正弦值(或余弦值)之间就是否也存在一种函数关系?若存在,请对这种函数关系下一个定义;若不存在,请说明理由. 1、正弦函数、余弦函数的定义 (1)正弦函数:R x x y ∈=,sin ; (2)余弦函数:R x x y ∈=,cos 【问题驱动2】——如何作出正弦函数R x x y ∈=,sin 、余弦函数R x x y ∈=,cos 的函数 图象? 2、正弦函数R x x y ∈=,sin 的图像 (1)[]π2,0,sin ∈=x x y 的图像 【方案1】——几何描点法 步骤1:等分、作正弦线——将单位圆等分,作三角函数线(正弦线)得三角函数值; 步骤2:描点——平移定点,即描点()x x sin ,; 步骤3:连线——用光滑的曲线顺次连结各个点 小结:几何描点法作图精确,但过程比较繁。 【方案2】——五点法 步骤1:列表——列出对图象形状起关键作用的五点坐标;
正弦函数和余弦函数的图像与性质
6.1正弦函数和余弦函数的图像与性质 一、复习引入 1、复习 (1)函数的概念 在某个变化过程中有两个变量x 、y ,若对于x 在某个实数集合D 内的每一个确定的值,按照某个对应法则f ,y 都有唯一确定的实数值与它对应,则y 就是x 的函数,记作 ()x f y =,D x ∈。 (2)三角函数线 设任意角α的顶点在原点O ,始边与x 轴的非负半轴重合,终边与单位圆相交于点(,)P x y ,过P 作x 轴的垂线,垂足为M ;过点(1,0)A 作单位圆的切线,设它与角α的终边(当α在第一、四象限角时)或其反向延长线(当α为第二、三象限角时)相交于T . 规定:当OM 与x 轴同向时为正值,当OM 与x 轴反向时为负值; 当MP 与y 轴同向时为正值,当MP 与y 轴反向时为负值; 当AT 与y 轴同向时为正值,当AT 与y 轴反向时为负值; 根据上面规定,则,OM x MP y ==, 由正弦、余弦、正切三角比的定义有: sin 1 y y y MP r α====; cos 1 x x x OM r α====; tan y MP AT AT x OM OA α= ===; 这几条与单位圆有关的有向线段,,MP OM AT 叫做角α的正弦线、余弦线、正切线。 二、讲授新课 【问题驱动1】——结合我们刚学过的三角比,就以正弦(或余弦)为例,对于每一个给定的 角和它的正弦值(或余弦值)之间是否也存在一种函数关系?若存在,请对这种函数关系下一个定义;若不存在,请说明理由. 1、正弦函数、余弦函数的定义 (1)正弦函数:R x x y ∈=,sin ; (2)余弦函数:R x x y ∈=,cos 【问题驱动2】——如何作出正弦函数R x x y ∈=,sin 、余弦函数R x x y ∈=,cos 的函数 图象? 2、正弦函数R x x y ∈=,sin 的图像 (1)[]π2,0,sin ∈=x x y 的图像 【方案1】——几何描点法 步骤1:等分、作正弦线——将单位圆等分,作三角函数线(正弦线)得三角函数值;
正弦和余弦教案一查表
正弦和余弦教案(四) 一、素质教育目标 (一)知识教学点 使学生会查“正弦和余弦表”,即由已知锐角求正弦、余弦值.(二)能力渗透点 逐步培养学生观察、比较、分析、概括等逻辑思维能力. (三)德育训练点 培养学生良好的学习习惯. 二、教学重点、难点 1.重点:“正弦和余弦表”的查法. 2.难点:当角度在0°~90°间变化时,正弦值与余弦值随角度变化而变化的规律. 三、教学步骤 (一)明确目标 1.复习提问 1)30°、45°、60°的正弦值和余弦值各是多少?请学生口答. 2)任意锐角的正弦(余弦)与它的余角的余弦(正弦)值之间的关系怎样?通过复习,使学生便于理解正弦和余弦表的设计方式. (二)整体感知 我们已经求出了30°、45°、60°这三个特殊角的正弦值和余弦值,但在生产和科研中还常用到其他锐角的正弦值和余弦值,为了使用上的方便,我们把0°—90°间每隔1′的各个角所对应的正弦值和余弦值(一般是含有四位有效数字的近似值),列成表格——正弦和余弦表.本节课我们来研究如何使用正弦和余弦表. (三)重点、难点的学习与目标完成过程 1.“正弦和余弦表”简介
学生已经会查平方表、立方表、平方根表、立方根表,对数学用表的结构与查法有所了解.但正弦和余弦表与其又有所区别,因此首先向学生介绍“正弦和余弦表”. (1)“正弦和余弦表”的作用是:求锐角的正弦、余弦值,已知锐角的正弦、余弦值,求这个锐角. 2)表中角精确到1′,正弦、余弦值有四位有效数字. 3)凡表中所查得的值,都用等号,而非“≈”,根据查表所求得的值进行近似计算,结果四舍五入后,一般用约等号“≈”表示. 2.举例说明 例4 查表求37°24′的正弦值. 学生因为有查表经验,因此查sin37°24′的值不会是到困难,完全可以自己解决. 例5 查表求37°26′的正弦值. 学生在独自查表时,在正弦表顶端的横行里找不到26′,但26′在24′~30′间而靠近24′,比24′多2′,可引导学生注意修正值栏,这样学生可能直接得答案.教师这时可设问“为什么将查得的5加在0.6074的最后一个数位上,而不是0.6074减去0.0005”.通过引导学生观察思考,得结论:当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小). 解:sin37°24′=0.6074. 角度增2′,值增0.0005. sin37°26′=0.6079. 例6 查表求sin37°23′的值. 如果例5学生已经理解,那么例6学生完全可以自己解决,通过对比,加强理解. 解:sin37°24′=0.6074 角度减1′,值减0.0002 sin37°23′=0.6072. 在查表中,还应引导学生查得:
正弦余弦函数之叠合
§3-6 正弦餘弦函數之疊合 我們考慮正餘弦函數圖形,如圖中虛線的圖,圖形像波動的形狀,有高有低,起伏很規則。高的地方就是波峰,低的地方就是波谷。如果兩個波動同時進行,疊合在一起後,會變成什麼樣子呢? 從上圖可以看出,y =sin x +cos x 的圖形基本上與y =sin x (或y =cos x )的圖形類似,只是振幅與位置有些改變或移動。進一步觀察,當sin x =cos x 時,此時y =sin x +cos x 的圖形出現波峰與波谷,且y =sin x +cos x 的圖形向右移動若干單位。 我們猜測y =sin x +cos x 可表為y =r sin(x +θ),要如何決定r 與θ 呢? y =r sin(x +θ)=r (sin x ?cos θ+cos x ?sin θ)=sin x +cos x ?r ?cos θ=1 且 r ?sin θ =1 ?r 2=2 ?r = 2 ?cos θ=12 且 sin θ =12 ?可取θ=π 4 ?y =sin x +cos x = 2 sin(x +π 4 ) (1)疊合的方法: 考慮y =f (x )=a ?sin x +b ?cos x ,a ,b 為實數,根據前面例子的推測,我們也按照前面例子的做法,將y =f (x )=a ?sin x +b ?cos x 化成y =f (x )=r sin(x +θ) y =r sin(x +θ)=r (sin x ?cos θ+cos x ?sin θ)=a sin x +b cos x ??? ????=????=?(**) sin (*)cos b r a r θθ ?(*)2+(**)2 ?r 2=a 2+b 2 ?r =a 2+b 2 ?cos θ= a a 2 +b 2 且 sin θ=b a 2 +b 2 。
正弦余弦值
1、sin0°=0 2、sin90°=1 3、sin180°=0 4、cos0°=1 5、cos90°=0 6、cos180°=-1 7、sin-30° 8、sin-45°=- 9、sin-60°=- 10、sin-90°=-1 11、cos- (1)特殊角三角函数值sin0=0 sin30= 0.5 sin45= 0.7071二分之根号2 sin60= 0.8660二分之根号3 sin90=1 cos0=1 cos30= 0.4二分之根号3 cos45= 0.1二分之根号2 cos60= 0.5 cos90=0 tan0=0 tan30= 0.9三分之根号3 tan45=1 tan60= 1.根号3 tan90=无cot0=无cot30=
1.根号3 cot45=1cot60= 0.9三分之根号3 cot90=0 附: 三角函数值表 sin0=0, sin15=(√6-√2)/4 , sin45=√ sin60=√ sin75=(√6+√2)/2 , sin90=1, sin105=√√ sin120=√√ (√6-√2)/4 sin180=0 sin270=-1 sin360=0 sin1= 0. 1.诱导公式 sin(-a)=-sin(a) cos(-a)=cos(a)
sin(2π-a)=cos(a) cos(2π-a)=sin(a) sin(2π+a)=cos(a) cos(2π+a)=-sin(a) sin(π-a)=sin(a) cos(π-a)=-cos(a) sin(π+a)=-sin(a) cos(π+a)=-cos(a) tgA=tanA=sinAcosA 2.两角和与差的三角函数 sin(a+b)=sin(a)cos(b)+cos(α)sin(b) cos(a+b)=cos(a)cos(b)-sin(a)sin(b) sin(a-b)=sin(a)cos(b)-cos(a)sin(b) cos(a-b)=cos(a)cos(b)+sin(a)sin(b) tan(a+b)=tan(a)+tan(b)1-tan(a)tan(b) tan(a-b)=tan(a)-tan(b)1+tan(a)tan(b) 3.和差化积公式 sin(a)+sin(b)=2sin(a+b2)cos(a-b2) sin(a)?sin(b)=2cos(a+b2)sin(a-b2) cos(a)+cos(b)=2cos(a+b2)cos(a-b2) cos(a)-cos(b)=-2sin(a+b2)sin(a-b2)
正弦函数和余弦函数的图像及性质
6.1正弦函数和余弦函数的图像与性质 一、复习引入 1、复习 (1)函数的概念 在某个变化过程中有两个变量x 、y ,若对于x 在某个实数集合D 的每一个确定的值,按照某个对应法则f ,y 都有唯一确定的实数值与它对应,则y 就是x 的函数,记作 ()x f y =,D x ∈。 (2)三角函数线 设任意角α的顶点在原点O ,始边与x 轴的非负半轴重合,终边与单位圆相交于点(,)P x y ,过P 作x 轴的垂线,垂足为M ;过点(1,0)A 作单位圆的切线,设它与角α的终边(当α在第一、四象限角时)或其反向延长线(当α为第二、三象限角时)相交于T . 规定:当OM 与x 轴同向时为正值,当OM 与x 轴反向时为负值; 当MP 与y 轴同向时为正值,当MP 与y 轴反向时为负值; 当AT 与y 轴同向时为正值,当AT 与y 轴反向时为负值; 根据上面规定,则,OM x MP y ==, 由正弦、余弦、正切三角比的定义有: sin 1 y y y MP r α====; cos 1 x x x OM r α====; tan y MP AT AT x OM OA α= ===; 这几条与单位圆有关的有向线段,,MP OM AT 叫做角α的正弦线、余弦线、正切线。 二、讲授新课 【问题驱动1】——结合我们刚学过的三角比,就以正弦(或余弦)为例,对于每一个给定的 角和它的正弦值(或余弦值)之间是否也存在一种函数关系?若存在,请对这种函数关系下一个定义;若不存在,请说明理由. 1、正弦函数、余弦函数的定义 (1)正弦函数:R x x y ∈=,sin ; (2)余弦函数:R x x y ∈=,cos 【问题驱动2】——如何作出正弦函数R x x y ∈=,sin 、余弦函数R x x y ∈=,cos 的函数 图象? 2、正弦函数R x x y ∈=,sin 的图像
正余弦值对应表
余弦值对应表:1°0.999848 2°0.999391 3°0.99863 4°0.997564 5°0.996195 6°0.994522 7°0.992546 8°0.990268 9°0.987688 10°0.984808 11°0.981627 12°0.978148 13°0.97437 14°0.970296 15°0.965926 16°0.961262 17°0.956305 18°0.951057 19°0.945519 20°0.939693 21°0.93358 22°0.927184 23°0.920505 24°0.913545 25°0.906308 26°0.898794 27°0.891007 28°0.882948 29°0.87462 30°0.866025 31°0.857167 32°0.848048 33°0.838671 34°0.829038 35°0.819152 36°0.809017 37°0.798636 38°0.788011 39°0.777146 40°0.766044 41°0.75471 42°0.743145 43°0.731354 44°0.71934 45°0.707107 46°0.694658 47°0.681998 48°0.669131 49°0.656059 50°0.642788 51°0.62932 52°0.615661 53°0.601815 54°0.587785 55°0.573576 56°0.559193 57°0.544639 58°0.529919 59°0.515038 60°0.5 61°0.48481 62°0.469472 63°0.45399 64°0.438371 65°0.422618 66°0.406737 67°0.390731 68°0.374607 69°0.358368 70°0.34202 71°0.325568 72°0.309017 73°0.292372 74°0.275637 75°0.258819 76°0.241922 77°0.224951 78°0.207912 79°0.190809 80°0.173648 81°0.156434 82°0.139173 83°0.121869 84°0.104528 85°0.0871557 86°0.0697565 87°0.052336 88°0.0348995 89°0.0174524 90° 0.
正弦和余弦表
正弦余弦表 A 0ˊ 6ˊ12ˊ 18ˊ 24ˊ 32ˊ 36ˊ 42ˊ 48ˊ 54ˊ 60ˊcosA 1ˊ 2ˊ 3ˊ sinA 0.0000 90°0.0003 0.0006 0.0009 0° 0.0000 0017 0035 0052 0070 0087 0105 0122 0140 0157 0175 89° 3 6 9 1° 0715 0192 0209 0227 0244 0262 0279 0297 0314 0332 0349 88° 3 6 9 2° 0349 0366 0364 0401 0419 0436 0545 0471 0448 0506 0523 87° 3 6 9 3° 0523 0541 0558 0576 0593 0610 0628 0645 0663 0680 0698 86° 3 6 9 4° 0689 0715 0732 0750 0767 0785 0802 0819 0837 0854 0872 85° 3 6 9 5° 0.0872 0889 0906 0924 0941 0958 0976 0993 1011 1028 1045 84° 3 6 9 6° 1045 1063 1080 1097 1115 1132 1139 1167 1184 1201 1219 83° 3 6 9 7° 1219 1236 1253 1271 1288 1305 1323 1340 1357 1374 1392 82° 3 6 9 8° 1392 1409 1427 1444 1461 1478 1495 1513 1530 1547 1564 81° 3 6 9 9° 1564 1582 1599 1616 1633 1650 1668 1685 1802 1819 0.1836 80° 3 6 9 10°0.1736 1754 1771 1788 1805 1822 1840 1857 1874 1891 1908 79° 3 6 9 11° 1908 1925 1942 1959 1977 1994 2011 2028 2045 2062 2079 78° 3 6 9 12° 2079 2096 2113 2130 2147 2164 2181 2198 2215 2233 2250 77° 3 6 9 13° 0.2250 2267 2284 2300 2317 2334 2351 2368 2385 2402 2419 76° 3 6 8 14° 2419 2436 2453 2470 2487 2504 2521 2538 2554 2571 2588 65° 3 6 8 15° 2588 2605 2622 2639 2656 2672 2689 2706 2723 2740 2756 74° 3 6 8 16° 2756 2773 2790 2807 2823 2840 2857 2874 2890 1907 2924 73° 3 6 8 17° 2924 2940 2957 2974 2990 3007 3024 3040 3057 3074 3090 72° 3 6 8 18° 3090 3107 3123 3140 3156 3173 3190 3206 3223 2339 3256 71° 3 6 8 19° 3256 3272 3289 3305 3322 3338 3355 3371 3387 3404 3420 70° 3 5 8 20° 3420 3437 3453 3469 3486 3502 3518 3535 3551 3567 3584 69° 3 5 8
正弦函数值表
.. 0.0{0.0000} 0.1{0.0017} 0.2{0.0035} 0.3{0.0052} 0.4{0.0070} 0.5{0.0087} 0.6{0.0105} 0.7{0.0122} 0.8{0.0140} 0.9{0.0157} 1.0{0.0175} 1.1{0.0192} 1.2{0.0209} 1.3{0.0227} 1.4{0.0244} 1.5{0.0262} 1.6{0.0279} 1.7{0.0297} 1.8{0.0314} 1.9{0.0332} 2.0{0.0349} 2.1{0.0366} 2.2{0.0384} 2.3{0.0401} 2.4{0.0419} 2.5{0.0436} 2.6{0.0454} 2.7{0.0471} 2.8{0.0488} 2.9{0.0506} 3.0{0.0523} 3.1{0.0541} 3.2{0.0558} 3.3{0.0576} 3.4{0.0593} 3.5{0.0610} 3.6{0.0628} 3.7{0.0645} 3.8{0.0663} 3.9{0.0680} 4.0{0.0698} 4.1{0.0715} 4.2{0.0732} 4.3{0.0750} 4.4{0.0767} 4.5{0.0785} 4.6{0.0802} 4.7{0.0819} 4.8{0.0837} 4.9{0.0854} 5.0{0.0872} 5.1{0.0889} 5.2{0.0906} 5.3{0.0924} 5.4{0.0941} 5.5{0.0958} 5.6{0.0976} 5.7{0.0993} 5.8{0.1011} 5.9{0.1028} 6.0{0.1045} 6.1{0.1063} 6.2{0.1080} 6.3{0.1097} 6.4{0.1115} 6.5{0.1132} 6.6{0.1149} 6.7{0.1167} 6.8{0.1184} 6.9{0.1201} 7.0{0.1219} 7.1{0.1236} 7.2{0.1253} 7.3{0.1271} 7.4{0.1288} 7.5{0.1305} 7.6{0.1323} 7.7{0.1340} 7.8{0.1357} 7.9{0.1374} 8.0{0.1392} 8.1{0.1409} 8.2{0.1426} 8.3{0.1444} 8.4{0.1461} 8.5{0.1478} 8.6{0.1495} 8.7{0.1513} 8.8{0.1530} 8.9{0.1547} 9.0{0.1564} 9.1{0.1582} 9.2{0.1599} 9.3{0.1616} 9.4{0.1633} 9.5{0.1650} 9.6{0.1668} 9.7{0.1685} 9.8{0.1702} 9.9{0.1719} 10.0{0.1736} 10.1{0.1754} 10.2{0.1771} 10.3{0.1788} 10.4{0.1805} 10.5{0.1822} 10.6{0.1840} 10.7{0.1857} 10.8{0.1874} 10.9{0.1891} 11.0{0.1908} 11.1{0.1925} 11.2{0.1942} 11.3{0.1959} 11.4{0.1977} 11.5{0.1994} 11.6{0.2011} 11.7{0.2028} 11.8{0.2045} 11.9{0.2062} 12.0{0.2079} 12.1{0.2096} 12.2{0.2113} 12.3{0.2130} 12.4{0.2147} 12.5{0.2164} 12.6{0.2181} 12.7{0.2198} 12.8{0.2215} 12.9{0.2233} 13.0{0.2250} 13.1{0.2267} 13.2{0.2284} 13.3{0.2300} 13.4{0.2317} 13.5{0.2334} 13.6{0.2351} 13.7{0.2368} 13.8{0.2385} 13.9{0.2402} 14.0{0.2419} 14.1{0.2436} 14.2{0.2453} 14.3{0.2470} 14.4{0.2487} 14.5{0.2504} 14.6{0.2521} 14.7{0.2538} 14.8{0.2554} 14.9{0.2571} 15.0{0.2588} 15.1{0.2605} 15.2{0.2622} 15.3{0.2639} 15.4{0.2656} 15.5{0.2672} 15.6{0.2689} 15.7{0.2706} 15.8{0.2723} 15.9{0.2740} 16.0{0.2756} 16.1{0.2773} 16.2{0.2790} 16.3{0.2807} 16.4{0.2823} 16.5{0.2840} 16.6{0.2857} 16.7{0.2874} 16.8{0.2890} 16.9{0.2907} 17.0{0.2924} 17.1{0.2940} 17.2{0.2957} 17.3{0.2974} 17.4{0.2990} 17.5{0.3007} 17.6{0.3024} 17.7{0.3040} 17.8{0.3057} 17.9{0.3074} 18.0{0.3090} 18.1{0.3107} 18.2{0.3123} 18.3{0.3140} 18.4{0.3156} 18.5{0.3173} 18.6{0.3190} 18.7{0.3206} 18.8{0.3223} 18.9{0.3239} 19.0{0.3256} 19.1{0.3272} 19.2{0.3289} 19.3{0.3305} 19.4{0.3322} 19.5{0.3338} 19.6{0.3355} 19.7{0.3371} 19.8{0.3387} 19.9{0.3404} 20.0{0.3420} 20.1{0.3437} 20.2{0.3453} 20.3{0.3469} 20.4{0.3486} 20.5{0.3502} 20.6{0.3518} 20.7{0.3535} 20.8{0.3551} 20.9{0.3567} 21.0{0.3584} 21.1{0.3600} 21.2{0.3616} 21.3{0.3633} 21.4{0.3649} 21.5{0.3665} 21.6{0.3681} 21.7{0.3697} 21.8{0.3714} 21.9{0.3730} 22.0{0.3746} 22.1{0.3762} 22.2{0.3778} 22.3{0.3795} 22.4{0.3811} 22.5{0.3827} 22.6{0.3843} 22.7{0.3859} 22.8{0.3875} 22.9{0.3891} 23.0{0.3907} 23.1{0.3923} 23.2{0.3939} 23.3{0.3955} 23.4{0.3971} 23.5{0.3987} 23.6{0.4003} 23.7{0.4019} 23.8{0.4035} 23.9{0.4051} 24.0{0.4067} 24.1{0.4083} 24.2{0.4099} 24.3{0.4115} 24.4{0.4131} 24.5{0.4147} 24.6{0.4163} 24.7{0.4179} 24.8{0.4195} 24.9{0.4210} 25.0{0.4226} 25.1{0.4242} 25.2{0.4258} 25.3{0.4274} 25.4{0.4289} 25.5{0.4305} 25.6{0.4321} 25.7{0.4337} 25.8{0.4352} 25.9{0.4368} 26.0{0.4384} 26.1{0.4399} 26.2{0.4415} 26.3{0.4431}
正弦和余弦
正弦和余弦(1) 重点难点 一定要理解并明确:在直角三角形中,当锐角固定时,它的对边、邻边与斜边的比值也是固定的. 内容速览 若一组直角三角形有一个锐角相等,可以把其 顶点A1,A2,A3重合在一起,记作A,并使直角边AC1,AC2,AC3……落在同一条直线上,则斜边AB1,AB2,AB3……落在另一条直线上. 易知,△AB1C1∽△AB2C2∽△AB3C3∽…… 形中,∠A的对边、邻边与斜边的比值,是一个固定值. 知识扩展 当锐角为30°时,它的对边与斜边比值我们知道.今天我们又发现,锐角任意时,它的对边与斜边的比值也是固定的. 如果知道这个比值,已知一边求其他未知边的问题就迎刃而解了.看来这个比值很重要,下再研究这个“比值”! 正弦和余弦(2) 重点难点
了解把握正弦、余弦概念;明确用含有几个字母的符号组sinA、cosA表示正弦、余弦. 内容速览 在△ABC中,∠C为直角,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA. 大家一定要亲自动笔计算,对一些特殊角三角函数值一定要认记. 典型一例 知识扩展 由以上知识,同学们应该明确对任意锐角A的正、余弦值都在0~1之间,即,0<sinA<1,0<cosA<1(∠A为锐角). 正弦值随角度增大而增大,余弦值随角度增大而减小.
正弦和余弦(3) 重点难点 了解把握一个锐角的正弦(余弦)值与它的余角的余弦(正弦)值之间的关系并会应用. 内容速览 任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值. sinA=cos(90°-A),cosA=sin(90°-A). 经典一例 (2)已知sin35°=0.5736,求cos55°; (3)已知cos47°6′=0.6807,求sin42°54′. 分析:(1)问比较简单,对照定理,即可解答.(2)、(3)比(1)则更深一步,因为(1)明确指出∠B与∠A互余,(2)、(3)没有,但是仔细看,你会发现35°与55°,47°6′与42°54′分别互余 解:(1)1/2,(2)0.5736,(3)0.6807. 知识扩展 任意一个锐角的正弦值等于它的余角的余弦值,任意一个锐角的余弦值等于它的余角的正弦值. 正弦和余弦(4) 重点难点 探索明确当角度在0°~90°间变化时,正弦值与余弦值随角度变化而变化的规律.
