分数阶傅里叶变换

分数阶傅里叶变换的MATLAB 仿真计算以及几点讨论
在Haldun M. Ozaktas 和 Orhan Arikan 等人的论文《Digital computation of the fractional Fourier transform 》中给出了一种快速计算分数阶傅里叶变换的算法, 其MATLAB 计算程序可在https://www.360docs.net/doc/e29149289.html,.tr/~haldun/fracF.m 上查到。现在基于该程序,对一方波?????<=其它
,01,1)(t t x 进行计算仿真。
注:网上流传较为广泛的FRFT 计算程序更为简洁,据称也是Haldun M. Ozaktas 和 Orhan Arikan 等人的论文《Digital computation of the fractional Fourier transform 》使用的算法。但是根据Adhemar Bultheel 和 Hector E. Martnez Sulbaran 的论文《Computation of the Fractional Fourier Transform 》中提到,Ozaktas 等人的分数阶傅里叶变换的计算程序仅有上述网站这一处,而两个程序的计算结果基本相符。本文使用较为简洁的计算程序,Ozaktas 等人的计算程序在附表中给出。
程序如下:
clear
clc
%构造方波?????<=其它
,01
,1)(t t x dt=0.05;
T=20;
t=-T:dt:T;
n=length(t);
m=1;
for k=1:n;
% tt=-36+k;
tt=-T+k*dt;
if tt>=-m && tt<=m
x(k)=1;
else
x(k)=0;
end
end
%确定α的值
alpha=0.01;
p=2*alpha/pi
%调用计算函数
Fx=frft(x,p);
Fx=Fx';
Fr=real(Fx);
Fi=imag(Fx);
A=abs(Fx);
figure,
subplot(2,2,1);
plot(t,Fr,'-',t,Fi,':');title(' α=0.01时的实部和虚部π'); axis([-4,4,-1.5,2]);
subplot(2,2,2);
plot(t,A,'-');title('α=0.01时的幅值');
axis([-4,4,0,2]);
分数阶傅里叶变换计算函数如下:
function Faf = frft(f, a)
% The fast Fractional Fourier Transform
% input: f = samples of the signal
% a = fractional power
% output: Faf = fast Fractional Fourier transform
error(nargchk(2, 2, nargin));
f = f(:);
N = length(f);
shft = rem((0:N-1)+fix(N/2),N)+1;
sN = sqrt(N);
a = mod(a,4);
% do special cases
if (a==0), Faf = f; return; end;
if (a==2), Faf = flipud(f); return; end;
if (a==1), Faf(shft,1) = fft(f(shft))/sN; return; end if (a==3), Faf(shft,1) = ifft(f(shft))*sN; return; end
% reduce to interval 0.5 < a < 1.5
if (a>2.0), a = a-2; f = flipud(f); end
if (a>1.5), a = a-1; f(shft,1) = fft(f(shft))/sN; end if (a<0.5), a = a+1; f(shft,1) = ifft(f(shft))*sN; end
% the general case for 0.5 < a < 1.5
alpha = a*pi/2;
tana2 = tan(alpha/2);
sina = sin(alpha);
f = [zeros(N-1,1) ; interp(f) ; zeros(N-1,1)];
% chirp premultiplication
chrp = exp(-i*pi/N*tana2/4*(-2*N+2:2*N-2)'.^2);
f = chrp.*f;
% chirp convolution
c = pi/N/sina/4;
Faf = fconv(exp(i*c*(-(4*N-4):4*N-4)'.^2),f);
Faf = Faf(4*N-3:8*N-7)*sqrt(c/pi);
% chirp post multiplication
Faf = chrp.*Faf;
% normalizing constant
Faf = exp(-i*(1-a)*pi/4)*Faf(N:2:end-N+1);
function xint=interp(x)
% sinc interpolation
N = length(x);
y = zeros(2*N-1,1);
y(1:2:2*N-1) = x;
xint = fconv(y(1:2*N-1), sinc([-(2*N-3):(2*N-3)]'/2)); xint = xint(2*N-2:end-2*N+3);
function z = fconv(x,y)
% convolution by fft
N = length([x(:);y(:)])-1;
P = 2^nextpow2(N);
z = ifft( fft(x,P) .* fft(y,P));
z = z(1:N);
从图中可见,当旋转角度0→α时,分数阶Fourier 变换将收敛为方波信号)(t x ;当2πα→时,收敛为c sin 函数。
对于线性调频chirp 信号X k =exp(-j0.01141t 2),k=-32,-31……32,变换后的信号波形图如下
几点讨论
一,目前的分数阶傅里叶变换主要有三种快速算法:
1,B. Santhanamand 和 J. H. McClellan 的论文《The discrete rotational Fourier transform 》中,先计算离散FRFT 的核矩阵,再利用FFT 来计算离散FRFT 。 2,本文中采用的在Haldun M. Ozaktas 和 Orhan Arikan 等人的论文《Digital computation of the fractional Fourier transform 》所述的算法,是将FRFT 分解为信号的卷积形式,从而利于FFT 计算FRFT 。
3,Soo-Chang Pei 和 Min-Hung Yeh 等人在《Two dimensional discrete fractional Fourier transform 》和《Discrete frac-tional fourier transformbased on orthogonal projections 》中,采用矩阵的特征值和特征向量来计算FRFT 。
二,Ozaktas 在《Digital computation of the fractional Fourier transform 》所述的算法,其实不是“离散”分数阶傅里叶变换的算法,而是对连续分数阶傅里叶变换
的数值计算。在C. Candan和M.A. Kutay等人的论文《The discrete Fractional Fourier Transform》中介绍了离散分数阶傅里叶变换的算法,并给出了计算仿真图形(错误!未找到引用源。)二者吻合得很好。
图1 C. Candan和M.A. Kutay等人离散分数阶傅里叶变换的算法与连续分数阶傅
里叶变换的比较
三,在Luis B. Almeida 的论文《The Fractional Fourier Transform and Time Frequency Representations》中给出了方波的分数阶傅立叶变换图形(图2)
图 2 Almeida 的论文中给出的方波的分数阶傅立叶变换图形
该图形与讲义中的图形相符。本文中的仿真结果大致与该图形也相符合,但是令人困惑的是无论用那种算法程序,怎样调整输入信号,在2πα→时,虚部都不为零,这与Almeida 和讲义中的图形并不一致。而在Haldun M. Ozaktas 和 Orhan Arikan 等人的论文《Digital computation of the fractional Fourier transform 》中只给出了幅值的绝对值的图形,并没有给出实部与虚部的结果,因此尚需进一步讨论
图 3 本文中计算的2πα→时,实部与虚部分布
附:
Haldun M. Ozaktas 和Orhan Arikan等人的论文《Digital computation of the fractional Fourier transform》所述的算法程序
%FAST COMPUTATION OF THE FRACTIONAL FOURIER TRANSFORM
%by M. Alper Kutay, September 1996, Ankara
%Copyright 1996 M. Alper Kutay
%This code may be used for scientific and educational purposes
%provided credit is given to the publications below:
%
%Haldun M. Ozaktas, Orhan Arikan, M. Alper Kutay, and Gozde Bozdagi, %Digital computation of the fractional Fourier transform,
%IEEE Transactions on Signal Processing, 44:2141--2150, 1996.
%Haldun M. Ozaktas, Zeev Zalevsky, and M. Alper Kutay,
%The Fractional Fourier Transform with Applications in Optics and
%Signal Processing, Wiley, 2000, chapter 6, page 298.
%
%The several functions given below should be separately saved
%under the same directory. fracF(fc,a) is the function the user
%should call, where fc is the sample vector of the function whose
%fractional Fourier transform is to be taken, and `a' is the
%transform order. The function returns the samples of the a'th
%order fractional Fourier transform, under the assumption that
%the Wigner distribution of the function is negligible outside a
%circle whose diameter is the square root of the length of fc. %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function[res]=fracF(fc,a)
% This function operates on the vector fc which is assumed to
% be the samples of a function, obtained at a rate 1/deltax
% where the Wigner distribution of the function f is confined
% to a circle of diameter deltax around the origin.
% (deltax^2 is the time-bandwidth product of the function f.)
% fc is assumed to have an even number of elements.
% This function maps fc to a vector, whose elements are the samples % of the a'th order fractional Fourier transform of the function f. % The lengths of the input and ouput vectors are the same if the
% input vector has an even number of elements, as required.
% Operating interval: -2 <= a <= 2
% This function uses the `core' function corefrmod2.m
N = length(fc);
% if fix(N/2) ~= N/2
% error('Length of the input vector should be even'); % end;
fc = fc(:);
fc = bizinter(fc);
fc = [zeros(N,1); fc ; zeros(N,1)];
flag = 0;
if (a>0) && (a<0.5)
flag = 1;
a = a-1;
end;
if (a>-0.5) && (a<0)
flag = 2;
a = a+1;
end;
if (a>1.5) && (a<2)
flag = 3;
a = a-1;
end;
if (a>-2) && (a<-1.5)
flag = 4;
a = a+1;
end;
res = fc;
if (flag==1) || (flag==3)
res = corefrmod2(fc,1);
end;
if (flag==2) || (flag==4)
res = corefrmod2(fc,-1);
end;
if (a==0)
res = fc;
else
if (a==2) || (a==-2)
res = flipud(fc);
else
res = corefrmod2(res,a);
end;
end;
res = res(N+1:3*N);
res = bizdec(res);
res(1) = 2*res(1); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function[res]=corefrmod2(fc,a)
% Core function for computing the fractional Fourier transform.
% Valid only when 0.5 <= abs(a) <= 1.5
% Decomposition used:
% chirp mutiplication - chirp convolution - chirp mutiplication deltax = sqrt(length(fc));
phi = a*pi/2;
N = fix(length(fc));
deltax1 = deltax;
alpha = 1/tan(phi);
beta = 1/sin(phi);
x = [-ceil(N/2):fix(N/2)-1]/deltax1;
fc = fc(:);
fc = fc(1:N);
f1 = exp(-1i*pi*tan(phi/2)*x.*x); %multiplication by chirp!
f1 = f1(:);
fc = fc.*f1;
x = x(:);
clear x;
t =[-N+1:N-1]/deltax1;
hlptc =exp(i*pi*beta*t.*t);
clear t;
hlptc = hlptc(:);
N2 = length(hlptc);
N3 = 2^(ceil(log(N2+N-1)/log(2)));
hlptcz = [hlptc;zeros(N3-N2,1)];
fcz = [fc;zeros(N3-N,1)];
Hcfft = ifft(fft(fcz).*fft(hlptcz)); % convolution with chirp clear hlptcz;
clear fcz;
Hc = Hcfft(N:2*N-1);
clear Hcfft;
clear hlptc;
Aphi = exp(-i*(pi*sign(sin(phi))/4-phi/2))/sqrt(abs(sin(phi))); xx = [-ceil(N/2):fix(N/2)-1]/deltax1;
f1 = f1(:);
res = (Aphi*f1.*Hc)/deltax1; % multiplication by chirp!
if (fix(N/2) ~=N/2)
res2(1:N-1) = res(2:N);
res2(N) = res(1);
res = res2;
end;
res = res(:);
clear f1
clear Hc %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function xint=bizinter(x)
N=length(x);
im = 0;
if sum(abs(imag(x)))>0
im = 1;
imx = imag(x);
x = real(x);
end;
x2=x(:);
x2=[x2.'; zeros(1,N)];
x2=x2(:);
xf=fft(x2);
if rem(N,2)==1 %N = odd
N1=fix(N/2+1); N2=2*N-fix(N/2)+1;
xint=2*real(ifft([xf(1:N1); zeros(N,1) ;xf(N2:2*N)].'));
else
xint=2*real(ifft([xf(1:N/2); zeros(N,1) ;xf(2*N-N/2+1:2*N)].')); end;
if ( im == 1)
x2=imx(:);
x2=[x2.'; zeros(1,N)];
x2=x2(:);
xf=fft(x2);
if rem(N,2)==1 %N = odd
N1=fix(N/2+1); N2=2*N-fix(N/2)+1;
xmint=2*real(ifft([xf(1:N1); zeros(N,1) ;xf(N2:2*N)].'));
else
xmint=2*real(ifft([xf(1:N/2); zeros(N,1) ;xf(2*N-N/2+1:2*N)].')); end;
xint = xint + i*xmint;
end;
xint = xint(:); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function xdec=bizdec(x)
k = 1:2:length(x);
xdec = x(k);
xdec = xdec(:); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function F2D=fracF2D(f2D,ac,ar)
[M,N] = size(f2D);
F2D = zeros(M,N);
if ac == 0
F2D = f2D;
else
for k = 1:N
F2D(:,k) = fracF(f2D(:,k),ac);
end;
end;
F2D = conj(F2D');
if ar ~= 0
for k = 1:M
F2D(:,k) = fracF(F2D(:,k),ar);
end;
end;
F2D = conj(F2D');
希尔伯特变换与傅立叶变换
在数学与信号处理的领域中,一个实数值函数的希尔伯特转换(Hilbert transform)——在此标示为——是将信号与做卷积,以得到。因此,希尔伯特转换结果可以被解读为输入是的线性非时变系统(linear time invariant system)的输出,而此一系统的脉冲响应为。这是一项有用的数学, 用在描述一个以实数值载波做调制的信号之复数包络(complex envelope),出现在通讯理论(应用方面的详述请见下文。) 希尔伯特转换是以著名数学家大卫·希尔伯特(David Hilbert)来命名。 希尔伯特转换定义如下: 其中 并考虑此积分为柯西主值(Cauchy principal value),其避免掉在以及 等处的奇点。 另外要指出的是: 若,则可被定义,且属于;其中。频率响应 希尔伯特转换之频率响应由傅立叶变换给出: , 其中 ?是傅立叶变换, ?i (有时写作j )是虚数单位, ?是角频率,以及
? 即为符号函数。 既然: , 希尔伯特转换会将负频率成分偏移+90°,而正频率成分偏移?90°。 反(逆)希尔伯特转换 我们也注意到:。因此将上面方程式乘上,可得到: 从中,可以看出反(逆)希尔伯特转换 傅里叶变换(Fourier变换)是一种线性的积分变换。因其基本思想首先由法国学者约瑟夫·傅里叶系统地提出,所以以其名字来命名以示纪念。 傅里叶变换在物理学、声学、光学、结构动力学、量子力学、数论、组合数学、概率论、统计学、信号处理、密码学、海洋学、通讯、金融等领域都有着广泛的应用。例如在信号处理中,傅里叶变换的典型用途是将信号分解成振幅分量和频率分量。 ?傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。最初傅里叶分析是作为热过程的解析分析的工具被提出的[1]。 ?傅里叶变换属于谐波分析。 ?傅里叶变换的逆变换容易求出,而且形式与正变换非常类似。 ?正弦基函数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解。在线性时不变的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取。
Chirp信号的傅里叶变换的特征比较.
Chirp信号的傅里叶变换的特征比较 Chirp信号即线性调频信号是瞬时频率在某个范围内随时间变化的正弦波,因其良好的频带利用率,具有较强的抗干扰、抗多途效应和抗多普勒衰减以及良好的频带利用率等优点,因此在通信、声呐、雷达等领域具有广泛的应用。本文就瞬时频率范围(信号的调频宽度)和信号的持续时间(信号的周期)对傅里叶变换后的chirp函数的频谱函数的影响做出讨论,运用MATLAB仿真分析比较。 一.信号的调频宽度上下限对频谱函数的影响 1)高频宽度300情况下的频谱函数。信号的采样频率为43000,扫描时间为0.05,初始频率设为19700,结束频率位置为20000。 2)低频宽度300情况下的频谱函数。信号的采样频率为2000,信号的持续时间为0.05,初始频率设为40,结束频率设置为340。 由上面两幅图可以看出,当它们满足,幅度谱的大小基本都在 0.01和0.015之间,这是因为它们的调频上下限之差相同都是300,且时间周 期都为0.05。由公式可知,幅度与信号的调频宽度(表示傅里叶变换后的频带宽度)和时间周期有关。 二.信号的调频宽度对频谱函数的影响 1)高频宽度10000情况下的频谱函数。信号的采样频率为48000,扫描时间为0.05,初始频率设为10000,结束频率位置为20000。
2)低频宽度80情况下的频谱函数。信号的采样频率为1000,信号的持续时间为0.05,初始频率设为40,结束频率设置为120。 上面两图在频带宽度内的幅度谱差异很明显,这是因为只有当时,近似程度才更高。 三.信号的持续时间对频谱函数的影响 1)低频宽度80情况下的频谱函数。信号的采样频率为1000,chirp 脉冲为0.05,信号的持续时间为2,初始频率设为40,结束频率设置为120。 上图的信号周期是2,发射脉冲长度为0.05与之前其它参数相同的图4比较可知,频带宽度基本相同,在频带宽度内的幅度谱没有太大变化,只是频点上的曲线多了些波动。
阶跃信号
2.5 冲激信号和阶跃信号的傅里叶变换 2.5.1 冲激信号 由傅里叶变换定义及冲激信号的抽样特性很容易求得(t)函数的FT为 冲激函数的频谱等于常数,也就是说,在整个频率范围内频谱都是均匀的。在时域中波形变化剧烈的冲激函数包含幅度相等的所有频率分量,这种频谱常称作"均匀谱"或"白色谱"。 2.5.2 直流信号 如前所述,冲激信号的频谱是常数,那么时域为常数的信号(直流信号)的频谱是否为冲激函数呢? 我们来考虑()的傅里叶逆变换,即 这也就是说 上式意味着 式中的E为常数。 这表明,直流信号的频谱是位于w=0的冲激函数,这与直流信号的物理概念是一致的。 2.5.3单位阶跃信号 单位阶跃函数同样不满足绝对可积条件,但仍存在傅里叶变换。前面我们已经讲述了符号函数的傅里叶变换,下面我们借助符号函数来求阶跃信号的FT。 单位阶跃函数U(t)可用符号函数来表示,即 再利用直流信号与符号函数的傅里叶变换
可得单位阶跃函数的傅里叶变换为 单位阶跃函数及其频谱如下图所示。由图可知,U(t)在t>0时等同于直流信号,但它又不是纯粹的直流信号,它在t=0处有跳变,因此其频谱不是仅在=0处有一个冲激函数(这对应于信号的直流特性),而且还会含有其它众多的频率分量。 为什么会有众多的频率分量呢?这是因为信号在时域零点处有跳变!由于时域的剧烈变化,相应的频域中的分量将是无限的。还记得我们在前面讲周期矩形脉冲信号所提及的"时域跳变将使频域包含无限的频率分量"的结论吗?这儿就是一个很好的例证。大家可以翻回去看看,是不是这样。 图2-11 (a) 单位阶跃函数的波形 (b) 信号的幅度谱
阶跃信号傅里叶变换的多种求解方法
阶跃信号傅里叶变换的多种求解方法
何勇福 皮小林 潘芳芳 南昌大学共青学院
[摘 要]因为阶跃信号不满足傅里叶变换所需的条件---信号绝对可积, 故不 能直接利用傅里叶变换的定义式来求阶跃信号的频谱密度函数, 本文从多个方面 给出求解其傅氏变换的方法。 [关键词]阶跃信号;频谱函数;傅里叶变换;拉普拉斯变换 我们在用傅里叶变换公式计算一个信号的频谱密度函数时, 要求该信号的积 分必须存在,这就意味着信号要满足绝对可积这个条件。对于单位阶跃信号来 说很显然不满足绝对可积,所以我们只能采用别的方法求其频谱函数,通常,用 取极限的方法是比较多的, 下面就结合信号与系统相关知识进一步研究其频谱函 数的多种求解。 一、按定义求解
F [e (t )] = ò e - jwt dt = ò cos( wt )dt - j ò sin( wt )dt
0 0 0
¥
¥
¥
= =
1 1 sin( wt ) ¥ cos( wt ) ¥ 0 0 w jw
lim ê ?
t ?¥
é cos( wt ) ù 1 é sin( wt ) ù é sin( wt ) ù - sin ê - lim ê ú+ ú w ú w ? t ?0 ? ? t ?¥ ? jw ? jw
上式中第一项即 pd ( w) ,中间两项都等于零,最后一项是
1 jw
1 ,所以可 jw
得阶跃信号的频谱函数为 pd ( w) + 二、利用求极限的方法
这是一种在很多教材上都采用了的一种方法。 将 e (t ) 看作单边指数信号衰减 信号 e - at e (t ) 当 a ? 0 时的极限,对于单边指数衰减信号的傅里叶变换容易求出:
F [e -at e (t )] = 1 a w = 2 -j 2 2 a + jw a + w a + w2 1 ,但实部满足以下关系: jw
当我们取 a ? 0 时容易求出虚部的极限为
分数傅里叶变换
分数傅里叶变换 分数傅里叶定义: 分数傅里叶变换的物理意义即做傅里叶变换次,其中不一定要为整数(比傅里叶变换更加广泛);通过分数傅里叶变换之后,图像或信号便会同时拥有时域与频域两者的特征。 1.1(维基百科) 第一种定义: 第二种定义: 1.2 从数学上分数傅立叶变换定义了积分形式: Wigner分布函数相空间定义的分数傅立叶变换 A.W.Lohmann在1993 年利用傅里叶变换相当于在Wigner分布函数相空间中角度为π/2的旋转这一性质,说明分数傅里叶变换在Wigner分布函数空间中相当于角度是pπ/2的旋转,这里,p是分数傅里叶变换的级次。
分数傅里叶变换的定义在数学上是等价的。当分数傅里叶变换的幂次p从0 连续增长到达1 时,分数傅里叶变换的结果相应地从原始信号的纯时间(空间)形式开始逐渐变化成为它的纯频域(谱)形式,幂次p在0到1之间的任何时刻对应的分数傅里叶变换采取了介乎于时(空)域和频域之间的一个过渡域的形式,形成一个既包含时(空)域信息同时也包含频(谱)域信息的混合信号。因此,这样定义的分数傅里叶变换确实是一种时(空)-频描述和分析工具 分数傅里叶的分类: 1.一维分数傅里叶变换 分数傅里叶变换的数学表达式有积分形式和级数表达式两种等价形式, 1.积分形式 2级数表达式形式 其中 2.二维分数傅里叶变换 其中C为相应常系数。当a=b时, 上式就是二维分数傅里叶变换的表 达式; 当a=b=1时, 上式转化为常规二维傅里叶变换; 当a与b不相等时, 我们称这种情况的二维分数傅里叶变换为不对称分数傅里叶变换。此时在x、y 方向实施的变换级次是不同的。 分数傅里叶变换的性质 1周期性:(k为整数) 2线性:(c1和c2是复常数)
常用傅里叶变换表
时域信号 弧频率表示的 傅里叶变换 注释 1 | 线性 2时域平移 3频域平移, 变换2的频域对应 \ 4 如果值较大,则会收缩 到原点附近,而会扩 散并变得扁平. 当| a | 趋向无 穷时,成为Delta函数。 5 傅里叶变换的二元性性质。通过 交换时域变量和频域变量 得到. 6 / 傅里叶变换的微分性质 7变换6的频域对应
8 表示和的卷积—这 就是卷积定理 - 9 矩形脉冲和归一化的sinc函数 10变换10的频域对应。矩形函数是理想的低通滤波器,sinc函数是这类滤波器对反因果冲击的响应。 11- tri是三角形函数 12变换12的频域对应 13高斯函数exp( ? αt2) 的傅里叶变换是他本身. 只有当Re(α) > 0时,这是可积的。 ¥14 15 16》 a>0
18δ(ω) 代表狄拉克δ函数分布. 这个变换展示了狄拉克δ函数的重要性:该函数是常函数的傅立叶变换 【 19 变换23的频域对应20由变换3和24得到. 21` 由变换1和25得到,应用了欧拉公 式: cos(at) = (e iat + e?iat) / 2. 22由变换1和25得到 23这里, n是一个自然数. δ(n)(ω) 是狄拉克δ函数分布的n阶微分。这个变换是根据变换7和24得到的。将此变换与1结合使用,我们可以变换所有多项式。 / 24此处sgn(ω)为符号函数;注意此变换与变换7和24是一致的. 25变换29的推广. 17变换本身就是一个公式
26【 变换29的频域对应. 27此处u(t)是单位阶跃函数; 此变换根据变换1和31得到. 28u(t)是单位阶跃函数,且a > 0. 34狄拉克梳状函数——有助于解释或理解从连续到离散时间的转变.
傅里叶变换在信号处理中的应用
傅里叶变换在信号处理中的应用 姓名董柱班级电气工程及其自动化学号1109141013 摘要: 傅里叶变换是一种特殊的积分变换。通过傅里叶变换把信号的从时域变换到频域研究,采用频域法较之经典时域的方法有很多突出的优点,虽然傅里叶分析不是信息科学与技术领域中唯一的变换域方法,但是不得不承认,在此领域中,傅里叶变换分析始终有着广泛的应用,通过傅里叶变换实现信号的滤波,调制,抽样是傅里叶变换在信号处理中最主要的作用。通过对信号的调制可以将信号的低频成分调制到高频,实现频谱搬移,减少马间串扰,提高抗噪声新能,有利于信号的远距离传输,另外,对信号采样可以使连续信号离散化,有利于用计算机对信号进行处理,总之,傅里叶变换在信号处理中有着非常重要的作用。傅里叶变换是学习其他频域变换的基础。 关键词: 傅里叶变换,时域,频域,信号处理,信息科学与技术,滤波,调制,抽样。 一傅里叶变换 1.定义 f(t)是t的函数,如果t满足狄里赫莱条件:具有有限个间断点;具有有限个极值点;绝对可积。则有下图①式成立。称为积分运算f(t)的傅立叶变换, ②式的积分运算叫做F(ω)的傅立叶逆变换。F(ω)叫做f(t)的像函数,f(t)叫做 F(ω)的像原函数。F(ω)是f(t)的像。f(t)是F(ω)原像。 ① 傅里叶变换 傅里叶逆变换 2.分类 连续傅立叶变换:一般情况下,若“傅立叶变换”一词的前面未加任何限定语,则指的是“连续傅立叶变换”。“连续傅立叶变换”将平方可积的函数f(t) 表示成复指数函数的积分或级数形式。 f(t) = \mathcal^[F(ω)] = \frac{\sqrt{2π}} \int\limits_{-\infty}^\infty F(ω)e^{iωt}\,dω.
基于分数阶Fourier变换的图像加密算法
Electronic Component & Device Applications 姨 ·exp(j (s 2+u 2)2tan α-jsu sin α )exp(j (t 2+v 2 )2tan β -jtv sin β ) (1) 其中,α=p 1π/2,β=p 2π/2,表示信号通过二维傅里叶变换后的旋转角度。应用二维傅里叶变换核K p1,p2(s ,t ,u ,v ),在变换阶数p 1和p 2给定的情况下,信号f (s ,t )的二维分数阶傅里叶变换定义为: F p1,p2(u ,v )= ∞-∞ 乙∞ -∞ 乙f (s ,t )K p1,p2 (s ,t ,u ,v )dsdt (2) 因为二维分数阶傅里叶变换核是可分离的, 即: K p1,p2(s ,t ,u ,v )=K p1(s ,u )×K p2(t ,v ) (3) 二维离散分数阶傅里叶变换和逆变换定义 为: X p1,p2(m ,n )=M -1m =0 ΣN -1 n =0 Σx (p ,q )K p1,p2(p ,q ,m ,n ) (4)x (m ,n )=M -1m =0 ΣN -1 n =0 ΣX p1,p2(m ,n )K -p1,-p2(p ,q ,m ,n ) (5) 收稿日期:2010-09-21 基于分数阶Fourier 变换的图像加密算法 尚宇雄,尚 宇 (西安工业大学电子信息工程学院,陕西 西安 710032) 摘 要:针对目前基于分数阶傅里叶变换的图像加密算法中存在的不足,设计了一种基于分 数阶傅里叶变换和混沌系统的图像加密新算法。该方案的安全性依赖于随机混沌图像、分数阶傅里叶变换阶数以及混沌系统的初始参数。理论分析和模拟实验结果表明该方案具有良好的图像加密效果。 关键词:分数阶Fourier 变换;混沌置乱;图像加密 doi:10.3969/j.issn.1563-4795.2011.03.017 52
阶跃信号傅里叶变换
阶跃信号为什么不满足傅里叶变换条件? 傅氏变换的充分条件是: 在时域内要绝对可积。 但是这并不是必要条件,一些非绝对可积的函数(阶跃函数)也是有傅里叶变换的,它们的傅氏变换按定义不太可能求得,一般是通过求极限的方式得到其傅氏变换。 2.5 冲激信号和阶跃信号的傅里叶变换 2.5.1 冲激信号 由傅里叶变换定义及冲激信号的抽样特性很容易求得(t)函数的FT为 可见,冲激函数的频谱等于常数,也就是说,在整个频率范围内频谱都是均匀的。在时域中波形变化剧烈的冲激函数包含幅度相等的所有频率分量,这种频谱常称作"均匀谱"或"白色谱"。 2.5.2 直流信号 如前所述,冲激信号的频谱是常数,那么时域为常数的信号(直流信号)的频谱是否为冲激函数呢? 我们来考虑()的傅里叶逆变换,即 这也就是说 上式意味着 式中的E为常数。 这表明,直流信号的频谱是位于w=0的冲激函数,这与直流信号的物理概念是一致的。
2.5.3单位阶跃信号 单位阶跃函数同样不满足绝对可积条件,但仍存在傅里叶变换。前面我们已经讲述了符号函数的傅里叶变换,下面我们借助符号函数来求阶跃信号的FT。 单位阶跃函数U(t)可用符号函数来表示,即 再利用直流信号与符号函数的傅里叶变换 可得单位阶跃函数的傅里叶变换为 单位阶跃函数及其频谱如下图所示。由图可知,U(t)在t>0时等同于直流信号,但它又不是纯粹的直流信号,它在t=0处有跳变,因此其频谱不是仅在=0处有一个冲激函数(这对应于信号的直流特性),而且还会含有其它众多的频率分量。 为什么会有众多的频率分量呢?这是因为信号在时域零点处有跳变!由于时域的剧烈变化,相应的频域中的分量将是无限的。还记得我们在前面讲周期矩形脉冲信号所提及的"时域跳变将使频域包含无限的频率分量"的结论吗?这儿就是一个很好的例证。大家可以翻回去看看,是不是这样。 图2-11 (a) 单位阶跃函数的波形(b) 信号的幅度谱
分数傅里叶变换产生分数泰伯效应
*国家自然科学基金资助项目。收稿日期∶1996—02—06;收到修改稿日期∶1996—03—28第24卷 第2期 中 国 激 光V o l.A24,N o.2 1997年2月C HIN ESE J O U RN AL O F LASERS February ,1997 分数傅里叶变换产生分数泰伯效应* 华建文 刘立人 (中国科学院上海光机所 上海201800) 提要 讨论了如何使用分数傅里叶变换来产生分数泰伯效应,导出了要产生这种双重变换的光学 条件,变换后的周期、变换比例因子和级联运算法则,并进行了实验验证。这种双重变换有助于光 学系统的设计、分析和计算。最后给出了应用实例。 关键词 光学变换,傅里叶变换,泰伯效应 1 引 言 分数傅里叶变换的概念是Namias [1]首先提出的。后来由McBride 和Kerr [2] 把它发展成一个较为完整的数学理论。它是傅里叶变换的全族。后来,Lohm ann [3]在分析Wig ner 函数的基础上建立了光学领域中的分数傅里叶变换,并给出了光学实现的两种方案。Mendlovic 和Oza-ktas [4,5]研究了分数傅里叶变换的某些特性以及在光纤中的光学实现。文献[6~11]报道了一些分数傅里叶变换的应用。泰伯效应是光栅在相干光照明下在自由空间中某些特定的距离Z 处自成像的现象。分数泰伯效应或称分数泰伯自成像是指这种成像过程发生在Z 的分数距离上,如Z /2处,Z /3处等等。关于它的基本理论及许多应用的回顾可在文献[12]及[13]中找到。本文主要研究如何利用分数傅里叶变换使光栅产生分数泰伯像,或者说如何使分数傅里叶变换和分数泰伯自成像同时发生。这两种过程同时发生有一定的实用意义。利用这双重的分数变换(自成像也可看作一种变换)有助于一些光学系统的设计和分析,也有助于光路级联计算的简化。我们把它用于位相物体观察系统的光学设计,得到的装置比波面成像剪切干涉系统简单,尺寸又小。而且还能满足观察不同大小物体的要求。2 分数泰伯效应和分数傅里叶变换 泰伯效应是一相干波照明一光栅,在自由空间中距光栅的某些特定的平面上能出现一些准确泰伯像和更多的分数泰伯像[13]。一块周期为T ,开口比为h 的朗奇光栅可用下式描述 g (x ,y )=rect(x /h )* n W (x -n T )(1)符号“*”表示卷积。用单色平面波照明光栅,其菲涅耳衍射场在光栅后方自由空间中传播,在离光栅距离为Z 的平面上,光强分布为[13]
傅里叶变换_百度文库.
傅里叶变换,拉普拉斯变换和Z 变换的意义来源:于理扬的日志 傅里叶变换在物理学、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用(例如在信号处理中, 傅里叶变换的典型用途是将信号分解成幅值分量和频率分量。 傅里叶变换能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数或者它们的积分的线性组合。在不同的研究领域, 傅里叶变换具有多种不同的变体形式, 如连续傅里叶变换和离散傅里叶变换。 傅里叶变换是一种解决问题的方法,一种工具,一种看待问题的角度。理解的关键是:一个连续的信号可以看作是一个个小信号的叠加, 从时域叠加与从频域叠加都可以组成原来的信号,将信号这么分解后有助于处理。 我们原来对一个信号其实是从时间的角度去理解的,不知不觉中,其实是按照时间把信号进行分割, 每一部分只是一个时间点对应一个信号值, 一个信号是一组这样的分量的叠加。傅里叶变换后, 其实还是个叠加问题, 只不过是从频率的角度去叠加, 只不过每个小信号是一个时间域上覆盖整个区间的信号, 但他确有固定的周期,或者说,给了一个周期,我们就能画出一个整个区间上的分信号,那么给定一组周期值(或频率值,我们就可以画出其对应的曲线,就像给出时域上每一点的信号值一样,不过如果信号是周期的话,频域的更简单,只需要几个甚至一个就可以了,时域则需要整个时间轴上每一点都映射出一个函数值。 傅里叶变换就是将一个信号的时域表示形式映射到一个频域表示形式;逆傅里叶变换恰好相反。这都是一个信号的不同表示形式。它的公式会用就可以,当然把证明看懂了更好。 对一个信号做傅里叶变换,可以得到其频域特性,包括幅度和相位两个方面。幅度是表示这个频率分量的大小, 那么相位呢, 它有什么物理意义?频域的相位与时域的相位有关系吗?信号前一段的相位(频域与后一段的相位的变化是否与信号的频率成正比关系。
(完整版)傅里叶变换分析
第一章 信号与系统的基本概念 1.信号、信息与消息的差别? 信号:随时间变化的物理量; 消息:待传送的一种以收发双方事先约定的方式组成的符号,如语言、文字、图像、数据等 信息:所接收到的未知内容的消息,即传输的信号是带有信息的。 2.什么是奇异信号? 函数本身有不连续点或其导数或积分有不连续点的这类函数统称为奇异信号或奇异函数。例如: 单边指数信号 (在t =0点时,不连续), 单边正弦信号 (在t =0时的一阶导函数不连续)。 较为重要的两种奇异信号是单位冲激信号δ(t )和单位阶跃信号u(t )。 3.单位冲激信号的物理意义及其取样性质? 冲激信号:它是一种奇异函数,可以由一些常规函数的广义极限而得到。 它表达的是一类幅度很强,但作用时间很短的物理现象。其重要特性是筛选性,即: ()()()(0)(0)t x t dt t x dt x δδ∞ ∞ -∞ -∞ ==? ? 4.什么是单位阶跃信号? 单位阶跃信号也是一类奇异信号,定义为: 10()00t u t t >?=?
12()()()x t ax t bx t =+,其中a 和b 是任意常数时, 输出信号()y t 是1()y t 和2()y t 的线性叠加,即:12()()()y t ay t by t =+; 且当输入信号()x t 出现延时,即输入信号是0()x t t -时, 输出信号也产生同样的延时,即输出信号是0()y t t -。 其中,如果当12()()()x t x t x t =+时,12()()()y t y t y t =+,则称系统具有叠加性; 如果当1()()x t ax t =时,1()()y t ay t =则称系统具有均匀性。 线性时不变系统是最基本的一类系统,是研究复杂系统,如非线性、时变系统的基础。 6.线性时不变系统的意义与应用? 线性时不变系统是我们本课程分析和研究的主要对象,对线性时不变性进行推广,可以得到线性时不变系统具有微分与积分性质,假设系统的输入与输出信号分别为()x t 和()y t ,则 当输入信号为 ()dx t dt 时,输出信号则为() dy t dt ; 或者当输入信号为()t x d ττ-∞ ?时,输出信号则为()t y d ττ-∞ ?。 另外,线性时不变系统对信号的处理作用可以用冲激响应(或单位脉冲响应)、系统函数或频率响应进行描述。而且多个系统可以以不同的方式进行连接,基本的连接方式为:级联和并联。 假设两个线性时不变系统的冲激响应分别为:1()h t 和2()h t , 当两个系统级联后,整个系统的冲激响应为:12()()*()h t h t h t =; 当两个系统并联后,整个系统的冲激响应为:12()()()h t h t h t =+; 当0t <时,若()0h t =, 则此系统为因果系统; 若|()|h t dt ∞ -∞<∞?, 则此系统为稳定系统。 第二章 连续时间系统的时域分析 1.如何获得系统的数学模型? 数学模型是实际系统分析的一种重要手段,广泛应用于各种类型系统的分析和控制之中。 不同的系统,其数学模型可能具有不同的形式和特点。对于线性时不变系统,其数学模型
信号处理中傅里叶变换简介
傅里叶变换 一、傅里叶变换的表述 在数学上,对任意函数f(x),可按某一点进行展开,常见的有泰勒展开和傅里叶展开。泰勒展开为各阶次幂函数的线性组合形式,本质上自变量未改变,仍为x,而傅里叶展开则为三角函数的线性组合形式,同时将自变量由x变成ω,且由于三角函数处理比较简单,具有良好的性质,故被广泛地应用在信号分析与处理中,可将时域分析变换到频域进行分析。 信号分析与处理中常见的有CFS(连续时间傅里叶级数)、CFT (连续时间傅里叶变换)、DTFT(离散时间傅里叶变换)、DFS(离散傅里叶级数)、DFT(离散傅里叶变换)。通过对连续非周期信号x c(t)在时域和频域进行各种处理变换,可推导出以上几种变换,同时可得出这些变换之间的关系。以下将对上述变换进行简述,同时分析它们之间的关系。 1、CFS(连续时间傅里叶级数) 在数学中,周期函数f(x)可展开为 由此类比,已知连续周期信号x(t),周期为T0,则其傅里叶级数为 其中,
为了简写,有 其中, 为了与复数形式联系,先由欧拉公式e j z=cos z+jsin z得 故有
令 则 对于D n,有 n≤0时同理。 故 CFS图示如下:
Figure 1 理论上,CFS对于周期性信号x(t)在任意处展开都可以做到无误差,只要保证n从-∞取到+∞就可以。在实践中,只要n取值范围足够大,就可以保证在某一点附近对x(t)展开都有很高的精度。 2、CFT(连续时间傅里叶变换) 连续非周期信号x(t),可以将其看成一连续周期信号的周期T0→∞。当然,从时域上也可以反过来看成x(t)的周期延拓。将x(t)进行CFS展开,有 若令 则 有
分数阶傅里叶变换
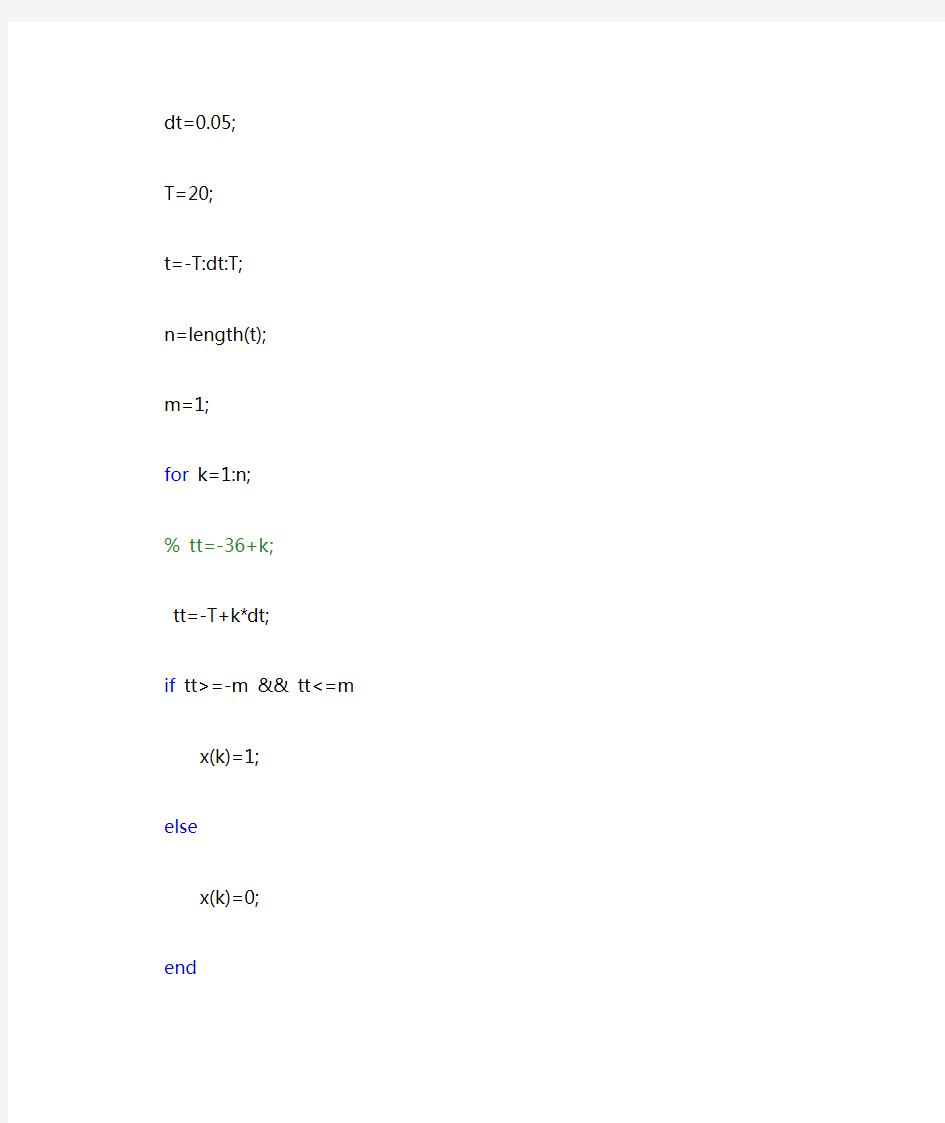
分数阶傅里叶变换的MATLAB 仿真计算以及几点讨论 在Haldun M. Ozaktas 和 Orhan Arikan 等人的论文《Digital computation of the fractional Fourier transform 》中给出了一种快速计算分数阶傅里叶变换的算法,其MATLAB 计算程序可在https://www.360docs.net/doc/e29149289.html,.tr/~haldun/fracF.m 上查到。现在 基于该程序,对一方波进行计算仿真。?????<=其它 ,01,1)(t t x 注:网上流传较为广泛的FRFT 计算程序更为简洁,据称也是Haldun M. Ozaktas 和 Orhan Arikan 等人的论文《Digital computation of the fractional Fourier transform 》使用的算法。但是根据Adhemar Bultheel 和 Hector E. Martnez Sulbaran 的论文《Computation of the Fractional Fourier Transform 》中提到,Ozaktas 等人的分数阶傅里叶变换的计算程序仅有上述网站这一处,而两个程序的计算结果基本相符。本文使用较为简洁的计算程序,Ozaktas 等人的计算程序在附表中给出。 程序如下: clear clc %构造方波?????<=其它 ,01 ,1)(t t x dt=0.05; T=20; t=-T:dt:T; n=length(t); m=1; for k=1:n; % tt=-36+k; tt=-T+k*dt; if tt>=-m && tt<=m x(k)=1; else
傅里叶变换算法详细介绍
从头到尾彻底理解傅里叶变换算法、上 前言 第一部分、 DFT 第一章、傅立叶变换的由来 第二章、实数形式离散傅立叶变换(Real DFT) 第三章、复数 第四章、复数形式离散傅立叶变换 /********************************************************** *****************************************/ 这一片的傅里叶变换算法,讲解透彻,希望对大家会有所帮助。感谢原作者们(July、dznlong)的精心编写。 /********************************************************** ****************************************/ 前言:
“关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解”---dznlong, 那么,到底什么是傅里叶变换算法列?傅里叶变换所涉及到的公式具体有多复杂列? 傅里叶变换(Fourier transform)是一种线性的积分变换。因其基本思想首先由法国学者傅里叶系统地提出,所以以其名字来命名以示纪念。 哦,傅里叶变换原来就是一种变换而已,只是这种变换是从时间转换为频率的变化。这下,你就知道了,傅里叶就是一种变换,一种什么变换列?就是一种从时间到频率的变化或其相互转化。 ok,咱们再来总体了解下傅里叶变换,让各位对其有个总体大概的印象,也顺便看看傅里叶变换所涉及到的公式,究竟有多复杂: 以下就是傅里叶变换的4种变体(摘自,维基百科) 连续傅里叶变换 一般情况下,若“傅里叶变换”一词不加任何限定语,则指的是“连续傅里叶变换”。连续傅里叶变换将平方可积的函数f(t)表示成复指数函数的积分或级数形式。
分数阶Fourier变换在通信中的应用
分数阶Fourier变换在通信中的应用 分数阶Fourier变换是对经典Fourier变换的推广。最早由Namias 以数学形式提出, 并很快在光学领域得到了广泛应用。而其在信号处 理领域的潜力直到20世纪90年代中期才逐渐得到发掘。尽管分数阶Fourier变换的定义式直观上看仅是chirp基分解, 而实质上分数阶Fourier 变换更具有时频旋转的特性,它是一种统一的时频变换,随 着变换阶数从0 连续增长到 1 而展示出信号从时域逐步变化到频域 的所有特征。 一、FRFT概述 FRFT是一种重要的时频分析工具,其根本特点可以理解为对傅 立叶变换特征值的分数化。酉性、旋转相加性和对信号时频形式的统 一性是FRFT的基本性质。由于对特征值分数化方式的不同,以及对FRFT性质约束的宽泛性,使得FRFT具有很多种不同的定义形式。 根据这些定义各自的出发点和基本特征,可以大致将其划分为两类,即:经典类FRFT(CFRFT)和加权类FRFT(WFRFT)。 CFRFT是提出比较早的一种FRFT形式,目前CFRFT定义主要有三种不同形式:一种是V. Namias在1980年从傅立叶变换的特征值与特征函数的角度定义了分数傅立叶变换,数学上表示为“无穷级数和”的形式;另一种是1987年,A. C. Mcbride和F. H. Kerr基于Namias 的标准Chirp类分数傅立叶变换提出的“积分形式”;最后一种是 A. W.Lohmann在1993年从Wigner分布函数相空间的角度定义的分数傅 立叶变换。三种定义形式研究角度不同,但可以证明是相互等价的。
由于经典FRFT具有chirp形式的正交基,因而经典类FRFT又被称为“chirp类FRFT”。经典FRFT在求解微分方程、量子力学、信号 分析和处理等科学研究中有着比较广泛的应用;工程技术方面,如光通信系统、光图像处理等光学相关领域是最早利用经典FRFT的,也是目前应用最成功的。但是受限于经典FRFT的离散算法问题,其在通信领域的应用受到了比较大的限制。 二、FRFT分类及通信中的应用 CFRFT在通信系统中的应用往往与Chirp 信号在通信中的使用密不可分。IEEE 802.15.4a中就有两种不同的采用Chirp信号作为传输信号的调制方式。其一是利用Chirp信号的扩频特性的CSS技术,它将Chirp信号的扫频率作为调制参数;其二是在脉冲超宽带系统中 利用Chirp信号设计脉冲波形。考虑到线性调频信号在分数域体现为 冲激函数,易于检测和识别,因此分数阶傅里叶变换常被应用于线性 调频信号的检测与参数估计;而IEEE802.15.4a技术体系下对于时延/频偏的估计,以及同步和测距的需求,都可利用CFRFT进行深入的研究。 Chirp信号在通信系统中的另一个主要应用方式是构造多载波系统。M. Martone针对在时间和频率双选择性衰落信道下传统正交频分 复用系统的子载波正交性容易受到破坏而导致系统性能下降的问题, 提出了基于分数傅里叶变换调制解调的多载波系统,其结果表明该系统是双弥散信道中近似最优的无线通信系统,可以在不增加额外计算的代价下,提升系统性能。其后,T. Erseghe等在Martone的工作基
常用函数傅里叶变换
信号与系统的基本思想:把复杂的信号用简单的信号表示,再进行研究。 怎么样来分解信号?任何信号可以用Delta 函数的移位加权和表示。只有系统是线性时不变系统,才可以用单位冲激函数处理,主要讨论各个单位冲激函数移位加权的响应的叠加能得到总的响应。 线性系统(齐次性,叠加定理) 时不变系统 对一个系统输入单位冲激函数,得到的响应为h(t).表征线性时不变系统的非常重要的东西,只要知道了系统对单位冲击函数的响应,就知道了它对任何信号的响应,因为任何信号都可以表示为单位冲激函数的移位加权和。 例如:d(t)__h(t) 那么a*d(t-t0)__a*h(t-t0) -()= ()(t-)d f t f τδττ∝∝? 的响应为-y()=()(-)t f h t d τττ∝ ∝ ? 记为y(t)=f(t)*h(t),称为f(t)和h(t)的卷积 总结为两点:对于现行时不变系统,任何信号可以用单位冲激信号的移位加权和表示,任何信号的响应可以用输入函数和单位冲激函数响应的卷积来表示 连续时间信号和系统的频域分析 时域分析的重点是把信号分解为单位冲激函数的移位加权和,只讨论系统对单位冲激函数的响应。而频域的分析是把信号分解为各种不同频率的正弦函数的加权和,只讨论系统对sinwt 的响应。都是把信号分解为大量单一信号的组合。
周期函数可以展开为傅里叶级数,将矩形脉冲展开成傅里叶级数,得到傅里叶级数的系数 n A sin F = T x x τ 其中0=2 nw x τ。 取样函数sin ()=x S a x 。产生一种震荡,0点的值最大,然后渐渐衰减直至0 第一:对于傅里叶级数的系数,n 是离散的,所以频谱也是离散状的每条谱线都出现在基波频率的整数倍上,其包络是取样函数。 第二:谱线的间距是0w .。零点是0=2nw x τ,02w =T π是谱的基波频率。如果τ不变,T 增大,那么0w 减小,当T 非常大的时候,0w 非常小,谱线近似连续,越来越密,幅度越来越小。 傅里叶变换:非周期函数 正变换:--F jw)= ()iwt f t e dt ∝ ∝?( 反变换:-1()=()2jnwt f t F jw e dw π ∝∝ ? 常用函数的傅里叶变换(典型非周期信号的频谱)
分数傅里叶变换
分数傅里叶变换的无透镜光学实现 杨虎李万松 提要:利用球面波照射物体的自由空间菲涅耳衍射,完成任意级次分数傅里叶变换的无透镜光学实现,给出了不同条件下无透镜模式基本参量的选择法则及其分数傅里叶变换的数学表达。计算机模拟实验证明了结论的可靠与可行。 关键词:傅里叶光学变换透镜 Non lens optical realization of fractional Fourier transform Yang Hu (Department of Physics,ShanXi Normal University,Linfen 041004) Li Wansong (Opto-Electronics Department,Sichuan Union University,Chengdu 610064) Abstract:In this paper,we describe the fact that arbitrary orders of fractional Fourier transform can be realized by the Fresnel diffraction in free space.In this case,the object should be illuminated by sphere light wave.We give out the select laws of the basic parameter under different conditions and the mathematic expression of the fractional Fourier transform.Its reliability and feasibility are demonstrated by computer simulation. Key words:Fourier,Optical transform,lens 1 引言 分数傅里叶变换的概念最早由Namias用于求解各种条件下的薛定谔方程〔1〕,Lohmann于1993年将其引入信息光学〔2〕,用单透镜模式和双透镜模式完成了它的光学实现,并把分数傅里叶变换理解为透镜的位相转换与菲涅耳衍射的组合。在Lohmann提供的光学实现装置中,透镜是必需的基本光学单元,且其焦距的选择条件较为严格,因此给应用环境带来不必要的限制。 本文基于分数傅里叶变换的物理本质,利用球面波照射物体的自由空间菲涅耳衍射,完成任意分数级傅里叶变换,提供了不同条件下无透镜模式基本参量的选择定则,弥补了有透镜模式的不足。计算机模拟实验证明了结论的可靠性与可行性。 2 理论分析
用Matlab对信号进行傅里叶变换实例
目录 用Matlab对信号进行傅里叶变换 (2) Matlab的傅里叶变换实例 (5) Matlab方波傅立叶变换画出频谱图 (7)
用Matlab对信号进行傅里叶变换 1.离散序列的傅里叶变换DTFT(Discrete Time Fourier Transform) 代码: 1 N=8; %原离散信号有8点 2 n=[0:1:N-1] %原信号是1行8列的矩阵 3 xn=0.5.^n; %构建原始信号,为指数信号 4 5 w=[-800:1:800]*4*pi/800; %频域共-800----+800 的长度(本应是无穷,高频分量很少,故省去) 6 X=xn*exp(-j*(n'*w)); %求dtft变换,采用原始定义的方法,对复指数分量求和而得 7 subplot(311) 8 stem(n,xn); 9 title('原始信号(指数信号)'); 10 subplot(312); 11 plot(w/pi,abs(X)); 12 title('DTFT变换') 结果: 分析:可见,离散序列的dtft变换是周期的,这也符合Nyquist采样定理的描述,连续时间信号经周期采样之后,所得的离散信号的频谱是原连续信号频谱的周期延拓。 2.离散傅里叶变换DFT(Discrete Fourier Transform)
与1中DTFT不一样的是,DTFT的求和区间是整个频域,这对 结果图:
分析:DFT只是DTFT的现实版本,因为DTFT要求求和区间无穷,而DFT只在有限点内求和。 3.快速傅里叶变换FFT(Fast Fourier Transform) 虽然DFT相比DTFT缩减了很大的复杂度,但是任然有相当大的计算量,不利于信息的实时有效处理,1965年发现的DFT解决了这一问题。 实现代码: 1 N=64; %原离散信号有8点 2 n=[0:1:N-1] %原信号是1行8列的矩阵 3 xn=0.5.^n; %构建原始信号,为指数信号 4 Xk=fft(xn,N); 5 subplot(221); 6 stem(n,xn); 7 title('原信号'); 8 subplot(212); 9 stem(n,abs(Xk)); 10 title('FFT变换') 效果图: 分析:由图可见,fft变换的频率中心不在0点,这是fft算法造成的,把fft改为fftshift可以将频率中心移到0点。
常用傅里叶变换
时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 1 线性 2 时域平移 3 频域平移,变换2 的频域对应 4 如果值较大,则 会收缩到原 点附近,而 会扩 散并变得扁平.当 | a | 趋向无穷 时,成为狄拉克δ 函数。 5 傅里叶变换的二元 性性质。通过交换 时域变量和频域 变量得到. 6 傅里叶变换的微分 性质
7 变换6的频域对应8 表示和 的卷积—这就是卷 积定理 9 变换8的频域对应。[编辑]平方可积函数 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 10 矩形脉冲和归一 化的sinc函数 11 变换10的频域对 应。矩形函数是理 想的低通滤波器, sinc函数是这类 滤波器对反因果 冲击的响应。
12 tri是三角形函数 13 变换12的频域对应 14 高斯函数exp( ? αt2)的傅里叶变换是他本身.只有当Re(α) > 0时,这是可积的。 15 光学领域应用较多 16 17 18 a>0 19 变换本身就是一个公式
20 J0(t)是0阶第一 类贝塞尔函数。 21 上一个变换的推 广形式; T n(t)是第 一类切比雪夫多 项式。 22 U n (t)是第二类切 比雪夫多项式。[编辑]分布 时域信号 角频率表示的 傅里叶变换 弧频率表示的 傅里叶变换 注释 23 δ(ω)代表狄拉克δ函数 分布.这个变换展示了狄 拉克δ函数的重要性:该 函数是常函数的傅立叶 变换 24 变换23的频域对应
25 由变换3和24得到. 26 由变换1和25得到,应用了欧拉公式: cos(at) = (e iat + e?iat) / 2. 27 由变换1和25得到 28 这里, n是一个自然数.δ(n)(ω)是狄拉克δ函数分布的n阶微分。这个变换是根据变换7和24得到的。将此变换与1结合使用,我们可以变换所有多項式。 29 此处sgn(ω)为符号函数;注意此变换与变换7和24是一致的. 30 变换29的推广. 31 变换29的频域对应. 32 此处u(t)是单位阶跃函数;此变换根据变换1和31得到.
