实验报告一主成分分析

《多元统计分析》
实验报告
姓名:张莉萍
学号: 176121113
日期: 2017年11月10日
评分标准
实验报告一主成分分析
实验目的:
1、熟练掌握利用MATLAB进行主成分分析的计算步骤。
2、掌握选择主成分个数的原则以及利用特征值建立权向量的方法。
3、能根据主成分的数学公式,针对实际问题给出主成分的合理解释。
4、掌握典型相关分析的方法。
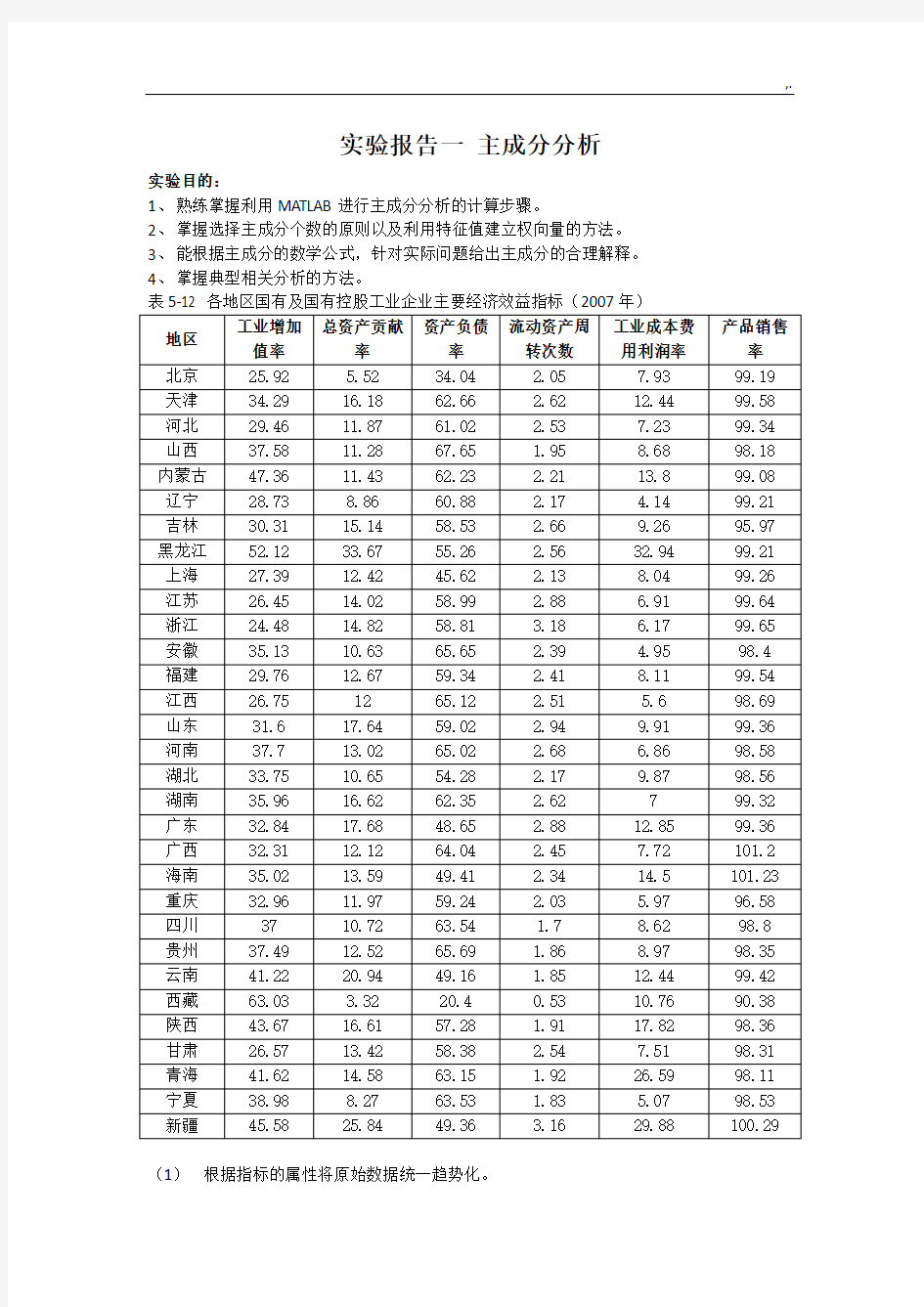
(1)根据指标的属性将原始数据统一趋势化。
(2)利用协方差、相关系数矩阵进行主成分分析,可否只用第一主成分排名。(3)构造新的实对称矩阵,使得可以只用第一主成分排名。
(4)排名的结果是否合理?为什么?
解:
(1)A=[25.92,5.52,34.04,2.05,7.93,99.19;
34.29,16.18,62.66,2.62,12.44,99.58;
…
45.58,25.84,49.36,3.16,29.88,100.29]
令:r=corrcoef(A); % 计算矩阵A的相关系数矩阵
得到的相关系数矩阵为:
r =
1.0000 0.2121 -0.3414 -0.5342 0.5812 -0.4993
0.2121 1.0000 0.1377 0.5214 0.7293 0.3818
-0.3414 0.1377 1.0000 0.3994 -0.1695 0.4629
-0.5342 0.5214 0.3994 1.0000 0.0838 0.6592
0.5812 0.7293 -0.1695 0.0838 1.0000 0.0909
-0.4993 0.3818 0.4629 0.6592 0.0909 1.0000
表明各个变量之间无明显的共性关系,可以进一步进行主成分分析的命令。
对原始数据进行数据统一趋势化,将资产负债率转化成效益型,其变换公式为
B=(b ij)n?p,b ij=
{
(x ij?x ij)
j
min
(x ij?x ij)
j
min
j
max
(效益型)
(x ij?x ij)
j
max
(x ij?x ij)
j
min
j
max
(成本型)
(|x ij?αj|?|x ij?αj|)
j
max
max||x ij?αj||?|x ij?αj|
j
min
(适度型)
令:[m,n]=size(A)
A1=(A(:,1)-min(A(:,1)))./(max(A(:,1))-min(A(:,1)));
A2=(A(:,2)-min(A(:,2)))./(max(A(:,2))-min(A(:,2)));
A3=(max(A(:,3))-A(:,3))./(max(A(:,3))-min(A(:,3)));
A4=(A(:,4)-min(A(:,4)))./(max(A(:,4))-min(A(:,4)));
A5=(A(:,5)-min(A(:,5)))./(max(A(:,5))-min(A(:,5)));
A6=(A(:,6)-min(A(:,6)))./(max(A(:,6))-min(A(:,6)));
B=[A1,A2,A3,A4,A5,A6]
得到矩阵B为:
B =
0.0374 0.0725 0.7113 0.5736 0.1316 0.8120
0.2545 0.4237 0.1056 0.7887 0.2882 0.8479
0.1292 0.2817 0.1403 0.7547 0.1073 0.8258
0.3398 0.2623 0 0.5358 0.1576 0.7189
0.5935 0.2672 0.1147 0.6340 0.3354 0.8018
0.1102 0.1825 0.1433 0.6189 0 0.8138
0.1512 0.3895 0.1930 0.8038 0.1778 0.5152
0.7170 1.0000 0.2622 0.7660 1.0000 0.8138
0.0755 0.2998 0.4662 0.6038 0.1354 0.8184
0.0511 0.3526 0.1833 0.8868 0.0962 0.8535
0 0.3789 0.1871 1.0000 0.0705 0.8544
0.2763 0.2409 0.0423 0.7019 0.0281 0.7392
0.1370 0.3081 0.1759 0.7094 0.1378 0.8442
0.0589 0.2860 0.0535 0.7472 0.0507 0.7659
0.1847 0.4718 0.1826 0.9094 0.2003 0.8276
0.3429 0.3196 0.0557 0.8113 0.0944 0.7558
0.2405 0.2415 0.2830 0.6189 0.1990 0.7539
0.2978 0.4382 0.1122 0.7887 0.0993 0.8240
0.2169 0.4731 0.4021 0.8868 0.3024 0.8276
0.2031 0.2900 0.0764 0.7245 0.1243 0.9972
0.2734 0.3384 0.3860 0.6830 0.3597 1.0000
0.2200 0.2850 0.1780 0.5660 0.0635 0.5714
0.3248 0.2438 0.0870 0.4415 0.1556 0.7760
0.3375 0.3031 0.0415 0.5019 0.1677 0.7346
0.4342 0.5806 0.3913 0.4981 0.2882 0.8332
1.0000 0 1.0000 0 0.2299 0
0.4978 0.4379 0.2195 0.5208 0.4750 0.7355
0.0542 0.3328 0.1962 0.7585 0.1170 0.7309
0.4446 0.3710 0.0952 0.5245 0.7795 0.7124
0.3761 0.1631 0.0872 0.4906 0.0323 0.7512
0.5473 0.7420 0.3871 0.9925 0.8938 0.9134(2)
令R=corrcoef(B) % 计算矩阵B的相关系数矩阵
得到的相关系数矩阵为:
R =
1.0000 0.2121 0.3414 -0.5342 0.5812 -0.4993
0.2121 1.0000 -0.1377 0.5214 0.7293 0.3818
0.3414 -0.1377 1.0000 -0.3994 0.1695 -0.4629
-0.5342 0.5214 -0.3994 1.0000 0.0838 0.6592
0.5812 0.7293 0.1695 0.0838 1.0000 0.0909
-0.4993 0.3818 -0.4629 0.6592 0.0909 1.0000
表明各个变量之间无明显的共性关系,可以进一步进行主成分分析的命令。
a.利用相关系数矩阵进行主成分分析
令:[v1,d1]=eig(corrcoef(B)) % 样本相关系数矩阵的特征值
得到结果如下:
v1 =
0.3973 0.4564 -0.3541 0.0499 -0.6454 -0.2990
-0.2931 0.5722 0.0316 -0.2765 -0.1388 0.7000
0.4030 0.1312 0.8834 0.1228 -0.1528 0.0399
-0.5513 0.0765 0.2943 -0.4985 -0.2307 -0.5494
-0.0061 0.6631 0.0031 0.1927 0.6371 -0.3423
-0.5384 0.0377 0.0813 0.7876 -0.2860 -0.0055
d1 =
2.5989 0 0 0 0 0
0 2.0777 0 0 0 0
0 0 0.6831 0 0 0
0 0 0 0.3671 0 0
0 0 0 0 0.1405 0
0 0 0 0 0 0.1327
因为,最大的特征值对应的不是正向量,所以不能用第一主成分进行排名。
b.利用协方差矩阵进行主成分分析
令:[v2,d2]=eig(cov(B)) % 样本协方差矩阵的特征值
得到结果如下:
v2 =
0.3165 -0.5994 -0.1127 -0.3839 -0.0469 -0.6150
-0.7289 -0.2252 -0.3177 0.0564 0.5328 -0.1733
-0.0180 -0.1808 0.0602 0.8683 -0.2758 -0.3652
0.5653 -0.1391 -0.5057 0.2953 0.4787 0.2983
0.2160 0.5656 0.2651 0.0348 0.5102 -0.5493
0.0453 -0.4670 0.7462 0.0837 0.3852 0.2601
d2 =
0.0050 0 0 0 0 0
0 0.0067 0 0 0 0
0 0 0.0122 0 0 0
0 0 0 0.0301 0 0
0 0 0 0 0.0931 0
0 0 0 0 0 0.1068
因为,最大的特征值对应的不是正向量,所以不能用第一主成分进行排名。(3)
利用R矩阵进行主成分分析
[m,n]=size(B); % 计算原始数据维数
fori=1:n
forj=1:n
R(i,j)=2*dot(B(:,i),B(:,j))./[sum(B(:,i).^2)+sum(B(:,j).^2)] % 计算R矩阵
[v3,d3]=eig(R); % R矩阵的特征值和特征向量q=sum(d3)/sum(sum(d3)) % 计算贡献率
得到结果如下:
v3 =
0.0573 0.1700 0.8123 -0.0311 -0.3650 0.4169
-0.2457 0.6976 -0.3708 -0.3348 0.0048 0.4510
-0.0216 -0.0427 -0.3306 0.7663 -0.4179 0.3558
0.7370 0.0253 -0.0286 0.1050 0.5246 0.4112
0.0936 -0.6149 -0.2584 -0.5160 -0.3343 0.4103
-0.6196 -0.3223 0.1606 0.1501 0.5524 0.3985
d3 =
0.0199 0 0 0 0 0
0 0.0947 0 0 0 0
0 0 0.1897 0 0 0
0 0 0 0.4629 0 0
0 0 0 0 0.9318 0
0 0 0 0 0 4.3011
q =
0.0033 0.0158 0.0316 0.0771 0.1553 0.7168
输出的结果显示,最大特征值(4.3011)对应的是正向量,且其贡献率为71.68%,所以能用第一主成分得分进行排名。
(4)
令F=[B-ones(m,1)*mean(B)]*d3(:,6); % 计算主成分得分
[F2,I1]=sort(F,’descend’); % I1给出各名次的序号
[F2,I2]=sort(I1); % I2给出各地区的排名
Plot(1:m,F,’*’); % 主成分得分图
排名的结果是合理的,因为第一主成分分析的贡献率为71.68%,可以用第一主成分代替原来的六个变量,对样本总体进行排名。
实验报告二聚类方法与聚类有效性
实验目的
1、熟练掌握应用MATLAB软件计算谱系聚类与K均值聚类的命令。
2、熟练掌握模糊C均值类与模糊减法聚类的MATLAB实现。
3、掌握最优聚类数的理论及其实现。
实验数据与内容
2008年我国34个地区中的29个地区的城镇居民人均收入见表6-6。解决以下问题:
(1)计算各样品间的欧氏距离、马氏距离和加权平方距离。
(2)运用谱系聚类法进行聚类,包括确定最优聚类数,选择合适的类间距离,同时作出谱系图。
(3)运用K均值聚类法进行聚类。
(4)运用模糊C均值聚类和模糊减法聚类法进行聚类。
(5)综合分析以上不同的聚类法所得的聚类结果,能得到什么样的结论?
解:
(1)
x=[15538.83,3161.87,1324.94,4955.14;
9302.38,959.43,293.92,3603.72;
…
9422.22,938.15,141.75,1976.49;
15538.83,3161.87,1324.94,4955.14]
a.计算欧氏距离
令:d1=pdist(x,'euclidean');% 计算各行之间的欧氏距离
D1=squareform(d1); % 将行向量d1转变成一个方阵
得到结果如下:
D1 =1.0e+03 *
Columns 1 through 8
0 6.8289 3.2383 7.1139 3.8914 7.0385 6.6887 6.8677
6.8289 0 3.6531 0.6653 3.6855 0.3609 0.3543 0.6582
3.2383 3.6531 0 3.8896 1.4431 3.8646 3.4843 3.7137
7.1139 0.6653 3.8896 0 3.8374 0.5765 0.5122 0.7867
3.8914 3.6855 1.4431 3.8374 0 3.9312 3.4790 3.9268
7.0385 0.3609 3.8646 0.5765 3.9312 0 0.4879 0.4492
6.6887 0.3543 3.4843 0.5122 3.4790 0.4879 0 0.6748
6.8677 0.6582 3.7137 0.7867 3.9268 0.4492 0.6748 0
1.8855 6.0788
2.5897 6.2476 2.5972 6.2953 5.8756 6.1899
5.8398 1.1261 2.6169 1.2885 2.6357 1.3377 0.8920 1.3174
7.1629 0.8571 3.9386 0.2824 3.9469 0.7151 0.7002 0.7781
5.5432 1.7003 2.4111 1.9004 2.0388 1.9708 1.5206 2.0766
7.0517 0.3956 3.8445 0.2871 3.8328 0.3323 0.3737 0.6430
8.3094 1.5183 5.1435 1.4386 5.1699 1.2948 1.7108 1.5136
7.3825 0.9266 4.2154 0.9349 4.3948 0.8254 1.0803 0.8295
6.0406 4.1092 3.6411 3.9171 2.4419 4.2993 3.8384 4.4258
6.6165 0.7045 3.4451 0.9702 3.2313 0.9910 0.6610 1.2965
8.0661 1.4281 4.8374 0.9818 4.6506 1.2772 1.4305 1.5688
7.6045 0.7866 4.4279 0.8051 4.3940 0.6154 0.9739 0.9903
7.1620 1.0854 4.0089 0.8704 4.2086 0.7836 1.0109 0.5317
7.2547 1.6389 4.0465 1.0782 3.6981 1.6299 1.3803 1.8010
0 6.8289 3.2383 7.1139 3.8914 7.0385 6.6887 6.8677 Columns 9 through 16
1.8855 5.8398 7.1629 5.5432 7.0517 8.3094 7.3825 6.0406
6.0788 1.1261 0.8571 1.7003 0.3956 1.5183 0.9266 4.1092
2.5897 2.6169
3.9386 2.4111 3.8445 5.1435
4.2154 3.6411 6.2476 1.2885 0.2824 1.9004 0.2871 1.4386 0.9349 3.9171 2.5972 2.6357 3.9469 2.0388 3.8328
5.1699 4.3948 2.4419
6.2953 1.3377 0.7151 1.9708 0.3323 1.2948 0.8254 4.2993
5.8756 0.8920 0.7002 1.5206 0.3737 1.7108 1.0803 3.8384
6.1899 1.3174 0.7781 2.0766 0.6430 1.5136 0.8295 4.4258
0 4.9953 6.3113 4.5580 6.2396 7.5801 6.7099 4.3822 4.9953 0 1.3891 0.8601 1.2489 2.5954 1.7883 3.3119 6.3113 1.3891 0 2.0698 0.4955 1.4660 0.8756 4.0086 4.5580 0.8601 2.0698 0 1.8586 3.1561 2.4874 2.7784
6.2396 1.2489 0.4955 1.8586 0 1.3611 0.8297 4.0519
7.5801 2.5954 1.4660 3.1561 1.3611 0 1.1485 5.2219 6.7099 1.7883 0.8756 2.4874 0.8297 1.1485 0 4.6805
4.3822 3.3119 4.0086 2.7784 4.0519
5.2219 4.6805 0
5.7324 0.9778 1.2242 1.1929 0.8523 2.0016 1.5268 3.5336 7.1291 2.2279 1.0281 2.6920 1.0998 1.0455 1.3239 4.3308
6.8261 1.8588 0.9523 2.3752 0.6569 0.7874 0.8963 4.5434 6.4400 1.6419 0.7362 2.4138 0.8824 1.4808 1.0046 4.5327 6.1396 1.6837 1.1038 2.0116 1.3337 2.2189 1.8901 3.1538 1.8855 5.8398
7.1629 5.5432 7.0517
8.3094 7.3825 6.0406 Columns 17 through 22
6.6165 8.0661
7.6045 7.1620 7.2547 0
0.7045 1.4281 0.7866 1.0854 1.6389 6.8289
3.4451
4.8374 4.4279 4.0089 4.0465 3.2383
0.9702 0.9818 0.8051 0.8704 1.0782 7.1139
3.2313
4.6506 4.3940 4.2086 3.6981 3.8914
0.9910 1.2772 0.6154 0.7836 1.6299 7.0385
0.6610 1.4305 0.9739 1.0109 1.3803 6.6887
1.2965 1.5688 0.9903 0.5317 1.8010 6.8677
5.7324 7.1291
6.8261 6.4400 6.1396 1.8855
0.9778 2.2279 1.8588 1.6419 1.6837 5.8398
1.2242 1.0281 0.9523 0.7362 1.1038 7.1629
1.1929
2.6920 2.3752 2.4138 2.0116 5.5432
0.8523 1.0998 0.6569 0.8824 1.3337 7.0517
2.0016 1.0455 0.7874 1.4808 2.2189 8.3094
1.5268 1.3239 0.8963 1.0046 1.8901 7.3825
3.5336
4.3308 4.5434 4.5327 3.1538 6.0406
0 1.6271 1.2276 1.6530 1.4831 6.6165
1.6271 0 0.8904 1.4649 1.2796 8.0661
1.2276 0.8904 0 1.1328 1.7086 7.6045
1.6530 1.4649 1.1328 0 1.7189 7.1620
1.4831 1.2796 1.7086 1.7189 0 7.2547
6.6165 8.0661
7.6045 7.1620 7.2547 0
矩阵D1中第i行j列的元素表示x中的第I个个体与第j个个体之间的欧氏距离。如矩阵D1中的第1行7列为6688.7,表示上海与北京的欧氏距离为6688.7,其余类推。
b.计算马氏距离
令d2=dpist(x,’mahalanobis’); % 计算各行之间的马氏距离
D2= D2=squareform(d2); % 将行向量d2转变成一个方阵
得到结果如下:
D2 =
Columns 1 through 8
0 2.9889 1.6549 3.0825 3.0150 3.1476 2.9034 3.0102
2.9889 0 2.2351 1.5806 2.1398 1.2879 0.9245 1.9664
1.6549
2.2351 0 1.8671 2.7424 2.5981 2.0782 2.3142
3.0825 1.5806 1.8671 0 2.5176 1.4008 0.9003 1.1807
3.0150 2.1398 2.7424 2.5176 0 2.3138 2.0222 2.9859
3.1476 1.2879 2.5981 1.4008 2.3138 0 0.6977 1.0949
2.9034 0.9245 2.0782 0.9003 2.0222 0.6977 0 1.2215
3.0102 1.9664 2.3142 1.1807 2.9859 1.0949 1.2215 0
2.5823
3.3811 2.7334 2.8738 2.1533 2.9077 2.7723 2.8911
2.5396 1.1557 1.3928 0.7547 2.0692 1.4401 0.7806 1.5214
3.2827 2.3879 1.8606 0.9581 3.2900 2.2649 1.8257 1.6247
3.2866 1.3819 2.8633 2.3843 1.1217 1.9344 1.6811 2.8411
2.9631 0.8988 1.9313 0.6904 2.2409 1.0274 0.4076 1.3048
3.4509 0.7805 2.6444 1.4813 2.6411 0.9746 0.9137 1.6196
4.1978 3.4728 2.8772 3.3915 4.8421 4.3299 3.7792 4.0955
4.9670 4.2320 3.9018 3.6136 3.2040 4.4813 3.9363 4.6242
3.5639 1.1696 3.0281 2.4936 1.8050 2.0451 1.7959 2.9686
3.5542 1.5347 2.3313 0.6418 2.4099 1.4915 0.9943 1.6287
3.4690 0.9355 2.9038 1.8003 2.1719 0.8155 0.9754 1.8531
4.1011 3.6530 3.5987 2.5386 4.1436 2.5494 2.8017 1.7380
3.9493 3.0381 2.6728 1.5736 3.1298 2.7078 2.3137 2.3051
0 2.9889 1.6549 3.0825 3.0150 3.1476 2.9034 3.0102 Columns 9 through 16
2.5823 2.5396
3.2827 3.2866 2.9631 3.4509
4.1978 4.9670
3.3811 1.1557 2.3879 1.3819 0.8988 0.7805 3.4728
4.2320
2.7334 1.3928 1.8606 2.8633 1.9313 2.6444 2.8772
3.9018
2.8738 0.7547 0.9581 2.3843 0.6904 1.4813
3.3915 3.6136
2.1533 2.0692
3.2900 1.1217 2.2409 2.6411
4.8421 3.2040
2.9077 1.4401 2.2649 1.9344 1.0274 0.9746 4.3299 4.4813
2.7723 0.7806 1.8257 1.6811 0.4076 0.9137
3.7792 3.9363
2.8911 1.5214 1.6247 2.8411 1.3048 1.6196 4.0955 4.6242
0 2.6860 3.2503 3.0554 3.0025 3.6517 5.5002 3.7280
2.6860 0 1.4352 1.9104 0.5955 1.4366
3.2038 3.5701
3.2503 1.4352 0 3.2665 1.5648 2.2806 3.0519 3.7338
3.0554 1.9104 3.2665 0 1.8598 1.9155
4.4495 3.7804
3.0025 0.5955 1.5648 1.8598 0 0.8965 3.3993 3.8620
3.6517 1.4366 2.2806 1.9155 0.8965 0 3.7011
4.5613
5.5002 3.2038 3.0519 4.4495 3.3993 3.7011 0 5.0014
3.7280 3.5701 3.7338 3.7804 3.8620
4.5613
5.0014 0
3.6718 2.0370 3.3527 0.7006 1.8798 1.6943
4.1677 4.1396
3.1370 1.0498 1.3973 2.1681 0.8050 1.4059 3.5438 3.3701
3.3517 1.6640 2.7238 1.4345 1.2125 0.7578
4.3140 4.4826
3.2658 3.0598 2.5637
4.2788 2.9179 3.2321
5.4376 5.2828
2.9302 2.0768 1.3862
3.4112 2.2027 2.9588
4.0895 2.8249
2.5823 2.5396
3.2827 3.2866 2.9631 3.4509
4.1978 4.9670 Columns 17 through 22
3.5639 3.5542 3.4690
4.1011 3.9493 0
1.1696 1.5347 0.9355 3.6530 3.0381
2.9889
3.0281 2.3313 2.9038 3.5987 2.6728 1.6549
2.4936 0.6418 1.8003 2.5386 1.5736
3.0825
1.8050
2.4099 2.1719 4.1436
3.1298 3.0150
2.0451 1.4915 0.8155 2.5494 2.7078
3.1476
1.7959 0.9943 0.9754
2.8017 2.3137 2.9034
2.9686 1.6287 1.8531 1.7380 2.3051
3.0102
3.6718 3.1370 3.3517 3.2658 2.9302 2.5823
2.0370 1.0498 1.6640
3.0598 2.0768 2.5396
3.3527 1.3973 2.7238 2.5637 1.3862 3.2827
0.7006 2.1681 1.4345 4.2788 3.4112 3.2866
1.8798 0.8050 1.2125
2.9179 2.2027 2.9631
1.6943 1.4059 0.7578 3.2321
2.9588
3.4509
4.1677 3.5438 4.3140
5.4376 4.0895 4.1978
4.1396 3.3701 4.4826
5.2828 2.8249 4.9670
0 2.2338 1.3634 4.5282 3.6772 3.5639
2.2338 0 1.6498 2.8944 1.6303
3.5542
1.3634 1.6498 0 3.3313 3.1319 3.4690
4.5282 2.8944 3.3313 0 2.6618 4.1011
3.6772 1.6303 3.1319 2.6618 0 3.9493
3.5639 3.5542 3.4690
4.1011 3.9493 0
矩阵D2中的第i行j列的元素表示x中的第I个个体与第j个个体之间的马氏距离。如矩阵D1中的第1行7列为2.9034,表示上海与北京的马氏距离为2.9034,其余类推。
c.计算加权平方距离
令d3=pdist(x, ‘seuclidean’);% 计算各行之间的方差加权距离
D3=squareform(d3); % 将行向量d3转变成一个方阵
得到结果如下:
D3 =
Columns 1 through 8
0 4.9684 2.3711 5.2381 4.3994 5.1121 5.0071 4.5744
4.9684 0 2.7457 0.7744 1.6677 0.4635 0.4030 0.8041
2.3711 2.7457 0 2.9177 2.2658 2.9177 2.7438 2.3904 5.2381 0.7744 2.9177 0 1.6036 0.7351 0.4562 0.9782
4.3994 1.6677 2.2658 1.6036 0 1.7799 1.4954 1.7975
5.1121 0.4635 2.9177 0.7351 1.7799 0 0.3862 0.6845 5.0071 0.4030 2.7438 0.4562 1.4954 0.3862 0 0.7258 4.5744 0.8041 2.3904 0.9782 1.7975 0.6845 0.7258 0 2.6878 3.2570 1.3978 3.2645 2.0791 3.3310 3.1282 2.9362
4.4267 0.8098 2.1132 0.8332 1.1589 0.9749 0.6757 0.7844
5.0090 1.0151 2.6661 0.4521 1.6519 1.0275 0.7459 0.9588 5.0727 0.8565 2.8538 0.9436 1.0673 0.9936 0.7554 1.3788 5.1416 0.4348 2.8567 0.3463 1.6229 0.4665 0.2044 0.8218 5.7408 0.8284 3.5293 1.0043 2.3289 0.7298 0.9079 1.2900 4.4109 1.5144 2.1988 1.6697 2.2867 1.8278 1.6420 1.5132
6.9990 3.6140 4.8384 3.0465 2.9212 3.6383 3.3494 3.9281
5.4993 0.7467 3.2747 0.9474 1.6662 0.8868 0.7883 1.4664
6.1879 1.4524 3.8617 0.9698 2.2233 1.3636 1.2579 1.8558 5.6785 0.7673 3.4740 0.9396 2.0863 0.6237 0.7857 1.2900 4.8578 1.2738 2.7071 1.0656 1.9789 0.9597 1.0152 0.6525 6.0901 1.9971 3.7621 1.2813 2.0555 1.9153 1.6774 2.1880
0 4.9684 2.3711 5.2381 4.3994 5.1121 5.0071 4.5744 Columns 9 through 16
2.6878 4.4267 5.0090 5.0727 5.1416 5.7408 4.4109 6.9990
3.2570 0.8098 1.0151 0.8565 0.4348 0.8284 1.5144 3.6140 1.3978 2.1132 2.6661 2.8538 2.8567 3.5293 2.1988
4.8384 3.2645 0.8332 0.4521 0.9436 0.3463 1.0043 1.6697 3.0465
2.0791 1.1589 1.6519 1.0673 1.6229 2.3289 2.2867 2.9212
3.3310 0.9749 1.0275 0.9936 0.4665 0.7298 1.8278 3.6383 3.1282 0.6757 0.7459 0.7554 0.2044 0.9079 1.6420 3.3494 2.9362 0.7844 0.9588 1.3788 0.8218 1.2900 1.5132 3.9281
0 2.5489 3.0839 3.0217 3.2766 4.0187 3.1843 4.4665
2.5489 0 0.7568 0.9572 0.7714 1.5368 1.3198
3.3933
3.0839 0.7568 0 1.2508 0.6719 1.3474 1.4209 3.1313 3.0217 0.9572 1.2508 0 0.8397 1.3499 2.0297 2.9808
3.2766 0.7714 0.6719 0.8397 0 0.8034 1.5885 3.3009
4.0187 1.5368 1.3474 1.3499 0.8034 0 2.0297 3.6878
3.1843 1.3198 1.4209 2.0297 1.5885 2.0297 0
4.1176
4.4665 3.3933 3.1313 2.9808 3.3009 3.6878 4.1176 0
3.5819 1.2726 1.3494 0.6019 0.7664 0.8910 2.0677 3.1562
4.1007 1.7645 1.3027 1.3954 1.1206 1.1036 2.4214 2.6767 3.8519 1.4478 1.3505 1.0824 0.7350 0.3631 2.1611 3.5048 3.0544 1.1621 1.0227 1.6466 1.0855 1.4947 1.9835 3.8002 3.7781 1.8935 1.3851 1.6940 1.5916 1.9537 2.6510 1.9492 2.6878 4.4267
5.0090 5.0727 5.1416 5.7408 4.4109
6.9990 Columns 17 through 22
5.4993
6.1879 5.6785 4.8578 6.0901 0
0.7467 1.4524 0.7673 1.2738 1.9971 4.9684
3.2747 3.8617 3.4740 2.7071 3.7621 2.3711
0.9474 0.9698 0.9396 1.0656 1.2813 5.2381
1.6662
2.2233 2.0863 1.9789 2.0555 4.3994
0.8868 1.3636 0.6237 0.9597 1.9153 5.1121
0.7883 1.2579 0.7857 1.0152 1.6774 5.0071
1.4664 1.8558 1.2900 0.6525
2.1880 4.5744
3.5819
4.1007 3.8519 3.0544 3.7781 2.6878
1.2726 1.7645 1.4478 1.1621 1.8935 4.4267
1.3494 1.3027 1.3505 1.0227 1.3851 5.0090
0.6019 1.3954 1.0824 1.6466 1.6940 5.0727
0.7664 1.1206 0.7350 1.0855 1.5916 5.1416
0.8910 1.1036 0.3631 1.4947 1.9537 5.7408
2.0677 2.4214 2.1611 1.9835 2.6510 4.4109
3.1562 2.6767 3.5048 3.8002 1.9492 6.9990
0 1.1062 0.6408 1.7513 1.7427 5.4993
1.1062 0 1.0375 1.8075 0.9824 6.1879
0.6408 1.0375 0 1.4736 1.8437 5.6785
1.7513 1.8075 1.4736 0 1.9915 4.8578
1.7427 0.9824 1.8437 1.9915 0 6.0901
5.4993
6.1879 5.6785 4.8578 6.0901 0
矩阵D3中的第i行j列的元素表示x中的第I个个体与第j个个体之间的方差加权距离。如矩阵D1中的第1行7列为5.0071,表示上海与北京的马氏距离为5.0071,其余类推。
(2)
由(1)可知,样本间的欧氏距离为D1
令z1=linkage(D1); % 选择类间距离为最短距离时
输出结果为:
z1 =1.0e+04 *
0.0001 0.0022 0 % 在0的水平,G1,G22合成一类为G23
0.0004 0.0011 0.0690 % 在0.0690的水平,G4,G11合成一类为G24
0.0013 0.0024 0.0739 % 在0.0739的水平,G24,G13合成一类为G25
0.0006 0.0025 0.0809 % 在0.0809的水平,G25,G6合成一类为G26
0.0002 0.0007 0.0893 % 在0.0893的水平,G2,G7合成一类为G27
0.0026 0.0027 0.1017 % 在0.1017的水平,G26,G27合成一类为G28
0.0008 0.0028 0.1118 % 在0.1118的水平,G28,G8合成一类为G29
0.0020 0.0029 0.1367 % 在0.1367的水平,G29,G20合成一类为G30
0.0015 0.0019 0.1553 % 在0.1553的水平,G15,G19合成一类为G31
0.0030 0.0031 0.1641 % 在0.1641的水平,G31,G30合成一类为G32
0.0017 0.0032 0.1860 % 在0.1860的水平,G32,G17合成一类为G33
0.0018 0.0033 0.2224 % 在0.2224的水平,G33,G18合成一类为G34
0.0014 0.0034 0.2375 % 在0.2375的水平,G34,G14合成一类为G35
0.0010 0.0035 0.2592 % 在0.2592的水平,G35,G10合成一类为G36
0.0003 0.0005 0.2631 % 在0.2631的水平,G3,G5合成一类为G37
0.0012 0.0036 0.2734 % 在0.2734的水平,G36,G12合成一类为G38
0.0021 0.0038 0.3181 % 在0.3181的水平,G38,G21合成一类为G39
0.0009 0.0023 0.5156 % 在0.5156的水平,G23,G9合成一类为G40
0.0016 0.0037 0.5625 % 在0.5625的水平,G37,G16合成一类为G41
0.0039 0.0041 0.8594 % 在0.8594的水平,G41,G39合成一类为G42
0.0040 0.0042 1.0415 % 在1.0415的水平,G42,G40合成一类
再令H=dendrogram(z1); % 作谱系聚类图
输出图形如下图所示:
令z2=linkage(D1,’complete’); % 选择类间距离为最长距离时输出结果为:
z2 =1.0e+04 *
0.0001 0.0022 0 % 在0的水平,G1,G22合成一类为G23
0.0004 0.0011 0.0690 % 在0.0690的水平,G4,G11合成一类为G24
0.0006 0.0013 0.0809 % 在0.0809的水平,G6,G13合成一类为G25
0.0002 0.0007 0.0893 % 在0.0893的水平,G2,G7合成一类为G26
0.0008 0.0020 0.1367 % 在0.1367的水平,G8,G20合成一类为G27
0.0024 0.0025 0.1487 % 在0.1487的水平,G24,G25合成一类为G28
0.0015 0.0019 0.1553 % 在0.1553的水平,G15,G19合成一类为G29
0.0026 0.0028 0.1934 % 在0.1934的水平,G26,G28合成一类为G30
0.0014 0.0018 0.2375 % 在0.2375的水平,G14,G18合成一类为G31
0.0027 0.0029 0.2471 % 在0.2471的水平,G27,G29合成一类为G32
0.0010 0.0017 0.2592 % 在0.2592的水平,G10,G17合成一类为G33
0.0003 0.0005 0.2631 % 在0.2631的水平,G3,G5合成一类为G34
0.0030 0.0032 0.3244 % 在0.3244的水平,G30,G32合成一类为G35
0.0021 0.0035 0.4113 % 在0.4113的水平,G21,G35合成一类为G36
0.0009 0.0023 0.5156 % 在0.5156的水平,G9,G23合成一类为G38
0.0031 0.0036 0.5929 % 在0.5929的水平,G31,G36合成一类为G39
0.0016 0.0034 0.7050 % 在0.7050的水平,G16,G34合成一类为G40
0.0037 0.0039 0.8993 % 在0.8993的水平,G37,G39合成一类为G41
0.0040 0.0041 1.5247 % 在1.5247的水平,G40,G41合成一类为G42
0.0038 0.0042 2.7548 % 在2.7548的水平,G38,G42合成一类
再令H=dendrogram(z2); % 作谱系聚类图
输出图形如下图所示:
令z3=linkage(D1,’average’); % 选择类间距离为类平均距离时输出结果为:
z3 =1.0e+04 *
0.0001 0.0022 0 % 在0的水平,G1,G22合成一类为G23
0.0004 0.0011 0.0690 % 在0.0690的水平,G4,G11合成一类为G24
0.0006 0.0013 0.0809 % 在0.0809的水平,G6,G13合成一类为G25
0.0002 0.0007 0.0893 % 在0.0893的水平,G2,G7合成一类为G26
0.0024 0.0025 0.1180 % 在0.1180的水平,G24,G25合成一类为G27
0.0008 0.0020 0.1367 % 在0.1367的水平,G8,G20合成一类为G28
0.0026 0.0027 0.1485 % 在0.1485的水平,G26,G27合成一类为G29
0.0015 0.0019 0.1553 % 在0.1553的水平,G15,G19合成一类为G30
0.0028 0.0029 0.1907 % 在0.1907的水平,G28,G29合成一类为G31
0.0014 0.0018 0.2375 % 在0.2375的水平,G14,G18合成一类为G32
0.0030 0.0031 0.2377 % 在0.2377的水平,G30,G31合成一类为G33
0.0010 0.0017 0.2592 % 在0.2592的水平,G10,G17合成一类为G34
0.0003 0.0005 0.2631 % 在0.2631的水平,G3,G5合成一类为G35
0.0012 0.0034 0.3662 % 在0.3662的水平,G12,G34合成一类为G36
0.0032 0.0037 0.4104 % 在0. 4104的水平,G32,G37合成一类为G38
0.0036 0.0038 0.5133 % 在0.5133的水平,G36,G38合成一类为G39
0.0009 0.0023 0.5156 % 在0.5156的水平,G9,G23合成一类为G40
0.0016 0.0035 0.6337 % 在0.6337的水平,G16,G35合成一类为G41
0.0039 0.0041 1.3582 % 在1.3582的水平,G39,G41合成一类为G42
0.0040 0.0042 2.3382 % 在2.3382的水平,G40,G42合成一类
再令H=dendrogram(z3); % 作谱系聚类图
输出图形如下图所示:
(3)
主成分分析法总结
主成分分析法总结 在实际问题研究中,多变量问题是经常会遇到的。变量太多,无疑会增加分析问题的难度与复杂性,而且在许多实际问题中,多个变量之间是具有一定的相关关系的。 因此,人们会很自然地想到,能否在相关分析的基础上,用较少的新变量代替原来较多的旧变量,而且使这些较少的新变量尽可能多地保留原来变量所反映的信息? 一、概述 在处理信息时,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠,例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。 为了解决这些问题,最简单和最直接的解决方案是削减变量的个数,但这必然又会导致信息丢失和信息不完整等问题的产生。为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。主成分分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。 主成分分析以最少的信息丢失为前提,将众多的原有变量综合成较少几个综合指标,通常综合指标(主成分)有以下几个特点: ↓主成分个数远远少于原有变量的个数 原有变量综合成少数几个因子之后,因子将可以替代原有变量参与数据建模,这将大大减少分析过程中的计算工作量。 ↓主成分能够反映原有变量的绝大部分信息 因子并不是原有变量的简单取舍,而是原有变量重组后的结果,因此不会造成原有变量信息的大量丢失,并能够代表原有变量的绝大部分信息。 ↓主成分之间应该互不相关 通过主成分分析得出的新的综合指标(主成分)之间互不相关,因子参与数据建模能够有效地解决变量信息重叠、多重共线性等给分析应用带来的诸多问题。 ↓主成分具有命名解释性 总之,主成分分析法是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子,如何使因子具有一定的命名解释性的多元统计分析方法。 主成分分析的具体步骤如下: (1)计算协方差矩阵 计算样品数据的协方差矩阵:Σ=(s ij )p ?p ,其中 1 1()() 1n ij ki i kj j k s x x x x n ==---∑i ,j=1,2,…,p (2)求出Σ的特征值 i λ及相应的正交化单位特征向量i a Σ的前m 个较大的特征值λ1≥λ2≥…λm>0,就是前m 个主成分对应的方差,i λ对应的单 位特征向量 i a 就是主成分Fi 的关于原变量的系数,则原变量的第i 个主成分Fi 为:
主成分分析实验报告
项目名称实验4―主成分分析 所属课程名称多元统计分析(英)项目类型综合性实验 实验(实训)日期2012年 4 月15 日
实验报告4 主成分分析(综合性实验) (Principal component analysis) 实验原理:主成分分析利用指标之间的相关性,将多个指标转化为少数几个综合指标,从而达到降维和数据结构简化的目的。这些综合指标反映了原始指标的绝大部分信息,通常表示为原始指标的某种线性组合,且综合指标间不相关。利用矩阵代数的知识可求解主成分。
实验题目:下表中给出了不同国家及地区的男子径赛记录:(t8a6) Country 100m (s) 200m (s) 400m (s) 800m (min) 1500m (min) 5000m (min) 10,000m (min) Marathon (mins) Argentina 10.39 20.81 46.84 1.81 3.7 14.04 29.36 137.72 Australia 10.31 20.06 44.84 1.74 3.57 13.28 27.66 128.3 Austria 10.44 20.81 46.82 1.79 3.6 13.26 27.72 135.9 Belgium 10.34 20.68 45.04 1.73 3.6 13.22 27.45 129.95 Bermuda 10.28 20.58 45.91 1.8 3.75 14.68 30.55 146.62 Brazil 10.22 20.43 45.21 1.73 3.66 13.62 28.62 133.13 Burma 10.64 21.52 48.3 1.8 3.85 14.45 30.28 139.95 Canada 10.17 20.22 45.68 1.76 3.63 13.55 28.09 130.15 Chile 10.34 20.8 46.2 1.79 3.71 13.61 29.3 134.03 China 10.51 21.04 47.3 1.81 3.73 13.9 29.13 133.53 Columbia 10.43 21.05 46.1 1.82 3.74 13.49 27.88 131.35 Cook Islands 12.18 23.2 52.94 2.02 4.24 16.7 35.38 164.7 Costa Rica 10.94 21.9 48.66 1.87 3.84 14.03 28.81 136.58 Czechoslovakia 10.35 20.65 45.64 1.76 3.58 13.42 28.19 134.32 Denmark 10.56 20.52 45.89 1.78 3.61 13.5 28.11 130.78 Dominican Republic 10.14 20.65 46.8 1.82 3.82 14.91 31.45 154.12 Finland 10.43 20.69 45.49 1.74 3.61 13.27 27.52 130.87 France 10.11 20.38 45.28 1.73 3.57 13.34 27.97 132.3 German (D.R.) 10.12 20.33 44.87 1.73 3.56 13.17 27.42 129.92 German (F.R.) 10.16 20.37 44.5 1.73 3.53 13.21 27.61 132.23 Great Brit.& N. Ireland 10.11 20.21 44.93 1.7 3.51 13.01 27.51 129.13 Greece 10.22 20.71 46.56 1.78 3.64 14.59 28.45 134.6 Guatemala 10.98 21.82 48.4 1.89 3.8 14.16 30.11 139.33 Hungary 10.26 20.62 46.02 1.77 3.62 13.49 28.44 132.58 India 10.6 21.42 45.73 1.76 3.73 13.77 28.81 131.98
烟道气体成分分析方案
a) 对烟气成分进行分析,在设备上选择质谱仪作为在线分析仪表。采用 1 台质谱仪、4套采样探头、2套前处理系统、1套后处理系统及1座分析小屋。质谱仪同时对两个采样点(余热锅炉入口、电收尘出口)进行分析,两采样点双流路切换分析,每个点的分析时间小于10S。 对于烟气成分分析选用上海舜宇恒平的工业连续在线质谱仪进行测量。质谱仪可快速响应,实时监测烟道气中成分变化,以便快速反映工艺状况、指导工艺生产。烟气中湿度测量选用瑞士ROTRONI(公司的高温湿度计进行测量,自带温度计算。 由于烟气中含有大量粉尘和水,系统难点在于预处理系统的处理,本系统主要采用采样探头的一备一用设计,同时自动控制反吹以防止堵塞,同时采用美国杜邦公司的nafion 管进行脱水。 整个方案主要由采样探头、前处理、后处理、及在线分析设备构成。 在现场需要布置单独的现场小屋用于放置在线分析设备。 样品采样探头安装在工艺现场取样点位置,针对余热锅炉入口和电收尘出口工况中高温、高粉尘、高水的特殊情况,每个采样点均采用一反吹的冗余设计,由PLC控制系统实现,正常工作时,PLC空制相应的电磁阀动作,一个采样探头正常工作取样、另外一套采样探头反吹电磁阀打开,氮气对另外一个采样探头进行反吹。以防止探头堵塞。 探头采用法兰对接,采样探针伸入烟道的至位置。由于烟道内的高温高粉尘工况,为防止粉尘的冲刷在探针外部设有保护套管,同时探针入口处设有金属网的过滤器,以减少进入取样管的粉尘,防止管线堵塞。 PLC控制系统安装在分析小屋内,同时控制4个采样点之间的切换和反吹,每个位号的采样点的双采样探头切换采用定时反吹,具体的切换间隔根据现场实际调试而定。 前处理箱就近安装在工艺现场取样点位置,用于样品的降温、除尘和脱水。样品的降温通过风冷方式实现,冷却用的仪表风先进行伴热,温度维持在
主成分分析原理及详解
第14章主成分分析 1 概述 1.1 基本概念 1.1.1 定义 主成分分析是根据原始变量之间的相互关系,寻找一组由原变量组成、而彼此不相关的综合变量,从而浓缩原始数据信息、简化数据结构、压缩数据规模的一种统计方法。 1.1.2 举例 为什么叫主成分,下面通过一个例子来说明。 假定有N 个儿童的两个指标x1与x2,如身高和体重。x1与x2有显著的相关性。当N较大时,N观测量在平面上形成椭圆形的散点分布图,每一个坐标点即为个体x1与x2的取值,如果把通过该椭圆形的长轴取作新坐标轴的横轴Z1,在此轴的原点取一条垂直于Z1的直线定为新坐标轴的Z2,于是这N个点在新坐标轴上的坐标位置发生了改变;同时这N个点的性质也发生了改变,他们之间的关系不再是相关的。很明显,在新坐标上Z1与N个点分布的长轴一致,反映了N个观测量个体间离差的大部分信息,若Z1反映了原始数据信息的80%,则Z2只反映总信息的20%。这样新指标Z1称为原指标的第 358
一主成分,Z2称为原指标的第二主成分。所以如果要研究N个对象的变异,可以只考虑Z1这一个指标代替原来的两个指标(x1与x2),这种做法符合PCA提出的基本要求,即减少指标的个数,又不损失或少损失原来指标提供的信息。 1.1.3 函数公式 通过数学的方法可以求出Z1和Z2与x1与x2之间的关系。 Z1=l11x1+ l12x2 Z2=l21x1+ l22x2 即新指标Z1和Z2是原指标x1与x2的线性函数。在统计学上称为第一主成分和第二主成分。 若原变量有3个,且彼此相关,则N个对象在3维空间成椭圆球分布,见图14-1。 通过旋转和改变原点(坐标0点),就可以得到第一主成分、第二主成分和第三主成分。如果第二主成分和第三主成分与第一主成高度相关,或者说第二主成分和第三主成分相对于第一主成分来说变异很小,即N个对象在新坐标的三维空间分布成一长杆状时,则只需用一个综合指标便能反映原始数据中3个变量的基本特征。 359
实验六主成分分析报告
实验六 主成分分析 一、实验目的 通过本次实验,掌握SPSS 及ENVI 的主成分分析方法。 二、有关概念 1. 主成分分析的概念 主成分分析(又称因子分析),是将多个实测变量转换为少数几个不相关的 综合指标的多元统计分析方法。代表各类信息的综合指标就称为因子或主成份。 主成分分析的数学模型可写为: m m x a x a x a x a z 131********++++= m m x a x a x a x a z 23232221212++++= m m x a x a x a x a z 33332321313++++= ……… m nm n n n n x a x a x a x a z ++++= 332211 其中,x 1、x 2、 x 3、 x 4 …x m 为原始变量;z 1、 z 2、 z 3、 z 4 …z n 为主成份,且有m ≥n 。 写成矩阵形式为:Z=AX 。Z 为主成份向量,A 为主成份变换矩阵,X 为原始变 量向量。主成份分析的目的是把系数矩阵A 求出,主成份Z1、Z2、Z3…在总方差中所占比重依次递减。 从理论上讲m=n 即有多少原始变量就有多少主成份,但实际上前面几个主成 份集中了大部分方差,因此取主成份数目远远小于原始变量的数目,但信息损失很小。 因子分析的一个重要目的还在于对原始变量进行分门别类的综合评价。如果 因子分析结果保证了因子之间的正交性(不相关)但对因子不易命名,还可以通过对因子模型的旋转变换使公因子负荷系数向更大(向1)或更小(向0)方向变化,使得对公因子的命名和解释变得更加容易。进行正交变换可以保证变换后各因子仍正交,这是比较理想的情况。如果经过正交变换后对公因子仍然不易解释,也可进行斜交旋转。 2. 因子提取方法 SPSS 提供的因子提取方法有: ①Principal components 主成份法。该方法假设变量是因子的纯线性组合。
浅谈商用燃气灶具烟气成分分析
浅谈商用燃气灶具烟气成分分析 浅谈商用燃气灶具烟气成分分析 摘要:针对商用燃气灶具烟气成分分析,讨论了影响因素和分析方法,并对新旧标准中烟气成分的计算公式进行对比分析。通过分析得出烟气成分最准确的分析方法。 关键词:商用燃气灶具取样方法空燃比烟气成分分析 中图分类号:TK01 前言 商用燃气灶具遍布机关、学校、医院食堂及宾馆饭店的厨房。随着人们生活水平的提高和生活节奏加快,越来越多的人选择在外就餐,商用燃气灶具的需求量大幅上升,国内生产企业上千家并且呈现与日俱增的势态。生产企业数量不断增加,产品质量却参差不齐。如果控制不好商用燃气灶具的质量不但会造成燃料的极大浪费,而且会排放有害气体污染环境。在国家大力倡导节能减排的今天,如何能够生产出低排放、高效能的产品是生产企业和质检部门日前关注的焦点。分析烟气成分是提高产品质量的关键措施之一。 根据烟气中氧含量的多少,可以推算出燃烧所用空气的多少,进而可以调整空气量,使燃气灶具具有更高的热效率。同时通过控制完全燃烧的程度,限制排放到大气的烟气中的有害物质,从而提高产品质量。因此,如何能够准确、及时地分析和检测商用燃气灶具的烟气是十分令人关心的问题。 1、烟气分析的影响因素 燃气燃烧后产生烟气中的成分有二氧化碳、水蒸气、氮气、氧气、一氧化碳、氧化物及硫化物等。但由于燃气成分与燃烧情况的不同,烟气中各种成分会有些变化。正确分析烟气成分的主要影响因素为取样方法和空燃比α(过剩空气系数)。 1.1取样方法 烟气成分正确分析的首要条件是分析的气体有代表性。因此燃烧产物的取样就显得特别重要。商用燃气灶具取样时特别注意取样的位
置和取样方式。取样要求:1)能连续自动地取样;2)取样点应尽可能避开有化学反应的位置;3)若有一级烟道的燃气灶具采用图11[1](a)所示取样管,在距烟道口100mm处的中心位置(图1[1](b)所示)取样,若无一级烟道需用特制的取样罩见图1[1](c),取样方式见图1[1](d)。4)取样须在等速的条件下进行,即进入取样探头进口的吸入速度与探头周围烟道中的烟气流速相等。为保证准确取样,取样器的截面通常为流通截面的1%~2%,最大也不应超过5%,烟气分析时须采用补偿式静止灵位探头结构。 1.2空燃比α 当鼓风量过大时(即空燃比α偏大),虽能充分燃烧,但烟气中过剩空气量偏大(O2含量高),过剩空气带走热损失Q1值增大,导致热效率η偏低,同时,过量的O2会与燃料中的S、烟气中的N2 反应生成SO2、NOx等有害物质;当鼓风量偏低时(即空燃比α减小),烟气中O2含量低,CO含量高,未完全燃烧,热损失Q2增大,热效率η也将降低,且会产生黑烟。空燃比与热效率的关系如图2[2]所示。 由于商用燃气灶具燃烧时空燃比α(过剩空气系数)不能准确的控制且其对商用燃气灶具的烟气成分和热效率有直接影响,商用燃气灶具国家标准规定检测干烟气中CO含量时均换算为α=1(没有过剩空气)状态。 2、烟气成分分析方法 烟气成分综合分析方法主要有:奥氏气体分析仪分析烟气、气相色谱仪分析烟气、烟气连续自动分析等。目前,多项成分连续自动分析设备应用最为广泛。多项成分的烟气分析仪分析过程如图3[3]所示。一般安装多个传感器,分为电化学传感器和红外传感器来分析烟气中的CO、CO2、O2、NOx、SO2等气体含量。商用燃气灶具烟气检测采用多项成分烟气分析仪和计算相结合的方法。 标准中的公式(1)和公式(2)称为“氧稀释法”,公式(3)称为“二氧化碳稀释法”。老标准中CO含量计算采用公式(1),新标准中采用公式(2)和公式(3)。公式(1)和公式(2)的使用条件是氧含量占空气的20.9%,在不同地区和不同海拔,空气中氧氮比
锅炉烟气成分分析
7.2锅炉烟气成分分析 在火力发电的过程中,对锅炉烟气含氧量、二氧化碳含量、一氧化碳含量的分析测量对于指导锅炉燃烧控制有重要的意义。 为保持锅炉处于最佳燃烧状态,应使实际供给的空气量大于理论空气量,锅炉机组热损失最小的炉膛出口的最佳过剩空气系数应保持在一定范围内。 对锅炉铟气中的过剩空气系数的分析测量要考虑到烟气取样点的选择或给予必要的修正。目前,一般把烟气取样点设计在过热器出口或省煤器出口处。燃烧理论指出:在燃料一定情况下,当完全燃烧时,过剩空气系数是烟气中氧量或二氧化碳含量的函数,此时一氧化碳的含量为零。当不完全燃烧时,因烟气中含有一氧化碳,过剩空气系数与氧量或二氧化碳含量的函数要受到一氧化碳含量的影响:因此对一氧化碳含量和氧气或二氧化碳含量的监视,对于指导燃烧更为有利。实际燃烧时,很多情况是烟气中一氧化碳含量比较少.因此,对于一氧化碳分析仪要求有较高的灵敏度和精确度。在不完全燃烧时,烟气中还会有未燃尽的可燃物含量对烟气中的一氧化碳的含量、二氧化碳含量和氧量都有影响。过剩空气系数α与一氧化碳含量二氧化碳含量和氧量的函数关系就更复杂,这种情况下.通过对一氧化碳含量和氧量的监测来指导燃烧会更有实际意义。目前,对于高压大型锅炉,烟气中未燃尽可燃物的含量很小.通常多是通过对烟气中的含氧量的监测来指导燃烧控制。
7.2.2 氧化锆氧量计 氧化锆氧量计属于电化学分析器中的一种。氧化锆(2 ZrO )是一种氧离子导电的固体电解质。氧化锆氧量计可以用来连续地分析各种锅炉烟气中的氧含量,然后控制送风量来调整过剩空气系数α值,以保证最佳的空气燃料比,达到节能效果。氧化锆传感器探头可以直接插人烟道中进行测量,氧化锆测量探头工作温度必须在850℃左右的高温下运行,否则灵敏度将会下降。所以氧化锆氧量计在探头上都装有测温传感器和电加热设备。 1) 氧化锆传感器测量原理 氧化锆在常温下为单斜晶体,当温度为 1150℃时,晶体排列由单斜晶体变为立方晶 体,同时有不到十分之一的体积收缩。如果 在氧化锆中加人一定量的氧化钙(CaO )和 氧化钇(32O Y ),则其晶型变为不随温度而 变的稳定的萤石型立方晶体,这时四价的锆 被二价的钙和三价的钇置换,同时产生氧离 子空穴。当温度为800℃以上时,空穴型的 氧化锆就变成了良好的氧离子导体,从而可以构成氧浓差电池。 氧浓差电池的原理如图7.13所示。在氧化锆电解质的两侧各烧结上一层多孔的铂电极,便形成了氧浓差电池。电池左边是被测的烟气,它的氧含量一般为4%~6%,设氧分压为1p ,氧浓度为1?。电池的右边是参比气体,如空气,它的氧含量一般为20.8%,氧分压为2p ,浓度为2?。在温度T=850℃时,氧化锆氧浓差电池的工作原理可用下式表示: Pt p O CaO ZrO p O Pt ),(,)(,22212分压力分压力 负极 电解质 正极 在正极上氧分子得到电子成为氧离子,即 -?→?+22224)(O e p O 分压力 在负极上氧离子失去电子成为氧分子,即 )(421 22p O e O 分压力?→?-- 这个过程就好像2 O 从正极渗透到负极上去一样。这也好像是图7.13氧浓差电池的原理
主成分分析法及其在SPSS中的操作
一、主成分分析基本原理 概念:主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。从数学角度来看,这是一种降维处理技术。 思路:一个研究对象,往往是多要素的复杂系统。变量太多无疑会增加分析问题的难度和复杂性,利用原变量之间的相关关系,用较少的新变量代替原来较多的变量,并使这些少数变量尽可能多的保留原来较多的变量所反应的信息,这样问题就简单化了。 原理:假定有n 个样本,每个样本共有p 个变量,构成一个n ×p 阶的数据矩阵, 记原变量指标为x 1,x 2,…,x p ,设它们降维处理后的综合指标,即新变量为 z 1,z 2,z 3,… ,z m (m ≤p),则 系数l ij 的确定原则: ①z i 与z j (i ≠j ;i ,j=1,2,…,m )相互无关; ②z 1是x 1,x 2,…,x P 的一切线性组合中方差最大者,z 2是与z 1不相关的x 1,x 2,…,x P 的所有线性组合中方差最大者; z m 是与z 1,z 2,……,z m -1都不相关的x 1,x 2,…x P , 的所有线性组合中方差最大者。 新变量指标z 1,z 2,…,z m 分别称为原变量指标x 1,x 2,…,x P 的第1,第2,…,第m 主成分。 从以上的分析可以看出,主成分分析的实质就是确定原来变量x j (j=1,2 ,…, p )在诸主成分z i (i=1,2,…,m )上的荷载 l ij ( i=1,2,…,m ; j=1,2 ,…,p )。 ?????? ? ???????=np n n p p x x x x x x x x x X 2 1 2222111211 ?? ??? ? ?+++=+++=+++=p mp m m m p p p p x l x l x l z x l x l x l z x l x l x l z 22112222121212121111............
主成分分析、因子分析实验报告--SPSS
对2009年我国88个房地产上市公司的因子分析 分析结果: 表1 KMO 和 Bartlett 的检验 取样足够度的 Kaiser-Meyer-Olkin 度量。.637 Bartlett 的球形度检验近似卡方398.287 df 45 Sig. .000 由表1可知,巴特利特球度检验统计量的观测值为398.287,相应的概率p值接近0,小于显著性水平 (取0.05),所以应拒绝原假设,认为相关系数矩阵与单位矩阵有显著差异。同时,KMO值为0.637,根据Kaiser给出的KMO度量标准(0.9以上表示非常适合;0.8表示适合;0.7表示一般;0.6表示不太适合;0.5以下表示极不适合)可知原有变量不算特别适合进行因子分析。 表2 公因子方差 初始提取市盈率 1.000 .706 净资产收益率 1.000 .609 总资产报酬率 1.000 .822 毛利率 1.000 .280 资产现金率 1.000 .731 应收应付比 1.000 .561 营业利润占比 1.000 .782 流通市值 1.000 .957 总市值 1.000 .928 成交量(手) 1.000 .858 提取方法:主成份分析。 表2为公因子方差,即因子分析的初始解,显示了所有变量的共同度数据。第一列是因子分析初始解下的变量共同度,它表明,对原有10个变量如果采用主成分分析方法提取所有特征根(10个),那么原有变量的所有方差都可被解释,变量的共同度均为1(原有变量标准化后的方差为1)。事实上,因子个数小于原有变量的个数才是因子分析的目标,所以不可提取全部特征根;第二列是在按指定提取条件(这里为特征根大于1)提取特征根时的共同度。可以看到,总资产报酬率、成交量、流
主成分分析法的原理应用及计算步骤..
一、概述 在处理信息时,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠,例如,高校科研状况评价中的立项课题数与项目经费、经费支出等之间会存在较高的相关性;学生综合评价研究中的专业基础课成绩与专业课成绩、获奖学金次数等之间也会存在较高的相关性。而变量之间信息的高度重叠和高度相关会给统计方法的应用带来许多障碍。 为了解决这些问题,最简单和最直接的解决方案是削减变量的个数,但这必然又会导致信息丢失和信息不完整等问题的产生。为此,人们希望探索一种更为有效的解决方法,它既能大大减少参与数据建模的变量个数,同时也不会造成信息的大量丢失。主成分分析正式这样一种能够有效降低变量维数,并已得到广泛应用的分析方法。 主成分分析以最少的信息丢失为前提,将众多的原有变量综合成较少几个综合指标,通常综合指标(主成分)有以下几个特点: ↓主成分个数远远少于原有变量的个数 原有变量综合成少数几个因子之后,因子将可以替代原有变量参与数据建模,这将大大减少分析过程中的计算工作量。 ↓主成分能够反映原有变量的绝大部分信息 因子并不是原有变量的简单取舍,而是原有变量重组后的结果,因此不会造成原有变量信息的大量丢失,并能够代表原有变量的绝大部分信息。 ↓主成分之间应该互不相关 通过主成分分析得出的新的综合指标(主成分)之间互不相关,因子参与数据建模能够有效地解决变量信息重叠、多重共线性等给分析应用带来的诸多问题。 ↓主成分具有命名解释性 总之,主成分分析法是研究如何以最少的信息丢失将众多原有变量浓缩成少数几个因子,如何使因子具有一定的命名解释性的多元统计分析方法。 二、基本原理 主成分分析是数学上对数据降维的一种方法。其基本思想是设法将原来众多的具有一定相关性的指标X1,X2,…,XP (比如p 个指标),重新组合成一组较少个数的互不相关的综合指标Fm 来代替原来指标。那么综合指标应该如何去提取,使其既能最大程度的反映原变量Xp 所代表的信息,又能保证新指标之间保持相互无关(信息不重叠)。 设F1表示原变量的第一个线性组合所形成的主成分指标,即 11112121...p p F a X a X a X =+++,由数学知识可知,每一个主成分所提取的信息量可 用其方差来度量,其方差Var(F1)越大,表示F1包含的信息越多。常常希望第一主成分F1所含的信息量最大,因此在所有的线性组合中选取的F1应该是X1,X2,…,XP 的所有线性组合中方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来p 个指标的信息,再考虑选取第二个主成分指标F2,为有效地反映原信息,F1已有的信息就不需要再出现在F2中,即F2与F1要保持独立、不相关,用数学语言表达就是其协方差Cov(F1, F2)=0,所以F2是与F1不
烟气成分分析
实验三 烟气成分分析 一、实验目的 锅炉中燃烧产物的计算和测定主要是求出燃烧后的烟气量和烟气组成。燃料燃烧后烟气的主要成分有:CO 2、SO 2 、O 2 、H 2 O 、N 2 、CO 等气体。本实验使用奥氏烟气分析器测定干烟气的容积成分百分数。通过实验使学生巩固烟气组成成分的概念,初步学会运用奥氏烟气分析器测定烟气成分的方法。 二、实验原理 奥氏烟气分析器是利用化学吸收法按容积测定气体成分的仪器。它主要由三个化学吸收瓶组成,利用不同化学药剂对气体的选择性吸收特性进行的。 吸收瓶Ⅰ内盛放氢氧化钾溶液(KOH ),它吸收烟气中的CO 2与SO 2气体。在烟气成分中常用RO 2表示CO 2与SO 2容积总和,即RO 2=CO 2+SO 2。 其化学反应式如下:2KOH+CO 2→K 2CO 3 ;KOH+SO 2→K 2SO 3 ; 吸收瓶Ⅱ内盛焦性没食子酸苛性钾溶液[C 6H 3(OK )3],它可吸收烟气中的RO 2与O 2气体。当RO 2被吸收瓶Ⅰ吸收后,吸收瓶Ⅱ则吸收的烟气容积中的O 2气体。 焦性没食子酸苛性钾溶液吸收O 2的化学反应式为: 4C 6H 3(OK )3 + O 2→2[(OK )3C 6H 2—C 6H 2(OK )3]+2 H 2 O 吸收瓶Ⅲ内盛氯化亚铜的氨溶液[Cu (NH 3)2Cl ],它可吸收烟气中的CO 气体。 其化学反应式为:Cu (NH 3)2Cl+2CO → Cu (CO )2Cl+ 2NH 3; 它同时也能吸收O 2气体。故烟气应先通过吸收瓶Ⅱ,使O 2被吸收后,这样通过吸收瓶Ⅲ吸收的烟气只剩下一氧化碳CO 气体了。 综上所述,三个吸收瓶的测定程序切勿颠倒。在环境温度下,烟气中的过饱和蒸汽将结露成水,因此在进入分析器前,烟气应先通过过滤器,使饱和蒸汽被吸收,故在吸收瓶中的烟气容积为干烟气容积,气体容积单位为Nm 3/Kg ,测定的成分为干烟气容积成分百分数,即CO 2+SO 2+O 2+CO+N 2=100% CO 2= %1002?gy CO V V (3-1) ; SO 2=%1002?gy SO V V (3-2) ; O 2 = %1002?gy O V V (3-3) ; CO = %100?gy CO V V (3-4);
教育信息处理(实验九因子分析与主成分分析)实验报告-示例
1、对北京18个区县中等职业教育发展水平进行聚类。X1:每万人中职在校生数;X2:每万人中职招生数;X3:每万人中职毕业生数;X4:每万人中职专任教师数;X5:本科以上学校教师占专任教师的比例;X6:高级教师占专任教师的比例;X7:学校平均在校生人数;X8:国家财政预算中职经费占国内生产总值的比例;X9:生均教育经费。 具体步骤如下: 1、导入数据,建立数据文件(data.sav) 2、选择聚类分析(分析—分类—系统聚类分析),选择变量,分群选择个 案方式 3、聚类分析描述统计(统计量—合并进程表;聚类成员—单一方案—聚类 数3) 4、聚类分析绘制(树状图;冰柱—所有聚类,方向—垂直) 5、聚类分析方法(聚类方法—组间联接,度量标准—区间—平方Euclidean
距离) 6、聚类分析保存(聚类成员—单一方案—聚类数3) 7、保存实验结果,并分析结果 结果与分析: (1)输出结果文件中的第一部分如下图1所示。 图1中可以看出18个样本都进入了聚类分析,但有效样本为14个,缺失14个。 (2)输出结果文件中的第二部分为系统聚类分析的凝聚状态表如图2所示。
第一列表示聚类分析的步骤,可以看出本例中共进行了17个步骤的分析; 第二列和第三列表示某步聚类分析中,哪两个样本或类聚成了一类; 第四列表示两个样本或类间的距离,从表格中可以看出,距离小的样本之间先聚类; 第五列和第六列表示某步聚类分析中,参与聚类的是样本还是类。0表示样本,数字n(非零)表示第n步聚类产生的类参与了本步聚类; 第七列表示本步聚类结果在下面聚类的第几步中用到。 图2给中第一行表示,第二个样本和第四个样本最先进行了聚类,样本间的距离为4803.026,这个聚类的结果将在后面的第六步
主成分分析原理
主成分分析原理 (一)教学目的 通过本章的学习,对主成分分析从总体上有一个清晰地认识,理解主成分分析的基本思想和数学模型,掌握用主成分分析方法解决实际问题的能力。 (二)基本要求 了解主成分分析的基本思想,几何解释,理解主成分分析的数学模型,掌握主成分分析方法的主要步骤。 (三)教学要点 1、主成分分析基本思想,数学模型,几何解释 2、主成分分析的计算步骤及应用 (四)教学时数 3课时 (五)教学内容 1、主成分分析的原理及模型 2、主成分的导出及主成分分析步骤 在实际问题中,我们经常会遇到研究多个变量的问题,而且在多数情况下,多个变量之间常常存在一定的相关性。由于变量个数较多再加上变量之间的相关性,势必增加了分析问题的复杂性。如何从多个变量中综合为少数几个代表性变量,既能够代表原始变量的绝大多数信息,又互不相关,并且在新的综合变量基础上,可以进一步的统计分析,这时就需要进行主成分分析。 第一节主成分分析的原理及模型 一、主成分分析的基本思想与数学模型 (一)主成分分析的基本思想 主成分分析是采取一种数学降维的方法,找出几个综合变量来代替原来众多的变量,使这些综合变量能尽可能地代表原来变量的信息量,而且彼此之间互不相关。这种将把多个变量化为少数几个互相无关的综合变量的统计分析方法就叫做主成分分析或主分量分析。
主成分分析所要做的就是设法将原来众多具有一定相关性的变量,重新组合为一组新的相互无关的综合变量来代替原来变量。通常,数学上的处理方法就是将原来的变量做线性组合,作为新的综合变量,但是这种组合如果不加以限制,则可以有很多,应该如何选择呢?如果将选取的第一个线性组合即第一个综合变量记为1F ,自然希望它尽可能多地反映原来变量的信息,这里“信息”用方差来测量,即希望)(1F Var 越大,表示1F 包含的信息越多。因此在所有的线性组合中所选取的1F 应该是方差最大的,故称1F 为第一主成分。如果第一主成分不足以代表原来p 个变量的信息,再考虑选取2F 即第二个线性组合,为了有效地反映原来信息,1F 已有的信息就不需要再出现在2F 中,用数学语言表达就是要求0),(21=F F Cov ,称2F 为第二主成分,依此类推可以构造出第三、四……第p 个主成分。 (二)主成分分析的数学模型 对于一个样本资料,观测p 个变量p x x x ,,21,n 个样品的数据资料阵为: ?? ? ? ? ? ? ??=np n n p p x x x x x x x x x X 2 1 22221 11211 ()p x x x ,,21= 其中:p j x x x x nj j j j ,2,1, 21=???? ?? ? ??= 主成分分析就是将 p 个观测变量综合成为p 个新的变量(综合变量),即 ?? ???? ?+++=+++=+++=p pp p p p p p p p x a x a x a F x a x a x a F x a x a x a F 22112222121212121111 简写为: p jp j j j x x x F ααα+++= 2211 p j ,,2,1 = 要求模型满足以下条件:
主成分分析实验报告
项目名称实验4—主成分分析 所属课程名称多元统计分析(英) 项目类型综合性实验_____________ 实验(实训)日期2012年4 月15日
二、实验(实训)容: 【项目容】 主成分分析。 【方案设计】 题目: 由原始数据求主成分。 【实验(实训)过程】(步骤、记录、数据、程序等)附后 【结论】(结果、分析) 附后 三、指导教师评语及成绩: 评语: 成绩:指导教师签名: 批阅日期: 实验报告4 主成分分析(综合性实验) (Prin cipal comp onent an alysis) 实验原理:主成分分析利用指标之间的相关性,将多个指标转化为少数几个综合指标,从而达到降维和数据结构简化的目的。这些综合指标反映了原始指标的绝
大部分信息,通常表示为原始指标的某种线性组合,且综合指标间不相关。利用矩阵代数的知识可求解主成分 实验题目:下表中给出了不同国家及地区的男子径赛记录:(t8a6) Country 100m 200m 400m 800m 1500m 5000m 10,000m Marathon (s) (s) (s) (min) (min) (min) (min) (mins) Argentina 10.39 20.81 46.84 1.81 3.7 14.04 29.36 137.72 Australia 10.31 20.06 44.84 1.74 3.57 13.28 27.66 128.3 Austria 10.44 20.81 46.82 1.79 3.6 13.26 27.72 135.9 Belgium 10.34 20.68 45.04 1.73 3.6 13.22 27.45 129.95 Bermuda 10.28 20.58 45.91 1.8 3.75 14.68 30.55 146.62 Brazil 10.22 20.43 45.21 1.73 3.66 13.62 28.62 133.13 Burma 10.64 21.52 48.3 1.8 3.85 14.45 30.28 139.95 Canada 10.17 20.22 45.68 1.76 3.63 13.55 28.09 130.15 Chile 10.34 20.8 46.2 1.79 3.71 13.61 29.3 134.03 China 10.51 21.04 47.3 1.81 3.73 13.9 29.13 133.53 Columbia 10.43 21.05 46.1 1.82 3.74 13.49 27.88 131.35 Cook Islands 12.18 23.2 52.94 2.02 4.24 16.7 35.38 164.7 Costa Rica 10.94 21.9 48.66 1.87 3.84 14.03 28.81 136.58 Czechoslovakia 10.35 20.65 45.64 1.76 3.58 13.42 28.19 134.32 Denmark 10.56 20.52 45.89 1.78 3.61 13.5 28.11 130.78 Dominican Republic 10.14 20.65 46.8 1.82 3.82 14.91 31.45 154.12 Finland 10.43 20.69 45.49 1.74 3.61 13.27 27.52 130.87 France 10.11 20.38 45.28 1.73 3.57 13.34 27.97 132.3 German (D.R.) 10.12 20.33 44.87 1.73 3.56 13.17 27.42 129.92 German (F.R.) 10.16 20.37 44.5 1.73 3.53 13.21 27.61 132.23 Great Brit.& N. Ireland 10.11 20.21 44.93 1.7 3.51 13.01 27.51 129.13
主成分分析法的步骤和原理
(一)主成分分析法的基本思想 主成分分析(Principal Component Analysis)是利用降维的思想,将多个变量转化为少数几个综合变量(即主成分),其中每个主成分都是原始变量的线性组合,各主成分之间互不相关,从而这些主成分能够反映始变量的绝大部分信息,且所含的信息互不重叠。[2] 采用这种方法可以克服单一的财务指标不能真实反映公司的财务情况的缺点,引进多方面的财务指标,但又将复杂因素归结为几个主成分,使得复杂问题得以简化,同时得到更为科学、准确的财务信息。 (二)主成分分析法代数模型 假设用p个变量来描述研究对象,分别用X1,X2…X p来表示,这p个变量构成的p维随机向量为X=(X1,X2…X p)t。设随机向量X的均值为μ,协方差矩阵为Σ。对X进行线性变化,考虑原始变量的线性组合: Z=μX+μX+…μX Z=μX+μX+…μX ……………… Z=μX+μX+…μX 主成分是不相关的线性组合Z1,Z2……Z p,并且Z1是X,X…X的线性组合中方差最大者,Z2是与Z1不相关的线性组合中方差最大者,…,Z是与Z1,Z2……Z p-1都不相关的线性组合中方差最大者。 (三)主成分分析法基本步骤 第一步:设估计样本数为n,选取的财务指标数为p,则由估计样本的原始数据可得矩阵X=(x ij)m×p,其中x ij表示第i家上市公司的第j项财务指标数据。 第二步:为了消除各项财务指标之间在量纲化和数量级上的差别,对指标数据进行标准化,得到标准化矩阵(系统自动生成)。 第三步:根据标准化数据矩阵建立协方差矩阵R,是反映标准化后的数据之间相关关系密切程度的统计指标,值越大,说明有必要对数据进行主成分分析。其中,R ij(i,j=1,2,…,p)为原始变量X i与X j的相关系数。R为实对称矩阵
密炼车间烟气排放成分分析
炼胶工艺 1混炼:通过适当的加工将生胶与配合剂均匀混合在一起,制成质量均一的混合物的工艺过程。 2密炼的混炼:密炼机混炼密炼机通过转子、上下顶栓在密炼室中产生复杂的流动方式和高剪切力,使橡胶配合剂和粒状添加剂很快粉碎和均匀分散,是一种高效的混炼方法。但是高剪切力会使物料温度在混炼中迅速上升,一般会达到130℃。这已超过了大多数硫化系统的活化温度,会使胶料发生早期硫化(焦烧)。一般的做法是将大部分物料在密炼机中混炼,然后将胶料从密炼机排放到开炼机上,在开炼机上加硫化剂或超速促进剂。由于开炼机实际上只在辊缝线上对胶料有挤压作用,而提供了很大的冷却面积,致物料的温度降低。在这一阶段加入硫化剂可以避免胶料发生早期硫化(焦烧)。 密炼机混炼方法主要有一段混炼法、二段混炼法、引料法和逆混法: (1)一段混炼法指经密炼机和压片机一次混炼制成混炼胶的方法。通常加料顺序为:生胶→小料→填充剂或1/2→1/2炭黑→油料软化剂→排料。胶料直接排入压片机,薄通数次后,使胶料降至100℃以下,再加入硫黄和超促进剂,翻炼均匀后下片冷却。此法的优点是比二段混炼法的胶料停放时间短和占地面积小,其缺点是胶料可塑性偏低,填充补强剂不易分散均匀,而且胶料在密炼机中的炼胶时间长,易产生早期硫化(焦烧)。此法较适用于天然橡胶胶料和合成橡胶比例不超过50%的胶料。 (2)二段混炼法将混炼过程分为两个阶段,其中第一段同一段混炼法一样,只是不加硫黄和活性较大的促进剂,首先制成一段混炼胶(炭黑母炼胶),然后下片冷却停放8小时以上。第二段是对第一段混炼胶进行补充加工,待捏炼均匀后排料至压片机加硫化剂、超促进剂,并翻炼均匀下片。为了使炭黑更好地在橡胶中分散,提高生产效率,通常第一段在快速密炼机(40r/min以上)中进行,第二段则采用慢速密炼机,以便在较低的温度加入硫化剂。一般当合成胶比例超过50%时,为改进并用胶的掺合和炭黑的分散,提高混炼胶的质量和硫化胶的物理机械性能,可以采用二段混炼法。 (3)引料法在投料同时投入少量(1.5~2Kg)预混好的未加硫黄的胶料,作为“引胶”或“种子胶”,当生胶和配合剂之间浸润性差、粉状配合剂混入有困难时,这样可大大加快粉状配合剂(填充补强剂)的混合分散速度。例如,丁基橡胶即可采取此法。而且不论是在一段、二段混炼法或是逆混法中,加入“引胶”均可获得良好的分散效果。 (4)逆混法加料顺序与上述诸法加料顺序相反的混炼方法,即先将炭黑等各种配合剂和软化剂按一定顺序投入混炼室,在混炼一段时间后再投入生胶(或塑炼胶)进行加压混炼。其优点是可缩短混炼时间。还可提高胶料的性能。该法适合于能大量添加补强填充剂(特别
主成分分析法介绍.doc
主成分分析方法 我们进行系统分析评估或医学上因子分析等时,多变量问题是 经常会遇到的。变量太多,无疑会增加分析问题的难度与复杂 性,而且在许多实际问题中,多个变量之间是具有一定的相关关 系的。因此,我们就会很自然地想到,能否在各个变量之间相关 关系研究的基础上,用较少的新变量代替原来较多的变量,而且使这些较少的新变量尽可能多地保留原来较多的变量所反映的 信息事实上,这种想法是可以实现的,本节拟介绍的主成分分析 方法就是综合处理这种问题的一种强有力的方法。 第一节主成分分析方法的原理 主成分分析是把原来多个变量化为少数几个综合指标的一种 统计分析方法,从数学角度来看,这是一种降维处理技术。假定 有 n 样本,每个样本共有 p 个变量描述,这样就构成了一个 n×p阶的数据矩阵: x 11 x 12 ... x 1 p x 21 x 22 ... x 2 p X ... ... ... ????(1) ... x n1 x n 2 ... x np
如何从这么多变量的数据中抓住事物的内在规律性呢要解决 这一问题, 自然要在 p 维空间中加以考察, 这是比较麻烦的。为了克服这一困难, 就需要进行降维处理, 即用较少的几个综合指标来代替原来较多的变量指标, 而且使这些较少的综合指标既能尽量多地反映原来较多指标所反映的信息, 同时它们之间又是彼此独立的。那么,这些综合指标(即新变量 )应如何选取呢显然,其最简单的形式就是取原来变量指标的线性组合, 适当调整组合系数,使新的变量指标之间相互独立且代表性最好。 如果记原来的变量指标为 x 1 , x 2 , x p ,它们的综合指标 —— 新 变量指标为 z 1 , z 2 , z m ( m ≤p)。则 z 1 l 11x 1 l 12 x 2 l 1 p x p z 2 l 21 x 1 l 22 x 2 l 2 p x p (2) z m l m1x 1 l m2 x 2 l mp x p 在( 2)式中,系数 l ij 由下列原则来决定: ( 1)z i 与 z j ( i ≠j;i ,j=1,2, , m)相互无关; ( 2)z 1 是 x 1,x 2,?,x p 的一切线性组合中方差最大者; z 2 是与 z 1 不相关的 x 1, x 2,?,x p 的所有线性组合中方差 最大者; ;z m 是与 z 1,z 2,??z m-1 都不相关的 x 1, x 2, ?, x p 的所有线性组合中方差最大者。
