运筹学--第四章 多目标规划

109 习题四
4.1 分别用图解法和单纯形法求解下述目标规划问题
(1) min z =p 1(+1d ++2d )+p 2-3d
st. -x 1+ x 2+ d -1- d +
1=1
-0.5x 1+ x 2+ d -
2-d +
2=2
3x 1+3x 2+ d -3- d +3=50
x 1,x 2≥0;d -i ,d +i ≥0(i =1,2,3)
(2) min z =p 1(2+1d +3+2d )+p 2-3d +p 3+4d st. x 1+ x 2+d -1-d +
1 =10
x 1 +d -2-d +2 =4
5x 1+3x 2+d -3-d +3 =56
x 1+ x 2+d -4-d +4 =12
x 1,x 2≥0;d -i ,d +i ≥0(i =1, (4)
4.2 考虑下述目标规划问题
min z =p 1(d +1+d +2)+2p 2d -4+p 2d -3+p 3d -1
st. x 1 +d -1-d +1=20
x 2+d -2-d +2=35
-5x 1+3x 2+d -
3-d +
3=220
x 1-x 2+d -4-d +4=60
x 1,x 2≥0;d -i ,d +i ≥0(i =1, (4)
(1)求满意解;
(2)当第二个约束右端项由35改为75时,求解的变化;
(3)若增加一个新的目标约束:-4x 1+x 2+d -5-d +5=8,该目标要求尽量达
到目标值,并列为第一优先级考虑,求解的变化;
(4)若增加一个新的变量x 3,其系数列向量为(0,1,1,-1)T ,则满意解如何变化?
4.3 一个小型的无线电广播台考虑如何最好地来安排音乐、新闻和商业节目时间。依据法律,该台每天允许广播12小时,其中商业节目用以赢利,每小时可收入250美元,新闻节目每小时需支出40美元,音乐节目每播一小时费用为17.50美元。法律规定,正常情况下商业节目只能占广播时间的20%,每小时至少安排5分钟新闻节目。问每天的广播节目该如何安排?优先级如下:
P 1:满足法律规定要求;
P 2:每天的纯收入最大。
试建立该问题的目标规划模型。
4.4 某企业生产两种产品,产品Ⅰ售出后每件可获利10元,产品Ⅱ售出后每件可获利8元。生产每件产品Ⅰ需3小时的装配时间,每件产品Ⅱ需2小时装配时间。可用的装配时间共计为每周120小时,但允许加班。在加班时间内生产两种产品时,每件的获利分别降低1元。加班时间限定每周不超过40小时,企业希望总获利最大。试凭自己的经验确定优先结构,并建立该问题的目标规划模型。
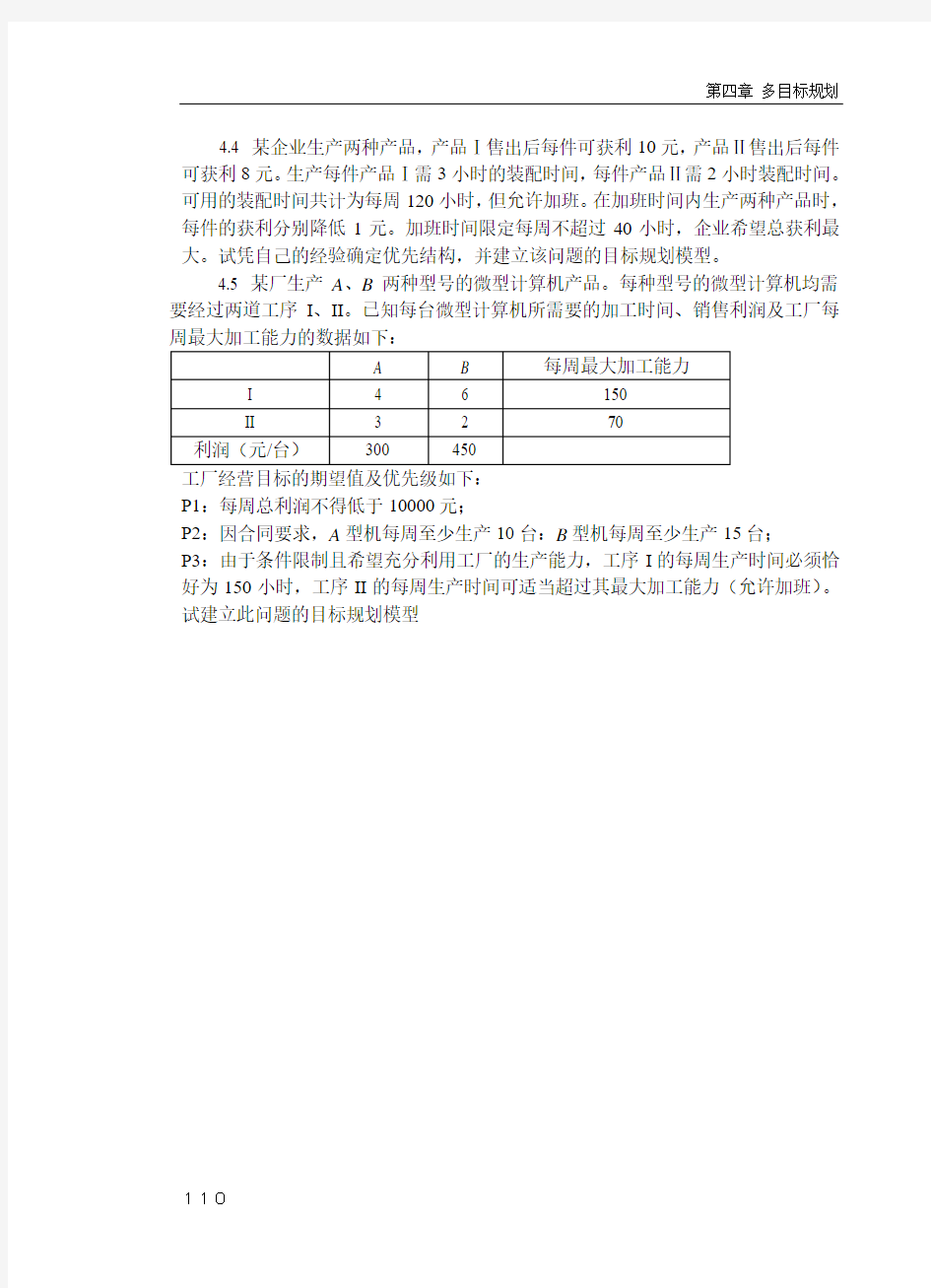
4.5 某厂生产A、B两种型号的微型计算机产品。每种型号的微型计算机均需要经过两道工序I、II。已知每台微型计算机所需要的加工时间、销售利润及工厂每
工厂经营目标的期望值及优先级如下:
P1:每周总利润不得低于10000元;
P2:因合同要求,A型机每周至少生产10台:B型机每周至少生产15台;
P3:由于条件限制且希望充分利用工厂的生产能力,工序I的每周生产时间必须恰好为150小时,工序II的每周生产时间可适当超过其最大加工能力(允许加班)。试建立此问题的目标规划模型
110
7运筹学之目标规划(胡运权版)
第七章 目标规划 §1 目标规划的提出 线性规划问题是讨论一个给定的线性目标函数在一组线性约束条件下的最大值或最小 值问题。对于一个实际问题,管理科学者根据管理层决策目标的要求,首先确定一个目标函数以衡量不同决策的优劣,且根据实际问题中的资源、资金和环境等因素对决策的限制提出相应的约束条件以建立线性规划模型;然后用计算机软件求出最优方案并作灵敏度分析以供管理层决策之用。而在一些问题中,决策目标往往不只一个,且模型中有可能存在一些互相矛盾的约束条件的情况,用已有的线性规划的理论和方法无法解决这些问题。因此,1961年美国学者查恩斯(A.Charnes )和库柏(W.W.Coopor )提出了目标规划的概念与数学模型,以解决经济管理中的多目标决策问题。 我们将通过几个例子来说明在实际应用中线性规划存在一系列的局限性。 例1 某厂生产A 、B 两种产品每件所需的劳动力分别为4个人工和6个人工,所需设备的单位台时均为1。已知该厂有10个单位机器台时提供制造这两种产品,并且至少能提供70个人工。又,A 、B 产品的利润,每件分别为300元和500元。试问:该厂各应生产多少件A 、B 产品,才能使其利润值最大? 解 设该厂能生产A 、B 产品的数量分别为12,x x 件,则有 12 1212max 30050010 ..46700, 1,2.j z x x x x s t x x x j =+?+≤? +≥??≥=? 图解法求解如下: 由上图可得,满足约束条件的可行解集为?,即机时约束和人工约束之间产生矛盾,因而该问题无解。但在实际中,该厂要增加利润,不可能不生产A 、B 两种产品,而由线性规划模型无法为其找到一个合适的方案。 例2 某厂为进行生产需采购A 、B 两种原材料,单价分别为70元/公斤和50元/公斤。现要求购买资金不超过5000元,总购买量不少于80公斤,而A 原材料不少于20公斤。问如
运筹学第四章多目标规划
习题四 4.1 分别用图解法和单纯形法求解下述目标规划问题 (1) min z =p 1(+1d ++2d )+p 2-3d st. -x 1+ x 2+ d -1- d + 1=1 -0.5x 1+ x 2+ d - 2-d + 2=2 3x 1+3x 2+ d -3- d +3=50 x 1,x 2≥0;d -i ,d +i ≥0(i =1,2,3) (2) min z =p 1(2+1d +3+2d )+p 2-3d +p 3+4d st. x 1+ x 2+d -1-d + 1 =10 x 1 +d -2-d +2 =4 5x 1+3x 2+d -3-d +3 =56 x 1+ x 2+d -4-d +4 =12 x 1,x 2≥0;d -i ,d +i ≥0(i =1, (4) 4.2 考虑下述目标规划问题 min z =p 1(d +1+d +2)+2p 2d -4+p 2d -3+p 3d -1 st. x 1 +d -1-d +1=20 x 2+d -2-d +2=35 -5x 1+3x 2+d - 3-d + 3=220 x 1-x 2+d -4-d +4=60 x 1,x 2≥0;d -i ,d +i ≥0(i =1, (4) (1)求满意解; (2)当第二个约束右端项由35改为75时,求解的变化; (3)若增加一个新的目标约束:-4x 1+x 2+d -5-d +5=8,该目标要求尽量达 到目标值,并列为第一优先级考虑,求解的变化; (4)若增加一个新的变量x 3,其系数列向量为(0,1,1,-1)T ,则满意解如何变化? 4.3 一个小型的无线电广播台考虑如何最好地来安排音乐、新闻和商业节目时间。依据法律,该台每天允许广播12小时,其中商业节目用以赢利,每小时可收入250美元,新闻节目每小时需支出40美元,音乐节目每播一小时费用为17.50美元。法律规定,正常情况下商业节目只能占广播时间的20%,每小时至少安排5分钟新闻节目。问每天的广播节目该如何安排?优先级如下: P 1:满足法律规定要求; P 2:每天的纯收入最大。 试建立该问题的目标规划模型。
运筹学第四章
运筹学第四章习题答案 4.1若用以下表达式作为目标规划的目标函数,其逻辑是否正确?为什么? (1)max {- d -+d } (2)max {-d ++ d } (3)min {-d ++d } (4)min {-d -+ d } (1)合理,令f (x )+- d -+ d =b,当f (x )取最小值时,- d -+ d 取最大值合理。 (2)不合理,+ d 取最大值时,f (x )取最大值,- d 取最大值时,f (x )应取最小值 (3)合理,恰好达到目标值时,- d 和+ d 都要尽可能的小。 (4)合理,令f (x )+- d -+ d =b,当f (x )取最大值时,- d -+ d 取最小值合理。 4.2用图解法和单纯形法解下列目标规划问题 (1)min {P 13 +d ,P 2- 2d ,P 3(- 1d ++ 1d )} 24261121=-+++- d d x x 52221=-+++- d d x x 155331=-++-d d x 3,2,1,0,,,21=≥+-i d d x x i i (2)min{P 1(+++43d d ),P 2+1d ,P 3-2d ,P 4(--+4 35.1d d )} 401121=-+++-d d x x 1002221=-++--d d x x 30331=-++-d d x 15442=-++-d d x 4,3,2,1,0,,,21=≥+-i d d x x i i (1)图解法
0 A B C X 1 由图可知,满足域为线段EG,这就是目标规划方程的解,可求得:E,G 的坐标分别为(0,12),(3,3) 故该问题的解为)312,3()3,3()12,0(21221a a a a a +=+ )1,0,(2121=+≥a a a a (2)图解法 2 1 由图可知,满足域为线段AB A(25,15),B(30,10)故该问题的解可 表示为)1015,3025()10,30()15,25(212121a a a a a a ++=+ )1,0(212,1=+≥a a a a
运筹学课件第四章目标规划
第四章目标规划 一、学习目的与要求 1、掌握目标规划的图解法模型; 2、掌握目标规划的单纯形的求解模型; 3、掌握目标规划的灵敏度分析。 二、课时6学时 第一节目标规划问题及其数学模型 一、问题的提出 应用线性规划可以处理许多线性系统的最优化问题,但线性规划,整数规划和非线性规划都只有一个目标函数,而在实际问题中,常常需要考虑多个目标:如设计一个新产品的工艺过程,不仅希望获利大,而且希望产量高,消耗低,质量好,投入少等。而这些目标之间通常是矛盾的。所以这类问题多目标问题比单目标问题要复杂得多,我们把这一类问题称为目标规划问题。 目标规划与线性规划相比,有以下优点: 1.线性规则只讨论一个线性目标函数在一组线性约束条件下的极值问题。 实际问题中,往往要考虑多个目标的决策问题,这些目标可能互相矛盾,也可能没有统一的度量单位,很难比较。目标规划就能够兼顾地处理多种目标的关系,求得更切合实际的解。 2.线性规划是在满足所有约束条件的可行解中求得最优解。而在实际问题 中往往存在一些相互矛盾的约束条件,如何在这些相互矛盾的约束条件下,找到一个满意解就是目标规划所要讨论的问题。 3.线性规划问题中的约束条件是不分主次、同等对待的,是一律要满足的“硬约束”。而在实际问题中,多个目标和多个约束条件不一定是同等重要的,而是有轻重缓急和主次之分的,如何根据实际情况确定模型和求解,使其更合实际是目标规划的任务。 4.线性规划的最优解可以说是绝对意义下的最优,为求得这个最优解,往往要花去大量的人力、物力和才力。而在实际问题中,却并不一定需要去找这种最优解。目标规划所求的满意解是指尽可能地达到或接近一个或几个已给定的指标值,这种满意解更能够满足实际的需要。 因此可以认为,目标规划更能够确切描述和解决经济管理中的许多实际问题。目前目标规划的理论和方法已经在经济计划、生产管理、经营管理、市场分析、财务管理等方面得到广泛的应用。 二、目标规划的数学模型 例1 某工厂生产两种产品,受到原材料和设备工时的限制。在单件利润等有关数据已知的条件下,要求制定一个获利最大的生产计划,具体数据见表:
多目标线性规划的若干解法及MATLAB实现
多目标线性规划的若干解法及MATLAB 实现 一.多目标线性规划模型 多目标线性规划有着两个和两个以上的目标函数,且目标函数和约束条件全是线性函 数,其数学模型表示为: 11111221221122221122max n n n n r r r rn n z c x c x c x z c x c x c x z c x c x c x =+++??=+++?? ??=+++? (1) 约束条件为: 1111221121122222112212,,,0 n n n n m m mn n m n a x a x a x b a x a x a x b a x a x a x b x x x +++≤??+++≤?? ??+++≤?≥?? (2) 若(1)式中只有一个1122i i i in n z c x c x c x =+++ ,则该问题为典型的单目标线性规划。我们记:()ij m n A a ?=,()ij r n C c ?=,12(,,,)T m b b b b = ,12(,,,)T n x x x x = , 12(,,,)T r Z Z Z Z = . 则上述多目标线性规划可用矩阵形式表示为: max Z Cx = 约束条件:0 Ax b x ≤?? ≥? (3) 二.MATLAB 优化工具箱常用函数[3] 在MA TLAB 软件中,有几个专门求解最优化问题的函数,如求线性规划问题的linprog 、求有约束非线性函数的fmincon 、求最大最小化问题的fminimax 、求多目标达到问题的fgoalattain 等,它们的调用形式分别为: ①.[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub) f 为目标函数系数,A,b 为不等式约束的系数, Aeq,beq 为等式约束系数, lb,ub 为x 的下 限和上限, fval 求解的x 所对应的值。 算法原理:单纯形法的改进方法投影法 ②.[x,fval ]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub ) fun 为目标函数的M 函数, x0为初值,A,b 为不等式约束的系数, Aeq,beq 为等式约束
多目标规划问题知识讲解
多目标规划问题
3.5 黑龙江省可持续农业产业结构优化模型的求解 鉴于上面的遗传算法的基本实现技术和理论分析,对标准遗传算法进行适当改进,将其用于求解黑龙江省可持续农业产业结构优化模型中。黑龙江省农业产业结构优化模型具有大系统、多目标、非线性等特点,传统的求解方法受到了模型复杂程度的限制,由引言可知,遗传算法对解决此类问题具有明显的优势。下面介绍具体采用的遗传多目标算法操作设计以及模型求解过程。 3.5.1遗传多目标算法操作设计 3.5.1.1 实数编码方法 在求解复杂优化问题时,二进制向量表示结构有时不太方便,并且浮点数编码的遗传算法对变异操作的种群稳定性比二进制编码好(徐前锋,2000)。以浮点数编码的遗传算法也叫实数遗传算法(Real number Genetic Algorithms ,简称RGA )。每一个染色体由一个浮点数向量表示,其长度与解向量相同。假如用向量),(21n x x x X 表示最优化问题的解,则相应的染色体就是 ),(21n x x x V ,其中n 是变量个数。 3.5.1.2 种群初始化方法 遗传算法中初始群体的个体是随机产生的,由于本文优化模型所涉及的变量容易给出一个相对较大的问题空间的变量分布范围,并且若给出一定的搜索空间也会加快遗传算法的收敛速度;因此本文采取3.3.2中的第一种策略,对每一个变量设置可能区间,然后在可能区间内随机产生初始种群。为保证不会遗漏最优解,选择区间跨度范围很大。 3.5.1.3 适应度函数设计
用遗传算法求解多目标优化问题中出现的一个特殊情况就是如何根据多个目标来确定个体的适应值。本文采用Gen 和Cheng 提出的适应性权重方法 (Adaptive Weight Approach ),该方法利用当前种群中一些有用的信息来重新调整权重,从而获得朝向正理想点的搜索压力(玄光男等,2004)。将目标函数按3.3.3所述转化成带有q 个目标(本文模型3 q )的最大化问题: )}(,),(),({max 2211x f z x f z x f z q q (3-14) 对于每代中待检查的解来说,在判据空间中定义两个极限点:最大极限点 z 和最小极限点 z 如下: },,,{} ,,,{m in m in 2m in 1m ax m ax 2m ax 1q q z z z z z z z z (3-15) 其中m in m ax k k z z 和是当前种群中第k 个目标的最大值和最小值。由两个极限点定义的超平行四边形是包含当前所有解的最小超平行四边形。两个极限点每代更新,最大极限点最终将接近正理想点。目标k 的适应性权重用下式计算: ),,2,1(1 min max q k z z k k k 因此,权重和目标(Weighted-sum Objective )函数由下面的公式确定 q k k k k q k k k z z x f x f x z 1m in m ax 1)()()( (3-16) 3.5.1.4 遗传操作 (1)选择操作。以比例选择法和最优个体保存法配合使用进行选择操作,即选择过程仍以旋转赌轮来为新的种群选择染色体,适应度越高的染色体被选中的概率越大;另一方面,为了保证遗传算法的全局收敛性,在选择作用后保留当前群体中适应度最高的个体,不参与交叉和变异,同时也确保当前最优个体不被随机进行的遗传操作破坏。
运筹学--第四章 多目标规划汇总
习题四 4.1 分别用图解法和单纯形法求解下述目标规划问题 (1)min z =p1(+)+p2 st. -x1+ x2+ d-1- d+1=1 -0.5x1+ x2+ d-2-d+2=2 3x1+3x2+ d-3- d+3=50 x1,x2≥0;d-i,d+i≥0(i =1,2,3) (2) min z =p1(2+3)+p2+p3 st. x1+ x2+d-1-d+1 =10 x1 +d-2-d+2 =4 5x1+3x2+d-3-d+3 =56 x1+ x2+d-4-d+4 =12 x1,x2≥0;d-i,d+i ≥0(i =1, (4) 4.2 考虑下述目标规划问题 min z =p1(d+1+d+2)+2p2d-4+p2d-3+p3d-1 st. x1 +d-1-d+1=20 x2+d-2-d+2=35 -5x1+3x2+d-3-d+3=220 x1-x2+d-4-d+4=60 x1,x2≥0;d-i,d+i ≥0(i =1, (4) (1)求满意解; (2)当第二个约束右端项由35改为75时,求解的变化;
(3)若增加一个新的目标约束:-4x1+x2+d-5-d+5=8,该目标要求尽量达到目标值,并列为第一优先级考虑,求解的变化; (4)若增加一个新的变量x3,其系数列向量为(0,1,1,-1)T,则满意解如何变化? 4.3 一个小型的无线电广播台考虑如何最好地来安排音乐、新闻和商业节目时间。依据法律,该台每天允许广播12小时,其中商业节目用以赢利,每小时可收入250美元,新闻节目每小时需支出40美元,音乐节目每播一小时费用为17.50美元。法律规定,正常情况下商业节目只能占广播时间的20%,每小时至少安排5分钟新闻节目。问每天的广播节目该如何安排?优先级如下: P1:满足法律规定要求; P2:每天的纯收入最大。 试建立该问题的目标规划模型。 4.4 某企业生产两种产品,产品Ⅰ售出后每件可获利10元,产品Ⅱ售出后每件可获利8元。生产每件产品Ⅰ需3小时的装配时间,每件产品Ⅱ需2小时装配时间。可用的装配时间共计为每周120小时,但允许加班。在加班时间内生产两种产品时,每件的获利分别降低1元。加班时间限定每周不超过40小时,企业希望总获利最大。试凭自己的经验确定优先结构,并建立该问题的目标规划模型。 4.5 某厂生产A、B两种型号的微型计算机产品。每种型号的微型计算机均需要经过两道工序I、II。已知每台微型计算机所需要的加工时间、销售利润及工厂每周最大加工能力的数据如下: A B每周最大加工能力 I 4 6 150 II 3 2 70 利润(元/台)300 450 工厂经营目标的期望值及优先级如下: P1:每周总利润不得低于10000元;
7.运筹学之目标规划(胡运权版)
页脚内容1 第七章 目标规划 §1 目标规划的提出 线性规划问题是讨论一个给定的线性目标函数在一组线性约束条件下的最大值或最小值问题。对于一个实际问题,管理科学者根据管理层决策目标的要求,首先确定一个目标函数以衡量不同决策的优劣,且根据实际问题中的资源、资金和环境等因素对决策的限制提出相应的约束条件以建立线性规划模型;然后用计算机软件求出最优方案并作灵敏度分析以供管理层决策之用。而在一些问题中,决策目标往往不只一个,且模型中有可能存在一些互相矛盾的约束条件的情况,用已有的线性规划的理论和方法无法解决这些问题。因此,1961年美国学者查恩斯(A.Charnes )和库柏(W.W.Coopor )提出了目标规划的概念与数学模型,以解决经济管理中的多目标决策问题。 我们将通过几个例子来说明在实际应用中线性规划存在一系列的局限性。 例1 某厂生产A 、B 两种产品每件所需的劳动力分别为4个人工和6个人工,所需设备的单位台时均为1。已知该厂有10个单位机器台时提供制造这两种产品,并且至少能提供70个人工。又,A 、B 产品的利润,每件分别为300元和500元。试问:该厂各应生产多少件A 、B 产品,才能使其利润值最大? 解 设该厂能生产A 、B 产品的数量分别为12,x x 件,则有 12 1212max 30050010..4670 0, 1,2.j z x x x x s t x x x j =+?+≤?+≥??≥=? 图解法求解如下:
页脚内容2 由上图可得,满足约束条件的可行解集为?,即机时约束和人工约束之间产生矛盾,因而该问题无解。但在实际中,该厂要增加利润,不可能不生产A 、B 两种产品,而由线性规划模型无法为其找到一个合适的方案。 例2 某厂为进行生产需采购A 、B 两种原材料,单价分别为70元/公斤和50元/公斤。现要求购买资金不超过5000元,总购买量不少于80公斤,而A 原材料不少于20公斤。问如何确定最好的采购方案(即花掉的资金最少,购买的总量最大)? 解 这是一个含有两个目标的数学规划问题。设12,x x 分别为购买两种原材料的公斤数,()112,f x x 为花掉的资金,()212,f x x 为购买的总量。建立该问题的数学模型形式如下: ()()11212 21212 1212 112 min ,7050 max , 70505000 80.. 20 ,0 f x x x x f x x x x x x x x s t x x x =+=++≤??+≥??≥??≥?
第1节多目标规划问题
第1节多目标规划问题 一、线性规划的局限性 第一,线性规划是在一组线性约束条件下,寻求某一项目标(如产量、利润或成本等)的最优值。而实际问题中往往要考虑多个目标的决策问题。 第二,线性规划最优解存在的前提条件是可行域为非空集,否则,线性规划无解。然而实际问题中,有时可能出现资源条件满足不了管理目标要求的情况,此时,仅做出无解的结论是没有意义的。现实中,也有可能各个目标相互矛盾,根本找不出一个全部目标都满足的解,但是在决策时,也必须找出一个满意的解。 第三,线性规划问题中的约束条件是不分主次、同等对待的,是一律要满足的“硬约束”,而在实际问题中,多个目标和多个约束条件并不一定是同等重要的,而是有轻重缓急和主次之分;有近期目标,也有远期目标;有定量的,也有定性的;有互相补充的,也有互相对立的,对这样复杂的决策问题,线性规划方法就无能为力了。 第四,线性规划的最优解可以说是绝对意义的最优,但很多实际情况只需(或只能)找出满意解。 上述原因限制了线性规划的应用范围。目标规划就是在解决以上问题的研究中应运而生,它能更确切地描述和解决经济管理中的许多实际问题。 二、多目标规划的提出 [例4—1]对于例1—1的生产计划问题,问如何安排甲、乙产品的产量,使企业利润为最大? 解设生产甲产品的产量为x1,乙产品的产量为x2,该问题的线性规划模型可以表示为: maxZ=3x1+5x2 s.t. 假设该厂根据市场需求或合同规定,希望尽量扩大产品甲的生产量,减少产品乙的生产,这时又增加了两个目标,则可建立如下的模型: maxZ1=3x1+5x2 maxZ2=x1 minZ3=x2 s.t.
容易看出,这是一个具有三个目标的线性规划模型,这些目标之间一般是相互矛盾的。从上述例子不难得出,多目标线性规划模型的原始一般形式如下: max(min)Z1=c11x1+c12x2+…+c1n x n max(min)Z2=c21x1+c22x2+…+c2n x n …… max(min)Z l=c l1x1+c l2x2+…+c ln x n 式中,有n个决策变量,m个约束条件,l个目标函数。当l=1时,即为我们熟悉的单目标线性规划模型。 三、多目标规划的解法 显然,对上述多目标线性规划模型,一般的线性规划方法不能求解。为此,许多学者提出了求解多目标规划问题的方法,其中不少方法已取得了富有成效的应用。而且,新的算法仍在不断地提出和改进。在这众多的算法中,绝大多数是基于以下加权系数法、优先等级法和有效解法的基本思想。 (一)加权系数法 这类方法的基本思想是试图在各目标之间寻找一种统一的度量标准,通过为每一目标赋一个加权系数,把多目标模型转化成单一目标的模型。从计算的角度看,这种方法确实吸引人。如果原模型是线性的,就可以用传统的单纯形法求解。但这类方法存在的一个明显的困难就是难以确定合理的加权系数。加权系数法一般应用于具有同一度量标准的多目标模型中。 (二)优先等级法 这类方法也是试图将多目标问题转化为单目标模型,但它避开了给各目标确定一个很难找到的加权系数,而是将各目标按其重要程度分成不同的优先等级,然后根据确定的目标优先等级的次序来求解。如果上一等级的目标得不到满足,则下一等级目标不予考虑。 (三)有效解法 这类方法的基本思想与前两类方法有很大的区别。在多目标规划问题中,最优解是使所有目标同时达到最优值的可行解。但是,在更多的情况下,由于众多的目标之间常常相互矛盾,因此,多目标规划问题的绝对最优解往往是不存在的,一部分目标的改善往往以牺牲另一部分目标的利益为代价。因而,多目标规划问题转而求能够照顾到各个目标,并使决策者感到满意的解。有效解或非劣解法就是找出可行域中全部的有效解或非劣解。如果能找到全部的有效
多目标规划问题Matlab示例_fgoalattain
多目标规划问题: x = fgoalattain(fun,x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon,... options) minimizes with the optimization options specified in the structure options. Use optimset to set these options. 例子:三个目标函数: 求最大值的: f(1)=0.082*x(1)+0.072*x(2)+0.065*x(3)+0.054*x(4)+0.038*x(5)+0.057*x(6)+0. 045*x(7) 求最小值的: f(2)=0.072*x(1)+0.063*x(2)+0.057*x(3)+0.05*x(4)+0.032*x(5)+0.0442*x(6)+0. 0675*x(7) f(3)=128*x(1)+78.1*x(2)+64.1*x(3)+43*x(4)+58.1*x(5)+36.9*x(6)+50.5*x(7)
约束条件: 0.082*x(1)+0.072*x(2)+0.065*x(3)+0.054*x(4)+0.038*x(5)+0.057*x(6)+0.045*x (7)>=7.2 0.072*x(1)+0.063*x(2)+0.057*x(3)+0.05*x(4)+0.032*x(5)+0.0442*x(6)+0.0675 *x(7)<=264.4 128*x(1)+78.1*x(2)+64.1*x(3)+43*x(4)+58.1*x(5)+36.9*x(6)+50.5*x(7)<=6971 9 lb=[0,0,0,0,0,0,0] ub=[426,390,430,374,445,534,476] f(1),f(2),f(3)的权值分别是:0.193,0.083,0.724 程序代码: %====================== function z=fgoalattain % 多目标最优化 clear all; clc % 给定目标,权重按目标比例确定,给出初值 options = optimset('TolCon',1e-008) goal = [-7 264 69000]; weight = [0.193 0.083 0.724]; x0 = [1 1 1 1 1 1 1]; % 给出约束条件的系数 A=[-0.082 -0.072 -0.065 -0.054 -0.038 -0.057 -0.045;0.072 0.063 0.057 0.05 0.032 0.0442 0.0675;128 78.1 64.1 43 58.1 36.9 50.5] B=[-7.2; 264.4;69719] Aeq = []; Beq = []; lb=[0,0,0,0,0,0,0] ub=[426,390,430,374,445,534,476] % 求解 [x,fval,attainfactor,exitflag] = fgoalattain(@ObjFun,x0,goal,weight,A,B,Aeq,Beq,lb,ub) % ------------------------------------------------------------------ function f = ObjFun(x) f1=0.082*x(1)+0.072*x(2)+0.065*x(3)+0.054*x(4)+0.038*x(5)+0.057*x(6)+0.04 5*x(7);
第四章 目标规划
第四章目标规划 (Goal programming)第一节目标规划问题及其数学模型第二节目标规划的图解法 第三节解目标规划的单纯形法 第四节目标规划的灵敏度分析 第五节目标规划应用举例
目标规划问题及其数学模型 一、目标规划问题的提出 例:某工厂生产两种产品,受到原材料供应和设备工时的限制。在单位利润等有关数据已知的前提条件下,要求制订一个获利最大的生产计划。具体数据见表 产品甲乙限量 原材料(kg/件)51060 设备工时(h/件)4440 利润(元/件)68
x 1和x 2,当用线性规划来描 述和解决这个问题时,其数学模型为 ?????≥≤+≤++=0,40 4 46010586max 2 121212 1x x x x x x x x z 其最优解,即最优生产计划为x 1=8件,x 2=2件, max z =64元。 从线性规划的角度看,问题似乎可以得到圆满解决。但线性规划是一个单目标最优化问题。如果站在工厂计划人员的立场上对此进行评价的话,问题就不是这么简单了。
、整数规划和非线性规划都只有一个目标函数,但在实际问题中往往要考虑多个目标。 例如,设计一个新产品的工艺过程,不仅希望利润大,而且希望: 产量高 消耗低 质量好 投入少等。 由于需要同时考虑多个目标,使这类多目标问题要比单目标问题复杂得多,不仅有主次之分, 而且有时会互相矛盾。 这就给用传统方法来解决多目标问题带来一定困难。
年,查恩斯(A. Charnes) 和库伯(W. W. Cooper)提出目标规划(goal programming),其目的就是为了解决多目标问题,该方法得到广泛重视和较快发展。 现代决策: 强调定量分析和定性分析相结合, 强调硬技术和软技术相结合, 强调矛盾和冲突的合理性, 强调妥协和让步的必要性。 目标规划在处理实际问题时,承认各项决策要求的存在有其合理性; 在作最终决策时,不强调绝对意义上的最优性,而是尽可能求出接近理想值的解——满意解。
运筹学--第四章 多目标规划
109 习题四 4.1 分别用图解法和单纯形法求解下述目标规划问题 (1) min z =p 1(+1d ++2d )+p 2-3d st. -x 1+ x 2+ d -1- d + 1=1 -0.5x 1+ x 2+ d - 2-d + 2=2 3x 1+3x 2+ d -3- d +3=50 x 1,x 2≥0;d -i ,d +i ≥0(i =1,2,3) (2) min z =p 1(2+1d +3+2d )+p 2-3d +p 3+4d st. x 1+ x 2+d -1-d + 1 =10 x 1 +d -2-d +2 =4 5x 1+3x 2+d -3-d +3 =56 x 1+ x 2+d -4-d +4 =12 x 1,x 2≥0;d -i ,d +i ≥0(i =1, (4) 4.2 考虑下述目标规划问题 min z =p 1(d +1+d +2)+2p 2d -4+p 2d -3+p 3d -1 st. x 1 +d -1-d +1=20 x 2+d -2-d +2=35 -5x 1+3x 2+d - 3-d + 3=220 x 1-x 2+d -4-d +4=60 x 1,x 2≥0;d -i ,d +i ≥0(i =1, (4) (1)求满意解; (2)当第二个约束右端项由35改为75时,求解的变化; (3)若增加一个新的目标约束:-4x 1+x 2+d -5-d +5=8,该目标要求尽量达 到目标值,并列为第一优先级考虑,求解的变化; (4)若增加一个新的变量x 3,其系数列向量为(0,1,1,-1)T ,则满意解如何变化? 4.3 一个小型的无线电广播台考虑如何最好地来安排音乐、新闻和商业节目时间。依据法律,该台每天允许广播12小时,其中商业节目用以赢利,每小时可收入250美元,新闻节目每小时需支出40美元,音乐节目每播一小时费用为17.50美元。法律规定,正常情况下商业节目只能占广播时间的20%,每小时至少安排5分钟新闻节目。问每天的广播节目该如何安排?优先级如下: P 1:满足法律规定要求; P 2:每天的纯收入最大。 试建立该问题的目标规划模型。
7.运筹学之目标规划(胡运权版)
第七章目标规划 §1 目标规划的提出 线性规划问题是讨论一个给定的线性目标函数在一组线性约束条件下的最大值或最小值问题。对于一个实际问题,管理科学者根据管理层决策目标的要求,首先确定一个目标函数以衡量不同决策的优劣,且根据实际问题中的资源、资金和环境等因素对决策的限制提出相应的约束条件以建立线性规划模型;然后用计算机软件求出最优方案并作灵敏度分析以供管理层决策之用。而在一些问题中,决策目标往往不只一个,且模型中有可能存在一些互相矛盾的约束条件的情况,用已有的线性规划的理论和方法无法解决这些问题。因此,1961年美国学者查恩斯(A.Charnes)和库柏(W.W.Coopor)提出了目标规划的概念与数学模型,以解决经济管理中的多目标决策问题。 我们将通过几个例子来说明在实际应用中线性规划存在一系列的局限性。 例1某厂生产A、B两种产品每件所需的劳动力分别为4个人工和6个人工,所需设备的单位台时均为1。已知该厂有10个单位机器台时提供制造这两种产品,并且至少能提供70个人工。又,A、B产品的利润,每件分别为300元和500元。试问:该厂各应生产多少件A、B产品,才能使其利润值最大? 解设该厂能生产A、B产品的数量分别为 ,x x件,则有 12
12 1212max 30050010..4670 0, 1,2.j z x x x x s t x x x j =+?+≤?+≥??≥=? 图解法求解如下: 由上图可得,满足约束条件的可行解集为?,即机时约束和人工约束之间产生矛盾,因而该问题无解。但在实际中,该厂要增加利润,不可能不生产A 、B 两种产品,而由线性规划模型无法为其找到一个合适的方案。 例2 某厂为进行生产需采购A 、B 两种原材料,单价分别为70元/公斤和50元/公斤。现要求购买资金不超过5000元,总购买量不少于80公斤,而A 原材料不少于20公斤。问如何确定最好的采购方案(即花掉的资金最少,购买的总量最大)? 解 这是一个含有两个目标的数学规划问题。设12,x x 分别为购买两种 原材料的公斤数,()112,f x x 为花掉的资金,()212,f x x 为购买的总量。建 立该问题的数学模型形式如下:
7.运筹学之目标规划(胡运权版)
盛年不重来,一日难再晨。及时宜自勉,岁月不待人。 第七章目标规划 §1 目标规划的提出 线性规划问题是讨论一个给定的线性目标函数在一组线性约束条件下的最大值或最小值问题。对于一个实际问题,管理科学者根据管理层决策目标的要求,首先确定一个目标函数以衡量不同决策的优劣,且根据实际问题中的资源、资金和环境等因素对决策的限制提出相应的约束条件以建立线性规划模型;然后用计算机软件求出最优方案并作灵敏度分析以供管理层决策之用。而在一些问题中,决策目标往往不只一个,且模型中有可能存在一些互相矛盾的约束条件的情况,用已有的线性规划的理论和方法无法解决这些问题。因此,1961年美国学者查恩斯(A.Charnes)和库柏(W.W.Coopor)提出了目标规划的概念与数学模型,以解决经济管理中的多目标决策问题。 我们将通过几个例子来说明在实际应用中线性规划存在一系列的局限性。 例1某厂生产A、B两种产品每件所需的劳动力分别为4个人工和6个人工,所需设备的单位台时均为1。已知该厂有10个单位机器台时提供制造这两种产品,并且至少能提供70个人工。又,A、B产品的利润,每件分别为300元和500元。试问:该厂各应生产多少件A、B产品,才能使其利润值最大? 解设该厂能生产A、B产品的数量分别为 ,x x件,则有 12
12 12 12 max300500 10 ..4670 0,1,2. j z x x x x s t x x x j =+ ?+≤ ? +≥ ? ?≥= ? 图解法求解如下: 由上图可得,满足约束条件的可行解集为?,即机时约束和人工约束之间产生矛盾,因而该问题无解。但在实际中,该厂要增加利润,不可能不生产A、B两种产品,而由线性规划模型无法为其找到一个合适的方案。 例2某厂为进行生产需采购A、B两种原材料,单价分别为70元/公斤和50元/公斤。现要求购买资金不超过5000元,总购买量不少于80公斤,而A原材料不少于20公斤。问如何确定最好的采购方案(即花掉的资金最少,购买的总量最大)? 解这是一个含有两个目标的数学规划问题。设 12 ,x x分别为购买两种 原材料的公斤数,() 112 , f x x为花掉的资金,() 212 , f x x为购买的总量。建立该问题的数学模型形式如下:
