地铁线路设计规划模型数学建模知识讲解

地铁线路设计规划模型

一、摘要

二、问题重述

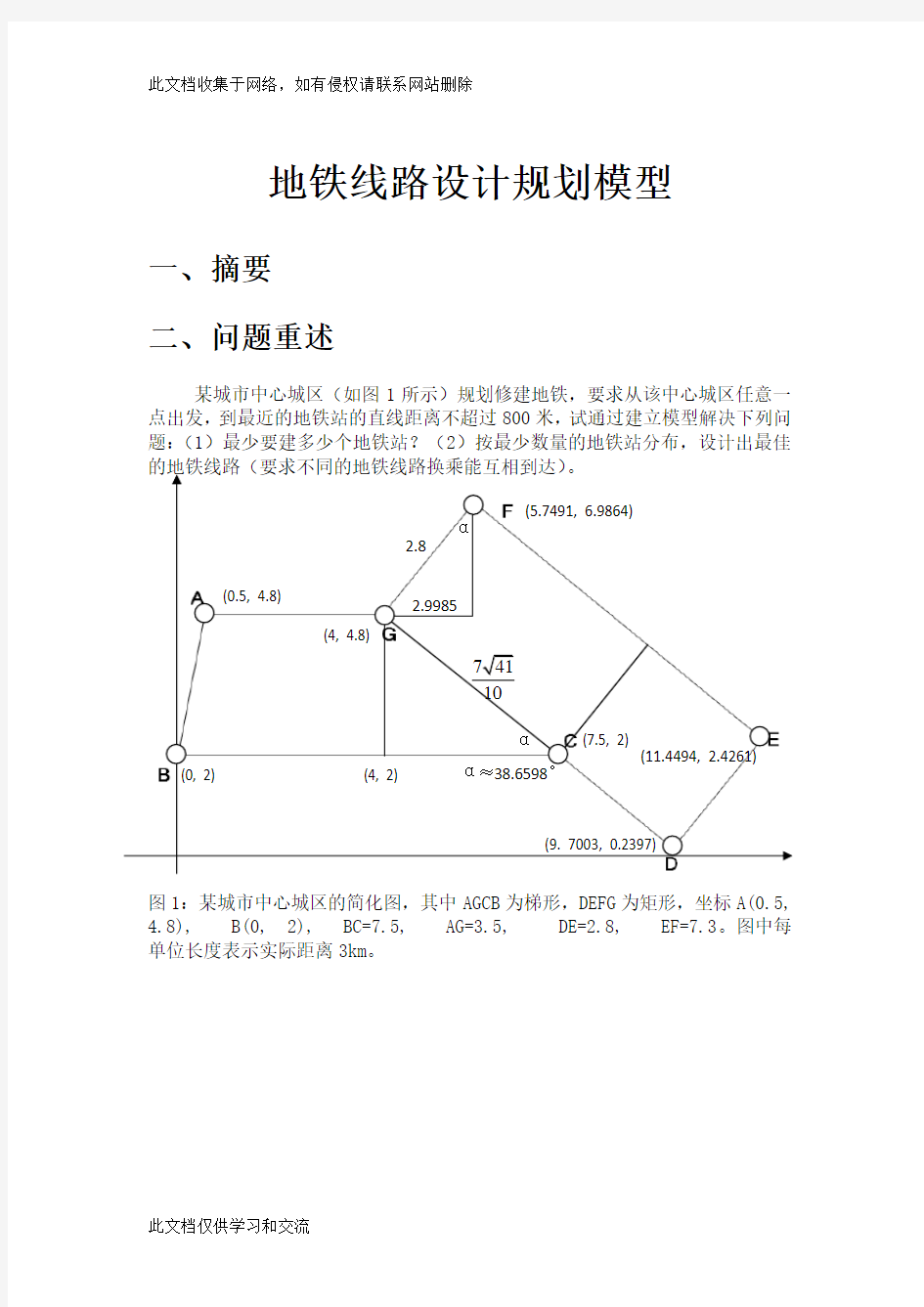
某城市中心城区（如图1所示）规划修建地铁，要求从该中心城区任意一点出发，到最近的地铁站的直线距离不超过800米，试通过建立模型解决下列问题：（1）最少要建多少个地铁站？（2）按最少数量的地铁站分布，设计出最佳

图1：某城市中心城区的简化图，其中AGCB为梯形，DEFG为矩形，坐标A(0.5, 4.8), B(0, 2), BC=7.5, AG=3.5, DE=2.8, EF=7.3。图中每单位长度表示实际距离3km。

三、名词和符号说明四、模型假设五、问题分析

本题中规划的中心城区是一个不规则的图形，所以地铁分布时不能简单的按规律建立。我们设想的是先建造一种拥有最佳有效面积的地铁站点。首先，我们利用微分的思想，以地铁站为圆心，800m 为半径画圆再在圆内画内接多边形，希望最后能将两个圆内内接多边形重叠之后重叠的面积尽量少。之后，我们又从化学原子排列规律中得到了另一种模型，从中我们再比较选出最佳的模型。之后，我们利用CAD 按比例画出题目的图与地铁站点阵进行比较，为了获取地铁站间的距离，我们用C 语言编了一个程序计算出每个地铁站的距离矩阵，最后再利用Matlab 画出地铁站点图的最小生成树，从中得出最佳路线。

思路一：我们抛开这个城市的图形，以地铁站为圆心，800m 为半径画圆，

如图5-1。

图 5-1

然后，为了使所有两个地铁站能无缝地接在一起，我们把这个图尽可能多地划分成内接多边形。如图（b ）~（e ）。

....

图 5-

2 图5-

3 图 5-

4 图 5-5

这里，我们又出现一个新的问题，要使内接多边形能接在一起，内接多边形的角度必须能整除360，n 边形内角和为(2)180n -?，每个内角为(2)180n n -?÷。满足整除360，只有n=3，4，6。

现在，我们先假设

n=3（图5-3），则每个点有效面积2

33r S a =

； n=4（图5-4），则这个点有效面积22r S a = ； n=6（图5-5），则这个点有效面积2

33r S a =

。所以可得，取n=6时，有效面积a S 最大，即将地铁站看成内接六边形时，两个地铁站之间衔接起来有效面积最大。

思路二:

考虑到每个地铁站建成后都会覆盖附近面积为S 的区域。但由思路一可知，

a S S <，所以思路二的基本想法就是允许S 有适当重叠，并得到重叠时的状态，

然后算出重叠状态下对于每个站点与其他站点交盖的面积'a S ，通过比较各种重合状态下的'a S ，选得最小的，就是我们要得到的最优设计。

具体实现：

1. 考虑四个圆的圆心组成矩形的情况

图 5-6 图 5-7 图 5-8

可以看到，中间的A 区域没有被覆盖，此时有两种解决方案，方案一是在A 区域的中心在建一个站，覆盖掉空白的部分，如图5-7；方案二是直接使四个圆重叠，覆盖空白部分，如图5-8。

很容易发现，对于上面两种情况，每一个圆与其他圆共同交盖的面积都是

2224 2.2832r r π-≈，即阴影所示区域。

2.考虑四个圆的圆心组成菱形的情况：

如果组成普通菱形（锐角不是60度），和正方形相比，每一个圆的交盖面积

'a S 增加。

3.考虑锐角为60度的菱形：

图 5-9 图5-10

方案三：如图5-9是正六边形，其中正六边形边长为r ,对每一个圆来说交

盖面积'a S 为222 1.0870r π-≈；

方案四：如图5-10，对每一个圆来

说交盖面积

a S 为22

2 3.68512

r r π-

≈。比较四种情况的'a S ，方案三的'a S 是最小的，从而有效面积

'22

a a S S S r =-

=。

综合上述两种思路，最后得出的最佳有效面积皆为2

a S r =，因此，接下来我们就选择将每个地铁站的覆盖面积视作正六边形。

六、模型建立与优化

问题一：最少要建多少个地铁站？

以一个地铁站的有效面积为内接六边形2

a S r =

，在 Auto CAD 中将边长为800单位的正六边形用阵列方法排出20×20的矩阵。将原题的城市图中各端点的坐标求出并放大比例按坐标画进地铁站六边形矩阵阵中，然后将城市图平移，旋转，比较不同情况下，城市图所含盖的正六边形数目最少的情况。

由于使用枚举法列举城市图与六边形之间关系的各种情况并清点城市图覆盖的六边形数目过于繁琐，我们考虑了一种优化方法。先让城市图的某一条边覆盖的正六边形数目最少，再考虑其他边覆盖的数目最少的情况，再通过平移等方法尽量减少七个边覆盖的正六边形的数目，以此逼近最优解。数六边形数目的时候为防止人工数数出错，我们采用将范围内的六边形载入选区并由电脑技术的方法保证了数据的真实性和准确性。

如下图6-1至图6-10列出了我们枚举的八种特殊情况。

图6-1 矩形短边横排233

图6-2 矩形短边斜排左对齐226

图6-3 矩形长边斜排左对齐226

图6-4 矩形长边斜排右对齐227

图6-5 矩形长边横排左对齐226

图6-6 矩形长边横排右对齐231

图6-7 梯形长边横排233

图6-8 梯形长边斜排230

由以上八张截图可发现，图6-2，图6-3，图6-5的六边形数目均为226，因此可以得出最小覆盖正六边形的数目为226个的结论，即最少要建226个地铁站才能完全铺满这个城市。经过多方比较，我们选取了最易于生成最小树的图6-5作为我们第二问的地铁线路设计目标。

问题二：按最少数量的地铁站分布，设计出最佳的地铁线路（要求不同的地铁线路换乘能互相到达）

我们在Auto CAD 中将图6-5情况下的226个正六边形替换为800半径的圆并按一定的顺序编号（图6-9），并且利用Auto CAD 的查询—列表显示功能将226个圆的圆心坐标全部输出（输出内容见附件8.1），通过Word 、Excel 等一系列Office 软件对数据的编辑操作，得到了226个点的有序坐标的txt 格式文件（数据见附件8.2）。用Visual C++编程软件将txt 文件中的所有数据依次导入并编程（C++文件见附件8.3）计算每一个点到其他225个点的距离导出至新的txt 文件（数据量过大不适合在附件中呈现）。用Matlab 软件将距离值全部导入，并利用Primf 最小生成树算法求出生成的最小树结果（结果与Primf 代码见附件8.4）。最后在Auto CAD 中绘出最小树（图6-10），并归纳了31条地铁线路（不拐弯的一条直线视为一条线路）共62组坐标点（见表6-1），在Visual C++中求出地铁线路总长度为311769m （编程代码见附件8.5）。

图 6-9 226个地铁站按顺序编号

3 6 8 1

2 4 5 7 9 10 11 12 1

3 14

15 16 17 18 19 20 21

22 23 24

28 29 35 34

32 31 30 36 42 41 40 39 38 37 49

48 47 46 45

43 56

55 54 53 52 51 50 57

63 6261 60 59 58 73 72 71 70 69 68 67 66 65

78 77 76 75 7492 91 90 89 88 87 86 85 84 83 102 101 100 99 98 97 96 95 94 93 114 113 112 111 110 109 108 107 106 105 104 103 126 125 124 123 122 121 120 119 118 117 116 115 139 138 137 136 135 134 133 132 131 130 129 128 127 152 151 150 149 148 147 146 145 144 143 142 141 140 166

165

164

163

162

161

160

159

158

157

156 155 154 153

181 180 179 178 177 176 175 174 173 172 171 170 169 168 167 190 189 188 187 186 185 184 183 182 208

207 206 205 204 203 202 201 200 216

215

214

213 212 211 210 209 222 221 220 219 218 217 199

198 197 196 195 194 193 192 191 225 224 223 226

图6-10 最小生成树地铁线路图

七、模型的评价与推广

八、附录

附录8.1：Auto CAD输出的226个圆的圆心坐标及其他

命令: _list 找到226 个

圆图层: 0

空间: 模型空间

句柄= 188e

圆心点，X=30400.0000 Y=15242.0471 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1880

圆心点，X=28000.0000 Y=19398.9690 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 187f

圆心点，X=28000.0000 Y=18013.3284 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 187e

圆心点，X=28000.0000 Y=16627.6878 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 187d

圆心点，X=28000.0000 Y=15242.0471 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 187c

圆心点，X=28000.0000 Y=13856.4065 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 187b

圆心点，X=28000.0000 Y=12470.7658 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1871

圆心点，X=25600.0000 Y=22170.2503 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1870

圆心点，X=25600.0000 Y=20784.6097 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 186f

圆心点，X=25600.0000 Y=19398.9690 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 186e

圆心点，X=25600.0000 Y=18013.3284 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 186d

圆心点，X=25600.0000 Y=16627.6878 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 186c

圆心点，X=25600.0000 Y=15242.0471 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 186b

圆心点，X=25600.0000 Y=13856.4065 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 186a

圆心点，X=25600.0000 Y=12470.7658 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1869

圆心点，X=25600.0000 Y=11085.1252 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 185f

圆心点，X=23200.0000 Y=20784.6097 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 185e

圆心点，X=23200.0000 Y=19398.9690 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 185d

圆心点，X=23200.0000 Y=18013.3284 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 185c

圆心点，X=23200.0000 Y=16627.6878 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 185b

圆心点，X=23200.0000 Y=15242.0471 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 185a

圆心点，X=23200.0000 Y=13856.4065 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1859

圆心点，X=23200.0000 Y=12470.7658 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1858

圆心点，X=23200.0000 Y=11085.1252 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1857

圆心点，X=23200.0000 Y=9699.4845 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 184c

圆心点，X=20800.0000 Y=18013.3284 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 184b

圆心点，X=20800.0000 Y=16627.6878 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 184a

圆心点，X=20800.0000 Y=15242.0471 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1849

圆心点，X=20800.0000 Y=13856.4065 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1848

圆心点，X=20800.0000 Y=12470.7658 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1847

圆心点，X=20800.0000 Y=11085.1252 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1846

圆心点，X=20800.0000 Y=9699.4845 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1845

圆心点，X=20800.0000 Y=8313.8439 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1844

圆心点，X=20800.0000 Y=6928.2032 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1843

圆心点，X=20800.0000 Y=5542.5626 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1842

圆心点，X=20800.0000 Y=4156.9219 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1841

圆心点，X=20800.0000 Y=2771.2813 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1840

圆心点，X=20800.0000 Y=1385.6406 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 183f

圆心点，X=20800.0000 Y= 0.0000 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 183a

圆心点，X=18400.0000 Y=16627.6878 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1839

圆心点，X=18400.0000 Y=15242.0471 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1838

圆心点，X=18400.0000 Y=13856.4065 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1837

圆心点，X=18400.0000 Y=12470.7658 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1836

圆心点，X=18400.0000 Y=11085.1252 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1835

圆心点，X=18400.0000 Y=9699.4845 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1834

圆心点，X=18400.0000 Y=8313.8439 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1833

圆心点，X=18400.0000 Y=6928.2032 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1832

圆心点，X=18400.0000 Y=5542.5626 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1831

圆心点，X=18400.0000 Y=4156.9219 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 1830

圆心点，X=18400.0000 Y=2771.2813 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 182f

圆心点，X=18400.0000 Y=1385.6406 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

空间: 模型空间

句柄= 182e

圆心点，X=18400.0000 Y= 0.0000 Z= 0.0000

半径800.0000

周长5026.5482

面积2010619.2983

圆图层: 0

规划模型求解指导老师：组员：组员分工实际的内容： 1·简要介绍线性规划的历史线性规划是运筹学中最基本、应用最广泛的分支。规划模型是一类有着广泛应用的确定性的系统优化模型，1939年，苏联数学家康托洛维奇出版《生产组织和计划中的数学方法》一书. 1947年，美国数学家丹兹格提出了线性规划问题的单纯形求解方法. 1951年，美国经济学家库普曼斯（J.C.Koopmans,1910—1985）出版《生产与配置的活动分析》一书. 1950～1956年，线性规划的对偶理论出现. 1960年，丹兹格与沃尔夫（P.Wolfe）建立大规模线性规划问题的分解算法. 1975年，康托洛维奇与库普曼斯因“最优资源配置理论的贡献”荣获诺贝尔经济学奖. 1978年，苏联数学家哈奇扬（L.G.Khachian）提出求解线性规划问题的多项式时间算法（内点算法），具有重要理论意义. 1984年，在美国贝尔实验室工作的印度裔数学家卡玛卡（N.Karmarkar）提出可以有效求解实际线性规划问题的多项式时间算法——Karmarkar算法.

线性规划的基本点就是在满足一定约束条件下，使预定的目标达到最优. 现在线性规划已不仅仅是一种数学理论和方法，而且成了现代化管理的重要手段，是帮助管理者与经营者做出科学决策的一个有效的数学技术. 历史表明，重要数学概念对数学发展的作用是不可估量的，函数概念对数学发展的影响，可以说是贯穿古今、旷日持久、作用非凡，回顾函数概念的历史发展，看一看函数概念不断被精炼、深化、丰富的历史过程，是一件十分有益的事情，它不仅有助于我们提高对函数概念来龙去脉认识的清晰度，而且更能帮助我们领悟数学概念对数学发展，数学学习的巨大作用。 2·线性规划的原理：线性规划是合理利用、调配资源的一种应用数学方法。它的基本思路就是在满足一定的约束条件下，使预定的目标达到最优。它的研究内容可归纳为两个方面：一是系统的任务已定，如何合理筹划，精细安排，用最少的资源(人力、物力和财力)去实现这个任务；二是资源的数量已定，如何合理利用、调配，使任务完成的最多。前者是求极小，后者是求极大。线性规划是在满足企业内、外部的条件下，实现管理目标和极值(极小值和极大值)问题，就是要以尽少的资源输入来实现更多的社会需要的产品的产出。因此，线性规划是辅助企业“转轨”、“变型”的十分有利的工具，它在辅助企业经营决策、计划优化等方面具有重要的作用。其一般形式为： n n n n n n b x a x a x a b x a x a x a x c x c x c x f =+++=+++→+++= 2 2222121112121112211min )(

数学建模线性规划模型数学建模教案,线性规划模型一、问题的提出在生产管理和经营活动中经常提出一类问题，即如何合理地利用有限的人力、物力、财力等资源，以便得到最好的经济效果。例1 若需在长为4000mm的圆钢上，截出长为698mm和518mm两种毛坯，问怎样截取才能使残料最少, 初步分析可以先考虑两种“极端”的情况: (1)全部截出长为698mm的甲件，一共可截出 EQ F(4000,698) ?5件，残料长为510mm。 (2)全部截出长为518mm的乙件，一共可截出 EQ F(4000,518) ?7件，残料长为374mm。由此可以想到，若将 x个甲件和y 个乙件搭配起来下料，是否可能使残料减少,把截取条件数学化地表示出来就是: 698 x + 518y ? 4000 x ，y都是非负整数目标是使:z = EQ F(698x + 518y,4000) (材料利用率)尽可能地接近或等于1。(尽可能地大) 该问题可用数学模型表示为: 目标函数 : max z = EQ F(698x + 518y,4000) 满足约束条件: 698 x + 518y ? 4000 ， (1) x ，y都是非负整数 . (2) 例2 某工厂在计划期内要安排生产I 、II两种产品，已知生产单位产品所需的设备台数及A、B两种原料的消耗，如下表所示。

I II 设备 1 2 8台数原材料A 4 0 16kg 原材料B 0 4 12kg 该工厂每生产一件产品I可获利 2 元，每生产一件产品II可获利 3 元，问应如何安排生产计划使工厂获利最多, 这问题可以用以下的数学模型来描述:设 x, x分别表示在计划期内产品I、II 的产量。 1 2 因为设备的有效台数为8 ，这是一个限制产量的条件，所以在确定I 、II的产量时，要考虑不超过设备的有效台数，即可用不等式表示为: x + 2x ? 8 . 1 2同理，因原材料A 、B的限量，可以得到以下不等式: 4 x ? 16 1 4 x ? 12. 2 该工厂的目标是在不超过所有资源限量的条件下，如何确定产量x、x以得到最大 1 2的利润。若用 z 表示利润，这时z = 2x + 3 x。综上所述，该计划问题可用数学模型表 1 2 示为: 目标函数 : max z = 2x + 3 x 1 2 满足约束条件: x + 2x ? 8 1 2 4 x ? 16 1 4 x ? 12. 2

整数规划的数学模型及解的特点整数规划IP (integer programming)：在许多规划问题中，如果要求一部分或全部决策变量必须取整数。例如，所求的解是机器的台数、人数、车辆船只数等，这样的规划问题称为整数规划，简记IP 。松弛问题(slack problem)：不考虑整数条件，由余下的目标函数和约束条件构成的规划问题称为该整数规划问题的松弛问题。若松弛问题是一个线性规化问题，则该整数规划为整数线性规划(integer linear programming)。一、整数线性规划数学模型的一般形式 ∑==n j j j x c Z 1 min)max(或中部分或全部取整数n j n j i j ij x x x m j n i x b x a t s ,...,,...2,1,...,2,10 ),(.211 ==≥=≥≤∑= 整数线性规划问题可以分为以下几种类型 1、纯整数线性规划(pure integer linear programming)：指全部决策变量都必须取整数值的整数线性规划。有时，也称为全整数规划。

2、混合整数线性规划(mixed integer liner programming)：指决策变量中有一部分必须取整数值，另一部分可以不取整数值的整数线性规划。 3、0—1型整数线性规划(zero —one integer liner programming)：指决策变量只能取值0或1的整数线性规划。 1 解整数规划问题 0—1型整数规划 0—1型整数规划是整数规划中的特殊情形，它的变量仅可取值0或1，这时的 ???? ? ????≥≤+≥+≤-+=且为整数0,5210453233max 2121212121x x x x x x x x x x z

数学建模第一章线性规划 §1 线性规划在人们的生产实践中，经常会遇到如何利用现有资源来安排生产，以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支—数学规划，而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。自从1947年G. B. Dantzig 提出求解线性规划的单纯形方法以来，线性规划在理论上趋向成熟，在实用中日益广泛与深入。特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划的适用领域更为广泛了，已成为现代管理中经常采用的基本方法之一。 1.1 线性规划的实例与定义例1 某机床厂生产甲、乙两种机床，每台销售后的利润分别为4000元与3000元。生产甲机床需用B A 、机器加工，加工时间分别为每台2小时和1小时；生产乙机床需用C B A 、、三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为A 机器10小时、B 机器8小时和C 机器7小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？上述问题的数学模型：设该厂生产1x 台甲机床和2x 乙机床时总利润最大，则21,x x 应满足（目标函数） 2134m ax x x z += (1) s.t. （约束条件） ?????? ?≥≤≤+≤+0 ,781022122 121x x x x x x x （2）这里变量21,x x 称之为决策变量，（1）式被称为问题的目标函数，（2）中的几个不等式是问题的约束条件，记为s.t.(即subject to)。

上述即为一规划问题数学模型的三个要素。由于上面的目标函数及约束条件均为线性函数，故被称为线性规划问题。总之，线性规划问题是在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。在解决实际问题时，把问题归结成一个线性规划数学模型是很重要的一步，但往往也是困难的一步，模型建立得是否恰当，直接影响到求解。而选取适当的决策变量，是我们建立有效模型的关键之一。 1.2 线性规划的Matlab 标准形式线性规划的目标函数可以是求最大值，也可以是求最小值，约束条件的不等号可以是小于号也可以是大于号。为了避免这种形式多样性带来的不便，Matlab 中规定线性规划的标准形式为 b Ax x c x T ≤ that such min 其中c 和x 为n 维列向量，b 为m 维列向量，A 为n m ?矩阵。例如线性规划 b Ax x c x T ≥ that such max 的Matlab 标准型为 b Ax x c x T -≤-- that such min 1.3 线性规划问题的解的概念一般线性规划问题的标准型为 ∑==n j j j x c z 1min (3) ∑==≤n j i j ij m i b x a 1,,2,1 s.t.Λ (4) 可行解满足约束条件（4）的解),,,(21n x x x x Λ=，称为线性规划问题的可行解，而使目标函数（3）达到最小值的可行解叫最优解。

甲乙公司不合作即竞争下所争取到的不同名专业推广者所建立的不同动态规划模型的组合方案如下：其中X 为可能竞争到的专业推广者人数，即动态规划模型中第一天的

专业推广者推广能力的份数，Y 为第二天需要的专业推广者推广能力的份数，即第三天安排从事推广工作的专业推广者的人数；Z 为第三天需要的专业推广者推广能力的份数，即第三天安排从事推广工作的专业推广者的人数；a 为x 名专业推广者累计从事培训工作出来的兼职推广者的批数（每批20 人），其中，有多种组合方案；甲公司雇佣这些兼职推广者均工作一天，从事推广工作，第二天辞退a ?b 批兼职推广员，其余的b 批继续从事推广工作一天后辞退，即兼职宣传员总共最多雇佣2 天；cost 为花费的成本，即资金的使用数量；F 为不同方案下所达到的总推广效益。上表可以提供给甲公司做决策依据，根据效益的大小甲公司可以决策的目标方向顺序是从①--⑧，即不合作的情况下甲公司可以尽量争取到9 人，如若不行，考虑争取4 人。 §5.4 0—1型整数规划模型 1、 0—1型整数规划模型概述整数规划指的是决策变量为非负整数值的一类线性规划，在实际问题的应用中，整数规划模型对应着大量的生产计划或活动安排等决策问题，整数规划的解法主要有分枝定界解法及割平面解法（这里不作介绍，感兴趣的读者可参考相关书籍）。在整数规划问题中，0—1型整数规划则是其中较为特殊的一类情况，它要求决策变量的取值仅为0或1，在实际问题的讨论中，0—1型整数规划模型也对应着大量的最优决策的活动与安排讨论，我们将列举一些模型范例，以说明这个事实。 0—1型整数规划的的数学模型为：目标函数 n n x c x c x c z M i n M a x +++= 2211)( 约束条件为： ???? ?? ?==≥≤++=≥≤++=≥≤++1 | 0 ) ,() ,() ,(2211222221211 1212111n m n mn m m n n n n x x x b x a x a x a b x a x a x a b x a x a x a , , ,21 这里，0 | 1表示0或1。 2、0—1型整数规划模型的解法

线性规划 1.简介：线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,它是辅助人们进行科学管理的一种数学方法.在经济管理、交通运输、工农业生产等经济活动中，提高经济效果是人们不可缺少的要求，而提高经济效果一般通过两种途径：一是技术方面的改进，例如改善生产工艺，使用新设备和新型原材料.二是生产组织与计划的改进，即合理安排人力物力资源. 线性规划所研究的是：在一定条件下，合理安排人力物力等资源，使经济效果达到最好.规划问题。一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性线性约束条件的解叫做可行解，由所有可行解组成的集合叫做可行域。 (x)都是线性函数，则该模型称为在优化模型中，如果目标函数f(x)和约束条件中的g i 线性规划。 2.线性规划的3个基本要素（1）决策变量（2）目标函数f(x) (x)≤0称为约束条件）（3）约束条件（g i 3.建立线性规划的模型（1）找出待定的未知变量（决策变量），并用袋鼠符号表示他们。（2）找出问题中所有的限制或者约束，写出未知变量的线性方程或线性不等式。

（3）找到模型的目标或判据，写成决策变量的线性函数，以便求出其最大值或最小值。以下题为例，来了解一下如何将线性规划用与实际的解题与生活中。生产计划问题某工厂生产甲乙两种产品，每单位产品消耗和获得的利润如表试拟订生产计划，使该厂获得利润最大解答：根据解题的三个基本步骤（1）找出未知变量，用符号表示：设甲乙两种产品的生产量分别为x 1与x 2 吨，利润为z万元。（2）确定约束条件：在这道题目当中约束条件都分别为：钢材，电力，工作日以及生产量不能为负的限制钢材：9x 1+5 x 2 ≤360，电力：4x 1+5 x 2 ≤200，工作日：3x 1+10 x 2 ≤300， x 1≥0 ，x 2 ≥0，（3）确定目标函数： Z=7x 1+12 x 2

整数规划模型

实际问题中 x x x x f z Max Min T n "),(),()(1==或的优化模型 m i x g t s i ",2,1,0)(..=≤x ~决策变量f (x )~目标函数g i (x )≤0~约束条件多元函数决策变量个数n 和数线性规划条件极值约束条件个数m 较大最优解在可行域学规非线性规划解的边界上取得划整数规划

Programming +Integer 所有变量都取整数，称为纯整数规划；有一部分取整数，称为混合整数规划；限制取0，1称为0‐1型整数规划。型整数规划

+整数线性规划 max(min) n z c x =1j j j n =∑1 s.t. (,) 1,2,,ij j i j a x b i m =≤=≥=∑"12 ,,,0 () n x x x ≥"且为整数或部分为整数

+例：假设有m 种不同的物品要装入航天飞机，它们的重量和体积分别为价值为w j 和v j ，价值为c j ，航天飞机的载重量和体积限制分别为W 和V ，如何装载使价值最大化？ m 1?1 max j j j c y =∑ 1 0j j y =?被装载 s.t. m j j v y V ≤∑0 j ?没被装载1 j m =1 j j j w y W =≤∑ 0 or 1 1,2,,j y j m =="

(Chicago)大学的Linus Schrage教授于1980年美国芝加哥(Chi)Li S h 前后开发, 后来成立LINDO系统公司（LINDO Systems Inc.），网址：https://www.360docs.net/doc/ed18074013.html, I）网址htt//li d LINDO: Interactive and Discrete Optimizer (V6.1) Linear(V61) LINGO: Linear Interactive General Optimizer (V8.0) LINDO——解决线性规划LP—Linear Programming，整数规划IP—Integer Programming问题。 LINGO——解决线性规划LP—Linear Programming，非线性规划NLP—Nonlinear Programming，整数规划IP—Integer Programming g g整划g g g 问题。

实验05 数学规划模型㈡（2学时）（第4章数学规划模型） 1.（求解）汽车厂生产计划（LP，整数规划IP）p101~102 (1) (LP)在模型窗口中输入以下线性规划模型 max z = 2x1 + 3x2 + 4x3 . + 3x2 + 5x3≤ 600 280x1 + 250x2 + 400x3≤ 60000 x1, x2, x3≥ 0 并求解模型。 ★(1) 给出输入模型和求解结果（见[101]）： model: TITLE汽车厂生产计划（LP）; !文件名：; max=2*x1+3*x2+4*x3; *x1+3*x2+5*x3<600; 280*x1+250*x2+400*x3<60000; end (2) (IP)在模型窗口中输入以下整数规划模型 max z = 2x1 + 3x2 + 4x3 . + 3x2 + 5x3≤ 600 280x1 + 250x2 + 400x3≤ 60000 x1, x2, x3均为非负整数

并求解模型。 LINGO函数@gin见提示。 ★(2) 给出输入模型和求解结果（见[102]模型、结果）：model: TITLE汽车厂生产计划（IP）; !文件名：; max=2*x1+3*x2+4*x3; *x1+3*x2+5*x3<600; 280*x1+250*x2+400*x3<60000; @gin(x1); @gin(x2); @gin(x3);!将x1,x2,x3限定为整数; end 2.（求解）原油采购与加工（非线性规划NLP，LP且IP）p104~107 模型：已知 ? ? ? ? ? ≤ ≤ + ≤ ≤ + ≤ ≤ = ) 1500 1000 ( 6 3000 ) 1000 500 ( 8 1000 ) 500 0( 10 ) ( x x x x x x x c 注：当500 ≤x≤ 1000时，c(x) = 10 × 500 + 8( x– 500 ) = (10 – 8 ) × 500 + 8x

《数学模型》教学大纲课程名称: 数学模型(Mathematical Model) 适用专业：应用数学、信息与计算科学课程学时: 48学时理论+32学时实验课程学分: 4 先修课程：微积分、线性代数、概率论考核方式：期末论文理论课教学大纲一、课程的性质与任务随着其它学科和计算机的迅速发展，数学已经向各个领域广泛渗透，数学已经由原来的高度抽象、严格推理和严密证明的理论课过渡成为解决许多边缘学科和交叉学科的关键技术。而数学一开始就是为了解决实际问题的需要而产生，数学模型或建立数学模型课程的开设就是一个朴素的回归。设立数学建模课程的主要目的是培养学生应用所学的数学基础知识（微积分、线性代数、概率统计）解决实际问题的能力，培养新型的应用型动手能力强的人才。本课程通过一系列典型案例的分析、学习和应用，使学生掌握解决实际问题的一般步骤和原理；通过一些必要的辅助计算软件（lingo优化软件、matlab科学计算软件等）的培训，培养学生新型的数学观：数学中很多的复杂而重复的计算，应该完全交给计算机去做，人就回到思考、分析、设计、评估等更重要的工作中去。由于实际问题的复杂性和广泛性，本课程在讲授不同类型的模型时，可以参考不同的教材和选取不同的计算软件，所以在教材的选取上本着灵活性和多样性，因而不同章节有不同的参考书。二、课程的内容第1章．数学建模概论 1.1 什么是数学模型

1.2 几个简单的建模案例 1.3 建立数学模型的基本方法和步骤 1.4 数学模型的特点和分类 1.5 数学建模能力的培养参考教材：《数学模型》.高教出版社.姜启源《数学建模与数学实验》.高教出版社.赵静《数学建模方法及其应用》高教出版社.韩中庚第2章. 初等数学模型 2.1 公平的席位分配问题 2.2 动物的身长和体重 2.3 空间点热源的扩散问题参考教材：《数学模型》.高教出版社.姜启源《数学建模与数学实验》.高教出版社.赵静第3章. 数学规划模型 3.1 线性和非线性规划模型相关概念 3.2 几种线性规划问题指派为问题运输问题材料切割问题配方问题排序问题多阶段生产计划问题生产流程问题参考教材：《数学模型》.高教出版社.姜启源《运筹学》.清华大学出版社.胡运权《管理运筹学》.高教出版社.韩伯棠《lingo优化软件》.清华大学出版社.谢金星第4章与图有关的优化问题 4.1 最短路径问题 4.2 流量问题 4.3 最优连线问题（最小树问题） 4.4 最优回路问题（哈密尔顿回路） 4.5 最小覆盖与最小配对问题参考教材：《运筹学》.清华大学出版社.胡运权《管理运筹学》.高教出版社.韩伯棠

-1- 第一章线性规划 §1 线性规划在人们的生产实践中，经常会遇到如何利用现有资源来安排生产，以取得最大经济效益的问题。此类问题构成了运筹学的一个重要分支—数学规划，而线性规划(Linear Programming 简记LP)则是数学规划的一个重要分支。自从1947 年G. B. Dantzig 提出求解线性规划的单纯形方法以来，线性规划在理论上趋向成熟，在实用中日益广泛与深入。特别是在计算机能处理成千上万个约束条件和决策变量的线性规划问题之后，线性规划的适用领域更为广泛了，已成为现代管理中经常采用的基本方法之一。 1.1 线性规划的实例与定义例1 某机床厂生产甲、乙两种机床，每台销售后的利润分别为4000 元与3000 元。生产甲机床需用A、B机器加工，加工时间分别为每台2 小时和1 小时；生产乙机床需用A、B、C三种机器加工，加工时间为每台各一小时。若每天可用于加工的机器时数分别为A 机器10 小时、B 机器8 小时和C 机器7 小时，问该厂应生产甲、乙机床各几台，才能使总利润最大？上述问题的数学模型：设该厂生产1 x 台甲机床和2 x 乙机床时总利润最大，则1 2 x , x 应满足（目标函数）1 2 max z = 4x + 3x (1) s.t.（约束条件） ?? ? ?? ? ? ≥ ≤ + ≤ + ≤ , 0 7 8 2 10 1 2 2 1 2 1 2 x x x x x x x （2）这里变量1 2 x , x 称之为决策变量，（1）式被称为问题的目标函数，（2）中的几个不等式是问题的约束条件，记为s.t.(即subject to)。由于上面的目标函数及约束条件均为线性

某银行经理计划用一笔资金进行有价证券的投资，可供购进的证券以及其信用等级、到期年限、收益如下表所示．按照规定，市政证券的收益可以免税，其他证券的收益需按50%的税率纳税．此表四问：（1）若该经理有1000万元资金，应如何投资？（2）如果能够以2.75%的利率借到不超过100万元资金，该经理应如何操作？（3）在1000万元资金情况下，若证券A 的税前收益增加为4.5%，投资应否改变？若证券C 的税前收益减少为4.8%，投资应否改变？解：设利润函数为M(x),投资A 、B 、C 、D 、E 五种类型的证券资金分别为12345,,,,x x x x x 万元，则由题设条件可知

12345123452341234512345123451234512345()0.0430.0270.0250.0220.0451000400 225 1.4()9154325(),,,,0 M x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =++++++++≤++≥++++≤++++++++≤++++≥ 利用MATLAB 求解最优解，代码如下： c=[-0.043 -0.027 -0.025 -0.022 -0.045]; A=[1 1 1 1 1;0 -1 -1 -1 0;0.6 0.6 -0.4 -0.4 3.6;4 10 -1 -2 -3]; b=[1000;-400;0;0]; Aeq=[]; beq=[]; vlb=[0;0;0;0;0]; vub=[]; [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub) 运行结果如下：

运筹学模型（一）本章重点：线性规划基础模型、目标规划模型、运输模型及其应用、图论模型、最小树问题、最短路问题复习要求： 1.进一步理解基本建模过程，掌握类比法、图示法以及问题分析、合理假设的内涵. 2.进一步理解数学模型的作用与特点. 本章复习重点是线性规划基础模型、运输问题模型和目标规划模型.具体说来，要求大家会建立简单的线性规划模型，把实际问题转化为线性规划模型的方法要掌握，当然比较简单.运输问题模型主要要求善于将非线性规划模型转化为运输规化模型，这种转化后求解相当简单.你至少把一个很实际的问题转化为用表格形式写出的模型，至于求解是另外一回事，一般不要求.目标模型一般是比较简单的线性规模模型在提出新的要求之后转化为目标规划模型.另外，关于图论模型的问题涉及到最短路问题，具体说来用双标号法来求解一个最短路模型.这之前恐怕要善于将一个实际问题转化为图论模型.还有一个最小数的问题，该如何把一个网络中的最小数找到.另外在个别场合可能会涉及一笔划问题. 1.营养配餐问题的数学模型 n n x C x C x C Z ++=211m i n ????? ?? ??=≥≥+++≥+++≥+++??) ,,2,1(0, ,, 22112222212111212111n j x b x a x a x a b x a x a x a b x a x a x a t s j m n mn m m n n n n 或更简洁地表为 ∑== n j j j x C Z 1 m i n ??? ??? ?==≥≥??∑=),,2,1,,2,1(01 n j m i x b x a t s j n j i j ij 其中的常数C j 表示第j 种食品的市场价格，a ij 表示第j 种食品含第i 种营养的数量，b i 表示人或动物对第i 种营养的最低需求量. 2.合理配料问题的数学模型有m 种资源B 1，B 2，…，B m ，可用于生产n 种代号为A 1，A 2，…，A n 的产品.单位产品A j 需用资源B i 的数量为a ij ，获利为C j 单位，第i 种资源可供给总量为b i 个单位.问如何安排生产，使总利润达到最大？设生产第j 种产品x j 个单位（j =1，2，…，n ），则有 n n x C x C x C Z +++= 2211m a x

长江学院课程设计报告课程设计题目：农业生产规划模型姓名1：袁珍珍学号： 08354230 姓名2：倪美丹学号： 08354213 姓名3：阮鹏娟学号： 08354216 专业土木工程班级083542 指导教师邱淑芳 2010年4月11号

摘要：通过对题目的分析可以看出本题是关于线性规划的问题，解决此类问题要找出决策变量，目标函数，约束条件等，在解题中我们建立了两种模型，通过比较来使问题更加的具有科学性。中国是一个农业大国，农民的生产生活可以直接影响到国家的经济，优化农业生产模型是一个不可忽视的问题。本题就是研究了农民在农业生产中种植农作物和养殖畜牧业的生产规划问题。以现有标准为参考，采用假设分析法提出了优化模型，计算出农民在农业生产中合理规划农作物的种植和畜牧业养殖的分配问题。让拥有有限经济实力和有限土地的农民，在有限的投资和有限的土地限制下，可以按照不同季节合理安排种植业和畜牧业的劳动时间，更可用赋予时间进行多项劳动，从而可以在规定的劳动力和劳动时间内收获最大净收益。这不仅可以发展我国的农业，更可使农民富裕起来，从而缩小了我国的贫富差距，对我国的经济发展有着重大促进作用。本文根据题目给出的数据和条件，假设出必要未知量，再列出必要方程式，运用Lingo等数学软件分析提出合理的数学模型。关键字：线性规划、数学建模、Lingo、农业生产、合理分配、最大净收益

阐述题目某农户拥有100亩土地和25000元可供投资，每年冬季（9月份中旬至来年5月中旬），该家庭的成员可以贡献 3500h的劳动时间，而夏季为4000h。如果这些劳动时间有赋予，该家庭中的年轻成员将去附近的农场打工，冬季每小时元，夏季每小时元。现金收入来源于三种农作物（大豆、玉米和燕麦）以及两种家禽（奶牛和母鸡）。农作物不需要付出投资，但每头奶牛需要400元的初始投资，每只母鸡需要3元的初始投资，每头奶牛需要使用亩土地，并且冬季需要付出100h劳动时间，夏季付出50h劳动时间，该家庭每年产生的净现金收入为450元；每只母鸡的对应数字为：不占用土地，冬季，夏季，年净现金收入元。养鸡厂房最多只能容纳3000只母鸡，栅栏的大小限制了最多能饲养32偷奶牛。根据估计，三种农作物每种植一亩所需要的劳动时间和收入如下表所示。建立数学模型，帮助确定每种农作物应该种植多少亩，以及奶牛和母鸡应该各蓄养多少，使年净现金收入最大。

第十三章线性规划与数学建模简介【授课对象】理工类专业学生【授课时数】6学时【授课方法】课堂讲授与提问相结合【基本要求】1、了解数学模型的基本概念、方法、步骤； 2、了解线性规划问题及其数学模型； 3、了解线性规划问题解的性质及图解法. 【本章重点】线性规划问题. 【本章难点】线性规划问题、线性规划问题解的性质、图解法. 【授课内容】本章简要介绍数学建模的基本概念、方法、步骤，并以几个典型线性规划问题为例，介绍构建数学模型的方法及其解的性质。 §1 数学建模概述一、数学建模数学建模是构造刻划客观事物原型的数学模型并用以分析、研究和解决实际问题的一种科学方法。运用这种科学方法，必须从实际问题出发，遵循从实践到认识再实践的认识规律，围绕建模的目的，运用观察力、想象力的抽象概括能力，对实际问题进行抽象、简化，反复探索，逐步完善，直到构造出一个能够用于分析、研究和解决实际问题的数学模型。因此，数学建模是一种定量解决实际问题的创新过程。二、数学模型的概念

模型是人们对所研究的客观事物有关属性的模拟。例如在力学中描述力、量和加速度之间关系的牛顿第二定律F＝ma就是一个典型的（数学）模型。一般地，可以给数学模型下这样的定义：数学模型是磁于以部分现实世界为一定目的而做的抽象、简化的数学结构。通俗而言，数学模型是为了一定目的对原型所作的一种抽象模拟，它用数学式子，数学符号以及程序、图表等描述客观事物的本质特征与内在联系。三建立数学模型的方法和步骤建立数学模型没有固定模式。下面介绍一下建立模型的大体过程： 1.建模准备建模准备是确立建模课题的过程。这类课题是人们在生产和科研中为了使认识和实践过一步发展必须解决的问题。因此，我们首先要发现这类需要解决的实际问题。其次要弄清所解决问题的目的要求并着手收集数据。进行建模筹划，组织必要的人力、物力等，确立建模课题。 2．模型假设作为建模课题的实际问题都是错综复杂的、具体的。如果不对这些实际问题进行抽象简化，人们就无法准确把握它的本质属性，而模型假设就是根据建模的目的对原型进行抽象、简化，抓住反映问题本质属性的主要因素，简化掉那些非本质的次要因素。有了这些假设，就可以在相对简单的条件下，弄清各因素之间的关系，建立相应的模型。合理的假设是建立理想模型的必要条件和基本保证。如果假设是合理的，则模型切合实际，能解决实际问题；如果假设不合理中或过于简化，则模型与实际情况不符或部分相符，就解决不了问题，就要修改假设，修改模型。 3．构造模型

四类基本模型 1 优化模型 1.1 数学规划模型线性规划、整数线性规划、非线性规划、多目标规划、动态规划。 1.2 微分方程组模型阻滞增长模型、SARS 传播模型。 1.3 图论与网络优化问题最短路径问题、网络最大流问题、最小费用最大流问题、最小生成树问题(MST)、旅行商问题(TSP)、图的着色问题。 1.4 概率模型决策模型、随机存储模型、随机人口模型、报童问题、Markov 链模型。 1.5 组合优化经典问题 ● 多维背包问题(MKP) 背包问题：n 个物品，对物品i ，体积为i w ，背包容量为W 。如何将尽可能多的物品装入背包。多维背包问题：n 个物品，对物品i ，价值为i p ，体积为i w ，背包容量为W 。如何选取物品装入背包，是背包中物品的总价值最大。多维背包问题在实际中的应用有：资源分配、货物装载和存储分配等问题。该问题属于NP 难问题。 ● 二维指派问题(QAP) 工作指派问题：n 个工作可以由n 个工人分别完成。工人i 完成工作j 的时间为ij d 。如何安排使总工作时间最小。二维指派问题（常以机器布局问题为例）：n 台机器要布置在n 个地方，机器i 与k 之间的物流量为ik f ，位置j 与l 之间的距离为jl d ，如何布置使费用最小。二维指派问题在实际中的应用有：校园建筑物的布局、医院科室的安排、成组技术中加工中心的组成问题等。 ● 旅行商问题(TSP) 旅行商问题：有n 个城市，城市i 与j 之间的距离为ij d ，找一条经过n 个城市的巡回（每个城市经过且只经过一次，最后回到出发点），使得总路程最小。 ● 车辆路径问题(VRP) 车辆路径问题（也称车辆计划）：已知n 个客户的位置坐标和货物需求，在

第一部分课后习题 1.学校共1000名学生，235人住在A宿舍，333人住在B宿舍，432人住在C宿舍。学生们要组织一个10人的委员会，试用下列办法分配各宿舍的委员数：（1）按比例分配取整数的名额后，剩下的名额按惯例分给小数部分较大者。（2）2.1节中的Q值方法。（3）d’Hondt方法：将A，B，C各宿舍的人数用正整数n=1，2，3，…相除，其商数如下表：将所得商数从大到小取前10个（10为席位数），在数字下标以横线，表中A，B，C行有横线的数分别为2，3，5，这就是3个宿舍分配的席位。你能解释这种方法的道理吗。如果委员会从10人增至15人，用以上3种方法再分配名额。将3种方法两次分配的结果列表比较。（4）你能提出其他的方法吗。用你的方法分配上面的名额。 2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。比如洁银牙膏50g 装的每支1.50元，120g装的3.00元，二者单位重量的价格比是1.2：1。试用比例方

法构造模型解释这个现象。（1）分析商品价格C与商品重量w的关系。价格由生产成本、包装成本和其他成本等决定，这些成本中有的与重量w成正比，有的与表面积成正比，还有与w无关的因素。（2）给出单位重量价格c与w的关系，画出它的简图，说明w越大c越小，但是随着w的增加c减少的程度变小。解释实际意义是什么。 3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生，打算按照放生的鱼的重量给予奖励，俱乐部只准备了一把软尺用于测量，请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼身的最大周长）：先用机理分析建立模型，再用数据确定参数 4.用宽w的布条缠绕直径d的圆形管道，要求布条不重叠，问布条与管道轴线的夹角应多大（如图）。若知道管道长度，需用多长布条（可考虑两端的影响）。如果管道是其他形状呢。

工作人员的最优时间分配问题的研究【摘要】对于一个事业单位，人力资源部门的合理分配对于一个事业单位的收益是至关重要的。众所周知，由于每个人的工作效率不尽不同，不同的分配方式所带来的收益也不同。本文建立了0-1规划模型对最少时间成本下的工作人员分配问题进行了研究。本问题中首先确定第i人做或者不做第j工作将问题定量化，根据不同的需要建立不同的目标函数。对于一个项目而言越早完成越好，对人力资源部门来说所花费的人力越少越好。本文利用运筹管理学的思想建立的0-1规划模型，最后使用Lingo对目标函数求最优解得出最终结果。关键词：最少时间运筹管理学最优解时间分配 0-1模型 Lingo 线性规划一、问题重述最优人力资源安排问题在企事业单位，人力资源部门经常要根据当前情况把人员分配给即将开始的项目。一般地，对项目而言，越早完成越好；而对人力资源部门而言，在该项目上所花费的人力越少越好。现有一个项目，需要把一份中文资料翻译成英语、法语、日语、德语和俄语。已知A、B、C、D、E、F和G七个人翻译该资料所需要花费的时间如表1所示，且这七个人均表示可参加该项目。【注意：为了译文的连贯性，不允许两人或两人以上做同一种译文的翻译工作。一个人在同一时间只能做一种译文的翻译工作。】试通过建立数学模型（而非枚举法）回答下述问题。问题1. 应该如何进行人力资源的安排使得该项目尽早完成？问题2. 在问题1中若规定每人最多承担一种译文的翻译工作，试求相应的最优人力资源安排方案。问题3. 接上级通知，为了保证翻译的质量，需要对翻译之后的译文进行审校且规定同一个语种的审校人和翻译者不能为同一人。显然，在这种新的要求下，该项目完成当且仅当所有的译文均审校完。已知这七人均表示可以参加审校工

数学建模论文

农业生产规划模型杨欢（2011级2班 1110500122）【摘要】本模型就是研究了农民在农业生产中种植农作物和养殖畜牧业的生产规划问题。以现有标准为参考，采用逐步分析法提出了线性规划模型，计算出农民在农业生产中该如何合理规划农作物的种植和畜牧业养殖的分配问题。本文根据题目给出的数据和条件，假设出了必要未知量，再根据题意列出必要方程和不等式，从而建立了完整而又合理的数学模型。最终建立的数学模型如下：目标函数 Max z=175*x1+300*x2+120*x3+400*x4+2*x5; 约束条件 x1+x2+x3+1.5*x4<=100; 400*x4+3*x5<=15000; 20*x1+35*x2+10*x3+100*x4+0.6*x5<=3500; 50*x1+75*x2+40*x3+50*x4+0.3*x5<=4000; x4<=32; x5<=3000; x1,……,x5>=0 最后我们运用LINDO等数学软件进行模型求解和分析，确保了结果的准确性和可行性。【关键词】农业规划投资最大净收益数学模型 LINDO软件 1问题的重述 1.1 问题背景：近年来，农业生产问题越来越收到人们的关注。人们对“农场”的热衷最初来自网络游戏带来的乐趣，同时带动和启发了人们积极投入到现实农场的建设和经营。当然，人们对农场的热衷还是日常生活的实际需求。中国是一个农业大

国，农民的农业生产生活问题不仅在很大程度上影响着我国的经济发展，更是决定着中国13亿人口的温饱问题。所以，对农场进行合理的规划，使其达到最优的效果，也即是最大的收益，是一个不可忽视的问题。

数学建模作业5数学规划模型----供应与选址的问题

一、问题提出某公司有6个建筑工地要开工，每个工地的位置（用平面坐标系(a，b)表示，距离单位：km）及水泥日用量d（吨）由下表给出。目前有两个料场位于A(5,1)，B(2,7)，日储量各有20吨。工地位置（a，b）及水泥日用量d 1 2 3456 a 1.25 8.75 0.5 5.75 3 7.25 b 1.25 0.75 4.75 5 6.5 7.75 d 3 5 4 7 6 11 （1）试制定每天的供应计划，即从A，B两料场分别向各工地运送多少水泥，可使运输费用（总的吨千米数）最小，并求出吨千米数。 ( 注：先画图，在坐标上标出各工地位置（用蓝色*标示）和料场位置（用红色o标示）) （2）目前公司准备建立两个新的料场，日储量各为20吨，为使运输费用最省，问新的料场应建在何处，并算出两料场分别向工地运输多少吨水泥和费用。（注：初始值取x0=[3 5 4 7 1 0 0 0 0 0 5 11 5 4 7 7]’）二、问题分析对于问题（1），确定用A，B两料场分别向各工地运送水泥，使运输费用（总的吨千米数）最小，即要知道两点间线段最小，料场到工地的路线是直的，而要满足六个工地的需求，又要考虑到A、B两个料场的供应量，即在各工地用量必须满足和各料场运送量不超过日储量的条件下，使总的吨千米数最小，这是线性问题。。对于问题（2），需要重新改建六个新的料场，使得在在各工地用量必须满足和各料场运送量不超过日储量的条件下，使总的吨千米数最小，则需要确定新的料场的具体位置，这是非线性问题。三、模型假设 1、假设料场和建筑工地之间都可以由直线到达； 2、运输费用由“吨千米数”来衡量； 3、两料场的日存储量够向各建筑工地供应；

1 整数规划的MATLAB 求解方法（一）用MATLAB 求解一般混合整数规划问题由于MATLAB 优化工具箱中并未提供求解纯整数规划和混合整数规划的函数，因而需要自行根据需要和设定相关的算法来实现。现在有许多用户发布的工具箱可以解决该类问题，例如比较著名的Y ALMIP ，读者可以自行到网上下载相关的工具包并进行学习。这里我们给出开罗大学的Sherif 和Tawfik 在MA TLAB Central 上发布的一个用于求解一般混合整数规划的程序，在此命名为intprog ，笔者在原程序的基础上做了简单的修改，将其选择分枝变量的算法由自然序改造成分枝变量选择原则中的一种，即：选择与整数值相差最大的非整数变量首先进行分枝。intprog 函数的调用格式如下： [x,fval,exitflag]=intprog(c,A,b,Aeq,beq,lb,ub,M,TolXInteger) 该函数解决的整数规划问题为： ????? ??????∈=≥≤≤=≤=）取整数（M j x n i x ub x lb b x A b Ax t s x c f j i eq eq T ) ,,2,1(0 ..min 在上述标准问题中，假设x 为n 维设计变量，且问题具有不等式约束1m 个，等式约束2m 个，那么：c 、x 均为n 维列向量，b 为1m 维列向量，eq b 为2m 维列向量，A 为n m ?1维矩阵，eq A 为n m ?2维矩阵。在该函数中，输入参数有c,A,b,A eq ,b eq ,lb,ub,M 和TolXInteger 。其中c 为目标函数所对应设计变量的系数，A 为不等式约束条件方程组构成的系数矩阵，b 为不等式约束条件方程组右边的值构成的向量。Aeq 为等式约束方程组构成的系数矩阵，b eq 为等式约束条件方程组右边的值构成的向量。lb 和ub 为设计变量对应的上界和下界。M 为具有整数约束条件限制的设计变量的序号，例如问题中设计变量为621,,,x x x ，要求32,x x 和6x 为整数，则M=[2;3;6]；若要求全为整数，则M=1:6，或者M=[1;2;3;4;5;6]。TolXInteger 为判定整数的误差限，即若某数x 和最邻近整数相差小于该误差限，则认为x 即为该整数。在该函数中，输出参数有x, fval 和exitflag 。其中x 为整数规划问题的最优解向量，fval 为整数规划问题的目标函数在最优解向量x 处的函数值，exitflag 为函数计算终止时的状态指示变量。例1 求解整数规划问题： ????? ?? ??≥≥≤+≥-+= 0, 12 1124 124 ..max 212212121，且取整数值x x x x x x x t s x x f