三角函数与复数

【知能目标】

1. 掌握同角的三角函数的基本关系式: 掌握正弦,余弦的诱导公式;掌握两角和与两角 差的正弦,余弦,正切公式;掌握二倍角的在正弦，余弦,正切公式.

2. 能正确运用三角公式,进行简单三角函数式的化简,求值和恒等式证明. 【综合脉络】

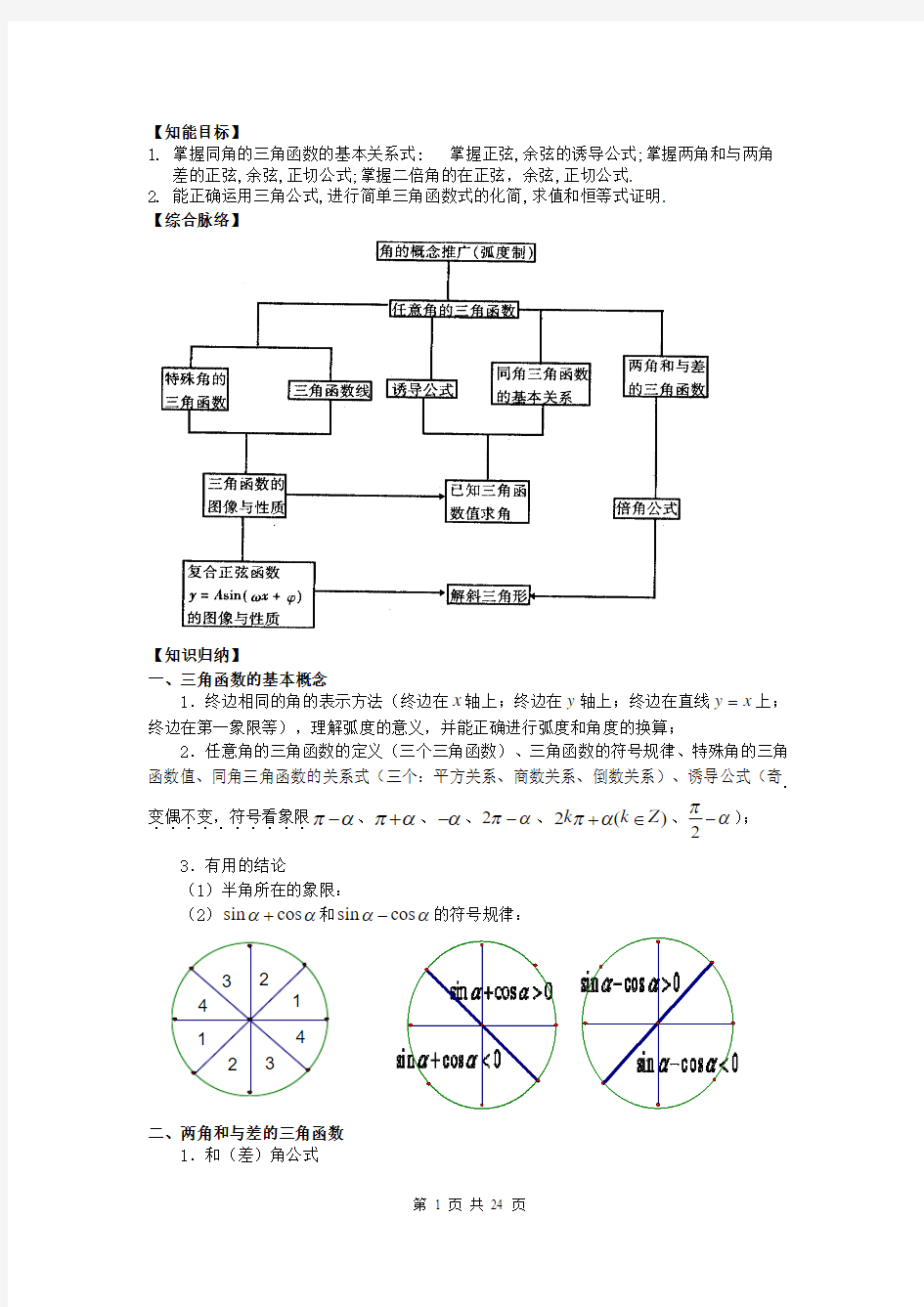
【知识归纳】

一、三角函数的基本概念

1．终边相同的角的表示方法（终边在x 轴上；终边在y 轴上；终边在直线y x =上；终边在第一象限等），理解弧度的意义，并能正确进行弧度和角度的换算；

2．任意角的三角函数的定义（三个三角函数）、三角函数的符号规律、特殊角的三角函数值、同角三角函数的关系式（三个：平方关系、商数关系、倒数关系）、诱导公式（奇．变偶不变，符号看象限．．．．．．．．．．πα-、πα+、α-、2πα-、2()k k Z πα+∈、2

π

α-）； 3．有用的结论

（1）半角所在的象限：

（2）sin cos αα+和sin cos αα-的符号规律：

二、两角和与差的三角函数

1．和（差）角公式

（1）sin()αβ+= ；（2）

sin()αβ-= .

（3）cos()αβ+= ；（4）cos()αβ-= .

（5）tan()αβ+= ；（6）tan()αβ-= .

2．二倍角公式

（1）sin 2α= ；（2）cos 2α= = = ；

（3）tan 2α= . 3．有用的公式

（1）升（降）幂公式：2

1cos 2sin 2αα-=

、2

1cos 2cos 2

αα+=、1

sin cos sin 22

ααα=；

（2）辅助角公式：sin cos )a b ααα?+=+（?由,a b 具体的值确定）； （3）正切公式的变形：tan tan tan()(1tan tan )αβαβαβ+=+-?. 4．有用的解题思路 （1）“变角找思路，范围保运算”； （2）“降幂——辅助角公式——正弦型函数”； （3）巧用sin cos αα±与sin cos αα?的关系； （4）巧用三角函数线——数形结合. 三、三角函数的图象与性质

1．列表综合三个三角函数sin y x =，cos y x =，tan y x =的图象与性质，并挖掘： （1）最值的情况；

（2）了解周期函数和最小正周期的意义．会求sin()y A x ω?=+的周期，或者经过简单的恒等变形可化为上述函数的三角函数的周期，了解加了绝对值后的周期情况．．．．．．．．．．．．．

； （3）会从图象归纳对称轴和对称中心；

sin y x =的对称轴是2

x k π

π=+

()k Z ∈，对称中心是(,0)k π()k Z ∈；

cos y x =的对称轴是x k π=()k Z ∈，对称中心是(,0)2

k π

π+

()k Z ∈

tan y x =的对称中心是(

,0)()2

k k Z π

∈ 注意加了绝对值后的情况变化. （4）写单调区间注意0ω>.

2．了解正弦、余弦、正切函数的图象的画法，会用“五点法”画正弦、余弦函数和函数sin()y A x ω?=+的简图，并能由图象写出解析式．

（1）“五点法”作图的列表方式；

（2）求解析式sin()y A x ω?=+时处相?的确定方法：代（最高、低）点法、公式

1x ?ω

=-

. 3．正弦型函数sin()y A x ω?=+的图象变换

切记：sin sin()y A x y A x ?ω

ωω?=???→=+平移

注意图象变换有时用向量表达，注意两者之间的转译. 四、解三角形

1．三个重要结论

（1）正弦定理：

2sin sin a b c

R A swinB C

===（2R 为三角形ABC 的外接圆直径）或写成 ::sin :sin :sin a b c A B C =

（2）余弦定理：A ab c b a cos 22

2

2

-+=，或写成ab

a c

b A 2cos 2

22-+=

（3）三角形ABC 面积公式：111

sin sin sin 222

S ab C bc A ca B === 2．在使用正弦定理时判断一解或二解的方法：⊿ABC 中，sin sin A B A B >?>

3．解三角形在测量等中的实践运用. 五、复数

1．虚数单位是i ，23444142431,,1,1,,1,.n n n n i i i i i i i i i i +++=-=-====-=- 2．复数为实数、虚数、纯虚数的充要条件分别是0,0,00b b a b =≠=≠且

两复数相等的充要条件为：实部与虚部分别相等；复数Z=a+bi 的共轭复数为a-bi ，在

复平面内它对应的点坐标为(a,b)，其模3．复数的加减法法则：实部与实部相加，虚部与虚部相加。 两复数乘法法则：与多项乘法法则相同。

两复数除法法则：分子分母同时乘以分线的共轭复数，再化简，使分母不含虚数。 【考点聚焦】

考点1：函数y =Asin()0,0)(>>+???A x 的图象与函数y =sin x 图象的关系以及根据图象写出函数的解析式

考点2：三角函数的定义域和值域、最大值和最小值；

考点3：三角函数的单调区间、最小正周期和三角函数图象的对称轴问题； 考点4：和、差、倍、半、、诱导公式、和差化积和积化和差公式、万能公式、同角的三角函数关系式；

考点5：三角形中的内角和定理、正弦定理、余弦定理； 考点6、复数的基本概念及运算. 【自我检测】

1． 同角三角函数基本关系式：＿＿＿＿＿＿＿＿，＿＿＿＿＿＿，＿＿＿＿＿＿＿. 2． 诱导公式是指α的三角函数与－α，180oα±,90oα±,270oα±,360o－α，

k 360o+α(k ∈Z)三角函数之间关系：奇变偶不变，符号看象限. 3． 两角和与差的三角函数：sin(α±β)=_______________________;

cos(α±β)=________________________;tan(α±β)=_________________________. 4． 二倍角公式：sin2α=__________;cos2α=_________=__________=___________ tan2α=_____________. 5． 半角公式：sin

2α=_______，cos 2α=_______,tan 2

α

=________=________=______.

6． 万能公式sin α=_____________,cos α=_____________,tan α=_____________.

【重点难点热点】

问题1：三角函数的图象问题

关于三角函数的图象问题，要掌握函数图象的平移变化、压缩变化，重点要掌握函数

y =Asin()0,0)(>>+???A x 的图象与函数y =sin x 图象的关系，注意先平移后伸缩与先

伸缩后平移是不同的，要会根据三角函数的图象写出三角函数的解析式.

例1．（05天津理）要得到y x 的图象，只需将函数)4

2sin(2π

+

=x y 的图象上

所有的点的

A 、横坐标缩短到原来的

1

2

倍（纵坐标不变）,再向左平行移动8π个单位长度

B 、横坐标缩短到原来的1

2

倍（纵坐标不变），再向右平行移动4π个单位长度

C 、横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动8π

个单位长度 D 、横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动4

π

个单位长度

思路点拨：将)42sin(2π+=x y 化为)4

2cos(2π

-=x y ，再进行变换.

解答：变换1：先将)42cos(2π-=x y 的图象向左平移8

π

个单位，得到

x x y 2cos 2]4

)8(2cos[2=-+=π

π的图象，再将x y 2cos 2=的图象的横坐标缩短

到原来的2倍得到x y cos 2=.

变换2：先将)4

2cos(2π

-

=

x y 的图象的横坐标缩短到原来的2倍，得到

)4

cos(2π

-

=x y 的图象，再将)4

cos(2π

-

=x y 的图象向左平移

4

π

个单位，得到x y cos 2=.

由上可得，应选C.

演变1：函数)

20,0,)(sin(π?ω?ω<≤>∈+=R x x y

的部分图象如图，则（ ）

A ．4

,2

π

?π

ω=

=

B ．6

,3

π

?π

ω=

=

C ．4,4π?πω==

D ．4

5,4π

?πω==

点拨与提示：根据图象得出函数的周期与振幅，再将（1,10坐标代入即可.

问题2：三角函数的求值问题

关干三角函数的求值问题,要注意根据已知条件,准确判断角所在的范围,合理选择公式,正确选择所求三角函数值的符号 例2：已知5

1cos sin ,02

=

+<<-

x x x π

. （I ）求sin x －cos x 的值； （Ⅱ）求x

x x x x x cot tan 2cos 2cos 2sin 22sin 322

++-的值.

思路分析：将sin x -cos x =

5

1

平方，求出sin x cos x 的值，进而求出（sin x -cos x ）2，然后由角的范围确定sin x -cos x 的符号.

解法一：（Ⅰ）由,25

1cos cos sin 2sin ,51cos sin 22=++=

+x x x x x x 平方得 即 .25

49cos sin 21)cos (sin .2524cos sin 22=-=--=x x x x x x 又,0cos sin ,0cos ,0sin ,02<-><∴<<-x x x x x π 故 .5

7

cos sin -=-x x

（Ⅱ）x x x x x x x

x x x x x sin cos cos sin 1

sin 2sin 2cot tan 2cos 2cos 2sin 2sin 3222+

+-=++-

125

108

)512()2512()sin cos 2(cos sin -=-?-=--=x x x x

解法二：（Ⅰ）联立方程??

???

=+=+.1cos sin ,

51cos sin 22x x x

由①得,cos 5

1

sin x x -=

将其代入②，整理得,012cos 5cos 252=--x x ???

???

?

=-=∴<<-=-=∴.

54cos ,53sin ,02.54cos 53cos x x x x x π 或 故 .5

7

cos sin -=-x x

①②

（Ⅱ）x x x x x x cot tan 2cos 2cos 2sin 2sin 322

++-x x x x sin cos 1sin 2sin 22+

+-=

125

108

)53542(54)53()sin cos 2(cos sin -=+-??-=--=x x x x

点评：本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基

本知识，以及推理和运算能力. 演变1：已知)3

tan(sin ,2572cos ,1027)4sin(π+αα=α=π-

α及求. 点拨与提示：用已知中的角表示所求的角.

问题3：三角函数的单调性、周期性、奇偶性等问题

有关三角函数的单调性、周期性等问题，通常需要先变形化简，然后求解. 例3：设函数)(),0( )2sin()(x f y x x f =<<-+=?π?图像的一条对称轴是直线8

π

=

x .

（Ⅰ）求?；（Ⅱ）求函数)(x f y =的单调增区间；（Ⅲ）画出函数)(x f y =在区间],0[π上的图像.

思路点拨：正弦y =sin x 的图象的对称轴为直线)(2

Z k k x ∈+=π

π，其对称轴与x 轴交点

的横坐标即是使函数取得最值的x 值. 解：（Ⅰ）)(8

x f y x ==

是函数π

的图像的对称轴，,1)8

2sin(±=+?

∴?π

.,2

4

Z k k ∈+

=+∴

π

πππ

.4

3,0π

??π-

=<<- （Ⅱ）由（Ⅰ）知).432sin(,43ππ?-=-

=x y 因此 由题意得 .,2243222Z k k x k ∈+≤-

≤-π

ππππ 所以函数.],85,8[)432sin(Z k k k x y ∈++-=πππππ的单调增区间为 （Ⅲ）由知)

32sin(π

-=x y 故函数上图像是在区间

],0[)(πx f y =

点评：本小题主要考查三角函数性质及图像的基本知识，考查推理和运算能力. 演变3：已知向量

x f x x x x ?=-+=+=)()),4

2tan(),42sin(2()),42tan(,2cos

2(令π

ππ. 求函数f (x )的最大值，最小正周期，并写出f (x )在[0，π]上的单调区间.

问题4：“拆项”与“添项”的问题 “拆项”与“添项”是指在作三角变换时，对角或三角函数可以分别进行面或添项处理.

例4：（1）求

8

sin 15sin 7cos 8sin 15cos 7sin ++的值； （2）已知：41)2tan(,52)tan(=-=

+πββα，求：)4

tan(απ

+的值. 思路分析：解此题的关健是能否抓住题中各角之间的内在联系.如（1）中的含有角7o、15o、8o，发现它们之间的关系是15o＝7o＋8o，故可将7o拆成15o－8o；同理在第（2）题中α

π

+4

可以拆成两角差，即)4

()(π

ββα-

-+.

解：（1） 8sin 15sin 7cos 8sin 15cos 7sin ++＝

8sin 15sin )815cos(8sin 15cos )815sin(+-+-＝

15cos 8cos 15sin 8cos ＝tan15o=

30

sin 30cos 1-=32- (2) ∵

απ

+4

=)4

()(π

ββα-

-+

∴tan(απ+4)=tan[)4

()(πββα--+]＝)4tan()tan(1)

4tan()tan(πββαπ

ββα-++--+＝

4

15214152?

+-＝223 点评：进行三角变换的技巧常常是变角――注意角的和、差、倍、半、互余、互补关系，根

据实际情况，对角进行“拆”或“添”变形，这样可以大大减少运算量.

演变4：求

20cos 20sin 10cos 2-的值

.

点拨与提示：10o＝30o－20o. 问题五：复数方程和共轭复数

复数方程常见解法是将复数方程转化为实数方程组；关于共轭复数有两个充要条件：①Z ∈R Z Z =?，②非零复数y 为纯虚数0=+?y y ，这两个充要条件是用整体观点处理复数的生要工具.

例5：求实数k 的值，使方程02)2(2=++++ki x i k x 至少有一个实根.

思路分析：已知方程是一元二次方程，系数含有参数，并且方程有一个实根，设出实根，利用复数相等可得出实数方程组，从而得解.

解：设α是方程的实根，则02)2(2=++++ki i k αα，

即0)2()2(2

=++++i k k ααα根据复数相等的充要条件得：?

??=+=++020

22k k ααα，消去α

得k 2

=8，∴k =22±

点评：如果利用一元二次方程的判别式△＝（k +2i ）2－4(2+k i)＝k 2

－12，要使方程至少有一个实根，只需△≥0，即k ≤32-,k ≥32，这样的解法是错误的.错误的原因在于：一元二次方程的判别式△＝b 2

-4ac ≥0是实系数一元二次方程有实根的充要条件，不适

合于复系数一元二次方程.对于这类虚数系数一元二次方程有实根的常见解法是设实根为α，将x ＝α代入方程，根据复数相等的条件来解.

演变5：解复数集中的方程：0)2()252(2

2

=--++-i x x x x 点拨与提示：整理成关于x 的一元二次方程，用求根公式求解. 例6：设z 是虚数，z z W 1+

=是实数，u

u u +-=11，求证：u 为纯虚数. 思路分析：本题证法很多，可以从共轭复数运算的角度给出证明. 证明：∵z z W 1+

=∈R ，∴z

z z z z z 1

11+=+=+，∴0)11(=-+-z z z z ∴0)|

|1

1)((2

=-

-z z z ，∵z 是纯虚数，∴0≠-z z ，∴|z |＝1，∴z z 1= ∵u z z z

z z z z z u -=+-=+-

=+-=+-=1

1111

111)11(.∴0=+u u .∵z 是虚数，∴1≠z ，∴0≠u ，∴u 为纯虚数.

点评：用整体观点处理复数问题时，应注意利用前面提到的充要条件. 演变6：设z 1,z 2为两个非零复数，且｜z 1+z 2｜=|z 1－z 2|，求证：2

2

1)(

z z 为负数.

点拨与提示：利用复数加、减法的几何意义求解. 专题小结

1．三角变换常用的方法技巧有切割化弦法，升幂降幂法、辅助元素法，“1”的代换法等．对于三角公式要记忆准确（在理解基础上），并要注意公式成立的条件，在应用时，要认真分析，合理转化，避免盲目性．

2．三角函数图象的对称性和有界性是高考命题的一个热点．最基本的三角函数图象的形状和位置特征，要准确掌握，它是利用数形结合思想解决三角函数问题的关键．三角函数图象各种变换的实质要熟练掌握，不能从形式上简单判断．

3．解三角形时，要根据条件正确选择正、余弦定理以及三角变换式．要充分发挥图形的作用，注意三角形外接圆半径在正弦定理中的转化功能 【活学巧练】 一、选择题

1．已知f (cos x )=cos3x ，则f (sin30o)的值为（ C ）

A 0

B 1

C －1 D

2

3 2．（2006年辽宁卷）ABC 的三内角,,A B C 所对边的长分别为,,a b c 设向量

(,)p a c b =+ ,(,)q b a c a =-- ,若//p q

,则角C 的大小为(B) (A)6π (B)3π (C) 2

π (D) 23π

3．（2006年安徽卷）将函数sin (0)y x ωω=>的图象按向量,06a π??

=- ???

平移，平移后的

图象如图所示，则平移后的图象所对应函数的解析式是（ C ）

A ．sin()6y x π

=+ B ．sin()6y x π

=- C ．sin(2)3y x π=+

D ．sin(2)3

y x π

=- 4．把函数)3sin 3(cos 2

2

x x y -=

的图象适当变动，就可得到y =－sin3x 的图象，这种变动可以是（ D ）

A 沿x 轴向右平移

4π B 沿x 轴向左平移4π C 沿x 轴向右平移12π D 沿x 轴向左平移12

π

5．已知复数z 1，z 2在复平面上对应的点分别是A ，B ，O 为坐标原点，当

z 1=2（cos60o+isin60o）?z 2,|z 2|=2，则△AOB 的面积为（ B ） A 34 B 32 C

3 D 2

6．复数z ＝1－cos θ－isin θ（3π＜θ＜4π）的辐角主值是（ B ） A

23θπ- B 23πθ- C 2

θπ+ D 23θ

π+

7．函数y =3sin(x +20o)+5sin(x +80o)的最大值为（ C ）

A

211 B 2

13 C 7 D 8 8．在△OAB 中，O 为坐标原点，]2

,0(),1,(sin ),cos ,1(π

θθθ∈B A ，则当△OAB 的面积

达最大值时，=θ（D ）

A ．6π

B ．4π

C ．3π

D ．2

π

9．在△ABC 中，若b

a b

a B A +-=-2tan ，其中a,

b 分别是∠A ，∠B 的对边，则△ABC 是（ D ）

A 等腰三角形

B 直角三角形

C 等腰直角三角形

D 等腰或直角三角形 10．函数y =2

3

cos 32sin 212+

-=

x x y 的最小正周期为（ D ） A 2π B π C 2π D 4

π

二、填空题

11 已知sin α=

53，α∈(2π，π)，tan(π－β)= 21，则tan(α－2β)=_ 247_____ 12 设α∈(43,4ππ)，β∈(0，4π)，cos(α－4

π)=53，sin(43π+β)=135

，则

sin(α+β)=__ 65

56

_______

13．已知复数：032z i =+，复数z 满足003z z z z ?=+，则复数z = 1-

3

2

i 14．设函数f (x )的图象与直线x =a ，x =b 及x 轴所围成图形的面积称为f (x )在[a ，

b ]上的面积，已知函数y ＝sin （nx ）在[0，

n

π]上的面积为n 2

（n ∈N * ），（i ）y ＝sin3x

在[0,32π]上的面积为43

；（ii ）y ＝sin （3x －π）＋1在[3π，34π]上的面积为

2

3

π+ 三、解答题

15 不查表求值：

.10cos 1)

370tan 31(100sin 130sin 2?

+?+?+?

16 （2006年安徽卷）已知

310,tan cot 43

παπαα<<+=- （Ⅰ）求tan α的值；

（Ⅱ）求

2

2

5sin 8sin

cos

11cos 8

2

2

2

2

2α

α

α

α

πα++-?

?

- ?

?

?的值.

17．在复数范围内解方程：i

i

i z z z

+-=

++23)(2

(i 为虚数单位). 18．（2006年四川卷）已知,,A B C 是三角形ABC ?三内角，向

量

((),cos ,sin m n A A =-=

，且1m n ?= .

（Ⅰ）求角A ；（Ⅱ）若

221sin 23cos sin B

B B

+=--，求tan B .

已知cos α+sin β=

3，sin α+cos β的取值范围是D ，x ∈D ，求函数

y =10

43

2log 2

1

++x x 的最小值，并求取得最小值时x 的值

参考答案

1．C 提示：1180cos )60(cos )30(sin -=?=?=?f f

2 B 提示：222//()()()p q a c c a b b a b a c ab ?+-=-?+-=

，利用余弦定理可得

2cos 1C =，即1cos 23

C C π

=?=，故选择答案B.

3．C 提示：将函数sin (0)y x ωω=>的图象按向量,06a π??

=- ???

平移，平移后的图象所

对应的解析式为sin ()6

y x π

ω=+，由图象知，73(

)1262

πππω+=，所以2ω=. 4．D 提示：)]12

(3sin[)4

3sin(π

π

-

-=-

-=x x y

5．B 提示∠AOB ＝60o，｜z 2|=2|z 1|=4，3260sin ||||2

1

21=??=

?z z S AOB 6．B 提示：)]23sin()23[cos(

2sin 2πθπθθ-+--=i z ，∵02

sin ,2223<-<<θ

πθπ，).3(2

1arg ,2230πθππθ-=∴<-

7．C 提示：y =3sin(x +20o)+5sin(x +80o)＝3sin(x +20o)+5sin[(x +20o)＋60o] ＝

7)20sin(7)20cos(2

35)20sin(211≤+?+=?++?+?x x x 8．D 提示：θθθθθθcos sin 2

1

21)sin 1)(cos 1(21cos 21sin 211-=-----

=?OAB S 11sin 224θ=

-， 当2θπ=即2

π

θ=时，面积最大.

9．D 提示：由正弦定理得：2

cos

2sin 22cos

2sin

2sin sin sin sin 2tan B A B A B

A B A B

a B A

b a b a B A -++-=

+-=+-=- ＝2cot 2tan B A B A +-，∴02tan =-B A 或12cot =+B A ∴02=-B A 或2

2π

=+B A ∴A ＝B 或A ＋B ＝90o 10．D 提示：)2

2sin(23232cos 232sin 21π

-=+--=x x x y ，则π=T 11．

247 提示 ∵sin α=53,α∈(2

π

,π),∴cos α=－54

则tan α=－43,又tan(π－β)=21可得tan β=－2

1

,

2212()

2tan 42tan 2.11tan 3

1()2

βββ?-==

=---- 2

34()tan tan 743tan(2)341tan tan 224

1()()43

αβαβαβ-----===+?+-?- 12

6556 提示 α∈(43,4ππ),α－4π∈(0, 2π),又cos(α－4π5

3

6556)sin(.655613554)1312(53)

4

3sin()4sin()43cos()4cos()]43()4cos[(]

2

)43()4sin[()sin(.13

12)43cos(,135)43sin().,43(43).4,0(,54)4sin(=

+=?+-?-=+?-++?--=++--=-++-=+∴-=+∴=+∈+∴∈=

-

∴βαβπ

παβππαβππαπ

βππαβαβπβπππβππβπ

α即 13．1-3

2i 提示：设z =a +b i,由(3+2i)(a +b i)=3(a +b i)+3+2i,得3a -2b =3a +3,2a +3b =3b +2, ∴a =1,b =3

2-.

14． π+32,34 提示：由题意得：，，x y 3

4232]320[3sin =?=上的面积为在π

上的图象在]343[1)3sin(πππ，x y +-=为一个半周期结合图象分析其面积为π+3

2

.

15 答案 2

16．解：(Ⅰ)由10tan cot 3

αα+=-

得2

3tan 10tan 30αα++=，即

1tan 3tan 3αα=-=-或，又34παπ<<，所以1

tan 3

α=-为所求.

（Ⅱ）225sin 8sin cos 11cos 822222αααα

πα++-?

?- ?

?

?

1-cos 1+cos 54sin 118ααα++-

=

=

= 17．解：原方程化简为i i z z z -=++1)(2

,

设z =x +y i(x 、y ∈R),代入上述方程得 x 2

+y 2

+2x i=1－i ，∴ x 2

+y 2

=1且2x =－1,解得x =－

2

1

且y =±

23, ∴原方程的解是z =-21±2

3

i.

18． 解：（Ⅰ）∵1m n ?=

∴(()cos ,sin 1A A -?=

cos 1A A -=

12sin cos 12A A ???= ? ???

, 1sin 62A π??-= ???

∵50,666A A π

π

ππ<<-

<-

<

∴66A ππ-= ∴3

A π

= （Ⅱ）由题知22

12sin cos 3cos sin B B

B B

+=--，整理得22sin sin cos 2cos 0B B B B --= ∴cos 0B ≠ ∴2

tan tan 20B B --= ∴tan 2B =或tan 1B =-

而tan 1B =-使22

cos sin 0B B -=，舍去 ∴tan 2

B = ∴()tan tan

C A B π=-+????()tan A B =-+tan tan 1tan tan A B A B +=-

-=

=

19 解 设u =sin α+cos β 则u 2+(3)2

=(sin α+cos β)2+(cos α+sin β)2

=2+2sin(α+β)≤4 ∴u 2

≤1,－1≤u ≤1 即D =［－1,1］,

设t=32+x ,∵－1≤x ≤1,∴1≤t

x 2

3

2-t

2max 0.5min 0.5

0.50.514248242,,8

log 0,5

log log log 8,82

1

.

2

t M t t t

t t M t y M M y t x ∴===≤=++====>∴======- 当且仅当即在时是减函数时此时 【挑战自我】

设a,b ,c 为△ABC 的三边，a ≤b ≤c ，R 是△ABC 的外接圆半径，令f =a+b －2R-8R 2

sin 2sin 2sin

C

B A ，试用

C 的大小来判定f 的符号. 解：f =2R （sinA+sinB －1－42

sin 2sin 2sin C

B A ）

＝2R[2sin )2cos 2(cos 212cos 2sin 2C

A B A B A B A B --++--+] ＝4R 2sin 2cos 42)2sin 2(sin 2cos C

C R R C A B A B -+--+-π ＝4R 2sin 42)2sin 2(sin 2cos 2C

R R C C A B +----π ＝2R )2

sin 2cos 2cos 2)(2sin 2(cos C C A B C C ---- 由a ≤b ≤c ，得A ≤B ≤C ，所以0＜B －A ＜B ＋A ，因此2

cos 2cos C

A B >-， 2sin 2cos 2cos C A B A B =+>-，所以2

sin 2cos 2cos 2C C A B +>-

故当f >0时，2sin 2cos C C >，则0＜C ＜2π 当f ＝0时，2sin 2cos C C =，则C ＝2π 当f ＜0时，2sin 2cos C C <，则C ＞2

π 【答案及点拨】

演变1：由图得

2,84T T =∴=,由T=2πω,得4πω=,在y =sin(4x π?+)中令x =1,y =1,得24

2

k π

π?π+=+

,24

k π

?π=+

,得4

π

?=

,选(C)

演变2：（解法一）由题设条件，应用两角差的正弦公式得

)

cos (sin 22

)4sin(1027α-α=π-α=，

即57cos sin =α-α ①

由题设条件，应用二倍角余弦公式得

)sin (cos 5

7

)sin )(cos sin (cos sin cos 2cos 25722α-α-=α+αα-α=α-α=α=

故5

1

sin cos -=α+α ②

由①式和②式得 54cos ,53sin -=α=α.因此，4

3

tan -=α，由两角和的正切公式

.11325483

343344

33143

3tan 313tan )4tan(-=+-=+

-

=α-+α=π+α 解法二：由题设条件，应用二倍角余弦公式得

α-=α=2sin 212cos 25

7

解得5

3sin ,259sin 2

±=α=

α即 由5

7cos sin ,1027)4sin(=α-α=π-

α可得 由于057sin cos ,0cos 57sin <-α=α>α+=

α且，故α在第二象限，于是5

3

sin =α. 从而5

4

57sin cos -=-α=α，以下同解法一.

演变3：)4

2tan()42tan()42sin(2cos 22)(π

ππ--++=?=x x x x x f

21tan tan 1

22)2221tan 1tan 22

2sin cos 2cos 1

222

x x x x x x x x +-=++?-+=+-

x x cos sin +==)4

sin(2π

+

x .

所以2)(的最大值为x f ，最小正周期为,2π]4

,0[)(π

在x f 上单调增加，[,]42

ππ上单调减少.

演变4：∵10o＝30o－20o，

∴原式＝

?

?

-??+??=??-?-?20cos 20sin )20sin 30sin 20cos 30(cos 220cos 20sin )2030cos(2

＝2cos30o=3.

演变5：原方程可化为022)5()2(2

=-++-+i x i x i

△＝[]i i i i i i 188241024)22)(2(4)5(2

=+-+=-+-+-.

而18i 的平方根为)1(3i +±，所以方程的根为)

2(2)

1(352,1i i i x ++±+=，

∴i x x 5

351,221-=

=. 演变6：提示：∵｜z 1+z 2｜=|z 1－z 2|（y 1y 20≠），∴|1||1|

2121-=+z z z z .即2

1z z

在复平面内对应的点到（－1,0）、（1,0）的距离相等，∴

21z z 对应的点在虚轴上，即2

1z z

为纯虚数. 演变题要有点拨，原创题有详解，一般题给答案

【实战演练】

一、选择题

1.函数4sin 21y x π?

?=++ ?3?

?的最小正周期为（B ）

Ａ．

π

2

Ｂ．π Ｃ．2π Ｄ．4π

2.（理科做）已知复数z 3i ）z ＝3i ，则z ＝（ D ）

A ．3

2 B. 34 C. 32 D.34 （文科做）已知α∈(

2π,π)，sin α=53,则tan(4

π

α+)等于(A)

A.71

B.7

C.－ 7

1

D.－7 3.（06湖北）若ABC ?的内角A 满足2

sin 23A =，则sin cos A A +=(A)

．．53 D ．53-

4．（06湖南）设点P 是函数x x f ωsin )(=的图象C 的一个对称中心，若点P 到图象

C 的对称轴上的距离的最小值4

π，则)(x f 的最小正周期是(B)

A ．2π B. π C. 2π D. 4

π

5.（理科做）已知

=+-=+ni m i n m ni i

m

是虚数单位，则是实数，，，其中11(C)

A.1+2i

B. 1-2i

C.2+i

D.2- i

（文科做）函数()tan 4f x x π?

?=+ ??

?的单调增区间为(C)

A ．,,22k k k Z ππππ?

?-+∈ ??

? B ．()(),1,k k k Z ππ+∈

C ．3,,44k k k Z ππππ??-+∈ ???

D ．3,,44k k k Z ππππ?

?

-+

∈ ??

?

6.（06安徽）对于函数()sin 1

(0)sin x f x x x

π+=

<<，下列结论正确的是（ B ） A ．有最大值而无最小值 B ．有最小值而无最大值 C ．有最大值且有最小值 D ．既无最大值又无最小值 7．若f (sin x )＝3－cos2x ，则f (cos x )＝(C)

A.3－cos2x

B.3－sin2x

C.3＋cos2x

D.3＋sin2x

8."等式sin(α+γ)=sin2β成立"是"α、β、γ成等差数列"的( A )

A.必要而不充分条件

B.充分而不必要条件

C.充分必要条件

D.既不充分又不必要条件

9.（06四川）下列函数中，图象的一部分如右图所示

的是(D)

A.sin 6y x π??=+ ???

B.sin 26y x π?

?=- ???

C.cos 43y x π??=- ???

D.cos 26y x π?

?=- ??

?

10.（06天津）已知函数()sin cos (f x a x b x a =-、b 为常数，0,)a x R ≠∈的图象关于直线4

x π

=对称，则函数3(

)4

y f x π

=-是(D)

A.偶函数且它的图象关于点(,0)π对称

B.偶函数且它的图象关于点3(

,0)2

π对称

C.奇函数且它的图象关于点3(

,0)2

π

对称 D.奇函数且它的图象关于点(,0)π对称

二、填空题

11.（理科做）设,x y 为实数，且

511213x y i i i

+=---，则x y += 4 。 （文科做）cos43°cos77°+sin43°cos167°的值为 －2

1

12.（理科做）若复数z 同时满足z －-z ＝2i ，-

z ＝iz （i 为虚数单位），则z ＝i －1

（文科做）如果αcos ＝51，且α是第四象限的角，那么)2cos(π

α+＝ 562

13.(06重庆)已知βα,??? ??∈ππ,43，sin(βα+)=－,53 sin ,13124=??? ?

?

-πβ则

cos ??? ?

?

+4πα=______6556-__.

14.已知函数()2sin (0)f x x ωω=>在区间,34ππ??

-????上的最小值是2-，则ω的最小

值是＿3

2

＿＿＿。

15.（06湖南）若()sin()sin()(0)44f x a x b x ab ππ

=++-≠是偶函数,则有序实数对

(,a b )可以是 a =1，b =－1. (注:只要填满足0a b +=的一组数即可)

16.（06全国I ）设函数())

()cos 0f x ??π=+<<。若()()/f x f x +是奇函

数，则?=___6

π

_______。 三、解答题

17. 已知5tan cot 2αα+=

，ππ42α??

∈ ???

，．求cos 2α和πsin(2)4α+的值． 18.（06福建）已知函数f (x )=sin 2x +3x cos x +2cos 2x ,x ∈R.

（I ）求函数f (x )的最小正周期和单调增区间；

（Ⅱ）函数f (x )的图象可以由函数y =sin2x (x ∈R )的图象经过怎样的变换得到？

19.（06山东）已知函数f (x )=A 2sin ()x ω?+(A >0,ω>0,0

π

函数，且y =f (x )

的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1，2）. （1）求?;

（2）计算f (1)+f (2)+… +f (2 008).

20.（理科做）（06浙江）如图，函数y=2sin(πx +φ),x ∈R,(其中0≤φ≤

2

π

)

的图象与y 轴交于点（0，1）.

(Ⅰ)求φ的值；

(Ⅱ)设P 是图象上的最高点，M 、N 是图象与x 轴的交点，求.的夹角与PN PM 本题主要考查三角函数的图像，已知三角函数求角，向量夹角的计算等基础知识和基本的运算能力。

（文科做）已知复数w 满足i (i )23(4w w -=-为虚数单位），|2|5

-+=w w

z ，求一个以z 为根的实系数一元二次方程.

答案与点拨：

1 B 解：T ＝22

π

π＝，故选B

2 （理） D 解：333

124i i z ）＝＝

故选D 。 （文） A 解：由3(,),sin ,25παπα∈=则3tan 4α=-，tan()4πα+=

1tan 1

1tan 7

αα+=-，选A.

3 A 解：由sin2A ＝2sinAcosA >0，可知A 这锐角，所以sinA ＋cosA >0，又

2

5(sin cos )1sin 23A A A +=+=，故选A

4 B 解：设点P 是函数x x f ωsin )(=的图象C 的一个对称中心，若点P 到图象C 的对称轴上的距离的最小值

4

π

，∴ 最小正周期为π，选B. 5 （理）C 解析：

()()i n n m ni i m

-++=?-=+1111，由m 、n 是实数，得???=+=-m

n n 101 ∴i ni m m n +=+????==221

，故选择C 。

（文）C

解：函数

()tan 4f x x π?

?=+ ??

?的单调增区间满足

2

4

2

k x k π

π

π

ππ-

<+

<+

，

∴ 单调增区间为3,,44k k k Z ππππ?

?-+∈ ??

?，选C.

6 B 解：令sin ,(0,1]t x t =∈，则函数()sin 1

(0)sin x f x x x

π+=

<<的值域为函数

11,(0,1]y t t =+∈的值域，而1

1,(0,1]y t t

=+∈是一个减函减，故选B 。

7 C 解:22(sin )3cos23(12sin )2sin 2f x x x x =-=--=+

所以2()22f x x =+,因此22(cos )2cos 2(2cos 1)33cos2f x x x x =+=-+=+故选C 本题主要考察函数解析式的变换和三角函数的二倍角公式,记忆的成分较重,难度 一般 8 A 解：若等式sin(α+γ)=sin2β成立，则α+γ=k π+(－1)k 22β，此时α、β、γ不一定成等差数列，若α、β、γ成等差数列，则2β=α+γ，等式sin(α+γ)=sin2β成立，所以“等式sin(α+γ)=sin2β成立”是“α、β、γ成等差数列”的．必要而不充分条件。选A ．

9 D 解：从图象看出，41T=1264

πππ

+=，所以函数的最小正周期为π，函数应为

y=sin 2x 向左平移了6

π

个单位，即

sin 2()6y x π=+=sin(2)cos(2)cos(2)3236x x x ππππ

+=-++=-，选D.

10 D 解：函数()sin cos f x a x b x =-(a 、b 为常数,0,)a x R ≠∈，∴

())f x x ?=-的周期为2π，

若函数的图象关于直线4

x π

=对称，不妨

设()sin()4f x x π=+，则函数3()4y f x π=-=3sin()sin()sin 44

x x x ππ

π-+=-=，所

以3()4

y f x π

=-是奇函数且它的图象关于点(,0)π对称，选D.

11（理） 4 解：

(1)(12)2()()112252525

x y x i y i x y x y i i y +++=+=+++--， 而

55(13)13131022i i i +==+- 所以123

252252

x y x y +=+=且，解得x ＝－1，y ＝5， 所以x ＋y ＝4。

（文）－

2

1

解：

cos43°cos77°+sin43°cos167°=cos 43cos77sin 43sin 77cos120??-??=?=－2

1． 12 （理）i －1解：已知221i Z iZ i Z i ?-=?==-；

（文）

5

6

2 解：已知cos()sin (παα?+=-=-