第15章 电路方程的矩阵形式

第十五章电路方程的矩阵形式
重点:
1.关联矩阵、基本回路矩阵及基本割集矩阵等基本概念
2.熟练掌握几种基本矩阵的列写及其相互间关系
3.熟练掌握基于矩阵的大规模电路分析方法的原理及应用前景难点:
1.掌握各种电路分析方法的矩阵应用
2.理解大规模电路分析方法对电路的计算机辅助分析与设计的作用我们以前在学习支路电流法、支路电压法以及网孔分析法、节点分析法、割集分析法、回路分析法时,都是凭观察来列出所需的独立方程组。在求解方程时可以用手算,也可以使用电子计算机。对于含元件较少的电路,这种做法是行得通的。但是现代的电子电路可以包含数百个元件,特别是集成电路技术的飞越发展,电路日益复杂。对于这类“大规模(Large scale)电路”,不可能再凭观察来列写方程。需要有一种系统化的步骤来处理这类电路,使列写方程和求解的工作都能由电子计算机去完成。本章初步地介绍了这种分析方法。其中要用到上章所述图论的一些基本概念以及线性代数中的矩阵方法。
§15-1 电网络图论的基本概念
网络图论与矩阵论、计算方法等构成电路的计算机辅助分析的基础。其中网络图论主要讨论电路分析中的拓扑规律性,从而便于电路方程的列写。
15.1.1 网络的图
1.网络图论——网络拓扑学
图论是数学中重要的分支,网络图论是图论在电路理论中的应用。主要通过电路的结构及其连接性质,对电路进行分析计算。
2.支路——Branch
每一个电路元件或多个电路元件的某种组合用一条线段代替,称为支路。
3.节点——node
每一个电路元件的端点,或多个电路元件相连接的点用一个圆点代替,称为节点。在电网络理论中,通常节点是指支路的汇集点,这一概念与数学图论中的“节点”概念略有不同。
4.网络的图——graph
节点和支路的集合,称为图,每一条支路的两端都连接到相应的节点上。有向图——Oriented graph是指各个支路规定了参考方向的图反之,称为无向图。
5.路径——path
从图G的某一节点出发,沿着一些支路连续移动,从而达到一个指定的节点,这一系列支路构成图的一条路径。
6.连通图——connected graph
当图G 中的任意两个节点之间至少存在一条路径时,称为连通图。 7.回路——loop
如果一条路径的起点和终点重合所形成的闭合路径,称为回路。 8.网孔——mesh
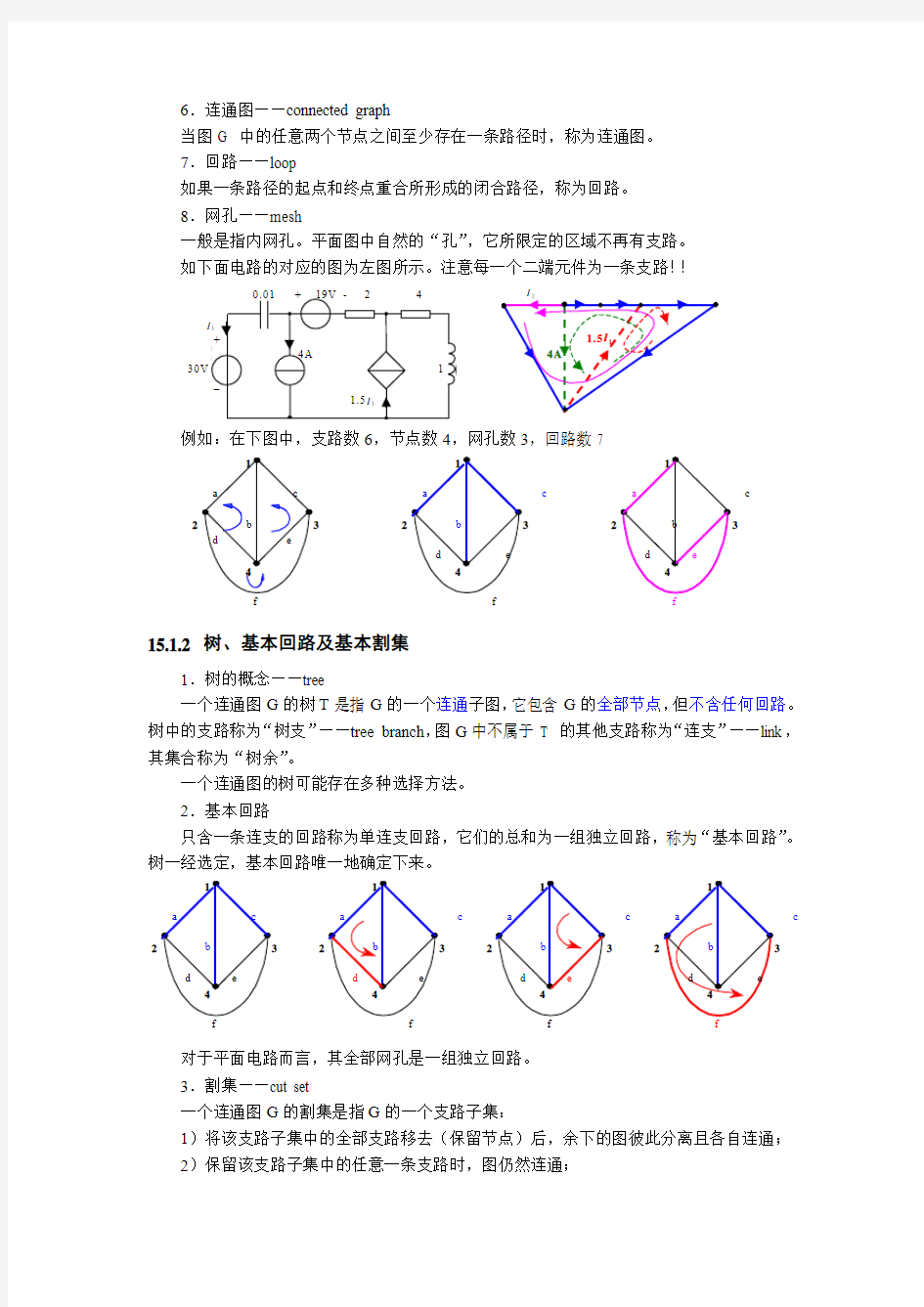
一般是指内网孔。平面图中自然的“孔”,它所限定的区域不再有支路。 如下面电路的对应的图为左图所示。注意每一个二端元件为一条支路!!
30V
例如:在下图中,支路数6,节点数4,网孔数3,回路数7
2
c 2
c 2
15.1.2 树、基本回路及基本割集
1.树的概念——tree
一个连通图G 的树T 是指G 的一个连通子图,它包含G 的全部节点,但不含任何回路。树中的支路称为“树支”——tree branch ,图G 中不属于T 的其他支路称为“连支”——link ,其集合称为“树余”。
一个连通图的树可能存在多种选择方法。 2.基本回路
只含一条连支的回路称为单连支回路,它们的总和为一组独立回路,称为“基本回路”。树一经选定,基本回路唯一地确定下来。
c
c
c
对于平面电路而言,其全部网孔是一组独立回路。 3.割集——cut set
一个连通图G 的割集是指G 的一个支路子集:
1)将该支路子集中的全部支路移去(保留节点)后,余下的图彼此分离且各自连通; 2)保留该支路子集中的任意一条支路时,图仍然连通;
基本割集
只含一条树支的割集称为单树支割集,它们的总和称为“基本割集”。树一经选定,基本割集唯一地确定下来。
c
c
c
2
15.1.3 关联矩阵a A与降阶关联矩阵A
给定一个定向图,各定向支路与各个节点之间的联接关系是十分清楚的,这种结构上的关系能否用代数的方法来表达呢?这对于企图用电子计算机来分析电路是个很重要的问题。运用矩阵可以解决这个问题。
一、关联矩阵Aa(又称增广关联矩阵)
1.定义
我们可以用定向图的各个节点组成矩阵的行,各定向支路组成矩阵的列,列表如下(其中,
,
2
1
b
b…等表示编号为1,2,…的支路,,...
,
2
1
n
n等表示编号为1,2,…的节点):以适当的数填入空档即可表明定向图中节点与支路的联接情况。这些数构成矩阵的元素。
1
b
2
b
3
b
4
b…
1
n
2
n
3
n
4
n
即定义关联矩阵(augmented incidence matrix),其中,a
A的行对应图的节点,列对应图的各个支路。]
[
ik
a
a
=
A
其中,当节点i与支路b k无关联时,0
=
ik
a
当节点i与支路b k关联,且支路电流的参考方向离开节点时,1
=
ik
a
当节点i与支路b k关联,且支路电流的参考方向指向节点时,1
-
=
ik
a 在一般情况下,对一个具有b条支路和n个节点的定向图来说,其增广关联矩阵为一个n行和b列的矩阵:
例如:
n
3
n
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
-
-
-
-
-
-
-
=
1
1
1
1
1
1
1
1
1
1
1
1
1
1
5
4
3
2
1
7
6
5
4
3
2
1
n
n
n
n
n
b
b
b
b
b
b
b
a
A
式15-1 图15-1 定向图一例 二、A a 的性质
由于每一支路都恰好与两个节点相关联,关联矩阵A a 中每一列都恰好有两个非零的元素,其一为+1,另一为-1。
把一个矩阵中的两行相加,就是把同一列中的元素相加。以(15-1)式所示矩阵为例,若矩阵中的第1行和第2行分别记为1R 和2R ,则
[][]01
1
10
1
001
00
10
10
01
01
121-=+-+++++-=+R R (15
-2)
如果把(15-1)式所示矩阵的各行相加,可得
054321=++++R R R R R
由此可见,增广关联矩阵的各行线性相关,这就是说,该矩阵中的任一行是其余各行的线性组合。
三、降阶关联矩阵A
由于增广关联矩阵的各行线性相关,即矩阵中的任一行是其余各行的线性组合。——也就是说,总可以通过矩阵的代数变换,使得其中某一行全为零元素——因此,除去增广关联矩阵中的任一行,矩阵仍具有同样的信息,足以表征定向图中节点对支路的关系。我们把这种()b n ?-1矩阵称为降阶(reduced )关联矩阵或径称为关联矩阵,记为A 。
在关联矩阵中有些列具有两个非零的元素(+1及-1),有些列只有一个非零元素。仍以图15-1所示定向图为例,若除去第2行,则
?
????????
???------=11
1
00011001000110
0011001
A (15-3)
再如:
问题:根据关联矩阵是否能够得到唯一的图??
四、矩阵A 的作用与KCL 定律及节点电压方程的矩阵表达式 1.关联矩阵A 与KCL 定律
电路的独立KCL 方程组可以用关联矩阵表示为向量方程。以上图为例,如果把节点2
选为参考节点,则由其余的4个节点可得独立的KCL 方程组如下:
节点1 05
2
1
=+--ΙΙΙ 节点3 04
5
1=++Ι
Ι
Ι
节点4 06
52=--Ι
Ι
Ι
(15-4)
?????
????
???------=11
1
01100110110000011143216 5 4 3 2 1a A
1 ?????
????
???------=11
1
01100110110000011143216 5 4 3 2 1a A
或写为
0=???
??????
?????????????????????----65432
111
1
011001000111
I I I I I I (15-5)
试把(15-5)式和(15-3)式加以比较,我们立即就可发现(15-5)式左端的系数矩阵与(15-3)式所示的矩阵A 完全相同。如设 []T
I 7
6
5
4
3
2
1
Ι
Ι
Ι
Ι
Ι
Ι
Ι
b =
并称b I 为支路电流向量,则(15-5)式
0AI
=b
(15-6)
虽然,这一方程是由图15-1所示的定向图得出的,但对任何定向图都可得出这一结果。 2.关联矩阵与支路电压、节点电压(——KVL )
仍然以上图为例,设各个支路电压分别为1u ,2u ,…,6u ,而以节点2为参考点的各个节点电压分别为1n u ,3n u ,4n u ,5n u
2
63532421312311n n n n n n n n n u u u u u u u u u u u u u u u ==+-=-=-=+-= ?????
???????????????
??????????----=??????????????
??
?321
65
4321 01
010********
01101
n n n u u u u u u u u u
可以推广之,设各个支路电压分别为1u ,2u ,…,b u ,用列相量表示
T
b u u u ] [21 =U
而以节点2为参考点的各个节点电压分别为1n u ,2n u ,…,
)
1(-n n u ,用列相量表示
T
n n n n u u u ]
[)1(21-= n U
则:n T
U A U =
15.1.4 回路矩阵及割集矩阵
一、增广回路矩阵B 1.定义
表明图中支路与回路之间的关系的矩阵。定义为:
设给定的定向图有b 条支路,a l 个回路。为每一回路规定一方向后,我们可以定义一个增广回路矩阵。它是一个b l a ?矩阵,记为a B ,
()ij
b =a B (15-7)
它的第()j i ,个元素确定如下: +1
如果支路j 在回路i 内,且它们的参考方向一致;
=
ij b -1
如果支路j 在回路i 内,且它们的参考方向不一致; 0
如果支路j 不在回路i 之内。
例如,图15-2所示定向图,具有六条支路和三个回路,如图中所示:
图15-2 定向图一例
设三个回路的方向均为顺时针方向。这定向图的增广回路矩阵为
6
54
3
2
1b b b b b b ????
?
?????----=00
1
1
1
1
111110
110001
321l l l a
B
(15-8)
显然可见,这矩阵的各行线性相关。 2.用B a 表示的KVL 方程矩阵表达式 如定义支路电压向量
[]
T
b U 65
4
3
2
1
U U U U U U =
则
0U B =b a
(15-9)
将表示该定向图所有回路的KVL 方程。 3.用B a 表示的KVL 方程矩阵表达式
设各个支路电流分别为1i ,2i ,…,b i ,用列相量表示
T
b i i i ] [21 =i
而各个回路电流分别为1l i ,2l i ,…,lm i ,用列相量表示
T
lm l l m i i i ] [21 =i
则:m i B i T
=
二、基本回路矩阵B
1.定义
由§2-5可知:独立回路数为()1--n b 个,因此在增广回路矩阵的a l 行中只有()1--n b 个是线性无关的。为了能直接获得独立的KVL 方程组,我们将运用§2-5所述的
基本回路的概念,并定义一个基本回路矩阵B ,它是一个()b n b ?+-1矩阵:
()ij
b =B (15-10)
它的第()j i ,个元素与a B 矩阵元素是一样的。
例如,对图15-3所示的定向图,选树如粗线所示,由连支确定基本回路,并选定其方向后,对应于该树的基本回路矩阵为
1
b
2
b
3
b 4b 5b 6
b
7
b
8b ?????
?
??????--=
10
1
1
0111000000011100
001000114321l l l l B (15-11)
2.用B 表示的KVL 方程矩阵表达式
电路的独立KVL 方程组可以用基本回路矩阵表示为向量方程。仍以图15-3的定向图为例,根据选定的基本回路,可得独立的KVL 方程组如下:
回路1l : 0261=++U U U
回路2l : 0543=++U U U
回路3l : 0765=+-U U U
(15-12) 回路4l : 0865=+-U U U
b b
23
图15-3 选定树后,定向图的基本回路
或写为
010
1
1
011100000001110000100011
87654321=??????
???
????
?????
???
?????????????????--U U U U U U U U (15-13)
由(15-11)式可知,上式可写为
0BU =b (15-14) 其中 []T
U 87
6
5
4
3
2
1
U U U U U U U U b =
虽然,这一方程是由图15-3所示的定向图得出的,但对任何定向图都可得出这一结果。 3.用B 表示的KCL 方程矩阵表达式
设各个支路电流分别为1i ,2i ,…,b i ,用列相量表示
T
b i i i ] [21 =I
而各个回路电流(即连支电流)分别为1l i ,2l i ,…,lm i ,用列相量表示
T
lm l l l i i i ] [21 =I
则:l I B I T
=
关于基本回路矩阵的说明
1)由于基本回路为单连支回路,所以其参考方向取为连支参考方向。 2)确定基本回路矩阵需要先选择一棵树
3)列写时,将矩阵的列按树支与连支分开排列的方式
????
?
???
??---=10
1
1
010110
001011 f e d f e d c b a B
三、基本割集矩阵Q 1. 定义
基本割集矩阵的行对应基本割集,列对应图的各个支路。][ik q =Q 其中, 当支路b k 与基本割集无关联时,0=ik q
当支路b k 与基本割集关联,且支路电流与基本割集的参考方向一致时,
1=ik q 当支路b k 与基本割集关联,且支路电流与基本割集的参考方向相反时,
1-=ik q
2. 关于基本割集矩阵的说明
1)由于基本割集为单树支回路,所以其参考方向取为树支参考方向。 2)确定基本割集矩阵需要先选择一棵树
3)列写时,将矩阵的列按树支与连支分开排列的方式 例如
????
?
???
??---=11
1
011010
101001
c b a f e
d c b a Q
再如图15-11所示定向图,对所示树来说
1b 2b
3b 4b 5b 6
b
图15-11 对选定树的三个基本割集
????
?
???
??---=11
1
100101
001011321q q q Q
3.用Q 表示的KCL 方程的矩阵表达式 对于每一个基本割集都应用一次KCL ,就可得到联系着b 个支路电流的()1-n 个线性
独立方程组。这组方程可表示为
0=b
QI
(KCL )
(15-46)
4.用Q 表示的KVL 方程的矩阵表达式 对于每一个基本割集都应用一次KCL ,就可得到联系着b 个支路电流的()1-n 个线性
独立方程组。这组方程可表示为
t T
U Q U = (KVL )
(15-46)
15.1.5 独立的KCL 方程和KVL 方程
一个含有n 个节点、b 条支路的电路,其独立的KCL (电流方程)方程数为(1-n )个,与这些独立的KCL 方程对应的节点称为独立节点;其独立的KVL (电压方程)方程数为 ()1(--n b )个。上述结论的具体说明与严格证明略去,有兴趣的同学可以在推荐的参考教材及有关的书籍中找到答案。一组独立回路就可对应一组独立的KVL 方程,因此,可以运用图论的一些基本概念来帮助我们简化电路问题的求解。
§15-2 支路方程的矩阵形式
从以上两节中我们得到两个基本
0AI
=b
(KCL )
0BU
=b
(KCL )
它们反映了电路的拓扑约束。我们还必须掌握支路的约束关系,才能得到完整的网络描述。本节推导支路约束关系的矩阵形式。
+ k
-
设电路中的每条支路有一个电阻,一个独立电压源和一个独立电流源,其一般形式如图15-4所示。如果支路中没有电源,则令电压源电压和电流源电流为零即可。由图15-4可得
sk k sk
k k k
U G Ι
U G Ι-+= b k ...2,1= (15-15)
其中
k
Ι
为第k 条支路电流,k U 为第k 条支路电压,k G 为第k 条支路电导,sk U 为第k
条支路的独立电压源的电压,sk
Ι为第k 条支路的独立电流源的电流。
把(3-15)式写成矩阵形式便得整个电路的支路约束。为此,定义支路电导矩阵G 如下
???????
????????
?=b G G G G
0000
000000321
G (15-16)
它是一个b b ?矩阵。定义独立电压源向量s U 为 []T
U 321s s s s U U U
= (15-17) 定义独立电流源向量s I 为 []T
I sb
s s s Ι
Ι
Ι
2
1
= (15-18)
于是,(15-15)式可改为
s
s b b G U
I G U I -+= (15-19)
这方程总括了网络中全部支路的约束关系。
支路方程也可用矩阵表示为
s s b
b AI U RI
U -+= (15-20)
其中
???????
????????
?=b R R R R
0000
000000321R (15-21)
称为支路电阻矩阵。
k k G R 1
=
b k ,2,1 =
根据两个约束关系,给定G I U ,,s s (或R )中的各元素值,我们就可求出电路中的各支路电流及支路电压。
§15-3 节点分析法
由第二章可知:在任何电路中必有一组电压是线性无关的,也必有一组电流是线性无关的。也就是说:电路中存在着一组独立电压变量,所有支路电压都可以表示为这组电压的线性组合;电路中存在着一组独立电流变量,所有支路电流都可以表示为这组电流的线性组合。
在第二章中我们已指出:电路中的()1-n 个节点电压是一组独立电压变量。若定义节点电压向量
()
[
]
T
U 12
1
-=n n n n n U U U
(15-22)
支路电压向量为
[]T
b U b U U U
2
1=
(15-23)
则这两向量间的关系可表为
n T
b U A U = (15-24)
其中T
A 为关联矩阵A 的转置。我们来证明这一关系。
设图3-5中所示为定向图中任一支路j ,联在节点i 与节点k 之间。任设支路电压j U
的极性如图中所示,则显然
nj
ni j
U U U
-=
这就是说,每一支路电压可表示为节点电压的线性组合。其一般形式应为
∑=-=1
1n i ni
ji j
U p U
(15-25)
i
+ j + ni
U
- nk
U
图15-5 借助于节点电压计算支路电压
其中
ji
p
为+1,-1或0。这就是说,支路电压向量与节点电压向量可表为
n b PU U = (15-26) 其中P 为()1-?n b 矩阵 ()ji
p =P (15-27)
它的第()i j ,个元素确定如下:
+1 如果支路j 与节点i 相关联,且离开该节点;
=
ji p -1 如果支路j 与节点i 相关联,且进入该节点; 0
如果支路j 与节点i 无关联。
上述
ji
p 的定义与关联矩阵A 中元素
ij
a 的定义完全相同,故得
ij
ji a p = 对所有的i 和j (15-28)
这表明
T
A P = (15-29)
于是(15-24)式得到了证明。
借助于()1-n 个节点电压来表示b 个支路电压,实际上是表达KVL 加于支路电压约束的一种方法。(15-24)式(KVL )连同(15-6)式(KCL )构成节点分析的两个基本方程。把它们和反映网络支路约束关系的(15-19)式相结合,就可得到具有()1-n 个未知量
()
121-n n n n U U U 、、的()1-n 个方程。为此,要进行消去支路变量的工作,其过程如下所
示:
KCL 0=b AI
(15-6) KVL n
T
b
U A U =
(15-24) VAR
s
s b
b GU I GU I -+=
(15-19) 以矩阵A 左乘方程(15-19)式,用
n
T
U A 代替b
U ,并应用(15-6)式,可得
=-+s
s n T
AGU
AI
U AGA
(15-30) 或
s
s
n T
AI
AGU
U AGA
-=
(15-31)
在上式中,T
AGA
是一个()()11-?-n n 方阵,而
s
AGU
和s AI -都是()1-n 维列向量。令
T
n
AGA
G
=
(15-32a )
s
s
n AI
AGU
I -=
(15-32b)
则(15-31)式成为
n
n n I U G =
(15-33)
方程组(15-33)式通常称为节点方程;n G 称为节点电导矩阵,n I 称为节点电流源向量。
在这个节点方程中,n G 和n I 是可以根据给定的电路结构、元件的参数和电源的电压以及电流算得的。由定向图能确定关联矩阵A ,由各支路的电导根据(15-16)式可确定支路电导矩阵G ,因而节点电导矩阵n G 就可由(15-32a )式确定。同样,由于电源向量s U 和s
I 是已知的,所以节点电流源向量n I 可按(15-32b )式确定。因此,向量方程(15-33)式把未知的()1-n 维列向量n U 同已知的()()11-?-n n 矩阵n G 和()1-n 维列向量n I 相联系。由此可解得n U 。n U 一旦求得,由(15-24)式可确定b 个支路电压,再由支路(15-19)可确定b 个支路电流。
节点方程(15-33)式是由()1-n 个以节点电压作未知量的线性代数方程组。(15-33)式是第二章(2-9)式的矩阵表示形式。我们过去是用视察法直接由电路列出这组方程的,并用任何一中方法求得解答。本节所述内容,可为节点分析法提供了一个严格的系统步骤,在任何情况下都适用。这种系统的方法在为运用计算机而编制程序时是必需的。
例15-1 电路如图15-6(a )所示,试列出编写节点方程和解出各支路变量的详细步骤。 解:(1)作该电路的图如图(b )所示。任选一参考节点,如节点5,其余节点分别标
以1、2、3、4。节点电压为4
321n n n n U U 、U U 、、。
(2)对支路1、2、3、4、5、6、7、8加以编号,并指定每一支路的参考方向。以变量
i
G 表示第i 支路的电导。
(3)建立关联矩阵A
1b 2b 3b 4b 5b 6b 7b 8b
84432101
1
1
100011000010001100011001
??
???????????------=
n n n n A
1n +
3Α -
(a ) (b) 图15-6 例15-1
(4)建立支路电导矩阵,由于电路具有8条支路,该矩阵为88?阶,且为对角线矩阵。
1b 2b 3b 4b 5b 6b 7b 8b
8
887654321210
001000000005100000000210000000010000000071000000001000000001??????????????
?????????????=
b b b b b b b b G
(5)根据T
n AGA
G =计算节点电导矩阵。
488
401
1000001000010101110010100011
03
10
7
11
21000171000051000110002151001
???????????????
?????????????------???
??????????------==T
n AGA
G
故得
4421317
11
71590511
051110
111017???
????????
??--------=
n
G
(6)确定独立电压源向量和独立电流源向量
[]T
s 000010000-=U
[]T
s 00000
03
-=I
注意,电压、电流的符号均根据图3-4,一般电阻支路所规定的方向与图3-6中支路的实际选定方向作比较而确定。
(7)根据s s
n AI AG U
I -=确定节点电流源向量
188
400001000003
10
7
11
2100017100005100011000211001??????????????????????
??????-???
??????????------=s
AGU
计算得
140202??
????????
???-=s
AGU
;
143030?????????????-=-s
AI
故得
?????
????
???--=-=3232s
s
n AI
AGU
I
(8)得节点方程n n n I U G =
?
????
?
??????--=???????????????????
??
?
??--------323
221317
11
71590511051110
11101743
21n n n n U U U U (9)我们可以通过逆矩阵1
-n G 来求解节点电压
??
???
?
??????--?????????
???=????????????--??
????
???
???--------=????????????-323
2253.1344
.0802
.0511
.0334.0322.1303.0334.0802.0303.014.1706.0511.0334.0706.0043.1323221317
11
170590511
051110
51110171
4321n n n n U U U U
解得
V
004.21=n U V
821.12
=n U V 067.23
-=n U V
999.04
-=n U
(10)求得各节点电压后,支路电压可由n T
b U A U =求得。
1
44
81887654321999.0067.2821
.1004.201
01000001000010101110010100011?????????
???
???--??????????????
?
??????
??????------=???????
???????????????????U U U U U U U U 解得
V 183.01=U V 820.22=U V
068.13-=U V 071.44
-=U V 004.25-=U V
821.16=U
V 999.07
=U V
067.28
-=U
(11)由s s b
b G U I G U
I -+=求各支路电流。得
A =183.01I A -=180.02
I
A -=152.03I A
=186.14I
A -=002.15I A =821.16I
A =333.07
I A
-=033.18
I
上例的建立方程和求解的工作可以由计算机完成。为此,我们应把计算程序以及网络的拓扑结构、元件的参数值输入计算机。计算结果由计算机的输出设备(例如行式打印机)获得。
一种输入数据的方式是:先输入节点数和支路数,以图3-6电路为例,输入数据的第一行为 5,8
“通知”计算机电路有5个节点,8条支路。其第二行为 1,1,2,1,0,0 其中第一位为支路编号,第二位为该支路的起始节点编号,第三位为该支路的终止节点编号,第四位为电阻值,第五位为电压源值,第六位为电流源值。
因此,图3-6电路的全部输入数据为 5,8
1,1,2,1,0,0
2,2,4,1,0,-3 (s I 与支路方向不一致) 3,3,4,7,0,0 4,3,1,5,-10,0 (s
U
与支路方向不一致)
5,5,1,2,0,0 6,2,5,5,0,0 7,5,4,3,0,0 8,3,5,2,0,0 根据这些数据,计算机即可形成
s
U G A 、、及
s
I 等矩阵。
计算机根据程序由A 形成T
A ,即可算出s
T
AGU AGA ,及s AI 等矩阵。在算出1-n
G
后,即可算出n U ,进而算出b b I U ,,并把结果打印出来。
§15-4 回路分析法
在前面我们已指出:选定树后,电路中的基本回路电流是一组独立电流变量,其个数为
()1--=n b l ,所有支路电流都可以表示为这组电流的线性组合。设基本回路电流向量为
[]T
ll l l l I I I
2
1
=I (15 -34)
这一向量与支路电流向量的关系可表示为
l T
b I B I = (15-35)
其中T
B 为基本回路矩阵的转置。我们来证明这一关系。
每一支路电流可表示为基本回路电流的线性组合。第j 条支路的电流可表示为 ∑==l
i li
ji j I c I 1 (15-36)
其中
ji
c 可为+1,-1或0。例如在图15-8所示定向图中,
()()()()432171110l l l l I I I I I -+++++=
写为一般形式,即为
l b CI I = (15-37)
其中C 为l b ?矩阵:
()
ji c =C (15-38)
它的第()i j ,个元素确定如下:
+1 如果支路j 在回路i 内,且它们的参考方向一致;
=
ji c -1 如果支路j 在回路i 内,且它们的参考方向不一致; 0 如果支路j 不在回路i 内。
图15-8 表明基本回路电流与支路电流关系用图
上述
ji
c 的定义与基本回路矩阵B 中的元素
ij
b 的定义完全相同,故得
ij
ji
b c = 对所有的i 和j
(15-39)
这表明
T
B C = (15-40)
于是(15-35)式得到了证明。
借助于()1--n b 个回路电流来表示b 个支路电流,实际上是表达KCL 加于支路电流约束的一种方法。(15-35)式(KCL )连同(3-34)式(KVL )构成回路分析的两个基本方程。把它们和反映网络支路约束条件的(15-20)式相结合,就可得到具有()1--n b 个未知量ll l l I 、、I I 21的()1--n b 个方程。为此,要进行消去支路变量的工作,其过程如下所示:
0BU =b (KVL )
(15-14)
l T
b I B I = (KCL )
(15-35)
s s b
b AI U RI
U -+= (V AR ) (15-20)
以矩阵B 左乘方程(15-20)式,用l T
I B 代替b I ,并考虑到(15-14)式,可得
s s l T
BU BRI I BRB -= (15-41)
在上式中,T
BRB 是一个()[]()[]11--?--n b n b 方阵,亦即l l ?方阵,而s BRI 和s
BU
-都是l 维向量。令
T
l B R B R =
(15-42) s s l BU BRI U -=
(3-43)
则(15-41)式成为
l l l U I R =
(15-44)
方程组(15-44)式通常称为回路方程;l R 称为回路电阻矩阵,l U 称为回路电压源向量。
以上所述内容,可为回路分析法提供一个严格的系统步骤,适宜于编制计算机程序。 例15-2 用回路分析法求解图15-6所示电路的支路电流。
图15-6 例15-2
解 作图15-6电路的定向图如图15-9所示,选树如图中粗线所示,基本回路为3
21l l l 、、和4l
8
487654321
4
32
1
10
1
1
0110001000110001000110001????????????????
?----=b b b b b b b b l l l l B
1b 2b 3b 4b 5b 6b 7b 8
b
888765432120
003000000005000000002000000005000000007000000001000000001
??????????????
?????????????=
b b b b b b b b R
4
492
2
2123003952058
???
????
??????--------==T
l BRB
R
1410030?????????????-=-=s
s
l BU
BRI
U
得回路方程
??
????
??????-=???????????????????
?????--------10030920
2
21230039520584321l l l l I I I I
?????
???????-??
???
?
?
?????--------=????????????-1003092
2
21230039520581
4321l l l l I I I I
A =1838.01l I A -=1806.02l I A
=1527.03l I A
=186.14
l I
求支路电流:
?????
?
?
???
??-??????????
??
?
?
????????????----=??????????????????????????186.11527.01806
.01838.011
00110001110011000
0100001000018765
4321I I I I I I I I
A
=1838.01
I A
-=1806.02I
A =1527.03I A =186.14I
A -=002.15I A
=3644.06I
A -=3333
.07I A -=033.18
I
§15-5 割集分析法
一、方法
以树支电流为变量,对用树支确定的基本割集列写KCL 方程,从而分析计算电路的方法。
在选择树时,应尽量将电压源或受控压源所在的支路选为树支,这样可以不再对由纯压源树支所确定的基本割集列写方程,从而进一步减少方程的数量。
解题方法与解题步骤基本与节点法相同,可以应用于非平面电路,而且在某些电路结构下可以简化计算。
二、割集分析法的矩阵形式
t t t J U G =?
其中:
◆ G t ——割集电导矩阵。其对角线上的元称为“自导”,其值为某一基本割集中联接的
支路上的电导之和,符号为正;其他各元称为“互导”, 其值为某两个基本割集共有支路上的电导之和,符号由两个割集的参考方向决定,如果一致,为正;相反则为负。
注意:割集之间参考方向的是否一致要依据其公共支路来判定。 ◆ U t ——树支电压向量。其元为各个树支的电压,为列向量。
◆ J t ——割集电流源向量。其元为与各个基本割集方向相反的电流源电流的代数和,
为列向量。 三、例题
1.已知:如图所示
求:
解:选树如图所示,则只需要对2Ω、4Ω支路(树支)所决定的基本割集列写方程即可。
1925305.144)42()425(11+--=?-?++?++I I
解得:A I 121-= 2.已知:如图所示
求:
解:选树如图所示,则只需要对2Ω、4Ω支路(树支)所决定的基本割集列写方程
网络拓扑和电路的矩阵形式
第十五章网络拓扑和电路方程的矩阵形式 第一节网络的拓扑图 一、网络的图:1、拓扑图: 在电路的分析中,不管电路元件的性质差别,只注意连接方式即网络拓扑的问题。若将每一条支路用一条线段(线段的长短、曲直不限)来表示,就组成拓扑图。如图15-1-1(a)对应电路的拓扑图为(b)。图15-1-2(a)对应电路的拓扑图为(b)。图15-1-3(a)对应电路在低频下的拓扑图为(b)。 此拓扑图是连通图。 (b) 是互感 电路的 分离图。 (b)是在低频下的拓扑图,是分离图,包括自环(自回路)、悬支、孤立结点。
2、有向图:如果标以支路电压、电流的(关联)参考方向,即成有向图。 3、子图:如果图G1的所有结点和支路是图G的结点和支路,则G1是G的子图。子图可以有很多。 第二节树、割集 一、树: 1、定义:连通图G的树T是G的一个子图。(1)它是连同的。(2)包括G中的所有结点。(3)不包含任何回路。树是连接图中所有结点但不包含回路的最少的支路集合。同一拓扑图可以有不同的树。对于一个有n个结点的全连通图可以选择出n n-2种不同的树。 2、树支和连支:当树确定后,凡是图G的支路又属于T的,称为树支,其它是连支。树支数T=n-1;连支数L=b-(n-1)。 二、割集: 定义:对连通图来说,割集C是一组支路的集合,如果把C的全部支路移去,将使原来的连通图分成两个分离部分,但在C的全部支路中,只要少移去一条支路,剩下的拓扑图仍是连通的。因此割集是把连通图分成两个分离部分的最少支路集合。 三、独立回路组的确定: 可以通过树确定一组独立回路,称为单连支回路组。如图15-2-1。 选择支路1、2、3、7为树支,4、5、6、 8为连支,则单连支回路组为: {1、2、4},{2、3、5},{2、3、6、7}, {1、3、7、8}。 又称为单连支回路组。 四、独立割集组的确定: 可以通过树确定一组独立割集,称为单树支割集组。如图15-2-2。 选择支路1、2、3、7为树支,4、5、 6、8为连支,则单树支割集组为: {1、4、8},{2、4、5、6},{3、5、6、 8},{6、7、8}。 又称为单树支割集组。 第三节关联矩阵、回路矩阵、
第十五章电路方程的矩阵形式
第十五章电路方程的矩阵形式 一、本章的核心、重点及前后联系 (一)本章的核心 列出结点电压方程的矩阵形式。 (二)本章重点 1.关联矩阵、回路矩阵、割集矩阵; 2.结点电压方程的矩阵形式。 (三)本章前后联系 本章是第三章电阻电路一般分析方法的扩充。 二、本章的基本概念、难点及学习方法指导 (一)本章的基本概念 1.割集定义 定义:连通图G 的一个割集是G 的一个支路集合,把这些支路移去将使G 分离为两个部分,但是如果少移去其中一条支路,图仍将是连通的。 割集:Q 1(a 、d 、f );Q 2(a 、b 、e );Q 3(b 、c 、f );Q 4(c 、d 、e );Q 5(b 、d 、e 、f ); Q 6(a 、c 、e 、f );Q 7(a 、b 、c 、d )。 图G 的割集 2.关联矩阵定义 定义:对于具有n 个节点、b 条支路的图,其关联矩阵(节点、支路关联矩阵)为一个 )(b n ?的矩阵,用a A 表示。行对应节点,列对应支路,它的任意元素jk a 定义如下: 1+=jk a ,表示支路k 与节点j 关联并且它的方向背离节点; 1-=jk a ,表示支路k 与节点j 关联并且它的方向指向节点; 0=jk a ,表示支路k 与节点j 不关联。 ? ???? ???????---++-++--++=0111001 0011001001110100143216 54321a A 划去a A 中的任意一行,剩下的b n ?-)1(矩阵用 A 表示,称为降阶关联矩阵: a b c d e f 5 Q 6 Q 7Q a b c d e f 1 Q 2 Q 3Q 4 Q 13
同济大学线性代数教案第一章线性方程组与矩阵
线性代数教学教案 第一章线性方程组与矩阵 授课序号01 1112121 2 n n m m mn a a a a a a ?? ?? ??? ,有时为了强调矩阵的行数和列数,也记为
n a ???. 212 n n n nn a a a ? ??? . 1112 00n n nn a a a a ?? ?? ? ? ?与上三角矩阵200 n nn a ? ??? . 000 0n a ??? ??? ,或记为100 1? ???? . 负矩阵的定义:对于矩阵()ij m n a ?=A ,称矩阵21 22 n m m m mn mn b a b a b ?? +++? ,
a b+
21 2 n m m mn a a a ????,转置矩阵212.m n n nm a ? ??? 矩阵的转置满足的运算规律(这里k 为常数,A 与B 为同型矩阵)阶方阵()ij a =A 如果满足222n n m mn n a x +21 2 n m m mn a a a ????称为该线性方程组的系数矩阵n x ???,m b = ? ??? β,有:
2221122221 21122n n n m m mn n m m mn n a a a x a x a x a x ??? ? =??? ???? ? ++ +????? . 再根据矩阵相等的定义,该线性方程组可以用矩阵形式来表示:=Ax β.
授课序号02 21 2 t s s st ????A A A ,21 2 t s s st ? = ? ??? B B B B ,的行数相同、列数相同,则有 21 22 t s s s st st ?? ±±±? B A B A B . 111221 2 t s s st ? ? ??? A A A A A ,都有21 2 t s s st k k ? ??? A A A .
知识点总结 矩阵的初等变换与线性方程组
第三章 矩阵的初等变换与线性方程组 第一节 矩阵的初等变换 初等行变换 ()1()i j r r ?对调两行,记作。 ()20()i k r k ≠?以数乘以某一行的所有元素,记作。 ()3()i j k r kr +把某一行所有元素的倍加到另一行对应的元素上去,记作。 初等列变换:把初等行变换中的行变为列,即为初等列变换,所用记号是把“r ”换成“c ”。 扩展 矩阵的初等列变换与初等行变换统称为初等变换,初等变换的逆变换仍为初等变换, 且类型相同。 矩阵等价 A B A B 如果矩阵经有限次初等变换变成矩阵,就称矩阵与等价。 等价关系的性质 (1)反身性 A~A 2 A ~B , B ~A;()对称性若则 3 A ~B,B ~C, A ~C ()传递性若则。(课本P59) 行阶梯形矩阵:可画出一条阶梯线,线的下方全为零,每个台阶只有一行,台阶数即是非零行的行数阶梯线的竖线(每段竖线的长度为一行)后面的第一个元素为非零元,也是非零行的第一个非零元。 行最简形矩阵:行阶梯矩阵中非零行的第一个非零元为1,且这些非零元所在的列的其他元素都为0. 标准型:对行最简形矩阵再施以初等列变换,可以变换为形如r m n E O F O O ???= ???的矩阵,称为标准型。标准形矩阵是所有与矩阵A 等价的矩阵中形状最简单的矩阵。 初等变换的性质
设A 与B 为m ×n 矩阵,那么 (1);r A B m P PA B ?=:存在阶可逆矩阵,使 (2)~;c A B n Q AQ B ?=存在阶可逆矩阵,使 (3)P ;A B m P n Q AQ B ?=:存在阶可逆矩阵,及阶可逆矩阵,使 初等矩阵:由单位矩阵经过一次初等变换得到的方阵称为初等矩阵。 初等矩阵的性质 设A 是一个m ×n 矩阵,则 (1)对A 施行一次初等行变换,相当于在A 的左边乘以相应的m 阶初等矩阵; ~;r A B m P PA B ?=即存在阶可逆矩阵,使 (2)对A 施行一次初等列变换,相当于在A 的右边乘以相应的n 阶初等矩阵; 即~;c A B n Q AQ B ?=存在阶可逆矩阵,使 (3)~P ;A B m P n Q AQ B ?=存在阶可逆矩阵,及阶可逆矩阵,使 (4)方阵A 可逆的充分必要条件是存在有限个初等方阵1212,,,,l l P P P A PP P =L L 使。 (5)~r A A E 可逆的充分必要条件是。(课本P ? ) 初等变换的应用 (1)求逆矩阵:()1(|)|A E E A -????→初等行变换或1A E E A -????????→ ? ????? 初等列变换。 (2)求A -1B :A (,) ~ (,),r A B E P 即() 1(|)|A B E A B -??→行,则P =A -1B 。或1E A B BA -????????→ ? ????? 初等列变换. 第二节 矩阵的秩
线性方程组的矩阵求解算法
线性方程组的矩阵求解算法 摘要 线性方程组的矩阵求解算法,只需在约当消元法的基础上,再对方程组的 增广矩阵的行最简形进行行(列)删除和增加行,交换行等运算即可得到方程组的解,并且这种方法既可求解有唯一解的方程组.因而算法简单,易于实现. 关键词 线性方程组;解向量;解法;约当消元法 1 矩阵求解算法 设有线性方程组m n A X b ?=,其增广矩阵())(1,m n A A b ?+=,算法的步骤如下: 第一步:利用约当消元法,把增广矩阵A 化为行最简形,设行最简形为()1m n B ?+.若()t i (),r A r =则方程组无解;否则设(),r A R =并执行以下步骤; 第二步:删除B 中的所有零行和每一行第一个非零元素(这个非零元素一定是1)所在的列,得到矩阵()1,r n r D ?-+并记录每行的第一个非零元所在的列标,放在一维数组()1,,t r L 中,如第i 行的第一个非零元在第j 列,则()t i j =; 第三步:构造矩阵() 1m n r D H F ?-+?? = ? ??,其中 ()()1100 001 0000 10n r n r F -?-+-?? ?- ? = ? ? -??L L L L L L L L 第四步:对矩阵H 中的行作交换运算:把H 中的第i 行(,1,1,i r r =-L 即从第r 行开始直到第一行)依次与其下一行交换,使之成为第()t i 行,交换运算结果后的矩阵记为G ,则G 中的前n r -个n 维列向量即为方程组的一个基础解系,最后一列向量即为方程组的一个特解; 第五步:写出方程组的通解. 2 算法证明 先证一个特殊情形,增广矩阵A 的行最简形矩阵B 的左上角为一r 阶的单位矩阵,即第i 行的第一个非零元的列标为i ,即()()1t i i i r =≤≤,所以设B 为
总结求线性方程组的方法
总结求线性方程组的方法-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII
华北水利水电大学 总结求线性方程组的方法 课程名称:线性代数 专业班级: 成员组成: 联系方式: 2014年12月31日
摘要:线性方程组的求解是当代代数学中的一个重要组成部分。它广泛应用在数学以及其他领域。它与矩阵、线性变换、行列式、向量组的线性相关性,二次型,这些型之间有着相当密切的联系。线性方程组是线性代数中一个相当基础的内容必须要学会以及熟悉内容。本文章主要说明和讨论线性方程组的基本结构,然后应用克拉莫法则,高斯消元法来来求解。 关键词:线性方程组、高斯消元法、克拉莫法则; Summary for the method of liner equations Abstract: Solution of the system of linear equations is an important component part of algebra. It is widely used in mathematics and other areas. It and determinant, matrix, linear transformation, linear correlation vector group, quadratic form, has the close relation. System of linear equations is a very basic content in linear algebra must grasp and familiar with the content. This article mainly explain and discuss the basic structure of system of linear equations, then apply law of kramer, gauss elimination method to solve.
第三章知识点总结 矩阵的初等变换与线性方程组
第三章矩阵的初等变换与线性方程组 第一节 矩阵的初等变换 初等行变换 ()1()i j r r ?对调两行,记作。 ()20()i k r k ≠?以数乘以某一行的所有元素,记作。 ()3()i j k r kr +把某一行所有元素的倍加到另一行对应的元素上去,记作。 初等列变换:把初等行变换中的行变为列,即为初等列变换,所用记号是把“r ”换成“c ”。 扩展 矩阵的初等列变换与初等行变换统称为初等变换,初等变换的逆变换仍为初等变换, 且类型相同。 矩阵等价 A B A B 如果矩阵经有限次初等变换变成矩阵,就称矩阵与等价。 等价关系的性质 (1)反身性 A~A 2 A ~B , B ~A;()对称性若则 3 A ~B,B ~C, A ~C ()传递性若则。(课本P59) 行阶梯形矩阵:可画出一条阶梯线,线的下方全为零,每个台阶只有一行,台阶数即是非零行的行数阶梯线的竖线(每段竖线的长度为一行)后面的第一个元素为非零元,也是非零行的第一个非零元。 行最简形矩阵:行阶梯矩阵中非零行的第一个非零元为1,且这些非零元所在的列的其他元素都为0. 标准型:对行最简形矩阵再施以初等列变换,可以变换为形如r m n E O F O O ???= ???的矩阵,称为标准型。标准形矩阵是所有与矩阵A 等价的矩阵中形状最简单的矩阵。 初等变换的性质 设A 与B 为m ×n 矩阵,那么 (1);r A B m P PA B ?= 存在阶可逆矩阵,使 (2)~;c A B n Q AQ B ?=存在阶可逆矩阵,使 (3)P ;A B m P n Q AQ B ?= 存在阶可逆矩阵,及阶可逆矩阵,使 初等矩阵:由单位矩阵经过一次初等变换得到的方阵称为初等矩阵。 初等矩阵的性质 设A 是一个m ×n 矩阵,则 (1)对A 施行一次初等行变换,相当于在A 的左边乘以相应的m 阶初等矩阵; ~;r A B m P PA B ?=即存在阶可逆矩阵,使
矩阵分解与线性方程组求解
一、 用列主元素高斯削去法求解下述线性方程组: ?????? ?-=+--=++---=--+=--+36 15531495102210762133421342143214 3214321x x x x x x x x x x x x x x x 程序: function x=gaussa(a) m=size(a); n=m(1); x=zeros(n,1); for k=1:n-1 [c,i]=max(abs(a(k:n,k))); q=i+k-1; if q~=k d=a(q,:);a(q,:)=a(k,:);a(k,:)=d end for i=k+1:n a(i,:)=a(i,:)-a(k,:)*a(i,k)/a(k,k) end end for j=n:-1:1 x(j)=(a(j,n+1)-a(j,j+1:n)*x(j+1:n))/a(j,j) end 执行过程: >> a=[1 13 -2 -34 13;2 6 -7 -10 -22;-10 -1 5 9 14; -3 -5 0 15 -36] a = -10 -1 5 9 14 2 6 -7 -10 -22 1 13 -2 -34 13 -3 -5 0 15 -36 >> gaussa(a) a = -10.0000 -1.0000 5.0000 9.0000 14.0000 0 5.8000 -6.0000 -8.2000 -19.2000 1.0000 13.0000 -2.0000 -34.0000 13.0000 -3.0000 -5.0000 0 15.0000 -36.0000 a = -10.0000 -1.0000 5.0000 9.0000 14.0000 0 5.8000 -6.0000 -8.2000 -19.2000 0 12.9000 -1.5000 -33.1000 14.4000 -3.0000 -5.0000 0 15.0000 -36.0000 a = -10.0000 -1.0000 5.0000 9.0000 14.0000 0 5.8000 -6.0000 -8.2000 -19.2000 0 12.9000 -1.5000 -33.1000 14.4000 0 -4.7000 -1.5000 12.3000 -40.2000
线性方程组的矩阵求法
线性方程组的矩阵求法 摘要: 关键词: 第一章引言 矩阵及线性方程组理论是高等代数的重要内容, 用矩阵 方法解线性方程组又是人们学习高等代数必须掌握的基本 技能,本文将给出用矩阵解线性方程组的几种方法,通过对线性方程组的系数矩阵(或增广矩阵)进行初等变换得到其解,并列举出几种用矩阵解线性方程组的简便方法。 第二章用矩阵消元法解线性方程组 第一节预备知识 定义1:一个矩阵中不等于零的子式的最大阶数叫作这个矩阵的秩。定理1:初等变换把一个线性方程组变为一个与它同解的线性方程组。 定义2:定义若阶梯形矩阵满足下面两个条件: (1)B的任一非零行向量的第一个非零分量(称为的 一个主元)为1; (2)B中每一主元是其所在列的唯一非零元。 则称矩阵为行最简形矩阵。 第二节 1.对一个线性方程组施行一个初等变换,相当于对它的增广矩
阵施行一个对应的行初等变换,而化简线性方程组相当于用行初等变换化简它的增广矩阵,因此,我们将要通过花间矩阵来讨论化简线性方程组的问题。这样做不但讨论起来比较方便,而且能给我们一种方法,就一个线性方程组的增广矩阵来解这个线性方程组,而不必每次都把未知量写出来。 下面以一般的线性方程组为例,给出其解法: (1) 11112211 21122222 1122 , , . n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b +++= +++= +++= L L L L L L L L L L L L L L L 根据方程组可知其系数矩阵为: (2) 11121 21222 12 n n m m mn a a a a a a a a a ?? ? ? ? ? ??? L L L L L L L L L L L L 其增广矩阵为: (3) 111211 212222 12 n n m m mn m a a a b a a a b a a a b ?? ? ? ? ? ??? L L L L L L L L L L L L L L L 根据(2)及矩阵的初等变换我们可以得到和它同解的线性方程组,并很容易得到其解。 定理2:设A是一个m行n列矩阵
线性方程组与矩阵
高代小练习 专业课研究部 一、填空题 1.设n 元齐次线性方程组的系数矩阵的秩r < n ,则方程组的基础解系由_n-r__个解向量组成. 2.向量组123,,ααα线性无关,则122331(,,)rank αααααα+++=__3____. 3.设向量组12,,,r βββ 可以由向量组12,,,s ααα 线性表出.如果向量组12,,,r βββ 线性无关,则r __<=___s (填大小关系). 4.在数域K 上的4维向量空间K 4内,给定向量组α1 =(1,-3,0,2)α2 =(-2,1,1,1)α3 =(-1,-2, 1,3),则此向量组的秩是_2____. 5.若V={(a+bi ,c+di)|a,b,c,d 属于R},则V 对于通常的加法和数乘,在复数域上是__2____维的,而在实数域上是__4_____维的. 6.设线性方程组AX=0的解都是线性方程组BX=0的解,则秩A ?>=??秩B. 7.设t ηηη,,,21 及t t ηληληλ+++ 2211都是)0(≠=b b AX 的解向量,则 =+++t λλλ 21______。 8.设任意一个n维向量都是齐次线性方程組0=AX 的解向量,则=)(A r ______。 9.已知321,,ααα是齐次方程组0=AX 的基础解系,那么基础解系还可以是______. (A) 332211αααk k k ++ (B) 133221,,αααααα+++ (C) 3221,αααα-- (D) 233211,,αααααα-+- 10.在三维几何空间中,用V 1表示通过原点的直线,V 2表示通过原点且与V 1垂直的平面,试求 21V V ?=_原点____,和21V V ?=_整个空间R 3 ____。 二.解答题 1.在4维向量空间中, (1)求基 到基 的过渡矩阵。
电路方程的矩阵形式
第十五章电路方程的矩阵形式 重点:1. 关联矩阵; 2. 结点电压方程的矩阵形式; 3. 状态方程。 难点: 电路状态方程列写的直观法和系统法。 §15.1 图的矩阵表示 1.有向图的关联矩阵 2.电路的图是电路拓扑结构的抽象描述。若图中每一支路都赋予一个参考方向,它成为有向图。有向图的拓扑性质可以用关联矩阵、回路矩阵和割集矩阵描述 3.关联矩阵是用结点与支路的关系描述有向图的拓扑性质。 4.回路矩阵是用回路与支路的关系描述有向图的拓扑性质。 5.割集矩阵是用割集与支路的关系描述有向图的拓扑性质。 6.本节仅介绍关联矩阵以及用它表示的基尔霍夫定律的矩阵形式。 7.一条支路连接某两个结点,则称该支路与这两个结点相关联。支路与结点的关联性质可以用关联矩阵描述。设有向图的结点数为n ,支路数为b ,且所有结点与支路均加以编号。 于是,该有向图的关联矩阵为一个阶的矩阵,用表示。它的每一行对应一个结 点,每一列对应一条支路,它的任一元素定义如下: 8.,表示支路k 与结点j 关联并且它的方向背离结点; 9.,表示支路k 与结点j 关联并且它指向结点; 10.,表示支路k 与结点j 无关联。 对于图 15.1 所示的有向图,它的关联矩阵是 关联矩阵的特点:图 15.1 ① 每一列只有两个非零元素,一个是+1,一个是-1,的每一列元素之和为零。
② 矩阵中任一行可以从其他 n-1 行中导出,即只有 n-1 行是独立的。 如果把的任一行划去,剩下的矩阵用表示,并称为降阶关联矩阵(今后主要用这种降阶关联矩阵,所以往往略去“降阶”二字),被划去的行对应的结点可以当作参考结点。 例如,若以结点 4 为参考结点,把上式中的第 4 行划去,得 若以结点 3 为参考结点,把上式中的第 3 行划去,得 矩阵的某些列将只具有一个 +1 或一个- 1 ,每一个这样的列必对应于与参考结点相关联的一条支路。 注意:给定可以确定,从而画出有向图。 2.用A表示矩阵形式的KCL 电路中的 b 个支路电流可以用一个 b 阶列向量表示,即 若用矩阵左乘电流列向量,则乘积是一个阶列向量,由矩阵相乘规则可知,它的每一元素即为关联到对应结点上各支路电流的代数和,即 因此,有 上式是用矩阵表示的KCL的矩阵形式。例如对图15.1,以结点4 为参考结点,有: 上式为n-1 个独立方程。
线性代数习题第三章 矩阵的初等变换与线性方程组
习题3-1 矩阵的初等变换及初等矩阵 1、用初等行变换化矩阵 1021 2031 3043 A - ?? ?? =?? ?? ?? 为行最简形、 2、用初等变换求方阵 321 315 323 A ?? ?? =?? ?? ?? 的逆矩阵、 3、设 412 221 311 A - ?? ?? =?? ?? - ?? , 3 22 31 - ?? ?? ?? ?? - ?? 1 B=,求X使AX B =、 4、设A就是n阶可逆矩阵,将A的第i行与第j行对换后得矩阵B、 (1) 证明B可逆(2)求1 AB-、
习题 3-2 矩阵的秩 1、求矩阵的秩: (1)310211211344A ????=--????-?? (2)111212122212n n n n n n a b a b a b a b a b a b B a b a b a b ??????=??????L L L L L L L 01,2,,i i a b i n ≠????=?? L 2、设12312323k A k k -????=--????-?? 问k 为何值,可使 (1)()1R A =; (2)()2R A =; (3)()3R A =、
3、 从矩阵A 中划去一行,得矩阵B ,则)(A R 与)(B R 的关系就是 、 .()()a R A R B = .()()b R A R B <; .()()1c R B R A >-; .()()() 1.d R A R B R A ≥≥- 4、 矩阵???? ??????-------815073*********的秩R= 、 a 、1; b 、 2; c 、 3; d 、 4、 5、 设n (n ≥3)阶方阵????? ???????=111ΛΛΛΛΛΛΛΛa a a a a a a a a A 的秩R (A )=n -1,则a = 、 a 、 1; b 、 n -11; c 、 –1; d 、 1 1-n 、 6、设A 为n 阶方阵,且2A A =,试证: ()()R A R A E n +-=
线性方程组AX=B的数值计算方法实验
线性方程组AX=B的数值计算方法实验 【摘要】在自然科学与工程技术中很多问题的解决常常归结为解线性代数方程组。例如电学中的网络问题,船体数学放样中建立三次样条函数问题,用最小二乘法验数据的曲线拟合问题,解非线性方程组的问题,用差分法或者有限元法解常微分方程,偏微分方程边值问题等都导致求解线性方程组。线性代数方面的计算方法就是研究求解线性方程组的一些数值解法与研究计算矩阵的特征值及特征向量的数值方法。关于线性方程组的数值解法一般有两类:直接法和迭代法。 关键字高斯消元法、三角分解法、高斯-赛德尔迭代、稀疏矩阵 一、实验目的 1.掌握高斯消元法、三角分解法、高斯—赛德尔迭代发的编程技巧。 2.掌握线性方程组AX=B的数值计算方法。 3.掌握矩阵的基本编程技巧。 二、实验原理 1.高斯消元法
数学上,高斯消元法是线性代数规划中的一个算法,可用来为线性方程组求解。高斯(Gauss )夏鸥按法其实是将一般的线性方程组变换为三角形(上三角)方程组求解问题(消元法),只是步骤规,便于编写计算机程序。 一般高斯消元法包括两过程:先把方程组化为同解的上三角形方程组,再按相反顺序求解上三角方程组。前者称为消去或消元过程,后者称回代过程。消去过程实际上是对增广矩阵作行初等变换。 对一般的n 阶方程组,消去过程分n-1步:第一步消去11a 下方元素。第二步消去22a 下方元素,......,第n-1步消去1-n 1-n a ,下方元素。即第k 步将第k 行的适当倍数加于其后各行,或可说是从k+1~n 行减去第k 行的适当倍数,使它们第k 列元素变为零,而其余列元素减去第k 行对应列元素的倍数。 2.三角分解法 三角分解法是将原正方 (square)矩阵分解成一个上三角形矩阵或是排列(permuted) 的上三角形矩阵和一个 下三角形矩阵,这样的分解法又称为LU 分解法。它的用途主要在简化一个大矩阵的行列式值的计算过程,求 反矩阵,和求解联立方程组。不过要注意这种分解法所得到的上下三角形矩阵并非唯一,还可找到数个不同 的一对上下三角形矩阵,此两三角形矩阵相乘也会得到原矩阵。
线性方程组和矩阵知识总结.doc
线性方程组和矩阵知识总结 吴荣魁 2013201363 线性方程组的基本概念 ???????=+++=+++=+++m mn m m n n n n b x a x a x a b x a x a x a b x a x a x a 322112222212111212111 其中未知数的个数n 和方程式的个数m 不必相等. 线性方程组的解是一个n 维向量它满足:当每个方中的未知数xi 都用ki 替代时都成为等式. 线性方程组的解的情况有三种:无解,唯一解,无穷多解. 对线性方程组讨论的主要问题两个:(1)判断解的情况.(2)求解 b1=b2=…=bm=0的线性方程组称为齐次线性方程组. n 维零向量总是齐次线性方程组的解,称为零解.因此齐次线性方程组解的情况只有两种:唯一解(即只要零解)和无穷多解(即有非零解). 把一个非齐次线性方程组的每个方程的常数项都换成0,所得到的齐次线性方程组称为原方程组的导出齐次线性方程组,简称导出组. 线性方程组的解法 ???????=+++=+++=+++m mn m m n n n n b x a x a x a b x a x a x a b x a x a x a 322112222212111212111 (1)、写出线性方程组的增广矩阵。 (2)、用初等行变换把增广矩阵化为阶梯形矩阵。 (3)、看阶梯形矩阵的最后一个非零行的首非零元是否在最后一列。如果是,则方程组无解;反之方程组有解。 (4)、在有解的情况下,找出阶梯形矩阵中非零行的个数r 。如果r=n ,则方程组有唯一解;如果r 第1 章矩阵与线性方程组 矩阵是描述和求解线性方程组最基本和最有用的工具。本章涉及向量和矩阵的基本 概念,归纳了向量和矩阵的基本运算。 1.1 主要理论与方法 1.1.1 矩阵的基本运算 一、矩阵与向量 a11x1 + a12x2 + ¢ ¢ ¢+ a1n x n = b1 a21x1 + a22x2 + ¢ ¢ ¢+ a2n x n = b2 ... a m1x1 + a m2x2 + ¢ ¢ ¢+ a mn x n = b m 9> >>>=>>>>; (1.1) 它使用m个方程描述n个未知量之间的线性关系。这一线性方程组很容易用矩阵||向量 形式简记为 Ax = b (1.2) 式中 A =26664 a11 a12 ¢ ¢ ¢ a1n a21 a22 ¢ ¢ ¢ a2n ... ... ... a m1 a m2 ¢ ¢ ¢ a mn 37775 (1.3) 称为m £ n矩阵,是一个按照长方阵列排列的复数或实数集合;而 x =26664 x1 x2 ... x n 37775 ; b =26664 b1 b2 ... b m 37775 (1.4) 分别为n £1向量和m£1向量,是按照列方式排列的复数或实数集合,统称列向量。类似地,按照行方式排列的复数或实数集合称为行向量,例如 a = [a1; a2; ¢ ¢ ¢ ; a n] (1.5) 是1 £ n向量。 二、矩阵的基本运算 1. 共轭转置:若A = [a ij ]是一个m£ n矩阵,则A的转置记作A T,是一个n £m矩阵, 定义为[A T]ij = a ji;矩阵A的复数共轭A¤定义为[A¤]ij = a¤ji;复共轭转置记作A H,定义 为 A H =26664 a¤11 a¤21 ¢ ¢ ¢ a¤m1 a¤12 a¤22 ¢ ¢ ¢ a¤m2 ... 第十五章 电路方程的矩阵形式 一、本章的核心、重点及前后联系 (一)本章的核心 列出结点电压方程的矩阵形式。 (二)本章重点 1. 关联矩阵、回路矩阵、割集矩阵; 2. 结点电压方程的矩阵形式。 (三)本章前后联系 本章是第三章电阻电路一般分析方法的扩充。 二、本章的基本概念、难点及学习方法指导 (一)本章的基本概念 1. 割集定义 定义:连通图G 的一个割集是G 的一个支路集合,把这些支路移去将使G 分离为两个部分,但是如果少移去其中一条支路,图仍将是连通的。 割集:Q 1(a 、d 、f );Q 2(a 、b 、e );Q 3(b 、c 、f );Q 4(c 、d 、e );Q 5(b 、d 、e 、f ); Q 6(a 、c 、e 、f );Q 7(a 、b 、c 、d )。 图G 的割集 2. 关联矩阵定义 定义:对于具有n 个节点、b 条支路的图,其关联矩阵(节点、支路关联矩阵)为一个 )(b n ?的矩阵,用a A 表示。行对应节点,列对应支路,它的任意元素jk a 定义如下: 1+=jk a ,表示支路k 与节点j 关联并且它的方向背离节点; 1-=jk a ,表示支路k 与节点j 关联并且它的方向指向节点; 0=jk a ,表示支路k 与节点j 不关联。 a b c d e f 5 Q 6 Q 7 Q a b c d e f 1 Q 2 Q 3 Q 4 Q ????? ? ??? ???---++-++--++=01110010011001001110100143216 54321a A 划去a A 中的任意一行,剩下的b n ?-)1(矩阵用 A 表示,称为降阶关联矩阵: ?? ?? ??????++-++--++=10011001001110100 1A A 阵表示的KCL 、KVL 方程: KCL :0Ai = KCL :n T u A u = 3. 回路矩阵定义 回路矩阵(回路、支路关联矩阵)用B 表示,行对应回路,列对应支路,任意元素b jk 定义如下: 1+=jk b ,表示支路k 与回路j 关联,且他们的方向一至; 1-=jk b ,表示支路k 与回路j 关联,且他们的方向相反; 0=jk b ,表示支路k 与回路j 不关联。 选树(1、2、5),则有单连支回路(1、4、5),(1、2、6),(2、3、5),回路方向为连支方向,所以: ?? ?? ? ?????-+++++-+-=0101101000110110013216 54321B 1 3 21 3 第三章 矩阵的初等变换与线性方程组 3.4.1 基础练习 1.已知121011251-?? ? = ? ?-??A ,求()R A . 2.已知3210 1032 100000200000-?? ?- ? = ?- ? ?? ?B ,求()R B . 3.若矩阵,,A B C 满足=A BC ,则( ). (A)()()R R =A B (B) ()()R R =A C (C)()()R R ≤A B (D) ()max{(),()}R R R ≥A B C 4. 设矩阵X 满足关系2=+AX A X ,其中423110123?? ? = ? ?-??A ,求X . 5. 设矩阵101210325?? ?= ? ?--?? A ,求1 ()--E A . 6.A 是m n ?矩阵,齐次线性方程组0=Ax 有非零解的充要条件是 . 7.若非齐次线性方程组=Ax b 中方程个数少于未知数个数,那么( ). (A) =Ax b 必有无穷多解; (B) 0=Ax 必有非零解; (C) 0=Ax 仅有零解; (D) 0=Ax 一定无解. 8. 求解线性方程组 (1)12312312312333332x x x x x x x x x +-=??+-=??-+=?, (2)72315 532151011536 x y z x y z x y z ++=?? -+=??-+=? (3)123412341 23420 202220 x x x x x x x x x x x x ++-=?? ++-=??+++=? 9.若方程组 12323232132(3)(4)(2)x x x x x x x λλλλλλ+-=-?? -=-??-=--+-? 有无穷多解,则λ= . 10.若12(1,0,2),(0,1,1)T T ==-αα都是线性方程组0=Ax 的解,则=A ( ). (A)()2,1,1- (B)201011-?????? (C)102011-????-?? (D)011422010-?? ??--?? ???? 3.4.2 提高练习 1.设A 为5阶方阵,且()3R =A ,则* ()R A = . 2.设矩阵12332354445037a a -????=-?? ??-?? A ,以下结论正确的是( ). (A)5a =时,()2R =A (B) 0a =时,()4R =A (C)1a =时,()5R =A (D) 2a =时,()1R =A 3.设A 是43?矩阵,且()2R =A ,而102020103?? ? = ? ?-??B ,则()R =AB . 4.设12243311t -?? ? = ? ?-??A ,B 为3阶非零矩阵,且0=AB ,则t = . 5.设12312323k k k -?? ? =-- ? ?-?? A , 问k 为何值,可使 (1)()1R =A (2)()2R =A (3)()3R =A . 6.设矩阵111111111111k k k k ?? ? ? = ? ? ??? A ,且()3R =A ,则k = . 线性方程组的几种解法 线性方程组形式如下: 常记为矩阵形式 其中 一、高斯消元法 高斯(Gauss)消元法的基本思想是:通过一系列的加减消元运算,也就是代数中的加减消去法,将方程组化为上三角矩阵;然后,再逐一回代求解出x 向量。现举例说明如下: (一)消元过程 第一步:将(1)/3使x 1的系数化为1 得 再将(2)、(3)式中x 1的系数都化为零,即由(2)-2×(1)(1) 得 )1(32)2( (03) 4 32=+x x )1(321)1(......23132=++ x x x 由(3)-4×(1)(1) 得 第二步:将(2)(1) 除以2/3,使x 2系数化为1,得 再将(3)(1) 式中x 2系数化为零,即 由(3)(1) -(-14/3)*(2)(2) ,得 第三步:将(3)(2) 除以18/3,使x 3系数化为1,得 经消元后,得到如下三角代数方程组: (二)回代过程 由(3)(3) 得 x 3=1, 将x 3代入(2)(2) 得x 2=-2, 将x 2 、x 3代入(1)(1) 得x 2=1 所以,本题解为[x]=[1,2,-1]T (三)、用矩阵演示进行消元过程 第一步: 先将方程写成增广矩阵的形式 第二步:然后对矩阵进行初等行变换 初等行变换包含如下操作 (1) 将某行同乘或同除一个非零实数 ) 3(3)3(......1-=x )2(3)3( (63) 18-=x ) 2(32) 2(......02=+x x ) 1(32)3( (63) 10 314-=-- x x (2)将某行加入到另一行 (3)将任意两行互换 第三步:将增广矩阵变换成上三角矩阵,即主对角线全为1,左下三角矩阵全为0,形式如下: 示例: (四)高斯消元的公式 综合以上讨论,不难看出,高斯消元法解方程组的公式为 1.消元 (1)令 a ij(1) = a ij , (i,j=1,2,3,…,n) b i(1) =b i , (i=1,2,3,…,n) (2)对k=1到n-1,若a kk(k)≠0,进行 l ik = a ik(k) / a kk(k) , (i=k+1,k+2,…,n) a ij(k+1) = a ij(k) - l ik * a kj(k), (i,j= k+1,k+2,…,n) b i(k+1) = b i(k) - l ik * b k(k), (i= k+1,k+2,…,n) 2.回代 若a nn(n) ≠0 x n = b n(n) / a nn(n) x i = (b i(i) – sgm(a ij(i) * x j)/- a ii(i),(i = n-1,n-2,…,1),( j = i+1,i+2,…,n ) (五)高斯消元法的条件 消元过程要求a ii(i) ≠0 (i=1,2,…,n),回代过程则进一步要求a nn(n) ≠0,但就方程组Ax=b 讲,a ii(i)是否等于0时无法事先看出来的。 注意A的顺序主子式D i(i=1,2,…,n),在消元的过程中不变,这是因为消元所作的变换是“将某行的若干倍加到另一行”。若高斯消元法的过程进行了k-1步(a ii(i) ≠0,i §1 消元法 引例 求解线性方程组 ?????=++=++=++288338 219432321321321x x x x x x x x x (1.1) 解: 用i r 表示方程组中的第i 个方程,采用消元法求解此线性方程组: 方程组(1.1)???→??21r r ?????=++=++=++2883319 43282321321321x x x x x x x x x ?? ???==+=++??????→?--423 0823,23323211312x x x x x x r r r r (1.2) ?????===???????→?÷+-23 12),(3213321x x x r r r r (1.3) 由于方程组(1.1)与(1.3)同解,从而得到(1.1)的解T x x x x ),,(321=T )2,3,1(= 定义 以下变换1,2,3称为线性方程组的初等变换。 1. 将某一方程乘以一个非零的倍数; 2. 将某一方程的某个倍数加到另外一方程上去; 3. 对调两方程的位置。 命题 初等变换总是把方程组变成同解的方程组。 用消元法求解线性方程组的过程:首先用初等变换化线性方程组为阶梯形方程组,把最后的恒等式“0=0”(如果出现的话)去掉。如果剩下的方程当中最后的一个等式是零等于一个非零的数,那么方程组无解,否则有解。在有解的情况下,如果阶梯形方程组中方程的个数等于未知量的个数,那么方程组有唯一的解;如果阶梯形方程组中方程的个数小于未知量的个数,那么方程组有无穷多个解。 定理 在齐次线性方程组 111122121122221122000 n n n n s s sn n a x a x a x a x a x a x a x a x a x +++=??+++=????+++=?L L L L L L L L L L L L L L 中,如果s 线性代数习题[第三章]矩阵的初等变换与线 性方程组 习题3-1矩阵的初等变换及初等矩阵 3 2 1 3 1 5的逆矩阵. 3 2 3 4.设A 是n 阶可逆矩阵 将A 的第i 行与第j 行对换后得矩阵B . (1)证明B 可逆 ⑵求AB 1. 1?用初等行变换化矩阵A 1 0 2 1 2 0 3 1 为仃取简形 3 0 4 3 4 1 2 1 3 2 2 1 ,B= 2 2 ,求X 使AX B 3 1 1 3 1 3.设A 2?用初等变换求方阵A 习题3-2矩阵的秩1?求矩阵的秩: (1)A 1 2 3k 2.设A 1 2k 3问k为何值,可使 k 2 3 (1)R(A) 1 ; ⑵R(A) 2; ⑶ R(A) 3 qb o i 1,2, |||,n &1 b| &1 b? a? b| a?b? Ill III a n E a n b 2 a2b n III a n b n 3.从矩阵A中划去一行,得矩阵B,则R(A)与R(B)的关系是_______ a. R(A) R(B) b. R(A) R(B); c. R(B) R(A) 1 ; d. R(A) R(B) R(A) 1. 3 2 1 3 1 4.矩阵2 1 3 1 3 的秩R= 7 0 5 1 8 a.1; b. 2; c.: 3; d. 4. 1 a a a 5.设n(n 3)阶方阵 a A 1 a a 的秩R(A)=n-1,则 a a a a 1 a. 1; b. 1 ; c.—; d . 1 1 n n 1 6.设A为n阶方阵,且A2A,试证: R(A) R(A E) n矩阵与线性方程组
第十五章电路方程的矩阵形式
矩阵的初等变换与线性方程组习题含答案
线性方程组的几种求解方法
求解线性方程组的几种方法
线性代数习题矩阵的初等变换与线性方程组讲课讲稿
