伪距测距原理
伪距测距原理
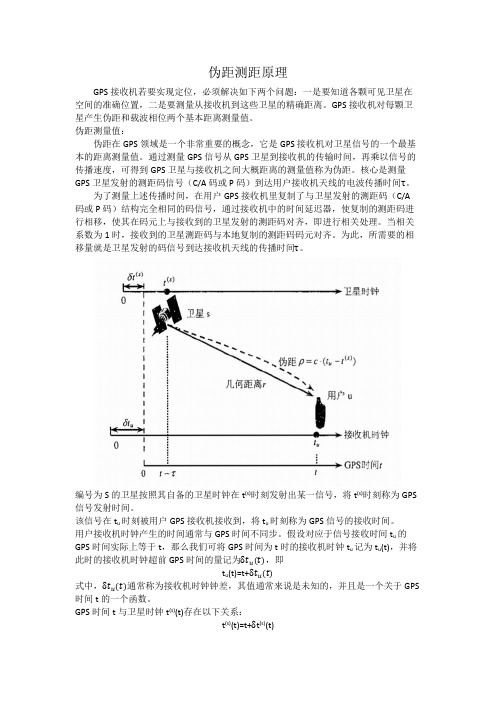
伪距测距原理GPS接收机若要实现定位,必须解决如下两个问题:一是要知道各颗可见卫星在空间的准确位置,二是要测量从接收机到这些卫星的精确距离。
GPS接收机对每颗卫星产生伪距和载波相位两个基本距离测量值。
伪距测量值:伪距在GPS领域是一个非常重要的概念,它是GPS接收机对卫星信号的一个最基本的距离测量值。
通过测量GPS信号从GPS卫星到接收机的传输时间,再乘以信号的传播速度,可得到GPS卫星与接收机之间大概距离的测量值称为伪距。
核心是测量GPS卫星发射的测距码信号(C/A码或P码)到达用户接收机天线的电波传播时间τ。
为了测量上述传播时间,在用户GPS接收机里复制了与卫星发射的测距码(C/A码或P码)结构完全相同的码信号,通过接收机中的时间延迟器,使复制的测距码进行相移,使其在码元上与接收到的卫星发射的测距码对齐,即进行相关处理。
当相关系数为1时,接收到的卫星测距码与本地复制的测距码码元对齐。
为此,所需要的相移量就是卫星发射的码信号到达接收机天线的传播时间τ。
编号为S的卫星按照其自备的卫星时钟在t(s)时刻发射出某一信号,将t(s)时刻称为GPS 信号发射时间。
该信号在t u时刻被用户GPS接收机接收到,将t u时刻称为GPS信号的接收时间。
用户接收机时钟产生的时间通常与GPS时间不同步。
假设对应于信号接收时间t u的GPS 时间实际上等于t,那么我们可将GPS时间为t时的接收机时钟t u记为t u(t),并将此时的接收机时钟超前GPS时间的量记为δt u(t),即t u(t)=t+δt u(t)式中,δt u(t)通常称为接收机时钟钟差,其值通常来说是未知的,并且是一个关于GPS 时间t的一个函数。
GPS时间t与卫星时钟t(s)(t)存在以下关系:t(s)(t)=t+δt(s)(t)其中卫星时钟钟差δt(s)(t)可以视为已知的,根据此式GPS时间与卫星时钟在信号发射时刻(t-τ)时的关系可表达成t(s)(t-τ)=t-τ+δt(s)(t-τ)GPS接收机根据接收机时钟在t u(t)时刻对GPS信号进行采样,然后对采样信号进行处理,可得到标记在GPS信号上的发射时间t(s)(t-τ)。
伪距定位原理.ppt

1、GPS伪距定位解的精度评定。
小结
Summary
本节课到此结束
3. 伪距定位观测方程的解
The Solution of Observation Equations
3.3 几个有关的问题
(4) 伪距定位的几何解释
三球定位原理
小结
Summary
伪距定位原理是《GPS原理与应用》的核心内容,主要介绍 了伪距定位观测方程的建立和伪距定位观测方程的解,得到了必 须同时观测4颗卫星才能进行定位的结论。
l j X m jY n j Z ctr 0j %j ct j I j T j
小结 Summary
伪距定位原理是《GPS原理与应用》的核心内容,主要介绍 了伪距定位观测方程的建立和伪距定位观测方程的解,得到了必 须同时观测4颗卫星才能进行定位的结论。
作业题
1.利用GPS进行伪距定位,为什么必须至少同时观测4颗卫星? 2.如何利用GP j T j
toc、a0、a1、a2
2. 伪距定位观测方程
The Observation Equations
2.3 信号传播时延
真实的信号传播时延:
j Tr T j
实测的信号传播时延:
%j tr t j
tj T j tj tr Tr tr
%j (Tr tr ) (T j t j )
2. 伪距定位观测方程
The Observation Equations
2.4 伪距
%j (Tr T j ) tr t j
j tr t j
c%j c j c tr c t j
%j j c tr c t j
伪距(Pseudo Range)是现代卫星导航系统的主要观测量之一。
伪距卡尔曼滤波

伪距卡尔曼滤波
伪距卡尔曼滤波是一种基于卡尔曼滤波的定位技术,利用伪距测量信息进行定位估计。
在GPS定位中,卫星和接收机之间的距离是通过测量信号传播时间来得到的。
由于信号传播速度接近光速,微小的测量误差会导致较大的定位误差。
为了提高定位精度,可以采用卡尔曼滤波对接收机的位置、速度和时钟参数进行最优估计。
伪距卡尔曼滤波的主要步骤包括:
建立状态方程:根据接收机的位置、速度和时钟参数建立状态方程,描述系统状态的变化规律。
建立观测方程:根据卫星的位置和信号传播时间建立观测方程,描述观测数据与系统状态之间的关系。
计算卡尔曼增益:根据当前状态估计和观测数据,计算卡尔曼增益,用于更新状态估计。
更新状态估计:根据卡尔曼增益和观测数据,更新接收机的位置、速度和时钟参数等状态变量的估计值。
迭代更新:重复步骤3和4,不断迭代更新状态估计,直到达到收敛或终止条件。
伪距卡尔曼滤波的优点包括:
可以对多个观测数据进行融合,提高定位精度和可靠性。
可以对系统状态进行平滑估计,减小噪声和干扰对定位结果的影响。
可以对系统状态进行预测,为后续的导航和路径规划提供支持。
在实际应用中,伪距卡尔曼滤波需要合理设置初始状态和参数,选择合适的观测数据和模型,以获得准确的定位结果。
伪距测量

(4)要保证测试结果的普适性并获取高可信度的设备时延值,伪距和钟差测量必须尽可能遍历各种技术状态, 如开关机、静态、低动态、高动态及多种信号接收强度等。
提高精度
(1)伪距、钟差、设备时延等基本物理量是密切相关的,而且都是时间的函数,因此其定义必须严格自洽。从 广义上讲,设备时延并不一定是真正意义上的时延,他们取决于时间参考点的选择。在一般情况下其取值可以为正, 也可以为负。
(2)在选择设备1pps输出端口为本地时间参考点的情况下,收发组合时延可以采用直接测量钟差的方法测定。 两台发射(或接收)设备的发射时延(或接收时延)的相对差值,可以通过与某一台参考接收(或发射)设备进行组合 时延测量得到。
谢谢观看
基本概念
测得的距离含有时钟误差和大气层折射延迟,而非“真实距离”,故称伪距。它是为实现伪距定位,利用测定 的伪距组成以接收机天线相位中心的三维坐标和卫星钟差为未知数的方程组,经最小二乘法解算以获得接收机天 线相位中心三维坐标,并将其归化为测站点的三维坐标。由于方程组含有4个未知数,必须有4个以上经伪距测量 而获得的伪距。此法既能用于接收机固定在地面测站上的静态定位,又适于接收机置于运动载体上的动态定位。 但后者的绝对定位精度较低,只能用于精度要求不高的导航。
真距
在无线电测量中,信号通过发射天线发射,经空间传播后由接收天线接收。所谓的信号空间传播时延是指信号 在空间传播过程中所花费的时间。信号空间传播时延反映了信号所走过的真实路程,可将其简单地称为真距。
gnss 伪距 钟差 -回复

gnss 伪距钟差-回复GNSS是全球导航卫星系统(Global Navigation Satellite System)的缩写,目前应用最广泛的是美国的GPS系统(Global Positioning System),同时还有俄罗斯的GLONASS系统、欧洲的Galileo系统以及中国的北斗系统。
这些系统通过一系列的卫星,提供全球范围内的定位、测量和导航服务。
在GNSS中,伪距是指接收机测量的信号从卫星到达接收机的时间间隔乘以光速所得到的距离。
以GPS为例,伪距是通过接收卫星发送的信号的到达时间与接收机中预设的接收时间之间的差值来计算得到的。
而钟差,则是指卫星和接收机钟表之间的时间差。
伪距和钟差是GNSS中必须要考虑的两个重要因素。
随着信号在大气层中的传播延迟和接收机钟表的不准确性,伪距的精度会受到一定程度的影响。
为了提高伪距的准确性,通常需要应用精密的测量技术和算法进行伪距解算。
同时,为了消除钟差带来的误差,接收机和卫星都使用了高稳定性的原子钟或石英钟。
具体来说,GNSS系统通过接收卫星发送的信号,并测量接收信号的到达时间,然后根据测量的时间间隔乘以光速来计算得到伪距。
这个伪距值会包含卫星钟差以及信号在大气中传播的延迟。
为了获得更准确的位置信息,接收机需要首先准确地估计卫星钟差,并校正伪距。
这通常通过接收多颗卫星的信号,将测量得到的信号延迟值与已知的卫星轨道信息进行比较来实现。
接下来,接收机需要计算出自己与每颗卫星之间的距离。
这需要考虑到地球的形状和卫星的轨道参数。
一种常用的方法是使用测距方程,将伪距与与卫星的几何参数进行联立求解,从而推导得出接收机与卫星之间的距离。
然而,伪距的测量误差和钟差的影响使得实际的距离计算存在一定的误差。
为了减小这些误差,并提高定位的精度,需要采用一些辅助措施。
例如,差分定位技术可以通过同时接收一个已知位置的参考站和未知位置的用户站的信号,进一步校正和消除伪距和钟差的误差。
matlab伪距单点定位

matlab伪距单点定位Matlab伪距单点定位伪距单点定位是一种利用卫星信号进行定位的方法,通过测量卫星信号的传播时间差来计算接收器与卫星之间的距离,并利用多个卫星的距离信息进行定位。
Matlab作为一种强大的数学计算工具,可以方便地实现伪距单点定位算法。
伪距单点定位的原理是利用接收器接收到的卫星信号的传播时间差来计算接收器与卫星之间的距离。
接收器通过测量卫星信号的到达时间差来计算伪距,然后利用伪距信息进行定位。
伪距是接收器接收到卫星信号的传播时间与光速之间的乘积,即伪距=传播时间×光速。
在实际应用中,接收器通常能够接收到多个卫星的信号,因此可以利用多个卫星的伪距信息进行定位。
伪距单点定位的核心是通过多个卫星的伪距信息求解接收器的位置坐标。
这个问题可以表示为一个数学模型,通过最小二乘法求解,得到接收器的位置坐标。
在Matlab中实现伪距单点定位算法需要以下几个步骤:1. 数据预处理:首先需要将接收器接收到的卫星信号数据进行预处理,包括数据解码、信号强度计算等。
2. 卫星位置计算:利用卫星星历数据,计算卫星在给定时刻的位置。
3. 伪距计算:通过测量卫星信号的传播时间差,计算接收器与卫星之间的伪距。
4. 伪距单点定位:利用多个卫星的伪距信息,通过最小二乘法求解接收器的位置坐标。
5. 定位结果分析:对定位结果进行分析和评估,包括精度评估、误差分析等。
在实际应用中,伪距单点定位算法还需要考虑多种误差的影响,包括钟差误差、大气延迟误差、多径效应等。
这些误差会对定位结果产生影响,需要进行误差补偿和校正。
Matlab伪距单点定位是一种利用卫星信号进行定位的方法,通过测量卫星信号的传播时间差来计算接收器与卫星之间的距离,并利用多个卫星的距离信息进行定位。
Matlab作为强大的数学计算工具,可以方便地实现伪距单点定位算法。
伪距单点定位的实现主要包括数据预处理、卫星位置计算、伪距计算、伪距单点定位和定位结果分析等步骤。
伪距残差公式

总之,伪距残差公式虽然听起来有点复杂,但它在我们的生活中默默地发挥着重要的作用,让我们的测量更加准确,让我们的生活更加便利。
希望通过我的这些介绍,能让您对伪距残差公式有了更清楚的认识。虽然它可能不像明星那样耀眼,但在测量的世界里,它可是当之无愧的大功臣!
伪距残差公式
伪距残差公式在测量领域可是个相当重要的家伙呢!
咱们先来聊聊啥是伪距。简单说,伪距就是通过测量信号传播时间和速度来估算出的距离,但这估算出来的距离可不那么准,会有误差。
而伪距残差公式呢,就是用来衡量这个估算距离和实际距离之间差距的工具。比如说,咱们想象一下,在一个大广场上,有一个测量小组正在努力工作。他们拿着各种仪器,想要精确测量从广场这头到那头的距离。
他们通过接收卫星信号,用公式算出了一个伪残差公式来帮忙找出来啦。
伪距残差公式就像是一个超级侦探,能敏锐地发现那些隐藏在测量数据中的小秘密。它的作用可大了去了!比如说在导航系统里,如果没有它帮忙找出误差,那咱们可能就会在陌生的地方迷路,找不到正确的方向。
在实际应用中,计算伪距残差可不是一件轻松的事儿。它需要考虑好多因素,像信号传播过程中的干扰啦,测量仪器的精度啦,甚至是天气情况都可能会有影响。
就拿天气来说吧,有一次我在参与一个测量项目的时候,那天刚好下着小雨,空气中湿度特别大。结果测量出来的伪距就出现了比较大的偏差,用伪距残差公式一分析,发现就是因为雨水对信号传播造成了一定的阻碍。
3.8-3.9伪距、载波相位测量原理

平方法
将所接收 到的调制信号 (卫星信号)自 乘。
平方法
技术要点
卫星信号(弱)自乘。
特点
优点:无需了解码的结构
缺点:无法获得导航电文,所获
载波波长为原来波长的一半,信 号质量较差(信噪比低,降低了 30dB)
(3)互相关(交叉相关)
方法
在不同频率的调制
信号(卫星信号) 进行相关处理,获 取两个频率间的伪 距差和相位差
测距码的调制与解调
在数字通讯技术中,为了有效地传播信息, 一般均将低频信号加载到高频的载波上, 这时原低频信号称为调制信号,而加载信 号后的载波就称为已调波。 GPS信号调制,是采用调相技术实现的。
卫星信号的调制
模二和
运算规则
二进制信号:“1”表示二进制“0”,“-1”表示二 进制“1”,则
利用测距码进行测距的 优点
易于捕获微弱的卫星信号 可提高测距精度 便于对系统进行控制和管 理(如AS)
每颗GPS卫星都采用特定的 伪随机噪声码
码相关伪距测量
特点 定位速度快,实时定位 精度较高 对信号的强度要求不高
3.9 卫星的载波信号及相位测量原理
3.9.1 3.9.2 3.9.3 3.9.4
1
0
1
1
0
1
(4)Z跟踪
技术要点:将卫星信号在一个W码码元内与 接收机复制出的P码进行相关处理。 在一个W码码元内进行卫星信号(弱)与复 制信号(强)进行相关。 特点 优点:无需了解Y码结构,可测定双频伪 距观测值,可获得导航电文,可获得全波 波长的载波,信号质量较平方法好(信噪 比降低了14dB)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
背景——GPS 系统定位原理
已知卫星的位置(通过广播描述卫星运动的星历参数和历书参数),测量得到卫星和用户之间的相对位置(伪距PRN ),用导航算法(最小二乘法或卡尔曼滤波法)解算得到用户的最可信赖位置。
图1
获得伪距后,按照下式解算定位结果:
11223344
(1)(2)(3)(4)(,i B Corr PR B Corr PR B Corr PR B Corr PR SVx SVy +=+=+=+=其中,,)(,,)i i i i SVz B Corr i PR i Rx Ry Rz 为卫星位置,为接收机钟差等效距离,
为第颗卫星的已知修正量,为对第颗卫星的观测伪距,为接收机位置
伪距测量原理
GPS 定位的基础就是测距,即通过测量信号从卫星传播到接收机所用的时间获得卫星和接收机之间的距离(i PR c t =⨯∆)。
图2
利用伪随机码的自相关特性如图3,令本地码片以一定速度移动如图4,当本地复现码与从卫星传到的码相关值达到最大时,本地码移动了的时间即为所求
t ∆。
图3 自相关函数
Δt
t 1
t 2
卫星t 1时刻产生的码相位,
Δt 后到达
从卫星传到的码
接收机产生的复现码
卫星产生的码
将接收机产生的码移动Δt
图4信号捕获过程。
