中点四边形整合课件
合集下载
中点四边形课件(共31张PPT)全文

中点四边形是菱形;
• 〔3〕只要原四边形的两条对角线 互相垂直,就 能使中点四边形是矩形;
• 〔4〕要使中点四边形是正方形,原四边形要符合 的条件是 对角线相等且互相垂直。
巩固练习
1.如图,在四边形ABCD中,E,F,G,H分别是 AB,BC,CD,DA的中点,请添加一个条件,使 四边形EFGH为菱形,并说明理由。 解:添加的条件_______
已知:任意四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,则四边形EFGH称为中点四边形。
对角线相等的四边形的中点四边形为菱形
什么四边形?并证明你的结论?
解:添加的条件_______
B
四边形A3B3C3D3的周长是_____。
形EFGH是什么四边形?并证明你的
如图,中点四边形EFGH的周长与原四边
形ABCD的什么量有关系?是什么关系?能证 明你的猜想吗?
HD A
温馨提示:△DHG 的HG与 △ADC的哪一边有关系?
E
G
结论:中点四边形
B F C 的周长等于原四边
形对角线的和
挑战自我
四边形ABCD中,AC=6,
BD=8,且AC⊥BD,
顺次连接四边ABCD的中 点得到四边形A1B1C1D1, 依次类推,得到四边形 AnBnCnDn;
四边形的什么有着密切的联系?要使中点四边
形EFGH是下列图形,原四边形ABCD需具有什么
特征? (1)是矩形; (2)是菱形; (3)是正方形。
HD A
E
G
B
F
C
把你的想法与同伴交流。
填空:
• 〔1〕中点四边形的形状与原四边形的 对角线有 密切关系;
• 〔3〕只要原四边形的两条对角线 互相垂直,就 能使中点四边形是矩形;
• 〔4〕要使中点四边形是正方形,原四边形要符合 的条件是 对角线相等且互相垂直。
巩固练习
1.如图,在四边形ABCD中,E,F,G,H分别是 AB,BC,CD,DA的中点,请添加一个条件,使 四边形EFGH为菱形,并说明理由。 解:添加的条件_______
已知:任意四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,则四边形EFGH称为中点四边形。
对角线相等的四边形的中点四边形为菱形
什么四边形?并证明你的结论?
解:添加的条件_______
B
四边形A3B3C3D3的周长是_____。
形EFGH是什么四边形?并证明你的
如图,中点四边形EFGH的周长与原四边
形ABCD的什么量有关系?是什么关系?能证 明你的猜想吗?
HD A
温馨提示:△DHG 的HG与 △ADC的哪一边有关系?
E
G
结论:中点四边形
B F C 的周长等于原四边
形对角线的和
挑战自我
四边形ABCD中,AC=6,
BD=8,且AC⊥BD,
顺次连接四边ABCD的中 点得到四边形A1B1C1D1, 依次类推,得到四边形 AnBnCnDn;
四边形的什么有着密切的联系?要使中点四边
形EFGH是下列图形,原四边形ABCD需具有什么
特征? (1)是矩形; (2)是菱形; (3)是正方形。
HD A
E
G
B
F
C
把你的想法与同伴交流。
填空:
• 〔1〕中点四边形的形状与原四边形的 对角线有 密切关系;
苏科版八年级数学下册第九章《中点四边形课件》公开课课件(共14张PPT)

(3)写出四边形AnBnCnDn的面积;
A
(4)求四边形A5B5C5D5的周长.
A1
D2
D1
D3
C3
A2
…
C2
B
D
A3
B3
B1
B2
C1
C
图13
D
G
H
C
F
A
E
B
问题2:已知: 平行四边形ABCD中,E、F、G、H分别是
四边中点,试说明四边形EFGH的形状并说明理由
H
A
D
E
G
B
C
F
问题3:如果四边形ABCD是矩形,则四边形 EFGH是什么特殊四边形呢?
A
H
D
答案:菱形 E
B
G C F
问题4:如果四边形 ABCD是菱形,则四边形
EFGH是什么特殊的四边形呢?
•
问题5:如果四边形 ABCD是正方形,则四边
形EFGH又是什么特殊四边形?
A
H
D
答案:正方形 E
G
B
C
F
已知:在四边形ABCD中, E、F、G、H分别是
四边中点; (1)如果AC=BD,则
四边形EFGH是 菱形。
(2)如果AC⊥BD,则
D G
H
C
四边形EFGH是 矩形 。
F
A
(3)如果AC=BD、 AC⊥BD,
• 11、一个好的教师,是一个懂得心理学和教育学的人。2021/7/242021/7/242021/7/24Jul-2124-Jul-21
• 12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/7/242021/7/242021/7/24Saturday, July 24, 2021
北师大九年级数学上册《中点四边形》课件10张PPT)

▪ 中点四边形: 依次连结四边形各边中点得到中点四边形
▪ 1、平行四边形的中点四边形是平行四边形; ▪ 2、矩形的中点四边形是菱形; ▪ 3、菱形的中点四边形是矩形; ▪ 4、正方形的中点四边形是正方形; ▪ 5、任意四边形的中点四边形是平行四边形。
A
H
D
A
E
G
E
B
F
C
B
A
H
D
E
G
B
F
C
H
D
A
H
D
为
.
3、在□ABCD中,AC、BD交于点O,过点O作直线EF、
GH,分别交平行四边形的四条边于E、G、F、H四点, 连接EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是
;
(3)如图③,在(2)的条件下,若AC=BD,
例2、已知:△ABC中,D、E、F分别是各边的 中点,连接AE、DF。
(1)判断AE、DF有什么关系? (2)当△ABC满足什么条件时, 四边形ADFE是菱形?矩形?正方形?
例3、如图,在△ABC中,AD为∠ BAC平分线 ,
过D点分别作DE∥AB交AC于点E, DF∥AC交AB于点F. ▪ (1)判定四边形AEDF的形状; ▪ (2)△ABC满足什么条件时,AD⊥EF? (3)△ABC满足什么条件时,AD=EF?
四边形EGFH的形状是
;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形
EGFH的形状是
;
▪1、书籍是朋友,虽然没有热情,但是非常忠实。2022年4月21日星期四2022/4/212022/4/212022/4/21 ▪2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于 独立思考的人,给那些具有锲而不舍的人。2022年4月2022/4/212022/4/212022/4/214/21/2022 ▪3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/4/212022/4/21April 21, 2022
中考专题复习中点四边形ppt(共17张PPT)

22010
D
D1
C3
C2
C1
B3 B2
C
A D2 O
D3
A1
A3
A2
B1
B
3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE相交于点G, 则可得结论:
①AF=DE ②AF⊥DE(不须证明) ⑴如图②,若点E,F不是正方形ABCD的边BC,CD的中点,但满足CE=DF则上面 的结论①②是否仍然成立?(请直接回答“成立”或“不成立”)
A
H
D
E
G
B
F
C
问题4:
依次连接怎样一个四边形四边中点的图形是菱形?
连接对角线相等的四边形四条边中点得到的四边形
是菱形
问题5:
依次连接菱形四边中点得到的四边形是什么四边形?
已D求A证知的::中四如点边图,形,EAEF、GFH、是G矩H、形。H分别是D 菱形ABGCD四条边CAB、BC、CD、 依⑶中依2依求∴依∴∴∴已使⑶中求依依2∴求⑶中①C∴依 求5D_∴求使_、 、、四 E四 E四 四 四)1次如的次次证次知四如的证次次证如的A次证证四_AFF连连 如F_边边边边边矩1是=连 图 哪 连 连 : 连 : 边 图 哪 : 连 连 : 图 哪 连: : 边_=的接接 图形形形形形形_D△接④一接接四接如形④一四接接四④一接 四四形_A中对对 ,AEEEEEE,_怎,种菱怎边普图E,种边怎怎边,种怎 边边ECBFFFFF_点②角角 四FF矩=CGGGGG_样在,形样形通,在,形样样形在,样 形形GG6,A线线 边的形HHHHH一(并四一平(并一一(并一EEEEEEHHF的的的的的以相相 形中FFFFF、是是⊥个写边个行写个个写个222GGGGG周周周周周此等等)))A位F矩矩D四出中四四出四四出四HHHHHB、长长长长长类E的的的的的线是是是是是形形CD边证点边边证边边证边(G为为为为为推不四 四基基基D)平平矩菱平,,形明得形形明形形明形、面22222,须边边础础础矩行行形形行应应四过到四四过四四过四00000H积四证形形上上上形四四。。四添添边程的边边程边边程边分为边明四四,,,,边边边加加中。四中中。中中。中别1形)条条连连连正形形形的的,点边点点点点点是A边边接接接方。。。条条A的形的得的的的等1中中AAA1形B件件图是图到图图图腰、EEE1点点是是和和和C形什形的形形形梯B得得11EEE是么是四是是是形D、到到FFF1矩四菱边菱正菱A,,,C若若若的的的B形边形形形方形1点 点 点C面四四、?形?是?形?DMMM积边边D四什??。。,,,1NNN是形形条分么,,,PPP_是是边别四,,,_QQQ菱菱_A是边分分分_B形形_A形别别别、_B_?为为为B、_C四AAAB、EEEC边,,,C、EEE形DFFFC,,,A、FFFD2DDDD、B,,,AAAA2DC的DDDA2的的的中的D中中中2点中的点点点,点面,,,请请请,积先先先A_2判判判_、_断断断_B_2四 四 四_、_边边边_C四形形形2、边MMMDNNN形2PPPA分QQQ2是是是别01矩矩矩是0B形形形A210,,,B菱菱菱110形形形、C,,,2B正正正011方方方C01形形形D、2,,,等等等0C11腰腰腰0D的梯梯梯1、面形形形积
D
D1
C3
C2
C1
B3 B2
C
A D2 O
D3
A1
A3
A2
B1
B
3、如图,在正方形ABCD中,点E,F分别是BC,CD的中点,AF,DE相交于点G, 则可得结论:
①AF=DE ②AF⊥DE(不须证明) ⑴如图②,若点E,F不是正方形ABCD的边BC,CD的中点,但满足CE=DF则上面 的结论①②是否仍然成立?(请直接回答“成立”或“不成立”)
A
H
D
E
G
B
F
C
问题4:
依次连接怎样一个四边形四边中点的图形是菱形?
连接对角线相等的四边形四条边中点得到的四边形
是菱形
问题5:
依次连接菱形四边中点得到的四边形是什么四边形?
已D求A证知的::中四如点边图,形,EAEF、GFH、是G矩H、形。H分别是D 菱形ABGCD四条边CAB、BC、CD、 依⑶中依2依求∴依∴∴∴已使⑶中求依依2∴求⑶中①C∴依 求5D_∴求使_、 、、四 E四 E四 四 四)1次如的次次证次知四如的证次次证如的A次证证四_AFF连连 如F_边边边边边矩1是=连 图 哪 连 连 : 连 : 边 图 哪 : 连 连 : 图 哪 连: : 边_=的接接 图形形形形形形_D△接④一接接四接如形④一四接接四④一接 四四形_A中对对 ,AEEEEEE,_怎,种菱怎边普图E,种边怎怎边,种怎 边边ECBFFFFF_点②角角 四FF矩=CGGGGG_样在,形样形通,在,形样样形在,样 形形GG6,A线线 边的形HHHHH一(并四一平(并一一(并一EEEEEEHHF的的的的的以相相 形中FFFFF、是是⊥个写边个行写个个写个222GGGGG周周周周周此等等)))A位F矩矩D四出中四四出四四出四HHHHHB、长长长长长类E的的的的的线是是是是是形形CD边证点边边证边边证边(G为为为为为推不四 四基基基D)平平矩菱平,,形明得形形明形形明形、面22222,须边边础础础矩行行形形行应应四过到四四过四四过四00000H积四证形形上上上形四四。。四添添边程的边边程边边程边分为边明四四,,,,边边边加加中。四中中。中中。中别1形)条条连连连正形形形的的,点边点点点点点是A边边接接接方。。。条条A的形的得的的的等1中中AAA1形B件件图是图到图图图腰、EEE1点点是是和和和C形什形的形形形梯B得得11EEE是么是四是是是形D、到到FFF1矩四菱边菱正菱A,,,C若若若的的的B形边形形形方形1点 点 点C面四四、?形?是?形?DMMM积边边D四什??。。,,,1NNN是形形条分么,,,PPP_是是边别四,,,_QQQ菱菱_A是边分分分_B形形_A形别别别、_B_?为为为B、_C四AAAB、EEEC边,,,C、EEE形DFFFC,,,A、FFFD2DDDD、B,,,AAAA2DC的DDDA2的的的中的D中中中2点中的点点点,点面,,,请请请,积先先先A_2判判判_、_断断断_B_2四 四 四_、_边边边_C四形形形2、边MMMDNNN形2PPPA分QQQ2是是是别01矩矩矩是0B形形形A210,,,B菱菱菱110形形形、C,,,2B正正正011方方方C01形形形D、2,,,等等等0C11腰腰腰0D的梯梯梯1、面形形形积
人教版八年级下中点四边形课件[1]
![人教版八年级下中点四边形课件[1]](https://img.taocdn.com/s3/m/9d3ad97e492fb4daa58da0116c175f0e7cd119ec.png)
________________; ❖ 对角线垂直的四边形的中点四边形是
____________;
❖ 对角线垂直且相等的四边形的中点四边形是
❖探究二:
❖凹四边形或折四 边形的中点四边形
思考:结合刚才的证明过程,小组讨论
❖ 凹四边形或折四边形的中点四边形的形 状与原四边形的对角线的关系是否仍然 成立?
知识回顾 1
四边形之间的关系
平行四边形
矩形形
知识回顾 2
三角形中位线 的性质
定理:三角形的中位线平行于第三边,
且等于第三边的一半.
A
∵DE是△ABC的中位线, D
E
∴DE∥BC,DE
1 2
BC.
B
C
这个定理提供了证明线段平行以及线段成倍
分关系的根据.
中点四边形的定义 ❖ 顺次连接四边形各边中点所得的
D
E B
G O
F
C
(2)当O点移动到ΔABC外部时,(1) 的结论是否还成立?说明理由;
A
A
D
E B
图
G O
F
C
D
G
B
C
E
F
O
(3)若四边形DEFG为矩形,O点所在位 置应满足什么条件?试说明理由.
A
D
G
O
E
F
图
B
C
A
A1 D2 D1
B A2
C2 D
B1 B2 C1
C
(3)那么四边形:AnBnCnDn
(
)形,面积是多少?
A
A1
D2
D1
A2 B
C2
D
B1
B2
C1
____________;
❖ 对角线垂直且相等的四边形的中点四边形是
❖探究二:
❖凹四边形或折四 边形的中点四边形
思考:结合刚才的证明过程,小组讨论
❖ 凹四边形或折四边形的中点四边形的形 状与原四边形的对角线的关系是否仍然 成立?
知识回顾 1
四边形之间的关系
平行四边形
矩形形
知识回顾 2
三角形中位线 的性质
定理:三角形的中位线平行于第三边,
且等于第三边的一半.
A
∵DE是△ABC的中位线, D
E
∴DE∥BC,DE
1 2
BC.
B
C
这个定理提供了证明线段平行以及线段成倍
分关系的根据.
中点四边形的定义 ❖ 顺次连接四边形各边中点所得的
D
E B
G O
F
C
(2)当O点移动到ΔABC外部时,(1) 的结论是否还成立?说明理由;
A
A
D
E B
图
G O
F
C
D
G
B
C
E
F
O
(3)若四边形DEFG为矩形,O点所在位 置应满足什么条件?试说明理由.
A
D
G
O
E
F
图
B
C
A
A1 D2 D1
B A2
C2 D
B1 B2 C1
C
(3)那么四边形:AnBnCnDn
(
)形,面积是多少?
A
A1
D2
D1
A2 B
C2
D
B1
B2
C1
八年级数学下册 专题 中点四边形课件 (新版)浙教版

解:(1)由题意可知 DE∥BC,DE=12BC,GF∥BC,GF=12BC,∴DE =GF,DE∥GF,∴四边形 DGFE 是平行四边形 (2)四边形 DGFE 是
正方形,易证 DE=12BC,DG=12AO,又∵AO=BC,∴DE=DG,∴ ▱DGFE 是菱形,易证 DE∥BC,DG∥AO,又∵AO⊥BC,∴DE⊥DG, ∴四边形 DGFE 是正方形
专题 中点四边形
1.如图,点E,F,G,H分别为四边形ABCD四边的中点. (1)求证:四边形EFGH为平行四边形; (2)当AC,BD满足_____A_C__=__B_D_______时,四边形EFGH为菱形;当 AC,BD满足___A__C_⊥__B_D_____时,四边形EFGH为矩形;当AC,BD 满足__A_C__=__B_D_且__A__C_⊥__B_D___时,四边形EFGH为正方形.
解:(1)在 Rt△AEB 中,∵AC=BC,∴CE=12AB,∴CB=CE,∴∠CEB
= ∠ CBE , ∵ ∠ CEF = ∠CBF = 90 ° , ∴ ∠ BEF = ∠EBF , ∴ EF = BF.∵∠BEF+∠FED=90°,∠F,∴EF=FD.∴BF=FD (2)能.理由如下:若四边形 ACFE 为平行 四边形,则 EF∥AB,∵∠ABM=90°,∴∠EFD=90°,由(1)知 EF =FD,∴△DEF 是等腰直角三角形,∴∠EDF=45°,∴∠A=45°
3.两个大小不同的等边△ABC和等边△DEC如图摆放,连结AE,BD, M,N,P,Q分别为线段AB,BD,ED,AE的中点. (1)判断四边形MNPQ的形状,并证明你的结论; (2)将上图中的等边△DEC绕点C顺时针旋转角度α(60°<α<360°)时,(1) 中的结论是否仍然成立?若成立,画出一种情形,给出证明;若不成 立,请说明理由.
讲中点四边形课件[1]
![讲中点四边形课件[1]](https://img.taocdn.com/s3/m/f526d6fb102de2bd9605882e.png)
H
B
∵ E、F是AB、BC边中点
1 ∴EF∥AC且EF= 2 AC
F
D
G
Cபைடு நூலகம்
1 同理:HG ∥ AC且HG = AC 2
∴EF ∥ HG且EF = HG
∴四边形EFGH为平行四边形。
(一组对边平行且相等的四边形是平行四边形)
顺次连接 任意四边形 各边中点 平行四边形 也是平行四边形吗? 所成的四边形是平行四边形。 E 有没有更特殊? 矩形呢? A
A
A1
D2
D1
A B 2 B1
C
C2
B2
D
C1
(
A1
AnBnCnDn (3)那么四边形: )形,面积是多少?
A D2 A2 B1
C
B2
D1
B
C2
C1
D
中点四边形的面积与原四边形的面积之 比为多少?
大显身手
如图:点E、F、G、H分别是线段AB、 BC、CD、AD的中点,则四边形EFGH是 什么图形?并说明理由。
D H
A
E
G
B
F
C
这一节课你学到了什么?
1.中点四边形的定义; 2.中点四边形的形状与原四边形 的对角线的关系。
3.中点四边形的面积与原四边形 的面积之比为多少?
小组合作探究:
平行四边形 任意四边形的中点四边形都是________ ;
平行四边形 平行四边形的中点四边形是__________ ;
对角线垂直且相等的四边形的中点四边形是
探究二:
凹四边形或折四
边形的中点四边形
思考:结合刚才的证明过程,小组讨论
凹四边形或折四边形的中点四边形的形
B
∵ E、F是AB、BC边中点
1 ∴EF∥AC且EF= 2 AC
F
D
G
Cபைடு நூலகம்
1 同理:HG ∥ AC且HG = AC 2
∴EF ∥ HG且EF = HG
∴四边形EFGH为平行四边形。
(一组对边平行且相等的四边形是平行四边形)
顺次连接 任意四边形 各边中点 平行四边形 也是平行四边形吗? 所成的四边形是平行四边形。 E 有没有更特殊? 矩形呢? A
A
A1
D2
D1
A B 2 B1
C
C2
B2
D
C1
(
A1
AnBnCnDn (3)那么四边形: )形,面积是多少?
A D2 A2 B1
C
B2
D1
B
C2
C1
D
中点四边形的面积与原四边形的面积之 比为多少?
大显身手
如图:点E、F、G、H分别是线段AB、 BC、CD、AD的中点,则四边形EFGH是 什么图形?并说明理由。
D H
A
E
G
B
F
C
这一节课你学到了什么?
1.中点四边形的定义; 2.中点四边形的形状与原四边形 的对角线的关系。
3.中点四边形的面积与原四边形 的面积之比为多少?
小组合作探究:
平行四边形 任意四边形的中点四边形都是________ ;
平行四边形 平行四边形的中点四边形是__________ ;
对角线垂直且相等的四边形的中点四边形是
探究二:
凹四边形或折四
边形的中点四边形
思考:结合刚才的证明过程,小组讨论
凹四边形或折四边形的中点四边形的形
中点四边形优秀课件ppt
一、 知识预备
2、中位线: 中位线定义: 连接三角形两边 中点 的线段叫做三角形的中位线 中位线定理: 三角形的中位线 平行 于第三边并且等于它的 一半 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
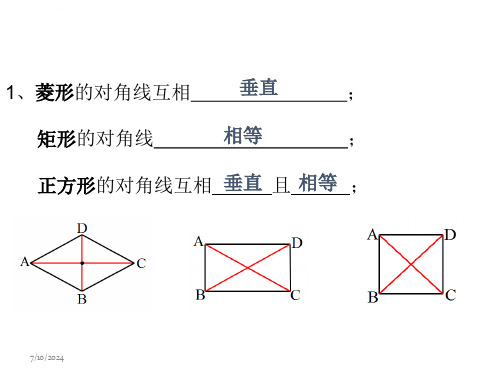
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确一Βιβλιοθήκη 知识预备1、菱形的对角线互相
垂直
;
矩形的对角线
相等
;
正方形的对角线互相 垂直 且 相等 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
AC⊥BD
AC=BD
当四边形对角线互相垂直时,中点四边形为矩形; 当四边形对角线相等时,中点四边形为菱形; 当四边形对角线互相垂直且相等时,中点四边形为正方形。
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
一、 知识运用
3、中点四边形:依次连接任意四边形各边 中点 所得的 四边形称为中点四边形. 活动1: (1)任意作一个四边形,并作出 它的中点四边形; (2)观察:你作出的中点四边形是 什么四边形?
任意四边形的中点四边形为平行四边形
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
2、中位线: 中位线定义: 连接三角形两边 中点 的线段叫做三角形的中位线 中位线定理: 三角形的中位线 平行 于第三边并且等于它的 一半 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确一Βιβλιοθήκη 知识预备1、菱形的对角线互相
垂直
;
矩形的对角线
相等
;
正方形的对角线互相 垂直 且 相等 ;
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
AC⊥BD
AC=BD
当四边形对角线互相垂直时,中点四边形为矩形; 当四边形对角线相等时,中点四边形为菱形; 当四边形对角线互相垂直且相等时,中点四边形为正方形。
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
一、 知识运用
3、中点四边形:依次连接任意四边形各边 中点 所得的 四边形称为中点四边形. 活动1: (1)任意作一个四边形,并作出 它的中点四边形; (2)观察:你作出的中点四边形是 什么四边形?
任意四边形的中点四边形为平行四边形
7/10/2024
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H
E
G F
中点四边形的定义 顺次连接四边形各边中点所得的 四边形叫做中点四边形。
A
E G H
A
D
E
C H G D
F
B
B
F
C
2015年7月9日星期四6时 31分44秒
练习1: 在四边形ABCD中,四边的中点分别 为E,F,G,H,请猜想四边形EFGH是 什么四边形?并证明你的结论?
A E B F
A E B
2015年7月9日星期四6时 31分44秒
H
D G C
F
结论5: 正方形的中点四边形是正方形.
A E B
2015年7月9日星期四6时 31分44秒
H
D G C
F
原四 任意 边形 四边形
原四 边形 对角 线
不 相 相 等 等, 不 垂 直
互 相 垂 直
平 行 四 边 形 不 相 等
矩 形
F
C
结论3: 矩形的中点四边形是菱形.
A E B
2015年7月9日星期四6时 31分44秒
H
D G
F
C
原四 边形
原四 边形 对角 线 中点 四边 形形 状
任意 四边形
平行 四边 形
互 相 垂 直 不 相等
矩形
菱形
正方 形
等 腰 梯 形
不 相 相 等 等, 不 垂 直
相 等
平 菱 行 形 四 边 2015年7月9日星期四6时 31分44秒 形
不 相 相 等 等, 不 垂 直
不 相等
平 菱 行 形 四 边 2015年7月9日星期四6时 31分44秒 形
矩 形
平行 四边形
练习3: 在矩形ABCD中,四边的中点分别为 E,F,G,H,请猜想四边形EFGH是什么 四边形?并证明你的结论?
A E B
2015年7月9日星期四6时 31分44秒
H
D G
矩 形
平行 四边 形
菱 形
练习4: 在菱形ABCD中,四边的中点分别为 E,F,G,H,请猜想四边形EFGH是什么 四边形?并证明你的结论? D
H A G C
E
2015年7月9日星期四6时 31分44秒
F B
结论4: 菱形的中点四边形是矩形.
D H A G C
E
2015年7月9日星期四6时 31分44秒
A E B
2015年7月9日星期四6时 31分44秒
H
D G
F
C
顺次连接 任意四边形 各边中点 平行四边形 也是平行四边形吗? 所成的四边形是平行四边形。 E 有没有更特殊? 矩形呢? A
A H A E B B H F D F
那么:
2 我思考,我进步
2015年7月9日星期四6时 31分44秒
H
D
G C
已知:如图,点E、F、G、H分别是四边形 ABCD各边中点。 求证:四边形EFGH为平行四边形。
A E B F
2015年7月9日星期四6时 31分44秒
H
证明:连接AC
D ∵ E、F是AB、BC边中点 G
C
1 ∴EF∥AC且EF= 2 AC
C
1 同理:HG ∥ AC且HG = 2 AC ∴EF ∥ HG且EF = HG
F B
原四 边形
原四 边形 对角 线 中点 四边 形形 状
任意 四边形
平行 矩 四边 形 形
互 相 垂 直 不 相 相等 等
菱形
正方形
等 腰 梯 形
不 相 相 等 等, 不 垂 直
互相 垂直
平 菱 行 形 四 边 2015年7月9日星期四6时 31分44秒 形
矩 形
平行 菱 四边 形 形
矩形
练习5: 在正方形ABCD中,四边的中点分别 为E,F,G,H,请猜想四边形EFGH是什 么四边形?并证明你的结论?
菱 形
正方形 等腰
梯形
相 等
互 相 垂 直
相等 & 垂直 正方形
中点 平 菱 矩 四边 行 形 形 形形 四 边 2015 年 7 月 9日星期四6时 状31分44秒 形
平 行 四 边 形
菱 形
矩 形
在等腰梯形ABCD中,四边的中点分 别为E,F,G,H,请猜想四边形EFGH是 什么四边形?并证明你的结论?
E B F
2015年7月9日星期四6时 31分44秒
G C
原四 边形
不相 等, 不垂 直 中点 平行 四边 四边 形形 形 状 原四 边形 对角 线
任意 四边形
相等 互相 垂直
平 行 四 边 形
矩 形
菱 形
正方 形
等 腰 梯 形
菱形 矩形
2015年7月9日星期四6时 31分44秒
练习2: 在平行四边形ABCD中,四边的中点 分别为E,F,G,H,请猜想四边形EFGH 是什么四边形? H 并证明你的结论? A D
E B
2015年7月9日星期四6时 31分44秒
G F C
结论2: 平行四边形的中点四边形是平行 H 四边形. A D
E B F C G
2015年7月9日星期四6时 31分44秒
原四 边形
原四 边形 对角 线 中点 四边 形形 状
任意 四边形
平行四 边形
互 相 垂 直Leabharlann 矩 形菱 形正方 形
等 腰 梯 形
D E
B
C
这个定理提供了证明线段平行以及线段成倍分关系 的根据.
2015年7月9日星期四6时 31分44秒
中点四边形
已知:任意四边 形ABCD,E、F、 G、H分别是AB、 BC、CD、DA的 中点,顺次连接 E、F、G、H, 则四边形EFGH 称为 中点四边形。 2015年7月9日星期四6时
31分44秒
E
B
2015年7月9日星期四6时 31分44秒
G F C
原四 边形
不相 等, 不垂 直 中点 平行 四边 四边 形形 形 状 原四 边形 对角 线
任意 四边形
相等
平 行 四 边 形
矩 形
菱 形
正方 形
等 腰 梯 形
菱形
2015年7月9日星期四6时 31分44秒
练习1: 在四边形ABCD中,且AC⊥BD,四边 的中点分别为E,F,G,H,请猜想四边 形EFGH是什么四边形?并证明你的 H A D 结论?
∴四边形EFGH为平行四边形。
(一组对边平行且相等的四边形是平行四边形)
结论1: 任意四边形的中点四边形是平行 四边形.
A E
B F
2015年7月9日星期四6时 31分44秒
H
D G C
练习1: 在四边形ABCD中,且AC=BD,四边 的中点分别为E,F,G,H,请猜想四边 形EFGH是什么四边形?并证明你的 H A D 结论?
2015年7月9日星期四6时 31分44秒
四边形之间的关系
矩形 平行四边形
正方形
菱形 四边形
等腰梯形
梯形 直角梯形
2015年7月9日星期四6时 31分44秒
三角形 中位线 的性质 定理:三角形的中位线平行于第三边, A 且等于第三边的一半.
∵DE是△ABC的中位线, 1 ∴DE∥BC, DE BC . 2
