北航张量分析课件12
合集下载
张量分析——初学者必看PPT

§A-2 矢量的基本运算
A 张量分析
四、矢量的并乘(并矢)
a ai ei , b b j e j
并乘
ab ai ei b j e j ai b j ei e j
a2b1e2 e1 a2b2 e2 e2 a2b3e2 e3 a3b1e3e1 a3b2 e3e2 a3b3e3e3
ab a1b1e1e1 a1b2 e1e2 a1b3e1e3
§A-3 坐标变换与张量的定义
A 张量分析
x x cos y sin y x sin y cos
x x cos y sin y x sin y cos
约定
S ai xi a j x j
用拉丁字母表示3维,希腊字母表2维
一、求和约定和哑指标
§ A-1 指标符号
双重求和
Aij xi y j
i 1 j 1
3
3
Aij xi y j A11x1 y1 A12 x1 y2 A13 x1 y3 A21x2 y1 A22 x2 y2 A23 x2 y3 A31x3 y1 A32 x3 y2 A33 x3 y3
两个二阶张量点积的结果为一个新的二阶张量,这 相当于矩阵相乘
§A-4 张量的代数运算
A 张量分析
五、张量的双点积
两个张量点积的结果仍为张量。新张量的阶数是 原两个张量的阶数之和减 4
A : B ( Aijk ei e j ek )( Brster es et ) Aijk Brst jr ks ei et Aijk B jkt ei et S
A B ( Aijk ei e j ek ) ( Brst er es et ) Aijk Brst ei e j kr es et Aijk Bkst ei e j es et S
张量分解学习PPT课件

.
26
CP分解
张量的低秩近似
◦ 然而在低秩近似方面,高阶张量的性质比矩阵SVD差
Kolda给出了一个例子,一个立方张量的最佳秩-1近似并不 包括在其最佳秩-2近似中,这说明张量的秩-k近似无法渐进 地得到
下面的例子说明,张量的“最佳”秩-k近似甚至不一定存在
X a1ob 1oc2a1ob2oc1a2ob 1oc1
纤维:x i j :
.
6
基本概念及记号
切片(slice)
水平切片:X i : :
侧面切片:X : j :
正面切片:X ::k ( X k )
.
7
基本概念及记号
内积和范数
◦ 设 X,Y¡I1× I2× L× IN
内积:
I1 I2
IN
X,Y
L x y i1i2LiN i1i2LiN
i11i21 iN1
R
X§A,B,C¨arobrocr r1
X
c1 b 1
c2 b2
L
cR b R
a1
a2
aR
三阶张量的CP分解
.
20
CP分解
CP分解的矩阵形式
◦ 因子矩阵:秩一张量中对应的向量组成的矩阵,如
A a 1 a2 LaR
◦ 利用因子矩阵,一个三阶张量的CP分解可以写成展开形式
X (1) A C e B T X (2) B C e A T X (3) C B e A T
◦ 对于高阶张量,有
X ┈ λ ;A (1 ),A (2 ),L ,A (N ) Rra ( r 1 )o a ( r 2 )o L o a ( r N ) r 1
其展开形式为
X ( n ) A ( n ) d i a g ( λ ) A ( N ) e L e A ( n 1 ) e A ( n 1 ) e L e A ( 1 )T
数学张量分析PPT课件

x y z
第6页/共92页
右散度表示为: diva a
diva a
ei i a je j
ij
a j xi
ai xi
iai
a1 a2 a3 x1 x2 x3
显然 diva diva
今后对于矢量场的左散度和右散度不加区别
第7页/共92页
张量的散度
关于二阶张量场 T T的P左散度定义为:
间点的位置。两者由下列坐标变换联系起来:
xi xi xi' i, i ' 1,2,3
第23页/共92页
若 xi'是的线性函数,则 x i' 也是一个斜角坐标,而且坐标变换为:
xi
Ai i'
x i'
x i
x i'
xi'
这里
Ai i'
为变换系数,它是常数。
若 x i不是 xi' 的线性函数,则 xi' 称为曲线坐标。
标量的梯度:
标量函数:
f f (r)
则梯度为:
f gradf eii f
展开后有:
原式 1 f e1 2 f e2 3 f e3
f i f j f k x y z
第1页/共92页
矢量的梯度: 左梯度
grad a a (i ei )(a j ej ) (eii )(a j e j )
a ai gi ai gi
由 eijk 的定义可知,下列混合积等式成立:
gig jgk gi g j gk gig jgk eijk gig jgk gi g j gk gig jgk eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为 和ijk 。ijk 由此定义可知
第6页/共92页
右散度表示为: diva a
diva a
ei i a je j
ij
a j xi
ai xi
iai
a1 a2 a3 x1 x2 x3
显然 diva diva
今后对于矢量场的左散度和右散度不加区别
第7页/共92页
张量的散度
关于二阶张量场 T T的P左散度定义为:
间点的位置。两者由下列坐标变换联系起来:
xi xi xi' i, i ' 1,2,3
第23页/共92页
若 xi'是的线性函数,则 x i' 也是一个斜角坐标,而且坐标变换为:
xi
Ai i'
x i'
x i
x i'
xi'
这里
Ai i'
为变换系数,它是常数。
若 x i不是 xi' 的线性函数,则 xi' 称为曲线坐标。
标量的梯度:
标量函数:
f f (r)
则梯度为:
f gradf eii f
展开后有:
原式 1 f e1 2 f e2 3 f e3
f i f j f k x y z
第1页/共92页
矢量的梯度: 左梯度
grad a a (i ei )(a j ej ) (eii )(a j e j )
a ai gi ai gi
由 eijk 的定义可知,下列混合积等式成立:
gig jgk gi g j gk gig jgk eijk gig jgk gi g j gk gig jgk eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为 和ijk 。ijk 由此定义可知
弹性力学张量分析学习—对于初学者很有用PPT课件

精选课件 31
符号ij 与erst
➢ erst 符号 (排列符号或置换符号,Eddington)
➢ 定义(笛卡尔坐标系)
1
e rst
1
0
当r, s, t为正序排列时 当r, s, t为逆序排列时 当r, s, t中两个指标值相同时
或
erst
1rssttr
2
(1,2,3)及其轮流换位得到的(2,3,1)和(3,1,2)称为正序排列。 (3,2,1)及其轮流换位得到精的选(课2件,1,3)和(1,3,2)称为逆序排列。
ij
1 0
(i = j) (i, j=1, 2, …, n) (i j)
➢ 特性
1. 对称性,由定义可知指标 i 和 j 是对称的,即
ij ji
精选课件 29
符号ij 与erst
2. ij 的分量集合对应于单位矩阵。例如在三维空间
11 12 13 1 0 0
21
22
23
0
1
0
31 32 33 0 0 1
3
➢ 分解式记法: uu1e1u2e2u3e3 uiei i1
➢ 分量记法: u i
精选课件
Appendix A.1
8
张量基本概念
➢ 指标符号用法
1. 三维空间中任意点 P 的坐标(x, y, z)可缩写成 xi , 其中x1=x, x2=y, x3=z。
2. 两个矢量 a 和 b 的分量的点积(或称数量积)为:
d s2 d x 1 2 d x 22 d x 32
可简写成: ds2 dxi dxi
场函数 f (x1, x2, x3) 的全微分: f
d f xi d xi
精选课件 24
符号ij 与erst
➢ erst 符号 (排列符号或置换符号,Eddington)
➢ 定义(笛卡尔坐标系)
1
e rst
1
0
当r, s, t为正序排列时 当r, s, t为逆序排列时 当r, s, t中两个指标值相同时
或
erst
1rssttr
2
(1,2,3)及其轮流换位得到的(2,3,1)和(3,1,2)称为正序排列。 (3,2,1)及其轮流换位得到精的选(课2件,1,3)和(1,3,2)称为逆序排列。
ij
1 0
(i = j) (i, j=1, 2, …, n) (i j)
➢ 特性
1. 对称性,由定义可知指标 i 和 j 是对称的,即
ij ji
精选课件 29
符号ij 与erst
2. ij 的分量集合对应于单位矩阵。例如在三维空间
11 12 13 1 0 0
21
22
23
0
1
0
31 32 33 0 0 1
3
➢ 分解式记法: uu1e1u2e2u3e3 uiei i1
➢ 分量记法: u i
精选课件
Appendix A.1
8
张量基本概念
➢ 指标符号用法
1. 三维空间中任意点 P 的坐标(x, y, z)可缩写成 xi , 其中x1=x, x2=y, x3=z。
2. 两个矢量 a 和 b 的分量的点积(或称数量积)为:
d s2 d x 1 2 d x 22 d x 32
可简写成: ds2 dxi dxi
场函数 f (x1, x2, x3) 的全微分: f
d f xi d xi
精选课件 24
2011张量ppt12

自由标的个数、 自由标的个数、符号及上下分布须相同 哑标必须成对上下分布
C
ns g gt
=A
mn
B
gs m gt
张量指标方程形式不变性
若张量指标方程在某一坐标系中成立, 若张量指标方程在某一坐标系中成立,则必在 任意坐标系中也成立 若
C
ns g gt
=A
mn
B
gs m gt
则
C′
ns g gt
= A′ B ′
gj p gk gj l gk
= δ β β β A′ B ′
C′
ij g gk
= β β β A′ B ′
li gj l gk
= A′ B ′
mn
C′
ns g gt
= A′ B ′
4.3 张量代数
gs m gt
7
张量分析
一般坐标系 的向量梯度
∂y j T : xi = xi (yj ) g = je ∂x v ∂v ∂yk i ∂v k ∂ i 左梯度 ∇v = e = i e k =g k i ∂x ∂y ∂y ∂x
z
张量分析
Tensor
x
v
y
第 12课
能源与动力工程学院
复习
张量的转置
A T = A ji g i g j = A g i g j = A jg i g i g j = A
ji gi j
g ig j
对称与反对称张量 张量 二阶张量
T
AT = A
A T = −A
% ] T [ B ] [T ′ ] = [ B ]T [T ] [ B ] T ′ = [ B % % ] = [ B ]−1 T [ B ] % % T ′ = [ B ] T [ B
C
ns g gt
=A
mn
B
gs m gt
张量指标方程形式不变性
若张量指标方程在某一坐标系中成立, 若张量指标方程在某一坐标系中成立,则必在 任意坐标系中也成立 若
C
ns g gt
=A
mn
B
gs m gt
则
C′
ns g gt
= A′ B ′
gj p gk gj l gk
= δ β β β A′ B ′
C′
ij g gk
= β β β A′ B ′
li gj l gk
= A′ B ′
mn
C′
ns g gt
= A′ B ′
4.3 张量代数
gs m gt
7
张量分析
一般坐标系 的向量梯度
∂y j T : xi = xi (yj ) g = je ∂x v ∂v ∂yk i ∂v k ∂ i 左梯度 ∇v = e = i e k =g k i ∂x ∂y ∂y ∂x
z
张量分析
Tensor
x
v
y
第 12课
能源与动力工程学院
复习
张量的转置
A T = A ji g i g j = A g i g j = A jg i g i g j = A
ji gi j
g ig j
对称与反对称张量 张量 二阶张量
T
AT = A
A T = −A
% ] T [ B ] [T ′ ] = [ B ]T [T ] [ B ] T ′ = [ B % % ] = [ B ]−1 T [ B ] % % T ′ = [ B ] T [ B
北航张量分析课件13

,
三、公式与计算(36分)
,
2
1。指标和谐的方程是(
)
Aij Aij
ij
ji
A j j R ii Ail R j (一般坐标系) ijl
j ik
1 jm gim gkm gki g k m i 2 y y y
16
15。向量(
)
的散度是向量梯度的缩并 的散度是2阶张量
左散度和右散度不相等 散度等于向量空间导数组与基向量的并积 17
16。向量的旋度(
)
是2阶张量 等于算子 与向量的点积 反映向量场的位移效应
反映向量场的旋转效应
18
17。协变基(
)
在物理空间与坐标面正交 与逆变基正交归一
解:
1 F N ij x j 2 xi
30
2。 将指标式展开为分量式
C B A B
j i k i l k
j l
解: C j B 1 A 1B j B 1 A 2 B j + B 1 A 3B j i i 1 1 i 1 2 i 1 3
B A B + B A B B A B
证毕。
27
d dT d (T ( ))= 2。证明卡氏张量求导法则 d d d
( T 为2阶张量, 为标量函数)
d d (T ( )) T ij e i e j 证: d d
d T ij e i e j d dT d dT ij d eie j d d d d d d
T 2
T12 T22 T32 00 2 2 x j x1 x2 x3
三、公式与计算(36分)
,
2
1。指标和谐的方程是(
)
Aij Aij
ij
ji
A j j R ii Ail R j (一般坐标系) ijl
j ik
1 jm gim gkm gki g k m i 2 y y y
16
15。向量(
)
的散度是向量梯度的缩并 的散度是2阶张量
左散度和右散度不相等 散度等于向量空间导数组与基向量的并积 17
16。向量的旋度(
)
是2阶张量 等于算子 与向量的点积 反映向量场的位移效应
反映向量场的旋转效应
18
17。协变基(
)
在物理空间与坐标面正交 与逆变基正交归一
解:
1 F N ij x j 2 xi
30
2。 将指标式展开为分量式
C B A B
j i k i l k
j l
解: C j B 1 A 1B j B 1 A 2 B j + B 1 A 3B j i i 1 1 i 1 2 i 1 3
B A B + B A B B A B
证毕。
27
d dT d (T ( ))= 2。证明卡氏张量求导法则 d d d
( T 为2阶张量, 为标量函数)
d d (T ( )) T ij e i e j 证: d d
d T ij e i e j d dT d dT ij d eie j d d d d d d
T 2
T12 T22 T32 00 2 2 x j x1 x2 x3
张量分析课件

P = ∑αij Ej (i=1,2,3) i
j =1
3
Pi′ = ∑ α i′j′ E j′ (i'=1,2,3)
j ′ =1
3
代 入
将一阶张量Ej和Pi的变换规律
Pi′ = ∑ Ai′i Pi
3
代 入
E j′ = ∑ Aj ′j E j
j =1
i =1 3
∑A
i =1
3
i ′i i
P = ∑∑ α i′j′ Aj′j E j
证: 刚体定轴转动:
ω
(Z轴)转轴
刚 体
(
)
v τi A ni O′ ri
v
刚体定轴转动
r2 r r I 质点:ij = m(rij δ ij − ( r )i ( r ) j ) O
v Ri
= m(δ ij xk xk − xi x j ) (i, j, k=1, 2, 3)
例3. 设质量为m的质点位于点(x1, x2, x3), 证明在 正交变换下,由九个分量构成的一个物理量Iij是一个 二阶张量, 其中: I ij = m(δ ij xk xk − xi x j ) (i, j=1, 2, 3) —称Iij为质点的惯性积,有Iij定义的物理量叫惯性矩. 证: 质点:I ij = m(δ ij xk xk − xi x j ) (i, j, k=1, 2, 3) 九个分量:
δij在坐标变换后,其各个分量的值不变. 即在任意坐 标系中按上式定义的二价对称δ符号是一个二阶张量.
例3. 设质量为m的质点位于点(x1, x2, x3), 证明在 正交变换下,由九个分量构成的一个物理量Iij是一个 二阶张量, 其中: I ij = m(δ ij xk xk − xi x j ) (i, j=1, 2, 3) —称Iij为质点的惯性积,有Iij定义的物理量叫惯性矩.
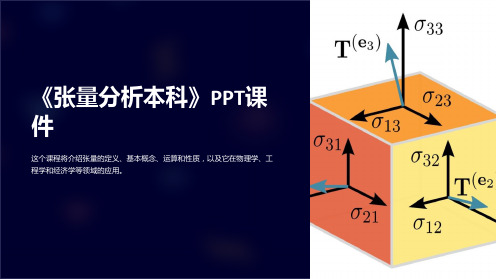
《张量分析本科》课件
2
流体力学
流体力学中的张量可描述液体和气体的流动性质,从而帮助工程师设计和优化流体系 统。
3
材料科学
张量在材料的力学行为、热膨胀和磁性等方面的研究中起着重要作用,有助于材料性 能的改进。
经济学中的张量应用
金融风险评估 市场分析 关联性, 对风险评估和投资决策具有重要意义。
《张量分析本科》PPT课 件
这个课程将介绍张量的定义、基本概念、运算和性质,以及它在物理学、工 程学和经济学等领域的应用。
张量的定义和基本概念
张量是一个多维数组,具有特定的变换规律。它在数学和物理学中扮演着重 要角色,能够描述物体在各个方向上的变化。
张量的运算和性质
张量可以进行加法、乘法等运算,还具有一些特殊的性质,如对称性、反对称性和行列式等。这些运算 和性质是研究和应用张量的基础。
学科交叉
张量分析作为一门综合性学科, 促进了不同学科之间的交流与 合作,推动了学科发展的跨越 性进展。
学习资源推荐
1 书籍和教材推荐
2 网上教程和视频
《张量分析导论》、《张量分析教程》等 是学习和研究张量分析的重要参考资源。
有许多免费的网上教程和视频,可以帮助 初学者快速入门和掌握张量分析的基本概 念和应用。
张量在市场需求、价格和产量之间的关系分 析中,能够提供深入洞察和科学决策支持。
张量分析可以用于挖掘大规模数据集中的模 式和趋势,为经济预测和决策提供准确和可 靠的依据。
张量分析的重要性
科学研究
张量分析在各个学科的科学研 究中发挥着重要作用,帮助解 决复杂问题和揭示自然规律。
技术发展
随着科技的发展和应用领域的 拓展,张量分析为新技术的发 展提供了关键理论基础。
张量的坐标表示和变换规律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H k v k y
j
g y
ijk vk
j
gi
g i
1 H 3 v 3 H 2 v 2 1 H1v1 H 3 v 3 g1 g 2 2 3 3 1 H 1 H 2 y y H 3 H1 y y 1 H 2 v 2 H1v1 g 3 1 2 H1 H 2 y y
k
1 kj gg j k y g y
2
gv k k g v v k g y k
2
k k
g kl kl
14
4.5 张量方程的转换
物质导数算子
T T y i t , t
场坐标
左散度
T T g k y
k
右散度
T T k gk y
ji i
gT j T
ij
i g j
T T
复习
gj
4
向量的旋度
v
v j gi
kji k
ijk vk gi j y
g y
ijk vk
j
gi
张量方程的转换 直角坐标系下的指标方程转换为曲线坐 标系下的指标方程 曲线坐标系实体方程、指标方程 转换为分量方程
7
正交曲线坐标系中的张量物理分量
正交坐标系
gi g g j gij ij gii
g i g g j gij ij g i i
jk k i
因
gij g
g
ii
1 gii
拉梅(Lam’s)系数
H i gii g i g i i
g i
gi gii
4.5 张量方程的转换 18
例:
转动惯量张量
I ij m ij x k x k x i x j
I
i gj
I ij I
ij
m g y y m g y y
i j k k ij ij k
m y yk y y j
i k k i j i
y y m g g y y y y y y m g g y y y y
复习
右梯度
T k T k g y
2
v vi k g k g i vi k g k g i vi l g l g i vi g l g i
l
向量的散度
gv k g v v k k g y k 二阶张量的散度
左散度
T T g k y
kl ij k l k i j j ij l i j kl
4.5 张量方程的转换 19
例:
不可压流体运动方程组(2维)
u j ux uy 0 v 0 0 x j x y ux p xx yx ux ux t ux x uy y f x x x y
i k
2
k
g
k
g g i v kj g g i v g i v k k k
j
i
kj
k k
g kl
kl
v k v k g i vi k g i
k
i k
k
例: 卡氏坐标系向量的L微分积
2 v i kl 2v 2v 2v 2v ei 2v vi kl g kl g i 2 2 2 x k xl x k x k x y z
k
右散度
T T k gk y
ji i
gT T
ij
i g j
T T
复习
gj
3
v vi k g k g i vi k g k g i vi l g l g i vi g l g i
l
向量的散度
gv k g v v k k g y k 二阶张量的散度
4.5 张量方程的转换 15
g i 与时间无关
直角到曲线坐标系的转换
1。转换步骤
把直角坐标系下的物理分量方程转换为直角坐 标系下的张量方程(实体、指标)
把直角坐标系下的张量方程转换为一般坐标
系下的张量方程 将一般坐标系下的张量方程在给定曲线坐标
系下展开为张量分量方程
④一般坐标系下的张量分量方程转换为物理分量方程
4.5 张量方程的转换 13
卡氏坐标系标量的L微分积
例: 一般坐标系标量的L微分
2 2 2 2 2 2 2 x y z
j jk j g j g j g gk y y
j
2
g k
kl
k ij
g i i H i H i j j y y i j
g ijl
k ij
i j k
9
4.5 张量方程的转换
k ii
H i H i kk g i i g i i g k k y gkk y H k H k y k
4.5 张量方程的转换 10
向量散度
g v v k k
gv k k g y
3
g
g ij g g HH H g 2
v i vi /
gii vi / H i
H H 2 H3 v k / Hk gv H H 2 H 3 y k
4.5 张量方程的转换 16
2。张量类型选择的基本原则
任意性:理论上可用任一种张量作转换 简单性:方程形式尽可能简单 一致性:满足指标一致原理,与相关方程一 致,与直角坐标系下的张量方程形式一致等。
针对性:根据具体需要选择
4.5 张量方程的转换
17
3。特殊张量对应关系
xi y
xk
ui ui uj x j t
4.5 张量方程的转换
p ji fi xi x j
20
u j x j
0 v 0
vj
j
gv j 1 0 j g y
ui ui uj x j t
p ji v fi v v f p xi x j t
u j
i ij j
e i gi
u j
k
g
ijk
i ijk
ij gij g i
ijk
xi
v v j i
gv j 1 j v v j x j g y j
2ui 2v x k x k
v kj g v
i kj
i k k
uk vk ijk vk ijk v ijk j x j y g y j
22
i ji
i k
i i j
H i H i i i g i i g i i g j j y gii y H i H i y k
i j
标量梯度
g k g k g k 1 k H k y k y k
g
1
1 2 1 2 1 +g +g 1 2 3 H1 y H 2 y H 3 y
例: 质点的加速度
Dv v vi j i k a ai g i v v gi v g j v k g gi Dt t t i v ui vi ui j i k k i gi v v k j gi v v k gi t uk x ei t t k
复习 5
张量的物理分量
g i gi gii
ii
v i v i gii
vij v j i g
g
jj
v j
g
jj
g
i
ii
g
jj
复习
6
第四章 一般张量
4.1 一般坐标系中的基向量 4.2 坐标变换与一般张量 4.3 张量代数 4.4 张量分析 4.5 张量方程的转换
ijk
i ik
iji
g i i H i H i g i k gk i g i i i k k j y y k y y y
i k
g i i g i j g j i i j i y y y
运动粒子坐标
dy j dT T T j dt t y dt
d~i y i ~i ~i t v v gi gi y y dt T T j T vjT j v t t y j
T T T i j T i j T v i v gi g v T j j t y t y t
j
i vi k i i ji v v k f p t
p g ik p k p g y k
ik
i
C
( )
:S
ji C jiklSkl
1 S v v 2
4.5 张量方程的转换
1 Skl vl k vl k 2
g i H i g i
g H H 2 H 3
4.5 张量方程的转换
vi H i vi
12
L(Laplacian)算子与物质导数算子
L算子
v v
2
L微分
v g k y
