QC 7种工具
QC七种工具

XXX XXX
2000年1月-6月
日期 班次 5月 332 245 144 82 16 819
2000.09.18 全部 6月 223 241 107 72 32 675 合计 1746 1537 913 493 130 4819
11欠铸 冷隔 小砂眼 粘 Nhomakorabea 其他 合计
4月 353 272 168 94 23 910
33
分层法
分层法示例
某空调维修部,帮助客户安装后经常发生制冷液泄 漏。通过现场调查,得知泄漏的原因有两个:一是 管子装接时,操作人员不同(有甲、乙、丙三个维 修人员按各自不同技术水平操作);二是管子和接 头的生产厂家不同(有A、B两家工厂提供配件)。 于是收集数据作分层法分析(见表一、表二),试 说明表一、表二的分层类别,并分析应如何防止渗 漏?
21
散布图
分 散 图 示 例
强正相关
X Y Y Y Y
强负相关
X
弱正相关
X
弱负相关
X 22
散布图
Y Y
不相关
X
曲线相关
X
散布图的分析和判断
对照典型图例法、简单象限法、回归分析法
23
散布图
1)对照典型图例法
实际画出的散布图与典型图例对照,就可得到两个变量之间是否相关 及属哪种相关的结论。
2)简单象限法
24
散布图
3)回归分析法 相关系数的定义
r= ∑(xi-x)(yi-y) ∑(xi-x)2 ∑(yi-y)2 Lxy= ∑(xi-x)(yi-y) Lxx= ∑(xi-x)2 Lyy= ∑(yi-y)2
25
=
Lxy Lxx Lyy
散布图
质量改进之新七种工具概述

图5-7 铸造质量问题、设备工装、工艺管 理关系分析Y型矩阵图
5.6 矩阵图的注意事项
– 1.正确选型,根据不同的因素分析选择适宜的 图形;
– 2.因素组内的各因素应在同一层次; – 3.因素组之间的相关关系应明显; – 4.QC小组使用矩阵图选择课题时,应关注矩阵
图中的着眼点; – 5.在进行矩阵分析时应独立考虑要选择的课题
•
QC小组在实施过程中可使用PDPC法辅助实现对策目标,
也可用它在构思新的设计方案时优化方案,实现小组目标。
4.5 PDPC法应用步骤
• 1.确定所要解决的课题,提出实现目标值; • 2.提出达到理想状态的手段、措施实施方案; • 3.对提出的措施,逐项进行可行性分析,充分预测可能
的结果及遇到困难时应采取的新的可行性措施和方案; • 4.综合考虑时间顺序、经济性、可靠性、难易程度和效
– 5.确认关联关系。 – 6.评价重要程度。
5.5 矩阵图的应用实例
• 例1:
– 某厂QC小组为提高某电机输入功率,通过运用 L型矩阵图法,对影响电机性能的相关关系进 行了比较分析。见下图。
图5-6 电机性能差原因分析L型矩阵图
• 例2:
• 某铸造厂QC小组为了解决汽车缸体铸 件产出率低的问题,针对涉及的设备工装 、工艺管理和铸造质量问题三个事项,选 用了Y型矩阵图进行了分析,见下图。
• 重要程度:
– 因直接到现场去接触事物有时是有限制的,所 以,为了广泛收集情况,这种间接调查方法也 是有效的。
③.头脑风暴法
• 含义:
– 头脑风暴法是采用会议的方式,引导每个参加 会议的人围绕某个中心议题广开言路,激发灵 感,在自己的头脑中掀起思想风暴,毫无顾忌 、畅所欲言地发表独立见解的一种集体创造性 思维的办法。
QC新老七种工具

0
2
0 0.39%
2
5
0 0.41%
2
0
0 0.09%
5
2
0 0.25%
1
0
0 0.09%
2
4
0 0.35%
1
1
0 0.47%
2
0
0 0.12%
0
2
0 0.41%
0
1
0 4.08%
16 34 1 0.34%
二、层别法
1、定义
层别法又称分类法、分组法,它是按照一定的 层别标志,把搜集到的大量有关某一特定主题的统 计数据加以归类、整理和汇总的一种方法,其主要 作用如图:
2
6
4
10
3
3
4
80 5461
4
37
6
12 38
1
2
176 9902
8
24
10
12
7
6
11
149 8503
2.5% 7.5% 5.0% 12.5% 3.8% 3.8% 5.0%
2.3% 21.0% 3.4% 6.8% 21.6% 0.6% 1.1% 5.4% 16.1% 6.7% 8.1% 4.7% 4.0% 7.4%
二、层别法
26078 1231
甲班 DA+DX
71
18
乙班 DA+DX
76
3
72
57
丙班 DA+DX
67 10
45
丁班 DA+DX
2
0
综合 综合DX DA+DX率 数
4.92% 27
3.02%
4
甲班 DX数
七种质量工具

员工
18
因果图事例(对策追求型)
此型表示期望结果(特性)与对策(要因)间的关系,目的是探求问题 点如何防止,目标之效果如何达成等的对策,实例见下图 。
业务量
职务
多少适当
轮调
命令
如
何 做 定时
建立业务计划
到
集
体 的 互相合作
重点分析图。 意大利经济学家Vilfredo Pareto在研究意大利当时的
(1897年)社会贫富现象时提出:80%的财富集中在20% 的人手中,人们称之为柏拉图原理(80-20原理,80/20法 则)。原意为当初意大利的贫富悬殊,全国的80%的财富 集中在约占人口数仅20%的富人手中,而另外的80%的人 为贫困者,他们所拥有的总财富,仅占全国总财富的20%, 故只要控制住此仅占20%人口的富人,即可控制全国的财 富。此项原理,被广泛应用于工厂内,一般来说,不良原 因虽然很多项,但是总是集中在那几项,而这少少的几项 (通常仅3~7项)加起来,却占了约70%~80%,所以如能集 中火力于这几项作改善时,可收事半功倍之效。
迎搭便车】 (6)不要太早下判断性的定论。 (7)讨论力求集中焦点,针对某一问题为目标加以讨论。 (8)破除阶级尊卑的观点,使大家无拘无束地一起讨论问题。 (9)不要让小团体私自交谈,有意见要向大家提出来。 (10)将个人的意见全记录下来。 (11)不要以个人意见冒充大家的意见,提出有碍新见解发展的言论或口气。 (12)大家提出的创意,到第二阶段讨论时,才予以整理、评价、活用。 【第二阶段为讨论可行者或追求真因,重在「质」】 简单综合起来,应用脑力激荡法之原则为下列四点: 不批评(禁止判断)。 自由奔放、愈新奇愈好。 多多益善。 欢迎搭便车。
qc7工具七大手法

qc7工具七大手法01qc七大手法是指企业质量管理中常用的质量管理工具,有“老七种”和“新七种”之分。
“老七种”有分层法、调查表、排列法、因果图、直方图、控制图和相关图,新的QC七种工具分别是系统图、关联图、亲和图、矩阵图、箭条图、PDPC法以及矩阵数据分析法等。
02“七大手法”主要是指企业质量管理中常用的质量管理工具,有“老七种”和“新七种”之分。
“老七种”有分层法、调查表、排列法、因果图、直方图、控制图和相关图,新的QC七种工具分别是系统图、关联图、亲和图、矩阵图、箭条图、PDPC法以及矩阵数据分析法等。
03QC七大手法:1、层别法:层别法就是将大量有关某一特定主题的观点、意见或想法按组分类,将收集到的大量的数据或资料按相互关系进行分组,加以层别。
层别法一般和柏拉图、直方图等其它七大手法结合使用,也可单独使用。
2、查检表检查表就是将需要检查的内容或项目一一列出,然后定期或不定期的逐项检查,并将问题点记录下来的方法,有时叫做查检表或点检表。
3、柏拉图柏拉图的使用要以层别法为前提,将层别法已确定的项目从大到小进行排列,再加上累积值的图形。
它可以帮助我们找出关键的问题,抓住重要的少数及有用的多数,适用于记数值统计,有人称为ABC图,又因为柏拉图的排序识从大到小,故又称为排列图。
044、直方图直方图是针对某产品或过程的特性值,利用常态分布(也叫正态分布)的原理,把50个以上的数据进行分组,并算出每组出现的次数,再用类似的直方图形描绘在横轴上。
5、因果分析图所谓因果图,又称特性要因图,主要用于分析品质特性与影响品质特性的可能原因之间的因果关系,通过把握现状、分析原因、寻找措施来促进问题的解决,是一种用于分析品质特性(结果)与可能影响特性的因素(原因)的一种工具。
又称为鱼骨图。
6、散布图将因果关系所对应变化的数据分别描绘在X-Y轴坐标系上,以掌握两个变量之间是否相关及相关的程度如何,这种图形叫做“散布图”,也称为“相关图”。
QC七种工具
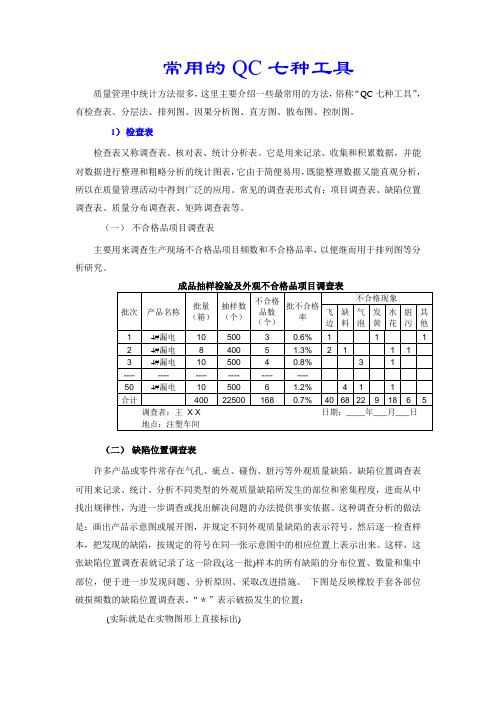
常用的QC七种工具质量管理中统计方法很多,这里主要介绍一些最常用的方法,俗称“QC七种工具”,有检查表、分层法、排列图、因果分析图、直方图、散布图、控制图。
1)检查表检查表又称调查表、核对表、统计分析表。
它是用来记录、收集和积累数据,并能对数据进行整理和粗略分析的统计图表,它由于简便易用,既能整理数据又能直观分析,所以在质量管理活动中得到广泛的应用。
常见的调查表形式有:项目调查表、缺陷位置调查表、质量分布调查表、矩阵调查表等。
(一)不合格品项目调查表主要用来调查生产现场不合格品项目频数和不合格品率,以便继而用于排列图等分析研究。
成品抽样检验及外观不合格品项目调查表(二)缺陷位置调查表许多产品或零件常存在气孔、疵点、碰伤、脏污等外观质量缺陷。
缺陷位置调查表可用来记录、统计、分析不同类型的外观质量缺陷所发生的部位和密集程度,进而从中找出规律性,为进一步调查或找出解决问题的办法提供事实依据。
这种调查分析的做法是:画出产品示意图或展开图,并规定不同外观质量缺陷的表示符号。
然后逐一检查样本,把发现的缺陷,按规定的符号在同一张示意图中的相应位置上表示出来。
这样,这张缺陷位置调查表就记录了这一阶段(这一批)样本的所有缺陷的分布位置、数量和集中部位,便于进一步发现问题、分析原因、采取改进措施。
下图是反映橡胶手套各部位破损频数的缺陷位置调查表,“*”表示破损发生的位置:(实际就是在实物图形上直接标出)(三) 质量分布调查表质量分布调查表是对计量数据进行现场调查的有效工具。
它是根据以往的资料,将某一质量特性项目的数据分布范围分成若干区间而制成的表格,用以记录和统计每一质量特性数据落在某一区间的频数。
见下表是一张某零件重量实测值分布调查表。
从表格的形式看,质量分布调查表与直方图的频数分布表相似。
不同点:质量分布调查表的区间范围是根据以往资料,首先划分区间范围,然后制成表格,以供现场调查记录数据;而频数分布表则是首先收集数据,再适当划分区间,然后制成图表,以供分析现场质量分布状况之用。
QC七种工具

第一概述一、起源新旧七种工具都是由日本人总结出来的。
日本人在提出旧七种工具推行并获得成功之后,1979年又提出新七种工具。
之所以称之为“七种工具”,是因为日本古代武士在出阵作战时,经常携带有七种武器,所谓七种工具就是沿用了七种武器。
有用的质量统计管理工具当然不止七种。
除了新旧七种工具以外,常用的工具还有实验设计、分布图、推移图等。
二、旧七种工具QC旧七大手法指的是:检查表、层别法、柏拉图、因果图、散布图、直方图、管制图。
三、新七种工具QC新七大手法指的是:关系图法、KJ法、系统图法、矩阵图法、矩阵数据分析法、PDPC法、网络图法。
相对而言,新七大手法在世界上的推广应用远不如旧七大手法,也从未成为顾客审核的重要方面。
第二层别法一、定义层别法是所有手法中最基本的概念,亦即将多种多样的资料,因应目的的需要分成不同的类别,使之方便以后的分析。
二、通常的层别方法使用的最多的是空间别:作业员:不同拉、班、组别机器:不同机器别原料、零件:不同供给厂家别作业条件:不同的温度、压力、湿度、作业场所产品:不同的产品别(如同时生产Ni-Cd和Ni-MH电池)时间别:不同批别、不同时间生产的产品其他:如使用不同的工艺方法生产的同种产品别三、应用层别法的应用,主要是一种系统概念,即在于要想把相当复杂的资料进行处理,就得懂得如何把这些资料加以有系统有目的的加以分门别类的归纳及统计。
第三检查表一、概述检查表是QC七大手法中最简单也是使用得最多的手法。
但或许正因为其简单而不受重视,所以检查表使用的过程中存在的问题不少。
不妨看看我们现在正在使用的各种报表,是不是有很多栏目空缺?是不是有很多栏目的内容用笔进行了修改?是不是有很多栏目内容有待修改?二、定义以简单的数据,用容易理解的方式,制成图形或表格,必要时记上检查记号,并加以统计整理,作为进一步分析或核对检查之用。
三、目的记录某种事件发生的频率。
四、时机1.当你必须记下某种事件发生的具体情况时;2.当你想了解某件事件发生的次数时;3.当你想收集资讯时。
QC七大手法(工具)完整版介绍

QC七大手法(工具)完整版介绍“七大手法”主要是指企业质量管理中常用的质量管理工具,有“老七种”和“新七种”之分。
“老七种”有分层法、调查表、排列法、因果图、直方图、控制图和相关图,新的QC七种工具分别是系统图、关联图、亲和图、矩阵图、箭条图、PDPC法以及矩阵数据分析法等。
今天我们一起来回顾一下“老七种”。
何为QC七手法:QC七手法又称为QC七工具,一般指旧QC七手法,即层别法、检查表、柏拉图、因果图、管制图、散布图和直方图。
是质量管理及改善运用的有效工具。
QC手法的适用范围:QC手法的用途非常广泛,可以用于企业管理的方方面面(包括计划管控、员工思想意识行为管理、质量管控、成本管控、交期管控、士气管理、环境管理、安全管理、效率管理、绩效考核、日常管理等等),但主要用于品质管理及改善。
七大手法口诀:因果追原因、检查集数据、柏拉抓重点、直方显分布、散布看相关、管制找异常、层别作解析。
因果图(特性要因图、石川图、鱼骨图):定义:当一个问题的特性(结果)受到一些要因(原因)影响时,将这些要因加以整理,成为有相互关系且有条理的图形,这个图形就称为特性要因图,又叫鱼骨图(Fish-Bone Diagram)。
用途说明:1.整理问题。
2.追查真正的原因。
3.寻找对策。
制作步骤:1. 决定问题或品质的特性——特性的选择不能使用看起来很抽象或含混不清的主题。
2. 决定大要因——须是简单的完整句,且具有某些程度或是方向性。
3. 决定中小要因。
4. 决定影响问题点的主要原因。
5. 填上制作目的、日期及制作者等资料。
应注意事项:1.脑力激荡。
2.以事实为依据。
3.无因果关系者,予以剔除,不予分类。
4.多加利用过去收集的资料。
5.重点放在解决问题上,并依结果提出对策,依5W2H原则执行。
.WHY——为什么?为什么要这么做?理由何在?原因是什么?.WHAT——是什么?目的是什么?做什么工作?.WHERE——何处?在哪里做?从哪里入手?.WHEN——何时?什么时间完成?什么时机最适宜?.WHO——谁?由谁来承担?谁来完成?谁负责?.HOW ——怎么做?如何提高效率?如何实施?方法怎样?.HOW MUCH——多少?做到什么程度?数量如何?质量水平如何?费用产出如何?6.依据特性别,分别制作不同的特性要因图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
QC 7种工具:(seven tools of QC)QC 7种工具:(seven tools of QC)1. 特性要因图(cause and effects diagram)●把对结果有影响的因子按4M整理,研究因果关系使用。
2. 柱状图(histogram)●用柱形表示的连续型Data的分布状态。
3. 排列图(Pareto diagram)●将各种问题按原因或状况分类统计,把数据从大到小排列后所做出的累计柱状图。
●2, 8法则:80%的不良发生在20%的主要工程上。
4. 检查表(check sheet)●用表格形式对Data进行整理和粗略分。
5. 管理图(graph)●统计方法使用于sample data监控及分析process变动。
6. 散点图(scatter plot)●判断两个连续型变量之间相互关系的点状图。
7. 阶层别(stratification)●把Data按特征分类,找到Data的散步规律。
数据类型:(data kinds)连续型:(continuous data)●可以连续测定的品质特性值。
如长度,重量。
离散型:(discrete data)●可以用个数测量的品质特性值。
○离散型data评价改善品质特性时,可信度比较低。
○尽量选定连续型data进行改善。
○选用离散型data时:用连续型特性值替代;增加sample数;收集时间记录参考。
母集团:(population)●data的全体集团,研究的对象。
○通过sample分析,得出母集团的某些特性值。
○品质特性值:平均值(X-bar),标准偏差(sigma)。
样本:(sample)●从母集团抽取的可以代表母集团性质的data。
●Sample种类:⒈random sample:母集团各种性质相同。
⒉层别sample:分类收集的data。
⒊系统sample:根据时间均匀的抽出。
⒋多阶段sample:分阶段收集的data。
有理数群:(rational subgroup)●在短时间内,同性质条件下的sample的集团。
○subgroup内只存在群内变动,subgroup间只存在群间变动。
○包含全部变动,subgroup no=6,subgroup size=5。
变动:(variation)●对于某种特性值,各data在平均值上离得多远,以平方和表示。
○为得出各因子对Y的影响度使用。
○变动大的因子是改善重要的因子。
○变动大,意味着各data与平均值相差大,即X与Y斜率大。
群内变动:(white noise)(Sum of Square Within)●所有工程中存在的由一般原因引起的变动。
(偶然原因)○偶然原因由作业者不熟练、周围环境等不可控制因素引起。
○影响工程样本的分布。
○一般由技术因素引起,可通过技术性改善减少。
群间变动:(black noise)(Sum of Square Between)●工程有外部影响时,由可查明的原因引起的变动。
(异常原因)○异常原因表现为与平时不一样的散布,不可控制与预测。
○通过管理可以控制的变动。
○影响平均值偏离目标值。
○表示随时间流逝实际的工程能力。
统计参数:(statistical parameter)⒈平均值:(average)算术平均,表示中心位置使用最广泛。
○集团平均用μ表示,sample用X-bar表示。
○计算时去掉异常点。
⒉中央值:(center)把data按大小排列,处在中间位置的值。
○n为奇数时,第(n+1)/2个数为中央值;n为偶数时,n/2和n/2+1个数的平均为中央值。
⒊最频值:最常出现的值。
数据分等级,最高等级即最频值的中间值最重要。
⒋散布:(distribute)表征data距离平均值大小的程度。
⒌分散:最大值到最小值的变动范围,有异常点不适用。
⒍标准偏差:(standard deviation)表征data散布大小的统计参数。
⒎四分位数:把data按大小顺序排列后,四等分。
○第一个数字叫第一四分位数。
(Q1)○第三个数字叫第三四分位数。
(Q3)○第二四分位数是中央值。
○四分位数的范围是Q3-Q1。
⒏变动系数:不同种类的散布比较时,数值差异大时使用。
V=S/X-bar。
Gage R&R:(gage repeatability & reproducibility)●评价测量系统本身的变动对工程变动影响程度。
○统计性工程管理依据测量的data。
如果data不可靠,导致工程能力出错,实验失败。
○测量误差是指测量值与参考值的差异。
○区分仪器不适合(反复性:EV)和测量方法不足(再现性:AV)评价。
○不是random sample,包含变动或者spec全范围准备。
统计性工程管理:SPC(statistical process control)●为生产出品质规格合格的产品按统计原理管理工程的方法。
○statistical:得出统计性资料和分析方法的帮助。
○process:掌握给出的品质规格和工程的能力状态。
○control:以我们的要求来管理。
统计:(statistical)●根据定量的data收集与分析导出结论掌握集团特性而使用。
自由度:●测定母集团参数必要的独立观察值数。
独立变量:(independent variable)●可控制对其它变量影响的变量。
○变量之间影响相互独立。
○实验计划时增加不必要的因子,不增加实验次数。
从属变量:(dependent variable)●由独立变量决定的变量。
CTQ:(critical to quality)●对产品的性能、功能、安全性等重要品质有致命影响的核心特性值。
○在顾客的观点进行FMEA和QFD。
○把顾客的要求以技术事项定量化再与具体SPEC相联系。
○CTQ是产品的功能、性能、不良都应该选定,并且可以测量。
○全部CTQ与关联部门确定,工程上判定。
CTP:(critical to quality)●对CTQ有影响的工程条件特性值。
规格上限:(Upper Spec Limit)/规格下限:(Lower Spec Limit)●技术性给出的公差尺寸的上限和下限。
○对象规格为10±0.5时:target是10,USL是9.5,LSL是10.5。
Z-bench:对于标准正态分布,用sigma scale衡量可满足规格的母集团品质的能力。
正态分布:(normal distribution)○统计性方法根据sample推测母集团特性。
○统计性参数包括平均值和标准偏差。
○X对于平均值μ左右对称,散布由sigma决定。
○连续型概率分布包括:正态分布,F-分布,T-分布,Chi-square 分布。
泊松分布:(Poisson distribution)●在一定时间或一定大小的空间上,事件无条件发生次数对应的概率分布。
○离散型概率分布包括:几何分布,多项分布,移值分布。
○前提条件:1. 对象区间应该分为某种事件发生可能性很小的单位区间。
2. 事件发生次数与单位时间应该独立。
3. 单位时间内两个以上的事件发生概率为‘0’。
业务流程图:(process mapping)○调查业务的流程,把process文件化用于明确改善的机会。
品质功能展开:(Quality Function Deployment)○是把顾客的要求转换成技术事项,有体系的接近获得CTQ的方法。
故障影响度分析:(Failure Modes & Effects Analysis)○明确产品设计中出现的问题,确定优先顺序,决定对故障Mode合适的action。
头脑风暴法:(brainstorming)○为了短时间内获得好的idea的方法。
种类:1. Free Wheeling:全体人员以对话形式得出idea。
2. Round Robin:成员轮流阐述idea。
3. Card Method:无讨论的形式下把idea写在卡片上。
注意事项:1. 任何idea不要批评。
2. 所有idea记录。
最少break down反映值在狭小范围上实验,致命因子也遵循2:8原则,改善20%的因子,改善效果是80%。
验证实验:(run confirmation)●实验计划法找出最佳工程条件,利用实际现物进行再现实验确认改善与否的实验。
○实验注意方面:潜在变量的影响,致命因子的遗漏,实验精度低。
回归分析:(regression analysis)●表示相关的独立变量和从属变量之间的函数关系。
○这个函数关系用数学方程式表示,利用这个方程式可以得到其它有用的情报。
○回归分析分类单纯回归:两个变量之间的关系是一次线性关系。
重回归分析:一个从属变量和两个以上独立变量。
曲线回归:两个变量之间是曲线关系。
○全部回归必须首先确认变数间是线性还是曲线关系。
○确认残差,残差图应为等分散,不是正态分布,无倾向性。
残差:(residual)●把从属变量与独立变量间的关系以回归线表示出来,由于回归线不能说明的误差。
○建立回归关系后,各测定值相同条件下存在潜在变数影响之外的散布。
○把这个值用变动量计算。
回归线不能说明的变动叫作残差。
○残差的值比较大的时候,用分散分析表验证,判断没有差异时,回归线无效。
○为减少残差,最大限度减少潜在变数,实验random进行。
决定系数:r2(coefficient of determination)是指以测定回归方程式的精度方法,在总变动中因回归线说明的变动所占有的距离,也叫回归线的奇与率。
○把两个因子间的相关关系以某种数学方程式表示,如果方程式存在全部data,则决定系数为1,回归方程式有用,决定系数接近0,则方程式无效。
○决定系数越接近1则精度越高,65%以上的相关系数回归线可以使用。
○决定系数越高对改善越有用。
相关关系:(correlation coefficient)●显示两个变量之间相关关系程度的统计值。
○相关系数大,关系就大。
最小平方法:(method of least squares)想把因子间的相关关系以方程式表示,让各data变动和最小而选定方程式的方法。
○假定两个变量Y和X之间有n个data,方程式可以表示为Y=a+bx1+e,这时想找到最佳关系式。
S=Σe2=Σ(Y-a-bx1)2上决定误差e的平方之和最小化选定a和b。
管理图:(control chart)●管理图按sampling计划收集一定期间的data,为了掌握工程是否在管理状态而使用。
可以随时分析,有很多优点。
○分为连续型和离散型管理图。
○连续型管理图对测定data不敏感,有工程stop,判断error少,用于事后管理。
○离散型管理图对测定data敏感,没有工程stop,判断error多,用于事前管理。
○不能说工程在管理状态就只生产良品。
○统计性品质问题有两种:平均值移动问题和散布问题。
