2017中考数学海淀二模(1)

合集下载

2017年中考数学真题试题与答案(word版)

XX★ 启用前2017 年中考题数学试卷一、选择题（本大题共 12 小题，每小题 3 分，共 36 分．在每小题给出的四个选项中，只有一个是符合题目要求的，把正确答案的标号填在答题卡内相应的位置上）1、计算2( 1) 的结果是（）1B、2C、1D、 22、若∠α的余角是30°，则 cosα的值是（）A 、213C、2D、3A 、B 、23223、下列运算正确的是（）A 、2a a 1 B、a a2a2C、a a a2 D 、( a)2a24、下列图形是轴对称图形，又是中心对称图形的有（）A、4 个B、3 个5、如图，在平行四边形∠1=（）C、2 个D、1 个ABCD 中，∠ B=80 °， AE平分∠BAD交 BC于点E， CF∥ AE交 AE于点F，则A、 40°B、 50°C、 60°D、80°6、已知二次函数y ax2的图象开口向上，则直线y ax 1 经过的象限是（）A 、第一、二、三象限 B、第二、三、四象限7、如图，你能看出这个倒立的水杯的俯视图是（C、第一、二、四象限）D、第一、三、四象限A B C D8、如图，是我市 5 月份某一周的最高气温统计图，则这组数据（最高气温）的众数与中位数分别是（）A 、 28℃， 29℃B 、 28℃， 29.5℃C、 28℃， 30℃D 、 29℃， 29℃9、已知拋物线 y1 x2 2，当 1 x 5 时， y 的最大值是（）2 35 7 A 、 2C 、B 、3D 、3 310、小英家的圆形镜子被打碎了，她拿了如图（网格中的每个小正方形边长为 1）的一块碎片到玻璃店，配制成形状、大小与原来一致的镜面，则这个镜面的半径是（）A 、 2B 、 5C 、22D 、311、如图，是反比例函数yk 1x和 yk 2 x（ k 1k 2 ）在第一象限的图象，直线AB ∥ x轴，并分别交两条曲线于A 、B 两点，若S AOB2 ，则k 2k 1 的值是（）A 、 1B 、 2C 、 4D 、 812、一个容器装有1 升水，按照如下要求把水倒出：第1 次倒出1升水，第2 次倒出的水量是1升的1 ，223第 3 次倒出的水量是1 升的314，第4 次倒出的水量是14升的1 ，⋯按照这种倒水的方法，倒了5 10 次后容器内剩余的水量是（）A 、10 升11B 、1 升9C 、110升D 、111升二、填空题（本大题共6 小题，每小题3 分，共 18 分 .把答案填在答题卡中的横线上）13、 2011的相反数是 __________14、近似数 0.618 有__________个有效数字．15、分解因式：a 3= __________16、如图，是某校三个年级学生人数分布扇形统计图，则九年级学生人数所占扇形的圆心角的度数为 __________C 'D 17、如图，等边△ ABC 绕点 B 逆时针旋转30°时，点 C 转到 C ′的位置，且 BC ′与 AC 交于点 D ，则CD的值为 __________16 题图17 题图18 题图18、如图， AB 是半圆 O 的直径，以 0A 为直径的半圆O ′与弦 AC 交于点 D ，O ′ E ∥ AC ，并交 OC 于点E ．则下列四个结论：①点 D 为 AC 的中点；② S O 'OE1S AOC ；③ AC 2AD；④四边形 O'DEO 是菱形．其中正确的结2论是 __________．（把所有正确的结论的序号都填上）三、解答题（本大题共 8 小题，满分共 66 分，解答过程写在答题卡上，解答应写出文字说明，证明过程或演算步骤） .19、计算： (1) 1(5) 034 ．220、假日，小强在广场放风筝．如图，小强为了计算风筝离地面的高度，他测得风筝的仰角为 60°，已知风筝线 BC 的长为 10 米，小强的身高 AB 为 1.55 米，请你帮小强画出测量示意图，并计算出风筝离地面的高度．（结果精确到 1 米，参考数据2 ≈ 1.41 ， 3≈ 1.73 ）21、如图， △ OAB 的底边经过⊙ O 上的点 C ，且 OA=OB ，CA=CB ，⊙O 与 OA 、OB 分别交于 D 、E 两点．（ 1）求证： AB 是⊙ O 的切线；（ 2）若 D 为 OA 的中点，阴影部分的面积为33，求⊙ O 的半径 r ．22、一个不透明的纸盒中装有大小相同的黑、白两种颜色的围棋，其中白色棋子 3 个（分别用白 A 、白 B 、白 C 表示），若从中任意摸出一个棋子，是白色棋子的概率为3 ．4（ 1）求纸盒中黑色棋子的个数；（ 2）第一次任意摸出一个棋子（不放回），第二次再摸出一个棋子，请用树状图或列表的方法，求两次摸到相同颜色棋子的概率．23、上个月某超市购进了两批相同品种的水果，第一批用了 2000 元，第二批用了 5500 元，第二批购进水果的重量是第一批的 2.5 倍，且进价比第一批每千克多 1 元．（ 1）求两批水果共购进了多少千克？（ 2）在这两批水果总重量正常损耗 10%，其余全部售完的情况下，如果这两批水果的售价相同，且总利润率不低于 26%，那么售价至少定为每千克多少元？利润（利润率 =100%）进价AG为边作一个正方形AEFG ，24、如图，点G 是正方形ABCD 对角线 CA 的延长线上任意一点，以线段线段 EB 和 GD 相交于点 H．（ 1）求证： EB=GD ；（ 2）判断 EB 与 GD 的位置关系，并说明理由；（ 3）若AB=2 ， AG=2，求EB的长．25、已知抛物线y ax22ax 3a ( a 0) 与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，点 D 为抛物线的顶点．（1）求 A 、 B 的坐标；（2）过点 D 作 DH 丄 y 轴于点 H，若 DH=HC ，求 a 的值和直线 CD 的解析式；（3）在第（ 2）小题的条件下，直线 CD 与 x 轴交于点 E，过线段 OB 的中点 N 作 NF 丄 x 轴，并交直线CD 于点 F，则直线 NF 上是否存在点 M ，使得点 M 到直线 CD 的距离等于点 M 到原点 O 的距离？若存在，求出点M 的坐标；若不存在，请说明理由．中考数学试题答案一、选择题题号123456789101112答案B A C C B D B A C B C D二、填空题13. 201114. 315.a(3 a)(3 a)°17.2318.①③④16. 144三、解答题19. 解：原式 =2-1-3+2 ，=0 ．故答案为： 0 ．20.解：∵一元二次方程 x2-4x+1=0 的两个实数根是 x1、 x2，∴ x1 +x 2=4 ， x1?x2=1 ，∴（ x1+x 2）2÷（）=4 2÷2=4 ÷421.解：在 Rt △ CEB 中，sin60 °=，∴CE=BC?sin60°=10×≈8.65m，∴CD=CE+ED=8.65+1.55=10.≈210m，答：风筝离地面的高度为 10m ．22.（ 1）证明：连 OC ，如图，∵ OA=OB ， CA=CB ，∴OC ⊥AB，∴AB 是⊙ O 的切线；（2）解：∵ D 为 OA 的中点， OD=OC=r ，∴ OA=2OC=2r ，∴∠ A=30°，∠ AOC=60°， AC=r，∴∠ AOB=120°， AB=2r，∴ S 阴影部分 =S △OAB -S 扇形ODE = ?OC?AB-=-，∴?r?2r- r2=-，∴ r=1 ，即⊙ O 的半径 r 为 1 ．23. 解：（ 1） 3÷-3=1 ．答：黑色棋子有 1 个；（ 2）共12 种情况，有 6 种情况两次摸到相同颜色棋子，所以概率为．24. 解：（ 1）设第一批购进水果x 千克，则第二批购进水果 2.5 千克，依据题意得：，解得 x=200 ，经检验 x=200 是原方程的解，∴x+2.5x=700 ，答：这两批水果功够进 700 千克；（ 2）设售价为每千克 a 元，则：，630a≥ 7500× 1.26，∴，∴a≥15，答：售价至少为每千克 15 元．25.（ 1 ）证明：在△ GAD 和△ EAB 中，∠ GAD=90° +∠ EAD ，∠ EAB=90° +∠ EAD ，∴∠ GAD= ∠ EAB ，又∵ AG=AE ， AB=AD ，∴△ GAD ≌△ EAB ，∴EB=GD ；（ 2） EB ⊥ GD ，理由如下：连接BD ，由（ 1 ）得：∠ ADG= ∠ ABE ，则在△ BDH 中，∠DHB=180° - （∠ HDB+ ∠ HBD ）=180°-90 °=90°，∴EB⊥GD ；（ 3）设BD与AC交于点O，∵ AB=AD=2在 Rt △ABD中， DB=，∴ EB=GD=．26. 解：（ 1）由y=0得， ax 2-2ax-3a=0，∵ a≠0，∴ x2 -2x-3=0，解得1=-1，x2=3，∴点 A 的坐标（ -1， 0），点 B 的坐标（ 3，0）；（2）由 y=ax 2 -2ax-3a ，令 x=0 ，得 y=-3a ，∴ C （ 0， -3a ），又∵ y=ax 2 -2ax-3a=a （ x-1 ）2-4a ，得 D （1 ， -4a ），∴ DH=1 ， CH=-4a- （ -3a ） =-a ，∴ -a=1 ，∴ a=-1 ，∴C（0， 3），D（1，4），设直线 CD 的解析式为y=kx+b ，把 C、 D 两点的坐标代入得，，解得，∴直线 CD 的解析式为y=x+3 ；（ 3）存在．由（ 2）得， E（-3，0），N（-，0）∴F（，），EN= ，作 MQ⊥CD 于 Q，设存在满足条件的点M（，m），则FM=-m ，EF==，MQ=OM=由题意得： Rt △ FQM ∽ Rt △ FNE ，∴=，整理得 4m 2+36m-63=0 ，∴m2+9m=，m 2+9m+=+（m+ ）2=m+ =±∴ m1=，m2=-，∴点 M 的坐标为M1（，），M2（，-）．”可见，一个人的心胸和眼光，决定了他志向的短浅或高远；一个清代“红顶商人”胡雪岩说：“做生意顶要紧的是眼光，看得到一省，就能做一省的生意；看得到天下，就能做天下的生意；看得到外国，就能做外国的生意。

2017年北京中考数学试卷及答案

（1）当的半径为2时，
①在点，，中，的关联点是；
②点P在直线上，若P为的关联点，求点P的横坐标的取值范围;
（2) 的圆心在x轴上,半径为2，直线与x轴、y轴分别交与点A,B.若线段AB上的所有点都是的关联点，直接写出圆心C的横坐标的取值范围.
13。如图，在△ABC中，M，N分别是AC,BC的中点，若，则。
14。如图，AB为的直径,C，D为上的点, 。若∠CAB=40°，则∠CAD=°.
15.如图，在平面直角坐标系xOy中,△AOB可以看成是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的，写出一种由△OCD得到△AOB的过程：.
（以上材料来源于《古证复原的原则》、《吴文俊与中国》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明: （+）.
易知， =，=.
可得：。
21.关于x的一元二次方程。
(1）求证：方程总有两个实数根；
（2）若方程有一个根小于1，求k的取值范围.
22。如图在四边形ABCD中,BD为一条射线，AD∥BC，AD=2BC，∠ABD=90°，E为AD的中点，
D。2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多
9。小苏和小林在右图的跑道上进行4×50米折返跑。在整个过程中，
跑步者距起跑线的距离y(单位：m）与跑步时间t（单位：s）的
对应关系如下图所示。下列叙述正确的是
A。两个人起跑线同时出发，同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
2017年北京市高级中等学校招生考试
数学试卷
学校：姓名：准考证号：
考
生
须
知

2017各地中考及北京各区一、二模数学试题分类整理——平行四边形、特殊平行四边形的性质与判定

类型2：平四与特殊平四的性质与判定（1）选填 1、（广东中考10）如图，已知正方形ABCD ，点E 是BC 边的中点，DE 与AC 相交于点F ，连接BF ，下列结论：①；②；③；④,其中正确的是( )A .①③B .②③C .①④D .②④ 2、（朝阳一模8）如图，广场中心的菱形花坛ABCD 的周长是40米，∠A =60°，则A ，C 两点之间的距离为（）A .5米B .53米C .10米D .103米3、（通州一模8）如图，将一张矩形的纸对折，旋转90°后再对折，然后沿着右图中的虚线剪下，则剪下的纸片打开后的形状一定为（） A ．三角形 B ．菱形 C ．矩形 D ．正方形4、（海淀二模4）如图，ABCD 中，AD =5，AB =3，∠BAD 的平分线AE 交BC 于E 点，则EC 的长为（）A ．4B ．3C ．2D ．1 5、（平谷一模2）把一个边长为1的正方形如图所示放在数轴上，以正方形的对角线为半径画弧交数轴于点A ，则点A对应的数是（） A ．1B ．2C ．3D ．26、（河南中考9）我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD 的边AB 在x 轴上，AB 的中点是坐标原点O ，固定点A ，B ，把正方形沿箭头方向推，使点D 落在y 轴正半轴上点D ′处，则点C 的对应点C ′的坐标为（）A ．（√3，1）B ．（2，1）C ．（1，√3）D ．（2，√3）7、（青岛中考7）如图，平行四边形ABCD 的对角线AC与BD 相交于点O ，AE ⊥BC ，垂足为E ，3=AB ，AC ＝2，BD ＝4，则AE 的长为（） A ．23 B ．23C ．721 D ．7212ABF ADF S S =△△4CDF CBF S S =△△2ADF CEF S S =△△2ADF CDF S S =△△A -13210B E CA D8、（德州中考11）如图放置的两个正方形，大正方形ABCD 边长为a ，小正方形CEFG 边长为b （a ＞b ），M 在BC 边上，且BM =b ，连接AM ，MF ，MF 交CG 于点P ，将△ABM 绕点A 旋转至△ADN ，将△MEF 绕点F 旋转至△NGF ．给出以下五个结论：①∠AND =∠MPC ；②CP =；③△ABM≌△NGF ；④S 四边形AMFN =a 2+b 2；⑤A ，M ，P ，D 四点共圆．其中正确的个数是（）A ．2B ．3C ． 4D ．59、（苏州中考10）如图，在菱形CD AB 中，60∠A =，D 8A =，F 是AB 的中点．过点F 作F DE ⊥A ，垂足为E ．将F ∆AE 沿点A 到点B 的方向平移，得到F '''∆A E ．设P 、'P 分别是F E 、F ''E 的中点，当点'A 与点B 重合时，四边形CD 'PP 的面积为（）A ．283B ．243C .323D ．3238-10、（顺义二模15）如图，在正方形ABCD 和正方形AEFG 中，顶点E 在边AD 上，连接DG 交EF 于点H ，若FH ＝1，EH ＝2，则DG 的长为． 11、（西城二模13）如图，正方形ABCD ，AC 为对角线，点E 在AC 上，且AE =AB ，则∠BED 的度数为 °．12、（怀柔一模13）如图，在ABCD 中，ED =2，BC =5，∠ABC的平分线交AD 于点E ，则AB 的长为_______________． 13、（通州一模15）如图，Rt △ABC ≌Rt △DCB ，两斜边交于点O ，如果AC =3，那么OD 的长为_____________．14、（苏州中考18）如图，在矩形CD AB 中，将C ∠AB 绕点A 按逆时针方向旋转一定角度后，C B 的对应边C ''B 交CD 边于点G ．连接'BB 、CC '，若D 7A =，CG 4=，G ''AB =B ，则CC '='BB _______________（结果保留根号）．2b b a-E DCB AOABCDH GF EDCB A D GC B AFEM NP15、（北京中考20）数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证. （以上材料源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》）请根据上图完成这个推论的证明过程．证明：()ADC ANF FGC NFGD S S S S ∆∆∆=-+矩形，ABC EBMF S S ∆=-矩形（____________+____________）．易知，ADC ABC S S ∆∆=，_____________=______________，______________=_____________．可得NFGD EBMF S S =矩形矩形．（2）解答题（基础、中等） 16、（顺义一模19）如图，□ABCD 中，BE ⊥CD 于E ，CE =DE ．求证：∠A =∠ABD ．17、（通州一模19）如图，在矩形ABCD 中，连接对角线AC ，BD ，延长BC 至点E ，使BC =CE ，连接DE . 求证：DE =AC .18、（燕山一模19）在△ABC 中, AD =BF ,点D ,E ,F 分别是AC ,BC ,BA 延长线上的点,四边形ADEF 为平行四边形. 求证: AB =ACAB C D EEDBA C FE DAB C19、（杭州中考21）如图，在正方形ABCD 中，点G 在对角线BD 上（不与点B ，D 重合），GE ⊥DC 于点E ，GF ⊥BC 于点F ，连结AG 。

2017北京中考数学一模27汇总

l2017中考一模27汇编27（西城）．在平面直角坐标系xOy 中，二次函数y =mx 2 -(2m + 1)x + m -5的图象与x 轴有两个公共点.（1）求m 的取值范围；（2）若m 取满足条件的最小的整数， ①写出这个二次函数的解析式；②当n ≤ x ≤ 1时，函数值y 的取值范围是-6 ≤ y ≤ 4-n ，求n 的值；③将此二次函数平移，使平移后的图象经过原点O .设平移后的图象对应的函数表达式为y =a (x -h )2 + k ，当x < 2时，y 随x 的增大而减小，求k 的取值范围.27(房山). 在平面直角坐标系xOy 中，直线32-=x y 与y 轴交于点A ，点A 与点B 关于x 轴对称，过点B 作y 轴的垂线l ，直线l 与直线32-=x y 交于点C. （1）求点C 的坐标；（2）如果抛物线n nx nx y 542+-= (n ＞0)与线段BC 有唯一公共点，求n 的取值范围．27（顺义）．如图，已知抛物线28(0)y ax bx a =++≠与x 轴交于A （-2，0），B 两点，与y 轴交于C 点，tan ∠ABC =2．（1）求抛物线的表达式及其顶点D 的坐标；（2）过点A 、B 作x 轴的垂线，交直线CD 于点E 、F ，将抛物线沿其对称轴向上平移m 个单位，使抛物线与线段EF （含线段端点）只有1个公共点．求m 的取值范围．27（平谷）．直线33y x =-+与x 轴，y 轴分别交于A ，B 两点，点A 关于直线1x =-的对称点为点C ．（1）求点C 的坐标；（2）若抛物线()230y mx nx m m =+-≠经过A ，B ，C 三点，求该抛物线的表达式；（3）若抛物线()230y ax bx a =++≠ 经过A ，B 两点，且顶点在第二象限，抛物线与线段AC 有两个公共点，求a 的取值范围．27（通州）．在平面直角坐标系xOy 中，抛物线2222+-+-=m m mx x y 的顶点为D.线段AB 的两个端点分别为A （-3，m ），B （1，m ）. （1）求点D 的坐标（用含m 的代数式表示）；（2）若该抛物线经过点B （1，m ），求m 的值；（3）若线段AB 与该抛物线只有一个公共点，结合函数的图象，求m 的取值范围.27（海淀）．平面直角坐标系xOy 中，抛物线2222y mx m x =-+交y 轴于A 点，交直线x =4于B 点．（1）抛物线的对称轴为x = （用含m 的代数式表示）；（2）若AB ∥x 轴，求抛物线的表达式；（3）记抛物线在A ，B 之间的部分为图象G （包含A ，B 两点），若对于图象G 上任意一点P （P x ，P y ），2P y ≤，求m 的取值范围．27（东城）．二次函数2(2)2(2)5y m x m x m =+-+-+，其中20m +>．（1）求该二次函数的对称轴方程；（2）过动点C (0,n )作直线l ⊥y 轴.① 当直线l 与抛物线只有一个公共点时, 求n 与m 的函数关系；② 若抛物线与x 轴有两个交点，将抛物线在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象. 当n =7时，直线l 与新的图象恰好有三个公共点，求此时m 的值；（3）若对于每一个给定的x 的值，它所对应的函数值都不小于1，求m 的取值范围．27（丰台）．在平面直角坐标系xOy 中，抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ，B 两点．（1）求抛物线的对称轴；（2）如果点A 的坐标是（-1，-2），求点B 的坐标；（3）抛物线的对称轴交直线AB 于点C ，如果直线AB 与y 轴交点的纵坐标为-1，且抛物线顶点D 到点C 的距离大于2，求m 的取值范围．27（门头沟）. 在平面直角坐标系xOy 中，抛物线()()13y a x x =+-与x 轴交于A ,B 两点，点A 在点B 的左侧，抛物线的顶点为P ,规定：抛物线与x 轴围成的封闭区域称为“G 区域”（不包含边界）.（1）如果该抛物线经过（1, 3），求a 的值，并指出此时“G 区域”有______个整数点；（整数点就是横纵坐标均为整数的点）（2）求抛物线()()13y a x x =+-的顶点P 的坐标（用含a 的代数式表示）；（3）在（2）的条件下，如果G 区域中仅有4个整数点时，直接写出a 的取值范围.27（石景山）．在平面直角坐标系xOy 中，抛物线2443(0)y ax ax a a =-+-≠的顶点为A ．（1）求顶点A 的坐标；（2）过点(0,5)且平行于x 轴的直线l ，与抛物线2443(0)y ax ax a a =-+-≠交于B ，C 两点．①当2a =时，求线段BC 的长；②当线段BC 的长不小于6时，直接写出a 的取值范围．。

2017海淀初中数学二模答案(终稿)(1)

海淀九年级第二学期期末练习数学答案2017．6一、选择题（本题共30分，每小题3分）二、填空题（本题共18分，每小题3分） 11．2x ≠12．答案不唯一，例如（0，0）13．1 14．答案不唯一，在10.89.6t -≤≤-范围内即可15．216．乙；乙的平均成绩更高，成绩更稳定．三、解答题（本题共72分，第17~26题，每小题5分，第27题7分，第28题7分，第29题8分） 17．原式 =23--------------------------------------------------------------------------4分 =5 --------------------------------------------------------------------------5分18．解：原不等式组为()3221213x x x x +-≥+>-⎧⎪⎨⎪⎩， ①． ②由不等式①，得362x x +-≥， ----------------------------------------------------------------- 1分解得2x ≥； -----------------------------------------------------------------2分由不等式①，得1233x x +>-，------------------------------------------------------------------ 3分解得4x <；-------------------------------------------------------------------4分∴ 原不等式组的解集是24x ≤<．--------------------------------------------------------------- 5分19．连接AC ，则△ABC ≌ △ADC ．----------------------------1分证明如下：在△ABC 与△ADC 中，AB AD AC AC CB CD ===⎧⎪⎨⎪⎩，，，----------------------------4分 ∴△ABC ≌ △ADC ．----------------------------5分 20．解：∵关于x 的方程412m xx-=的根是2，∴4124m -=．------------------------------------------------------------------------------1分∴4m =．------------------------------------------------------------------------------2分∴()2428m m --+DCBA()244248=--⨯+ ------------------------------------------------------------------------------ 4分0=．-------------------------------------------------------------------------------- 5分21．解：（1）∵直线3l y mx =-：过点A （2，0），∴023m =-． ------------------------------------------------------------------------------ 1分 ∴32m =． ------------------------------------------------------------------------------ 2分 ∴直线l 的表达式为332y x =-．-----------------------------------------------------3分（2）n =32-或92．------------------------------------------------------------------------- 5分22．（1）C ； ---------------------------------------------------------------------------------------------- 2分（2）① B ； ---------------------------------------------------------------------------------------------- 4分 ② 100． ---------------------------------------------------------------------------------------------- 5分 23．（1）证明：∵EF 垂直平分AC ，∴F A =FC ，EA =EC ，----------------------------------------------------------------1分 ∵ AF ∥BC ， ∴∠1=∠2． ∵AE =CE ， ∴∠2=∠3． ∴ ∠1=∠3． ∵EF ⊥AC ，∴∠ADF =∠ADE =90°．∵ ∠1+∠4=90°，∠3+∠5=90°． ∴∠4=∠5．∴ AF =AE ．----------------------------------------------------------------2分 ∴AF =FC =CE =EA ．∴四边形AECF 是菱形．----------------------------------------------------------------3分（2）解：∵∠BAC =∠ADF =90°， ∴AB ∥FE ． ∵AF ∥BE ， ∴四边形ABEF 为平行四边形． ∵AB =10，∴FE =AB =10．-----------------------------------------------------------------------------------4分 ∵∠ACB =30°，∴tan ABAC ACB==∠∴12AECF S AC FE ⋅==菱形----------------------------------------------------------5分54321F E DCB A24．（1）北京市2016年研究生、普通高校本专科学生、成人本专科学生招生人数和在校生人数统计表（单位：万人）北京市2016年研究生、普通高校本专科学生、成人本专科学生招生人数和在校生人数统计图（单位：万人）---------------------------------- 2分（2）35.1；-------------------------------------------------------------------------------------------------- 3分（3）答案不唯一，预估理由与预估结果相符即可．--------------------- 5分25．（1）证明：∵D 为 AC的中点，∴∠CBA =2∠CBE ．------------------------------------ 1分 ∵AB 是⊙O 的直径，∴∠ACB =90°，∴∠1+∠CBA =90°． ∴∠1+2∠CBE =90°． ∵AP 是⊙O 的切线，∴∠P AB =∠1+∠P AC =90°．----------------------------- 2分∴∠P AC =2∠CBE ．--------------------------------------3分（2）思路：①连接AD ，由D 是 AC的中点，∠2=∠CBE ，由∠ACB =∠P AB =90°，得∠P =∠3=∠4，故AP =AE ； ②由AB 是⊙O 的直径，可得∠ADB =90°；由AP =AE ，得PE =2PD =2m ，∠5=12∠P AC =∠CBE =α-------- 4分③在Rt △P AD 中，由PD =m ，∠5=α，可求P A 的长； ④在Rt △P AB 中，由P A 的长和∠2=α，可求BP 的长；由BE PB PE =-可求BE 的长；⑤在Rt △BCE 中，由BE 的长和CBE α∠=，可求CE 的长．------------------- 5分A26．（1）答案不唯一，例如6y x=，28y x =-+，2611y x x =-+等；-------------------------------2分（2）答案不唯一，符合题意即可；-----------------------------------------------------------------4分（3）所写的性质与图象相符即可．----------------------------------------------------------------- 5分 27．（1）解：∵抛物线()222244y x mx m x m =-+-=--，其对称轴为1x =，∴1m =．∴该抛物线的表达式为223y x x =--．------------------------------------------------- 2分（2）解：当0y =时，2230x x --=，解得11x =-，23x =，∴抛物线与x 轴的交点为A （1-，0），B （3，0）． --------------------------------- 3分 ∴4AB =．当0x =时，3y =-，∴抛物线与y 轴的交点为C （0，3-）． ------------------------------------------- 4分 ∵12CD AB =， ∴CD =2．∵CD ∥x 轴，点D 在点C 的左侧，∴点D 的坐标为（2-，3-）． --------------------------------------------------5分（3）11t -≤≤．------------------------------------------------------------------------------------ 7分28．（1）证明：∵AB =AC ，AD 为BC 边上的高，∠BAD =20°， ∴∠BAC =2∠BAD =40°． --------------------------------------1分 ∵CF ⊥AB ， ∴∠AFC =90°． ∵E 为AC 中点， ∴EF =EA =12AC ．∴∠AFE =∠BAC =40°． ----------------------------------------2分（2）①画出一种即可． ----------------------------------------------------------------------------------3分MPN ECDB AFEAPN ECB A②证明：想法1：连接DE．∵AB=AC，AD为BC边上的高，∴D为BC中点．∵E为AC中点，∴ED∥AB，∴∠1=∠APE．--------------------------------- 4分∵∠ADC=90°，E为AC中点，∴12AE DE CE AC===．同理可证12AE NE CE AC===．∴AE=NE=CE=DE．∴A，N，D，C在以点E为圆心，AC为直径的圆上．-----5分∴∠1=2∠MAD．------------------------------------------ 6分∴∠APE=2∠MAD．------------------------------------------- 7分想法2：设∠MAD=α，∠DAC=β，∵CN⊥AM，∴∠ANC=90°．∵E为AC中点，∴12AE NE AC==．∴∠ANE=∠NAC=∠MAD+∠DAC=α+β．--------------------- 4分∴∠NEC=∠ANE+∠NAC=2α+2β．------------------------ 5分∵AB=AC，AD⊥BC，∴∠BAC=2∠DAC=2β．∴∠APE=∠PEC-∠BAC=2α．--------------------------------- 6分∴∠APE=2∠MAD．--------------------------------------------- 7分想法3：在NE上取点Q，使∠NAQ=2∠MAD，连接AQ，∴∠1=∠2．∵AB=AC，AD⊥BC，∴∠BAD=∠CAD．∴∠BAD-∠1=∠CAD-∠2，即∠3=∠4．----------------------------------------- 4分∴∠3+∠NAQ=∠4+∠NAQ，即∠P AQ=∠EAN．∵CN⊥AM，ED C BAPMN4321QNMPABCDE∴∠ANC =90°． ∵E 为AC 中点， ∴12AE NE AC ==． ∴∠ANE =∠EAN ．---------------------------------------------------------------- 5分 ∴∠P AQ =∠ANE ． ∵∠AQP =∠AQP ，∴△P AQ ∽△ANQ ．---------------------------------------------------------------- 6分 ∴∠APE =∠NAQ =2∠MAD ．-------------------------------------------------------- 7分29．（1）①R ，S ；----------------------------------------------------------------------------------------------- 2分 ②（4-，0）或（4，0）；------------------------------------------------------------------------ 4分（2）①由题意，直线3y x =-与x 轴交于C （3，0），与y 轴交于D （0，3-）．点M 在线段CD 上，设其坐标为（x ，y ），则有：0x ≥，0y ≤，且3y x =-．点M 到x 轴的距离为y ，点M 到y 轴的距离为x ，则3x y x y +=-=．∴点M 的同族点N 满足横纵坐标的绝对值之和为3．即点N 在右图中所示的正方形CDEF 上． ∵点E 的坐标为（3-，0），点N 在直线x n =上，∴33n -≤≤．--------------------------------------------------------------------------------------- 6分 ②m ≤1-或m ≥1．------------------------------------------------------------------------------------ 8分x。

(完整版)2017年北京市中考数学试题及答案

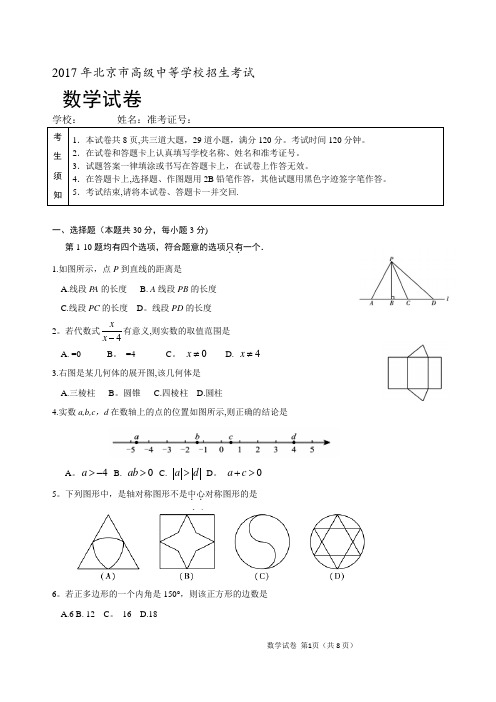
2017年北京市高级中等学校招生考试数学试题一、选择题（本题共30分，每小题3分）1.如图所示，点P 到直线l 的距离是（）A ．线段PA 的长度B ．线段PB 的长度C ．线段PC 的长度D ．线段PD 的长度 2.若代数式4xx -有意义，则实数x 的取值范围是（） A ．0x = B ．4x = C ．0x ≠ D ．4x ≠ 3. 右图是某个几何题的展开图，该几何体是（）A ．三棱柱B ．圆锥C ．四棱柱D ．圆柱4. 实数,,,a b c d 在数轴上的对应点的位置如图所示，则正确的结论是（）A ．4a >-B ．0bd > C. a b > D ．0b c +> 5.下列图形中，是轴对称图形但不是中心对称图形的是（）A ．B ． C. D ．6.若正多边形的一个内角是150°，则该正多边形的边数是（） A ． 6 B ． 12 C. 16 D ．187. 如果2210a a +-=，那么代数式242a a a a ⎛⎫- ⎪-⎝⎭g 的值是（）A ． -3B ． -1 C. 1 D ．38.下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况. 2011-2016年我国与东南亚地区和东欧地区的贸易额统计图（以上数据摘自《“一带一路”贸易合作大数据报告（2017）》）根据统计图提供的信息，下列推理不合理的是（）A．与2015年相比，2016年我国与东欧地区的贸易额有所增长B．2011-2016年，我国与东南亚地区的贸易额逐年增长C. 2011-2016年，我国与东南亚地区的贸易额的平均值超过4200亿美元D．2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多9.小苏和小林在右图所示的跑道上进行4×50米折返跑.在整个过程中，跑步者距起跑线的距离y（单位：m）与跑步时间t（单位：s）的对应关系如下图所示.下列叙述正确的是（）A ．两人从起跑线同时出发，同时到达终点B ．小苏跑全程的平均速度大于小林跑全程的平均速度 C. 小苏前15s 跑过的路程大于小林前15s 跑过的路程 D ．小林在跑最后100m 的过程中，与小苏相遇2次10. 下图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.下面有三个推断：① 当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616； ② 随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；③ 若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620. 其中合理的是（）A ．①B ．② C. ①② D ．①③二、填空题（本题共18分，每题3分）11. 写出一个比3大且比4小的无理数：______________．12. 某活动小组购买了4个篮球和5个足球，一共花费了435元，其中篮球的单价比足球的单价多3元，求篮球的单价和足球的单价.设篮球的单价为x 元，足球的单价为y 元，依题意，可列方程组为____________． 13.如图，在ABC ∆中，M N 、分别为,AC BC 的中点.若1CMN S ∆=，则ABNM S =四边形．14.如图，AB 为O e 的直径，C D 、为O e 上的点，AD CD =.若040CAB ∠=，则CAD ∠= ．15.如图，在平面直角坐标系xOy 中，AOB ∆可以看作是OCD ∆经过若干次图形的变化（平移、轴对称、旋转）得到的，写出一中由OCD ∆得到AOB ∆的过程：．16.下图是“作已知直角三角形的外接圆”的尺规作图过程已知：0,90Rt ABC C ∆∠=，求作Rt ABC ∆的外接圆.作法：如图．（1）分别以点A 和点B 为圆心，大于12AB 的长为半径作弧，两弧相交于,P Q 两点；（2）作直线PQ ，交AB 于点O ；（3）以O 为圆心，OA 为半径作O e .O e 即为所求作的圆.请回答：该尺规作图的依据是．三、解答题（本题共72分，第17题-26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、证明过程或演算步骤.17.计算：(4cos3012+--.18. 解不等式组：()21571023x x x x ⎧+>-⎪⎨+>⎪⎩19.如图，在ABC ∆中，0,36AB AC A =∠=，BD 平分ABC ∠交AC 于点D . 求证：AD BC =.20. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证.（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》）请根据上图完成这个推论的证明过程．证明：()ADC ANF FGC NFGD S S S S ∆∆∆=-+矩形，ABC EBMF S S ∆=-矩形（____________+____________）．易知，ADC ABC S S ∆∆=，_____________=______________，______________=_____________．可得NFGD EBMF S S =矩形矩形．21.关于x 的一元二次方程()23220x k x k -+++=. （1）求证：方程总有两个实数根；（2）若方程有一根小于1，求k 的取值范围.22. 如图，在四边形ABCD 中，BD 为一条对角线，0//,2,90AD BC AD BC ABD =∠=，E 为AD 的中点，连接BE .（1）求证：四边形BCDE 为菱形；（2）连接AC ，若AC 平分,1BAD BC ∠=，求AC 的长. 23. 如图，在平面直角坐标系xOy 中，函数()0ky x x=>的图象与直线2y x =-交于点()3,A m . （1）求k m 、的值；（2）已知点()(),0P n n n >，过点P 作平行于x 轴的直线，交直线2y x =-于点M ，过点P 作平行于y 轴的直线，交函数()0ky x x=>的图象于点N . ①当1n =时，判断线段PM 与PN 的数量关系，并说明理由； ②若PN PM ≥，结合函数的图象，直接写出n 的取值范围.24.如图，AB 是O e 的一条弦，E 是AB 的中点，过点E 作EC OA ⊥于点C ，过点B 作O e 的切线交CE 的延长线于点D . （1）求证：DB DE =；（2）若12,5AB BD ==，求O e 的半径.25.某工厂甲、乙两个部门各有员工400人，为了解这两个部门员工的生产技能情况，进行了抽样调查，过程如下，请补充完整. 收集数据从甲、乙两个部门各随机抽取20名员工，进行了生产技能测试，测试成绩（百分制）如下：甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77 乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40 整理、描述数据按如下分数段整理、描述这两组样本数据：（说明：成绩80分及以上为生产技能优秀，70--79分为生产技能良好，60--69分为生产技能合格，60分以下为生产技能不合格）分析数据两组样本数据的平均数、中位数、众数如下表所示：得出结论：a .估计乙部门生产技能优秀的员工人数为____________；b .可以推断出_____________部门员工的生产技能水平较高，理由为_____________.（至少从两个不同的角度说明推断的合理性）26.如图，P 是AB 所对弦AB 上一动点，过点P 作PM AB ⊥交AB 于点M ，连接MB ，过点P 作PN MB ⊥于点N .已知6AB cm =，设A P 、两点间的距离为xcm ，P N 、两点间的距离为ycm .（当点P 与点A 或点B 重合时，y 的值为0）小东根据学习函数的经验，对函数y 随自变量x 的变化而变化的规律进行了探究．下面是小东的探究过程，请补充完整：（1）通过取点、画图、测量，得到了x 与y 的几组值，如下表：（说明：补全表格时相关数值保留一位小数）（2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象.（3）结合画出的函数图象，解决问题：当PAN ∆为等腰三角形时，AP 的长度约为____________cm . 27.在平面直角坐标系xOy 中，抛物线243y x x =-+与x 轴交于点A B 、（点A 在点B 的左侧），与y 轴交于点C .（1）求直线BC 的表达式；（2）垂直于y 轴的直线l 与抛物线交于点()()1122,,,P x y Q x y ，与直线BC 交于点()33,N x y ，若123x x x <<，结合函数的图象，求123x x x ++的取值范围.28.在等腰直角ABC ∆中，090ACB ∠=，P 是线段BC 上一动点（与点B C 、不重合），连接AP ，延长BC 至点Q ，使得CQ CP =，过点Q 作QH AP ⊥于点H ，交AB 于点M . （1）若PAC α∠=，求AMQ ∠的大小（用含α的式子表示）. （2）用等式表示线段MB 与PQ 之间的数量关系，并证明.29．在平面直角坐标系xOy 中的点P 和图形M ，给出如下的定义：若在图形M 上存在一点Q ，使得P Q 、两点间的距离小于或等于1，则称P 为图形M 的关联点．（1）当O e 的半径为2时，①在点123115,0,,,,02222P P P ⎛⎛⎫⎛⎫⎪ ⎪ ⎝⎭⎝⎭⎝⎭中，O e 的关联点是_______________． ②点P 在直线y x =-上，若P 为O e 的关联点，求点P 的横坐标的取值范围．（2）C e 的圆心在x 轴上，半径为2，直线1y x =-+与x 轴、y 轴交于点A B 、．若线段AB 上的所有点都是C e 的关联点，直接写出圆心C 的横坐标的取值范围．。

中考数学二模 25题

1.（2017年嘉定宝山）已知：8=AB ，⊙O 经过点A 、B .以AB 为一边画平行四边形ABCD ，另一边CD 经过点O （如图8）.以点B 为圆心，BC 为半径画弧，交线段OC 于点E （点E 不与点O 、点C 重合）.（1）求证：OE OD =；（2）如果⊙O 的半径长为5（如图9），设x OD =，y BC =，求y 关于x 的函数解析式，并写出它的定义域；（3）如果⊙O 的半径长为5，联结AC ，当AC BE ⊥时，求OD 的长.2.（2017年普陀）如图10，半圆O 的直径AB ＝10，有一条定长为6的动弦CD 在弧AB 上滑动（点C 、点D 分别不与点A 、点B 重合），点E 、F 在AB 上，EC ⊥CD ，FD ⊥CD ．（1）求证：EO OF =；（2）联结OC ，如果△ECO 中有一个内角等于45 ，求线段EF 的长；（3）当动弦CD 在弧AB 上滑动时，设变量CE x =，四边形CDFE 面积为S ，周长为l ，问：S 与l 是否分别随着x 的变化而变化？试用所学的函数知识直接写出它们的函数解析式及函数定义域，以说明你的结论．图9 B O A 备用图 B OA 图8 E CB A O D 图103.（2017年崇明）如图，梯形ABCD 中，AB CD ∥，90ABC ∠=︒，6AB =，8BC =，tan 2D =，点E 是射线CD 上一动点（不与点C 重合），将BCE ∆沿着BE 进行翻折，点C 的对应点记为点F ．（1）如图1，当点F 落在梯形ABCD 的中位线MN 上时，求CE 的长；（2）如图2，当点E 在线段CD 上时，设CE x =，BFC EFCS y S ∆∆=，求y 与x 之间的函数关系式，并写出定义域；（3）如图3，联结AC ，线段BF 与射线CA 交于点G ，当CBG ∆是等腰三角形时，求CE 的长．ABCDEFM NEDCFABEDC FAB GD CAB（第25题图1）（第25题图2）（第25题图3）（第25题备用图）4.（2017年杨浦）已知：以O 为圆心的扇形AOB 中，∠AOB =90°，点C 为»AB 上一动点，射线AC 交射线OB 于点D ，过点D 作OD 的垂线交射线OC 于点E ，联结AE . （1）如图1，当四边形AODE 为矩形时，求∠ADO 的度数；（2）当扇形的半径长为5，且AC =6时，求线段DE 的长；（3）联结BC ，试问：在点C 运动的过程中，∠BCD 的大小是否确定？若是，请求出它的度数；若不是，请说明理由.5.（2017年奉贤）已知：如图9，线段AB =4，以AB 为直径作半圆O ，点C 为弧AB 的中点，点P 为直径AB 上一点，联结PC ，过点C 作CD //AB ，且CD =PC ，过点D 作DE//PC ，交射线PB 于点E ，PD 与CE 相交于点Q ．（1）若点P 与点A 重合，求BE 的长；（2）设PC = x ，y CEPD，当点P 在线段AO 上时，求y 与x 的函数关系式及定义域；（3）当点Q 在半圆O 上时，求PC 的长．图9ACPOBD E Q备用图AO BCA OBCD E（备用图） A O B CD E （图1）6.（2017年闵行）如图，在梯形ABCD 中，AD // BC ，∠B = 90°，AB = 4，BC = 9，AD = 6．点E 、F 分别在边AD 、BC 上，且BF = 2DE ，联结FE ．FE 的延长线与CD 的延长线相交于点P ．设DE = x ，PEy EF ．（1）求y 关于x 的函数解析式，并写出函数的定义域；（2）当以ED 为半径的⊙E 与以FB 为半径的⊙F 外切时，求x 的值；（3）当△AEF ∽△PED 时，求x 的值．7.（2017年长宁金山）如图，△ABC 的边AB 是⊙O 的直径，点C 在⊙O 上，已知AC =6 cm ，BC =8 cm ，点P 、Q 分别在边AB 、BC 上，且点P 不与点A 、B 重合，BQ =k ·AP （k >0），连接PC 、PQ ．（1）求⊙O 的半径长；（2）当k =2时，设AP =x ，△CPQ 的面积为y ，求y 关于x 的函数关系式，并写出定义域；（3）如果△CPQ ∽△ABC ，且∠ACB =∠CPQ ，求k 的值.第25题图A B CDE F P （第25题图）A B C D （备用图）EP 第25题图 C AB D8.（2017年虹口）如图，在△ABC 中，AB=AC =5，cos B =45，点P 为边BC 上一动点，过点P 作射线PE 交射线BA 于点D ，∠BPD=∠BAC ．以点P 为圆心，PC 长为半径作⊙P 交射线PD 于点E ，联结CE ，设BD=x ，CE=y ．（1）当⊙P 与AB 相切时，求⊙P 的半径；（2）当点D 在BA 的延长线上时，求y 关于x 的函数解析式，并写出定义域；（3）如果⊙O 与⊙P 相交于点C 、E ，且⊙O 经过点B ，当OP=54时，求AD 的长．9.（2017年浦东新区）如图所示，︒=∠45MON ，点P 是MON ∠内一点，过点P 作OM PA ⊥于点A 、ON PB ⊥于点B ，且22=PB ．取OP 的中点C ，联结AC 并延长，交OB 于点D ．（1）求证：OPB ADB ∠=∠；（2）设x PA =，y OD =，求y 关于x 的函数解析式；（3）分别联结AB 、BC ，当ABD △与CPB △相似时，求PA 的长．（第25题图）（备用图）10.（2016年崇明）如图，已知BC 是半圆O 的直径，8BC =，过线段BO 上一动点D ，作AD BC ⊥交半圆O 于点A ，联结AO ，过点B 作BH AO ⊥，垂足为点H ，BH 的延长线交半圆O 于点F ．（1）求证：AH BD =；（2）设BD x =，BE BF y ⋅=，求y 关于x 的函数关系式；（3）如图2，若联结FA 并延长交CB 的延长线于点G ，当FAE ∆与FBG ∆相似时，求BD 的长度．11.（2016年宝山嘉定）如图8，⊙O 与过点O 的⊙P 相交于AB ，D 是⊙P 的劣弧OB 上一点，射线OD 交⊙O 于点E ，交AB 的延长线于点C .如果AB =24，32tan =∠AOP . (1) 求⊙P 的半径长；(2) 当△AOC 为直角三角形时，求线段OD 的长； (3) 设线段OD 的长度为x ，线段CE 的长度为y ，求y 与x 之间的函数关系式及其定义域．（第25题图1）ABDOE HFC（第25题图2） CO D B G A F H E 图8_C _ E _B _O_P_A_ D12.（2016年长宁金山）如图, 已知在Rt △ABC 中, ∠ACB =90°, AB =5, 4sin 5A, P 是边BC 上的一点, PE ⊥AB , 垂足为E , 以点P 为圆心, PC 为半径的圆与射线PE 相交于点Q , 线段CQ 与边AB 交于点D . （1）求AD 的长;（2）设CP =x , △PCQ 的面积为y , 求y 关于x 的函数解析式, 并写出定义域;（3）过点C 作CF ⊥AB , 垂足为F , 联结PF 、QF , 如果△PQF 是以PF 为腰的等腰三角形, 求CP 的长.13.（2016年闸北）如图，在△ABC 中，AB=AC=6，BC=4，⊙B 与边AB 相交于点D ，与边BC 相交于点E ，设⊙B 的半径为x ．（1）当⊙B 与直线AC 相切时，求x 的值；（2）设DC 的长为y ，求y 关于x 的函数解析式，并写出定义域；（3）若以AC 为直径的⊙P 经过点E ，求⊙P 与⊙B 公共弦的长．BCAP EQDBCACB ADE （第25题图）14.（2016年闵行）如图，已知在△ABC 中，AB = AC = 6，AH ⊥BC ，垂足为点H ．点D 在边AB 上，且AD = 2，联结CD 交AH 于点E ．（1）如图1，如果AE = AD ，求AH 的长；（2）如图2，⊙A 是以点A 为圆心，AD 为半径的圆，交线段AH 于点F ．设点P 为边BC 上一点，如果以点P 为圆心，BP 为半径的圆与⊙A 外切，以点P 为圆心，CP 为半径的圆与⊙A 内切，求边BC 的长；（3）如图3，联结DF ．设DF = x ，△ABC 的面积为y ，求y 关于x 的函数解析式，并写出自变量x 的取值范围．15.（2016年松江）已知：如图1，在梯形ABCD 中，AD //BC ，∠BCD =90º， BC=11，CD=6，tan ∠ABC =2，点E 在AD 边上，且AE=3ED ，EF //AB 交BC 于点F ，点M 、N 分别在射线FE 和线段CD 上．（1）求线段CF 的长；（2）如图2，当点M 在线段FE 上，且AM ⊥MN ，设FM ·cos ∠EFC =x ，CN =y ，求y 关于x 的函数解析式，并写出它的定义域；（3）如果△AMN 为等腰直角三角形，求线段FM 的长．AB C H D （第25题图1) E AB C H D E（第25题图3) F P AB C H D E（第25题图2) F （第25题图1）AC B DE F（第25题图2）AC B DE FNM （备用图）A CBDE F16.（2016年黄埔）如图7，在Rt △ABC 中，90ACB ∠=︒，1AC =，BC =7，点D 是边CA 延长线上的一点，AE ⊥BD ，垂足为点E ，AE 的延长线交CA 的平行线BF 于点F ，联结CE 交AB 于点G ．（1）当点E 是BD 的中点时，求tan AFB ∠的值；（2）CE AF 的值是否随线段AD 长度的改变而变化，如果不变，求出CE AF 的值；如果变化，请说明理由；（3）当BGE ∆与BAF ∆相似时，求线段AF 的长．19.（2016年杨浦）已知：半圆O 的直径AB =6，点C 在半圆O 上，且tan 22ABC ∠=，点D 为AC 上一点，联结DC （如图）．（1）求BC 的长；（2）若射线DC 交射线AB 于点M ，且△MBC 与△MOC 相似，求CD 的长；（3）联结OD ，当OD//BC 时，作∠DOB 的平分线交线段DC 于点N ，求ON 的长．图7AB C DEF G （第25题备用图） A B O C A B O C D（第25题图）20.（2016年奉贤）已知：如图，在边长为5的菱形ABCD 中，cos A =35，点P 为边AB 上一点，以A 为圆心、AP 为半径的⊙A 与边AD 交于点E ，射线CE 与⊙A 另一个交点为点F ．（1）当点E 与点D 重合时，求EF 的长；（2）设AP =x ，CE =y ，求y 关于x 的函数关系式及定义域；（3）是否存在一点P ，使得 2EF PE =⋅，若存在，求AP 的长，若不存在，请说明理由．21.（2016年普陀）如图9，在Rt △ABC 中，90C ∠= ，14AC =，3tan 4A =，点D 是边AC 上的一点，8AD =．点E 是边AB 上一点，以点E 为圆心，EA 为半径作圆，经过点D ．点F 是边AC 上一动点（点F 不与A 、C 重合），作FG EF ⊥，交射线BC 于点G ．（1）用直尺圆规作出圆心E ，并求圆E 的半径长（保留作图痕迹）；（2）当点G 在边BC 上时，设AF x =，CG y =，求y 关于x 的函数解析式，并写出它的定义域；（3）联结EG ，当△EFG 与△FCG 相似时，推理判断以点G 为圆心、CG 为半径的圆G 与圆E 可能产生的各种位置关系．DCBA E F第25题图P DCBA备用图DCBA图9DCBA图9备用图22.(2016年浦东）如图，Rt △ABC 中，90ACB ∠= ，6BC =，点D 为斜边AB 的中点，点E 为边AC 上的一个动点．联结DE ，过点E 作DE 的垂线与边BC 交于点F ，以,DE EF 为邻边作矩形DEFG ．（1）如图1，当8AC =，点G 在边AB 上时，求DE 和EF 的长；（2）如图2，若12DE EF =，设AC x =，矩形DEFG 的面积为y ，求y 关于x 的函数解析式；（3）若23DE EF =，且点G 恰好落在Rt △ABC 的边上，求AC 的长．23.(2015年黄埔）如图8，Rt △ABC 中，90C ︒∠=，30A ︒∠=，BC =2，CD 是斜边AB 上的高，点E 为边AC 上一点（点E 不与点A 、C 重合），联结DE ，作CF ⊥DE ，CF 与边AB 、线段DE 分别交于点F 、G ．（1）求线段CD 、AD 的长；（2）设CE x =，DF y =，求y 关于x 的函数解析式，并写出它的定义域；（3）联结EF ，当△EFG 与△CDG 相似时，求线段CE 的长．GFED C BA 第25题图2A BC D EFG 第25题图1 ABCD备用图DCBA(备用图）图8GFDCB A E23.(2015年奉贤）已知：如图，线段AB =8，以A 为圆心，5为半径作圆A ，点C 在⊙A 上，过点C 作CD //AB 交⊙A 于点D （点D 在C 右侧），联结BC 、AD ．（1）若CD=6，求四边形ABCD 的面积；（2）设CD =x ，BC =y ，求y 与x 的函数关系式及自变量x 的取值范围；（3）设BC 的中点为M ，AD 的中点为N ，线段MN 交⊙A 于点E ，联结CE ，当CD 取何值时，CE //AD ．23.(2015年松江区）如图，已知在直角梯形ABCD 中，AD ∥BC ，∠ABC =90º，AB =4，AD=3，552sin =∠BCD ，点P 是对角线BD 上一动点，过点P 作PH ⊥CD ，垂足为H ．（1）求证：∠BCD =∠BDC ；（2）如图1，若以P 为圆心、PB 为半径的圆和以H 为圆心、HD 为半径的圆外切时，求DP 的长；（3）如图2，点E 在BC 延长线上，且满足DP =CE ，PE 交DC 于点F ，若△ADH 和△ECF 相似，求DP 的长．DCB （第25题图）AB（备用图）AABCHPD （第25题图1）ABCHPD EF（第25题图2）23.(2015年闵行区）如图，已知在梯形ABCD 中，AD // BC ，AB = DC = 5，AD = 4．M 、N 分别是边AD 、BC 上的任意一点，联结AN 、DN ．点E 、F 分别在线段AN 、DN 上，且ME // DN ，MF // AN ，联结EF ．（1）如图1，如果EF // BC ，求EF 的长；（2）如果四边形MENF 的面积是△ADN 的面积的38，求AM 的长；（3）如果BC = 10，试探索△ABN 、△AND 、△DNC 能否两两相似？如果能，求AN 的长；如果不能，请说明理由．23.(2015年嘉定）在Rt △ABC 中，︒=∠90C ，2=BC ，Rt △ABC 绕着点B 按顺时针方向旋转，使点C 落在斜边AB 上的点D ，设点A 旋转后与点E 重合，联结AE ，过点E 作直线EM 与射线CB 垂直，交点为M ．（1）若点M 与点B 重合如图10，求BAE ∠cot 的值；（2）若点M 在边BC 上如图11，设边长x AC =，y BM =，点M 与点B 不重合，求y 与x 的函数关系式，并写出自变量x 的取值范围；（3）若EBM BAE ∠=∠，求斜边AB 的长．A B C D M N E F（图1）A B C D M NE F （第25题图）A CB (M )ED 图10ACBMED图11。

中考中的费马点详解加练习

皮耶·德·费马（Pierre de Fermat）是一个17世纪的法国律师，也是一位业余数学家。

之所以称业余，是由于皮耶·德·费马具有律师的全职工作。

他的姓氏根据法文与英文实际发音也常译为“费尔玛”（注意“玛”字）。

费马最后定理在中国习惯称为费马大定理，西方数学界原名“最后”的意思是：其它猜想都证实了，这是最后一个。

著名的数学史学家贝尔（E. T. Bell）在20世纪初所撰写的著作中，称皮耶·德·费马为”业余数学家之王。

“贝尔深信，费马比皮耶·德·费马同时代的大多数专业数学家更有成就，然而皮耶·德·费马并未在其他方面另有成就，本人也渐渐退出人们的视野，考虑到17世纪是杰出数学家活跃的世纪，因而贝尔认为费马是17世纪数学家中最多产的明星。

费马点问题最早是由法国数学家皮埃尔·德·费马在一封写给意大利数学家埃万杰利斯塔·托里拆利（气压计的发明者）的信中提出的。

托里拆利最早解决了这个问题，而19世纪的数学家斯坦纳重新发现了这个问题，并系统地进行了推广，因此这个点也称为托里拆利点或斯坦纳点，相关的问题也被称作费马-托里拆利-斯坦纳问题。

这一问题的解决极大推动了联合数学的发展，在近代数学史上具有里程碑式的意义。

“费马点”是指位于三角形内且到三角形三个顶点距离之和最短的点。

若给定一个三角形△ABC的话，从这个三角形的费马点P到三角形的三个顶点A、B、C的距离之和比从其它点算起的都要小。

这个特殊点对于每个给定的三角形都只有一个。

1.若三角形3个内角均小于120°，那么3条距离连线正好三等分费马点所在的周角，即该点所对三角形三边的X角相等，均为120°。

所以三角形的费马点也称为三角形的等角中心。

2.若三角形有一内角大于等于120°，则此钝角的顶点就是距离和最小的点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6 5 4 3 2 1 –6 –5 –4 –3 –2 –1
O
–1 –2 –3 –4 –5 –6
1
2
3
4
5
6
x
普通高校本专科学生成人本专科学生
招生人数
17.2
在校生人数
研பைடு நூலகம்生
在科技方面，2016 年全年研究与试验发展（R&D）经费支出 1479.8 亿元，比 2015 年增长了 6.9%，全市研究与试验发展（R&D）活动人员 36.2 万人，比上年增长 1.1 万人． 2013 年， 2014 年， 2015 年全年研究与试验发展（R&D）经费支出分别为 1185.0 亿元， 1268.8 亿元，1384.0 亿元，分别比前一年度增长 11.4%，7.1%，9.1%．
（1）请用统计图或统计表将北京市2016年研究生、普通高校本专科学生、成人本专科学生的招生人数和在校生人数表示出来；
北京市 2016 年研究生、普通高校本专科学生、成人本专科学生招生人数和在校生人数统计图（单位：万人）
70 60 50 40 30 20 10 0 58.8
29.2 9.7 15.5 6.1
2
B． y 3 x 1 D． y
1 x
9．如图，在等边三角形三个顶点和中心处的每个“○”中各填有一个式子，若图中任意三个“○”中的式子之和均相等，则 a 的值为 A．3 C．1 B．2
3 a b 2a 2
D．0
10．利用量角器可以制作“锐角正弦值速查卡” ．制作方法如下：如图，设 OA=1，以 O 为圆心，分别以 0.05，0.1，0.15，0.2，„，0.9，0.95 长为半径作半圆，再以 OA 为直径作⊙M．利用“锐角正弦值速查卡”可 sin 60 0.87 ， sin 45 0.71 ．以读出相应锐角正弦的近似值．例如：下列角度中正弦值最接近 0.94 的是 A．70° B．50° C．40° D．30°
y
l A O B
2
x
频数/人 240 210 180 150 120 90 60 30 20
O
240 200 160
100 80 80 50 25 25
40 60
15
5
20
80 100 120 140 160 180 200 220 240 月均花费/元
23．如图，在△ABC 中，∠BAC=90°，线段 AC 的垂直平分线交 AC 于 D 点，交 BC 于 E 点，过点 A 作 BC 的平行线交直线 ED 于 F 点，连接 AE，CF．（1）求证：四边形 AECF 是菱形；（2）若 AB=10，∠ACB=30°，求菱形 AECF 的面积．
P D E A O C B
26．已知 y 是 x 的函数，该函数的图象经过 A（1，6），B（3，2）两点．（1）请写出一个符合要求的函数表达式；
（2）若该函数的图象还经过点 C（4，3），自变量 x 的取值范围是 x≥0 ，该函数无最小值． ①如图，在给定的坐标系 xOy 中，画出一个符合条件的函数的图象；．．
y P 3 2 1 –3 –2 –1 O –1 1 2 3 x Q
（1）已知点 A 的坐标为（ 3 ，1）， ①在点 R（0，4），S（2，2），T（2， 3 ）中，为点 A 的同族点的是； ②若点 B 在 x 轴上，且 A，B 两点为同族点，则点 B 的坐标为；
（2）直线 l： y x 3 ，与 x 轴交于点 C，与 y 轴交于点 D， ①M 为线段 CD 上一点，若在直线 x n 上存在点 N，使得 M， N 两点为同族点，求 n 的取值范围；
想法3：在NE上取点Q，使∠NAQ=2∠MAD，要证∠APE=2∠MAD，只需证 △NAQ∽△APQ．
P
29．在平面直角坐标系 xOy 中，对于 P，Q 两点给出如下定义：若点 P 到两坐标轴的距离之和等于点 Q 到两坐标轴的距离之和，则称 P， Q 两点为同族点．下图中的 P，Q 两点即为同族点．
（2）2015年北京市研究与试验发展（R&D）活动人员为_____ 万人；（3）根据材料中的信息，预估2017年北京市全年研究与试验发展（R&D）经费支出约亿元，你的预估理由是__________ ．
的中点，AC， 25．如图，AB 是⊙O 的直径，BC 为弦，D 为 AC BD 相交于 E 点，过点 A 作⊙O 的切线交 BD 的延长线于 P 点．（1）求证：∠PAC=2∠CBE；（2）若 PD=m，∠CBE=α，请写出求线段 CE 长的思路．
A
E F B D C
（2）若 M 为线段 BD 上的动点（点 M 与点 D 不重合），过点 C 作 CN⊥AM 于 N 点，射线 EN，AB 交于 P 点． ①依题意将图 2 补全； ②小宇通过观察、实验，提出猜想：在点 M 运动的过程中，始终有∠APE=2∠MAD．
P P
（2）若 M 为线段 BD 上的动点（点 M 与点 D 不重合），过点 C 作 CN⊥AM 于 N 点，射线 EN，AB 交于 P 点． ①依题意将图 2 补全； ②小宇通过观察、实验，提出猜想：在点 M 运动的过程中，始终有∠APE=2∠MAD．
1 （2）若 CD∥x 轴，点 D 在点 C 的左侧，CD AB ，求点 D 的坐标； 2
（3）在（2）的条件下，将抛物线在直线x=t右侧的部分沿直线x=t翻折后的图形记为G，若图形G与线段CD有公共点，请直接写出t的取值范围．
28．在锐角△ABC 中，AB=AC，AD 为 BC 边上的高，E 为 AC 中点．（1）如图 1，过点 C 作 CF⊥AB 于 F 点，连接 EF．若∠BAD=20°，求∠AFE 的度数；
80 100 90 70 110 60 110 100 1 A 80 120 70 50 120 130 60 0.9 50 0.8 40 130 140 0.7 140 40 30 150 0.6 150 30 0.5 M 20 160 0.4 160 20 0.3 10 170 0.2 10 170 0.1 0 180 0 180
0.9
1.5
4.1
2.0
7.0
若每向上攀登 1 km，所在位置的气温下降幅度基本一致，则向上攀登的海拔高度为 2.5 km 时，登山队所在位置的气温约为 ℃．
15．下图是测量玻璃管内径的示意图，点 D 正对“10mm”刻度线，点 A 正对“30mm”刻度线，DE∥AB．若量得 AB 的长为 6mm，则内径 DE 的长为 mm．
A D
F
B
E
C
在教育方面，全市共有 58 所普通高校和 81 个科研机构培养研究生，全年研究生招生 9.7 万人，在校研究生 29.2 万人．全市 91 所普通高校全年招收本专科学生 15.5 万人，在校生 58.8 万人．全市成人本专科招生 6.1 万人，在校生 17.2 万人．
（1）请用统计图或统计表将北京市2016年研究生、普通高校本专科学生、成人本专科学生的招生人数和在校生人数表示出来；
甲
乙
17．计算： 12
1 3 2 2 tan 60 ° ． 3
1
20．若关于 x 的方程
4 x

m 2x
1 的根是 2，求 m 4 2m 8 的值．
2
21．如图，在平面直角坐标系 xOy 中，过点 A（2，0）的直线 l： y mx 3 与 y 轴交于点 B．（1）求直线 l 的表达式； n （2）若点 C 是直线 l 与双曲线 y 的 x 一个公共点，AB=2AC，直接写出 n 的值．
B E
10 15 20 25 30
C
D
A
16．在一次飞镖比赛中，甲、乙两位选手各扔 10 次飞镖，下图记录了他们的比赛结果．你认为两人中技术更好的是理由是
1 2 3 4 5 6 7 8 9 10 9 8 7 6 5 4 3 2 1
，你的
．
1 2 3 4 5 6 7 8 9 10 9 8 7 6 5 4 3 2 1
y
6 5 4 3 2 1 –6 –5 –4 –3 –2 –1
O
–1 –2 –3 –4 –5 –6
1
2
3
4
5
6
x
（2）直线 l： y x 3 ，与 x 轴交于点 C，与 y 轴交于点 D， ②M 为直线 l 上的一个动点，若以（m，0）为圆心， 2 为半径的圆上存在点 N，使得 M，N 两点为同族点，直接写出 m y 的取值范围．
北京市 2016 年研究生、普通高校本专科学生、成人本专科学生招生人数和在校生人数统计表（单位：万人）人数类别项目招生人数在校生人数 9.7 29.2 研究生普通高校本专科学生 15.5 58.8 成人本专科学生 6.1 17.2
在教育方面，全市共有 58 所普通高校和 81 个科研机构培养研究生，全年研究生招生 9.7 万人，在校研究生 29.2 万人．全市 91 所普通高校全年招收本专科学生 15.5 万人，在校生 58.8 万人．全市成人本专科招生 6.1 万人，在校生 17.2 万人．
车 APP，如图， “ ” 为小白同学的位置， “★”为检索到的共享单车停放点．为
了到达距离最近的共享单车停放点，下列四个区域中，小白同学应该前往的是 A．F6 C．D5
5 D
B．E6 D．F7
6 7
★ ★
E
★
F
★
★
8．在下列函数中，其图象与 x 轴没有交点的是 A． y 2 x C． y x
y
8 6 A 4 2 B 2 4 6 8
C
O
-2 -4
x