聚类分析
合集下载
聚 类 分 析
阵 D0，列于表6.2.1。
表 6.2.1
D0
G1
G2
G3
G4
G5
G1 0
G2 G3
1 5 7
0
4
0
6
2
0
G4 10
9
5
3
0
G5
（2） D0 中最小元素是 D12 1 ，于是将 G1 和G2合并 成 G6 ，并利用（6.3.2）式计算 G6与其他类的距离，列于
表6.2.2
表6.2.2
D1
G6
样品（变量）第一次归类后形成一个新的类，再计算 新类与其他样品（变量）之间的距离（相似系数），按 最小距离（最大相似系数）再进行合并，直至所有的样 品（变量）合并为一类为止。接着将合并过程用谱系图 表示出来，表明样品（变量）之间的亲疏关系，并将所 有的样品（变量）合并成较少的几大类。
三、聚类分析的基本步骤
表6.2.4
D3
G6
G8
G6
0
G8
4
0
（5）最后将G6 和 G8 合并为 G9 ，这时所有五个样品聚
为一类，过程终止。
将上述聚类过程画成一张树形图（或称谱系图， dendrogram），如图6.2.1 所示。
G1 1
G6
G2 2
G3 6
G4 8
G7
G9
G5 11
G8
0 12 34
D
图6.2.1 最短距离法树形图
市场调查
聚类分析
一、聚类分析在市场调查中的应用：
（一）细分市场 （二）研究消费者行为 （三）市场选择 （四）简化数据
二、聚类分析的基本原理
聚类分析根据分类的对象不同，可以分为Q型聚类分 析和R型聚类分析 。Q型聚类是指对样品进行聚类，R型 聚类是指对变量进行聚类。
表 6.2.1
D0
G1
G2
G3
G4
G5
G1 0
G2 G3
1 5 7
0
4
0
6
2
0
G4 10
9
5
3
0
G5
（2） D0 中最小元素是 D12 1 ，于是将 G1 和G2合并 成 G6 ，并利用（6.3.2）式计算 G6与其他类的距离，列于
表6.2.2
表6.2.2
D1
G6
样品（变量）第一次归类后形成一个新的类，再计算 新类与其他样品（变量）之间的距离（相似系数），按 最小距离（最大相似系数）再进行合并，直至所有的样 品（变量）合并为一类为止。接着将合并过程用谱系图 表示出来，表明样品（变量）之间的亲疏关系，并将所 有的样品（变量）合并成较少的几大类。
三、聚类分析的基本步骤
表6.2.4
D3
G6
G8
G6
0
G8
4
0
（5）最后将G6 和 G8 合并为 G9 ，这时所有五个样品聚
为一类，过程终止。
将上述聚类过程画成一张树形图（或称谱系图， dendrogram），如图6.2.1 所示。
G1 1
G6
G2 2
G3 6
G4 8
G7
G9
G5 11
G8
0 12 34
D
图6.2.1 最短距离法树形图
市场调查
聚类分析
一、聚类分析在市场调查中的应用：
（一）细分市场 （二）研究消费者行为 （三）市场选择 （四）简化数据
二、聚类分析的基本原理
聚类分析根据分类的对象不同，可以分为Q型聚类分 析和R型聚类分析 。Q型聚类是指对样品进行聚类，R型 聚类是指对变量进行聚类。
第九章聚类分析
• 为定义个体间的距离应先将每个样本数据看成k维 空间的一个点，通常，点与点之间的距离越小，意 味着他们越“亲密”，越有可能聚成一类，点与点 之间的距离越大，意味着他们越“疏远”，越有可 能分别属于不同的类。
• 例：下表是同一批客户对经常光顾的五座商场在购物环境和
服务质量两方面的平均得分，现希望根据这批数据将五座商
7、如果参与聚类分析的变量存在数量级上的差异， 应在Transform Values框中的Standardize选项 中选择消除数量级差的方法。并指定处理是针对变 量的还是针对样本的。By variable表示针对变量， 适于 Q 型聚类分析；By case 表示针对样本，适 于R型聚类分析。
8、单击Statistics按钮指定输出哪些统计量
R型聚类：对变量进行聚类，使具有相似性的变量聚集在 一起，差异性大的变量分离开来，可在相似变量中选择 少数具有代表性的变量参与其他分析，实现减少变量个 数，达到变量降维的目的。
凝聚方式聚类：其过程是，首先，每个个体自成一类； 然后，按照某种方法度量所有个体间的亲疏程度，并将 其中最“亲密”的个体聚成一小类，形成n-1个类；接下 来，再次度量剩余个体和小类间的亲疏程度，并将当前 最亲密的个体或小类再聚到一类；重复上述过程，直到 所有个体聚成一个大类为止。可见，这种聚类方式对n个 个体通过n-1步可凝聚成一大类。
平方欧式距离（Squared Euclidean distance ） 切比雪夫（Chebychev）距离
max xi yi max( 7366 , 6864 )
Block距离
k
xi yi 73 66 68 64 i1
2、计数变量个体间距离的计算方式
卡方（Chi-Square measure）距离 Phi方（Phi-Square measure）距离
• 例：下表是同一批客户对经常光顾的五座商场在购物环境和
服务质量两方面的平均得分，现希望根据这批数据将五座商
7、如果参与聚类分析的变量存在数量级上的差异， 应在Transform Values框中的Standardize选项 中选择消除数量级差的方法。并指定处理是针对变 量的还是针对样本的。By variable表示针对变量， 适于 Q 型聚类分析；By case 表示针对样本，适 于R型聚类分析。
8、单击Statistics按钮指定输出哪些统计量
R型聚类：对变量进行聚类，使具有相似性的变量聚集在 一起，差异性大的变量分离开来，可在相似变量中选择 少数具有代表性的变量参与其他分析，实现减少变量个 数，达到变量降维的目的。
凝聚方式聚类：其过程是，首先，每个个体自成一类； 然后，按照某种方法度量所有个体间的亲疏程度，并将 其中最“亲密”的个体聚成一小类，形成n-1个类；接下 来，再次度量剩余个体和小类间的亲疏程度，并将当前 最亲密的个体或小类再聚到一类；重复上述过程，直到 所有个体聚成一个大类为止。可见，这种聚类方式对n个 个体通过n-1步可凝聚成一大类。
平方欧式距离（Squared Euclidean distance ） 切比雪夫（Chebychev）距离
max xi yi max( 7366 , 6864 )
Block距离
k
xi yi 73 66 68 64 i1
2、计数变量个体间距离的计算方式
卡方（Chi-Square measure）距离 Phi方（Phi-Square measure）距离
什么是聚类分析,它有哪些应用？
什么是聚类分析，它有哪些应用？
一、聚类分析的实现方式
聚类分析的实现方式有很多种，如下面几种：
1. 基于距离的聚类：
这种方法将数据点之间的距离作为相似性的度量，然后将距离最近的数据点聚在一起，并逐渐地将距离较远的数据点加入到不同的簇中。
2. 基于密度的聚类：
这种方法通过计算数据点的密度来确定簇边界，而不是使用距离来度量相似性。
将密度较高的数据点聚集在一起，而将密度较低的数据点单独作为一个簇。
3. 基于层次的聚类：
这种方法将数据点逐层进行聚合，每一层都是由多个子层组成的。
聚类过程一直持续到所有数据点都被分配到一个簇中，或者簇的数量达到预设的值。
二、聚类分析的应用领域
聚类分析作为一种重要的数据挖掘技术，在多个领域中都有着广泛的应用，下面介绍一些主要应用领域：
1. 市场细分：
聚类分析可以帮助企业将市场分割成不同的细分市场，然后根据每个细分市场的特点定制相应的市场策略。
2. 生物分类：
聚类分析在生物学领域中应用非常广泛，例如，可以用于分类分子或组分、成本分析以及微生物学等方面。
3. 网络流量分析：
聚类分析可以帮助网络管理员对网络流量进行分类，以便更好地了解网络中流动的数据类型，从而更好地优化网络性能。
4. 风险评估：
聚类分析可以用于对风险进行分类和评估，例如，可以将客户分类成高风险、中风险和低风险客户，以快速响应某些意外事件。
结论
聚类分析是一种非常有用的技术，可以用于许多不同的领域。
以上只是聚类分析的一些基本理解和应用，随着技术的不断发展，聚类分析在未来也将有着更广泛的应用。
聚类分析
C
E
A
F B
重心距离
D
4.中间距离法（Median clustering ）
如果类与类之间的距离既不采用两类之间最近的距离,也 不采用两类之间最远的距离,而是采用两者之间的距离, 则称为中间距离法.当两类 G p 和 Gq 合并成新类 Gr Gp Gq 时, Gr 与任一类 Gk 的距离如何决定呢? Gkq 、 G pq 为边作三角形，可设 Gkq Gkp ，按最短 以Gkp、 距离法核算类间距离；若 Gkq Gkp ，按最远距离法核 算类间距离；若 Gkq Gkp 取其中线，由初等几何知这 个中线的平方等于任一类 Gk 与 Gr 间的距离。计算公式 如下： 1 2 1 2 1 2 2 Gkr Gkp Gkq G pq 2 2 4
得到新矩阵
G6 G1 G 2 G 5 G 6 0 D1 G1 13.12 0 G 2 24.06 11.67 0 G 5 2.21 12.80 23.54 0
合并类6和类5，得到新类7
类7与剩余的1、2之间的距离分别为：
d(5,6)1=min(d51,d61)=min(12.80,13.12)=12.80 d(5,6)2=min(d52,d62)=min(23.54,24.06)=23.54
0 2.20 3.51
因此将3.4合并为一类，为类6，替代了3、4两类 类6与剩余的1、2、5之间的距离分别为：
d(3,4)1=min(d31,d41)=min(13.80,13.12)=13.12 d(3,4)2=min(d32,d42)=min(24.63,24.06)=24.06 d(3,4)5=min(d35,d45)=min(3.51,2.21)=2.21
聚类分析
聚类分析也是一种分类技术。
与多元分析的其他方法相比，该方法较为粗糙，理论上还不完善，但应用方面取得了很大成功。
与回归分析、判别分析一起被称为多元分析的三大方法。
聚类的目的。
根据已知数据，计算各观察个体或变量之间亲疏关系的统计量（距离或相关系数）。
根据某种准则（最短距离法、最长距离法、中间距离法、重心法），使同一类内的差别较小，而类与类之间的差别较大，最终将观察个体或变量分为若干类。
聚类分析又叫群分析、点群分析或者簇分析，是直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。
1、聚类分析聚类分析也称群分析、点群分析。
例如，我们可以根据各个银行网点的储蓄量、人力资源状况、营业面积、特色功能、网点级别、所处功能区域等因素情况，将网点分为几个等级，再比较各银行之间不同等级网点数量对比状况。
1、基本思想：我们所研究的样品（网点）或指标（变量）之间存在程度不同的相似性（亲疏关系——以样品间距离衡量）。
于是根据一批样品的多个观测指标，具体找出一些能够度量样品或指标之间相似程度的统计量，以这些统计量为划分类型的依据。
把一些相似程度较大的样品（或指标）聚合为一类，把另外一些彼此之间相似程度较大的样品（或指标）又聚合为另一类，直到把所有的样品（或指标）聚合完毕，这就是分类的基本思想。
在聚类分析中，通常我们将根据分类对象的不同分为Q型聚类分析和R型聚类分析两大类。
R型聚类分析是对变量进行分类处理，Q型聚类分析是对样本进行分类处理。
R型聚类分析的主要作用是：1、不但可以了解个别变量之间的关系的亲疏程度，而且可以了解各个变量组合之间的亲疏程度。
2、根据变量的分类结果以及它们之间的关系，可以选择主要变量进行回归分析或Q型聚类分析。
Q型聚类分析的优点是：1、可以综合利用多个变量的信息对样本进行分类；2、分类结果是直观的，聚类谱系图非常清楚地表现其数值分类结果；3、聚类分析所得到的结果比传统分类方法更细致、全面、合理。
聚类分析应用
聚类分析简介
▪ 聚类分析的算法选择
1.根据数据集的特点和聚类目的选择合适的聚类算法，例如对于大规模数据集可以采用高效的 划分聚类算法，对于形状复杂的簇可以采用密度聚类算法。 2.对于不同的聚类算法，需要了解它们的优缺点和适用场景，以便在实际应用中选择最合适的 算法。 3.聚类算法的选择需要考虑数据的维度、规模、分布等因素，以及聚类结果的解释性和可用性 。 以上是关于聚类分析简介的三个主题内容，希望能够帮助到您。
聚类分析应用
目录页
Contents Page
1. 聚类分析简介 2. 聚类分析方法 3. 数据预处理 4. 距离度量方法 5. 聚类质量评估 6. 常见聚类算法 7. 聚类应用案例 8. 总结与展望
聚类分析应用
聚类分析简介
聚类分析简介
▪ 聚类分析简介
1.聚类分析是一种无监督学习方法，用于将数据集中的对象根据相似性进行分组，使得同一组 （即簇）内的对象尽可能相似，而不同组的对象尽可能不同。 2.聚类分析可以应用于各种领域，如数据挖掘、模式识别、图像处理、生物信息学等，帮助研 究者发现数据中的内在结构和规律。 3.常见的聚类算法包括划分聚类、层次聚类、密度聚类、网格聚类等，不同的算法有着不同的 优缺点和适用场景。
▪ 共享最近邻聚类
1.共享最近邻聚类是一种基于数据点之间共享最近邻信息的聚 类方法，通过计算数据点之间的相似度，实现簇的划分。 2.共享最近邻聚类算法对噪声和异常点有较好的鲁棒性，可以 处理形状复杂的簇和高维数据，但计算复杂度较高。 3.通过改进相似度计算方式、引入近似算法或结合其他技术， 可以优化共享最近邻聚类的性能和可扩展性。
常见聚类算法
▪ 密度峰值聚类
1.密度峰值聚类是一种基于密度的聚类方法，通过寻找具有最 高局部密度的数据点作为聚类中心，实现簇的划分。 2.密度峰值聚类算法不需要预先设定簇的数量，对形状复杂的 簇和噪声有较好的鲁棒性，但计算复杂度较高。 3.通过优化密度峰值定义方式、引入核函数或结合其他算法， 可以提高密度峰值聚类的性能和效率。
聚类分析
11
步骤：
• • • • • • • 1、对数据进行变换处理，消除量纲 2、构造n个类，每个类只包含一个样本计算 3、n个样本两两间的距离{dij} 4、合并距离最近的两类为一新类 5、计算新类与当前各类的距离，重复（4） 6、画聚类图 7、决定类的个数和类
12
类与类间距离的确定
一、最短距离法 二、最长距离法 三、中间距离法 四、重心距离法 五、类平均法 六、离差平方和
聚类分析
(Cluster Analysis)
1
聚类分析(Cluster Analysis)
• 一、聚类分析基本原理 • 二、层次聚类法(Hierarchical Cluster) • 三、K-均值聚类法(K-means cluster)
2
一、聚类分析(Cluster analysis)基本原理 • 聚类分析又称群分析或点群分析，它是研
G8={G1,G2}
17
d78=min{d71,d72}=12.80 7 D4= 7 8 河南3 甘肃4 青海5 辽宁1 浙江2 0 12.8 0 8
18
最长距离法(furthest neighbor)
• 用两类之间最远点 的距离代表两类之 间的距离。
例2：对例1的数据以最长距离法聚类。
19
d13=13.80 d14=13.12 d15=12.80 d23=24.63 d24=24.06 d25=23.54 d34=2.2 d35=3.51 d45=2.21 1 D1= 1 2 3 4 5 0 11.67 0 13.80 24.63 0 13.12 24.06 2.20 0 0 12.80 23.54 3.51 2.21 2 3 4 5 河南与甘肃的距离最近， 先将二者（3和4）合 为一类G6={G3，G4}
步骤：
• • • • • • • 1、对数据进行变换处理，消除量纲 2、构造n个类，每个类只包含一个样本计算 3、n个样本两两间的距离{dij} 4、合并距离最近的两类为一新类 5、计算新类与当前各类的距离，重复（4） 6、画聚类图 7、决定类的个数和类
12
类与类间距离的确定
一、最短距离法 二、最长距离法 三、中间距离法 四、重心距离法 五、类平均法 六、离差平方和
聚类分析
(Cluster Analysis)
1
聚类分析(Cluster Analysis)
• 一、聚类分析基本原理 • 二、层次聚类法(Hierarchical Cluster) • 三、K-均值聚类法(K-means cluster)
2
一、聚类分析(Cluster analysis)基本原理 • 聚类分析又称群分析或点群分析，它是研
G8={G1,G2}
17
d78=min{d71,d72}=12.80 7 D4= 7 8 河南3 甘肃4 青海5 辽宁1 浙江2 0 12.8 0 8
18
最长距离法(furthest neighbor)
• 用两类之间最远点 的距离代表两类之 间的距离。
例2：对例1的数据以最长距离法聚类。
19
d13=13.80 d14=13.12 d15=12.80 d23=24.63 d24=24.06 d25=23.54 d34=2.2 d35=3.51 d45=2.21 1 D1= 1 2 3 4 5 0 11.67 0 13.80 24.63 0 13.12 24.06 2.20 0 0 12.80 23.54 3.51 2.21 2 3 4 5 河南与甘肃的距离最近， 先将二者（3和4）合 为一类G6={G3，G4}
聚类分析(共8张PPT)
第4页，共8页。
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中，形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中，一般可以用三种方式采集数据：二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
研究个案 A B C
受教育年限 10 16 6
年收入（万元） 2
1.5 1
年收入（元） 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位：万元
第6页，共8页。
单位：元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形，由用户指定须聚类的 类数之后，系统采用标准迭代算法进行运算，把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值，加以分类，使类与类间的异质性达到最大，而同一类的几个观察值同质性很高。 ③对数据进行变换处理，（如标准化或规格化）；
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离，就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组，而聚类分析 按照这种方则法是不断将进“行合观并察，直值到个把所体有”的样予品以合为分一组个，大类亦为即止。因子分析时，根据因变量（题项）间关系密切与 四⑦、最常 后用绘两制否种系，聚统类聚将分类变析谱方系量法图予，按以不分同的类分（类标分准为或不几同个的层分类面原因则，子得）出不；同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观，因察子值分析，是加一种以“横分向类合并，”的使方类法，与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法，。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高，度。由测用度户了指研定究须对聚象类的的相类似数性之。后，系统采用标准迭代算法进行运算，把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平：等等横，向都需简要化对研，究聚对象类进分行分析类：。纵向分组
聚类分析
三、聚类分析中的测度与标准化
在聚类分析技术的发展过程中，形成了很多种测度相似性的方法。每一种方法 都从不同的角度测度了研究对象的相似性。
在数据采集过程中，一般可以用三种方式采集数据：二分类型数据、等级类型 数据和连续类型数据。在进行聚类分析时可以根据不同的数据特点采用相应的测度 方法。
尽量避免绝对数据。
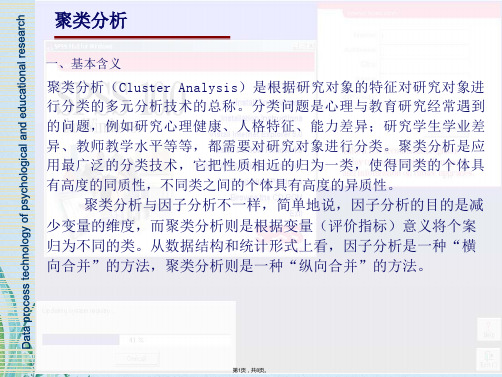
研究个案 A B C
受教育年限 10 16 6
年收入（万元） 2
1.5 1
年收入（元） 20000 15000 10000
A、B、C在不同距离单位时的距离图
A
B
B
10.01
C
A
10000
C
单位：万元
第6页，共8页。
单位：元
聚类分析
四、常用两种聚类分析方法
1.快速聚类法
快速聚类过程是初始分类的有效方法。适用于大容量样本的情形，由用户指定须聚类的 类数之后，系统采用标准迭代算法进行运算，把所有的个案归并在不同的类中。
m维空间中点与点之间的某种距离就可用来描述样品之间的亲疏程度。 而聚类分析则较常使用于将变量属性相似程度较高的观察值，加以分类，使类与类间的异质性达到最大，而同一类的几个观察值同质性很高。 ③对数据进行变换处理，（如标准化或规格化）；
mm维维空 空间间中中点点与与点点实之之际间间的的应某某用种种距距时离离，就就可可两用用者来来描描的述述主样样品品要之之差间间的的别亲亲在疏疏程程于度度因。。子分析是针对“变量”予以分组，而聚类分析 按照这种方则法是不断将进“行合观并察，直值到个把所体有”的样予品以合为分一组个，大类亦为即止。因子分析时，根据因变量（题项）间关系密切与 四⑦、最常 后用绘两制否种系，聚统类聚将分类变析谱方系量法图予，按以不分同的类分（类标分准为或不几同个的层分类面原因则，子得）出不；同而的分聚类类结果分。析则较常使用于将变量属性相似 从数据结构程和度统计较形高式上的看观，因察子值分析，是加一种以“横分向类合并，”的使方类法，与聚类类分间析的则是异一质种“性纵向达合到并”最的方大法，。 而同一类的几个观察值 适每用一于 种大方容法同量都质样从本不性的同很情的形角高，度。由测用度户了指研定究须对聚象类的的相类似数性之。后，系统采用标准迭代算法进行运算，把所有的个案归并在不同的类中。 研究学生学业差异、因教师素教分学水析平：等等横，向都需简要化对研，究聚对象类进分行分析类：。纵向分组
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6
§2 相似系数和距离 一、变量测量尺度的类型 为了将样本进行分类，就需要研究样品之间的关 系；而为了将指标进行分类，就需要研究指标之间 的关系。但无论是样品之间的关系，还是指标之间 的关系，都是用变量来描述的，变量的类型不同， 描述方法也就不同。通常，变量按照测量它们的尺 度不同，可以分为三类。 (1)间隔尺度。指标度量时用数量来表示，其数 值由测量或计数、统计得到，如长度、重量、收入、 支出等。一般来说，计数得到的数量是离散数量， 测量得到的数量是连续数量。
dij2 (xi x j ) 1 (xi x j )
分别表示第i个样品和第j样品的p指标观测值所 组成的列向量，即样本数据矩阵中第i个和第j个行 向量的转置，表示观测变量之间的协方差短阵。 在实践应用中，若总体协方差矩阵未知，则可用 样本协方差矩阵作为估计代替计算。
16
马氏距离又称为广义欧氏距离。显然，马氏距离与上 述各种距离的主要不同就是马氏距离考虑了观测变量之间
18
• 相似系数 • 聚类分析方法不仅用来对样品进行分类，而且可用 来对指标（或变量）进行分类，在对变量进行分类 时，常常采用相似系数来度量变量之间的相似性。相 似系数越大（或其绝对值越大），认为变量之间的相 似程度就越高；反之，则越低。聚类时，比较相似的 变量倾向于归为一类，不太相似的变量归属不同的 类。
37
2、最长距离法 用最长距离法对5个样品进行分类。首 先采用绝对距离计算距离矩阵：
G1 G1 G2 G3 G4 G5
0
G2
0
1.5 5 7
G3
G4
G5
1
2.5 6 8
0 3.5 5.5 0 2 0
38
然后和被聚为新类，得：
G6 G6 G3
0 2.5 6
8
G3
0 3.5
5.5
G4
G5
G4
G5
0
2 0
Gq
Gp
G1
0
G2
d12
0
┇
… …
Gn
d1n
d2n
┇
G1 G2
┇ ┇
d 21
Gn
d n1
dn2
…
0
22
四、样本数据与小类、小类与小类之间的度量
1 、最短距离（Nearest Neighbor)
x11•
d13
x22•
x21•
x12•
23
组间平均连接（Between-group Linkage)
•
•
29
3、利用递推公式计算新类与其它类之间的 距离。分别删除D（0）表的第p，q行和第p， q列，并新增一行和一列添上的结果，产生 D（1）表。
30
4、在D（1）表再选择最小的非零数，其 对应的两类有构成新类，再利用递推公式 计算新类与其它类之间的距离。分别删除D （1）表的相应的行和列，并新增一行和一 列添上的新类和旧类之间的距离。结果， 产生D（2）表。类推直至所有的样本点归 为一类为止。
13
(2)杰氏距离 这是杰斐瑞和马突斯塔(Jffreys & Matusita) 所定义的一种距离，其计算公式为：
dij ( J )
k 1
p
( xik x jk )
2
12
14
(3)兰氏距离
这是兰思和维廉姆斯(Lance & Williams)所给定的一种
距离，其计算公式为：
dij ( L)
28
§3
（一）方法
系统聚类方法
开始各样本自成一类。 1、根据样品的特征，规定样品之间的距离
，
共有d 个。将所有列表，记为D（0）表，该表 Cn2 ij 是一张对称表。所有的样本点各自为一类。
2、选择D（0）表中最小的非零数，不妨假设 于是将 和 G p Gq 合并为一类，记为 d pq Gr Gp，Gq ， 。
19
2、相似系数的算法 （1）相关系数 变量
xi
与x j 之间的相似测度为:
ij
(x
k 1 n k 1
n
ki
xi )( xkj x j )
n 2 2
[ ( xki xi ) ][ ( xkj x j ) ]
k 1
20
（2）夹角余弦
夹角余弦时从向量集合的角度所定义的一种测度变 量之间亲疏程度的相似系数。设在n维空间的向量
39
各步聚类的结果： (1,2) (3) (4) (5) (1,2,) (3) (4 ,5) (1,2,3) (4,5) (1,2,3,4,5)
40
3、离差平方和法
G1 和 G2 被聚为新类，重心为 X 6 (1 2) / 2 1.5
如G1 和G2 为一类，则离差平方和
S12 (1 1.5)2 (2 1.5)2 0.5
k 1
p
xik x jk xik x jk
这是一个自身标准化的量，由于它对大的奇异值不 敏感，这样使得它特别适合于高度偏倚的数据。虽然这
个距离有助于克服明氏距离的第一个缺点，但它也没有
考虑指标之间的相关性。
15
(4)马氏距离 这是印度著名统计学家马哈拉诺比斯 (P．C．Mahalanobis)所定义的一种距离，其 计算公式为：
其中 S r2 是由Gp 和Gq 合并成的Gr 类的类内离差平方和。
42
G1 G1 G2 G3 G4 G5
0 0.5
G2
0
G3
G4
G5
3.125
18 32
1.125
12.50 24.50
0
6.125
15.125
0 2 0
43
4、重心法
用重心法对5个样品进行分类。首先采用
绝对距离计算距离平方矩阵：
3
例 对10位应聘者做智能检验。3项指标X，Y
和Z分别表示数学推理能力，空间想象能力和语
言理解能力。其得分如下，选择合适的统计方 法对应聘者进行分类。
应聘者 X Y Z 1 28 29 28 2 18 23 18 3 11 22 16 4 21 23 22 5 26 29 26 6 20 23 22 7 16 22 22 8 14 23 24 9 24 29 24 10 22 27 24
如 G1和 G3为一类，则离差平方和
S13 (1 2.25) 2 (2 2.25) 2 3.125
如 G2和 G3 为一类，则离差平方和
S23 (2 2.75) (3.5 2.75) 1.125
2 2
41
2 2 定义距离为离差平方和 的增量：Dpq Sr2 S p Sq2
dij 0对一切的i和j成立; dij 0当且仅当i j成立;
dij d ji 对一切的i和j成立;
dij dik d kj 对于一切的i和j成立.
11
2、常用距离的算法
(1) 明氏距离测度 设 x i xi1 , xi 2 , , xip 和 x j ( x j1 , x j 2 ,, x jp ) 是第i和 j 个样品的观测值，则二者之间的距离 为：
然后
G1 和 G2 被聚为新类 G6 ，得 D (1) ：
G6 G3
0 3.5 0
G4
G5
G6 G3
0 1.5 5
G4 G5
7
5.5
2
0
33
G7 G7 G4 G5
0 3.5 5.5
G4
G5
0 2 0
35
G8 G8 G7
0
G7
3.5
0
36
各步聚类的结果： (1,2) (3) (4) (5) (1,2,3) (4) (5) (1,2,3) (4,5) (1,2,3,4,5)
26
离差平方和法连接
(2 3)2 (4 3) 2 2
2，4
(6 5.5) (5 5.5) 0.5
2 2
6，5
1，5
(1 3)2 (5 3) 2 8
27
红绿（2，4，6，5）8.75 离差平方和增加8.75－2.5＝6.25 黄绿（6，5，1，5）14.75 离差平方和增加14.75－8.5＝6.25 黄红（2，4，1，5）10－10＝0 故按该方法的连接和黄红首先连接。
的相关性。
17
(5) 斜交空间距离 由于各变量之间往往存在着不同的相关 关系，用正交空间的距离来计算样本间的 距离易变形，所以可以采用斜交空间距离。
1 p p dij 2 ( xih x jh )( xik x jk ) hk p h1k 1
12
当各变量之间不相关时，斜交空间退化为欧氏距离。
9
指标（或变量）之间的聚类即R型聚类分 析，常用相似系数来测度变量之间的亲疏程 度。而样品之间的聚类即Q型聚类分析，则 常用距离来测度样品之间的亲疏程度。
注:变量聚类放到因子分析后面
10
1、定义距离的准则
定义距离要求满足第i个和第j个样品之间的距离如下四 个条件（距离可以自己定义，只要满足距离的条件）
明氏距离
dij ( k1| xik x jk |g )
p
1 g
特别，欧氏距离
dij
k 1
( xik
p
x jk ) 2
12
明考夫斯基距离主要有以下两个缺点： ①明氏距离的值与各指标的量纲有关。
②明氏距离的定义没有考虑各个变量之间 的相关性和重要性。实际上，明考夫斯基距离 是把各个变量都同等看待，将两个样品在各个 变量上的离差简单地进行了综合。
G1
G2
0
2.25