高等数学李伟版课后习题答案第五章
高等数学李伟版课后习题答案第三章

⾼等数学李伟版课后习题答案第三章习题3—1(A )1.判断下列叙述是否正确,并说明理由:(1)函数的极值与最值是不同的,最值⼀定是极值,但极值未必是最值;(2)函数的图形在极值点处⼀定存在着⽔平的切线;(3)连续函数的零点定理与罗尔定理都可以⽤来判断函数是否存在零点,⼆者没有差别;(4)虽然拉格朗⽇中值公式是⼀个等式,但将()f ξ'进⾏放⼤或缩⼩就可以⽤拉格朗⽇中值公式证明不等式,不过这类不等式中⼀定要含(或隐含)有某函数的两个值的差.答:(1)不正确.最值可以在区间端点取得,但是由于在区间端点处不定义极值,因此最值不⼀定是极值;⽽极值未必是最值这是显然的.(2)不正确.例如32x y =在0=x 点处取极值,但是曲线在点)00(,却没有⽔平切线.(3)不正确.前者是判断)(x f 是否有零点的,后者是判断)(x f '是否有零点的.(4)正确.⼀类是明显含有)()(a f b f -的;另⼀类是暗含着)()(0x f x f -的. 2.验证函数2)1(e x y -=在区间]20[,上满⾜罗尔定理,并求出定理中的ξ.解:显然2)1(e x y -=在闭区间]20[,上连续,在开区间)20(,内可导,且e )2()0(==y y ,于是函数2)1(ex y -=在区间]20[,上满⾜罗尔定理的条件,2)1(e )1(2)(x x x y ---=',由0)(='ξy ,有0e )1(22)1(=---ξξ,得1=ξ,∈ξ)20(,,所以定理的结论也成⽴.3.验证函数1232-+=x x y 在区间]11[,-上满⾜拉格朗⽇中值定理,并求出公式中的ξ.解:显然1232-+=x x y 在闭区间]11[,-连续,在开区间)11(,-内可导,于是函数1232-+=x x y 在区间]11[,-上满⾜拉格朗⽇中值定理的条件,26)(+='x x y ,2)1(1)1()1(=----y y ,由)()1(1)1()1(ξy y y '=----,有226=+ξ,得0=ξ,∈ξ)11(,-,所以定理的结论也成⽴.4.对函数x x x f cos )(+=、x x g cos )(=在区间]20[π,上验证柯西中值定理的正确性,并求出定理中的ξ.解:显然函数x x x f cos )(+=、x x g cos )(=在闭区间]20[π,上连续,在开区间)20(π,内可导,且x x f sin 1)(-=',x x g sin )(-=',在区间)20(π,内0)(≠'x g ,于是函数x x x f cos )(+=、x x g cos )(=在区间]20[π,上满⾜柯西定理的条件,⼜21)0()2/()0()2/(πππ-=--g g f f ,由)()()0()2/()0()2/(ξξππg f g g f f ''=--,有ξξπsin sin 121--=-,即πξ2sin =,由于∈ξ)20(π,,得πξ2arcsin=,所以定理的结论也成⽴.5.在)(∞+-∞,内证明x x cot arc arctan +恒为常数,并验证2cot arc arctan π≡+x x .证明:设x x x f cot arc arctan )(+=,显然)(x f 在)(∞+-∞,内可导,且-+='211)(x x f 0112≡+x,由拉格朗⽇定理的推论,得在)(∞+-∞,内x x cot arc arctan +恒为常数,设C x f ≡)(,⽤0=x 代⼊,得2π=C ,所以2cot arc arctan π≡+x x .6.不求出函数2()(4)f x x x =-的导数,说明0)(='x f 有⼏个实根,并指出所在区间.解:显然2()(4)f x x x =-有三个零点20±==x x ,,⽤这三点作两个区间]20[]02[,、,-,在闭区间]02[,-上)(x f 连续,在开区间)02(,-内)(x f 可导,⼜0)0()2(==-f f 于是)(x f 在]02[,-满⾜罗尔定理,所以⾄少有∈1ξ)02(,-,使得0)(1='ξf ,同理⾄少有∈2ξ)20(,,使得0)(2='ξf ,所以0)(='x f ⾄少有两个实根.⼜因为)(x f 是三次多项式,有)(x f '时⼆次多项式,于是0)(='x f 是⼆次代数⽅程,由代数基本定理,得0)(='x f ⾄多有两个实根.综上,0)(='x f 恰有两个实根,且分别位于区间)02(,-与)20(,内.7.证明下列不等式:(1)对任何实数b a ,,证明cos cos a b a b -≤-;(2)当0>x 时,x x xx<+<+)1ln(1.证明:(1)当b a =时,cos cos a b a b -≤-显然成⽴.当b a <时,取函数x x f cos )(=,显然)(x f 在闭区间][b a ,上连续,在开间)(b a ,内可导,由拉格朗⽇定理,有∈ξ)(b a ,,使得))(()()(b a f b f a f -'=-ξ,即)(sin cos cos b a b a -?-=-ξ,所以)()(sin cos cos b a b a b a -≤-?-=-ξ.当b a >时,只要将上⾯的区间][b a ,换为][a b ,,不等式依然成⽴.所以,对任何实数b a ,,都有cos cos a b a b -≤-.(2)取函数)1ln()(t t f +=,当0>x 时,函数)1ln()(t t f +=在闭区间]0[x ,上连续,在开区间)0(x ,内可导,根据拉格朗⽇定理,有∈ξ)0(x ,,使得ξξ+='1)(xf .因为x <<ξ0,则x xx x x =+<+<+0111ξ,所以x x x x <+<+)1ln(1. 8.若函数)(x f 在区间),(b a 具有⼆阶导数,且)()()(321x f x f x f ==,其中21x x a <<b x <<3,证明在区间)(3,1x x 内⾄少有⼀点ξ,使得0)(=''ξf .证明:根据已知,函数)(x f 在区间][21x x ,及][32x x ,上满⾜罗尔定理,于是有∈1ξ)(21x x ,,∈2ξ)(32x x ,(其中21ξξ<),所得0)(1='ξf ,0)(2='ξf .再根据已知及)()(21ξξf f '=',函数)(x f '在区间][21ξξ,上满⾜罗尔定理,所以有∈ξ)(21ξξ,?)(3,1x x ,所得0)(=''ξf ,即在区间)(3,1x x 内⾄少有⼀点ξ,使得0)(=''ξf .习题3—1(B )1.在2004年北京国际马拉松⽐赛中,我国运动员以2⼩时19分26秒的成绩夺得了⼥⼦组冠军.试⽤微分中值定理说明她在⽐赛中⾄少有两个时刻的速度恰好为18. 157km/h (马拉松⽐赛距离全长为42.195km ).解:设该运动员在时刻t 时跑了)(t s s =(km ),此刻才速度为)()(t s t v v '==(km/h ),为解决问题的需要,假定)(t s 有连续导数.设起跑时0=t ,到达终点时0t t =,则3238888889.20≈t ,对函数)(t s 在区间]0[0t ,上⽤拉格朗⽇定理,有00t <<ξ,所得)()(0)0()(00ξξv s t s t s ='=--,⽽15706.183238888889.2195.420)0()(00≈=--t s t s km/h ,所以157.1815706.18)(>≈ξv .对)(t v 在区间]0[ξ,及][0t ,ξ上分别使⽤连续函数的介值定理(注意,0)0(=v0)(0=t v ,则数值18. 157分别介于两个区间端点处函数值之间),于是有)0(1ξξ,∈,)0(2,ξξ∈,使得157.18)(1=ξv ,157.18)(2=ξv,这表明该运动员在⽐赛中⾄少有两个时刻的速度恰好为18. 157km/h .2.若函数)(x f 在闭区间][b a ,上连续,在开区间),(b a 内可导,且0)(>'x f ,证明⽅程0)(=x f 在开区间),(b a 内⾄多有⼀个实根.证明:采⽤反证法,若⽅程0)(=x f 在开区间),(b a 有两个(或两个以上)不同的实根21x x <,即0)()(21==x f x f ,根据已知函数)(x f 在][21x x ,上满⾜罗尔定理,于是有∈ξ)()(21b a x x ,,?,使得0)(='ξf ,与在开区间),(b a 内0)(>'x f ⽭盾,所以⽅程0)(=x f 在开区间),(b a 内⾄多有⼀个实根.(注:本题结论也适⽤于⽆穷区间) 3.证明⽅程015=-+x x 只有⼀个正根.证明:设1)(4-+=x x x f ()(∞+-∞∈,x ),则014)(4>+='x x f ,根据上题结果,⽅程015=-+x x 在)(∞+-∞,内⾄多有⼀个实根.取闭区间]10[,,函数1)(4-+=x x x f 在]10[,上连续,且01)0(<-=f ,01)1(>=f ,由零点定理,有)10(,∈ξ,使得0)(=ξf ,从⽽⽅程015=-+x x 在)0(∞+,内⾄少有⼀个实根.综上,⽅程015=-+x x 只有⼀个正根,且位于区间)10(,内. 4.若在),(+∞-∞内恒有k x f =')(,证明b kx x f +=)(.证明:(⽅法1)设函数kx x f x F -=)()(,则0)()(≡-'='k x f x F ,根据拉格朗⽇定理的推论)(x F 恒为常数,设C kx x f x F ≡-=)()(,⽤0=x 代⼊,得)0(f C =,记b f =)0(,则b C kx x f x F ==-=)()(,所以b kx x f +=)(.(⽅法2)记b f =)0(,∈?x ),(+∞-∞,若0=x ,则满⾜b kx x f +=)(;若0≠x ,对函数)(t f 以x t t ==,0为端点的闭区间上⽤拉格朗⽇定理,则有ξ介于0与x 之间,使得)0)(()0()(-'=-x f f x f ξ,即kx b x f =-)(,所以b kx x f +=)(.5.若函数)(x f 在区间)0(∞+,可导,且满⾜0)()(2≡-'x f x f x ,1)1(=f ,证明x x f =)(.证明:设函数xx f x F )()(=(∈x )0(∞+,),则xx x f x f x x x x f x x f x F 2)()(22/)()()(-'=-'=',由0)()(2≡-'x f x f x ,得0)(≡'x F ,根据拉格朗⽇定理的推论)(x F 恒为常数,设C xx f x F ==)()(,⽤1=x 代⼊,且由1)1(=f ,得1=C ,所以1)()(==xx f x F ,即x x f =)(.6.证明下列不等式(1)当0>x 时,证明x x+>1e ;(2)对任何实数x ,证明x x arctan ≥.证明:(1)取函数t t f e )(=(]0[x t ,∈)显然函数)(t f 在区间]0[x ,上满⾜拉格朗⽇定理,则有∈ξ)0(x ,,使得)0)(()0()(-'=-x f f x f ξ,即x xξe 1e =-,所以 x x x+>+=1e 1e ξ.(2)当0=x 时,显然x x arctan ≥.当0≠x 时,取函数t t f arctan )(=,对)(t f 在以x t t ==,0为端点的闭区间上⽤拉格朗⽇定理,则有ξ介于0与x 之间,使得)0)(()0()(-'=-x f f x f ξ,即21arct an ξ+=xx ,所以x x x <+=21arctan ξ.综上,对任何实数x ,都有x x arctan ≥.7.若函数)(x f 在闭区间[1-,1]上连续,在开区间(1-,1)内可导,M f =)0((其中0>M ),且M x f <')(.在闭区间[1-,1]上证明M x f 2)(<.证明:对∈?x [1-,1],当0=x 时,M M f 2)0(<=,.不等式成⽴.当0≠x 时,根据已知,函数)(t f 在以x t t ==,0为端点的区间上满⾜拉格朗⽇定理,则有ξ介于0与x 之间,使得)0)(()0()(-'=-x f fx f ξ,即x f M x f )()(ξ'=-,所以,M x f x f +'=)()(ξ,从⽽M M f M x f M x f x f 2)()()()(<+'≤+'≤+'=ξξξ.综上,在闭区间[1-,1]上恒有M x f 2)(<.8.若函数)(x f 在闭区间]0[a ,上连续,在开区间)0(a ,内可导,且0)(=a f ,证明在开区间)0(a ,内⾄少存在⼀点ξ,使得0)()(='+ξξξf f .证明:设函数)()(x xf x F =(∈x ]0[a ,),则0)(0)0(==a F F ,,再根据已知,函数)(x F 在区间],0[a 满⾜罗尔定理,则有∈ξ)0(a ,,使得0)(='ξf .⽽)()()(ξξξξf f f '+=',于是0)()(='+ξξξf f .所以,在开区间)0(a ,内⾄少存在⼀点ξ,使得0)()(='+ξξξf f .习题3—2(A )1.判断下列叙述是否正确?并说明理由(1)洛必达法则是利⽤函数的柯西中值定理得到的,因此不能利⽤洛必达法则直接求数列极限;(2)凡属“00”,“∞∞”型不定式,都可以⽤洛必达法则来求其的极限值;(3)型如””,“”,“”,“”,““0100∞∞-∞∞?∞型的不定式,要想⽤洛必达法则,需先通过变形.⽐如“0?∞”型要变型成为“00”,“∞∞”型,”,”,““00∞-∞””,““01∞∞型要先通过变型,转化为“0?∞”型的不定式,然后再化为基本类型.答:(1)正确.因为数列是离散型变量,对它是不能求导的,要想对数列的“不定式”极限使⽤洛必达法则,⾸先要根据“海涅定理”将数列极限转换为普通函数极限,然后再使⽤洛必达法则.(2)不正确.如0sin 1sinlim 20=→xx x x (00型)、1cos sin lim -=-+∞→x x x x x (∞∞型)、11lim 2=++∞→x x x (∞∞型)都不能⽤洛⽐达法则求得极限值.(3)正确.可参见本节3.其他类型的不定式极限的求法,但是“∞-∞”型通常是直接化为“00”,“∞∞”型. 2.⽤洛必达法则求下列极限:(1)x x x --→e 1ln lim e ;(2)11lim 1--→n m x x x (0≠mn );(3)x x x 5tan 3sin limπ→;(4)2e e cos 1lim 0-+--→x x x x;(5)1sec tan 2lim0-→x x x x ;(6)xxx 3tan tan lim 2/π→;(7)x x x 2cot lim 0→;(8)x x x cot arc lim +∞→;(9))sin 11(lim 0x x x -→;(10)111lim()ln 1x x x →--;(11)xx x tan 0lim +→;(12))1ln(1)(lim x x x ++∞→;(13)21)(cos lim x x x →;(14)nn n ln lim∞→;解:(1)e11/1lim e 1ln lime e -=-=--→→x x x x x .(2)==----→→1111lim 11lim n m x nm x nx mx x x nm.(3)=-?-==→→22)1(535sec 53cos 3lim 5tan 3sin limx x x x x x ππ53-.(4)=+=-=-+--→-→-→x x x x x x x x x x x x e e cos lim e e sin lim 2e e cos 1lim00021.(5)===-=-→→→→xxx x x x x x x x x x x x tan 4lim tan sec 4lim 1sec 2lim 1sec tan 2lim002004. (6) =---=-=?=→→→→x xx x xx x x x x x x x x sin 3sin 3lim cos 3cos lim )cos 3cos 3sin sin (lim 3tan tan lim2/2/2/2/ππππ3.(7)===→→→x x x x x x x x 2sec 21lim 2tan lim 2cot lim 200021.(8)=+=-+-==+∞→+∞→+∞→+∞→22221lim /1)1/(1lim 1/cot arc lim cot arc lim xx x x x x x x x x x x 1.(9)=-=-=-=-=-→→→→→2sin lim 21cos lim sin lim sin sin lim )sin 11( lim 002000xx x x x x x x x x x x x x x x x 0.(10)xx x x x x x x x x x x x /)1(ln /11lim ln )1(ln 1lim )11ln 1(lim 111-+-=---=--→→→=+=-+-=→→2ln 1lim 1ln 1lim11x x x x x x x 21.(11)设xxy tan =,则x x y ln tan ln =,因为0lim /1/1lim /1ln lim ln lim ln tan lim ln lim 0200=-=-====++++++→→→→→→x xxx x x x x x y x x x x x x ,所以, ==+→0tan 0e lim xx x 1.(12)设)1ln(1)(x x y +=,则)1ln(ln 21)1ln(ln ln x xx x y +=+=,因为 21)11(lim 21)1/(1/1lim 21)1ln(ln lim 21ln lim =+=+=+= +∞→+∞→+∞→+∞→x x x x x y x x x x ,所以 ==++∞→21)1ln(1e )(lim x x x e .(13)设21)(cos x x y =,则2cos ln ln x xy =,因为 21cos 2sin lim cos ln lim ln lim 0200-=-==→→→x x x x x y x x x ,所以==-→2 110e )(cos lim 2x x x e1.(14)根据海涅定理,====+∞→+∞→+∞→∞→xxx xx nn x x x n 2lim2/1/1limln limln lim0.3.验证极限xx xx x cos 2sin 2lim -+∞→存在,并说明不能⽤洛必达法则求得.解:=-+=-+=-+∞→∞→0102/)cos 2(1/)(sin 2lim cos 2sin 2limx x x x x x x x x x 2.因为极限xxx x x x x x sin 21cos 2lim )cos 2()sin 2(lim++='-'+∞→∞→不存在,因为此极限不能⽤洛必达法则求得.4.验证极限x x x x sin )/1sin(lim 20→存在,并说明不能⽤洛必达法则求得.解:=?=?=→→→011sin lim sin lim sin )/1sin(lim0020xx x x x x x x x x 0.因为极限xx x x x x x x x cos )/1sin()/1sin(2lim)(sin ])/1sin([lim 020-=''→→不存在,因为此极限不能⽤洛必达法则求得.习题3—2(B )1.⽤洛必达法则求下列极限:(1)311lnarctan 2limx x xx x -+-→;(2)xx x x 30sin arcsin lim -→(3))tan 11(lim 220xx x -→;(4)]e )11[(lim -+∞→xx x x ; (5) 260)sin (lim x x xx →;(6)n n nn b a )2(lim +∞→(00>>b a ,).解:(1)原式30)1ln()1ln(arctan 2limx x x x x -++-=→=--=--+-+=→→)1(34lim 3111112lim 40220x x x x x x x 34-.(2)原式2220220301311lim 31/11lim arcsin lim xx x x x x x x x x x ---=--=-=→→→=-=--=→→22022032/lim 311lim xx x x x x 61-.(3)原式30022220tan lim tan lim tan tan lim xxx x x x x x x x x x x -?+=-=→→→ ==-=-=→→→22022030tan lim 3231sec lim 2tan lim 2x x xx x x x x x x 32.(4)令t x 1=,则原式21010)1ln()1()1(lim e )1(lim tt t t t t t t t tt ++-+=-+→→ =+-=-+-=++-=→→→t t t t t t t t t t t )1ln(lim 2e 21)1ln(1lim e )1ln()1(lim e 002 02 e -.(5)令6)sin (x x x y =,则2sin ln 6ln x x xy =,因为 30200sin cos lim 3)sin cos 2sin /6(lim ln lim xxx x x x x x x x x y x x x -=-?=→→→ 13sin lim 320-=-=→x x x x ,所以==-→160e )sin (lim x x xx e 1.(6)令=n x nn nb a )2(+,则]2ln )[ln(ln -+=n n n b a n x ,再令x t 1=,因为 tb a b a x x t t t xx x n n 2ln )ln(lim ]2ln )[ln(lim ln lim 011-+=-+=→+∞→∞→ ab b a ba b b a a t t t t t ln 2ln ln ln ln lim 0=+=++=→,所以==+∞→abnn nn b a ln e )2(lim ab .2.当0→x 时,若)(e )(2c bx ax x f x ++-=是⽐2x ⾼阶的⽆穷⼩,求常数c b a 、、.解:根据已知,有0)(e lim220=++-→x c bx ax x x ,由分母极限为零,则有分⼦极限也为零,于是01)]([e lim 2x =-=++-→c c bx ax x ,得1=c ,此时02)2(e lim )(e lim 0220=+-=++-→→x b ax x c bx ax x x x x ,再由分⼦极限为零,同样得1=b ,进⽽022122e lim 2)12(e lim )(e lim 00220=-=-=+-=++-→→→a a x ax x c bx ax x x x x x x ,得21=a ,所以1121===c b a ,,时,当0→x 时,)(e )(2c bx ax x f x ++-=是⽐2x ⾼阶的⽆穷⼩.3.若函数)(x f 有⼆阶导数,且2)0(,1)0(,0)0(=''='=f f f ,求极限2)(limxxx f x -→.解:1)0(210)0()(lim 2121)(lim )(lim002=''=-'-'=-'=-→→→f x f x f x x f x x x f x x x .(注:根据题⽬所给条件,不能保证)(x f ''连续,所以只能⽤⼀次洛⽐达法则,再⽤⼆阶导数的分析定义)习题3—3(A )1.判断下列叙述是否正确?并说明理由:(1)只要函数在点0x 有n 阶导数,就⼀定能写出该函数的泰勒多项式.⼀个函数的泰勒多项式永远都不会与这个函数恒等,⼆者相差⼀个不恒为零的余项;(2)⼀个函数在某点附近展开带有拉格朗⽇余项的n 阶泰勒公式是它的n 次泰勒多项式加上与该函数的n 阶导数有关的所谓拉格朗⽇型的余项;(3)在应⽤泰勒公式时,⼀般⽤带拉格朗⽇型余项的泰勒公式⽐较⽅便.答:(1)前者正确,其根据是泰勒多项式的定义;后者不正确.当)(x f 本⾝是⼀个n 次多项式时,有0)(≡x R n ,这时函数的泰勒多项式恒等于这个函数.(2)不正确.拉格朗⽇型的余项与函数)(x f 的1+n 阶导数有关.(3)不正确.利⽤泰勒公式求极限时就要⽤带有⽪亚诺余项的泰勒公式,⼀般在对余项进⾏定量分析时使⽤带拉格朗⽇型余项的泰勒公式,在对余项进⾏定性分析时使⽤带⽪亚诺型余项的泰勒公式.2.写出函数x x f arctan )(=的带有佩亚诺型余项的三阶麦克劳林公式.解:因为211)(x x f +=',)1(2)(2x x x f +-='',322)1(62)(x x x f ++-=''',于是 2)0(0)0(1)0(0)0(-='''=''='=f f f f ,,,,代⼊到)(!3)0(!2)0()0()0()(332x o x f x f x f f x f +'''+'+'+=中,得 )(3arctan 33x o x x x +-=. 3.按1-x 的乘幂形式改写多项式1)(234++++=x x x x x f .解:因为1234)(23+++='x x x x f ,2612)(2++=''x x x f ,624)(+='''x x f ,24)()4(=x f ,更⾼阶导数都为零,于是,,,20)1(10)1(5)1(=''='=f f f 30)1(='''f ,24)0()4(=f ,将其带⼊到)()1(!4)1()1(!3)1()1(!2)1()1)(1()1()(44)4(32x R x f x f x f x f f x f +-+-'''+-'+-'+=中,得 432)1()1(5)1(10)1(105)(-+-+-+-+=x x x x x f(其中5)5(4)1(!5)()(-=x f x R ξ恒为零). 4.将函数1)(+=x xx f 在1x =点展开为带有佩亚诺型余项的三阶泰勒公式.解:因为111)(+-=x x f ,则2)1(1)(+='x x f ,3)1(2)(+-=''x x f ,4)1(6)(+='''x x f ,于是83)1(41)0(41)1(21)1(='''-=''='=f f f f ,,,,将其带⼊到 ))1(()1(!3)1()1(!2)1()1)(1()1()(332-+-'''+-'+-'+=x o x f x f x f f x f 中,得))1((16)1(8)1(41211332-+-+---+=+x o x x x x x . 5.写出函数xx x f e )(=的带有拉格朗⽇型余项的n 阶麦克劳林公式.解:因为)(e )()(k x x f x k +=(1321+=n n k ,,,,,)(参见习题2.5(B )3),于是,k fk =)0()((n k ,,,,210=),=+=++1)1()!1()()(n n n x n x f x R θ1)!1(e )1(++++n x x n x n θθ,将其带⼊到)(!)0(!2)0()0()0()()(2x R x n f x f x f f x f n nn +++'+'+= ,得 132)!1(e )1()!1(!2e +++++-++++=n x n xx n x n n x x x x x θθ )10(<<θ.6.将函数xx f 1)(=按(1)x +的乘幂展开为带有拉格朗⽇型余项的n 阶泰勒公式.解:因为1)(!)1()(+-=k k k xk x f,于是!)1()(k f k -=-(13210+=n n k ,,,,,,), 1211211)1()1()1()1()!1()!1()1()1()!1()()(+++++++++-=+++-=++=n n n n n n n n n x x n n x n f x R ξξξ,将其代⼊到中)()1(!)1()1(!2)1()1)(1()1()()(2x R x n f x f x f f x f n n n ++-+++-'++-'+-= ,得2112)1()1()1()1()1(11++++-++--+-+--=n n n nx x x x x ξ(ξ介于1-与x 之间).习题3—3(B )1.为了修建跨越沙漠的⾼速公路,测量员测量海拔⾼度差时,必须考虑地球是⼀个球体⽽表⾯不是⽔平,从⽽对测量的结果加以修正.(1)如果R 表⽰地球的半径,L 是⾼速公路的长度.证明修正量为R RLR C -=sec . (2)利⽤泰勒公式证明3422452R L R L C +≈.(3)当⾼速公路长100公⾥时,⽐较(1)和(2)中两个修正量(地球半径取6370公⾥).证明:(1)由αR L =,有R L =α,⼜在直⾓三⾓形ODB 中,CR R+=αcos ,于是R C R L+==1s e cs e c α,由此得R RLR C -=sec .(2)先将x x f sec )(=展开为4阶麦克劳林公式,为此求得x x x f tan sec )(=',x x x x f 32s e c t a n s e c )(+='',x x x x x f tan sec 5tan sec )(33+=''',x x x x x x f5234)4(s e c 5t a n s e c 18tan sec )(++=,,,,,,5)0(0)0(1)0(0)0(1)0()4(=='''=''='=f f f f f 于是 )(245211sec 442x R x x x +++=;当1<2245211sec x x x ++≈,取R L x =,得442224521sec RL R L R L ++≈,于是≈-=R R L R C sec 3422452R L R L +.(3)按公式R RLR C -=sec计算,得修正量为785010135.0)1(≈C ,按公式3422452RL R L C +≈计算,得修正量为785009957.0)2(≈C ,它们相差⼤约为000000178.0)2()1(≈-C C .2.写出函数212e)(x x f -=的带佩亚诺型余项的n 2阶麦克劳林公式.解:由)(!!3!21e 32nn tt o n t t t t ++++++= ,令22x t -=,得 )]2(!2)1(!62!42!221[e eee223624222122n n n nn x x x o n x x x x +?-++?-?+?-==--)(]!)!2()1(!!6!!4!!21[e 22642n n n x o n x x x x +-++-+-= ,按规律,由于nx2项的后⼀项为22+n x,所以余项也可以⽤)(12+n xo .3.写出函数x x f 2sin )(=的带⽪亚诺型余项的m 2阶麦克劳林公式.解:x x 2cos 2121sin 2-=)2()!2()2()1(!6)2(!4)2(!2)2(1[2121222642m m mn x o m x x x x +-++-+--=)()!2(2)1(4523122121642m m m m x o x m x x x +-+-+-=-- ,同上⼀题,余项也可以⽤)(12+m x o .(注意:像2、3题⽤变量代换写泰勒公式的⽅法只使⽤于带有佩亚诺型余项的泰勒公式,不适⽤带有拉格朗⽇型余项的泰勒公式,否则得到的余项不再是拉格朗⽇型余项) 4.应⽤三阶泰勒公式计算下列各数的近似值,并估计误差:(1)330;(2)18sin .解:(1)取函数31)(x x f +=,展开为三阶麦克劳林公式,有31154323)1(3108159311)(x xx x x x x f θ+?-+-+=+=,3339/11332730+?=+=,现取9/1=x ,)59049572912711(3303+-+≈,误差为54431089.19310-?R , 10725.3)000085.0001372.0037037.01(3)59049572912711(3303=+-+≈+-+≈;(2)⽤x sin 的麦克劳林公式,取1018π==x ,得53)10(!5)cos()10(!311018sin πθππx +-=,则3)10(!311018sin ππ-≈,误差为5531055.2)10(!51-?≈<≤πR3090.030899.000517.031416.018sin ≈=-≈.5.利⽤泰勒公式求下列极限:(1)642/012/e cos lim 2x x x x x +--→;(2)x x x x x x x sin )1(sin e lim 20+-→.解:(1)原式64636426 642012/)](!32821[)](!62421[lim xx x o x x x x o x x x x ++?-+--+-+-=→ 3607)(360/7lim 6660=+=→x x o x x .(2)原式3233220)](6/)][(2/1[lim x x x x o x x x o x x x --+-+++=→ 31)(3/lim3330=+=→x x o x x .6.设函数)(x f 在区间][b a ,上有⼆阶连续导数,证明:有)(b a ,∈ξ使得)(4)()2(2)()(2ξf a b b a f b f a f ''-=+-+.证明:将函数)(x f y =在20ba x +=点展开为⼀阶泰勒公式,有 20000)(!2)())(()()(x x f x x x f x f x f -''+-'+=η.(η介于x 与0x 之间)分别⽤b x a x ==、代⼊上式,得 201000)(!2)())(()()(x a f x a x f x f a f -''+-'+=η 4)(!2)(2)2()2(21b a f b a b a f b a f -''+-+'++=η(21b a a +<<η),202000)(!2)())(()()(x b f x b x f x f b f -''+-'+=η 4)(!2)(2)2()2(22a b f a b b a f b a f -''+-+'++=η(b b a <<+22η),上两式相加,得]2)()([4)()2(2)()(212ηηf f a b b a f b f a f ''+''-++=+,由)(x f ''连续,根据习题1-7(B )4,得)(2)()(21ξηηf f f ''=''+''()(b a ,∈ξ),于是,)(4)()2(2)()(2ξf a b b a f b f a f ''-++=+,所以,有)(b a ,∈ξ使得)(4)()2(2)()(2ξf a b b a f b f a f ''-=+-+. 7.若函数)(x f 有⼆阶导数,0)(>''x f ,且1)(lim=→xx f x ,⽤泰勒公式证明x x f ≥)(. 证明:由函数)(x f 可导,及1)(lim=→xx f x ,得1)0(0)0(='=f f ,,将)(x f 展开为⼀阶麦克劳林公式,有22)()(x f x x f ξ''+=(ξ介于0与x 之间),由0)(>''x f ,得x x f x x f ≥''+=22)()(ξ.8.设函数)(x f 在区间]20[,上⼆次可微,)2()0(f f =,且M x f ≤'')(,对任何]20[,∈x ,证明M x f ≤')(.证明:对任何∈x ]20[,,将函数)(t f y =在x t =点展开为⼀阶泰勒公式,有 2)(!2)())(()()(x t f x t x f x f t f -''+-'+=ξ.(ξ介于x 与t 之间)分别⽤20==t t 、代⼊上式,得 21!2)()()()0(x f x x f x f f ξ''+'-=,(x <<10ξ)(1) 22)2(!2)()2)(()()2(x f x x f x f f -''+-'+=ξ,(22<<ξx )(2)(2)-(1),并由条件)2()0(f f =,有 ])()2)(([21)(202122x f x f x f ξξ''--''+'=,即])()2)(([41)(2122x f x f x f ξξ''--''-=',所以M x x M x x M x f =+-?≤+-≤'222])2[(4])2[(4)(.习题3—4(A )1.下列叙述是否正确?并按照你的判断说明理由:(1)设函数()f x 在区间[,]a b 上连续,在(,)a b 内可导,那么()f x 在区间[,]a b 上单调增加(减少)的充分必要条件是对任意的(,)x a b ∈,0)(>'x f (0)(<'x f );(2)函数的极⼤值点与极⼩值点都可能不是唯⼀的,并且在其驻点与不可导点处均取得极值;(3)判定极值存在的第⼀充分条件是根据驻点两侧导数的符号来确定该驻点是否为极值点,第⼆充分条件是根据函数在其驻点处⼆阶导数的符号来判定该驻点是否为极值点;(4)在区间I 上连续的函数,其最⼤值点或最⼩值点⼀定是它的极值点.答:(1)不正确.如3x y =在]11[,-上单调增加,⽽032≥='x y .(2)前者正确,后者不正确.驻点与不可导点是取得极值必要条件不是充分条件,如函数3x y =有驻点0=x ,⽽3x y =在0=x 点不取极值;⼜如函数3x y =有不可导点0=x ,⽽3x y =在0=x 点也不取极值.(3)前者不正确,后者正确.第⼀充分条件对连续函数的不可导点也适⽤.(4)不正确.函数的最⼤(⼩)值点可以是闭区间端点,这时的最值点就不是极值点. 2.证明函数x x x f arcsin )(-=在]11[,-上单调减少.解:在开区间)11(,-内,0111)(2≤--='xx f ,且等号只在0=x 点成⽴,所以)(x f 在开区间)11(,-内单调减少,⼜因为函数x x x f arcsin )(-=在区间]11[,-的左、右端点处分别右连续、左连续,所以x x x f arcsin )(-=在]11[,-上单调减少. 3.求下列函数的单调区间和极值:(1)323y x x =-;(2)xx y 12+=;(3)3232x x y +?=;(4)2exy x =;(5)x x y -+=)1ln(;(6))1ln(2-=x y .解:(1)定义域为)(∞+-∞,,)2(3632-=-='x x x x y ,由0='y ,得驻点0=x ,2=x ,函数没有不可导点.单增区间为:)2[]0(∞+-∞,、,,单减区间为:]20[,,极⼤值为:0)0(=y ,极⼩值为:4)2(-=y .(2)定义域为)0()0(∞+-∞,,,221xx y -=',由0='y ,得驻点1±=x ,在定义域内函数没有不可导点.单增区间为:)1[]1(∞+--∞,、,,单减区间为:]10()01[,、,-,极⼤值为:2)1(-=-y ,极⼩值为:2)1(=y .(3)定义域为)(∞+-∞,,2233)1(2xx y ?+=',由0='y ,得驻点1-=x ,不可导点0=x .单增区间为:)1[∞+-,,单减区间为:]1(--∞,,⽆极⼤值,极⼩值为:1)1(-=-y .(4)定义域为)0()0(∞+-∞,,,3)2(e xx y x -=',由0='y ,得驻点2=x ,在定义域内函数没有不可导点.单增区间为:、,)0(-∞)2[∞+,,单减区间为:]20(,,⽆极⼤值,极⼩值为:4/e )2(2=y .(5)定义域为)1(∞+-,,xxy +-='1,由0='y ,得驻点0=x ,在定义域内函数没有不可导点.单增区间为:]01(,-,单减区间为:)0[∞+,,极⼤值为:0)0(=y ,⽆极⼩值.(6)定义域为)1()1(∞+--∞,,,122-='x xy ,在定义域内0≠'y ,且没有不可导点.单增区间为:)1(∞+,,单减区间为:)1(--∞,,既⽆极⼤值,也⽆极⼩值.4.求下列函数在指定区间的最⼤值M 和最⼩值m :(1)163)(24+-=x x x f ,]20[,∈x ;(2)11)(+-=x x x f ,]40[,∈x .解:(1))1(121212)(23-=-='x x x x x f ,由0)(='x f ,得1=x (10-==x x ,都不在)20(,内),⽐较数值25)2(2)1(1)0(=-==f f f ,,,得163)(24+-=x x x f 在。
大学高等数学第五章 定积分及其应用答案
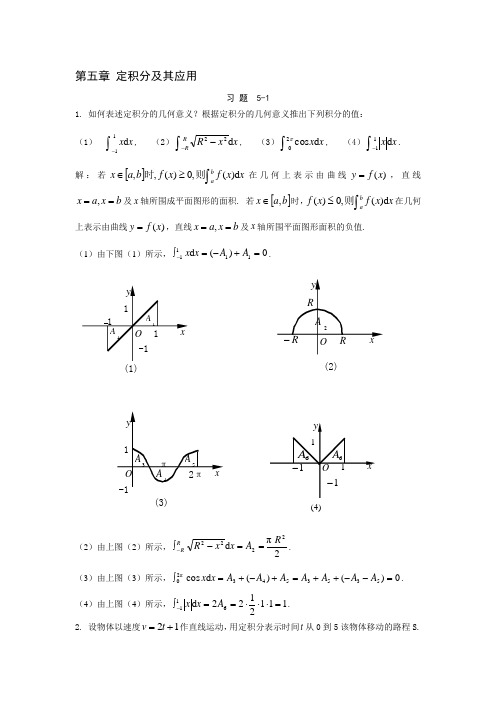
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义?根据定积分的几何意义推出下列积分的值: (1)⎰-x x d 11, (2)⎰--x x R R R d 22, (3)⎰x x d cos 02π, (4)⎰-x x d 11.解:若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时,⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =,直线b x a x ==,及x 轴所围平面图形面积的负值. (1)由下图(1)所示,0)(d 1111=+-=⎰-A A x x .(2)由上图(2)所示,2πd 2222R A x x R R R==-⎰-.(3)由上图(3)所示,0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . (4)由上图(4)所示,1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动,用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解:=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解:任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =,小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式:∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解:上在]1,0[)(2x x f =连续函数,故可积,因此为方便计算,我们可以对[]0,1 n 等分,分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点,故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ(即时∞→n ),由定积分的定义得: 120d x x ⎰=31.5. 利用定积分的估值公式,估计定积分⎰-+-1134)524(x x x d 的值.解:先求524)(34+-=x x x f 在[]1,1-上的最值,由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小,知min max 5093,111024f f ==,由定积分的估值公式,得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ,哪个积分值较大?解:在[]0,1区间内:22xx x x e e ≥⇒≥ 由性质定理知道:⎰1d xe x≥⎰1d 2x e x7. 证明:⎰---<<2121212d 22x e ex 。
高等数学李伟版课后习题答案第八章.

习题8—1(A)1.判断下列论述是否正确,并说明理由:(1)一个点集的内点一定属于,其外点一定不属于,其边界点一定不属于,其聚点一定属于;(2)开集的所有点都是其内点,开集也称为开区域;(3)一个有界集一定能包含在以坐标原点为圆心,适当长的线段为半径的圆内;(4)考查二元函数的定义域时,应从两方面去考虑:用解析式表达的函数要考虑使该解析式有意义的所对应的点的集合(自然定义域).对有实际意义的函数还应该从自然定义域中找出使实际问题有意义的点集;(5)当沿某一条曲线趋于时,函数的极限存在,并不能说明极限存在,但如果当沿某一条使函数有定义的曲线趋于时,函数的极限不存在,则一定不存在;(6)为说明极限不存在,通常也采取用当沿两条不同曲线趋于时,函数的极限不相等的方法;(7)如果函数在点连续,点必须是函数定义域的内点;(8)若是二元函数的间断点,那么一定不存在.答:(1)前两者都正确,这是根据内点、外点的定义;后两者都不正确,无论是边界点还是聚点它们都可以是的点,也可以是非的点,如当是闭集是,的边界点是的点当是开集时的边界点就不是的点;又如点是集合的聚点,但是它不是的点.(2)前者正确,这是有开集定义决定的;后者不正确,连通的开集才是开区域,不连通的开集不是开区域,如是开集,但是不是开区域.(3)正确,这就是有界集的定义.(4)正确,求多元函数的自然定义域如同一元函数的定义域,要从以下几个方面考虑:①分式中分母不能为零,②开偶次方底数要大于等于零,③对数中真数要于零,④、中要求,⑤若干个式子的四则运算中,取每个式子有意义的交集,等等.(5)两者都正确,如:不存在,但是沿取极限时值为1;后者是由极限的定义决定.(6)正确,这是证明多元函数极限不存在的基本方法,它源于在中,是以(定义域内的)任意方式实现的.(7)不正确.如:在点连续,但是点不是函数定义域的内点.(8)不正确.如:点是函数的间断点,但是极限.2.判定下列平面点集中哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点所组成的集合(称为导集,用表示)和边界:(1);(2);(3);(4).解:(1)是有界闭区域,其导集,其边界.(2)是非开非闭的有界区域,其导集,其边界.(3)是无界区域,其导集,.(4)是有界开集(不是区域),其导集,其边界.3.设函数,求,.解:,.4.设函数,求.解:.5.设函数,已知时,,求及的表达式.解:由时,,有,即,所以;而.6.设函数,求的表达式.解:(方法1)因为,所以.(方法2)令,则,于是,所以.7.求下列各函数的定义域,并作定义域草图:(1);(2);(3);(4).解:(1)由且,得定义域.(2)由及,有,得定义域.(3)由,有,得定义域.(4)由,有,或,得定义域.8.求下列极限:(1);(2);(3);(4);(5);(6).解:(1).(2).(3).(4)因为有界,而,所以.(5).(6).9.证明下列极限不存在:(1);(2).证明:(1)沿取极限,则,当取不同值时,该极限值不同,所以极限不存在.(2)先沿取极限,则;再沿取极限,则,由于沿两种不同方式取极限其极限值不同,所以极限不存在.10.找出下列函数的间断点的集合:(1);(2);(3).解:三个函数都是初等函数,找间断点只需找函数无定义的点,并且这些点又是定义域的聚点.(1)函数只在点无定义,且是定义域的聚点,所以断点的集合.(2)函数在圆周上无定义,且圆周上的点都是定义域的聚点,所以断点的集合.(3)函数的定义域,函数在及上无定义,这些点中只有,及()是定义域的聚点,所以断点的集合.习题8—1(B)1.某厂家生产的一种产品在甲、乙两个市场销售,销售价格分别为(单位:元),两个市场的销售量各自是销售价格的均匀递减函数,当售价为10元时,销售量分别为2400、850件,当售价为12元时,销售量分别为2000、700件.如果生产该产品的成本函数是,试用表示该厂生产此产品的利润.解:根据已知,设,由时,;时,,有得,于是.由时,;时,,有得,于是.两个市场销售该产品的收入为,该产品的成本.根据利润等于收入减去成本,得.2.设函数求函数值.解:当时,则,于是;当时,则,于是.3.求函数的定义域.解:由,有且,即且,或写作且;或且,即且,或写作且,所以定义域.4.求下列极限:(1);(2);(3);(4).解:(1)令,则当时,,所以.或者:因为时,与是等价无穷小,所以.(2).(3)令,则当时,(其中在区间内任意变化),所以.(4)因为,而,,根据“夹逼准则”得.5.证明极限不存在.证明:先沿取极限,,再取极限,,由于沿两种不同方式取极限其极限值不同,所以极限不存在.6.讨论函数的连续性.解:当时,是连续函数.当时,满足的点是轴上点或轴上点,对轴上点,极限,这些点是函数的连续点.对轴上点(除去),当时,极限不存在(极限不是零,震荡),所以这些点是间断点.综上,函数在点()处不连续,其余点处都连续.习题8—2(A)1.判断下列论述是否正确,并说明理由:(1)极限既是的一元函数在点处的导数,也是二元函数在点处对变量的偏导数;(2)二元函数在某一点处连续是在这点偏导数存在的必要条件;(3)二元函数的两个二阶混合偏导数与只要存在就一定相等.答:(1)正确,这是根据导数与偏导数的定义.(2)不正确,例如函数在点处连续,但是都不存在.事实上:因为不存在,所以不存在;由变量的对称性得,也不存在.(3)不正确.还需要与连续,否则它们不一定相等,如函数在点处,,从而.事实上,,特别,,特别,,.2.求下列函数对各个自变量的一阶偏导数:(1)();(2);(3);(4);(5)();(6);(7);(8);(9);(10).解:(1)将函数改写为,则,.(2),.(3),.(4),.(5),.(6),.(7),.(8),由变量的对称性,得.(9),,.(10),,.3.求下列函数在指定点的偏导数:(1)设,求及;(2)设,求及.解:(1)在时,将函数改写为,则,,.(2)因为,所以,因为,所以.4.求曲线在点处的切线与轴正向的夹角.解:,,用表示曲线在点处的切线与轴正向的夹角,则,所以.5.求下列函数的高阶偏导数:(1)设,求,,和;(2)设,求,和;(3)设,求,和.解:(1),,,,,,.(2),,,,,.(3),,,,.6.设函数,求,和.解:因为,则,因为,则,.7.设函数,证明.证明:因为,所以.8.设函数,证明.证明:因为,所以.9.设函数,证明.证明:因为,,,,,,所以.10.若函数都可导,设,证明.证明:因为,,,所以.习题8—2(B)1.设一种商品的需求量是其价格及某相关商品价格的函数,如果该函数存在偏导数,称为需求对价格的弹性、为需求对价格的交叉弹性.如果某种数码相机的销售量与其价格及彩色喷墨打印机的价格有关,为,当,时,求需求对价格的弹性、需求对价格的交叉弹性.解:由,,有,,当,时,需求对价格的弹性:,需求对价格的交叉弹性:.2.已知满足,证明.证明:由,有,由,有,由,有,得.3.设函数,证明.证明:将函数改写为,则,,由变量的对称性,有,,所以.4.设函数满足,且,,求.解:由,两边同时对求不定积分,有,用代入该式,有,根据条件,得,于是.上式两边同时再对求不定积分,有,由条件,得,所以.5.设函数,求及.解:,(或由变量的对称性求得).6.设函数证明在点处的两个偏导数都不存在.证明:因为极限不存在,极限不存在,所以在点处的两个偏导数都不存在.习题8—3(A)1.判断下列论述是否正确,并说明理由:(1)称函数在可微分,如果在这一点函数的两个偏导数都存在,并且,其中为函数在点的全增量,;(2)函数在一点可微分,它在这点必连续;(3)函数在一点可微分的充分必要条件是,在这点的偏导数都存在;(4)函数在一点的偏导数连续,能保证在这点附近曲面可以用平面来近似替代,其中.答:(1)正确,可微的必要条件是两个偏导数存在,且,再根据,有,即.,这就是函数可微的定义.(2)正确,事实上,由可微,根据定义有,于是,这表明函数在该点连续.(3)不正确,偏导数存在仅仅是可微的必要条件,而不是可微的充分条件,如函数在两个偏导数都存在且等于零(习题8-2(B)5),但是函数在不可微.事实上,若可微,则,但是不存在(分别沿、取极限,其值为0及),这与矛盾,所以函数在不可微.函数可微的充分条件是偏导数在该点连续.(4)正确,若记,则,由此得,这表明在点附近曲面可以用平面来近似替代,这就是所谓的局部线性化.2.求下列函数的全微分:(1);(2);(3);(4);(5);(6).解:(1)因为,,所以.(2)因为,,所以.(3)因为,,所以.(4)因为,,所以(5)因为,,,所以.(6)因为,,,所以.3.当,时,求函数的全微分和局部线性化.解:因为,,,,所以,而,.4.当,,,时,求函数的全增量及全微分.解:,,,,当,,,时:全增量,全微分.习题8—3(B)1.一个圆柱形构件受压后发生形变,它的半径由cm增加到cm,高由cm减少到cm,求此构件体积变化的近似值.解:设构件的高为、底半径为、体积为,则.,,于是,当时,(,即体积大约减少了628 (.2.计算的近似值.解:考虑函数,取,而,,、、,则.3.设函数在点的某个邻域内可微,且,其中,求函数在点处的全微分及局部线性化.解:在中,令,得.在点考虑函数的全增量:,(其中)根据全微分的定义,有,并且得..4.设函数在点处讨论偏导数的存在性、偏导数的连续性以及函数的可微性.解:因为,,所以在点处函数的两个偏导数都存在,且.再讨论可微性,函数在处的全增量用表示,则,记,则不存在(沿取极限,其值为;沿取极限,其值为),所以函数在点处不可微.进而得偏导(函)数在点处不连续(若偏导(函)数在点处连续,根据可微的充分条件,则函数一点可微,与函数不可微矛盾).习题8—4(A)1.判断下列论述是否正确,并说明理由:(1)对多元复合函数来说,欲求其对自变量的偏导数,借助于树形图比较方便.不论中间变量是几元函数,最终求出的偏导数所含的项数等于从因变量到达该自变量的路径数目,某一项有几个因式,取决于与该项相对应的路径中所含有的线段数目;(2)对于可微的复合函数,,对于的偏导数;(3)利用全微分形式的不变性,对一个多元复合函数来说可以先求其全微分,最后再得出该复合函数对各自变量的偏导数.答:(1)正确,这是复合函数的链式求导法则决定的,如若函数由函数复合而成,复合函数的树形图为右图,而在图中我们可以看到从变量到变量有四条路径,由此导数公式中有四项之和,而每一项中(如第一项)偏导数或导数的个数(3个)等于这条路径上从到段数(3段).(2)不正确,左、右式中的含义不同,左式中表示对自变量求导,它涉及图中三个,而右式中的仅表示对中间变量(一)求导,(当某一个变量在复合函数中有双重身份,既是自变量又是中间变量时会出现这种记号混淆情况),为了与左式中区别,此处应当用记号(同时分别用)表示,即写作.(3)正确,即若某个复合函数的全微分是(通常这个全微分是由微分法则与微分形式不变性求得),则、,这是多元复合函数求偏导数的方法之一.2.设函数,而,,求.解:(方法1)函数的复合关系如图,则.(方法2)消去中间变量,有,按一元函数求导,得.(注:具体函数的复合函数都有以上两种方法,并且方法2简单,但是本节的目的在于练习复合函数链式求导方法,所以后面只用方法1求导)3.设函数而是的可微函数,求.解:.4.设函数,而,求.解:.5.设函数,而,,求和.解:,.6.设函数,求和.解:这是幂指函数求导,为方便求导,将它写作复合函数,为此令,则,.(注:可以由变量的对称性直接写出)7.求下列函数的一阶偏导数(其中函数具有一阶连续的偏导数或导数):(1);(2);(3);(4).解:(1),.(2),.(3),.(4),,.8.设函数,其中是可微函数,证明.证明:因为,,所以.9.设函数,其中是可微函数,证明.证明:因为,,所以.10.用微分形式不变性求函数的偏导数和.解:令,则,则根据微分法则与微分形式不变性,得所以,,.习题8—4(B)1.在解偏微分方程(含有未知函数的偏导数的方程,也称为数理方程)时,常常要用变量代换将一个复杂的方程化为一个简单的方程,从而可以求其解.设具有二阶连续偏导数,若用变量代换将偏微分方程化为,求的值.解:,,,,.由,有,即,要化为,必须,且,由,即,得或,但是由,所以只能是.2.设有一阶连续偏导数,且满足,,,求.解:令,等式两边同时对求导,有,(*)由于,,则(*)式化为,所以.3.若函数有二阶导数,且,又函数满足方程,求.解:令,则,于是,,,,由,有,即,这是二阶常系数线性齐次微分方程,特征方程是,特征根为,方程的通解是,,由条件,有,,得,所求所求函数是.4.若函数可微,且对任何正实数有,证明.证明:等式两边同时对导,则,记,则上式为,令,得,将该式中的分别用表示,则,即.5.求下列函数的二阶偏导数(其中函数具有二阶连续偏导数):(1);(2);解:(1),,,,.(2),,,,.6.设,其中函数、有二阶导数,求、及.解:,,,,.7.设,其中函数、有二阶导数,证明.证明:因为,,.所以.习题8—5(A)1.判断下列论述是否正确,并说明理由:(1)要使方程确定一个隐函数,如果将定理5.1中的条件换为而其它不变,则该方程仍能确定一个隐函数;(2)如果函数满足类似于定理5.1的条件,对各个自变量有连续偏导数,且对某个变量的偏导数不为零,则元方程可以确定一个具有连续偏导数的元函数;(3)若按照教材中的说法,一个方程组可以确定一组多元函数.那么函数的个数等于方程组中方程的个数,函数的元数等于方程中所含变量的总个数减去方程的个数;(4)若方程组能确定两个二元隐函数那么通过对该方程组中的各个方程的两边对同一个变量求导,就可以得到含有的方程组,通过解这个方程组,就可以求得.答:(1)不正确,如方程(其中),在点处有,但是它不能确定一个隐函数,因为在这点左侧附近给定一个对应有两个值,在这点右侧附近没有值对应;当且其它条件不变时,可以确定一个一元函数.(2)正确,这是定理5.1的推广.(3)正确,但是要注意两点,一是变量的个数需大于方程的个数(否则方程组可能只确定一点,或者无解);二是要满足隐函数存在的条件(超出教学要求,此处略去).(4)正确,如同例5.4、例5.5等的解法.2.若函数分别由下列方程确定,求.(1);(2);(3);(4).解:(1)(方法1)设,则,所以(方法2)方程两边同时对求导,有,解得.(注:两种方法最大的差别在于:方法1中在求时都看作自变量,而方法2在求导过程中要看作的函数.尽管方法1简单一些,但是它有局限性,只适用于求一个方程确定的隐函数的一阶导数或偏导数,而方法2适用于各类隐函数的各阶导数或偏导数的求法,后面一般都按方法2作)(2)方程两边同时对求导,有,解得.(3)方程两边同时对求导,有,得.(4)方程两边取对数,有,该式两边同时对求导,有,即,解得.3.设函数分别由下列方程确定,求.(1);(2).解:(1)方程两边同时对求导,有,得,.(2)方程两边同时对求导,有,解得,.4.若函数分别由下列方程确定,求及.(1);(2);(3);(4).解:(1)(方法1)设,则,所以.(方法2)方程两边对求导,有,得,方程两边对求导,有,得.(以下都按方法2作)(2)方程两边同时对求导,有,得,方程两边同时对求导,有,得(或由变量的对称性,得).(3)方程两边对求导,有,即,而,所以,得,由变量对称性有.(4)方程改写为,方程两边对求导,有,得,方程两边对求导,有,得.5.若函数,,都是由方程确定的隐函数,其中有一阶连续非零的偏导数,证明.证明:因为,所以.6.设函数,而函数由方程确定,求全导数.解:方程两边同时对求导,有,得,.7.设函数,而函数、分别由方程及确定,求全导数.解:方程两边同时对求导,有,得,方程两边同时对求导,有,得,所以.8.设函数,而由方程确定,求.解:方程两边同时对求导,有,用、代入,有,得.于是,所以.习题8—5(B)1.某工件的外表面是一个椭球面,方程由给出,现在点处要将其局部线性化(即做一个切平面),求局部线性化表达式.解:设方程在点确定的隐函数为,方程两边对求导,有,用、代入,有,得,由变量对称性,得.所以.2.若函数由方程确定,求.解:方程两边对求导,有,得,由变量的对称性,得.等式两边同时对求导,有,即所以.或.3.若函数由方程确定,其中是可微函数,求、.解:方程两边同时对求导,有,解得,方程两边同时对求导,有,解得.4.若函数由方程确定,其中是可微函数,证明.证明:方程两边同时对求导,有,得,方程两边同时对求导,有,得,所以.5.设函数,而由方程确定,其中函数连续,、可微,且,求.解:方程两边对求导,有,得,方程两边对求导,有,得.,所以.6.求由下列方程组所确定函数的导数或偏导数:(1)求和.(2)求及.解:(1)方程组两边同时对求导,有消去,有,得,而.(2)方程组两边同时对求导,有(1)(2),有,得,再代入到(2)之中得.方程组两边同时对求导,有与前面解法类似,得,.习题8—6(A)1.判断下列论述是否正确,并说明理由:(1)如果曲线的参数方程为(),那么它就对应一个向量值方程若存在并且不同时为零,那么,曲线在相应点处的切向量为,由此利用直线的点向式方程就可写出该点处的切线方程;(2)求曲线的切线方程与法平面方程的关键是求切向量,而其中又以参数方程为基础,其它形式的曲线方程都划归为参数方程,找出相应的切向量,然后写出要求的方程;(3)曲面的切平面方程是以曲面的一般方程为基础进行讨论的,如果曲面方程为的形式,那么必须把它化为的形式,其中,因而它在点处的法向量一定为,切平面方程为:;(4)如果曲线为一般方程那么,曲线在点的切向量可取为.答:(1)正确,这就是曲线为参数方程时,切线方向向量的求法.此时切线方程为;法平面方程为.(2)正确,对参数方程,在处的切向量;对形如的取向方程,将变量看作参数,在处的切向量对一般方程按隐函数它可以确定两个一元函数,如,按隐函数求导方法得到,从而得在处的切向量.(3)不确切,曲面的法向量可以直接由给出,也可以由给出.(4)正确,设曲面在点处的法向量为,曲面在点处的法向量为,根据法平面的定义有,于是可取.2.空间一质点在时刻时的位置为,求质点在时刻的速度.解:.3.求曲线在点处的切线及法平面方程.解:点对应参数为,切向量,切线方程为,法平面方程为,即.4.求曲线,在对应于的点处的切线及法平面方程.解:切点为,切向量,切线方程为,法平面方程为,即.5.求曲线在点处的切线及法平面方程.解:,切向量,切线方程为,法平面方程为,即.6.求曲线在点处的切线及法平面方程.解:设,则切向量,切线方程为,法平面方程为,即.7.求曲面在点处的切平面及法线方程.解:设,则法向量,切平面方程是,即,法线方程是.8.求曲面在点处的切平面及法线方程.解:法向量切平面方程是,即,法线方程是.习题8—6(B)1.求曲线()上平行于平面的切线方程,并写出该点处的法平面方程.解:设切点坐标为,该点对应参数,曲线在该点的切向量为,由切线与平面平行,有,得,即,由于,所以.切点坐标为,切向量,切线方程为,法平面方程为,即.2.在椭球面上求平行于平面的切平面方程.解:设切点坐标为,,则法向量,由切平面平行于平面,有,即,代入到曲面方程之中,有,得,切点为或,在点,切平面为,即;在点,切平面为,即.3.问旋转抛物面上哪一点处的切平面过曲线,,在点处的切线.解:设切点坐标为,则法向量,切平面方程为,即.曲线,,在点对应参数,曲线在点处的切向量.由在曲面上,有.①由切平面过,有.②曲线,,在点处的切线在切平面上,有所以,即.③由方程①、②、③式解得或,于是所求点为或.4.证明二次曲面在点处的切平面方程为:.证明:设,则曲面在的法向量。
高等数学课后习题答案第五章
解:
.
(6) (7) 抛物线 y = − x 2 +4 x − 3 及其在(0,−3)和(3,0)处的切线; 解:y′ = − 2 x +4 . ∴y ′(0)=4 , y ′(3)= − 2 . ∵ 抛物线在点(0 , − 3) 处切线方程是 y =4 x − 3 在 (3 , 0) 处的切线是 y = − 2 x +6 两切线交点是( , 3) . 故 所 求 面 积 为 (7)
(8) 摆线 x = a ( t − sin t ) , y = a (1 − cos t ) 的一拱 (0≤t ≤2π)与 x 轴; 解:当 t =0 时, x =0, 当 t =2π时, x =2πa . 所以
S=∫
2πa
0
ydx = ∫ a (1 − cos t ) da (t − sin t )
(图 22)
kmρ ds kmρ kmρ = 2 ( Rdθ ) = dθ 2 R R R kmρ dFx = dF cos θ = cos θ dθ , R
dF =
则
Fx = ∫
ϕ 2 ϕ − 2
ϕ km ρ km ρ 2kmρ ϕ cosθ dθ = 2 ∫ 2 cos θ dθ = sin 0 R R R 2
(19) 设水的比重为 1, ,则将这薄水层吸出池面所作的微功为 dw=x·60 g d x =60 gx d x . 于是将水全部抽出所作功为
. 13. 有一等腰梯形闸门,它的两条底边各长 10m 和 6m,高为 20m,较长的底边与水面相 齐,计算闸门的一侧所受的水压力. 解:如图 20,建立坐标系,直线 AB 的方程为 . 压力元素为 所求压力为 =1467(吨) =14388(KN) 14. 半径为 R 的球沉入水中,球的顶部与水面相切,球的密度 (20)
高等数学参考解答 (5)

5.对所给方程配方可知
可见,是球面方程,球心坐标 半径5
6.(1)椭圆柱面(2)双曲线柱面(3)抛物柱面(4)椭圆柱面
7.椭球
B组
1.选择练习题
(1)空间点 关于 轴的对称点是
A B
C D
(2)在空间直角坐标系中,点 位于
A第5卦限B第4卦限
C第2卦限D第3卦限
(3)在 坐标面上与已知三点 , 和 等距的点是
解之得
又在(2,1)点有 , , ,因此
,
从而函数在(2,1)点处有极小值 。
⑵求偏导,联立求驻点
解之得 ,
在(-3,-2)点有 , , ,因此
,
从而函数在(-3,-2)点处有极大值 ;
另一方面,在(-3,2)点有 , , ,因此此点处有
从而,驻点 不是极值点.
7.设长方体的长宽高分别为x, y, z,先给出体积函数
2.(1)(-x,y,z),(x,-y,-z),(0,0,z)(2)
(3)c(y-b)+b(z-c)=0。
3.(1)过z轴,则平面的方程为
又过点( ,1, ),则有 ,因此平面方程为
x+3y=0
(2)平行于x轴的平面方程为
又过点A( ,1, )和B(3,0,5),从而
得
从而所求平面的方程为
(3)平行于xOy面的平面方程为
3.⑴ ,
⑵ ,
⑶ ,
⑷ ,
⑸ ,
⑹ ,
4.⑴先求一阶偏导数
,
因此
, ,
⑵先求一阶偏导数
,
因此
, ,
⑶先求一阶偏导数
,
因此
, ,
⑷先求一阶偏导数
高教线性代数第五章 二次型课后习题答案

第五章 二次型1.用非退化线性替换化下列二次型为标准形,并利用矩阵验算所得结果。
1)323121224x x x x x x ++-;2)23322221214422x x x x x x x ++++; 3)32312122216223x x x x x x x x -+--;4)423243418228x x x x x x x x +++; 5)434232413121x x x x x x x x x x x x +++++;6)4342324131212422212222442x x x x x x x x x x x x x x x ++++++++; 7)43322124232221222x x x x x x x x x x ++++++。
解 1)已知 ()323121321224,,x x x x x x x x x f ++-=, 先作非退化线性替换(1) 则()312221321444,,y y y y x x x f ++-=2223233121444y y y y y y ++-+-=()222333142y y y y ++--=, 再作非退化线性替换(2) 则原二次型的标准形为()2322213214,,z z z x x x f ++-=,最后将(2)代入(1),可得非退化线性替换为 (3) 于是相应的替换矩阵为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-=100211212102110001021021100011011T , 且有。
2)已知()=321,,x x x f 23322221214422x x x x x x x ++++,由配方法可得()()()233222222121321442,,x x x x x x x x x x x f +++++=()()2322212x x x x +++=,于是可令, 则原二次型的标准形为()2221321,,y y x x x f +=,且非退化线性替换为, 相应的替换矩阵为 , 且有⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--='000010001100210211420221011122011001AT T 。
高等数学第五章课后习题答案

班级姓名学号1 第五章定积分1.证明定积分性质:òò=b abadxx f kdx x kf )()((k 是常数). 证:òåòå=D =D ==®=®banii ban ii x kf x kf x f k x f k)()(lim )(lim )(1010x x l l 2.估计下列积分值:(1)dxx )sin 1(4542ò+p p解:令x x f 2sin 1)(+=,则02sin cos sin 2)(===x x x x f ‘得驻点:,,221p p==x x 由23)4(,23)4(,1)(,2)2(====p p p pf f f f ,得2)(max ,1)(min ==x f x f 由性质,得pp p p2)(454££òdx x f (2)ò333arctan xdxx 解:令x x x f arctan )(=,01arctan )(2>++=xxx x f ‘,所以)(x f 在]333[,上单调增加,p p33)(max ,36)(min ==\x f x f ,)()(33333arctan 33336333-££-\òp pxdx x ,即pp32a r c t a n 9333££òx d x x班级班级 姓名姓名 学号学号3.比较下列积分值的大小:.比较下列积分值的大小: (1)dx x ò12与dxx ò13解:当10££x 时,有23x x £,且23x x -不恒等于0,0312>-\òdx x x )(,即,即 dxx dxx òò>1212。
(2)ò6pxdx 与ò6sin pxdx解:当60p££x 时,有x x £sin ,且x x sin -不恒等于0,0sin 10>-\òdx x x )(,即,即 dx x dx x òò>1010sin 。
高等数学李伟版课后习题答案第八章.

习题8—1(A)1.判断下列论述是否正确,并说明理由:(1)一个点集的内点一定属于,其外点一定不属于,其边界点一定不属于,其聚点一定属于;(2)开集的所有点都是其内点,开集也称为开区域;(3)一个有界集一定能包含在以坐标原点为圆心,适当长的线段为半径的圆内;(4)考查二元函数的定义域时,应从两方面去考虑:用解析式表达的函数要考虑使该解析式有意义的所对应的点的集合(自然定义域).对有实际意义的函数还应该从自然定义域中找出使实际问题有意义的点集;(5)当沿某一条曲线趋于时,函数的极限存在,并不能说明极限存在,但如果当沿某一条使函数有定义的曲线趋于时,函数的极限不存在,则一定不存在;(6)为说明极限不存在,通常也采取用当沿两条不同曲线趋于时,函数的极限不相等的方法;(7)如果函数在点连续,点必须是函数定义域的内点;(8)若是二元函数的间断点,那么一定不存在.答:(1)前两者都正确,这是根据内点、外点的定义;后两者都不正确,无论是边界点还是聚点它们都可以是的点,也可以是非的点,如当是闭集是,的边界点是的点当是开集时的边界点就不是的点;又如点是集合的聚点,但是它不是的点.(2)前者正确,这是有开集定义决定的;后者不正确,连通的开集才是开区域,不连通的开集不是开区域,如是开集,但是不是开区域.(3)正确,这就是有界集的定义.(4)正确,求多元函数的自然定义域如同一元函数的定义域,要从以下几个方面考虑:①分式中分母不能为零,②开偶次方底数要大于等于零,③对数中真数要于零,④、中要求,⑤若干个式子的四则运算中,取每个式子有意义的交集,等等.(5)两者都正确,如:不存在,但是沿取极限时值为1;后者是由极限的定义决定.(6)正确,这是证明多元函数极限不存在的基本方法,它源于在中,是以(定义域内的)任意方式实现的.(7)不正确.如:在点连续,但是点不是函数定义域的内点.(8)不正确.如:点是函数的间断点,但是极限.2.判定下列平面点集中哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点所组成的集合(称为导集,用表示)和边界:(1);(2);(3);(4).解:(1)是有界闭区域,其导集,其边界.(2)是非开非闭的有界区域,其导集,其边界.(3)是无界区域,其导集,.(4)是有界开集(不是区域),其导集,其边界.3.设函数,求,.解:,.4.设函数,求.解:.5.设函数,已知时,,求及的表达式.解:由时,,有,即,所以;而.6.设函数,求的表达式.解:(方法1)因为,所以.(方法2)令,则,于是,所以.7.求下列各函数的定义域,并作定义域草图:(1);(2);(3);(4).解:(1)由且,得定义域.(2)由及,有,得定义域.(3)由,有,得定义域.(4)由,有,或,得定义域.8.求下列极限:(1);(2);(3);(4);(5);(6).解:(1).(2).(3).(4)因为有界,而,所以.(5).(6).9.证明下列极限不存在:(1);(2).证明:(1)沿取极限,则,当取不同值时,该极限值不同,所以极限不存在.(2)先沿取极限,则;再沿取极限,则,由于沿两种不同方式取极限其极限值不同,所以极限不存在.10.找出下列函数的间断点的集合:(1);(2);(3).解:三个函数都是初等函数,找间断点只需找函数无定义的点,并且这些点又是定义域的聚点.(1)函数只在点无定义,且是定义域的聚点,所以断点的集合.(2)函数在圆周上无定义,且圆周上的点都是定义域的聚点,所以断点的集合.(3)函数的定义域,函数在及上无定义,这些点中只有,及()是定义域的聚点,所以断点的集合.习题8—1(B)1.某厂家生产的一种产品在甲、乙两个市场销售,销售价格分别为(单位:元),两个市场的销售量各自是销售价格的均匀递减函数,当售价为10元时,销售量分别为2400、850件,当售价为12元时,销售量分别为2000、700件.如果生产该产品的成本函数是,试用表示该厂生产此产品的利润.解:根据已知,设,由时,;时,,有得,于是.由时,;时,,有得,于是.两个市场销售该产品的收入为,该产品的成本.根据利润等于收入减去成本,得.2.设函数求函数值.解:当时,则,于是;当时,则,于是.3.求函数的定义域.解:由,有且,即且,或写作且;或且,即且,或写作且,所以定义域.4.求下列极限:(1);(2);(3);(4).解:(1)令,则当时,,所以.或者:因为时,与是等价无穷小,所以.(2).(3)令,则当时,(其中在区间内任意变化),所以.(4)因为,而,,根据“夹逼准则”得.5.证明极限不存在.证明:先沿取极限,,再取极限,,由于沿两种不同方式取极限其极限值不同,所以极限不存在.6.讨论函数的连续性.解:当时,是连续函数.当时,满足的点是轴上点或轴上点,对轴上点,极限,这些点是函数的连续点.对轴上点(除去),当时,极限不存在(极限不是零,震荡),所以这些点是间断点.综上,函数在点()处不连续,其余点处都连续.习题8—2(A)1.判断下列论述是否正确,并说明理由:(1)极限既是的一元函数在点处的导数,也是二元函数在点处对变量的偏导数;(2)二元函数在某一点处连续是在这点偏导数存在的必要条件;(3)二元函数的两个二阶混合偏导数与只要存在就一定相等.答:(1)正确,这是根据导数与偏导数的定义.(2)不正确,例如函数在点处连续,但是都不存在.事实上:因为不存在,所以不存在;由变量的对称性得,也不存在.(3)不正确.还需要与连续,否则它们不一定相等,如函数在点处,,从而.事实上,,特别,,特别,,.2.求下列函数对各个自变量的一阶偏导数:(1)();(2);(3);(4);(5)();(6);(7);(8);(9);(10).解:(1)将函数改写为,则,.(2),.(3),.(4),.(5),.(6),.(7),.(8),由变量的对称性,得.(9),,.(10),,.3.求下列函数在指定点的偏导数:(1)设,求及;(2)设,求及.解:(1)在时,将函数改写为,则,,.(2)因为,所以,因为,所以.4.求曲线在点处的切线与轴正向的夹角.解:,,用表示曲线在点处的切线与轴正向的夹角,则,所以.5.求下列函数的高阶偏导数:(1)设,求,,和;(2)设,求,和;(3)设,求,和.解:(1),,,,,,.(2),,,,,.(3),,,,.6.设函数,求,和.解:因为,则,因为,则,.7.设函数,证明.证明:因为,所以.8.设函数,证明.证明:因为,所以.9.设函数,证明.证明:因为,,,,,,所以.10.若函数都可导,设,证明.证明:因为,,,所以.习题8—2(B)1.设一种商品的需求量是其价格及某相关商品价格的函数,如果该函数存在偏导数,称为需求对价格的弹性、为需求对价格的交叉弹性.如果某种数码相机的销售量与其价格及彩色喷墨打印机的价格有关,为,当,时,求需求对价格的弹性、需求对价格的交叉弹性.解:由,,有,,当,时,需求对价格的弹性:,需求对价格的交叉弹性:.2.已知满足,证明.证明:由,有,由,有,由,有,得.3.设函数,证明.证明:将函数改写为,则,,由变量的对称性,有,,所以.4.设函数满足,且,,求.解:由,两边同时对求不定积分,有,用代入该式,有,根据条件,得,于是.上式两边同时再对求不定积分,有,由条件,得,所以.5.设函数,求及.解:,(或由变量的对称性求得).6.设函数证明在点处的两个偏导数都不存在.证明:因为极限不存在,极限不存在,所以在点处的两个偏导数都不存在.习题8—3(A)1.判断下列论述是否正确,并说明理由:(1)称函数在可微分,如果在这一点函数的两个偏导数都存在,并且,其中为函数在点的全增量,;(2)函数在一点可微分,它在这点必连续;(3)函数在一点可微分的充分必要条件是,在这点的偏导数都存在;(4)函数在一点的偏导数连续,能保证在这点附近曲面可以用平面来近似替代,其中.答:(1)正确,可微的必要条件是两个偏导数存在,且,再根据,有,即.,这就是函数可微的定义.(2)正确,事实上,由可微,根据定义有,于是,这表明函数在该点连续.(3)不正确,偏导数存在仅仅是可微的必要条件,而不是可微的充分条件,如函数在两个偏导数都存在且等于零(习题8-2(B)5),但是函数在不可微.事实上,若可微,则,但是不存在(分别沿、取极限,其值为0及),这与矛盾,所以函数在不可微.函数可微的充分条件是偏导数在该点连续.(4)正确,若记,则,由此得,这表明在点附近曲面可以用平面来近似替代,这就是所谓的局部线性化.2.求下列函数的全微分:(1);(2);(3);(4);(5);(6).解:(1)因为,,所以.(2)因为,,所以.(3)因为,,所以.(4)因为,,所以(5)因为,,,所以.(6)因为,,,所以.3.当,时,求函数的全微分和局部线性化.解:因为,,,,所以,而,.4.当,,,时,求函数的全增量及全微分.解:,,,,当,,,时:全增量,全微分.习题8—3(B)1.一个圆柱形构件受压后发生形变,它的半径由cm增加到cm,高由cm减少到cm,求此构件体积变化的近似值.解:设构件的高为、底半径为、体积为,则.,,于是,当时,(,即体积大约减少了628 (.2.计算的近似值.解:考虑函数,取,而,,、、,则.3.设函数在点的某个邻域内可微,且,其中,求函数在点处的全微分及局部线性化.解:在中,令,得.在点考虑函数的全增量:,(其中)根据全微分的定义,有,并且得..4.设函数在点处讨论偏导数的存在性、偏导数的连续性以及函数的可微性.解:因为,,所以在点处函数的两个偏导数都存在,且.再讨论可微性,函数在处的全增量用表示,则,记,则不存在(沿取极限,其值为;沿取极限,其值为),所以函数在点处不可微.进而得偏导(函)数在点处不连续(若偏导(函)数在点处连续,根据可微的充分条件,则函数一点可微,与函数不可微矛盾).习题8—4(A)1.判断下列论述是否正确,并说明理由:(1)对多元复合函数来说,欲求其对自变量的偏导数,借助于树形图比较方便.不论中间变量是几元函数,最终求出的偏导数所含的项数等于从因变量到达该自变量的路径数目,某一项有几个因式,取决于与该项相对应的路径中所含有的线段数目;(2)对于可微的复合函数,,对于的偏导数;(3)利用全微分形式的不变性,对一个多元复合函数来说可以先求其全微分,最后再得出该复合函数对各自变量的偏导数.答:(1)正确,这是复合函数的链式求导法则决定的,如若函数由函数复合而成,复合函数的树形图为右图,而在图中我们可以看到从变量到变量有四条路径,由此导数公式中有四项之和,而每一项中(如第一项)偏导数或导数的个数(3个)等于这条路径上从到段数(3段).(2)不正确,左、右式中的含义不同,左式中表示对自变量求导,它涉及图中三个,而右式中的仅表示对中间变量(一)求导,(当某一个变量在复合函数中有双重身份,既是自变量又是中间变量时会出现这种记号混淆情况),为了与左式中区别,此处应当用记号(同时分别用)表示,即写作.(3)正确,即若某个复合函数的全微分是(通常这个全微分是由微分法则与微分形式不变性求得),则、,这是多元复合函数求偏导数的方法之一.2.设函数,而,,求.解:(方法1)函数的复合关系如图,则.(方法2)消去中间变量,有,按一元函数求导,得.(注:具体函数的复合函数都有以上两种方法,并且方法2简单,但是本节的目的在于练习复合函数链式求导方法,所以后面只用方法1求导)3.设函数而是的可微函数,求.解:.4.设函数,而,求.解:.5.设函数,而,,求和.解:,.6.设函数,求和.解:这是幂指函数求导,为方便求导,将它写作复合函数,为此令,则,.(注:可以由变量的对称性直接写出)7.求下列函数的一阶偏导数(其中函数具有一阶连续的偏导数或导数):(1);(2);(3);(4).解:(1),.(2),.(3),.(4),,.8.设函数,其中是可微函数,证明.证明:因为,,所以.9.设函数,其中是可微函数,证明.证明:因为,,所以.10.用微分形式不变性求函数的偏导数和.解:令,则,则根据微分法则与微分形式不变性,得所以,,.习题8—4(B)1.在解偏微分方程(含有未知函数的偏导数的方程,也称为数理方程)时,常常要用变量代换将一个复杂的方程化为一个简单的方程,从而可以求其解.设具有二阶连续偏导数,若用变量代换将偏微分方程化为,求的值.解:,,,,.由,有,即,要化为,必须,且,由,即,得或,但是由,所以只能是.2.设有一阶连续偏导数,且满足,,,求.解:令,等式两边同时对求导,有,(*)由于,,则(*)式化为,所以.3.若函数有二阶导数,且,又函数满足方程,求.解:令,则,于是,,,,由,有,即,这是二阶常系数线性齐次微分方程,特征方程是,特征根为,方程的通解是,,由条件,有,,得,所求所求函数是.4.若函数可微,且对任何正实数有,证明.证明:等式两边同时对导,则,记,则上式为,令,得,将该式中的分别用表示,则,即.5.求下列函数的二阶偏导数(其中函数具有二阶连续偏导数):(1);(2);解:(1),,,,.(2),,,,.6.设,其中函数、有二阶导数,求、及.解:,,,,.7.设,其中函数、有二阶导数,证明.证明:因为,,.所以.习题8—5(A)1.判断下列论述是否正确,并说明理由:(1)要使方程确定一个隐函数,如果将定理5.1中的条件换为而其它不变,则该方程仍能确定一个隐函数;(2)如果函数满足类似于定理5.1的条件,对各个自变量有连续偏导数,且对某个变量的偏导数不为零,则元方程可以确定一个具有连续偏导数的元函数;(3)若按照教材中的说法,一个方程组可以确定一组多元函数.那么函数的个数等于方程组中方程的个数,函数的元数等于方程中所含变量的总个数减去方程的个数;(4)若方程组能确定两个二元隐函数那么通过对该方程组中的各个方程的两边对同一个变量求导,就可以得到含有的方程组,通过解这个方程组,就可以求得.答:(1)不正确,如方程(其中),在点处有,但是它不能确定一个隐函数,因为在这点左侧附近给定一个对应有两个值,在这点右侧附近没有值对应;当且其它条件不变时,可以确定一个一元函数.(2)正确,这是定理5.1的推广.(3)正确,但是要注意两点,一是变量的个数需大于方程的个数(否则方程组可能只确定一点,或者无解);二是要满足隐函数存在的条件(超出教学要求,此处略去).(4)正确,如同例5.4、例5.5等的解法.2.若函数分别由下列方程确定,求.(1);(2);(3);(4).解:(1)(方法1)设,则,所以(方法2)方程两边同时对求导,有,解得.(注:两种方法最大的差别在于:方法1中在求时都看作自变量,而方法2在求导过程中要看作的函数.尽管方法1简单一些,但是它有局限性,只适用于求一个方程确定的隐函数的一阶导数或偏导数,而方法2适用于各类隐函数的各阶导数或偏导数的求法,后面一般都按方法2作)(2)方程两边同时对求导,有,解得.(3)方程两边同时对求导,有,得.(4)方程两边取对数,有,该式两边同时对求导,有,即,解得.3.设函数分别由下列方程确定,求.(1);(2).解:(1)方程两边同时对求导,有,得,.(2)方程两边同时对求导,有,解得,.4.若函数分别由下列方程确定,求及.(1);(2);(3);(4).解:(1)(方法1)设,则,所以.(方法2)方程两边对求导,有,得,方程两边对求导,有,得.(以下都按方法2作)(2)方程两边同时对求导,有,得,方程两边同时对求导,有,得(或由变量的对称性,得).(3)方程两边对求导,有,即,而,所以,得,由变量对称性有.(4)方程改写为,方程两边对求导,有,得,方程两边对求导,有,得.5.若函数,,都是由方程确定的隐函数,其中有一阶连续非零的偏导数,证明.证明:因为,所以.6.设函数,而函数由方程确定,求全导数.解:方程两边同时对求导,有,得,.7.设函数,而函数、分别由方程及确定,求全导数.解:方程两边同时对求导,有,得,方程两边同时对求导,有,得,所以.8.设函数,而由方程确定,求.解:方程两边同时对求导,有,用、代入,有,得.于是,所以.习题8—5(B)1.某工件的外表面是一个椭球面,方程由给出,现在点处要将其局部线性化(即做一个切平面),求局部线性化表达式.解:设方程在点确定的隐函数为,方程两边对求导,有,用、代入,有,得,由变量对称性,得.所以.2.若函数由方程确定,求.解:方程两边对求导,有,得,由变量的对称性,得.等式两边同时对求导,有,即所以.或.3.若函数由方程确定,其中是可微函数,求、.解:方程两边同时对求导,有,解得,方程两边同时对求导,有,解得.4.若函数由方程确定,其中是可微函数,证明.证明:方程两边同时对求导,有,得,方程两边同时对求导,有,得,所以.5.设函数,而由方程确定,其中函数连续,、可微,且,求.解:方程两边对求导,有,得,方程两边对求导,有,得.,所以.6.求由下列方程组所确定函数的导数或偏导数:(1)求和.(2)求及.解:(1)方程组两边同时对求导,有消去,有,得,而.(2)方程组两边同时对求导,有(1)(2),有,得,再代入到(2)之中得.方程组两边同时对求导,有与前面解法类似,得,.习题8—6(A)1.判断下列论述是否正确,并说明理由:(1)如果曲线的参数方程为(),那么它就对应一个向量值方程若存在并且不同时为零,那么,曲线在相应点处的切向量为,由此利用直线的点向式方程就可写出该点处的切线方程;(2)求曲线的切线方程与法平面方程的关键是求切向量,而其中又以参数方程为基础,其它形式的曲线方程都划归为参数方程,找出相应的切向量,然后写出要求的方程;(3)曲面的切平面方程是以曲面的一般方程为基础进行讨论的,如果曲面方程为的形式,那么必须把它化为的形式,其中,因而它在点处的法向量一定为,切平面方程为:;(4)如果曲线为一般方程那么,曲线在点的切向量可取为.答:(1)正确,这就是曲线为参数方程时,切线方向向量的求法.此时切线方程为;法平面方程为.(2)正确,对参数方程,在处的切向量;对形如的取向方程,将变量看作参数,在处的切向量对一般方程按隐函数它可以确定两个一元函数,如,按隐函数求导方法得到,从而得在处的切向量.(3)不确切,曲面的法向量可以直接由给出,也可以由给出.(4)正确,设曲面在点处的法向量为,曲面在点处的法向量为,根据法平面的定义有,于是可取.2.空间一质点在时刻时的位置为,求质点在时刻的速度.解:.3.求曲线在点处的切线及法平面方程.解:点对应参数为,切向量,切线方程为,法平面方程为,即.4.求曲线,在对应于的点处的切线及法平面方程.解:切点为,切向量,切线方程为,法平面方程为,即.5.求曲线在点处的切线及法平面方程.解:,切向量,切线方程为,法平面方程为,即.6.求曲线在点处的切线及法平面方程.解:设,则切向量,切线方程为,法平面方程为,即.7.求曲面在点处的切平面及法线方程.解:设,则法向量,切平面方程是,即,法线方程是.8.求曲面在点处的切平面及法线方程.解:法向量切平面方程是,即,法线方程是.习题8—6(B)1.求曲线()上平行于平面的切线方程,并写出该点处的法平面方程.解:设切点坐标为,该点对应参数,曲线在该点的切向量为,由切线与平面平行,有,得,即,由于,所以.切点坐标为,切向量,切线方程为,法平面方程为,即.2.在椭球面上求平行于平面的切平面方程.解:设切点坐标为,,则法向量,由切平面平行于平面,有,即,代入到曲面方程之中,有,得,切点为或,在点,切平面为,即;在点,切平面为,即.3.问旋转抛物面上哪一点处的切平面过曲线,,在点处的切线.解:设切点坐标为,则法向量,切平面方程为,即.曲线,,在点对应参数,曲线在点处的切向量.由在曲面上,有.①由切平面过,有.②曲线,,在点处的切线在切平面上,有所以,即.③由方程①、②、③式解得或,于是所求点为或.4.证明二次曲面在点处的切平面方程为:.证明:设,则曲面在的法向量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题5—1(A)1.判断下列叙述是否正确?并说明理由:(1)如果函数)(x f 仅在区间],[b a 上有界,它在],[b a 上未必可积,要使其可积,它在],[b a 上必须连续;(2)如果积分⎰b ax x f d )((b a <)存在,那么nab i n a b a f x x f ni n ba--+=∑⎰=∞→)(lim d )(1; (3)性质5也常称为积分不等式,利用它(包括推论)结合第三章的有关知识,可以估计积分的值、判定积分的符号,也可证明关于定积分的某些不等式;(4)定积分的中值定理是一个非常重要的定理,利用它能去掉积分号,同时该“中值”)(ξf 还是被积函数在积分区间上的平均值. 答:(1)前者正确.如狄利克雷函数⎩⎨⎧∈∈=cQx Q x x D ,,,01)(在区间][b a ,(其中a b >)上有界,但是它在区间][b a ,上不可积,事实上:将][b a ,任意分成n 个小区间][1i i x x ,- )21(n i ,,, =,(其中b x a x n ==,0)记第i 个小区间长度为i x ∆,先在][1i i x x ,-上取i ξ为有理数,则a b x x D ni i n i i i -=∆=∆∑∑=→=→0lim )(lim λλξ,再在][1i i x x ,-上取i ξ为无理数,则00lim )(lim=∆⋅=∆∑∑=→=→ni i ni iix xD λλξ,对于i ξ的不同取法黎曼和的极限不同,所以)(x D 在区间][b a ,上不可积;后者不正确,参见定理1.2.(2)正确.事实上:由于)(x f 在区间][b a ,上可积,则对][b a ,的任意分法,i ξ的任意取法,都有i ni i b ax f x x f ∆=∑⎰=→)(lim d )(1ξλ,现在对][b a ,区间n 等分,i ξ去在小区间的右分点,则i n a b a i -+=ξ,nab x i -=∆,并且0→λ等价于∞→n ,所以 i ni i b ax f x x f ∆=∑⎰=→)(lim d )(1ξλnab i n a b a f ni n --+=∑=∞→)(lim 1. (3)正确.它是证明关于定积分不等式的基础,参见例题1.3、1.4、1.5等. (4)正确.它可以起到去掉积分号的作用))((d )(a b f x x f b a-=⎰ξ;也可以用来表示连续函数在区间][b a ,上的平均值ab -1)(d )(⎰=b af x x f ξ,但是由于ξ位置不好确定,一般不用它来计算平均值,而是直接计算⎰-b ax x f a b d )(1.2.自由落体下落的速度gt v =,用定积分表示前10秒物体下落的距离.解:根据定积分引入的实例,变速直线运动的路程=s ⎰b at t v d )(,所以⎰=100d t gt s .3.一物体在力)(x F F =作用下,沿x 轴从a x =点移动到b x =点,用定积分表示力)(x F 所做的功W .解:将位移区间][b a ,任意分成n 个小区间][1i i x x ,-)21(n i ,,, =,(其中b x a x n ==,0)记第i 个小区间长度为i x ∆,在][1i i x x ,-上任取一点i ξ,用)(i F ξ近似代替物体从1-=i x x 移动到i x x =时所受的力,则物体从1-=i x x 移动到i x x =时所做的功近似为i i i x F W ∆≈∆)(ξ,于是∑∑==∆≈∆=ni iin i ixF W W 11)(ξ,记}21m a x {n i x i ,,, =∆=λ,则⎰∑=→=∆=b ani iix x F x F W d )()(lim1ξλ(假定极限∑=→∆ni i i x F 1)(lim ξλ存在).4.用定积分的几何意义求下列积分值:(1)x x a a ad 22⎰--; (2)⎰-21d x x .解:(1)如图,上半圆的面积2/2πa A =,根据定积分几何意义A x x a a a=-⎰-d 22,所以,=-⎰-x x a a ad 222/2πa .(2)如图,面积22/41==A ,2/12=A ,根据定积分几何意义2/3d 2121=-=⎰-A A x x ,所以,=⎰-21d x x 2/3.5.若函数)(x f y =在区间],[a a -上连续,用定积分的几何意义说明:(1) 当)(x f 为奇函数时,0d )(=⎰-a a x x f ;(2) 当)(x f 为偶函数时,⎰⎰=-aa ax x f x x f 0d )(2d )(.解:(1)如图1,当)(x f 是奇函数时,由对称性,面积21A A =,根据定积分几何意义,0d )(21=-=⎰-A A x x f a a.(2)如图2,当)(x f 是偶函数时,由对称性,面积21A A =,根据定积分几何意义,⎰⎰==+=-aa ax x f A A A x x f 0121d )(22d )(.6.比较下列各组定积分的大小:(1)x x I d 1021⎰=与x x I d 1032⎰=; (2)x x I d 211⎰=与x x I d 2132⎰=;(3)x x I d sin 21⎰=π与x x I d sin 2031⎰=π;(4)x x I d ln 531⎰=与x x I d )(ln 2532⎰=.解:(1)因为在区间]10[,上32x x ≥,所以≥⎰x x d 102x x d 103⎰,即21I I ≥.(2)因为在区间]21[,上3x x ≥,所以≥⎰x x d 21x x d 213⎰,即21I I ≥.(3)因为在区间]2/0[π,上x x 3sin sin ≥,所以≥⎰x x d sin 2πx x d sin 203⎰π,即21I I ≥.(4)因为在区间]53[,上2)(ln ln x x ≤,所以≤⎰x x d ln 53x x d )(ln 253⎰,即21I I ≤.7.估计下列定积分的值:(1)⎰+=π20d )sin 2(x x I ; (2)⎰=1d arctan x x I ;(3)⎰+=212d 1x xx I ; (4)⎰+-=202)d 32(x x x I . 解:(1)设x x f sin 2)(+=,在区间]20[π,上显然有3)(1≤≤x f ,又,1)2/3(=πf 3)2/(=πf ,于是函数)(x f 在区间]20[π,上的最小值为1=m ,最大值3=M ,而区间长度π2=-a b ,根据)(d )()(a b M x x f a b m b a-≤≤-⎰,得ππ62≤≤I .(2)设x x f arctan )(=,由于函数)(x f 在区间]10[,上单调增加,于是)(x f 在区间]10[,上的最小值为0)0(==f m ,最大值4/)1(π==f M ,而区间长度1=-a b ,根据)(d )()(a b M x x f a b m b a-≤≤-⎰,得4/0π≤≤I .(3)设21)(x x x f +=,则222)1(1)(x x x f +-=',在区间]21[,上0)(≤'x f ,于是函数)(x f 在区间]21[,上单调减少,所以)(x f 在区间]21[,上的最小值为2/5)2(==f m ,最大值2/1)1(==f M ,而区间长度1=-a b ,根据)(d )()(a b M x x f a b m b a-≤≤-⎰,得2/15/2≤≤I .(4)设32)(2+-=x x x f ,则22)(-='x x f ,有0)(='x f ,在区间)20(,内得驻点1=x ,又3)2(2)1(3)0(===f f f ,,,所以函数)(x f 在区间]20[,上的最小值为2)1(==f m ,最大值3)2()0(===f f M ,而区间长度2=-a b ,根据)(d )()(a b M x x f a b m ba-≤≤-⎰,得64≤≤I .8.证明下列不等式:(1)x x x x d cos d sin 404⎰⎰≤ππ; (2)x x x x d )1(d e 110⎰⎰+≥.证明:(1)在区间]4/0[π,上显然有x x cos sin ≤,所以x x x x d cos d sin 404⎰⎰≤ππ.(2)设x x f x--=1e )(,在区间]10[,上,01e )(≥-='xx f ,于是函数)(x f 在区间]10[,上单调增加,从而0)0()(=≥f x f ,即在区间]10[,上x x +≥1e ,所以x x x x d )1(d e 110⎰⎰+≥.习题5—1(B)1.右图给出了做直线运动的某质点在0到9s 内的速度图象,求它在这段时间间隔内所走的路程. 解:质点在0到9s 内所走的有效路程为阴影面积的 代数和,即2810d )(90=-=⎰t t v (单位); 质点在0到9s 内所实际走的路程为阴影面积的和,即18810d )(90=+=⎰t t v (单位)2.用定积分中值定理求下列极限:(1)x xx x n nn d 2lim 82⎰+∞→; (2)x xx n nn d 1arctan lim1⎰+∞→.解:(1)由定积分中值定理,nnn n n n nx x x x ξξξ+=+⎰26d 282(其中82≤≤n ξ),于是 3/126lim 26lim d 2lim 182=+=+=+-∞→∞→∞→⎰n nn n n n n n n n n n x x x x ξξξξ. (2)由定积分中值定理,nn n nx x x ξξ1arctan d 1arctan 1=⎰+(其中1+≤≤n n n ξ),由1+≤≤n n n ξ,有∞→n 等价于+∞→n ξ,于是11lim 1arctan lim d 1arctan lim 1=⋅==+∞→+∞→+∞→⎰nn n n n nn n n x x x ξξξξξξ.3.若函数)()(x g x f ,在区间][b a ,(b a <)上连续,)()(x g x f ≤,且)(x f 不恒等于)(x g ,证明⎰⎰<bab ax x g x x f d )(d )(.证明:设)()()(x f x g x F -=,由题目条件知,在区间][b a ,上函数)(x F 连续且0)(≥x F 又不恒等于零,于是有∈0x ][b a ,,使得0)(0>=ηx F ,由连续函数的性质,0>∃δ,在区间][][00b a x x ,, δδ+-内恒有2/)(η>x F ,设区间][][00b a x x ,, δδ+-][21c c ,=(12c c >),所以02/)(/2d d )(d )(122121>-=≥≥⎰⎰⎰c c x x x F x x F c c c c baηη,即0]d )()([>-⎰b ax x f x g ,再由定积分的线性性,得⎰⎰<babax x g x x f d )(d )(.4.证明下列不等式: (1)4/1022e 2d e e 22---≤≤-⎰x xx;(2)211d 2211<+<⎰nx x x (其中n 是正整数). 证明:(1)设xxx f -=2e )(,则xxx x f --='2e )12()(,由0)(='xf ,在区间)20(,内得驻点2/1=x ,又24/1e )2(e )2/1(1)0(===-f f f ,,,于是函数)(x f 在区间]20[,的最小值为4/1e-=m ,最大值为2e =M ,从而≤-4/1e2220e 2d e 2≤⎰-x xx,因为=⎰-02d e 2x xx⎰--2d e 2x xx,所以4/1022e 2d e e 22---≤≤-⎰x xx.(2)在区间]10[,上显然有x xx x n≤+≤12,且等号不恒成立,而函数nxx x +12、、x 都连续,根据本节习题(B )3,有⎰⎰⎰<+<11010d 1d d 2x x xx x x x n,而由定积分的几何意义得21d 10=⎰x x ,221d 21d 21010==⎰⎰x x x x ,所以211d 22110<+<⎰nx x x . 习题5—2(A)1.判断下列叙述是否正确?并说明理由:(1)在定理2.1的证明中,被积函数连续的条件是不可缺少的; (2)若()f x 连续、)(x ϕ可导,则⎰=)(0d )()(x t t f x F ϕ的导数等于被积函数在上限处的值;(3)在()f x 连续、)(x ϕ及)(x ψ可导时,通过将⎰=)()(d )()(x x t t f x F ϕψ化成两个变上限定积分,可求得()(())()(())()'''=-F x f x x f x x ϕϕψψ;(4)使用牛顿—莱布尼兹公式计算定积分,首先要找到被积函数在积分区间上的一个原函数,然后求该原函数在积分区间上的增量.答:(1)正确.定理的证明中两次用到连续性,一次是使用定积分中值定理时,再一次是最后求极限时.(2)不正确.应该是)()]([)(x x f x F ϕϕ'=',即被积函数在上限处的值与上限处函数)(x ϕ的导数之积.(3)正确.将函数)(x F 改写为⎰⎰-=)()(d )(d )()(x ax ax x f x x f x F ψϕ,再根据(2)求导.(4)正确.这就是牛顿—莱布尼兹公式)()(d )(a F b F x x f b a-=⎰(其中)(x F 是)(x f 在区间][b a ,上的一个原函数),但是要注意被积函数的连续性,对分段函数(或分区间连续函数)要分区间求. 2.计算下列定积分:(1)x x x d )123(1024⎰-+; (2)x a x a x ad ))((0⎰+-;(3)x x x d )11(94+⎰; (4)x x d 1123⎰--+;(5)x x x d 12134⎰-; (6)⎰+33/121d x x; (7)x x x d 31102⎰+-; (8)⎰-21021d x x ; (9)x x d )sin 21(0⎰-π; (10)x x d tan 32⎰π(11)⎰-40sin 1d πxx; (12)x x d cos 0⎰π;(13)x x x d 12202⎰+-; (14)x x f d )(20⎰,其中⎩⎨⎧≥<=.11e )(x x x x f x ,,, 解:(1)154]3253[d )123(10341024=-+=-+⎰x x x x x x . (2)=-=-=-=+-⎰⎰3333022033d )(d ))((a a a x x a x x a x a x aaa322a -.(3)=-=+=+=+⎰⎰32824]232[d )1(d )11(942/39494x x x xx x x x 344. (4)=-=+=+----⎰2ln 01ln d 112323xx x 2ln -.(5)=-=+=-=-⎰⎰1817]212[d )1(d 121222132134x x x x x x x x 89. (6)=-==+⎰63arctan 1d 33/133/12ππx x x 6π. (7)=+-=+-=+-⎰3ln 214ln 2136)]3ln(213arctan 31[d 31103102πx x x x x 43ln 2136+π. (8)=-==-⎰06arcsin 1d 2/10212πx x x 6π. (9)=--+=+=-⎰)11(2cos 2d )sin 21(00ππππx x x 4-π.(10)=--=-=-=⎰⎰3033tan d )1(sec d tan 3/0302302πππππx x x x x 33π-.(11)=-+=+=+=-⎰⎰121]sec [tan cos )d sin (1sin 1d 4/040240πππx x xx x x x 2. (12)=---=-=-=⎰⎰⎰)10(01sin sin d cos d cos d cos 2/2/02200πππππππx x x x x x x x 2.(13)x x x x x x x x x d )(d )1(d 1d 122112202⎰⎰⎰⎰--+-=-=+-=+=-+--=2121)1(21)1(21212102x x 1. (14)=-+-=+=+=⎰⎰⎰2121e 2ed de d )(2121021120x x x x x x f x x21e +. 3.求下列函数)(x y y =的导数xyd d : (1)⎰-=x t t y 0d e 2; (2)⎰=1d sin x t tty ; (3)⎰=xt t y 02d sin ; (4)⎰=xxt x y e 2d ln .解:(1)=x yd d 2e x -. (2)=x y d d xx sin -. (3)=⋅=x x x y 21)sin(d d 2xx 2sin . (4)='⋅-'⋅=)()ln()e ()e ln(d d 22x x xyx x )ln 2e (2x x x -. 4.求下列极限:(1)xtx t x ln d e lim112⎰→; (2)320d sin limx t t x x ⎰→;(3)xx t t x x 502sin d cos lim⎰-→; (4)⎰⎰→2202d cos )d sin (limx xx tt t tt.解:(1)===→→→⎰222e lim /1e lim ln d e lim1111x x x x xt x x x x te . (2)==→→⎰2203203sin lim d sin limx x x t t x x x 31. (3)=-=-=-=-→→→→⎰⎰440420520502052/lim 51cos lim d cos limsin d cos limx x x x x x t t xx t t x x x x x x 101-.(4)===⋅=→→→→⎰⎰⎰⎰1sin lim d sin lim cos 2sin d sin 2lim d cos )d sin (lim000400020202x xx t t t x x x x t t t t t t t t x x x x x x xx 1. 习题5—2(B)1. 求变力2)(t t t F -=沿数轴从点1=t 到点2=t 所做的功.解:根据习题5-1(A )3,x t t t t F W d )(d )(21221⎰⎰-==3324313238324]332[2132/3-=+--=-=t t . 2.设函数)(x y y =由方程0d 1d 1202202=-++⎰⎰x y t t t t ,求xyd d . 解:方程0d 1d 122202=-++⎰⎰x y t t t t 两边同时对x 求导,有012d d 41242=-++x x x y y ,解得24411d d yx x x y +--=. 3.若函数)(x f 连续,设⎰=xt t xf y 1d )(,求xyd d . 解:⎰=x t t f xy 1d )(,根据乘积求导法则,x yd d )(d )(1x xf t t f x +=⎰.4.证明:当0=x 时,函数t t x I x t d e )(02⎰-=取得最小值.证明:函数)(x I 在)(∞+-∞,内有定义,2e )(x x x I -=',由0)(='x I 得唯一驻点0=x ,又22e 2e )(2x x x x I ---='',01)0(>=''I ,于是0=x 是函数t t x I xtd e )(02⎰-=的唯一极小值点,从而也是最小值点,所以当0=x 时,函数t t x I x t d e )(02⎰-=取得最小值.5.若函数)(x f 在区间][b a ,上连续,在)(b a ,内可导,且0)(<'x f ,设 ⎰-=x a t t f ax x F d )(1)(, 证明:在区间)(b a ,内0)(≤'x F . 证明:2)(d )())(()(a x tt f a x x f x F xa---='⎰.(方法1)由定积分中值定理,a x f x f a x a x f a x x f x F --=----=')()()())(())(()(2ξξ (其中x a ≤≤ξ),由0)(<'x f ,有函数)(x f 单调减少,而x ≤ξ,得)()(ξf x f ≤,所以在区间)(b a ,内证明0)(≤'x F . (方法2)因为))((d )(a x x f t x f x a-=⎰,所以22)(d )]()([)(d )(d )()(a x t t f x f a x tt f t x f x F x axax a--=--='⎰⎰⎰(t x ≥),由0)(<'x f ,有函数)(x f 单调减少,而t x ≥,于是0)()(≤-t f x f ,得0d )]()([≤-⎰x at t f x f ,所以在区间)(b a ,内证明0)(≤'x F . (方法3)设=)(x g ⎰--x at t f a x x f d )())((,则0))(()(≤-'='a x x f x g ,于是函数)(x g 在区间][b a ,上单调减少,0)()(=≤a g x g ,所以0)(≤'x F . 6.若函数)(x f 可导,且0)0(=f ,2)0(='f ,求极限2d )(limx t t f x x ⎰→.解:='=-==→→→⎰)0(21)0()(lim 212)(limd )(lim00200f x f x f x x f xtt f x x x x 1. (注:由于)(x f '未必连续,因此极限xx f x 2)(lim 0→不能再用洛必达法则)7.设函数)(x f 在闭区间]10[,连续,且1)(<x f ,证明方程-x 21d )(0=⎰x t t f 在开区间)10(,有且仅有一个实根.证明:设-=x x F 2)(1d )(0-⎰x t t f ,根据已知,函数)(x F 在闭区间]10[,连续,又 01)0(<-=F ,-=1)1(F ⎰10d )(t t f ,由于连续函数1)(<x f ,则1d )(1<⎰t t f ,从而0)1(>F ,由零点定理得方程-x 21d )(0=⎰x t t f 在开区间)10(,至少有一个实根.而0)(2)(>-='x f x F ,)(x F 单调增加,于是方程0)(=x F 至多有一个实根,即方 程-x 21d )(0=⎰x t t f 在开区间)10(,至多有一个实根.综上,证明方程-x 21d )(0=⎰x t t f 在开区间)10(,有且仅有一个实根.8.若函数⎩⎨⎧≤≤-=其它,,,,010)(6)(2x x x x f 求函数⎰=Φx t t f x 0d )()(在),(+∞-∞内的表达式.解:当0<x 时,0d 0d )()(0===Φ⎰⎰xx t t t f x ;当10<≤x 时,3203202023]23[d )66(d )()(x x t t t t t t t f x xxx -=-=-==Φ⎰⎰;当1≥x 时,10]23[d 0d )66(d )()(1032112=+-=+-==Φ⎰⎰⎰t t t t t t t t f x xx ,所以,⎪⎩⎪⎨⎧≥<≤-<=Φ.11102300)(32x x x x x x ,,,,,习题5—3(A)1.判断下列叙述是否正确?并说明理由:(1)在定积分的换元积分法中,要求被积函数)(x f 在区间],[b a 上连续,函数()x t ϕ=在以βα、为端点的区间上有连续的导数,以保证[()]()f t t ϕϕ'在[,]αβ或],[αβ上可积; (2)对定积分进行换元时,需要注意的是换元的同时要换积分限,这时还要特别注意换元后积分的下限要小于上限;(3)定积分也有与不定积分类似的凑微分法与三角代换法等换元法,具体采取哪种换元法,其依据与不定积分是相同的;(4)在利用奇、偶函数的积分性质时,不仅要注意被积函数的奇偶性,而且还要注意积分区间关于坐标原点必须是对称的.答:(1)正确.此时[()]()f t t ϕϕ'在[,]αβ或],[αβ上是连续的,因此它可积. (2)不正确.如t x cos =,则t t x x d sin d 102/2102⎰⎰-=-π,其中下限大,上限小;对积分⎰b ax x f d )(作换元)(t x ϕ=,原积分下限a x =对应的t 值在换元后积分的下限上,原积分上限b x =对应的t 值在换元后积分的上限上. (3)正确.(4)正确.但是还需注意函数是可积的. 2.计算下列定积分:(1)x xx d 191⎰+; (2)⎰-++01311d x x ;(3)x xx d 4511⎰--; (4)x x x d 1213-⎰;(5)⎰+31221d xxx ; (6)⎰-12122d 1x xx ; (7)⎰-2122d 1x x x ; (8)⎰-324)28(d x x;(9)⎰+302d 1x x x ; (10)x x x d sin cos 04⎰π(11)x x d )sin 1(03⎰+π; (12)x x x d e 12⎰;(13)x x xd ln 1e1⎰+; (14)x x x d 1sin /3/22⎰ππ;(15)⎰-++212102d x x x ; (16)x x x d sin sin 03⎰-π. 解:(1)令t x =,则2t x =,t t x d 2d =,于是t t t t t t x xxd )111(2d 12d 13131291⎰⎰⎰++-=+=+=++-=31312)1ln(24t t 2ln 24+. (2)令t x =+31,则13-=t x ,t t x d 3d 2=,于是=++-=++-=+=++--⎰⎰⎰01210102013)]1ln(3323[)d 111(31d 311d t t t t t t t t t x x232ln 3-. (3)令t x =-45,则4/)5(2t x -=,2/d d t t x -=,于是=---=--=-⎰⎰-)310(81d 8)5(d 4513313211t x t t t x x x61. (4)令t x sin =,则t t x d cos d =,于是t t t t t t x x xcos d )cos (cos d cos sin d 1220420232103-==-⎰⎰⎰ππ1525131]3cos 5cos [2/035=-=-=πt t .(5)令t x tan =,则t t x d sec d 2=,于是=-===+⎰⎰⎰3/4/3/4/23/4/223122]sin 1[sin d c sec tan d sec 1d ππππππt t t ost t t t t xx x 3322-. (6)令t x sin =,则t t x d cos d =,于是=--=-==-⎰⎰⎰4cot d )1(csc d cot d 12/4/2/4/22/4/212122πππππππt t t t t x xx 41π-. (7)令t x sec =,则t t t x d sec tan d =,于是⎰⎰⎰-==-3/03/022122d )cos (sec d cos sin d 1ππt t t t t t x xx3/0]sin sec tan [ln πt t t -+=23)32ln(-+=. (8)=-=-=---=-⎰⎰)64181(61)28(61)28()2d(821)28(d 323324324x x x x x 3847. (9)=-=+=++=+⎰⎰)18(31)1(31)d(1121d 1302/323022302x x x x x x 37. (10)===⎰⎰πππ050404sin 51dsin sin d sin cos x x x x x x 0.(11)=-+=-+=+⎰⎰πππππ03023]cos 3cos [dcos )1(cos d )sin 1(x x x x x x 34+π. (12)===⎰⎰121010222e 21)d(e 21d e x x x x x x )1e (21-. (13)=+=+=+=+⎰⎰321)(ln 321dln ln ln d ln 1e 12/3e 1e 1e1x x x x x x x 35. (14)=-==-=⎰⎰0211cos )1d(1sin d 1sin /3/2/3/2/3/22ππππππx•x x x x x 21.(15)=-=+=+++=++---⎰⎰)04(3131arctan 313)1()1d(102d 212122212πx x x x x x 12π. (16)x x x x x x x x x d cos sin d cos sin d sin sin 023⎰⎰⎰==-πππx x x x x x d cos sin d cos sin 2/2/0⎰⎰⋅-⋅=πππ x x x x dsin sin dsin sin 2/2/0⎰⎰⋅-⋅=πππ=+=-=3232sin 32sin 322/2/32/02/3πππx x 34. 3.计算下列定积分:(1)x x x d sin 02⎰π; (2)x x x d e 1⎰-;(3)x x d ln e 1⎰; (4)⎰41d ln x xx ;(5)⎰102d arctan x x x ; (6)⎰21d arcsin x x ;(7)x x xd cose 2/0⎰π; (8)⎰+4d )1ln(x x .解:(1))d sin sin (2d cos 2cos d sin 02022x x xx x x x xx x x x ⎰⎰⎰-+=+-=ππππππ4cos 2202-=+=πππx .(2)=--=+-=----⎰⎰101110e e 1d e ed e x x x xx x x x e21-. (3)=--=-=⎰⎰)1e (e d ln d ln e 1e1e 1x xx x x x x 1.(4)=--=-=-=⎰⎰)12(42ln 842ln 8d 2ln 2d ln 41414141x x xxx x x xx 42ln 8-.(5)⎰⎰⎰+-=+-=102221023103102)d(16112d 131arctan 3d arctan x x x x x x x x x x x π ])d(111[6112)d(1611210221210222⎰⎰++--=+-=x xx x x x ππ=+--=])1ln(1[6112102x π)2ln 1(6112--π. (6)⎰⎰--=21022/10210d 1arcsin d arcsin x x x xx x x =-+=2/102112x π12312-+π. (7)因为x x x x x x x x d sin e sin e d cos e 2/02/02/0⎰⎰-=πππx x x x x x xx d cos e 1e d cos e cos e e 2/022/02/02⎰⎰--=-+=πππππ,有=⎰x x xd cose 22/0π1e 2-π,所以=⎰x x xd cose 2/0π)1e (212-π.(8)⎰⎰⎰+-=+-+=+4040440d )1(23ln 4d )1(2)1ln(d )1ln(x x x x x x x x x x x对积分⎰+40d )1(2x x x ,令t x =,则2t x =,t t x d 2d =,于是3ln )]1ln(2[)d 111(d 1d )1(22022020240=++-=++-=+=+⎰⎰⎰t t t t t t t t t x x x, 所以,=-=+⎰3ln 3ln 4d )1ln(40x x 3ln 3.4.试选择简便的方法计算下列定积分:(1) x xx d sin 147⎰-+ππ; (2) x x x x d )e e (113--+⎰;(3)x x x d 1112⎰-+; (4)x x x d cos sin 2/52/343⎰ππ.解:(1)因为x x x f 47sin 1)(+=是奇函数,所以=+⎰-x xx d sin 147ππ0. (2)设)e e ()(3xx x x f -+=,)()e e ()(3x f x x f x x -=+-=--,于是)(x f 是奇函数,所以=+--⎰x x x x d )e e (1130.(3)因为21)(xx x f +=是偶函数,所以=+=+=+⎰⎰-1210211212d 12d 1x x xx x xx )12(2-.(4)因为x x x f 43cos sin )(=是π2为周期的奇函数,所以==⎰⎰-x x x x x x d cos sin d cos sin 2/2/432/52/343ππππ0.5.若函数)(x f 连续,证明下列定积分等式:(1)⎰⎰-=aa x x a f x x f 0d )(d )(;(2)⎰⎰=2020d )(cos d )(sin ππx x f x x f .(3)⎰⎰-=-110d )1(d )1(x x x x x x m n n m ;(4)⎰⎰+=+x x x x x x /112121d 1d )0(>x .证明:(1)令t a x -=,则⎰⎰⎰⎰-=-=--=a aaa x x a f t t a f t t a f x x f 000d )(d )()d )((d )(.(2)令t x -=2π,则⎰⎰⎰⎰==--=2020022d )(cos d )(cos )dt )](2[sin(d )(sin πππππx x f t t f t f x x f .(3)令t x -=1,则⎰⎰⎰⎰-=-=--=-1100110d )1(d )1()d ()1(d )1(x x x t t t t t t x x x m n m n n m n m .(4)令tx 1=,则⎰⎰⎰⎰+=+=+-=+x x x x x x t x t t t x x /112/1121/122121d 1d )/1(1/d 1d .习题5—3(B)1.计算下列定积分:(1)⎰-2ln 22ln 1e d x x ; (2))0(d 2202>-⎰a x x ax x a ;(3)x x f d )1(20⎰-, 其中⎪⎩⎪⎨⎧≥+<+=.0110e 11)(x xx x f x ,,,(4)⎰''102d )2(x x f x , 其中⎰=='=201d )(0)2(21)2(x x f f f ,,. 解:(1)令t x =-1e ,则)1ln(2t x +=,21d 2d tt t x +=,于是6)43(2a r c t a n 2d 121e d 313122ln 22ln πππ=-==+=-⎰⎰t t tx x . (2)令t a a x sin =-,则t t a x d cos d =,于是x a x a x x x ax x a a d )(d 22022202⎰⎰--=-⎰-+=2223d cos )sin 1(ππt t t a=⋅⋅==⎰2212d cos 23223ππa t t aπ23a .或:令t a x =-,则t x d d =,于是⎰⎰⎰--+=--=-a aa a t t a t a x a x a x x x ax x d )(d )(d 2222022202=⋅=-=⎰22242d 2a a t t a a a ππ23a . (3)令t x =-1,则t t f t t f t t f x x f d )(d )(d )(d )1(1011120⎰⎰⎰⎰+==---10011001)1ln(d )e 1e 1(1d e 1d t t t t t t t t+++-=+++=⎰⎰⎰-- =+++-=++-=--2ln )e 1ln(2ln 12ln )e 1ln(1101t )e 1ln(+. (4)⎰⎰'-'=''10102102d )2()2(21d )2(x x f x x f x x x f x ⎰+-'=1010d )2(21)2(212)2(x x f x xf f ⎰+-=1d )2(2141x x f .对积分⎰10d )2(x x f ,令t x =2,则21d )(21d )2(201==⎰⎰t t f x x f ,所以 0212141d )2(12=⋅+-=''⎰x x f x . 2.设x x I nn d tan 40⎰=π,证明211---=n n I n I .并计算⎰404d tan πx x .证明:240224024tan d tan d )1(sec tand tan ----=-==⎰⎰⎰n n n nn I x x x x x x x I πππ224/01111tan -----=--=n n n I n I n x π. =-=+-=-=⎰⎰32d 13131d tan 4002404ππx I I x x 324-π. 3.证明⎰⎰+=+2020d sin cos sin d sin cos cos ππx xx x x x x x ,并由此计算该积分值. 证明:记=1I ⎰+2d sin cos sin πx xx x,=2I ⎰+20d sin cos cos πx xx x,令t x -=2π,则=-+=+⎰⎰0220)d (cos sin cos d sin cos sin ππt t t t x x x x ⎰+2d sin cos cos πx xx x.=⋅=++=+==+⎰⎰221d sin cos cos sin 21)(21d sin cos sin 2021120πππx x x x x I I I x x x x 4π. 4.若函数)(x f 连续,设⎰+=21d )ln ()(t x t f x F ,求)(x F '.解:(方法1)令u x t =+ln ,则⎰⎰++=+=x xu u f t x t f x F ln 2ln 121d )(d )ln ()(,所以=⋅+-⋅+='x x f x x f x F 1)ln 1(1)ln 2()(xx f x f )ln 1()ln 2(+-+. (方法2)设)(x f 的原函数为)(x G (连续函数一定有原函数),则 212121)ln ()ln d()ln (d )ln ()(x t G x t x t f t x t f x F +=++=+=⎰⎰)ln 1()ln 2(x G x G +-+=, 所以,=⋅+'-⋅+'='x x G x x G x F 1)ln 1(1)ln 2()(xx f x f )ln 1()ln 2(+-+. 5.若函数)(x f 连续,证明下列定积分等式:(1)⎰⎰=πππd )(sin 2d )(sin x x f x x xf ;(2)⎰⎰-+-=1d ])([()(d )(x x a b a f a b x x f b a;(3)⎰⎰-+=aa x x a f x f x x f 020d )]2()([d )(.证明:(1)令t x -=π,则⎰⎰⎰-=---=ππππππ000d )(sin )()d )]([sin()(d )(sin tt f t t t f t x x xf⎰⎰⎰⎰-=-=ππππππ0d )(sin d )(sin d )(sin d )(sin x x xf x x f t t tf t t f ,于是,⎰⎰=πππ0d )(sin d )(sin 2x x f x x xf , 所以,⎰πd )(sin x x xf ⎰=ππd )(sin 2x x f .(2)令t a b a x )(-+=,则⎰⎰⎰-+-=--+=110d ])([()(d )]()([(d )(x x a b a f a b t a b t a b a f x x f b a.(3)⎰⎰⎰+=a a aa x x f x x f x x f 0220d )(d )(d )(,在右式第二个积分中,令t a x -=2,则⎰⎰⎰⎰-=-=--=aa aa a x x a f t t a f t t a f x x f 002d )2(d )2()d )(2(d )(,所以⎰⎰⎰⎰⎰-+=+=a aa a aa x x a f x x f x x f x x f x x f 00220d )2(d )(d )(d )(d )(⎰-+=a x x a f x f 0d )]2()([.6.设函数)(x f 在区间],[ππ-上连续,且满足⎰-++=ππx x x f x x x f d sin )(cos 1)(2,求)(x f .解:记I x x x f =⎰-ππd sin )(,则I xxx f ++=2cos 1)(,此等式两边同时乘x sin ,然后再区间],[ππ-上求积分,有⎰⎰⎰---++=ππππππx x I x x x x x x x f d sin d cos 1sin d sin )(2,即 ⎰⎰⎰+=+=⋅++=--πππππ0222d cos 1sin 2d cos 1sin 0d cos 1sin x x x x x x x x I x xx x I ⎰⎰-=+-=+=ππππππ00202)a r c t a n (c o s c o s 1os d d cos 1sin x x x c x xx 2)44(2ππππ=----=,所以,2cos 1)(22π++=x x x f . 习题5—4(A)1.下列叙述是否正确?并按照你的判断说明理由:(1)无论是无穷(限)积分还是无界函数的积分(瑕积分),它们的收敛性都是利用“定积分”与“极限”这两个基本概念作“已知”来定义的; (2)积分⎰+∞-∞x x f d )(收敛,是指⎰-∞0d )(x x f 与⎰+∞0d )(x x f 都收敛,若⎰+∞-∞x x f d )(发散,则⎰-∞0d )(x x f 与⎰+∞0d )(x x f 都发散;(3) 无论是无穷(限)积分还是无界函数的积分(瑕积分),在它们收敛时,要计算其值,一般可以利用推广的牛顿—莱布尼兹公式,而不必再利用定义转化为求定积分的极限. 答:(1)正确.参见定义4.1及定义4.2.(2)前者正确.参见教材260P 第8至12行,(注意积分限中的“0”可以是某一个实数c );后者不正确.若⎰+∞-∞x x f d )(发散,则两个积分⎰-∞0d )(x x f 与⎰+∞0d )(x x f 中可能只有一个发散,如x xd e ⎰+∞∞-;也可以两个都发散如x x xd 12⎰+∞∞-+.(3)正确.参见教材260P 第13至17行及262P 第1至7行. 2.先判断下列广反常积分是否收敛,然后对于收敛的积分再计算其值:(1)⎰+∞13d x x; (2)⎰+∞+01d x x ; (3)x axd e⎰+∞-(0>a ); (4)⎰-∞+021d x xx ;(5)⎰+∞-∞++32d 2x x x; (6)⎰+∞121d e x x x; (7)⎰-∞d e x x x; (8)⎰-+011d x x ;(9)⎰-1021d xx x ; (10)⎰-101d xx ;(11)⎰-202)1(d x x; (12)⎰⋅e 1ln d x x x .解:(1)21)2121(lim ]21[lim d lim d 2121313=-=-==+∞→+∞→+∞→+∞⎰⎰b x x x x x b b b b b ,所以,此无穷积分收敛,且积分值为21. (2)+∞=-+=+=+=++∞→+∞→+∞→+∞⎰⎰)11(lim 2]12[lim 1d lim1d 000b x x x x x b b b b b ,所以,此无穷积分发散.(3)aa a x x abb b ax b b ax b ax 1)e 1(lim 1]e [lim 1d e lim d e 000=-=-==-∞→-∞→-∞→+∞-⎰⎰, 所以,此无穷积分收敛,且积分值为a1.(4)-∞=+-=+=+=+-∞→-∞→-∞→-∞⎰⎰)1ln(lim 21)]1[ln(lim 211d lim 1d 2020202a x x x x x x x a aa a a , 所以,此无穷积分发散. (5)因为2221arctan212)1()1d(32d 11212π=+=+++=++-∞---∞--∞⎰⎰x x x x x x ,2221arctan2132d 112π=+=++∞+-+∞-⎰x x x x ,以上两个积分都收敛,所以⎰+∞-∞++32d 2x x x收敛,且 ⎰+∞-∞++32d 2x x x +++=⎰--∞1232d x x x ⎰+∞-++1232d x x x22222πππ=+=. (6)1e e )1d(e d e 1111121-=-=-=∞++∞+∞⎰⎰x xxx xx ,所以,此无穷积分收敛,且积分值为1e -. (7)11e 1lime e limd e ed e 00-=-=--=-=--∞→∞---∞→-∞∞--∞⎰⎰xx xxx x x xx x x x x ,所以,此无穷积分收敛,且积分值为1-. (8)因为∞=++-→x x 11lim 1,所以下限1-=x 是瑕点.+∞=+-=+=+=++++-→-→-→-⎰⎰)1ln(lim )]1[ln(lim 1d lim 1d 110101a x x x x x a a a a a , 所以,此瑕积分发散.(9)因为∞=--→211lim xx x ,所以上限1=x 是瑕点. 11lim 1]1[lim 1d lim 1d 2102121102=--=--=-=----→→→⎰⎰b x x x x x x x b b b b b , 所以,此瑕积分收敛,且积分值为1.(10)因为∞=--→xx 11lim 1,所以上限1=x 是瑕点. 21lim 22]1[lim 21d lim 1d 101110=--=--=-=----→→→⎰⎰b x xx xx b b b b b , 所以,此瑕积分收敛,且积分值为2. (11)因为∞=-→21)1(1limx x ,所以1=x 是瑕点.此积分分为⎰-102)1(d x x 与⎰-212)1(d x x讨论, 因为∞=--=-=---=--→⎰⎰111lim 11)1()d(1)1(d 11102102xx x x x x x , 所以,瑕积分⎰-102)1(d x x 发散,从而瑕积分⎰-202)1(d x x也发散. (12)因为∞=⋅+→x x x ln 1lim 1,所以下限1=x 是瑕点.2ln 2lim 2ln 2ln dln ln d 1e1e 1e 1=-===⋅+→⎰⎰x xxx xx x x ,所以,此瑕积分收敛,且积分值为2.习题5—4(B)1.有一个长为l 的细杆AB 均匀带电,总电量为q ,若在杆的延长线上距点A 为0x 处有一个单位正电荷,现将单位正电荷从0x 处沿杆的延长线方向移动到无穷远处,试求克服电场引力所做的功W .解:如图取坐标,A 点为原点,设单位正电荷位于x 处时,受细杆产生的电场力为)(x F ,则)11(1d )(/)(002xl x l kq tx l kq t t x l kq x F ll--=-=-=⎰(其中k 是引力系数). lx x l kqxlx l kq x x l x l kq x x F W x x x -=-=--==∞++∞+∞⎰⎰00ln ln d )11(d )(000. 2.下列反常积分是否收敛?(1)⎰+∞12d arctan x xx; (2)x x x a a d 220⎰-(0>a ). 解:(1)⎰⎰⎰+∞+∞∞++∞+-+=++-=1212112d )11(4d )1(1arctan d arctan x x xx x x x x xx x x π2ln 21421ln 2141ln214122+=-=++=∞+πππx x . (2)因为∞=-+→xxa x 2lim 0,所以下限0=x 是瑕点. (方法1)令t x x a =-2,则212t ax +=,于是πa ta t ta t at t a t x x x a a ==+-+=+=-∞++∞∞++∞⎰⎰⎰220220arctan 21d 21212d d 2.(方法2)令t a x 2sin 2=,则t t t a x d cos sin 4d =,于是ππππa a t t a t t t a t t x x x a a =⋅==⋅=-⎰⎰⎰44d cos 4d cos sin 4sin cos d 22022020.(方法3)令t a a x sin =-,则t t a x d cos d =,于是x xa x a x x x ax x x x a a a a d )(d 2d 2202220220⎰⎰⎰--=-=-πππππππa t a t t a t t t a ==-=+=⎰⎰⎰---2222222d d )sin 1(d sin 1cos .3.建立x x I x n n d e 0⎰+∞-=的递推公式,并由此计算n I .解:11010elim d e ed e --+∞→+∞--∞+-+∞-=+-=+-==⎰⎰n n x nx xn x nxnn nI nI x x xn x x x I .321)2)(1()1(-----=-==n n n n I n n n I n n nI I!]e [!d e !!000n n x n I n x x =-====∞+-+∞-⎰.4.已知反常积分,2d sin 0π=⎰+∞x x x 求反常积分x x x d sin 022⎰+∞. 解:由于1sin lim 220=+→xxx ,所以0=x 不是瑕点.。
