中考数学第三轮复习综合题5

合集下载

2021年中考数学第三轮专题冲刺复习：圆的综合(含答案)

2021年中考数学第三轮专题冲刺复习：圆的综合1、如图，AB 是⊙O 的直径，点C 在AB 的延长线上，AD 平分∠CAE 交⊙O 于点D ，且AE ⊥CD ，垂足为点E ．（1）求证：直线CE 是⊙O 的切线．（2）若BC=3，CD=3，求弦AD 的长．2、如图，AN 是M 的直径，//NB x 轴，AB 交M 于点C ．（1）若点()()00,6,0,2,30A N ABN ∠=，求点B 的坐标；（2）若D 为线段NB 的中点，求证：直线CD 是M 的切线．3、如图，⊙O 与Rt △ABC 的直角边AC 和斜边AB 分别相切于点C 、D ，与边BC 相交于点F ，OA 与CD 相交于点E ，连接FE 并延长交AC 边于点G ．（1）求证：DF ∥AO ；（2）若AC=6，AB=10，求CG 的长．4、如图，以AB边为直径的⊙O经过点P,C是⊙O上一点，连结PC交AB于点E，且PA=.∠ACP，PD=60（1）试判断PD与⊙O的位置关系，并说明理由；（2）若点C是弧AB的中点，已知4CE⋅的值.AB=，求CP5、如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为6，BC=8，求弦BD的长．6、如图，AB是⊙O的直径，点E是上的一点，∠DBC=∠BED．（1）求证：BC是⊙O的切线；（2）已知AD=3，CD=2，求BC的长．7、如图，BF为⊙O的直径，直线AC交⊙O于A，B两点，点D在⊙O上，BD平分∠OBC，DE⊥AC于点E．（1）求证：直线DE是⊙O的切线；（2）若 BF=10，sin∠BDE=，求DE的长．8、如图，Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O交AC于点D，E是BC 的中点，连接DE、OE．(1)判断DE与⊙O的位置关系并说明理由；(2)若ta n C＝，DE＝2，求AD的长．9、如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，延长BC到点D，连接OA，AD，使得∠FAC=∠AOD，∠D=∠BAF．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为5，CE=2，求EF的长．10、如图，AB是⊙O的直径，C是⊙O上一点，过点O作OD⊥AB，交BC的延长线于D，交AC于点E，F是DE的中点，连接CF．（1）求证：CF是⊙O的切线．（2）若∠A＝22.5°，求证：AC＝DC．11、如图，AB为⊙O的直径，C为⊙O上一点，D为BA延长线上一点，∠ACD=∠B．（1）求证：DC为⊙O的切线；（2）线段DF分别交AC，BC于点E，F且∠CEF=45°，⊙O的半径为5，sinB=，求CF的长．12、如图，△ABC内接于⊙O，AB是⊙O的直径，AC＝CE，连接AE交BC于点D，延长DC至F点，使CF＝CD，连接AF．（1）判断直线AF与⊙O的位置关系，并说明理由．（2）若AC＝10，tan∠CAE＝，求AE的长．13、（1）如图1，有一个残缺圆，请作出残缺圆的圆心O（保留作图痕迹，不写作法）．（2）如图2，设AB是该残缺圆⊙O的直径，C是圆上一点，∠CAB的角平分线AD交⊙O于点D，过D作⊙O的切线交AC的延长线于点E．①求证：AE⊥DE；②若DE＝3，AC＝2，求残缺圆的半圆面积．14、如图，⊙O是△ABC的外接圆，O点在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线，与AB的延长线相交于点P．（1）求证：PD是⊙O的切线；（2）求证：△PBD∽△DCA；（3）当AB=6，AC=8时，求线段PB的长．15、如图，AB是⊙O的直径,点E为线段OB上一点（不与O、B重合），作，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，于点F，连结CB.（1）求证：CB是的平分线；（2）求证：CF=CE;（3）当时，求劣弧BC的长度（结果保留π）.16、如图，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是上任意一点，AH=2，CH=4．（1）求⊙O的半径r的长度；（2）求sin∠CMD；（3）直线BM交直线CD于点E，直线MH交⊙O于点N，连接BN交CE于点F，求HE•HF的值．17、如图，△ABC内接于⊙O，CD平分∠ACB交⊙O于D，过点D作PQ∥AB分别交CA、CB延长线于P、Q，连接BD．（1）求证：PQ是⊙O的切线；（2）求证：BD2=ACBQ；（3）若AC、BQ的长是关于x的方程x+=m的两实根，且tan∠PCD=，求⊙O的半径．18、（1）方法选择如图①，四边形ABCD是⊙O的内接四边形，连接AC，BD，AB＝BC＝AC．求证：BD＝AD+CD．小颖认为可用截长法证明：在DB上截取DM＝AD，连接AM…小军认为可用补短法证明：延长CD至点N，使得DN＝AD…请你选择一种方法证明．（2）类比探究【探究1】如图②，四边形ABCD是⊙O的内接四边形，连接AC，BD，BC是⊙O的直径，AB＝AC．试用等式表示线段AD，BD，CD之间的数量关系，井证明你的结论．【探究2】如图③，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，∠ABC＝30°，则线段AD，BD，CD之间的等量关系式是BD＝CD+2AD．（3）拓展猜想如图④，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，BC：AC：AB＝a：b：c，则线段AD，BD，CD之间的等量关系式是BD＝CD+ AD．参考答案2021年中考数学第三轮专题冲刺复习：圆的综合1、如图，AB是⊙O的直径，点C在AB的延长线上，AD平分∠CAE交⊙O于点D，且AE⊥CD，垂足为点E．（1）求证：直线CE是⊙O的切线．（2）若BC=3，CD=3，求弦AD的长．【解答】（1）证明：连结OC，如图，∵AD平分∠EAC，∴∠1=∠3，∵OA=OD，∴∠1=∠2，∴∠3=∠2，∴OD∥AE，∵AE⊥DC，∴OD⊥CE，∴CE是⊙O的切线；（2）∵∠CDO=∠ADB=90°，∴∠2=∠CDB=∠1，∵∠C=∠C，∴△CDB∽△CAD，∴==，∴CD 2=CB •CA ，∴（3）2=3CA ，∴CA=6，∴AB=CA ﹣BC=3， ==，设BD=K ，AD=2K ，在Rt △ADB 中，2k 2+4k 2=5，∴k=， ∴AD=．2、如图，AN 是M 的直径，//NB x 轴，AB 交M 于点C ．（1）若点()()00,6,0,2,30A N ABN ∠=，求点B 的坐标；（2）若D 为线段NB 的中点，求证：直线CD 是M 的切线．解：（1）∵A 的坐标为（0，6），N （0，2）∴AN =4，∵∠ABN =30°，∠ANB =90°，∴AB =2AN =8，∴由勾股定理可知：NB =，∴B （，2）（2）连接MC ，NC ∵AN 是⊙M 的直径，∴∠ACN =90°，∴∠NCB =90°在Rt △NCB 中，D 为NB 的中点，∴CD =12NB =ND ，∴∠CND=∠NCD，∵MC=MN，∴∠MCN=∠MNC．∵∠MNC+∠CND=90°，∴∠MCN+∠NCD=90°，即MC⊥CD．∴直线CD是⊙M的切线．3、如图，⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D，与边BC 相交于点F，OA与CD相交于点E，连接FE并延长交AC边于点G．（1）求证：DF∥AO；（2）若AC=6，AB=10，求CG的长．【解答】（1）证明：连接OD．∵AB与⊙O相切与点D，又AC与⊙O相切与点，∴AC=AD，∵OC=OD，∴OA⊥CD，∴CD⊥OA，∵CF是直径，∴∠CDF=90°，∴DF⊥CD，∴DF ∥AO ．（2）过点作EM ⊥OC 于M ，∵AC=6，AB=10，∴BC==8，∴AD=AC=6，∴BD=AB ﹣AD=4，∵BD 2=BF •BC ，∴BF=2，∴CF=BC ﹣BF=6．OC=CF=3，∴OA==3， ∵OC 2=OE •OA ，∴OE=， ∵EM ∥AC ，∴===，∴OM=，EM=，FM=OF+OM=， ∴===，∴CG=EM=2．4、如图，以AB 边为直径的⊙O 经过点P ,C 是⊙O 上一点，连结PC 交AB 于点E ，且 60=∠ACP ，PD PA =.（1）试判断PD 与⊙O 的位置关系，并说明理由；（2）若点C 是弧AB 的中点，已知4AB =，求CP CE ⋅的值.解：（1）如图，PD 是⊙O 的切线.证明如下：连结OP ， 60=∠ACP ，∴ 120=∠AOP ，OP OA = ，∴ 30=∠=∠OPA OAP ，PD PA =，∴ 30=∠=∠D PAO ，∴ 90=∠OPD ，∴PD 是⊙O 的切线. （2）连结BC ，AB 是⊙O 的直径， ∴ 90=∠ACB ，又C 为弧AB 的中点， ∴ 45=∠=∠=∠APC ABC CAB ，4=AB ，2245== sin AB AC .APC CAB C C ∠=∠∠=∠, ，∴CAE ∆∽CPA ∆， ∴CACE CP CA =，∴82222===⋅)(CA CE CP .5、如图，△ABD 是⊙O 的内接三角形，E 是弦BD 的中点，点C 是⊙O 外一点且∠DBC=∠A ，连接OE 延长与圆相交于点F ，与BC 相交于点C ．（1）求证：BC 是⊙O 的切线；（2）若⊙O 的半径为6，BC=8，求弦BD 的长．【解答】（1）证明：连接OB，如图所示：∵E是弦BD的中点，∴BE=DE，OE⊥BD， =，∴∠BOE=∠A，∠OBE+∠BOE=90°，∵∠DBC=∠A，∴∠BOE=∠DBC，∴∠OBE+∠DBC=90°，∴∠OBC=90°，即BC⊥OB，∴BC是⊙O的切线；（2）解：∵OB=6，BC=8，BC⊥OB，∴OC==10，∵△OBC的面积=OC•BE=OB•BC，∴BE===4.8，∴BD=2BE=9.6，即弦BD的长为9.6．6、如图，AB是⊙O的直径，点E是上的一点，∠DBC=∠BED．（1）求证：BC是⊙O的切线；（2）已知AD=3，CD=2，求BC的长．解：（1）证明：∵AB是⊙O的切直径，∴∠ADB=90°，又∵∠BAD=∠BED，∠BED=∠DBC，∴∠BAD=∠DBC，∴∠BAD+∠ABD=∠DBC+ABD=90°，∴∠ABC=90°，∴BC是⊙O的切线；（2）解：∵∠BAD=∠DBC，∠C=∠C，∴△ABC∽△BDC，∴=，即BC2=AC•CD=（AD+CD）•CD=10，∴BC=．7、如图，BF为⊙O的直径，直线AC交⊙O于A，B两点，点D在⊙O上，BD平分∠OBC，DE⊥AC于点E．（1）求证：直线DE是⊙O的切线；（2）若 BF=10，sin∠BDE=，求DE的长．【解答】解：（1）如图所示，连接OD，∵OD=OB，∴∠ODB=∠OBD，∵BD平分∠OBC，∴∠OBD=∠DBE，∴∠ODB=∠DBE，∴OD∥AC，∵DE⊥AC，∴OD⊥DE，∵OD是⊙O的半径，∴直线DE是⊙O的切线；（2）如图，连接DF，∵BF是⊙O的直径，∴∠FDB=90°，∴∠F+∠OBD=90°，∵∠OBD=∠DBE，∠BDE+∠DBE=90°，∴∠F=∠BDE，在Rt△BDF中，=sinF=sin∠BDE=，∴BD=10×=2，∴在Rt△BDE中，sin∠BDE==，∴BE=2×=2，∴在Rt△BDE中，DE===4．8、如图，Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O交AC于点D，E是BC 的中点，连接DE、OE．(1)判断DE与⊙O的位置关系并说明理由；(2)若ta n C＝，DE＝2，求AD的长．解：(1)DE与⊙O相切，理由如下：连接OD，BD，∵AB是直径，∴∠ADB＝∠BDC＝90°，∵E是BC的中点，∴DE＝BE＝CE，∴∠EDB＝∠EBD，∵OD＝OB，∴∠OBD＝∠ODB．∴∠EDO＝∠EBO＝90°，(用三角形全等也可得到)∴DE与⊙O相切．(2)∵ta n C＝，可设BD＝x，CD＝2x，∵在Rt△BCD中，BC＝2DE＝4，BD2＋CD2＝BC2∴(x)2＋(2x)2＝16，解得：x＝±(负值舍去)∴BD＝x＝，∵∠ABD＝∠C，∴ta n∠ABD＝ta n CAD＝BD＝×＝．答：AD的长是．9、如图，△ABC内接于⊙O，BC是⊙O的直径，弦AF交BC于点E，延长BC到点D，连接OA，AD，使得∠FAC=∠AOD，∠D=∠BAF．（1）求证：AD是⊙O的切线；（2）若⊙O的半径为5，CE=2，求EF的长．【解答】解：（1）∵BC是⊙O的直径，∴∠BAF+∠FAC=90°，∵∠D=∠BAF，∠AOD=∠FAC，∴∠D+∠AOD=90°，∴∠OAD=90°，∴AD是⊙O的切线；（2）连接BF，∴∠FAC=∠AOD，∴△ACE∽△OCA，∴，∴，∴AC=AE=，∵∠CAE=∠CBF，∴△ACE∽△BFE，∴，∴=，∴EF=．10、如图，AB是⊙O的直径，C是⊙O上一点，过点O作OD⊥AB，交BC的延长线于D，交AC于点E，F是DE的中点，连接CF．（1）求证：CF是⊙O的切线．（2）若∠A＝22.5°，求证：AC＝DC．【解答】（1）证明：∵AB是⊙O的直径，∴∠ACB＝∠ACD＝90°，∵点F是ED的中点，∴CF＝EF＝DF，∴∠AEO＝∠FEC＝∠FCE，∵OA＝OC，∴∠OCA＝∠OAC，∵OD⊥AB，∴∠OAC+∠AEO＝90°，∴∠OCA+∠FCE＝90°，即OC⊥FC，∴CF与⊙O相切；（2）解：∵OD⊥AB，AC⊥BD，∴∠AOE＝∠ACD＝90°，∵∠AEO＝∠DEC，∴∠OAE＝∠CDE＝22.5°，∵AO＝BO，∴AD＝BD，∴∠ADO＝∠BDO＝22.5°，∴∠ADB＝45°，∴∠CAD＝∠ADC＝45°，∴AC＝CD．11、如图，AB为⊙O的直径，C为⊙O上一点，D为BA延长线上一点，∠ACD=∠B．（1）求证：DC为⊙O的切线；（2）线段DF分别交AC，BC于点E，F且∠CEF=45°，⊙O的半径为5，sinB=，求CF的长．【解答】（1）证明：连接OC，∵AB为⊙O的直径，∴∠ACB=∠BCO+∠OCA=90°，∵OB=OC，∴∠B=∠BCO，∵∠ACD=∠B，∴∠ACD=∠BCO，∴∠ACD+∠OCA=90°，即∠OCD=90°，∴DC为⊙O的切线；（2）解：Rt△ACB中，AB=10，sinB=，∴AC=6，BC=8，∵∠ACD=∠B，∠ADC=∠CDB，∴△CAD∽△BCD，∴，设AD=3x，CD=4x，Rt△OCD中，OC2+CD2=OD2，52+（4x）2=（5+3x）2，x=0（舍）或，∵∠CEF=45°，∠ACB=90°，∴CE=CF，设CF=a，∵∠CEF=∠ACD+∠CDE，∠CFE=∠B+∠BDF，∴∠CDE=∠BDF，∵∠ACD=∠B，∴△CED∽△BFD，∴，∴，a=，∴CF=．12、如图，△ABC内接于⊙O，AB是⊙O的直径，AC＝CE，连接AE交BC于点D，延长DC至F点，使CF＝CD，连接AF．（1）判断直线AF与⊙O的位置关系，并说明理由．（2）若AC＝10，tan∠CAE＝，求AE的长．【解答】解：（1）直线AF是⊙O的切线，理由是：连接AC，∵AB为⊙O直径，∴∠ACB＝90°，∴AC⊥BC，∵CF＝CD，∴∠CAF＝∠EAC，∵AC＝CE，∴∠E＝∠EAC，∵∠B＝∠E，∴∠B＝∠FAC，∵∠B+∠BAC＝90°，∴∠FAC+∠BAC＝90°，∴OA⊥AF，又∵点A在⊙O上，∴直线AF是⊙O的切线；（2）过点C作CM⊥AE，∵tan∠CAE＝，∴＝，∵AC＝10，∴设CM＝3x，则AM＝4x，在Rt△ACM中，根据勾股定理，CM2+AM2＝AC2，∴（3x）2+（4x）2＝100，解得x＝2，∴AM＝8，∵AC＝CE，∴AE＝2AE＝2×8＝16．13、（1）如图1，有一个残缺圆，请作出残缺圆的圆心O（保留作图痕迹，不写作法）．（2）如图2，设AB是该残缺圆⊙O的直径，C是圆上一点，∠CAB的角平分线AD交⊙O于点D，过D作⊙O的切线交AC的延长线于点E．①求证：AE⊥DE；②若DE＝3，AC＝2，求残缺圆的半圆面积．【解答】（1）解：如图1：点O即为所求．（2）①证明：如图2中，连接OD交BC于F．∵AD平分∠BAC，∴∠DAC＝∠DAB，∴＝，∴OD⊥BC，∴CF＝BF，∠CFD＝90°，∵DE是切线，∴DE⊥OD，∴∠EDF＝90°，∵AB是直径，∴∠ACB＝∠BCE＝90°，∴四边形DECF是矩形，∴∠E＝90°，∴AE⊥DE．②∵四边形DECF是矩形，∴DE＝CF＝BF＝3，在Rt△ACB中，AB＝＝2，∴残缺圆的半圆面积＝•π•（2）2＝20π．14、如图，⊙O是△ABC的外接圆，O点在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线，与AB的延长线相交于点P．（1）求证：PD是⊙O的切线；（2）求证：△PBD∽△DCA；（3）当AB=6，AC=8时，求线段PB的长．【解答】（1）证明：∵圆心O在BC上，∴BC是圆O的直径，∴∠BAC=90°，连接OD，∵AD平分∠BAC，∴∠BAC=2∠DAC，∵∠DOC=2∠DAC，∴∠DOC=∠BAC=90°，即OD⊥BC，∵PD∥BC，∴OD⊥PD，∵OD为圆O的半径，∴PD是圆O的切线；（2）证明：∵PD∥BC，∴∠P=∠ABC，∵∠ABC=∠ADC，∴∠P=∠ADC，∵∠PBD+∠ABD=180°，∠ACD+∠ABD=180°，∴∠PBD=∠ACD，∴△PBD∽△DCA；（3）解：∵△ABC为直角三角形，∴BC2=AB2+AC2=62+82=100，∴BC=10，∵OD垂直平分BC，∴DB=DC，∵BC为圆O的直径，∴∠BDC=90°，在Rt△DBC中，DB2+DC2=BC2，即2DC2=BC2=100，∴DC=DB=5，∵△PBD∽△DCA，∴=，则PB===．15、如图，AB是⊙O的直径,点E为线段OB上一点（不与O、B重合），作，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，于点F，连结CB.（1）求证：CB是的平分线；（2）求证：CF=CE;（3）当时，求劣弧BC的长度（结果保留π）.证明：连接AC，∵AB为直径，∴∠ACB=90°∴∠1+∠2=90°，∠2+∠3=90°∴∠1=∠3又∵CP为切线∴∠OCP=90°∵DC为直径∴∠DBC=90°∴∠4+∠DCB=90°，∠DCB+∠D=90°∴∠4=∠D又∵弧BC=弧BC∴∠3=∠D∴∠1=∠4即：CB 是∠ECP 的平分线（2）∵∠ACB =90°∴∠5+∠4=90°，∠ACE +∠1=90°由（1）得∠1=∠4∴∠5=∠ACE在Rt △AFC 和Rt △AEC 中AEC AFC AC AC ECA FCA AEC F ≌△△∴⎪⎩⎪⎨⎧=∠=∠︒=∠=∠90 ∴CF =CE（3）延长CE 交DB 于Qx x x EQ xCQ CP PQCB QCB CB xCE CF xCP x CF CP CF =-=∴==∴⊥∠=====344324343的角平分线是∵）得由（，设： ππ332321806032346060-60-18060333tan 33290219019022=⨯∴=∴=︒=︒︒︒=∠∴︒=∠∴===∠=∴=⋅⋅=∴=∴∴∠=∠∴︒=∠+∠︒=∠+∠︒=∠⊥的长度为：弧∵中，在△即∽△△，，，BC OB AB CBE CBE x x EB CE CBE CEB xEB EB x x EQ CE EB EQEB EB CE BEQCEB CQBCQB CBQ EB CE16、如图，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是上任意一点，AH=2，CH=4．（1）求⊙O的半径r的长度；（2）求sin∠CMD；（3）直线BM交直线CD于点E，直线MH交⊙O于点N，连接BN交CE于点F，求HE•HF的值．【解答】解：（1）如图1中，连接OC．∵AB⊥CD，∴∠CHO=90°，在Rt△COH中，∵OC=r，OH=r﹣2，CH=4，∴r2=42+（r﹣2）2，∴r=5．（2）如图1中，连接OD．∵AB⊥CD，AB是直径，∴==，∴∠AOC=∠COD，∵∠CMD=∠COD，∴∠CMD=∠COA，∴sin∠CMD=sin∠COA==．（3）如图2中，连接AM．∵AB是直径，∴∠AMB=90°，∴∠MAB+∠ABM=90°，∵∠E+∠ABM=90°，∴∠E=∠MAB，∴∠MAB=∠MNB=∠E，∵∠EHM=∠NHFM∴△EHM∽△NHF，∴=，∴HE•HF=HM•HN，∵HM•HN=AH•HB，∴HE•HF=AH•HB=2•（10﹣2）=16．17、如图，△ABC内接于⊙O，CD平分∠ACB交⊙O于D，过点D作PQ∥AB分别交CA、CB延长线于P、Q，连接BD．（1）求证：PQ是⊙O的切线；（2）求证：BD2=ACBQ；（3）若AC、BQ的长是关于x的方程x+=m的两实根，且tan∠PCD=，求⊙O 的半径．【解答】（1）证明：∵PQ∥AB，∴∠ABD=∠BDQ=∠ACD，∵∠ACD=∠BCD，∴∠BDQ=∠ACD，如图1，连接OB，OD，交AB于E，则∠OBD=∠ODB，∠O=2∠DCB=2∠BDQ，在△OBD中，∠OBD+∠ODB+∠O=180°，∴2∠ODB+2∠O=180°，∴∠ODB+∠O=90°，∴PQ是⊙O的切线；（2）证明：如图2，连接AD，由（1）知PQ是⊙O的切线，∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD，∴AD=BD，∵∠DBQ=∠ACD，∴△BDQ∽△ACD，∴=，∴BD2=ACBQ；（3）解：方程x+=m可化为x2﹣mx+4=0，∵AC、BQ的长是关于x的方程x+=m的两实根，∴ACBQ=4，由（2）得BD2=ACBQ，∴BD2=4，∴BD=2，由（1）知PQ是⊙O的切线，∴OD⊥PQ，∵PQ∥AB，∴OD⊥AB，由（1）得∠PCD=∠ABD，∵tan∠PCD=，∴tan∠ABD=，∴BE=3DE，∴DE2+（3DE）2=BD2=4，∴DE=，∴BE=，设OB=OD=R，∴OE=R﹣，∵OB2=OE2+BE2，∴R2=（R﹣）2+（）2，解得：R=2，∴⊙O的半径为2．18、（1）方法选择如图①，四边形ABCD是⊙O的内接四边形，连接AC，BD，AB＝BC＝AC．求证：BD＝AD+CD．小颖认为可用截长法证明：在DB上截取DM＝AD，连接AM…小军认为可用补短法证明：延长CD至点N，使得DN＝AD…请你选择一种方法证明．（2）类比探究【探究1】如图②，四边形ABCD是⊙O的内接四边形，连接AC，BD，BC是⊙O的直径，AB＝AC．试用等式表示线段AD，BD，CD之间的数量关系，井证明你的结论．【探究2】如图③，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，∠ABC＝30°，则线段AD，BD，CD之间的等量关系式是BD＝CD+2AD．（3）拓展猜想如图④，四边形ABCD是⊙O的内接四边形，连接AC，BD．若BC是⊙O的直径，BC：AC：AB＝a：b：c，则线段AD，BD，CD之间的等量关系式是BD＝CD+ AD．【解答】解：（1）方法选择：∵AB＝BC＝AC，∴∠ACB＝∠ABC＝60°，如图①，在BD上截取DEMAD，连接AM，∵∠ADB＝∠ACB＝60°，∴△ADM是等边三角形，∴AM＝AD，∵∠ABM＝∠ACD，∵∠AMB＝∠ADC＝120°，∴△ABM≌△ACD（AAS），∴BM＝CD，∴BD＝BM+DM＝CD+AD；（2）类比探究：如图②，∵BC是⊙O的直径，∴∠BAC＝90°，∵AB＝AC，∴∠ABC＝∠ACB＝45°，过A作AM⊥AD交BD于M，∵∠ADB＝∠ACB＝45°，∴△ADM是等腰直角三角形，∴AM＝AD，∠AMD＝45°，∴DM＝AD，∴∠AMB＝∠ADC＝135°，∵∠ABM＝∠ACD，∴△ABM≌△ACD（AAS），∴BM＝CD，∴BD＝BM+DM＝CD+AD；【探究2】如图③，∵若BC是⊙O的直径，∠ABC＝30°，∴∠BAC＝90°，∠ACB＝60°，过A作AM⊥AD交BD于M，∵∠ADB＝∠ACB＝60°，∴∠AMD＝30°，∴MD＝2AD，∵∠ABD＝∠ACD，∠AMB＝∠ADC＝150°，∴△ABM∽△ACD，∴＝，∴BM＝CD，∴BD＝BM+DM＝CD+2AD；故答案为：BD＝CD+2AD；（3）拓展猜想：BD＝BM+DM＝CD+AD；理由：如图④，∵若BC是⊙O的直径，∴∠BAC＝90°，过A作AM⊥AD交BD于M，∴∠MAD＝90°，∴∠BAM＝∠DAC，∴△ABM∽△ACD，∴＝，∴BM＝CD，∵∠ADB＝∠ACB，∠BAC＝∠NAD＝90°，∴△ADM∽△ACB，∴＝＝，∴DM＝AD，∴BD＝BM+DM＝CD+AD．故答案为：BD＝CD+AD。

2021年中考数学第三轮专题复习：四边形的综合练习

2021年中考数学第三轮专题复习：四边形的综合练习1、如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．2、如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．3、如图，在正方形ABCD中，点G在边BC上（不与点B，C重合），连结AG，作DE⊥AG于点E，BF⊥AG于点F，设=k．（1）求证：AE=BF．（2）连结BE，DF，设∠EDF=α，∠EBF=β．求证：tanα=ktanβ．（3）设线段AG与对角线BD交于点H，△AHD和四边形CDHG的面积分别为S1和S2，求的最大值．4、如图，在正方形ABCD中，点E、G分别是边AD、BC的中点，AF=AB．（1）求证：EF⊥AG；（2）若点F、G分别在射线AB、BC上同时向右、向上运动，点G运动速度是点F运动速度的2倍，EF⊥AG是否成立（只写结果，不需说明理由）？（3）正方形ABCD的边长为4，P是正方形ABCD内一点，当S△PAB =S△OAB，求△PAB周长的最小值．5、如图，在矩形ABCD中,AB= 2cm,∠ADB =30°. P，Q两点分别从A，B同时出发，点P沿折线AB--BC运动，在AB上的速度是2cm/s,在BC上的速度是23cm/s;点Q在BD上以2cm/s的速度向终点D运动.过点P作PN⊥AD，垂足为点N.连接PQ，以PQ，PN 为邻边作▱PQMN.设运动的时间为x(s)，▱PQMN与矩形ABCD重叠部分的图形面积为y(cm2).(1)当PQ⊥AB时，x= ；(2)求y关于x的函数解析式，并写出x的取值范围；(3)直线AM将矩形ABCD的面积分成1:3两部分时，直接写出x的值.6、在▱ABCD中，BE平分∠ABC交AD于点E．（1）如图1，若∠D＝30°，AB=√6，求△ABE的面积；（2）如图2，过点A作AF⊥DC，交DC的延长线于点F，分别交BE，BC于点G，H，且AB＝AF．求证：ED﹣AG＝FC．7、定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1，等腰直角四边形ABCD，AB=BC，∠ABC=90°，①若AB=CD=1，AB//CD，求对角线BD的长.②若AC⊥BD，求证：AD=CD.(2)如图2，在矩形ABCD中，AB=5，BC=9，点P是对角线BD上一点，且BP=2PD，过点P作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形.求AE的长.8、如图，矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上，线段OA、OC的长度满足方程|x﹣15|+=0（OA＞OC），直线y=kx+b分别与x轴、y轴交于M、N两点，将△BCN 沿直线BN折叠，点C恰好落在直线MN上的点D处，且tan∠CBD=（1）求点B的坐标；（2）求直线BN的解析式；（3）将直线BN以每秒1个单位长度的速度沿y轴向下平移，求直线BN扫过矩形AOCB的面积S关于运动的时间t（0＜t≤13）的函数关系式．9、在四边形ABCD中，∠B+∠D=180°，对角线AC平分∠BAD．（1）如图1，若∠DAB=120°，且∠B=90°，试探究边AD、AB与对角线AC的数量关系并说明理由．（2）如图2，若将（1）中的条件“∠B=90°”去掉，（1）中的结论是否成立？请说明理由．（3）如图3，若∠DAB=90°，探究边AD、AB与对角线AC的数量关系并说明理由．10、在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．11、在图1，2，3中，已知▱ABCD，∠ABC＝120°，点E为线段BC上的动点，连接AE，以AE 为边向上作菱形AEFG，且∠EAG＝120°．（1）如图1，当点E与点B重合时，∠CEF＝°；（2）如图2，连接AF．①填空：∠FAD∠EAB（填“＞”，“＜“，“＝”）；②求证：点F在∠ABC的平分线上；（3）如图3，连接EG ，DG ，并延长DG 交BA 的延长线于点H ，当四边形AEGH 是平行四边形时，求BCAB 的值．12、如图①，在△ABC 中，∠ACB =90°，∠B =30°，AC =1，D 为AB 的中点，EF 为△ACD 的中位线，四边形EFGH 为△ACD 的内接矩形（矩形的四个顶点均在△ACD 的边上）．（1）计算矩形EFGH 的面积；（2）将矩形EFGH 沿AB 向右平移，F 落在BC 上时停止移动．在平移过程中，当矩形与△CBD时，求矩形平移的距离；（3）如图③，将（2）中矩形平移停止时所得的矩形记为矩形1111E FG H ，将矩形1111E FG H 绕1G 点按顺时针方向旋转，当1H 落在CD 上时停止转动，旋转后的矩形记为矩形2212E F G H ，设旋转角为α，求cos α的值．13、邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依次类推，若第n 次操作余下的四边形是菱形，则称原平行四边形为n 阶准菱形，如图1，□ABCD 为1阶准菱形. （1）猜想与计算邻边长分别为3和5的平行四边形是阶准菱形；已知□ABCD 的邻边长分别为b a ,（b a >），满足r b a +=8，r b 5=，请写出□ABCD 是阶准菱形. （2）操作与推理小明为了剪去一个菱形，进行如下操作：如图2，把□ABCD 沿BE 折叠（点E 在AD 上），使点A 落在BC 边上的点F 处，得到四边形ABEF .请证明四边形ABEF 是菱形.14、如图，矩形ABCD的对角线AC，BD相交于点O，△COD关于CD的对称图形为△CED．（1）求证：四边形OCED是菱形；（2）连接AE，若AB=6cm，BC=cm．①求sin∠EAD的值；②若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，再以1.5cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动，当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间．15、在现实生活中，我们会看到许多“标准”的矩形，如我们的课本封面、A4的打印纸等，其实这些矩形的长与宽之比都为：1，我们不妨就把这样的矩形称为“标准矩形”，在“标准矩形”ABCD中，P为DC边上一定点，且CP=BC，如图所示．（1）如图①，求证：BA=BP；（2）如图②，点Q在DC上，且DQ=CP，若G为BC边上一动点，当△AGQ的周长最小时，求的值；（3）如图③，已知AD=1，在（2）的条件下，连接AG并延长交DC的延长线于点F，连接BF，T为BF的中点，M、N分别为线段PF与AB上的动点，且始终保持PM=BN，请证明：△MNT的面积S为定值，并求出这个定值．16、已知：如图，四边形ABCD，AB∥DC，CB⊥AB，AB=16cm，BC=6cm，CD=8cm，动点P从点D 开始沿DA边匀速运动，动点Q从点A开始沿AB边匀速运动，它们的运动速度均为2cm/s．点P和点Q同时出发，以QA、QP为边作平行四边形AQPE，设运动的时间为t（s），0＜t＜5．根据题意解答下列问题：（1）用含t的代数式表示AP；（2）设四边形CPQB的面积为S（cm2），求S与t的函数关系式；（3）当QP⊥BD时，求t的值；（4）在运动过程中，是否存在某一时刻t，使点E在∠ABD的平分线上？若存在，求出t的值；若不存在，请说明理由．17、定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．18、已知四边形ABCD的一组对边AD、BC的延长线交于点E．（1）如图1，若∠ABC=∠ADC=90°，求证：ED•EA=EC•EB；（2）如图2，若∠ABC=120°，cos∠ADC=，CD=5，AB=12，△CDE的面积为6，求四边形ABCD 的面积；（3）如图3，另一组对边AB、DC的延长线相交于点F．若cos∠ABC=cos∠ADC=，CD=5，CF=ED=n，直接写出AD的长（用含n的式子表示）19、在菱形ABCD中，∠ABC=60°,点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随点P的位置变化而变化.（1）如图1，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是，CE与AD的位置关系是；（2）当点E在菱形ABCD外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由(选择图2，图3中的一种情况予以证明或说理).(3) 如图4，当点P在线段BD的延长线上时，连接BE，AB=2√3 ,BE=2√19 ,求四边形ADPE 的面积.20、问题呈现如图1，在边长为1的正方形网格中，连接格点D，N和E，C，DN和EC相交于点P，求tan∠CPN的值．方法归纳求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形．观察发现问题中∠CPN不在直角三角形中，我们常常利用网格画平行线等方法解决此类问题，比如连接格点M，N，可得MN∥EC，则∠DNM=∠CPN，连接DM，那么∠CPN就变换到Rt△DMN中．问题解决（1）直接写出图1中tan∠CPN的值为；（2）如图2，在边长为1的正方形网格中，AN与CM相交于点P，求cos∠CPN的值；思维拓展（3）如图3，AB⊥BC，AB=4BC，点M在AB上，且AM=BC，延长CB到N，使BN=2BC，连接AN 交CM的延长线于点P，用上述方法构造网格求∠CPN的度数．。

2020年九年级数学中考三轮专题复习：函数及其图象(含答案)

2020年中考数学三轮专题复习函数及其图象（含答案）一、选择题（本大题共6道小题）1. 二次函数y=(x-1)2+3的图象的顶点坐标是 ()A.(1，3)B.(1，-3)C.(-1，3)D.(-1，-3)2. 若二次函数y=ax2+bx+c(a<0)的图象经过点(2，0)，且其对称轴为直线x=-1，则使函数值y>0成立的x的取值范围是()A.x<-4或x>2B.-4≤x≤2C.x≤-4或x≥2D.-4<x<23. 如图是雷达屏幕在一次探测中发现的多个目标，其中对目标A的位置表述正确的是()A.在南偏东75°方向处B.在5 km处C.在南偏东15°方向5 km处D.在南偏东75°方向5 km处4. 第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛，则下列函数图象可以体现这次比赛过程的是()5. 从某容器口以均匀地速度注入酒精，若液面高度h随时间t的变化情况如图所示，则对应容器的形状为()6. 如图，☉O的半径为2，双曲线的解析式分别为y=和y=-，则阴影部分的面积为()A.4πB.3πC.2πD.π二、填空题（本大题共5道小题）7. 星期天，小明上午8:00从家里出发，骑车到图书馆去借书，再骑车回到家，他离家的距离y(千米)与时间t(分)的关系如图所示，则上午8:45小明离家的距离是千米.8. 如图，直线y=kx+b(k<0)经过点A(3，1)，当kx+b<x时，x的取值范围为.9. 已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:x…-1 0 1 2 3 …y… 3 0 -1 0 m…(1)观察上表可求得m的值为;(2)这个二次函数的解析式为;(3)若点A(n+2，y1)，B(n，y2)在该抛物线上，且y1>y2，则n的取值范围为.10. 已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1，其部分图象如图所示，下列说法中:①b>0;②a-b+c<0;③b+2c>0;④当-1<x<0时，y>0，正确的是__________________(填写序号).11. 如图，矩形OABC的顶点A，C分别在y轴、x轴的正半轴上，D为AB的中点，反比例函数y=(k>0)的图象经过点D，且与BC交于点E，连接OD，OE，DE，若△ODE的面积为3，则k的值为.三、解答题（本大题共6道小题）12. 为了节能减排，我市某校准备购买某种品牌的节能灯，已知3只A型节能灯和5只B型节能灯共需50元，2只A型节能灯和3只B型节能灯共需31元.(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?(2)学校准备购买这两种型号的节能灯共200只，要求A型节能灯的数量不超过B型节能灯的数量的3倍，请设计出最省钱的购买方案，并说明理由.13. 小王骑车从甲地到乙地，小李骑车从乙地到甲地，小王的速度小于小李的速度，两人同时出发，沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.请你根据图象进行探究:(1)小王和小李的速度分别是多少?(2)求线段BC所表示的y与x之间的函数解析式，并写出自变量x的取值范围.14. 如图，二次函数的图象与x轴交于A(-3，0)，B(1，0)两点，交y轴于点C(0，3)，点C，D是二次函数图象上的一对对称点，一次函数的图象过点B，D.(1)请直接写出点D的坐标;(2)求二次函数的解析式;(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.15. 如图，抛物线y=-x2+bx+c与x轴交于A，B两点(A在B的左侧)，与y轴交于点N，过A点的直线l:y=kx+n与y轴交于点C，与抛物线y=-x2+bx+c的另一个交点为D，已知A(-1，0)，D(5，-6)，P点为抛物线y=-x2+bx+c上一动点(不与A，D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值;(3)设M为直线l上的点，探究是否存在点M，使得以点N，C，M，P为顶点的四边形为平行四边形.若存在，求出点M的坐标;若不存在，请说明理由.16. 某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙(墙足够长)，已知计划中的建筑材料可建围墙的总长度为50 m.设饲养室长为x(m)，占地面积为y(m2).(1)如图①，问饲养室长x为多少时，占地面积y最大?(2)如图②，现要求在图中所示位置留2 m宽的门，且仍使饲养室的占地面积最大.小敏说:“只要饲养室长比(1)中的长多2 m就行了.”请你通过计算，判断小敏的说法是否正确.17. 在画二次函数y=ax2+bx+c(a≠0)的图象时，甲写错了一次项的系数，列表如下:x…-1 0 1 2 3 …y甲… 6 3 2 3 6 …乙写错了常数项，列表如下:x…-1 0 1 2 3 …y乙…-2 -1 2 7 14 …通过上述信息，解决以下问题:(1)求原二次函数y=ax2+bx+c(a≠0)的表达式;(2)对于二次函数y=ax2+bx+c(a≠0)，当x时，y的值随x的值增大而增大;(3)若关于x的方程ax2+bx+c=k(a≠0)有两个不相等的实数根，求k的取值范围. 2020年中考数学三轮专题复习函数及其图象-答案一、选择题（本大题共6道小题）1. 【答案】A2. 【答案】D[解析]∵二次函数y=ax2+bx+c(a<0)的图象经过点(2，0)，且其对称轴为直线x=-1，∴二次函数的图象与x轴另一个交点为(-4，0)，∵a<0，∴抛物线开口向下，则使函数值y>0成立的x的取值范围是-4<x<2.3. 【答案】D[解析]目标A的位置在南偏东75°方向5 km处，故选D.4. 【答案】B[解析]根据题意可知兔子先让乌龟跑了一段距离，但是比乌龟晚到终点，故选项B正确.5. 【答案】C6. 【答案】C[解析]根据反比例函数y=，y=-及圆的中心对称性和轴对称性知，将二、四象限的阴影部分旋转到一、三象限对应部分，显然所有阴影部分的面积之和等于一、三象限内两个扇形的面积之和，也就相当于一个半径为2的半圆的面积.=π×22=2π.故选C.∴S阴影二、填空题（本大题共5道小题）7. 【答案】1.58. 【答案】x>3[解析]当x=3时，x=×3=1，∴点A在一次函数y=x的图象上，且一次函数y=x的图象经过第一、三象限，∴当x>3时，一次函数y=x的图象在y=kx+b的图象上方，即kx+b<x.9. 【答案】解:(1)3[解析]观察表格，根据抛物线的对称性可得x=3和x=-1时的函数值相等，∴m的值为3，故答案为:3.(2)y=(x-1)2-1[解析]由表格可得，二次函数y=ax2+bx+c图象的顶点坐标是(1，-1)，∴y=a(x-1)2-1.又当x=0时，y=0，∴a=1，∴这个二次函数的解析式为y=(x-1)2-1.(3)n>0[解析]∵点A(n+2，y1)，B(n，y2)在该抛物线上，且y1>y2，∴结合二次函数的图象和性质可知n>0.10. 【答案】①③④[解析]根据图象可得:a<0，c>0，对称轴:直线x=-=1，∴b=-2a.∵a<0，∴b>0，故①正确;把x=-1代入y=ax2+bx+c，得y=a-b+c.由抛物线的对称轴是直线x=1，且过点(3，0)，可得当x=-1时，y=0，∴a-b+c=0，故②错误;当x=1时，y=a+b+c>0.∵b=-2a，∴-+b+c>0，即b+2c>0，故③正确;由图象可以直接看出④正确.故答案为:①③④.11. 【答案】4[解析]过点D作DH⊥x轴于H点，交OE于M，∵反比例函数y=(k>0)的图象经过点D，E，∴S△ODH=S△ODA=S△OEC=，∴S△ODH-S△OMH=S△OEC-S△OMH，即S△OMD=S四边形EMHC，∴S△ODE=S梯形DHCE=3，设D(m，n)，∵D为AB的中点，∴B(2m，n).∵反比例函数y=(k>0)的图象经过点D，E，∴E2m，，∴S梯形=+n m=3，DHCE∴k=mn=4.三、解答题（本大题共6道小题）12. 【答案】解:(1)设1只A型节能灯的售价是x元，1只B型节能灯的售价是y元，根据题意，得解得答:1只A型节能灯的售价是5元，1只B型节能灯的售价是7元.(2)设购买A型节能灯a只，则购买B型节能灯(200-a)只，总费用为w元，w=5a+7(200-a)=-2a+1400，∵a≤3(200-a)，∴a≤150，∵-2<0，w随a的增大而减小，∴当a=150时，w取得最小值，此时w=1100，200-a=50.答:最省钱的购买方案是:购买A型节能灯150只，B型节能灯50只.13. 【答案】解:(1)从线段AB得:两人从相距30 km的两地同时出发，1 h后相遇，则v小王+v小李=30 km/h，小王从甲地到乙地行驶了3 h，∴v小王=30÷3=10(km/h)，∴v小李=20 km/h.(2)C点的意义是小李骑车从乙地到甲地用了30÷20=1.5(h)，此时小王和小李的距离是1.5×10=15(km)，∴C点坐标是(1.5，15).设直线BC的解析式为y=kx+b，将B(1，0)，C(1.5，15)分别代入解析式，得解得:∴线段BC的解析式为y=30x-30(1≤x≤1.5).14. 【答案】解:(1)D(-2，3).(2)设二次函数的解析式为y=ax2+bx+c(a，b，c为常数，且a≠0)，根据题意，得解得∴二次函数的解析式为y=-x2-2x+3.(3)x<-2或x>1.15. 【答案】[分析] (1)将点A，D的坐标分别代入直线表达式、抛物线的表达式，即可求解;(2)设出P点坐标，用参数表示PE，PF的长，利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况，分别求解即可.解:(1)将点A，D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A，D的坐标代入抛物线表达式，得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1，∴C(0，-1)，则直线l与x轴的夹角为45°，即∠OAC=45°，∵PE∥x轴，∴∠PEF=∠OAC=45°.又∵PF∥y轴，∴∠EPF=90°，∴∠EFP=45°.则PE=PF.设点P坐标为(x，-x2+3x+4)，则点F(x，-x-1)，∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18，∵-2<0，∴当x=2时，PE+PF有最大值，其最大值为18.(3)由题意知N(0，4)，C(0，-1)，∴NC=5，①当NC是平行四边形的一条边时，有NC∥PM，NC=PM.设点P坐标为(x，-x2+3x+4)，则点M的坐标为(x，-x-1)，∴|y M-y P|=5，即|-x2+3x+4+x+1|=5，解得x=2±或x=0或x=4(舍去x=0)，则点M坐标为(2+，-3-)或(2-，-3+)或(4，-5);②当NC是平行四边形的对角线时，线段NC与PM互相平分.由题意，NC的中点坐标为0，，设点P坐标为(m，-m2+3m+4)，则点M(n'，-n'-1)，∴0==，解得:n'=0或-4(舍去n'=0)，故点M(-4，3).综上所述，存在点M，使得以N，C，M，P为顶点的四边形为平行四边形，点M的坐标分别为:(2+，-3-)，(2-，-3+)，(4，-5)，(-4，3).16. 【答案】解:(1)∵y=x·=-(x-25)2+，∴当x=25时，占地面积y最大.(2)y=x·=-(x-26)2+338，∴当x=26时，占地面积y最大.即当饲养室长为26 m时，占地面积最大.∵26-25=1≠2，∴小敏的说法不正确.17. 【答案】解:(1)根据甲同学的错误可知x=0时，y=c=3是正确的，由甲同学提供的数据，选择x=-1，y=6;x=1，y=2代入y=ax2+bx+3，得解得a=1是正确的.根据乙同学提供的数据，选择x=-1，y=-2;x=1，y=2代入y=x2+bx+c，得解得b=2是正确的，∴y=x2+2x+3.(2)≥-1[解析]抛物线y=x2+2x+3的对称轴为直线x=-1，∵二次项系数为1，故抛物线开口向上，∴当x≥-1时，y的值随x值的增大而增大.故答案为≥-1.(3)∵方程ax2+bx+c=k(a≠0)有两个不相等的实数根，即x2+2x+3-k=0有两个不相等的实数根，∴Δ=4-4(3-k)>0，解得k>2.。

2013年中考数学三轮复习每天30分综合训练(05)

2013年中考数学三轮复习每天30分综合训练（05）一、填空题（共10小题，每小题3分，满分30分）1．（3分）（防城港）计算：1×（﹣3）=_________．2．（3分）（防城港）当x=_________时，分式没有意义．3．（3分）（无锡）分解因式：4a2﹣1=_________．4．（3分）（防城港）在梯形ABCD中，AD∥BC，当添加一个条件_________时，梯形ABCD是等腰梯形．（不添加辅助线或字母，只需填一个条件）．5．（3分）（防城港）如图，已知直线a∥b，则y°与x°的函数关系式是_________．6．（3分）（防城港）下列说法：1：圆柱体的左视图必是一个圆；2：任意一个三角形必有一个内切圆．正确说法正确的序号是_________．7．（3分）（2010•枣庄）下列一串梅花图案是按一定规律排列的，请你仔细观察，在前2009个梅花图案中，共有_________个“”图案．8．（3分）（防城港）一组数据：1，﹣2，a的平均数是0，那么这组数据的方差是_________．9．（3分）（防城港）如图，网格的小正方形的边长均为1，小正方形的顶点叫做格点．△ABC 的三个顶点都在格点上，那么△ABC的外接圆半径是_________．10．（3分）（防城港）将直线y=x向左平移1个单位长度后得到直线α，如图，直线α与反比例函数y=（x＞0）的图象相交于A，与x轴相交于B，则OA2﹣OB2=_________．二、选择题（共8小题，每小题4分，满分32分） 11．（4分）（防城港）计算（）2的结果是（）A ． 9B ． ﹣9C ． 3D ． ﹣312．（4分）（防城港）跑步是一项增强体质的简易体育活动．某校某天早上参加晨跑人数有2318人，用科学记数法表示这个数是（）A ． 2.318×103B ． 0.2318×104C ． 23.18×102D ． 231.8×10113．（4分）（防城港）下列图形是轴对称图形的是（）A ．B ．C ．D ．14．（4分）（防城港）方程的解是（） A ． x =1 B ． x =2 C ． x =3 D ． x =415．（4分）（防城港）小刚准备用自己节省的零花钱购买一台MP4来学习英语，他已存有50元，并计划从本月起每月节省30元，直到他至少有280元．设x 个月后小刚至少有280元，则可列计算月数的不等式为（）A ． 30x+50＞280B ． 30x ﹣50≥280C ． 30x ﹣50≤280D ．30x+50≥28016．（4分）（防城港）如图，射线PQ 是⊙O 相切于点A ，射线PO 与⊙O 相交于B ，C 两点，连接AB ，若PB ：BC=1：2上，则∠PAB 的度数等于（）A ． 26°B ． 30°C ． 32°D ． 45°17．（4分）（防城港）二次函数y=﹣x 2+1的图象与x 轴交于A ，B 两点，与y 轴相交于点C ．下列说法中，错误的是（）A ． △ABC 是等腰三角形B ．点C 的坐标是（0，1）C ． AB 的长为2D ． y 随x 的增大而减小18．（4分）（防城港）如图，点A 1，A 2，A 3，A 4是某市正方形道路网的部分交汇点，且它们都位于同一对角线上．某人从点A 1出发，规定向右或向下行走，那么到达点A 3的走法共有（）A ． 4种B ． 6种C ． 8种D ． 10种三、解答题（共4小题，满分38分）19．（8分）（防城港）计算：2tan60°﹣．20．（8分）（防城港）解不等式组：，并把解集在数轴上表示出来．21．（10分）（防城港）如图，矩形ABCD中，点E、F分别在AB、BC上，△DEF为等腰直角三角形，∠DEF=90°，AD+CD=10，AE=2，求AD的长．22．（12分）（防城港）如图，⊙O的半径为2，直径CD经过弦AB的中点G，若的长等于圆周长的．（1）填空：cos∠ACB=_________；（2）求的值．。

重庆市大足区双路 2022年中考数学第三轮压轴题：四边形综合复习

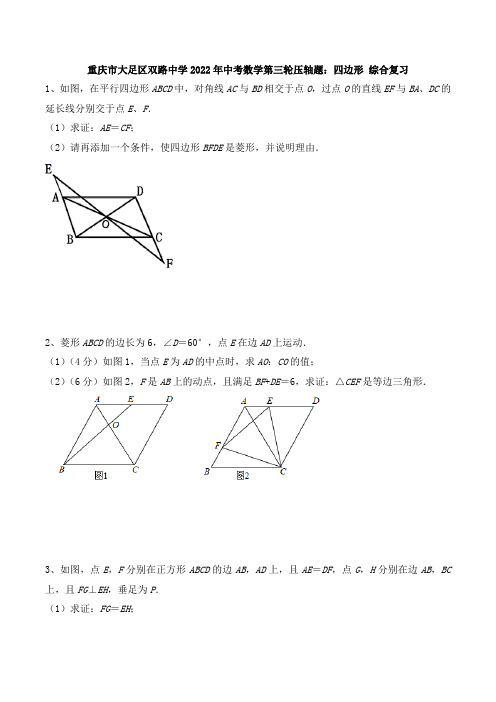
重庆市大足区双路中学2022年中考数学第三轮压轴题：四边形综合复习1、如图，在平行四边形ABCD中，对角线AC与BD相交于点O，过点O的直线EF与BA、DC的延长线分别交于点E、F．（1）求证：AE＝CF；（2）请再添加一个条件，使四边形BFDE是菱形，并说明理由．2、菱形ABCD的边长为6，∠D＝60°，点E在边AD上运动．（1）（4分）如图1，当点E为AD的中点时，求AO：CO的值；（2）（6分）如图2，F是AB上的动点，且满足BF+DE＝6，求证：△CEF是等边三角形．3、如图，点E，F分别在正方形ABCD的边AB，AD上，且AE＝DF，点G，H分别在边AB，BC 上，且FG⊥EH，垂足为P．（1）求证：FG＝EH；（2）若正方形ABCD边长为5，AE＝2，tan∠AGF＝，求PF的长度．4、如图，平行四边形ABCD的对角线AC，BD相交于点O，AB⊥AC，AB＝6cm，BC＝10cm，点P 从点A出发，沿AD方向以每秒1cm的速度向终点D运动，连接PO，并延长交BC于点Q．设点P的运动时间为t秒．（1）求BQ的长（用含t的代数式表示）；（2）当四边形ABQP是平行四边形时，求t的值；（3）当时，点O是否在线段AP的垂直平分线上？请说明理由．5、如图，在边长为1的正方形ABCD中，动点E，F分别在边AB，CD上，将正方形ABCD沿直线EF折叠，使点B的对应点M始终落在边AD上（点M不与点A，D重合），点C落在点N处，MN与CD交于点P．（1）当AM =13时，AE 的值是；（2）随着点M 在边AD 上位置的变化，△PDM 的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值；（3）设四边形BEFC 的面积为S ，求出S 的最小值．6、有公共顶点A 的正方形ABCD 与正方形AEGF 按如图1所示放置，点E ，F 分别在边AB 和AD 上，连接BF ，DE ，M 是BF 的中点，连接AM 交DE 于点N ．【观察猜想】（1）线段DE 与AM 之间的数量关系是，位置关系是；【探究证明】（2）将图1中的正方形AEGF 绕点A 顺时针旋转45°，点G 恰好落在边AB 上，如图2，其他条件不变，线段DE 与AM 之间的关系是否仍然成立？并说明理由．7、在正方形ABCD 中，点E 是边BC 上一动点（不含端点B 、C ）．（1）如图1，AE ⊥EF ，AE ＝EF ，连接CF ． ①求∠ECF 的大小；②如图2，N 为CF 的中点，连接DN 、DE ，求证：DE =√2DN ；（2）如图3．若AD ＝1+√3，直接写出12BE +DE 的最小值．8、如图，将正方形纸片ABCD 折叠使点D 落在射线BA 上的点E ，将纸片展平，折痕交AD 边于点F ，交BC 边于点G ，DC 的对应边EC '所在的直线交直线BC 于点H ，连接DE ．(1)若点E 在AB 边上， ①求证：AED DEH ∠=∠． ②当23AE EB =时，求sin BHE ∠的值． (2)若AE k EB=，求BHCH 的值（用含k 的代数式表示）。

2021年九年级中考数学第三轮压轴题：二次函数的综合专题复习(含答案)

2021年中考数学第三轮压轴题：二次函数的综合专题复习1、如图，抛物线y=x2+bx+c与y轴交于点A（0，2），对称轴为直线x=﹣2，平行于x轴的直线与抛物线交于B、C两点，点B在对称轴左侧，BC=6．（1）求此抛物线的解析式．（2）点P在x轴上，直线CP将△ABC面积分成2：3两部分，请直接写出P点坐标．2、如图，已知点A（﹣1，0），B（3，0），C（0，1）在抛物线y=ax2+bx+c上．（1）求抛物线解析式；（2）在直线BC上方的抛物线上求一点P，使△PBC面积为1；（3）在x轴下方且在抛物线对称轴上，是否存在一点Q，使∠BQC=∠BAC？若存在，求出Q点坐标；若不存在，说明理由．3、如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC 面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．4、如图，已知二次函数y=ax2+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．（1）求这个二次函数的表达式；（2）点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；（3）直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．5、如图，抛物线顶点P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED 的边长；如果不存在，请说明理由．6、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点（A在B 的左侧），且OA=3，OB=1，与y轴交于C（0，3），抛物线的顶点坐标为D（﹣1，4）．（1）求A、B两点的坐标；（2）求抛物线的解析式；（3）过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B、D两点间的一个动点（点P不与B、D两点重合），PA、PB与直线DE分别交于点F、G，当点P 运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．7、如图，在平面直角坐标系中，抛物线y=x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．（1）求点A，B，C的坐标；（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．8、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y 轴于点C（0，﹣），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=．（1）求抛物线的解析式；（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P 运动到点A时，点Q也停止运动，设运动时间为t秒．①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．9、如图，已知二次函数y=ax2−5√3x+c(a>0)的图象抛物线与x轴相交于不同的两点A(x1,0)，B(x2,0)，且x1<x2，(1)若抛物线的对称轴为x=√3求的a值；(2)若a=15，求c的取值范围；(3)若该抛物线与y轴相交于点D，连接BD，且∠OBD=60∘，抛物线的对称轴l，连接AF，满与x轴相交点E，点F是直线l上的一点，点F的纵坐标为3+12a足∠ADB=∠AFE，求该二次函数的解析式．10、如图1，已知抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．（1）求抛物线的表达式；（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．（3）如图2，连接BC，PB，PC，设△PBC的面积为S．①求S关于t的函数表达式；②求P点到直线BC的距离的最大值，并求出此时点P的坐标．11、如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+3．（1）求抛物线的表达式；（2）在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；（3）在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．12、如图1，经过原点O的抛物线y=ax2+bx（a、b为常数，a≠0）与x轴相交于另一点A（3，0）．直线l：y=x在第一象限内和此抛物线相交于点B（5，t），与抛物线的对称轴相交于点C．（1）求抛物线的解析式；（2）在x轴上找一点P，使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似，求满足条件的点P的坐标；（3）直线l沿着x轴向右平移得到直线l′，l′与线段OA相交于点M，与x 轴下方的抛物线相交于点N，过点N作NE⊥x轴于点E．把△MEN沿直线l′折叠，当点E恰好落在抛物线上时（图2），求直线l′的解析式；（4）在（3）问的条件下（图3），直线l′与y轴相交于点K，把△MOK绕点O 顺时针旋转90°得到△M′OK′，点F为直线l′上的动点．当△M'FK′为等腰三角形时，求满足条件的点F的坐标．13、如图1，抛物线y=ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0）．（1）求该抛物线所对应的函数解析式；（2）如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．①求四边形ACFD的面积；②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q 的坐标．14、已知抛物线y=x2+bx+c经过点A（﹣2，0），B（0、﹣4）与x轴交于另一点C，连接BC．（1）求抛物线的解析式；（2）如图，P是第一象限内抛物线上一点，且S△PBO =S△PBC，求证：AP∥BC；（3）在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A，B，C，E中的三点为顶点的三角形相似（不重合）？若存在，请求出点D的坐标；若不存在，请说明理由．参考答案1、如图，抛物线y=x2+bx+c与y轴交于点A（0，2），对称轴为直线x=﹣2，平行于x轴的直线与抛物线交于B、C两点，点B在对称轴左侧，BC=6．（1）求此抛物线的解析式．（2）点P在x轴上，直线CP将△ABC面积分成2：3两部分，请直接写出P点坐标．【解答】解：（1）由题意得：x=﹣=﹣=﹣2，c=2，解得：b=4，c=2，则此抛物线的解析式为y=x2+4x+2；（2）∵抛物线对称轴为直线x=﹣2，BC=6，∴B横坐标为﹣5，C横坐标为1，把x=1代入抛物线解析式得：y=7，∴B（﹣5，7），C（1，7），设直线AB解析式为y=kx+2，把B坐标代入得：k=﹣1，即y=﹣x+2，作出直线CP，与AB交于点Q，过Q作QH⊥y轴，与y轴交于点H，BC与y轴交于点M，可得△AQH∽△ABM，∴=，∵点P在x轴上，直线CP将△ABC面积分成2：3两部分，∴AQ：QB=2：3或AQ：QB=3：2，即AQ：AB=2：5或AQ：QB=3：5，∵BM=5，∴QH=2或QH=3，当QH=2时，把x=﹣2代入直线AB解析式得：y=4，此时Q（﹣2，4），直线CQ解析式为y=x+6，令y=0，得到x=﹣6，即P（﹣6，0）；当QH=3时，把x=﹣3代入直线AB解析式得：y=5，此时Q（﹣3，5），直线CQ解析式为y=x+，令y=0，得到x=﹣13，此时P （﹣13，0），综上，P的坐标为（﹣6，0）或（﹣13，0）．2、如图，已知点A（﹣1，0），B（3，0），C（0，1）在抛物线y=ax2+bx+c上．（1）求抛物线解析式；（2）在直线BC上方的抛物线上求一点P，使△PBC面积为1；（3）在x轴下方且在抛物线对称轴上，是否存在一点Q，使∠BQC=∠BAC？若存在，求出Q点坐标；若不存在，说明理由．【解答】解：（1）设抛物线的解析式为y=a（x+1）（x﹣3），将C（0，1）代入得﹣3a=1，解得：a=﹣，∴抛物线的解析式为y=﹣x2+x+1．（2）过点P作PD⊥x，交BC与点D．设直线BC的解析式为y=kx+b，则，解得：k=﹣，∴直线BC的解析式为y=﹣x+1．设点P（x，﹣x2+x+1），则D（x，﹣x+1）∴PD=（﹣x2+x+1）﹣（﹣x+1）=﹣x2+x，=OB•DP=×3×（﹣x2+x）=﹣x2+x．∴S△PBC又∵S=1，△PBC∴﹣x2+x=1，整理得：x2﹣3x+2=0，解得：x=1或x=2，∴点P的坐标为（1，）或（2，1）．（3）存在．∵A（﹣1，0），C（0，1），∴OC=OA=1∴∠BAC=45°．∵∠BQC=∠BAC=45°，∴点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点．设△ABC外接圆圆心为M，则∠CMB=90°．设⊙M的半径为x，则Rt△CMB中，由勾股定理可知CM2+BM2=BC2，即2x2=10，解得：x=（负值已舍去），∵AC的垂直平分线的为直线y=﹣x，AB的垂直平分线为直线x=1，∴点M为直线y=﹣x与x=1的交点，即M（1，﹣1），∴Q的坐标为（1，﹣1﹣）．3、如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．（1）求线段OC的长度；（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC 面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．【解答】解：（1）由题可知当y=0时，a（x﹣1）（x﹣3）=0，解得：x1=1，x2=3，即A（1，0），B（3，0），∴OA=1，OB=3∵△OCA∽△OBC，∴OC：OB=OA：OC，∴OC2=OA•OB=3，则OC=；（2）∵C是BM的中点，即OC为斜边BM的中线，∴OC=BC，∴点C的横坐标为，又OC=，点C在x轴下方，∴C（，﹣），设直线BM的解析式为y=kx+b，把点B（3，0），C（，﹣）代入得：，解得：b=﹣，k=，∴y=x﹣，又∵点C（，﹣）在抛物线上，代入抛物线解析式，解得：a=，∴抛物线解析式为y=x2﹣x+2；（3）点P存在，设点P坐标为（x，x2﹣x+2），过点P作PQ⊥x轴交直线BM于点Q，则Q（x，x﹣），∴PQ=x﹣﹣（x2﹣x+2）=﹣x2+3x﹣3，当△BCP面积最大时，四边形ABPC的面积最大，=PQ（3﹣x）+PQ（x﹣）=PQ=﹣x2+x﹣，S△BCP有最大值，四边形ABPC的面积最大，此时点P的坐标为当x=﹣=时，S△BCP（，﹣）．4、如图，已知二次函数y=ax2+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．（1）求这个二次函数的表达式；（2）点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；（3）直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．【解答】解：（1）将A（1，0），B（3，0）代入函数解析式，得，解得，这个二次函数的表达式是y=x2﹣4x+3；（2）当x=0时，y=3，即点C（0，3），设BC的表达式为y=kx+b，将点B（3，0）点C（0，3）代入函数解析式，得，解这个方程组，得直线BC的解析是为y=﹣x+3，过点P作PE∥y轴，交直线BC于点E（t，﹣t+3），PE=﹣t+3﹣（t﹣4t+3）=﹣t2+3t，∴S△BCP =S△BPE+SCPE=（﹣t2+3t）×3=﹣（t﹣）2+．∵﹣＜0，∴当t=时，S△BCP最大=（3）M（m，﹣m+3），N（m，m2﹣4m+3）MN=m2﹣3m，BM=|m﹣3|，当MN=BM时，①m2﹣3m=（m﹣3），解得m=，②m2﹣3m=﹣（m﹣3），解得m=﹣当BN=MN时，∠NBM=∠BMN=45°，m2﹣4m+3=0，解得m=1或m=3（舍）当BM=BN时，∠BMN=∠BNM=45°，﹣（m2﹣4m+3）=﹣m+3，解得m=2或m=3（舍），当△BMN是等腰三角形时，m的值为，﹣，1，2．5、如图，抛物线顶点P（1，4），与y轴交于点C（0，3），与x轴交于点A，B．（1）求抛物线的解析式．（2）Q是抛物线上除点P外一点，△BCQ与△BCP的面积相等，求点Q的坐标．（3）若M，N为抛物线上两个动点，分别过点M，N作直线BC的垂线段，垂足分别为D，E．是否存在点M，N使四边形MNED为正方形？如果存在，求正方形MNED 的边长；如果不存在，请说明理由．【解答】解：（1）设y=a（x﹣1）2+4（a≠0），把C（0，3）代入抛物线解析式得：a+4=3，即a=﹣1，则抛物线解析式为y=﹣（x﹣1）2+4=﹣x2+2x+3；（2）由B（3，0），C（0，3），得到直线BC解析式为y=﹣x+3，∵S△OBC =S△QBC，∴PQ∥BC，①过P作PQ∥BC，交抛物线于点Q，如图1所示，∵P（1，4），∴直线PQ解析式为y=﹣x+5，联立得：，解得：或，即Q（2，3）；②设G（1，2），∴PG=GH=2，过H作直线Q2Q3∥BC，交x轴于点H，则直线Q2Q3解析式为y=﹣x+1，联立得：，解得：或，∴Q2（，），Q3（，）；（3）存在点M，N使四边形MNED为正方形，如图2所示，过M作MF∥y轴，过N作NF∥x轴，过N作NH∥y轴，则有△MNF 与△NEH都为等腰直角三角形，设M（x1，y1），N（x2，y2），设直线MN解析式为y=﹣x+b，联立得：，消去y得：x2﹣3x+b﹣3=0，∴NF2=|x1﹣x2|2=（x1+x2）2﹣4x1x2=21﹣4b，∵△MNF为等腰直角三角形，∴MN2=2NF2=42﹣8b，∵NH2=（b﹣3）2，∴NF2=（b﹣3）2，若四边形MNED为正方形，则有NE2=MN2，∴42﹣8b=（b2﹣6b+9），整理得：b2+10b﹣75=0，解得：b=﹣15或b=5，∵正方形边长为MN=，∴MN=9或．6、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点（A在B 的左侧），且OA=3，OB=1，与y轴交于C（0，3），抛物线的顶点坐标为D（﹣1，4）．（1）求A、B两点的坐标；（2）求抛物线的解析式；（3）过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B、D两点间的一个动点（点P不与B、D两点重合），PA、PB与直线DE分别交于点F、G，当点P 运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．【解答】解：（1）由抛物线y=ax2+bx+c交x轴于A、B两点（A在B的左侧），且OA=3，OB=1，得A点坐标（﹣3，0），B点坐标（1，0）；（2）设抛物线的解析式为y=a（x+3）（x﹣1），把C点坐标代入函数解析式，得a（0+3）（0﹣1）=3，解得a=﹣1，抛物线的解析式为y=﹣（x+3）（x﹣1）=﹣x2﹣2x+3；（3）EF+EG=8（或EF+EG是定值），理由如下：过点P作PQ∥y轴交x轴于Q，如图．设P（t，﹣t2﹣2t+3），则PQ=﹣t2﹣2t+3，AQ=3+t，QB=1﹣t，∵PQ∥EF，∴△AEF∽△AQP，∴=，∴EF===×（﹣t2﹣2t+3）=2（1﹣t）；又∵PQ∥EG，∴△BEG∽△BQP，∴=，∴EG===2（t+3），∴EF+EG=2（1﹣t）+2（t+3）=8．7、如图，在平面直角坐标系中，抛物线y=x2﹣x﹣4与x轴交于A，B两点（点A在点B左侧），与y轴交于点C．（1）求点A，B，C的坐标；（2）点P从A点出发，在线段AB上以每秒2个单位长度的速度向B点运动，同时，点Q从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，当其中一个点到达终点时，另一个点也停止运动．设运动时间为t秒，求运动时间t为多少秒时，△PBQ的面积S最大，并求出其最大面积；（3）在（2）的条件下，当△PBQ面积最大时，在BC下方的抛物线上是否存在点M，使△BMC的面积是△PBQ面积的1.6倍？若存在，求点M的坐标；若不存在，请说明理由．【解答】解：（1）当x=0时，y=x2﹣x﹣4=﹣4，∴点C的坐标为（0，﹣4）；当y=0时，有x2﹣x﹣4=0，解得：x1=﹣2，x2=3，∴点A的坐标为（﹣2，0），点B的坐标为（3，0）．（2）设直线BC的解析式为y=kx+b（k≠0），将B（3，0）、C（0，﹣4）代入y=kx+b，，解得：，∴直线BC的解析式为y=x﹣4．过点Q作QE∥y轴，交x轴于点E，如图1所示，当运动时间为t秒时，点P的坐标为（2t﹣2，0），点Q的坐标为（3﹣t，﹣t），∴PB=3﹣（2t﹣2）=5﹣2t，QE=t，∴S△PBQ=PB•QE=﹣t2+2t=﹣（t﹣）2+．∵﹣＜0，∴当t=时，△PBQ的面积取最大值，最大值为．（3）当△PBQ面积最大时，t=，此时点P的坐标为（，0），点Q的坐标为（，﹣1）．假设存在，设点M的坐标为（m，m2﹣m﹣4），则点F的坐标为（m，m﹣4），∴MF=m﹣4﹣（m2﹣m﹣4）=﹣m2+2m，∴S△BMC=MF•OB=﹣m2+3m．∵△BMC的面积是△PBQ面积的1.6倍，∴﹣m2+3m=×1.6，即m2﹣3m+2=0，解得：m1=1，m2=2．∵0＜m＜3，∴在BC下方的抛物线上存在点M，使△BMC的面积是△PBQ面积的1.6倍，点M 的坐标为（1，﹣4）或（2，﹣）．8、如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y 轴于点C（0，﹣），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=．（1）求抛物线的解析式；（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P 运动到点A时，点Q也停止运动，设运动时间为t秒．①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．解：（1）∵OA=1，OB=4∴A（1，0），B（﹣4，0）设抛物线的解析式为y=a（x+4）（x﹣1）∵点C（0，﹣）在抛物线上∴﹣解得a=∴抛物线的解析式为y=（2）存在t，使得△ADC与△PQA相似．理由：①在Rt△AOC中，OA=1，OC=则tan∠ACO=∵tan∠OAD=∴∠OAD=∠ACO∵直线l的解析式为y=∴D（0，﹣）∵点C（0，﹣）∴CD=由AC2=OC2+OA2，得AC=在△AQP中，AP=AB﹣PB=5﹣2t，AQ=t由∠PAQ=∠ACD，要使△ADC与△PQA相似只需或则有或解得t1=，t2=∵t1＜2.5，t2＜2.5∴存在t=或t=，使得△ADC与△PQA相似②存在t，使得△APQ与△CAQ的面积之和最大理由：作PF⊥AQ于点F，CN⊥AQ于N在△APF中，PF=AP•sin∠PAF=在△AOD中，由AD2=OD2+OA2，得AD=在△ADC中，由S△ADC=∴CN=∴S△AQP +S△AQC==﹣∴当t=时，△APQ与△CAQ的面积之和最大9、如图，已知二次函数y=ax2−5√3x+c(a>0)的图象抛物线与x轴相交于不同的两点A(x1,0)，B(x2,0)，且x1<x2，(1)若抛物线的对称轴为x=√3求的a值；(2)若a=15，求c的取值范围；(3)若该抛物线与y轴相交于点D，连接BD，且∠OBD=60∘，抛物线的对称轴l 与x轴相交点E，点F是直线l上的一点，点F的纵坐标为3+12a，连接AF，满足∠ADB=∠AFE，求该二次函数的解析式．【答案】解：(1)抛物线的对称轴是：x=−b2a =−−5√32a=√3，解得：a=52；(2)由题意得二次函数解析式为：y=15x2−5√3x+c，∵二次函数与x轴有两个交点，∴△>0，∴△=b2−4ac=(−5√3)2−4×15c，∴c<54；(3)∵∠BOD=90∘，∠DBO=60∘，∴tan60∘=ODOB =cOB=√3，∴OB=√33c，∴B(√33c,0)，把B(√33c,0)代入y =ax 2−5√3x +c 中得：ac 23−5√3⋅√3c 3+c =0，ac 23−5c +c =0，∵c ≠0， ∴ac =12， ∴c =12a，把c =12a代入y =ax 2−5√3x +c 中得： y =a(x 2−5√3x a+12a 2)=a(x −4√3a)(x −√3a)， ∴x 1=4√3a，x 2=√3a， ∴A(√3a ,0)，B(4√3a ,0)，D(0,12a)， ∴AB =4√3a−√3a=3√3a ，AE =3√32a， ∵F 的纵坐标为3+12a ， ∴F(5√32a ,6a+12a)，过点A 作AG ⊥DB 于G ， ∴BG =12AB =AE =3√32a，AG =92a ，DG =DB −BG =8√3a−3√32a=13√32a， ∵∠ADB =∠AFE ，∠AGD =∠FEA =90∘， ∴△ADG ∽△AFE ， ∴AE AG =FEDG ， ∴3√32a 92a=6a+12a 13√32a，∴a =2，c =6， ∴y =2x 2−5√3x +6．10、如图1，已知抛物线y=﹣x 2+bx+c 与x 轴交于A （﹣1，0），B （3，0）两点，与y 轴交于C 点，点P 是抛物线上在第一象限内的一个动点，且点P 的横坐标为t ．（1）求抛物线的表达式；（2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．（3）如图2，连接BC，PB，PC，设△PBC的面积为S．①求S关于t的函数表达式；②求P点到直线BC的距离的最大值，并求出此时点P的坐标．【解答】解：（1）将A（﹣1，0）、B（3，0）代入y=﹣x2+bx+c，，解得：，∴抛物线的表达式为y=﹣x2+2x+3．（2）在图1中，连接PC，交抛物线对称轴l于点E，∵抛物线y=﹣x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点，∴抛物线的对称轴为直线x=1．当t=2时，点C、P关于直线l对称，此时存在点M，使得四边形CDPM是平行四边形．∵抛物线的表达式为y=﹣x2+2x+3，∴点C的坐标为（0，3），点P的坐标为（2，3），∴点M的坐标为（1，6）；当t≠2时，不存在，理由如下：若四边形CDPM是平行四边形，则CE=PE，∵点C的横坐标为0，点E的横坐标为0，∴点P的横坐标t=1×2﹣0=2．又∵t≠2，∴不存在．（3）①在图2中，过点P作PF∥y轴，交BC于点F．设直线BC的解析式为y=mx+n（m≠0），将B（3，0）、C（0，3）代入y=mx+n，，解得：，∴直线BC的解析式为y=﹣x+3．∵点P的坐标为（t，﹣t2+2t+3），∴点F的坐标为（t，﹣t+3），∴PF=﹣t2+2t+3﹣（﹣t+3）=﹣t2+3t，∴S=PF•OB=﹣t2+t=﹣（t﹣）2+．②∵﹣＜0，∴当t=时，S取最大值，最大值为．∵点B的坐标为（3，0），点C的坐标为（0，3），∴线段BC==3，∴P点到直线BC的距离的最大值为=，此时点P的坐标为（，）．11、如图，以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点，交y轴于点C，直线BC的表达式为y=﹣x+3．（1）求抛物线的表达式；（2）在直线BC上有一点P，使PO+PA的值最小，求点P的坐标；（3）在x轴上是否存在一点Q，使得以A、C、Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．【解答】解：（1）把x=0代入y=﹣x+3，得：y=3，∴C（0，3）．把y=0代入y=﹣x+3得：x=3，∴B（3，0），A（﹣1，0）将C（0，3）、B（3，0）代入y=﹣x2+bx+c得：，解得b=2，c=3．∴抛物线的解析式为y=﹣x2+2x+3．（2）如图所示：作点O关于BC的对称点O′，则O′（3，3）．∵O′与O关于BC对称，∴PO=PO′．∴OP+AP=O′P+AP≤AO′．∴OP+AP的最小值=O′A==5．（3）y=﹣x2+2x+3=﹣（x﹣1）2+4，∴D（1，4）．又∵C（0，3，B（3，0），∴CD=，BC=3，DB=2．∴CD2+CB2=BD2，∴∠DCB=90°．∵A（﹣1，0），C（0，3），∴OA=1，CO=3．∴==．又∵∠AOC=DCB=90°，∴△AOC∽△DCB．∴当Q的坐标为（0，0）时，△AQC∽△DCB．如图所示：连接AC，过点C作CQ⊥AC，交x轴与点Q．∵△ACQ为直角三角形，CO⊥AQ，∴△ACQ∽△AOC．又∵△AOC∽△DCB，∴△ACQ∽△DCB．∴=，即=，解得：AQ=10．∴Q（9，0）．综上所述，当Q的坐标为（0，0）或（9，0）时，以A、C、Q为顶点的三角形与△BCD相似．12、如图1，经过原点O的抛物线y=ax2+bx（a、b为常数，a≠0）与x轴相交于另一点A（3，0）．直线l：y=x在第一象限内和此抛物线相交于点B（5，t），与抛物线的对称轴相交于点C．（1）求抛物线的解析式；（2）在x轴上找一点P，使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似，求满足条件的点P的坐标；（3）直线l沿着x轴向右平移得到直线l′，l′与线段OA相交于点M，与x 轴下方的抛物线相交于点N，过点N作NE⊥x轴于点E．把△MEN沿直线l′折叠，当点E恰好落在抛物线上时（图2），求直线l′的解析式；（4）在（3）问的条件下（图3），直线l′与y轴相交于点K，把△MOK绕点O 顺时针旋转90°得到△M′OK′，点F为直线l′上的动点．当△M'FK′为等腰三角形时，求满足条件的点F的坐标．【解答】解：（1）由已知点B坐标为（5，5）把点B（5，5），A（3，0）代入y=ax2+bx，得解得∴抛物线的解析式为：y=（2）由（1）抛物线对称轴为直线x=，则点C坐标为（，）∴OC=，OB=5当△OBA∽△OCP时，∴∴OP=当△OBA∽△OPC时，∴∴OP=5∴点P坐标为（5，0）或（，0）（3）设点N坐标为（a，b），直线l′解析式为：y=x+c ∵直线l′y=x+c与x轴夹角为45°∴△MEN为等腰直角三角形．当把△MEN沿直线l′折叠时，四边形ENE′M为正方形∴点′E坐标为（a﹣b，b）∵EE′平行于x轴∴E、E′关于抛物线对称轴对称∵∴b=2a﹣3则点N坐标可化为（a，2a﹣3）把点N坐标带入y=得：2a﹣3=解得a1=1，a2=6∵a=6时，b=2a﹣3=﹣9＜0∴a=6舍去则点N坐标为（1，﹣1）把N坐标带入y=x+c则c=﹣2∴直线l′的解析式为：y=x﹣2（4）由（3）K点坐标为（0，﹣2）则△MOK为等腰直角三角形∴△M′OK′为等腰直角三角形，M′K′⊥直线l′∴当M′K′=M′F时，△M'FK′为等腰直角三角形∴F坐标为（1，0）或（﹣1，﹣2）13、如图1，抛物线y=ax2+bx+3交x轴于点A（﹣1，0）和点B（3，0）．（1）求该抛物线所对应的函数解析式；（2）如图2，该抛物线与y轴交于点C，顶点为F，点D（2，3）在该抛物线上．①求四边形ACFD的面积；②点P是线段AB上的动点（点P不与点A、B重合），过点P作PQ⊥x轴交该抛物线于点Q，连接AQ、DQ，当△AQD是直角三角形时，求出所有满足条件的点Q 的坐标．【解答】解：（1）由题意可得，解得，∴抛物线解析式为y=﹣x2+2x+3；（2）①∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴F（1，4），∵C（0，3），D（2，3），∴CD=2，且CD∥x轴，∵A（﹣1，0），∴S四边形ACFD =S△ACD+S△FCD=×2×3+×2×（4﹣3）=4；②∵点P在线段AB上，∴∠DAQ不可能为直角，∴当△AQD为直角三角形时，有∠ADQ=90°或∠AQD=90°，i．当∠ADQ=90°时，则DQ⊥AD，∵A（﹣1，0），D（2，3），∴直线AD解析式为y=x+1，∴可设直线DQ解析式为y=﹣x+b′，把D（2，3）代入可求得b′=5，∴直线DQ解析式为y=﹣x+5，联立直线DQ和抛物线解析式可得，解得或，∴Q（1，4）；ii．当∠AQD=90°时，设Q（t，﹣t2+2t+3），设直线AQ的解析式为y=k1x+b1，把A、Q坐标代入可得，解得k1=﹣（t﹣3），设直线DQ解析式为y=k2x+b2，同理可求得k2=﹣t，∵AQ⊥DQ，∴k1k2=﹣1，即t（t﹣3）=﹣1，解得t=，当t=时，﹣t2+2t+3=，当t=时，﹣t2+2t+3=，∴Q点坐标为（，）或（，）；综上可知Q点坐标为（1，4）或（，）或（，）．14、已知抛物线y=x2+bx+c经过点A（﹣2，0），B（0、﹣4）与x轴交于另一点C，连接BC．（1）求抛物线的解析式；（2）如图，P是第一象限内抛物线上一点，且S△PBO =S△PBC，求证：AP∥BC；（3）在抛物线上是否存在点D，直线BD交x轴于点E，使△ABE与以A，B，C，E中的三点为顶点的三角形相似（不重合）？若存在，请求出点D的坐标；若不存在，请说明理由．【解答】解：（1）把点A（﹣2，0），B（0、﹣4）代入抛物线y=x2+bx+c中得：，解得：，∴抛物线的解析式为：y=x2﹣x﹣4；（2）当y=0时，x2﹣x﹣4=0，解得：x=﹣2或4，∴C（4，0），如图1，过O作OE⊥BP于E，过C作CF⊥BP于F，设PB交x轴于G，∵S△PBO =S△PBC，∴，∴OE=CF，易得△OEG≌△CFG，∴OG=CG=2，设P（x，x2﹣x﹣4），过P作PM⊥y轴于M，tan∠PBM===，∴BM=2PM，∴4+x2﹣x﹣4=2x，x2﹣6x=0，x 1=0（舍），x2=6，∴P（6，8），易得AP的解析式为：y=x+2，BC的解析式为：y=x﹣4，∴AP∥BC；（3）以A，B，C，E中的三点为顶点的三角形有△ABC、△ABE、△ACE、△BCE，四种，其中△ABE重合，不符合条件，△ACE不能构成三角形，∴当△ABE与以A，B，C，E中的三点为顶点的三角形相似，存在两个三角形：△ABC和△BCE，①当△ABE与以A，B，C中的三点为顶点的三角形相似，如图2，∵∠BAE=∠BAC，∠ABE≠∠ABC，∴∠ABE=∠ACB=45°，∴△ABE∽△ACB，∴，∴，∴AE=，∴E（，0），∵B（0，﹣4），易得BE：y=，则x2﹣x﹣4=x﹣4，x 1=0（舍），x2=，∴D（，）；②当△ABE与以B，C、E中的三点为顶点的三角形相似，如图3，∵∠BEA=∠BEC，∴当∠ABE=∠BCE时，△ABE∽△BCE，∴==，设BE=2m，CE=4m，Rt△BOE中，由勾股定理得：BE2=OE2+OB2，∴，3m2﹣8m+8=0，（m﹣2）（3m﹣2）=0，m 1=2，m2=，∴OE=4m﹣4=12或，∵OE=＜2，∠AEB是钝角，此时△ABE与以B，C、E中的三点为顶点的三角形不相似，如图4，∴E（﹣12，0）；同理得BE的解析式为：y=﹣x﹣4，﹣x﹣4=x2﹣x﹣4，x=或0（舍）∴D（，﹣）；综上，点D的坐标为（，）或（，﹣）．。

2021年中考数学第三轮冲刺专题复习：四边形的综合 (含答案)

2021年中考数学第三轮冲刺专题复习：四边形的综合专项练习1、如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．2、如图，▱ABCD的对角线AC、BD相交于点O，EF经过O，分别交AB、CD于点E、F，EF的延长线交CB的延长线于M．（1）求证：OE＝OF；（2）若AD＝4，AB＝6，BM＝1，求BE的长．3、如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．4、如图，在平行四边形ABCD中，AE平分∠DAB，已知CE＝6，BE＝8，DE＝10．（1）求证：∠BEC＝90°；（2）求cos∠DAE．5、如图，已知平行四边形ABCD中，AB＝5，BC＝3，AC＝2．（1）求平行四边形ABCD的面积；（2）求证：BD⊥BC．6、如图所示，已知正方形OEFG的顶点O为正方形ABCD对角线AC、BD的交点，连接CE、DG．（1）求证：△DOG≌△COE；（2）若DG⊥BD，正方形ABCD的边长为2，线段AD与线段OG相交于点M，AM＝，求正方形OEFG 的边长．7、如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE，过点C作CG⊥AB交AB的延长线于点G．（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB＝，∠CBG＝45°，BC＝4，则▱ABCD的面积是24．8、如图，四边形ABCD是正方形，△EFC是等腰直角三角形，点E在AB上，且∠CEF＝90°，FG⊥AD，垂足为点C．（1）试判断AG与FG是否相等？并给出证明；（2）若点H为CF的中点，GH与DH垂直吗？若垂直，给出证明；若不垂直，说明理由．9、定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB 是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．10、如图，在平行四边形ABCD中，点E在边BC上，连结AE，EM⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP．（1）若DP＝2AP＝4，CP＝，CD＝5，求△ACD的面积．（2）若AE＝BN，AN＝CE，求证：AD＝CM+2CE．11、如图，在正方形ABCD中，分别过顶点B，D作BE∥DF交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使BH＝DG，连接EG，FH．（1）求证：四边形EHFG是平行四边形；（2）已知：AB＝2，EB＝4，tan∠GEH＝2，求四边形EHFG的周长．12、如图，四边形ABCD是矩形，AB＝20，BC＝10，以CD为一边向矩形外部作等腰直角△GDC，∠G＝90°．点M在线段AB上，且AM＝a，点P沿折线AD﹣DG运动，点Q沿折线BC﹣CG运动（与点G 不重合），在运动过程中始终保持线段PQ∥AB．设PQ与AB之间的距离为x．（1）若a＝12．①如图1，当点P在线段AD上时，若四边形AMQP的面积为48，则x的值为；②在运动过程中，求四边形AMQP的最大面积；（2）如图2，若点P在线段DG上时，要使四边形AMQP的面积始终不小于50，求a的取值范围．13、在矩形ABCD中，AE⊥BD于点E，点P是边AD上一点．（1）若BP平分∠ABD，交AE于点G，PF⊥BD于点F，如图①，证明四边形AGFP是菱形；（2）若PE⊥EC，如图②，求证：AE•AB＝DE•AP；（3）在（2）的条件下，若AB＝1，BC＝2，求AP的长．14、已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM 的面积为S（cm2），S与t的函数关系如图②所示．（1）直接写出动点M的运动速度为cm/s，BC的长度为cm；（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）①求动点N运动速度v（cm/s）的取值范围；②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由．15、如图1，正方形ABDE和BCFG的边AB，BC在同一条直线上，且AB＝2BC，取EF的中点M，连接MD，MG，MB．（1）试证明DM⊥MG，并求的值．（2）如图2，将图1中的正方形变为菱形，设∠EAB＝2α（0＜α＜90°），其它条件不变，问（1）中的值有变化吗？若有变化，求出该值（用含α的式子表示）；若无变化，说明理由．16、综合与实践动手操作：第一步：如图1，正方形纸片ABCD沿对角线AC所在的直线折叠，展开铺平．在沿过点C的直线折叠，使点B，点D都落在对角线AC上．此时，点B与点D重合，记为点N，且点E，点N，点F三点在同一条直线上，折痕分别为CE，CF．如图2．第二步：再沿AC所在的直线折叠，△ACE与△ACF重合，得到图3．第三步：在图3的基础上继续折叠，使点C与点F重合，如图4，展开铺平，连接EF，FG，GM，ME．如图5，图中的虚线为折痕．问题解决：（1）在图5中，∠BEC的度数是，的值是．（2）在图5中，请判断四边形EMGF的形状，并说明理由；（3）在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形（正方形除外），并写出这个菱形：．17、已知：在矩形ABCD中，E，F分别是边AB，AD上的点，过点F作EF的垂线交DC于点H，以EF为直径作半圆O．（1）填空：点A（填“在”或“不在”）⊙O上；当＝时，tan∠AEF的值是；（2）如图1，在△EFH中，当FE＝FH时，求证：AD＝AE+DH；（3）如图2，当△EFH的顶点F是边AD的中点时，求证：EH＝AE+DH；（4）如图3，点M在线段FH的延长线上，若FM＝FE，连接EM交DC于点N，连接FN，当AE＝AD 时，FN＝4，HN＝3，求tan∠AEF的值．参考答案2021年中考数学第三轮冲刺专题复习：四边形的综合专项练习1、如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．【解答】解：（1）设正方形CEFG的边长为a，∵正方形ABCD的边长为1，∴DE＝1﹣a，∵S1＝S2，∴a2＝1×（1﹣a），解得，（舍去），，即线段CE的长是；（2）证明：∵点H为BC边的中点，BC＝1，∴CH＝0.5，∴DH＝＝，∵CH＝0.5，CG＝，∴HG＝，∴HD＝HG．2、如图，▱ABCD的对角线AC、BD相交于点O，EF经过O，分别交AB、CD于点E、F，EF的延长线交CB的延长线于M．（1）求证：OE＝OF；（2）若AD＝4，AB＝6，BM＝1，求BE的长．【解答】（1）证明：∵四边形ABCD是平行四边形，∴OA＝OC，AB∥CD，BC＝AD，∴∠OAE＝∠OVF，在△AOE和△COF中，，∴△AOE≌△COF（ASA），∴OE＝OF；（2）解：过点O作ON∥BC交AB于N，则△AON∽△ACB，∵OA＝OC，∴ON＝BC＝2，BN＝AB＝3，∵ON∥BC，∴△ONE∽△MBE，∴＝，即＝，解得，BE＝1．3、如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．【解答】解：（1）∵四边形EFGH是矩形，∴EH＝FG，EH∥FG，∴∠GFH＝∠EHF，∵∠BFG＝180°﹣∠GFH，∠DHE＝180°﹣∠EHF，∴∠BFG＝∠DHE，∵四边形ABCD是菱形，∴AD∥BC，∴∠GBF＝∠EDH，∴△BGF≌△DEH（AAS），∴BG＝DE；（2）连接EG，∵四边形ABCD是菱形，∴AD＝BC，AD∥BC，∵E为AD中点，∴AE＝ED，∵BG＝DE，∴AE＝BG，AE∥BG，∴四边形ABGE是平行四边形，∴AB＝EG，∵EG＝FH＝2，∴AB＝2，∴菱形ABCD的周长＝8．4、如图，在平行四边形ABCD中，AE平分∠DAB，已知CE＝6，BE＝8，DE＝10．（1）求证：∠BEC＝90°；（2）求cos∠DAE．【解答】（1）证明：∵四边形ABCD是平行四边形，∴DC＝AB＝，AD＝BC，DC∥AB，∴∠DEA＝∠EAB，∵AE平分∠DAB，∴∠DAE＝∠EAB，∴∠DAE＝∠DEA∴AD＝DE＝10，∴BC＝10，AB＝CD＝DE+CE＝16，∵CE2+BE2＝62+82＝100＝BC2，∴△BCE是直角三角形，∠BEC＝90°；（2）解：∵AB∥CD，∴∠ABE＝∠BEC＝90°，∴AE＝＝＝8，∴cos∠DAE＝cos∠EAB＝＝＝．5、如图，已知平行四边形ABCD中，AB＝5，BC＝3，AC＝2．（1）求平行四边形ABCD的面积；（2）求证：BD⊥BC．【解答】解：（1）作CE⊥AB交AB的延长线于点E，如图：设BE＝x，CE＝h在Rt△CEB中：x2+h2＝9①在Rt△CEA中：（5+x）2+h2＝52②联立①②解得：x＝，h＝∴平行四边形ABCD的面积＝AB•h＝12；（2）作DF⊥AB，垂足为F∴∠DF A＝∠CEB＝90°∵平行四边形ABCD∴AD＝BC，AD∥BC∴∠DAF＝∠CBE又∵∠DF A＝∠CEB＝90°，AD＝BC∴△ADF≌△BCE（AAS）∴AF＝BE＝，BF＝5﹣＝，DF＝CE＝在Rt△DFB中：BD2＝DF2+BF2＝（）2+（）2＝16∴BD＝4∵BC＝3，DC＝5∴CD2＝DB2+BC2∴BD⊥BC．6、如图所示，已知正方形OEFG的顶点O为正方形ABCD对角线AC、BD的交点，连接CE、DG．（1）求证：△DOG≌△COE；（2）若DG⊥BD，正方形ABCD的边长为2，线段AD与线段OG相交于点M，AM＝，求正方形OEFG 的边长．【解答】解：（1）∵正方形ABCD与正方形OEFG，对角线AC、BD∴DO＝OC∵DB⊥AC，∴∠DOA＝∠DOC＝90°∵∠GOE＝90°∴∠GOD+∠DOE＝∠DOE+∠COE＝90°∴∠GOD＝∠COE∵GO＝OE∴在△DOG和△COE中∴△DOG≌△COE（SAS）（2）如图，过点M作MH⊥DO交DO于点H∵AM＝，DA＝2∴DM＝∵∠MDB＝45°∴MH＝DH＝sin45°•DM＝，DO＝cos45°•DA＝∴HO＝DO﹣DH＝﹣＝∴在Rt△MHO中，由勾股定理得MO＝＝＝∵DG⊥BD，MH⊥DO∴MH∥DG∴易证△OHM∽△ODG∴＝＝＝，得GO＝2则正方形OEFG的边长为27、如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE，过点C作CG⊥AB交AB的延长线于点G．（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB＝，∠CBG＝45°，BC＝4，则▱ABCD的面积是24．【解答】（1）证明：∵AE＝CF，∴AE﹣EF＝CF﹣EF，即AF＝CE，∵DF∥BE，∴∠DF A＝∠BEC，∵DF＝BE，∴△ADF≌△CBE（SAS），∴AD＝CB，∠DAF＝∠BCE，∴AD∥CB，∴四边形ABCD是平行四边形；（2）解：∵CG⊥AB，∴∠G＝90°，∵∠CBG＝45°，∴△BCG是等腰直角三角形，∵BC＝4，∴BG＝CG＝4，∵tan∠CAB＝，∴AG＝10，∴AB＝6，∴▱ABCD的面积＝6×4＝24，故答案为：24．8、如图，四边形ABCD是正方形，△EFC是等腰直角三角形，点E在AB上，且∠CEF＝90°，FG⊥AD，垂足为点C．（1）试判断AG与FG是否相等？并给出证明；（2）若点H为CF的中点，GH与DH垂直吗？若垂直，给出证明；若不垂直，说明理由．【解答】解：（1）AG＝FG，理由如下：如图，过点F作FM⊥AB交BA的延长线于点M∵四边形ABCD是正方形∴AB＝BC，∠B＝90°＝∠BAD∵FM⊥AB，∠MAD＝90°，FG⊥AD∴四边形AGFM是矩形∴AG＝MF，AM＝FG，∵∠CEF＝90°，∴∠FEM+∠BEC＝90°，∠BEC+∠BCE＝90°∴∠FEM＝∠BCE，且∠M＝∠B＝90°，EF＝EC∴△EFM≌△CEB（AAS）∴BE＝MF，ME＝BC∴ME＝AB＝BC∴BE＝MA＝MF∴AG＝FG，（2）DH⊥HG理由如下：如图，延长GH交CD于点N，∵FG⊥AD，CD⊥AD∴FG∥CD∴，且CH＝FH，∴GH＝HN，NC＝FG∴AG＝FG＝NC又∵AD＝CD，∴GD＝DN，且GH＝HN∴DH⊥GH9、定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB 是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．【解答】解：（1）∵AB＝AC，AD是△ABC的角平分线，∴AD⊥BC，∴∠ADB＝90°，∴∠DAB+∠DBA＝90°，∴∠FBA与∠EBA互余，∴四边形ABEF是邻余四边形；（2）如图所示（答案不唯一），四边形AFEB为所求；（3）∵AB＝AC，AD是△ABC的角平分线，∴BD＝CD，∵DE＝2BE，∴BD＝CD＝3BE，∴CE＝CD+DE＝5BE，∵∠EDF＝90°，点M是EF的中点，∴DM＝ME，∴∠MDE＝∠MED，∵AB＝AC，∴∠B＝∠C，∴△DBQ∽△ECN，∴，∵QB＝3，∴NC＝5，∵AN＝CN，∴AC＝2CN＝10，∴AB＝AC＝10．10、如图，在平行四边形ABCD中，点E在边BC上，连结AE，EM⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P是AD上一点，连接CP．（1）若DP＝2AP＝4，CP＝，CD＝5，求△ACD的面积．（2）若AE＝BN，AN＝CE，求证：AD＝CM+2CE．【解答】（1）解：作CG⊥AD于G，如图1所示：设PG＝x，则DG＝4﹣x，在Rt△PGC中，GC2＝CP2﹣PG2＝17﹣x，在Rt△DGC中，GC2＝CD2﹣GD2＝52﹣（4﹣x）2＝9+8x﹣x2，∴17﹣x2＝9+8x﹣x2，解得：x＝1，即PG＝1，∴GC＝4，∵DP＝2AP＝4，∴AD＝6，∴S△ACD＝×AD×CG＝×6×4＝12；（2）证明：连接NE，如图2所示：∵AH⊥AE，AF⊥BC，AE⊥EM，∴∠AEB+∠NBF＝∠AEB+∠EAF＝∠AEB+∠MEC＝90°，∴∠NBF＝∠EAF＝∠MEC，在△NBF和△EAF中，，∴△NBF≌△EAF（AAS），∴BF＝AF，NF＝EF，∴∠ABC＝45°，∠ENF＝45°，FC＝AF＝BF，∴∠ANE＝∠BCD＝135°，AD＝BC＝2AF，在△ANE和△ECM中，，∴△ANE≌△ECM（ASA），∴CM＝NE，又∵NF＝NE＝MC，∴AF＝MC+EC，∴AD＝MC+2EC．11、如图，在正方形ABCD中，分别过顶点B，D作BE∥DF交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使BH＝DG，连接EG，FH．（1）求证：四边形EHFG是平行四边形；（2）已知：AB＝2，EB＝4，tan∠GEH＝2，求四边形EHFG的周长．【解答】解：（1）∵四边形ABCD是正方形，∴AB＝CD，AB∥CD，∴∠DCA＝∠BAC，∵DF∥BE，∴∠CFD＝∠BEA，∵∠BAC＝∠BEA+∠ABE，∠DCA＝∠CFD+∠CDF，∴∠ABE＝∠CDF，在△ABE和△CDF中，∵，∴△ABE≌△CDF（AAS），∴BE＝DF，∵BH＝DG，∴BE+BH＝DF+DG，即EH＝GF，∵EH∥GF，∴四边形EHFG是平行四边形；（2）如图，连接BD，交EF于O，∵四边形ABCD是正方形，∴BD⊥AC，∴∠AOB＝90°，∵AB＝2，∴OA＝OB＝2，Rt△BOE中，EB＝4，∴∠OEB＝30°，∴EO＝2，∵OD＝OB，∠EOB＝∠DOF，∵DF∥EB，∴∠DFC＝∠BEA，∴△DOF≌△BOE（AAS），∴OF＝OE＝2，∴EF＝4，∴FM＝2，EM＝6，过F作FM⊥EH于M，交EH的延长线于M，∵EG∥FH，∴∠FHM＝∠GEH，∵tan∠GEH＝tan∠FHM＝＝2，∴，∴HM＝1，∴EH＝EM﹣HM＝6﹣1＝5，FH＝＝＝，∴四边形EHFG的周长＝2EH+2FH＝2×5+2＝10+2．12、如图，四边形ABCD是矩形，AB＝20，BC＝10，以CD为一边向矩形外部作等腰直角△GDC，∠G＝90°．点M在线段AB上，且AM＝a，点P沿折线AD﹣DG运动，点Q沿折线BC﹣CG运动（与点G 不重合），在运动过程中始终保持线段PQ∥AB．设PQ与AB之间的距离为x．（1）若a＝12．①如图1，当点P在线段AD上时，若四边形AMQP的面积为48，则x的值为3；②在运动过程中，求四边形AMQP的最大面积；（2）如图2，若点P在线段DG上时，要使四边形AMQP的面积始终不小于50，求a的取值范围．【解答】（1）解：①P在线段AD上，PQ＝AB＝20，AP＝x，AM＝12，四边形AMQP的面积＝（12+20）x＝48，解得：x＝3；故答案为：3；②当P，在AD上运动时，P到D点时四边形AMQP面积最大，为直角梯形，∴0＜x≤10时，四边形AMQP面积的最大值＝（12+20）10＝160，当P在DG上运动，10＜x≤20，四边形AMQP为不规则梯形，作PH⊥AB于M，交CD于N，作GE⊥CD于E，交AB于F，如图2所示：则PM＝x，PN＝x﹣10，EF＝BC＝10，∵△GDC是等腰直角三角形，∴DE＝CE，GE＝CD＝10，∴GF＝GE+EF＝20，∴GH＝20﹣x，由题意得：PQ∥CD，∴△GPQ∽△GDC，∴＝，即＝，解得：PQ＝40﹣2x，∴梯形AMQP的面积＝（12+40﹣2x）×x＝﹣x2+26x＝﹣（x﹣13）2+169，∴当x＝13时，四边形AMQP的面积最大＝169；（2）解：P在DG上，则10≤x≤20，AM＝a，PQ＝40﹣2x，梯形AMQP的面积S＝（a+40﹣2x）×x＝﹣x2+x，对称轴为：x＝10+，∵0≤x≤20，∴10≤10+≤15，对称轴在10和15之间，∵10≤x≤20，二次函数图象开口向下，∴当x＝20时，S最小，∴﹣202+×20≥50，∴a≥5；综上所述，a的取值范围为5≤a≤20．13、在矩形ABCD中，AE⊥BD于点E，点P是边AD上一点．（1）若BP平分∠ABD，交AE于点G，PF⊥BD于点F，如图①，证明四边形AGFP是菱形；（2）若PE⊥EC，如图②，求证：AE•AB＝DE•AP；（3）在（2）的条件下，若AB＝1，BC＝2，求AP的长．【解答】（1）证明：如图①中，∵四边形ABCD是矩形，∴∠BAD＝90°，∵AE⊥BD，∴∠AED＝90°，∴∠BAE+∠EAD＝90°，∠EAD+∠ADE＝90°，∴∠BAE＝∠ADE，∵∠AGP＝∠BAG+∠ABG，∠APD＝∠ADE+∠PBD，∠ABG＝∠PBD，∴∠AGP＝∠APG，∴AP＝AG，∵P A⊥AB，PF⊥BD，BP平分∠ABD，∴P A＝PF，∴PF＝AG，∵AE⊥BD，PF⊥BD，∴PF∥AG，∴四边形AGFP是平行四边形，∵P A＝PF，∴四边形AGFP是菱形．（2）证明：如图②中，∵AE⊥BD，PE⊥EC，∴∠AED＝∠PEC＝90°，∴∠AEP＝∠DEC，∵∠EAD+∠ADE＝90°，∠ADE+∠CDE＝90°，∴∠EAP＝∠EDC，∴△AEP∽△DEC，∴＝，∵AB＝CD，∴AE•AB＝DE•AP；（3）解：∵四边形ABCD是矩形，∴BC＝AD＝2，∠BAD＝90°，∴BD＝＝，∵AE⊥BD，∴S△ABD＝•BD•AE＝•AB•AD，∴AE＝，∴DE＝＝，∵AE•AB＝DE•AP；∴AP＝＝．14、已知矩形ABCD中，AB＝5cm，点P为对角线AC上的一点，且AP＝2cm．如图①，动点M从点A出发，在矩形边上沿着A→B→C的方向匀速运动（不包含点C）．设动点M的运动时间为t（s），△APM 的面积为S（cm2），S与t的函数关系如图②所示．（1）直接写出动点M的运动速度为2cm/s，BC的长度为10cm；（2）如图③，动点M重新从点A出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N从点D出发，在矩形边上沿着D→C→B的方向匀速运动，设动点N的运动速度为v（cm/s）．已知两动点M，N经过时间x（s）在线段BC上相遇（不包含点C），动点M，N相遇后立即同时停止运动，记此时△APM与△DPN的面积分别为S1（cm2），S2（cm2）①求动点N运动速度v（cm/s）的取值范围；②试探究S1•S2是否存在最大值，若存在，求出S1•S2的最大值并确定运动时间x的值；若不存在，请说明理由．【解答】解：（1）∵t＝2.5s时，函数图象发生改变，∴t＝2.5s时，M运动到点B处，∴动点M的运动速度为：＝2cm/s，∵t＝7.5s时，S＝0，∴t＝7.5s时，M运动到点C处，∴BC＝（7.5﹣2.5）×2＝10（cm），故答案为：2，10；（2）①∵两动点M，N在线段BC上相遇（不包含点C），∴当在点C相遇时，v＝＝（cm/s），当在点B相遇时，v＝＝6（cm/s），∴动点N运动速度v（cm/s）的取值范围为cm/s＜v≤6cm/s；②过P作EF⊥AB于F，交CD于E，如图3所示：则EF∥BC，EF＝BC＝10，∴＝，∵AC＝＝5，∴＝，解得：AF＝2，∴DE＝AF＝2，CE＝BF＝3，PF＝＝4，∴EP＝EF﹣PF＝6，∴S1＝S△APM＝S△APF+S梯形PFBM﹣S△ABM＝×4×2+（4+2x﹣5）×3﹣×5×（2x﹣5）＝﹣2x+15，S2＝S△DPM＝S△DEP+S梯形EPMC﹣S△DCM＝×2×6+（6+15﹣2x）×3﹣×5×（15﹣2x）＝2x，∴S1•S2＝（﹣2x+15）×2x＝﹣4x2+30x＝﹣4（x﹣）2+，∵2.5＜＜7.5，在BC边上可取，∴当x＝时，S1•S2的最大值为．15、如图1，正方形ABDE和BCFG的边AB，BC在同一条直线上，且AB＝2BC，取EF的中点M，连接MD，MG，MB．（1）试证明DM⊥MG，并求的值．（2）如图2，将图1中的正方形变为菱形，设∠EAB＝2α（0＜α＜90°），其它条件不变，问（1）中的值有变化吗？若有变化，求出该值（用含α的式子表示）；若无变化，说明理由．【解答】（1）证明：如图1中，延长DM交FG的延长线于H．∵四边形ABCD，四边形BCFG都是正方形，∴DE∥AC∥GF，∴∠EDM＝∠FHM，∵∠EMD＝∠FMH，EM＝FM，∴△EDM≌△FHM（AAS），∴DE＝FH，DM＝MH，∵DE＝2FG，BG＝DG，∴HG＝DG，∵∠DGH＝∠BGF＝90°，MH＝DM，∴GM⊥DM，DM＝MG，连接EB，BF，设BC＝a，则AB＝2a，BE＝2a，BF＝a，∵∠EBD＝∠DBF＝45°，∴∠EBF＝90°，∴EF＝＝a，∵EM＝MF，∴BM＝EF＝a，∵HM＝DM，GH＝FG，∴MG＝DF＝a，∴＝＝．（2）解：（1）中的值有变化．理由：如图2中，连接BE，AD交于点O，连接OG，CG，BF，CG交BF于O′．∵DO＝OA，DG＝GB，∴GO∥AB，OG＝AB，∵GF∥AC，∴O，G，F共线，∵FG＝AB，∴OF＝AB＝DF，∵DF∥AC，AC∥OF，∴DE∥OF，∴OD与EF互相平分，∵EM＝MF，∴点M在直线AD上，∵GD＝GB＝GO＝GF，∴四边形OBFD是矩形，∴∠OBF＝∠ODF＝∠BOD＝90°，∵OM＝MD，OG＝GF，∴MG＝DF，设BC＝m，则AB＝2m，易知BE＝2OB＝2•2m•sinα＝4m sinα，BF＝2BO°＝2m•cosα，DF＝OB＝2m•sinα，∵BM＝EF＝＝，GM＝DF＝m•sinα，∴＝＝．16、综合与实践动手操作：第一步：如图1，正方形纸片ABCD沿对角线AC所在的直线折叠，展开铺平．在沿过点C的直线折叠，使点B，点D都落在对角线AC上．此时，点B与点D重合，记为点N，且点E，点N，点F三点在同一条直线上，折痕分别为CE，CF．如图2．第二步：再沿AC所在的直线折叠，△ACE与△ACF重合，得到图3．第三步：在图3的基础上继续折叠，使点C与点F重合，如图4，展开铺平，连接EF，FG，GM，ME．如图5，图中的虚线为折痕．问题解决：（1）在图5中，∠BEC的度数是67.5°，的值是．（2）在图5中，请判断四边形EMGF的形状，并说明理由；（3）在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形（正方形除外），并写出这个菱形：菱形EMCH或菱形FGCH．【解答】解：（1）由折叠的性质得：BE＝EN，AE＝AF，∠CEB＝∠CEN，∠BAC＝∠CAD，∵四边形ABCD是正方形，∴∠EAF＝90°，∴∠AEF＝∠AFE＝45°，∴∠BEN＝135°，∴∠BEC＝67.5°，∴∠BAC＝∠CAD＝45°，∵∠AEF＝45°，∴△AEN是等腰直角三角形，∴AE＝EN，∴＝＝；故答案为：67.5°，；（2）四边形EMGF是矩形；理由如下：∵四边形ABCD是正方形，∴∠B＝∠BCD＝∠D＝90°，由折叠的性质得：∠BCE＝∠ECA＝∠ACF＝∠FCD，CM＝CG，∠BEC＝∠NEC＝∠NFC＝∠DFC，∴∠BCE＝∠ECA＝∠ACF＝∠FCD＝＝22.5°，∠BEC＝∠NEC＝∠NFC＝∠DFC＝67.5°，由折叠可知：MH、GH分别垂直平分EC、FC，∴MC＝ME＝CG＝GF，∴∠MEC＝∠BCE＝22.5°，∠GFC＝∠FCD＝22.5°，∴∠MEF＝90°，∠GFE＝90°，∵∠MCG＝90°，CM＝CG，∴∠CMG＝45°，∵∠BME＝∠BCE+∠MEC＝22.5°+22.5°＝45°，∴∠EMG＝180°﹣∠CMG﹣∠BME＝90°，∴四边形EMGF是矩形；（3）连接EH、FH，如图所示：∵由折叠可知：MH、GH分别垂直平分EC、FC，同时EC、FC也分别垂直平分MH、GH，∴四边形EMCH与四边形FGCH是菱形，故答案为：菱形EMCH或菱形FGCH．17、已知：在矩形ABCD中，E，F分别是边AB，AD上的点，过点F作EF的垂线交DC于点H，以EF为直径作半圆O．（1）填空：点A在（填“在”或“不在”）⊙O上；当＝时，tan∠AEF的值是；（2）如图1，在△EFH中，当FE＝FH时，求证：AD＝AE+DH；（3）如图2，当△EFH的顶点F是边AD的中点时，求证：EH＝AE+DH；（4）如图3，点M在线段FH的延长线上，若FM＝FE，连接EM交DC于点N，连接FN，当AE＝AD 时，FN＝4，HN＝3，求tan∠AEF的值．【解答】解：（1）连接AO，∵∠EAF＝90°，O为EF中点，∴AO＝EF，∴点A在⊙O上，当＝时，∠AEF＝45°，∴tan∠AEF＝tan45°＝1，故答案为：在，1；（2）∵EF⊥FH，∴∠EFH＝90°，在矩形ABCD中，∠A＝∠D＝90°，∴∠AEF+∠AFE＝90°，∠AFE+∠DFH＝90°，∴∠AEF＝∠DFH，又FE＝FH，∴△AEF≌△DFH（AAS），∴AF＝DH，AE＝DF，∴AD＝AF+DF＝AE+DH；（3）延长EF交HD的延长线于点G，∵F分别是边AD上的中点，∴AF＝DF，∵∠A＝∠FDG＝90°，∠AFE＝∠DFG，∴△AEF≌△DGF（ASA），∴AE＝DG，EF＝FG，∵EF⊥FG，∴EH＝GH，∴GH＝DH+DG＝DH+AE，∴EH＝AE+DH；（4）过点M作MQ⊥AD于点Q．设AF＝x，AE＝a，∵FM＝FEEF⊥FH，∴△EFM为等腰直角三角形，∴∠FEM＝∠FMN＝45°，∵FM＝FE，∠A＝∠MQF＝90°，∠AEF＝∠MFQ，∴△AEF≌△QFM（ASA），∴AE＝EQ＝a，AF＝QM，∵AE＝AD，∴AF＝DQ＝QM＝x，∵DC∥QM，∴，∵DC∥AB∥QM，∴，∴，∵FE＝FM，∴，∠FEM＝∠FMN＝45°，∴△FEN～△HMN，∴，∴．。

2021年中考数学第三轮：三角形的综合解答题专题复习(含答案)

2021年中考数学第三轮：三角形的综合解答题专题复习1、已知，如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．（1）求证：△ACE≌△BCD；（2）求证：2CD2=AD2+DB2．2、如图，在△ABC中，BC＞AC，点E在BC上，CE=CA，点D在AB上，连接DE，∠ACB+∠ADE=180°，作CH⊥AB，垂足为H．（1）如图a，当∠ACB=90°时，连接CD，过点C作CF⊥CD交BA的延长线于点F．①求证：FA=DE；②请猜想三条线段DE，AD，CH之间的数量关系，直接写出结论；（2）如图b，当∠ACB=120°时，三条线段DE，AD，CH之间存在怎样的数量关系？请证明你的结论．3、如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．（1）求证：AD=AF；（2）求证：BD=EF；（3）试判断四边形ABNE的形状，并说明理由．4、在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．（1）如图1，若点F与点A重合，求证：AC=BC；（2）若∠DAF=∠DBA，①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．5、如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．（1）如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．（2）如图2，若∠ACB=∠DCE=120°，CM为△DCE中DE边上的高，BN为△ABE中AE边上的高，试证明：AE=2CM+BN．6、在△ABC中，P为边AB上一点．(1) 如图1，若∠ACP＝∠B，求证：AC2＝AP·AB；(2) 若M为CP的中点，AC＝2，①如图2，若∠PBM＝∠ACP，AB＝3，求BP的长；②如图3，若∠ABC＝45°，∠A＝∠BMP＝60°，直接写出BP的长．7、小颖在学习“两点之间线段最短”查阅资料时发现：△ABC内总存在一段P与三个顶点的连线的夹角相等，此时该点到三个顶点的距离之和最小．【特例】如图①，点P为等边△ABC的中心，将△ACP绕点A逆时针旋转60°得到△ADE，从而有DE=PC，连接PD得到PD=PA，同时∠APB+∠APD=120°+60°=180°，∠ADP+∠ADE=180°，即B、P、D、E四点共线，故PA+PB+PC=PD+PB+DE=BE．在△ABC中，另取一点P'，易知点P'与三个顶点连线的夹角不相等，可证明B、P'、D'、E'四点不共线，所以P'A+P'B+P'C>PA+PB+PC，即点P到三个顶点距离之和最小．【探究】（1）如图②，P为△ABC内一点，∠APB=∠BPC=120°，证明PA+PB+PC的值最小；【拓展】（2）如图③，△ABC中，AC=6，BC=8，∠ACB=30°，且点P为△ABC内一点，求点P 到三个顶点的距离之和的最小值．8、如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE、BD．（1）猜想PM与PN的数量关系及位置关系，请直接写出结论；α，得到图②，AE与MP、BD分别（2）现将图①中的△CDE绕着点C顺时针旋转)︒α<90<0(︒交于点G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；（3）若图②中的等腰直角三角形变成直角三角形，使BC=k AC，CD=k CE，如图③，写出PM与PN的数量关系，并加以证明．9、如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．（1）请判断四边形EBGD的形状，并说明理由；（2）若∠ABC=30°，∠C=45°，ED=2，点H是BD上的一个动点，求HG+HC的最小值．10、（1）已知：△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC＝∠DCE，若∠A＝60°（如图①）．求证：EB＝AD；（2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其它条件不变（如图②），（1）的结论是否成立，并说明理由；（3）若将（1）中的“若∠A＝60°”改为“∠A＝90°”，其它条件不变，则EBAD的值是多少？（直接写出结论，不要求写解答过程）11、问题引入：（1）如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A＝α，则∠BOC＝____________（用α表示）；如图②，∠CBO＝13∠ABC，∠BCO＝13∠ACB，∠A＝α，则∠BOC＝____________（用α表示）. 拓展研究：（2）如图③，∠CBO＝13∠DBC，∠BCO＝13∠ECB，∠A＝α，猜想∠BOC＝____________（用α表示），并说明理由.（3）BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO＝1n∠DBC，∠BCO＝1n∠ECB，∠A＝α，请猜想∠BOC＝____________ .12、已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．①当点M与点C、D不重合时，连接CM，求∠CMD的度数；②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．13、在△ABC中，AB=6，AC=BC=5，将△ABC绕点A按顺时针方向旋转，得到△ADE，旋转角为α（0°＜α＜180°），点B的对应点为点D，点C的对应点为点E，连接BD，BE．（1）如图，当α=60°时，延长BE交AD于点F．①求证：△ABD是等边三角形；②求证：BF⊥AD，AF=DF；③请直接写出BE的长；（2）在旋转过程中，过点D作DG垂直于直线AB，垂足为点G，连接CE，当∠DAG=∠ACB，且线段DG与线段AE无公共点时，请直接写出BE+CE的值．温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．14、阅读下面材料：小明遇到这样一个问题：如图1，△ABC中，AB=AC，点D在BC边上，∠DAB=∠ABD，BE⊥AD，垂足为E，求证：BC=2AE．小明经探究发现，过点A作AF⊥BC，垂足为F，得到∠AFB=∠BEA，从而可证△ABF≌△BAE（如图2），使问题得到解决．（1）根据阅读材料回答：△ABF与△BAE全等的条件是 AAS（填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个）参考小明思考问题的方法，解答下列问题：（2）如图3，△ABC中，AB=AC，∠BAC=90°，D为BC的中点，E为DC的中点，点F在AC的延长线上，且∠CDF=∠EAC，若CF=2，求AB的长；（3）如图4，△ABC中，AB=AC，∠BAC=120°，点D、E分别在AB、AC边上，且AD=kDB（其中0＜k＜），∠AED=∠BCD，求的值（用含k的式子表示）．15、如图①，在△ABC中，∠ACB=90°，∠B=30°，AC=1，D为AB的中点，EF为△ACD的中位线，四边形EFGH为△ACD的内接矩形（矩形的四个顶点均在△ACD 的边上）．（1）计算矩形EFGH的面积；（2）将矩形EFGH沿AB向右平移，F落在BC上时停止移动．在平移过程中，当矩形与△CBD重叠部分的面积为时，求矩形平移的距离；（3）如图③，将（2）中矩形平移停止时所得的矩形记为矩形E1F1G1H1，将矩形E1F1G1H1绕G1点按顺时针方向旋转，当H1落在CD上时停止转动，旋转后的矩形记为矩形E2F2G1H2，设旋转角为α，求cosα的值．16、尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．求证：a2+b2=5c2该同学仔细分析后，得到如下解题思路：先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证（1）请你根据以上解题思路帮尤秀同学写出证明过程．（2）利用题中的结论，解答下列问题：在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO 的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求MG2+MH2的值．17、如图①，△ABC中，∠ABC＝45°，AH⊥BC于点H，点D在AH上，且DH＝CH，连接BD．⑴求证：BD＝AC；⑵将△BHD绕点H旋转，得到△EHF(点B、D分别与点E、F对应)，连接AE．i) 如图②，当点F落在AC上时(F不与C重合)，若BC＝4，tan C＝3，求AE的长；ii)如图③，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH．试探究线段GH与EF之间满足的等量关系，并说明理由．参考答案2021年中考数学第三轮：三角形的综合解答题专题复习1、已知，如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点．（1）求证：△ACE≌△BCD；（2）求证：2CD2=AD2+DB2．【解答】证明：（1）∵△ABC和△ECD都是等腰直角三角形，∴AC=BC，CD=CE，∵∠ACB=∠DCE=90°，∴∠ACE+∠ACD=∠BCD+∠ACD，∴∠ACE=∠BCD，在△ACE和△BCD中，，∴△AEC≌△BDC（SAS）；（2）∵△ACB是等腰直角三角形，∴∠B=∠BAC=45度．∵△ACE≌△BCD，∴∠B=∠CAE=45°∴∠DAE=∠CAE+∠BAC=45°+45°=90°，∴AD2+AE2=DE2．由（1）知AE=DB，∴AD2+DB2=DE2，即2CD2=AD2+DB2．2、如图，在△ABC中，BC＞AC，点E在BC上，CE=CA，点D在AB上，连接DE，∠ACB+∠ADE=180°，作CH⊥AB，垂足为H．（1）如图a，当∠ACB=90°时，连接CD，过点C作CF⊥CD交BA的延长线于点F．①求证：FA=DE；②请猜想三条线段DE，AD，CH之间的数量关系，直接写出结论；（2）如图b，当∠ACB=120°时，三条线段DE，AD，CH之间存在怎样的数量关系？请证明你的结论．【解答】证明：（1）①∵CF⊥CD，∴∠FCD=90°，∵∠ACB=90°，∴∠FCA+∠ACD=∠ACD+∠DCE，∴∠FCA=∠DCE，∵∠FAC=90°+∠B，∠CED=90°+∠B，∴∠FAC=∠CED，∵AC=CE，∴△AFC≌△EDC，∴FA=DE，②DE+AD=2CH，理由是：∵△AFC≌△EDC，∴CF=CD，∵CH⊥AB，∴FH=HD，在Rt△FCD中，CH是斜边FD的中线，∴FD=2DH，∴AF+AD=2CH，∴DE+AD=2CH；（2）AD+DE=2CH，理由是：如图b，作∠FCD=∠ACB，交BA延长线于F，∵∠FCA+∠ACD=∠ACD+∠DCB，∴∠FCA=∠DCB，∵∠EDA=60°，∴∠EDB=120°，∵∠FAC=120°+∠B，∠CED=120°+∠B，∴∠FAC=∠CED，∵AC=CE，∴△FAC≌△DEC，∴AF=DE，FC=CD，∵CH⊥FD，∴FH=HD，∠FCH=∠HCD=60°，在Rt△CHD中，tan60°=，∴DH=CH，∵AD+DE=AD+AF=FD=2DH=2CH，即：AD+DE=2CH．3、如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．（1）求证：AD=AF；（2）求证：BD=EF；（3）试判断四边形ABNE的形状，并说明理由．【解答】（1）证明：∵AB=AC，∠BAC=90°，∴∠ABC=∠ACB=45°，∴∠ABF=135°，∵∠BCD=90°，∴∠ABF=∠ACD，∵CB=CD，CB=BF，∴BF=CD，在△ABF和△ACD中，，∴△ABF≌△ACD（SAS），∴AD=AF；（2）证明：由（1）知，AF=AD，△ABF≌△ACD，∴∠FAB=∠DAC，∵∠BAC=90°，∴∠EAB=∠BAC=90°，∴∠EAF=∠BAD，在△AEF和△ABD中，，∴△AEF≌△ABD（SAS），∴BD=EF；（3）解：四边形ABNE是正方形；理由如下：∵CD=CB，∠BCD=90°，∴∠CBD=45°，由（2）知，∠EAB=90°，△AEF≌△ABD，∴∠AEF=∠ABD=90°，∴四边形ABNE是矩形，又∵AE=AB，∴四边形ABNE是正方形．4、在Rt△ABC中，∠C=90°，Rt△ABC绕点A顺时针旋转到Rt△ADE的位置，点E在斜边AB上，连结BD，过点D作DF⊥AC于点F．（1）如图1，若点F与点A重合，求证：AC=BC；（2）若∠DAF=∠DBA，①如图2，当点F在线段CA的延长线上时，判断线段AF与线段BE的数量关系，并说明理由；②当点F在线段CA上时，设BE=x，请用含x的代数式表示线段AF．【解答】解：（1）由旋转得，∠BAC=∠BAD，∵DF⊥AC，∴∠CAD=90°，∴∠BAC=∠BAD=45°，∵∠ACB=90°，∴∠ABC=45°，∴AC=CB，（2）①由旋转得，AD=AB，∴∠ABD=∠ADB，∵∠DAF=∠ABD，∴∠DAF=∠ADB，∴AF∥BB，∴∠BAC=∠ABD，∵∠ABD=∠FAD由旋转得，∠BAC=∠BAD，∴∠FAD=∠BAC=∠BAD=×180°=60°，由旋转得，AB=AD，∴△ABD是等边三角形，∴AD=BD，在△AFD和△BED中，，∴△AFD≌△BED，∴AF=BE，②如图，由旋转得，∠BAC=∠BAD，∵∠ABD=∠FAD=∠BAC+∠BAD=2∠BAD，由旋转得，AD=AB，∴∠ABD=∠ADB=2∠BAD，∵∠BAD+∠ABD+∠ADB=180°，∴∠BAD+2∠BAD+2∠BAD=180°，∴∠BAD=36°，设BD=x，作BG平分∠ABD，∴∠BAD=∠GBD=36°∴AG=BG=BC=x，∴DG=AD﹣AG=AD﹣BG=AD﹣BD，∵∠BDG=∠ADB，∴△BDG∽△ADB，∴．∴，∴，∵∠FAD=∠EBD，∠AFD=∠BED，∴△AFD∽△BED，∴，∴AF==x．5、如图，△ACB和△DCE均为等腰三角形，点A，D，E在同一直线上，连接BE．（1）如图1，若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．（2）如图2，若∠ACB=∠DCE=120°，CM为△DCE中DE边上的高，BN为△ABE中AE边上的高，试证明：AE=2CM+BN．【解答】（1）①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°，∴∠ACB=∠DCE=180°﹣2×50°=80°．∵∠ACB=∠ACD+∠DCB，∠DCE=∠DCB+∠BCE，∴∠ACD=∠BCE．∵△ACB和△DCE均为等腰三角形，∴AC=BC，DC=EC．在△ACD和△BCE中，有，∴△ACD≌△BCE（SAS），∴AD=BE．②解：∵△ACD≌△BCE，∴∠ADC=∠BEC．∵点A，D，E在同一直线上，且∠CDE=50°，∴∠ADC=180°﹣∠CDE=130°，∴∠BEC=130°．∵∠BEC=∠CED+∠AEB，且∠CED=50°，∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．（2）证明：∵△ACB和△DCE均为等腰三角形，且∠ACB=∠DCE=120°，∴∠CDM=∠CEM=×（180°﹣120°）=30°．∵CM⊥DE，∴∠CMD=90°，DM=EM．在Rt△CMD中，∠CMD=90°，∠CDM=30°，∴DE=2DM=2×=2CM．∵∠BEC=∠ADC=180°﹣30°=150°，∠BEC=∠CEM+∠AEB，∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°，∴∠BEN=180°﹣120°=60°．在Rt△BNE中，∠BNE=90°，∠BEN=60°，∴BE==BN．∵AD=BE，AE=AD+DE，∴AE=BE+DE=BN+2CM．6、在△ABC中，P为边AB上一点．(1) 如图1，若∠ACP＝∠B，求证：AC2＝AP·AB；(2) 若M为CP的中点，AC＝2，①如图2，若∠PBM＝∠ACP，AB＝3，求BP的长；②如图3，若∠ABC＝45°，∠A＝∠BMP＝60°，直接写出BP的长．【解析】（1）证明：∵∠ACP＝∠B，∠BAC＝∠CAP，∴△ACP∽△ABC，∴AC：AB＝AP：AC，∴AC2＝AP·AB；（2）①如图，作CQ∥BM交AB延长线于Q，设BP＝x，则PQ＝2x∵∠PBM＝∠ACP，∠PAC＝∠CAQ，∴△APC∽△ACQ，由AC2＝AP·AQ得：22＝（3－x）（3＋x），∴x即BP②如图：作CQ ⊥AB 于点Q ，作CP 0＝CP 交AB 于点P 0，∵AC ＝2，∴AQ ＝1，CQ ＝BQ ，设P 0Q ＝PQ ＝1－x ，BP －1＋x ，∵∠BPM ＝∠CP 0A ，∠BMP ＝∠CAP 0，∴△AP 0C ∽△MPB ，∴00AP P CMP BP=，∴MP ∙ P0C ＝2012P C =AP 0∙BP ＝x －1＋x ），解得x∴BP 1＋1．7、小颖在学习“两点之间线段最短”查阅资料时发现：△ABC 内总存在一段P 与三个顶点的连线的夹角相等，此时该点到三个顶点的距离之和最小．【特例】如图①，点P 为等边△ABC 的中心，将△ACP 绕点A 逆时针旋转60°得到△ADE ，从而有DE=PC ，连接PD 得到PD=PA ，同时∠APB+∠APD=120°+60°=180°，∠ADP+∠ADE=180°，即B 、P 、D 、E 四点共线，故PA+PB+PC=PD+PB+DE=BE ．在△ABC 中，另取一点P'，易知点P'与三个顶点连线的夹角不相等，可证明B 、P'、D'、E'四点不共线，所以P'A +P'B +P'C >PA+PB+PC ，即点P 到三个顶点距离之和最小．【探究】（1）如图②，P 为△ABC 内一点，∠APB=∠BPC=120°，证明PA+PB+PC 的值最小；【拓展】（2）如图③，△ABC 中，AC=6，BC=8，∠ACB=30°，且点P 为△ABC 内一点，求点P 到三个顶点的距离之和的最小值．解：(1)将△APC 绕点A 逆时针旋转60°得到△ADE ，从而有DE=PC ，连接PD 得到PD=PA ，同时∠APB+∠APD=120°+60°=180°，∠ADP+∠ADE=180°，即B 、P 、D 、E 四点共线，故PA+PB+PC=PD+PB+DE=BE ．在△ABC 中，另取一点P'，易知点P'与三个顶点连线的夹角不相等，可证明B 、P'、D'、E'四点不共线，所以P'A +P'B +P'C >PA+PB+PC ，即点P 到三个顶点距离之和最小．(2)将△ACP 绕点A 逆时针旋转60°得到△ADE ，从而有DE=PC ，连接PD 得到PD=PA ，同时∠APB+∠APD=120°+60°=180°，∠ADP+∠ADE=180°，即B 、P 、D 、E 四点共线，故PA+PB+PC=PD+PB+DE=BE ．此时点P 到三个顶点距离之和最小．连接CE ，∵∠CAE=60°，AC=AE ， ∴△ACE 为等边三角形， ∴CE=AC=6，∠ACE=60°， ∵∠ACB=30°， ∴∠BCE=90°， ∵BC=8，∴10682222=+=+=CE BC BE ，即点P 到三个顶点的距离之和的最小值为10．8、如图①，△ABC 与△CDE 是等腰直角三角形，直角边AC 、CD 在同一条直线上，点M 、N 分别是斜边AB 、DE 的中点，点P 为AD 的中点，连接AE 、BD ．（1）猜想PM 与PN 的数量关系及位置关系，请直接写出结论；（2）现将图①中的△CDE 绕着点C 顺时针旋转)900(︒<<︒αα，得到图②，AE 与MP 、BD 分别交于点G 、H ．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；（3）若图②中的等腰直角三角形变成直角三角形，使BC =k AC ，CD =k CE ，如图③，写出PM 与PN 的数量关系，并加以证明．解：（1）PM =PN ,PM ⊥PN .(2) ∵△ACB 和△ECD 是等腰直角三角形， ∴AC=BC ,EC=CD ,∠ACB =∠ECD =90°．∴∠ACB +∠BCE =∠ECD +∠BCE ． ∴∠ACE =∠BCD ． ∴△ACE ≌△BCD ．∴AE =BD ，∠CAE =∠CBD ．又∵∠AOC =∠BOE ， ∠CAE =∠CBD ，∴∠BHO =∠ACO =90°. ∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴PM =21BD ， PM ∥BD ；PN =21AE ， PN ∥AE .∴PM =PN ． ∴∠MGE+∠BHA =180°． ∴∠MGE=90°． ∴∠MPN=90°． ∴PM ⊥PN ．(3) PM = kPN∵△ACB 和△ECD 是直角三角形， ∴∠ACB =∠ECD =90°．∴∠ACB +∠BCE =∠ECD +∠BCE ． ∴∠ACE =∠BCD ． ∵BC =kAC ，CD =kCE ， ∴k CECDAC BC ==． ∴△BCD ∽△ACE ． ∴BD = kAE ．∵点P 、M 、N 分别为AD 、AB 、DE 的中点，∴PM =21BD ，PN =21AE ．∴PM = kPN ．9、如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．（1）请判断四边形EBGD的形状，并说明理由；（2）若∠ABC=30°，∠C=45°，ED=2，点H是BD上的一个动点，求HG+HC的最小值．【解答】解：（1）四边形EBGD是菱形．理由：∵EG垂直平分BD，∴EB=ED，GB=GD，∴∠EBD=∠EDB，∵∠EBD=∠DBC，∴∠EDF=∠GBF，在△EFD和△GFB中，，∴△EFD≌△GFB，∴ED=BG，∴BE=ED=DG=GB，∴四边形EBGD是菱形．（2）作EM⊥BC于M，DN⊥BC于N，连接EC交BD于点H，此时HG+HC最小，在RT△EBM中，∵∠EMB=90°，∠EBM=30°，EB=ED=2，∴EM=BE=，∵DE∥BC，EM⊥BC，DN⊥BC，∴EM∥DN，EM=DN=，MN=DE=2，在RT△DNC中，∵∠DNC=90°，∠DCN=45°，∴∠NDC=∠NCD=45°，∴DN=NC=，∴MC=3，在RT△EMC中，∵∠EMC=90°，EM=．MC=3，∴EC===10．∵HG+HC=EH+HC=EC，∴HG+HC的最小值为10．10、（1）已知：△ABC是等腰三角形，其底边是BC，点D在线段AB上，E是直线BC上一点，且∠DEC＝∠DCE，若∠A＝60°（如图①）．求证：EB＝AD；（2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其它条件不变（如图②），（1）的结论是否成立，并说明理由；的值是多少？（3）若将（1）中的“若∠A＝60°”改为“∠A＝90°”，其它条件不变，则EBAD（直接写出结论，不要求写解答过程）证明：（1）过D点作BC的平行线交AC于点F．∵△ABC是等腰三角形，∠A＝60°∴△ABC是等边三角形．∴∠ABC＝60 °∵DF∥BC，∴∠ADF＝∠ABC＝60 °，∴△ADF是等边三角形．∴AD＝DF，∠AFD＝60 °．∴∠DFC＝180°－60 °＝120°，∵∠DBE＝180°－60 °＝120°，∴∠DFC＝∠DBE．又∵∠FDC＝∠DCE，∠DCE＝∠DEC，∴∠FDC＝∠DEC，ED＝CD．∴△DBE≌△CFD（AAS），∴BE＝DF，∴BE＝AD．（2）BE＝AD成立．理由如下：过D点作BC的平行线交AC的延长线于点F．同（1）可证△ADF是等边三角形，∴AD＝DF，∠AFD＝60 °．∵∠DBE＝∠ABC＝60 °，∴∠DBE＝∠AFD．∵∠FDC＝∠DCE，∠DCE＝∠DEC，∴∠FDC＝∠DEC，ED＝CD．∴△DBE≌△CFD（AAS），∴BE＝DF，∴BE＝AD．（3）EBAD过D点作BC的平行线交AC于点G，∵△ABC是等腰三角形，∠A＝90°∴∠ABC＝∠ACB＝45°，∴∠DBE＝180°－45°＝135°．∵DG∥BC，∴∠GDC＝∠DCE，∠DGC＝180°－45°＝135°，∴∠DBE＝∠DGC，∵∠DCE＝∠DEC，∴ED＝CD，∠DEC＝∠GDC．∴△DBE≌△CGD（AAS），∴BE＝GD．∵∠ADG＝∠ABC＝45°，∠A＝90°，∴△ADG是等腰直角三角形．∴DG，∴BE，∴EBAD11、问题引入：（1）如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A＝α，则∠BOC＝____________（用α表示）；如图②，∠CBO＝13∠ABC，∠BCO＝13∠ACB，∠A＝α，则∠BOC＝____________（用α表示）. 拓展研究：（2）如图③，∠CBO＝13∠DBC，∠BCO＝13∠ECB，∠A＝α，猜想∠BOC＝____________（用α表示），并说明理由.（3）BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线，它们交于点O，∠CBO＝1n∠DBC，∠BCO＝1n∠ECB，∠A＝α，请猜想∠BOC＝____________ .解：（1）如图①，在△ABC中，∵点O是∠ABC和∠ACB平分线的交点，∴∠CBO＝12∠ABC，∠BCO＝12∠ACB.∵∠A＝α，∴∠BOC＝180°－12（∠ABC＋∠ACB）＝180°－12（180°－∠A）＝180°－12（180°－∠α）＝180°－90°＋12∠α＝90°＋12∠α.如图②，∵∠CBO＝13∠ABC，∠BCO＝13∠ACB，∠A＝α，∴∠BOC＝180°－13（∠ABC＋∠ACB）＝180°－13（180°－∠A）＝180°－13（180°－∠α）＝180°－60°＋13∠α＝120°＋13∠α.故答案为90°＋12∠α，120°＋13∠α.（2）如图③，∵∠CBO＝13∠DBC，∠BCO＝13∠ECB，∠A＝α，∴∠BOC＝180°－13（∠DBC＋∠ECB）＝180°－13[360°－（∠ABC＋∠ACB）]＝180°－13[360°－（180°－∠A）]＝180°－13（180°＋∠α）＝180°－60°－13∠α＝120°－13∠α.故答案为120°－13∠α.（3）∵∠CBO＝1n∠DBC，∠BCO＝1n∠ECB，∠A＝α，∴∠BOC＝180°－1n（∠DBC＋∠ECB）＝180°－1n[360°－（∠ABC＋∠ACB）]＝180°－1n[360°－（180°－∠A）]＝180°－1n（180°＋∠α）＝1nn-×180°－1n∠α.＝1180-nnα-⋅∠（）故答案为1180-nnα-⋅∠（）.12、已知△ABC是等腰直角三角形，AC=BC=2，D是边AB上一动点（A、B两点除外），将△CAD绕点C按逆时针方向旋转角α得到△CEF，其中点E是点A的对应点，点F是点D的对应点．（1）如图1，当α=90°时，G是边AB上一点，且BG=AD，连接GF．求证：GF∥AC；（2）如图2，当90°≤α≤180°时，AE与DF相交于点M．①当点M与点C、D不重合时，连接CM，求∠CMD的度数；②设D为边AB的中点，当α从90°变化到180°时，求点M运动的路径长．【解答】解：（1）如图1中，∵CA=CB，∠ACB=90°，∴∠A=∠ABC=45°，∵△CEF是由△CAD旋转逆时针α得到，α=90°，∴CB与CE重合，∴∠CBE=∠A=45°，∴∠ABF=∠ABC+∠CBF=90°，∵BG=AD=BF，∴∠BGF=∠BFG=45°，∴∠A=∠BGF=45°，∴GF∥AC．（2）①如图2中，∵CA=CE，CD=CF，∴∠CAE=∠CEA，∠CDF=∠CFD，∵∠ACD=∠ECF，∴∠ACE=∠CDF，∵2∠CAE+∠ACE=180°，2∠CDF+∠DCF=180°，∴∠CAE=∠CDF，∴A、D、M、C四点共圆，∴∠CMF=∠CAD=45°，∴∠CMD=180°﹣∠CMF=135°．②如图3中，O是AC中点，连接OD、CM．∵AD=DB，CA=CB，∴CD⊥AB，∴∠ADC=90°，由①可知A、D、M、C四点共圆，∴当α从90°变化到180°时，点M在以AC为直径的⊙O上，运动路径是弧CD，∵OA=OC，CD=DA，∴DO⊥AC，∴∠DOC=90°，∴的长==．∴当α从90°变化到180°时，点M运动的路径长为．13、在△ABC中，AB=6，AC=BC=5，将△ABC绕点A按顺时针方向旋转，得到△ADE，旋转角为α（0°＜α＜180°），点B的对应点为点D，点C的对应点为点E，连接BD，BE．（1）如图，当α=60°时，延长BE交AD于点F．①求证：△ABD是等边三角形；②求证：BF⊥AD，AF=DF；③请直接写出BE的长；（2）在旋转过程中，过点D作DG垂直于直线AB，垂足为点G，连接CE，当∠DAG=∠ACB，且线段DG与线段AE无公共点时，请直接写出BE+CE的值．温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．【解答】解：（1）①∵△ABC绕点A顺时针方向旋转60°得到△ADE，∴AB=AD，∠BAD=60°，∴△ABD是等边三角形；②由①得△ABD是等边三角形，∴AB=BD，∵△ABC绕点A顺时针方向旋转60°得到△ADE，∴AC=AE，BC=DE，又∵AC=BC，∴EA=ED，∴点B、E在AD的中垂线上，∴BE是AD的中垂线，∵点F在BE的延长线上，∴BF⊥AD，AF=DF；③由②知BF⊥AD，AF=DF，∴AF=DF=3，∵AE=AC=5，∴EF=4，∵在等边三角形ABD中，BF=AB•sin∠BAF=6×=3，∴BE=BF﹣EF=3﹣4；（2）如图所示，∵∠DAG=∠ACB，∠DAE=∠BAC，∴∠ACB+∠BAC+∠ABC=∠DAG+∠DAE+∠ABC=180°，又∵∠DAG+∠DAE+∠BAE=180°，∴∠BAE=∠ABC，∵AC=BC=AE，∴∠BAC=∠ABC，∴∠BAE=∠BAC，∴AB⊥CE，且CH=HE=CE，∵AC=BC，∴AH=BH=AB=3，则CE=2CH=8，BE=5，∴BE+CE=13．14、阅读下面材料：小明遇到这样一个问题：如图1，△ABC中，AB=AC，点D在BC边上，∠DAB=∠ABD，BE⊥AD，垂足为E，求证：BC=2AE．小明经探究发现，过点A作AF⊥BC，垂足为F，得到∠AFB=∠BEA，从而可证△ABF≌△BAE（如图2），使问题得到解决．（1）根据阅读材料回答：△ABF与△BAE全等的条件是 AAS（填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个）参考小明思考问题的方法，解答下列问题：（2）如图3，△ABC中，AB=AC，∠BAC=90°，D为BC的中点，E为DC的中点，点F在AC的延长线上，且∠CDF=∠EAC，若CF=2，求AB的长；（3）如图4，△ABC中，AB=AC，∠BAC=120°，点D、E分别在AB、AC边上，且AD=kDB（其中0＜k＜），∠AED=∠BCD，求的值（用含k的式子表示）．【解答】证明：（1）如图2，作AF⊥BC，∵BE⊥AD，∴∠AFB=∠BEA，在△ABF和△BAE中，，∴△ABF≌△BAE（AAS），∴BF=AE∵AB=AC，AF⊥BC，∴BF=BC，∴BC=2AE，故答案为AAS（2）如图3，连接AD，作CG⊥AF，在Rt△ABC中，AB=AC，点D是BC中点，∴AD=CD，∵点E是DC中点，∴DE=CD=AD，∴tan∠DAE===，∵AB=AC，∠BAC=90°，点D为BC中点，∴∠ADC=90°，∠ACB=∠DAC=45°，∴∠F+∠CDF=∠ACB=45°，∵∠CDF=∠EAC，∴∠F+∠EAC=45°，∵∠DAE+∠EAC=45°，∴∠F=∠DAE，∴tan∠F=tan∠DAE=，∴，∴CG=×2=1，∵∠ACG=90°，∠ACB=45°，∴∠DCG=45°，∵∠CDF=∠EAC，∴△DCG∽△ACE，∴，∵CD=AC，CE=CD=AC，∴，∴AC=4；∴AB=4；（3）如图4，过点D作DG⊥BC，设DG=a，在Rt△BGD中，∠B=30°，∴BD=2a，BG=a，∵AD=kDB，∴AD=2ka，AB=BD+AD=2a+2ka=2a（k+1），过点A作AH⊥BC，在Rt△ABH中，∠B=30°．∴BH=a（k+1），∵AB=AC，AH⊥BC，∴BC=2BH=2a（k+1），∴CG=BC﹣BG=a（2k+1），过D作DN⊥AC交CA延长线与N，∵∠BAC=120°，∴∠DAN=60°，∴∠ADN=30°，∴AN=ka，DN=ka，∵∠DGC=∠AND=90°，∠AED=∠BCD，∴△NDE∽△GDC．∴，∴，∴NE=3ak（2k+1），∴EC=AC﹣AE=AB﹣AE=2a（k+1）﹣2ak（3k+1）=2a（1﹣3k2），∴=．15、如图①，在△ABC中，∠ACB=90°，∠B=30°，AC=1，D为AB的中点，EF为△ACD的中位线，四边形EFGH为△ACD的内接矩形（矩形的四个顶点均在△ACD 的边上）．（1）计算矩形EFGH的面积；（2）将矩形EFGH沿AB向右平移，F落在BC上时停止移动．在平移过程中，当矩形与△CBD重叠部分的面积为时，求矩形平移的距离；（3）如图③，将（2）中矩形平移停止时所得的矩形记为矩形E1F1G1H1，将矩形E1F1G1H1绕G1点按顺时针方向旋转，当H1落在CD上时停止转动，旋转后的矩形记为矩形E2F2G1H2，设旋转角为α，求cosα的值．【解答】解：（1）如图①，在△ABC中，∵∠ACB=90°，∠B=30°，AC=1，∴AB=2，又∵D是AB的中点，∴AD=1，，又∵EF是△ACD的中位线，∴，在△ACD中，AD=CD，∠A=60°，∴∠ADC=60°，在△FGD中，GF=DF•sin60°=，∴矩形EFGH的面积；（2）如图②，设矩形移动的距离为x，则，当矩形与△CBD重叠部分为三角形时，则，，∴．（舍去），当矩形与△CBD重叠部分为直角梯形时，则，重叠部分的面积S=，∴，即矩形移动的距离为时，矩形与△CBD重叠部分的面积是；（3）如图③，作H2Q⊥AB于Q，设DQ=m，则，又，．在Rt△H2QG1中，，解之得（负的舍去）．∴．16、尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．求证：a2+b2=5c2该同学仔细分析后，得到如下解题思路：先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证（1）请你根据以上解题思路帮尤秀同学写出证明过程．（2）利用题中的结论，解答下列问题：在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO 的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求MG2+MH2的值．【解答】解：（1）设PF=m，PE=n，连结EF，如图1，∵AF，BE是△ABC的中线，∴EF为△ABC的中位线，AE=b，BF=a，∴EF∥AB，EF=c，∴△EFP∽△BPA，∴，即==，∴PB=2n，PA=2m，在Rt△AEP中，∵PE2+PA2=AE2，∴n2+4m2=b2①，在Rt△AEP中，∵PF2+PB2=BF2，∴m2+4n2=a2②，①+②得5（n2+m2）=（a2+b2），在Rt△EFP中，∵PE2+PF2=EF2，∴n2+m2=EF2=c2，∴5•c2=（a2+b2），∴a2+b2=5c2；（2）∵四边形ABCD为菱形，∴BD⊥AC，∵E，F分别为线段AO，DO的中点，由（1）的结论得MB2+MC2=5BC2=5×32=45，∵AG∥BC，∴△AEG∽△CEB，∴==，∴AG=1，同理可得DH=1，∴GH=1，∴GH∥BC，∴===，∴MB=3GM，MC=3MH，∴9MG2+9MH2=45，∴MG2+MH2=5．17、如图①，△ABC中，∠ABC＝45°，AH⊥BC于点H，点D在AH上，且DH＝CH，连接BD．⑴求证：BD＝AC；⑵将△BHD绕点H旋转，得到△EHF(点B、D分别与点E、F对应)，连接AE．i) 如图②，当点F落在AC上时(F不与C重合)，若BC＝4，tan C＝3，求AE的长；ii)如图③，当△EHF是由△BHD绕点H逆时针旋转30°得到时，设射线CF与AE相交于点G，连接GH．试探究线段GH与EF之间满足的等量关系，并说明理由．解：⑴∵AH ⊥BC ，∴∠BHD ＝∠AHC ＝90°，∵∠ABC ＝45°，∴∠ABH ＝∠BAH ＝45°，∴BH ＝AH ，又∵DH ＝CH ，∴△BDH ≌△ACH ，∴BD ＝AC ；⑵i)过点H 作HG ⊥AC 于点G ，由题意可知△EHF ≌△AHC ，∴∠EHF ＝∠AHC ＝90°，EH ＝AH ，HF ＝CH ，∴∠AHE ＝∠FHC ，EH AH HF CH =，∴△AEH ∽△CFH ，∴AE AH CF CH =，在Rt △AHC 中，tan C ＝AH CH＝3，∴BH ＝AH ＝3CH ，∵BC ＝BH ＋CH ＝4，∴AH ＝3，CH ＝1，∴AC∵S △AHC ＝12AH HC ⋅＝12AC HG ⋅，∴HG ＝AH HC AC ⋅CG＝，∴CF ＝2CG，∴AE ＝CF AH CH⋅＝351ii) 设CG 、AH 交于点Q ，由题意可知EH ＝AH ，HF ＝CH ，∠AHE ＝∠FHC ＝90°＋30°＝120°，∴∠HAE ＝∠HEA＝1802AHE ︒-∠，∠FCH ＝∠CFH ＝1802FHC ︒-∠＝30°，又∵∠AQG ＝∠CQH ，∴△AQG ∽△CQH ，∴AQ GQ CQ HQ =，又∵∠AQC ＝∠GQH ，∴△AQC ∽△GQH ，∴GH QH AC CQ =＝sin30°，∵AC ＝EF ，∴12GH EF =．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2011第三轮复习综合题5 九年级班号A 姓名
1.我们知道：有两条边相等的三角形叫做等腰三角形．类似地，我们定义：至少有一组对
边相等的四边形叫做等对边四边形．
（1）请写出一个你学过的特殊四边形中是等对边四边形的图形的名称；
（2）如图，在ABC △中，点D E ，分别在AB AC ，上，设CD BE ，相交于点O ，若
60A ∠=°，12
DCB EBC A ∠=∠=∠．请你写出图中一个与A ∠相等的角，并猜想图中哪个四边形是等对边四边形；
（3）在ABC △中，如果A ∠是不等于60°的锐角，点D E ，分别在AB AC ，上，且
12
DCB EBC A ∠=∠=∠．探究：满足上述条件的图形中是否存在等对边四边形，并证明你的结论． B O A
D
E
C
2.四边形一条对角线所在直线上的点，如果到这条对角线的两端点的距离不相等，但到另
一对角线的两个端点的距离相等，则称这点为这个四边形的准等距点．如图1，点P 为四边形ABCD 对角线AC 所在直线上的一点，PD ＝PB ，PA ≠PC ，则点P 为四边形ABCD 的准等距点．
（1）如图2，画出菱形ABCD 的一个准等距点．
（2）如图3，作出四边形ABCD 的一个准等距点(尺规作图，保留作图痕迹，不要求写作法)．
（3）如图4，在四边形ABCD 中，P 是AC 上的点，PA ≠PC ，延长BP 交CD 于点E ，延长DP
交BC 于点F ，且∠CDF ＝∠CBE ，CE ＝CF ．求证：点P 是四边形AB CD 的准等距点．
（4）试研究四边形的准等距点个数的情况(说出相应四边形的特征及准等距点的个数，（不
必证明)．
1.
2. 解：(1)如图2，点P即为所画点．……………………1分(答案不唯一．画图正确，无文字说明不扣分；点P画在AC中点不给分)
(2)如图3，点P即为所作点．……………………3分(答案不唯一．作图正确，无文字说明不扣分；无痕迹或痕迹不清晰的酌情扣分)
(3)略
(4)①当四边形的对角线互相垂直且任何一条对角线不平分另一对角线或者对角线互相平分且不垂直时，准等距点的个数为0个；………………………………………………9分
②当四边形的对角线不互相垂直，又不互相平分，且有一条对角线的中垂线经过另一对角线的中点时，准等距点的个数为1个；…………………………………………10分
③当四边形的对角线既不互相垂直又不互相平分，且任何一条对角线的中垂线都不经过另一条对角线的中点时，准等距点的个数为2个；……………………………………11分
④四边形的对角线互相垂直且至少有一条对角线平分另一对角线时，准等距点有无数个．1分(．答案不唯一．画图正确，无文字说明不扣分；点P画在 A C中点不给分) …………………………………………………………………………12分(第(4)小题只说出准等距点的个数，不能给满分)。