ON SELECTION OF SOLUTIONS TO VECTORIAL HAMILTON-JACOBI SYSTEM
c++ vector 选择题

c++ vector 选择题英文回答:1. Which of the following is not a member function of the vector class?(A) push_back.(B) pop_back.(C) front.(D) reverse.2. What is the time complexity of inserting an element at the beginning of a vector?(A) O(1)。
(B) O(log n)。
(C) O(n)。
(D) O(n^2)。
3. Which of the following iterators can be used to iterate over a vector in reverse order?(A) begin()。
(B) end()。
(C) rbegin()。
(D) rend()。
4. What is the default capacity of a vector?(A) 0。
(B) 1。
(C) The size of the vector.(D) The maximum possible size of the vector.5. Which of the following is not an advantage of usinga vector over an array?(A) Dynamic size.(B) Faster access.(C) More efficient memory usage.(D) Easier to iterate over.中文回答:1. 以下哪些不是 vector 类的成员函数?(A) push_back.(B) pop_back.(C) front.(D) reverse.2. 在向量的开头插入一个元素的时间复杂度是多少?(A) O(1)。
Sparse Subspace Clustering

(RANSAC) [11], fit a subspace of dimension d to randomly chosen subsets of d points until the number of inliers is large enough. The inliers are then removed, and the process is repeated to find a second subspace, and so on. RANSAC can deal with noise and outliers, and does need to know the number of subspaces. However, the dimensions of the subspaces must be known and equal, and the number of trials needed to find d points in the same subspace grows exponentially with the number and dimension of the subspaces. Factorization-based methods [6, 12, 16] find an initial segmentation by thresholding the entries of a similarity matrix built from the factorization of the matrix of data points. Such methods are provably correct when the subspaces are independent, but fail when this assumption is violated. Also, these methods are sensitive to noise. Spectralclustering methods [30, 10, 28] deal with these issues by using local information around each point to build a similarity between pairs of points. The segmentation of the data is then obtained by applying spectral clustering to this similarity matrix. These methods have difficulties dealing with points near the intersection of two subspaces, because the neighborhood of a point can contain points from different subspaces. This issue can be resolved by looking at multiway similarities that capture the curvature of a collection of points within an affine subspace [5]. However, the complexity of building a multi-way similarity grows exponentially with the number of subspaces and their dimensions. Algebraic methods, such as Generalized Principal Component Analysis (GPCA) [25, 18], fit the data with a polynomial whose gradient at a point gives a vector normal to the subspace containing that point. Subspace clustering is then equivalent to fitting and differentiating polynomials. GPCA can deal with subspaces of different dimensions, and does not impose any restriction on the relative orientation of the subspaces. However, GPCA is sensitive to noise and outliers, and its complexity increases exponentially with the number of subspaces and their dimensions. Informationtheoretic approaches, such as Agglomerative Lossy Compression (ALC) [17], model each subspace with a degenerate Gaussian, and look for the segmentation of the data that minimizes the coding length needed to fit these points with a mixture of Gaussians. As this minimization problem 1
美国赛博空间作战行动Cyberspace _Operations

CHAPTER II
CYBERSPACE OPERATIONS CORE ACTIVITIES
Introduction................................................................................................................II-1
3.应用
a、本出版物中确立的联合原则适用于联合参谋部、作战司令部指挥官、下属统一司令部、联合特遣部队、这些司令部的下属部门、各军种和作战支持机构。
b、本出版物中的指南具有权威性;因此,除非指挥官认为特殊情况另有规定,否则将遵循这一原则。如果本出版物的内容与出版物的内容发生冲突,则以本出版物为准,除非参谋长联席会议通常与其他参谋长联合会成员协调,提供了更为现行和具体的指导。作为多国(联盟或联盟)军事指挥部一部分的部队指挥官应遵循美国批准的多国原则和程序。对于未经美国批准的条令和程序,指挥官应评估并遵循多国司令部的条令与程序,如果适用并符合美国法律、法规和条令。
•联合职能部门和网络空间运作
第三章权限、角色和职责
•简介III-1
•当局III-2
•角色和职责
•法律考虑因素III-11
第四章规划、协调、执行和评估
•联合规划过程和网络空间运营
•网络空间运营规划考虑因素
•对网络空间的情报和操作分析支持
运营计划IV-6
•针对性IV-8
•网络空间部队的指挥与控制
SmartSolutions для муравье

SmartSolutions for AntsA guide to ant management on-structure, off-structure and inside Photos by Ed Freytag, New Orleans Mosquito, Termite and Rodent Control BoardThe Problemwith AntsThe SmartSolutionfor Ants Ants are the number one reason homeowners call a pest management professional. Given this reality, ants take on a particular importance not only as a frequently encountered pest control challenge, but, quite often, as the foundation of your ongoing relationship with a customer.Unfortunately, due to their complex social structures, foraging habits, nomadic nesting tendencies and more, ants can be quite difficult to control. The cost of failure, at best, will be callbacks, wasted time and resources. At worst, it will be the loss of a potential, profitable, long-term customer.The SmartSolution for Ants from BASF Pest Control Solutions was created to help you control ant problems the first time you’re called, establish longstanding customer relationships and build a foundation for future business. It combines Termidor® termiticide/ insecticide with complementary ant control products and Prescription Treatment® IPM techniques that exploit unique ant behavior and biology.This guide will explore the unique challenges involved in modern ant control and introduce you to the unique products you need to overcome them. It will also give you the guidance you need to understand why, how and when you should use these products.The #1 Nuisance Pest can be Much More than a NuisanceAnts account for more new customer calls than any other pest. What’s not so good is that ants also account for more retreatment calls from current customers than any other pest.This suggests that existing ant control solutions quite simply aren’t cutting it. Callbacks can prove costly on a number of fronts, including:Not to mention the potential for actual structural damage for which some ant species are known.Special Challenges from AntsComplex social colonies and unique behaviors set ants distinctly apart from most other perimeter pests. They are active foragers, which means they are likely to invade homes looking for food and other resources. When they find it, they recruit nest mates, often in large numbers.Trying to keep these ants out with repellent chemical barriers often proves futile, as ants are particularly adept at circumnavigating them. Killing individual workers is equally futile. Some colonies have thousands or even millions of ants, so they just keep on coming.Assuming that you’ve found the heart of an ant problem by locating a nest can be equally misguided. Finding and treating individual nests may control certain species, however, some ants have supercolonies or satellite nests that can infest multiple properties.Finally, the wide range of ant species can exhibit variable feeding preferences, foraging patterns, nesting choices and colony structures, requiring different treatment strategies and products to choose from.n Aggravated customers n Damage to your reputationn Lost customer confidence/satisfactionn Lost future business n Frustrated techniciansn Wasted time, labor and resourcesLayer 1: Exterior On StructureFight ants with Termidor,®America’s #1 GPC product*Termidor termiticide/insecticide is the core product ofthe SmartSolution for Ants and provides the most effective outdoor low-dose control of ants available. A Termidor treatment creates a treated zone of nonrepellent protection around the home. This is the key to Termidor’s uniqueTransfer Effect.™Ants passing through the treated area pick up Termidor on their bodies and transfer the active ingredient to nest mates through routine social contact. The Transfer Effect enables Termidor to control ants that never make direct contact with a treated surface. They need only to contact other ants that have been exposed to T ermidor . Ants interact with each other as a means of communication, grooming and feeding, which makes the concept of transfer so important to ant control.Termidor stands alone in terms of its ability to control ants through its Transfer Effect. In a study by Choe and Rust (UC Riverside), ants exposed to Termidor “readily transferred the insecticide to other individuals in the colony, resulting in high mortality… The other insecticides were not transferred and ants exhibited mortality rates similar to that of the controls.” On its own, Termidor significantly reduces nuisance ant callbacks. As part of the SmartSolution for Ants, it becomes a powerful “first layer” of control, providing an incomparably effective base for the other important layers.Layer 2: Exterior Off StructureReduce ant pressure around the structure and stop colonies from invadingTreatments away from the structure where ants are observed trailing or near resource sites (including trees, planting beds) reduce the ant pressure around the structure and helpprevent invading colonies from setting up close to the house. The Alpine ® WSG/Advance ® Ant Bait combination is ideal.n A lpine WSGAlpine WSG combines a versatile label that allows treatment of ant trails or even curative broadcast applications to lawns, with its nonrepellent,undetectable transferability to kill ants where they are found. This is an excellent complement to both Termidor on structure treatments and Advance Ant Bait applications.n A dvance Ant BaitsAdvance Ant Baits take advantage of the practice of social food sharing common among ants. Ants recruit their nest mates to help collect food and carry it back to the nest and then distribute it throughout the colony. Advance Ant Baits are designed to be extremely attractive for fast acceptance by ants and are available in several formulations to attract a wide variant of ants. Baiting does not interfere with the effects of a Termidor treatment, and in fact, using both treatments together has been shown to lead to more reliable results.Controlling Ants Inside and OutThe SmartSolution for Ants includes carefully selected products that address the special challenges of ant control. These products, delivered in “Layers of Treatment” outside and inside, expand the transfer zone and take advantage of distinct ant biology and social behaviors.Cumulative number of dead ants in a horizontal transfer study by Dr. Rustday 3day 7C u m u l a t i v e n u m b e r o f d e a d a n t sTreatmentTermidorArilon Talstar Optigard Flex Tempo UltraControl*SPC, LLC 2008.-40-200 20 406080 100 P e r c e n t R e d u c t i o nOdorous House Ant Population ReductionLayer 3: Inside StructureTarget problem areas with nonrepellent products without risk of “locking them in”Because there are so many species of ants and so many treatment situations inside a structure, a PMP should have a broad choice of indoor control products at hand to treat them. The SmartSolution for Ants includes a flexible range of nonrepellent indoor ant control products and application methods that complement Termidor ® without the risk of “budding” or “lock-in” that can occur with repellents.n A lpine ® products*Alpine products utilize advanced nonrepellent technology to eliminate ant populations. All Alpine products are labeled for use indoors and outdoors. Alpine WSG is an odorless, non-staining formulation that can beapplied indoors as a spot or crack and crevice treatment where ants may be foraging. The fact that it contains the reduced risk active ingredient dinotefuran will be a comfort to your customers.n T ermidor FoamTermidor Foam is the preferred void treatment productfor ants. Featuring the same Transfer Effect ™ as other Termidor products, this formulation is designed to treat voids and ant galleries wherever ants enter, hide or harbor, both indoors and outdoors.n A dvance ® Ant Baits(See description on previous page.)*Where Alpine is not yet registered, Phantom ®products offer an excellent treatment option indoors.20 40 60 80 100 142423714Carpenter Ants: Percent Mortality at TimeConclusion: Termidor Foam termiticide/insecticide provided good residual (24 hours after treatment) efficacy against carpenter ants. Laurel D. Hansen, Biology Department MS 3180, Spokane Falls Community College, 3410 W. Fort Wright Drive, Spokane Falls, WA 99224, Report Number: 806.Termidor Foam and Water12 HAT 1 DAT2 DAT3 DATAverage Percent Mortality of Recipients (Transfer Effect)Black Carpenter Ants, C. pennsylvanicus, with Alpine WSG (0.1%)**The label states 0.2% for carpenter antsDr. Buczkowski Purdue 2013Alpine WSG 1:50Control 1:50As a part of an overall ant IPM program, integrating several layers of treatment can be useful in attacking antsin ways that address symptoms, control the source and help to prevent future reinfestations. An example of the SmartSolution for Ants three-layered approach may include: Layer 1: Exterior On the StructureCreate a Termidor® termiticide/insecticide treatment zone on and around the structure. Following the label directions, spray along the foundation exterior perimeter to an area one foot up and one foot out from where the ground meetsthe foundation. Termidor can also be applied to areas where ants enter the structure, where they trail or crawl and hide, or where their nests are found. Spray up to 18 inches in width around doors, windows, vents, pipes or any other exterior openings and/or with a Crack & Crevice® injection tip into foundation cracks or drilled holes where ants could enter the structure. Be especially careful to treat the joint where exterior siding meets the cement block or brick foundation. Treat areas where any wires (electrical, cable or telephone) enter the house. Termidor exterior applications can be applied two times per year. We suggest that the applications be made when ants are active and pest pressure is evident. Layer 2: Exterior Off from the StructureGarbage areas, planting beds, trees and overgrown and cluttered areas are great examples of resource sites likelyto foster the growth of ant populations. These areas can be dealt with through baiting with Advance® Granular Ant Baits and/or the use of Alpine WSG to expand the transfer zone. Ants are known to prefer crawling along structural guidelines when trailing, so in addition to treating the suspected nesting areas, focus on edges of sidewalks and driveways, garden borders, fences and other areas where ants may trail.Layer 3: Inside the StructureAnts indoors can be dealt with by crack and crevice,spot or void treatments of nonrepellent products. Choose the best formulation based on where the ants are trailingor suspected to be nesting — for instance: Prescription Treatment® brand Alpine® Pressurized Insecticide for crack and crevice, Termidor Foam for voids and Alpine WSG for spot treatments. These products won’t trap ants indoors,or interfere with the movement through the transfer zone created outside by Termidor. If Advance Ant Baits are used indoors, be sure to place baits near ant trails in areas where increased ant activity from recruitment won’t be a problem for the customer. Attics, basements and crawlspaces aregood indoor placement choices for baiting.Always read and follow label directions.© 2014 BASF Corporation. All rights reserved.Arilon is a trademark of E. I. du Pont de Nemours and Company or its affiliates, Talstar is a registered trademark of FMC Corporation or its subsidiaries, affiliates or licensors in the U.S. and other countries, Optigard is a trademark of a Syngenta Group Company and Tempo is a registered trademark of Bayer.10-21-155-033PRESSURIZED INSECTICIDEBASF Pest Control Solutions believes a sound Integrated Pest Management strategy is the cornerstone of successful pest control and good stewardship. Our Prescription Treatment approach includes the core IPM practices you should always employ in conjunction with any BASF SmartSolution.CO MM U N I C A TEwith the clientto promote cooperation, establish expectations and convey value.I N S P E C Tto gather the informationthat leads to good decisions. P RE S C R I B Ea treatment strategy to achieve specific goalsin the account.T R E A Tusing effectivetechniques and materials that support the strategy.F OL L O W U Pwith the client to assess the results of the treatment.。
Discontinuous Dynamical Systems

Discontinuous Dynamical Systems
A tutorial on notions of solutions, nonsmooth analysis, and stability
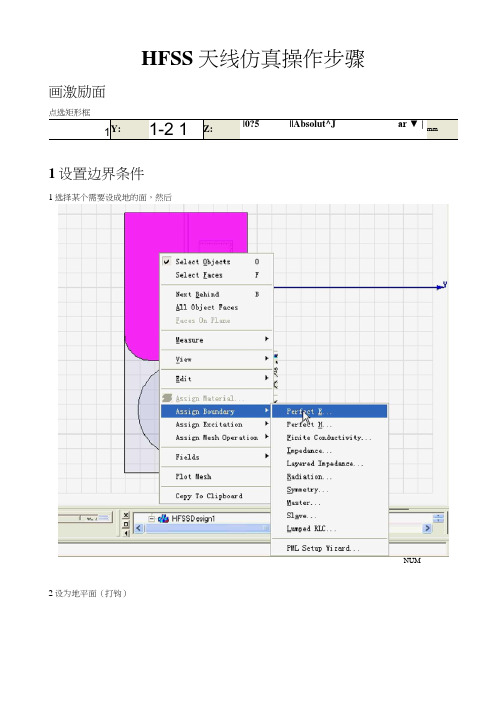
HFSS天线仿真操作步骤
XSize
YSize
ZSize
£
Command |
2£l
口
§
pper
teri all
Box2
Copy To Clipboard
Copy To Clipboard
Delete Start Point
Delete End Point
Delete Start Point
Delete End Point
选择金属化通孔,
点
Draw 3D Model er HFSS Tools Window KelpX□®El凰遂型倉P匕劉[、*2厂吧]口ooorfT®7q13刁险。矗1V] (gi |Object
!J
l±l・:®';s.・.T•♦••・田・4十••・田…田±•:田…田丄十
…甲由:
Cyl1naer1
Cylinder1
O Sheets
-匸]Perfect E
Mesh
Optim
Resul
Port
Field
Radi注tion
Edit Imp a dance Mult
Li st..・
Delete All
MM
Vi sualization..・
Reorder Matrix.・・
+ l£j Defini tions
"Wave Port”,弹出一个菜单。
HFSS
画激励面
点选矩形框
1
Y:
1-21
Z:
|0?5 ||Absolut^J ar ▼ |
mm
1设置边界条件
1选择某个需要设成地的面,然后
NUM
2设为地平面(打钩)
VectorCalculus

6.1 VECTOR FIELDS EXAMPLE 1.5
Graphing Vector Fields and Flow Lines Graph the vector fields y,−x and 2, 1 + 2xy and sketch-in approx. flow lines through the points (0, 1), (0, −1) and (1, 1). Solution:
Slide 4
6.1 VECTOR FIELDS EXAMPLE 1.1
Plotting a Vector Field For the vector field F(x, y) = x + y, 3y − x, evaluate (a) F(1, 0), (b) F(0, 1) and (c) F(−2, 1).
Slide 27
6.1 VECTOR FIELDS EXAMPLE 1.8
Finding Gradient Fields Solution (cont.):
Slide 28
6.1 VECTOR FIELDS EXAMPLE 1.9
Finding Potential Functions Determine whether each of the following vector fields is conservative. If it is, find a corresponding potential function f (x, y): (a) F(x, y) = 2xy − 3, x2 + cos y (b) G(x, y) = 3x2y2 − 2y, x2y − 2x. Solution:
Plot each vector F(x, y) using the point (x, y) as the initial point. Solution:
科技英语试题及答案

科技英语试题及答案一、选择题(每题2分,共20分)1. The term "nanotechnology" refers to the manipulation of matter on an atomic, molecular, and supramolecular scale.A. TrueB. False2. Which of the following is NOT a characteristic of renewable energy sources?A. Infinite in supplyB. Environmentally friendlyC. Dependent on weather conditionsD. Non-renewable3. The process of converting solar energy into electrical energy is known as:A. SolarizationB. Photovoltaic effectC. Solar distillationD. Thermal radiation4. In the context of computer science, what does "AI" stand for?A. Artificial IntelligenceB. Advanced InterfaceC. Automated InputD. Application Interface5. The term "genome" is associated with:A. The complete set of genes in an organismB. The structure of a cellC. The study of geneticsD. The process of cell division6. What is the primary function of a transistor in an electronic circuit?A. To amplify signalsB. To store dataC. To convert light into electricityD. To filter signals7. The "Internet of Things" (IoT) refers to:A. A network of interconnected devicesB. The global network of computersC. A collection of internet protocolsD. The study of internet security8. Which of the following is a type of biotechnology?A. Genetic engineeringB. Quantum computingC. NanolithographyD. Nuclear fusion9. The "Greenhouse Effect" is related to:A. The warming of the Earth's surfaceB. The cooling of the Earth's surfaceC. The process of photosynthesisD. The formation of the ozone layer10. What does "CRISPR" stand for in the field of molecular biology?A. Clustered Regularly Interspaced Short Palindromic RepeatsB. Computer-Aided Research in Scientific ProjectsC. Comprehensive Research in Innovative ScienceD. Computational Research in Systematic Processes二、填空题(每题1分,共10分)1. The unit of electrical resistance is the ______.2. The process of converting sound waves into electrical signals is known as ______.3. In physics, the term "entropy" is used to describe the level of ______ in a system.4. The study of the chemical composition of planets is known as ______.5. The term "cybersecurity" refers to the protection of______ from cyber threats.6. The process of converting electrical energy into light is known as ______.7. The smallest unit of life that can replicate itself is called a ______.8. The process of creating new substances from existing ones is known as ______.9. The study of the structure and function of cells is known as ______.10. The process of converting light energy into chemical energy is known as ______.三、简答题(每题5分,共30分)1. Explain the concept of "machine learning" in artificialintelligence.2. Describe the role of a semiconductor in modern electronics.3. What is the significance of biodiversity in the context of environmental science?4. Discuss the potential impact of nanotechnology on medicine.四、论述题(共40分)1. Discuss the ethical considerations involved in the development and use of genetic engineering technologies. (20分)2. Analyze the potential benefits and challenges of implementing a global Internet of Things (IoT) network. (20分)答案:一、选择题1. A2. D3. B4. A5. A6. A7. A8. A9. A10. A二、填空题1. ohm2. transduction3. disorder4. cosmochemistry5. information systems6. electroluminescence7. cell8. synthesis9. cytology10. photosynthesis三、简答题1. Machine learning is a subset of artificial intelligence that enables computers to learn from and make decisions based on data, improving at tasks over time through experience without being explicitly programmed.2. Semiconductors are materials with electrical conductivity between that of a conductor and an insulator. They arecrucial in electronic devices like transistors and diodes, allowing for the control of electrical current and the amplification of signals.3. Biodiversity is significant in environmental science as it ensures the stability of ecosystems, supports ecological processes, and provides a variety of services and resources that are vital for human survival and well-being.4. Nanotechnology has the potential to。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ON SELECTION OF SOLUTIONS TO VECTORIALHAMILTON-JACOBI SYSTEMBAISHENG YANAbstract.In this paper,we discuss some principles on the selection ofthe solutions of a special vectorial Hamilton-Jacobi system defined by(1.1)below.Wefirst classify the equivalent solutions based on a well-known construction and then discuss some selection principles usingintuitive descriptions of coarseness or maximality of solutions.We alsodiscuss a selection principle based on comparison of the projections of asolution with certain smooth functions and introduce a notion of partialviscosity solutions for the vectorial Hamilton-Jacobi equation,whichgeneralizes the well-known notion of viscosity solutions in the scalarcase.Since we mainly work in the framework of Sobolev solutions,weshow that,as in the scalar case,for certain domains the partial viscosityprinciple may rule out many interesting Lipschitz solutions.1.IntroductionIn this paper,we discuss some principles on the selection of the solutions of a special vectorial Hamilton-Jacobi system defined by(1.1)Du(x)∈K a.e.x∈Ω,where K is a given set of m×n real matrices,Ωis a bounded domain in R n,u is a mapping fromΩto R m and Du is the gradient matrix of u: Du(x)=(∂u i/∂x j),i=1,2,...,m,j=1,2,...,n.We study the solutions of system(1.1)in the usual Sobolev space W1,p(Ω;R m)for some1≤p≤∞with an affine Dirichlet boundary condition(1.2)u|∂Ω=ξx+b,whereξis a given m×n matrix and b is a given vector in R m.As usual,the(Ω;R m),the closure boundary condition(1.2)means that u−ξx−b∈W1,pin W1,p(Ω;R m)of the set of smooth mappings compactly supported inΩ. It is clear that ifξ∈K the affine map u=ξx+b is always a solu-tion to problem(1.1)-(1.2)and,in view of regularity,this trivial solution is considered as being more favorable than other solutions(if exist).Of Key words and phrases.Selection of solutions,coarse,L p-maximal,and partial viscosity solutions.12BAISHENG YANcourse,a real interest of studying problem(1.1)-(1.2)lies in that even when ξ/∈K the problem may have solutions.The reason we study system(1.1) in the Sobolev spaces rather than some smooth function spaces,such as C1(Ω;R m),is that in application to the phase transition problem for a martensitic material the set K models the set of homogeneous strains min-imizing the material’s elastic potential energy,the so-called energy well, which often has several disjoint connected components;usually,a smooth solution u of(1.1)will force Du to lie only on one of the components of K and thus prohibit the formation of physically important structures in the phase transition(see[2,11]).In the Sobolev space setting,the nontrivial solutions of(1.1)-(1.2),if exist,are not unique and may have differentfine structures(microstructures).However,physically,these solutions may all exhibit the same effective(macroscopically observable)quantities of the ma-terial.This paper is devoted to a mathematical issue regarding the selection of solutions of problem(1.1)-(1.2)in a Sobolev space.The existence of certain weak solutions to the problem(1.1)-(1.2)has been established in a series of papers of Dacorogna and Marcellini[6,7]and M¨u ller andˇSver´a k[9,10],using different methods.They showed that if K is compact and has a sufficiently rich structure then the Dirichlet problem (1.1)-(1.2)possesses infinitely many Lipschitz solutions for certain boundary dataξx+b withξ/∈K(note that the constant b is irrelevant).Their methods seem not applicable to the systems(1.1)defined by unbounded sets K.Nevertheless,in the present paper,we shall assume that,for certain given boundary dataξ,problem(1.1)-(1.2)has solutions in W1,p(Ω;R m). Wefirst classify the equivalent solutions using a principle motivated by a well-known construction of self-similarity(see the proof of Proposition2.1) and then discuss some selection principles based on an intuitive descrip-tion of coarseness or maximality of a solution also motivated by the same construction.All these principles rely essentially on the comparison of all equivalent solutions.For example,an L p-maximal solution defined later is a solution for which a certain L p-norm is not smaller than the norm of other equivalent solutions.Since the class of equivalent solutions is usually difficult to study,these selection principles can hardly be effective in appli-cations;however,they provide some new understanding of the structures of Sobolev solutions to the problem(1.1)-(1.2).To discuss yet another selection principle,we note that if u∈W1,p(Ω;R m) is a solution to the problem(1.1)-(1.2)then,for any unit vector h∈R m, the functionϕ(x)=h·u(x)∈W1,p(Ω)is a solution of the problem(1.3)Dϕ(x)∈Γ a.e.x∈Ω,ϕ|∂Ω=(h tξ)x,ON SELECTION OF SOLUTIONS3 whereΓ=K h={h tη|η∈K}is a subset of M1×n∼=R n.The equation Dϕ(x)∈Γcan be considered as a special scalar Hamilton-Jacobi equation H(Dϕ(x))=0defined by certain Hamiltonians H(p),i.e.,functions vanish-ing exactly onΓ.In the setting of Sobolev solutions,the choice of different Hamiltonians does not affect the solutions of problem(1.3).However,later on,we shall use a particular Hamiltonian to impose some constraints on these solutions.In the scalar case,an important and elegant method to generalize weak solutions of the scalar Hamilton-Jacobi equations to the class of continuous functions is the well-known viscosity solution method introduced by Crandall and Lions[5](see also[4,8]),which is based on the comparison of a solution with certain smooth functions and is compatible with certain regularizing procedures(the vanishing viscosity method).We generalize the notion of the viscosity solutions to the special vectorial Hamilton-Jacobi equations as given by(1.1).Since there is no direct way to compare the vector valued functions,our comparison will be restricted to the projections of a solution in certain directions.This leads us to studying the equations(1.3).Although these equations may be far from completely char-acterizing the original vectorial Hamilton-Jacobi equation,they certainly impose some reasonable partial restrictions on the solutions.In this regard, we define a partial viscosity solution(in direction h)of(1.1)-(1.2)to be those solutions u for whichϕ(x)=h·u(x)is a viscosity solution relevant to prob-lem(1.3).This principle does not involve comparison with other equivalent solutions.Finally,since we mainly work in the framework of Sobolev solutions,even in a scalar case,the existence of W1,p-viscosity solutions seems to depend strongly on the geometry of the domain,as has been recently shown in the paper[3].For instance,they showed that in the scalar case(m=1),for certain domainsΩand boundary dataξx+b,there may exist infinitely many Lipschitz solutions to problem(1.1)-(1.2)but no Lipschitz-viscosity solutions at all.In the vectorial case,we shall see that the partial viscosity principle also rules out many interesting Lipschitz solutions for certain domains(for example,all smooth domains).As an example,we show that for smooth domains the M¨u ller-ˇSver´a k solutions of the two-well problem in[9]are nota partial viscosity solution(in certain directions).2.Classification of Sobolev solutionsIn the rest of the paper,we assumeΩ⊂R n is a bounded domain with Lipschitz boundary∂Ω,although most of the results hold for any open4BAISHENG YANbounded setsΩwith|∂Ω|=0.We use M to denote the space M m×n of all m×n real matrices with norm|ξ|=(ξtξ)1/2.Definition2.1.Let1≤p≤∞,K⊆M be given.We defineβp(K)to be the set of allξ∈M such that the problem(2.1)Du(x)∈K a.e.x∈Ω;u|∂Ω=ξxhas a solution u in W1,p(Ω;R m).Moreover,forξ∈βp(K),let S p(Ω)be the set of solutions u of problem(2.1)in W1,p(Ω;R m).Clearly,K⊆βp(K)andβp(K)⊆βq(K)if p>q.Since any Sobolev map with essentially bounded gradient can be considered as a Lipschitz map,it follows thatβp(K)=βq(K)for all1≤q<p≤∞for a bounded set K. Later,we shall give an example of an unbounded set K such thatβp(K) is strictly contained inβq(K)for p>q.For general sets K,we have the following result.Proposition 2.1.The setβp(K)is independent of the smooth bounded domainΩ.Moreover,if S p(Ω)contains a nontrivial solution u=ξx then it must contain infinitely many solutions.Proof.The proof of this result is not difficult,but involves an important construction that motivates much of the consideration of the present paper. We discuss this construction in the proof.To prove the independence ofβp(K)onΩ,suppose for a bounded Lip-schitz domainΩproblem(2.1)has a solution u∈W1,p(Ω;R m).Let U be another bounded Lipschitz domain in R n.(Note that U can beΩitself.) We show that the Dirichlet problem(2.2)Dv(y)∈K a.e.y∈U;v|∂U=ξyalso has a solution v in W1,p(U;R m);this proves the independence result. To construct a solution to problem(2.2),we define open setsΩa,ǫfor a∈R n,ǫ>0by(2.3)Ωa,ǫ≡a+ǫΩ={a+ǫx|x∈Ω}.Then,for any y∈U,there exists r y>0such thatΩy,r⊂U for all r∈(0,r y).Notice that the family{Ωy,r|y∈U,0<r<r y}forms a Vitali cover for U;thus by the Vitali covering lemma,there exist disjoint setsΩk,and a set N of measure (k=1,2,...),whereΩk=y k+r kΩ,0<r k<r ykzero such that U=∪∞k=1Ωk∪N.Define a map v:U→R m by (2.4)v(y)= ξy k+r k u(y−y k r k),y∈Ωk,k=1,2,...;ξy,otherwise in U.ON SELECTION OF SOLUTIONS5It is easy to verify that v−ξy∈W1,p(U;R m)and that Dv(y)∈K for a.e. y∈U.Therefore v is a solution to the problem(2.2).To prove the second part of the proposition,we choose U=Ω.Let u=ξx be a nontrivial solution of(2.1).The construction above shows that v is a solution of(2.1)and v−ξy L p(Ω)≤(sup y∈Ωr y) u−ξx L p(Ω).Hence,by choosing r y<ǫfor all y∈Ω,we can construct a sequence of solutions{vǫ} in S p(Ω)such that vǫ(y)→ξy in L p(Ω)asǫ→0.This proves that problem (2.1)has infinitely many solutions.The proof of the proposition is now completed. Note that the map v defined by(2.4)above satisfies(2.5)1|U| Uψ(Dv(x))dx=1|Ω|Ωψ(Du(x))dxfor all continuous functionsψsatisfying|ψ(η)|≤C(|η|p+1)(for p=∞we need|ψ(η)|<∞).In the following,we denote by C p(M)the linear space of all such continuous functionsψ.Definition2.2.We say two solutions u,v in S p(Ω)are equivalent and write u∼v if for allψ∈C p(M)(2.6) Ωψ(Dv(x))dx= Ωψ(Du(x))dx.This relation is indeed an equivalence relation on S p(Ω).Any solution v (with U=Ω)as constructed in the proof above is equivalent to u.We denote the quotient set of the equivalence classes by S p(Ω).Therefore the solution set S p(Ω)is decomposed as the union of the disjoint equivalence classes:S p(Ω)=∪{[u]|[u]∈S p(Ω)}.Each[u]in S p(Ω)defines a linear functionalµ[u]on C p(M)throughµ[u],ψ =1|Ω| Ωψ(Du(x))dx,which,by the Riesz representation theorem,also induces a probability Radon measureµ[u]on M supported on the closure¯K.For applications in non-linear elasticity,ifψ(Du(x))is a quantity depending on the deformation gradient Du(x),solutions in an equivalence class all give the same effective or macroscopically observable quantity µ[u],ψ ,although microscopically these solutions are distinct and have differentfine structures.For general energy minimizing sequences,such a description of macroscopically observ-able quantities has been successfully given in terms of Young measures(see [2]).6BAISHENG YANLemma2.2.For each p∈[1,∞],the functionΨ([u])= Du−ξ L p(Ω)is a well-defined function on S p(Ω).Proof.If1≤p<∞we chooseψ(η)=|η−ξ|p in(2.6).While,if p=∞we chooseψ(η)=|η−ξ|q for any q<∞,raise the equality(2.6)to the power 1/q and then let q→∞.Therefore Dv−ξ p= Du−ξ p if v∼u for all 1≤p≤∞;soΨ([u])is well-defined on S p(Ω). Note thatΨ([u])=0if and only ifξ∈K and[u]=[ξx];in this case,the class[ξx]contains only the trivial solutionξx.Therefore,to some extent,the functionΨ([u])provides a scale to measure the L p-deviation of the gradient Du from the constant matrixξ.To keep the L p-deviation as small as possible, the solution class[u]is preferable over the class[v]ifΨ([u])<Ψ([v]).In this sense,it would be interesting to study the problemΨ([u]).¯m=inf[u]∈S p(Ω)Since we do not know much about the structure of S p(Ω),it seems impossible to analyze this minimum problem.In the following,we shallfix a solution class[u]so thatΨ([u])is close to the number¯m with some precision and study the selection principles for solutions in the same class[u].Finally,we give an example of set K for whichβp(K)may depend on p≥1dramatically.Example.Let n≥3and K=C1={ξ∈M n×n||ξ|n=n n/2detξ}be the set of conformal matrices.Supposeξ∈βp(C1).Then there exists a map u∈W1,p(Ω;R n)such that(2.7)|Du(x)|n=n n/2det Du(x) a.e.x∈Ω;u|∂Ω=ξx.If p≥n,we can integrate the equation above overΩand use the boundary condition,the Jensen inequality,and a property of the determinant function to obtain|ξ|n≤n n/2detξ.Hence,by Hadamard’s inequality,ξ∈C1.This showsβn(C1)=C1.Let J be an n×n matrix with J t J=I,det J=−1and let u0(x)= Jx/|x|2.Then an easy calculation shows that u0∈W1,p(B;R n)for all p< n/2,where B is the unit ball in R n,and that u=u0solves(2.7)withΩ=B,ξ=J.This shows J∈βp(C1)for all p<n/2;henceβn(C1)=βp(C1)for all p<n/2.For further information onβp(C1)when n/2≤p<n,see [12,13].3.Selection of solutions in the same classFor any given solution u of problem(2.1),the map v constructed as in the proof of Proposition2.1is an equivalent solution and hasfiner structuresON SELECTION OF SOLUTIONS7 and perhaps more singularities.We don’t know whether or not all solutions v∈[u]are obtained this way.But certainly this construction renders us some reasonable and intuitive standards on selecting solutions in the same solution class.Intuitively,all our selection principles should conform to the principle that solutions with lessfine structures or singularities be more preferable.3.1.Coarseness of solutions.In the construction(2.4),a“patch”of v, v|Ωa,ǫ,totally determines u inΩand has the same intrinsic structure as u (e.g.,boundary data,singularities);such solutions v are considered as having morefine structures or singularities than u and thus being unfavorable. Definition3.1.Let u,v∈S p(Ω).We say u is coarsened from v and write u≻v provided that u∼v and there exists a“patch”Ωa,ǫ⊂⊂Ωsuch that u(y)=ǫ−1(v(a+ǫy)−ξa)for almost every y∈Ω.We say u is self-similar if u≻u.We say u is a coarse solution if no solutions are coarsened from u. Note that the relation“≻”is transitive:u≻v,v≻w=⇒u≻w. Indeed,if forΩa,ǫ,Ωb,δ⊂⊂Ωwe have u(y)=ǫ−1(v(a+ǫy)−ξa)and v(y)=δ−1(w(b+δy)−ξb)for y∈Ω,then for the patchΩc,γ⊂⊂Ω,where c=a+ǫb,γ=ǫδ,we have(3.1)u(y)=γ−1(w(c+γy)−ξc) a.e.y∈Ω.Therefore,if u≻v and v≻u then u,v are both self-similar.Proposition3.1.Let u∈S p(Ω)andΩa,ǫ⊂⊂Ω.Suppose u(y)=ǫ−1(u(a+ǫy)−ξa)for almost every y∈Ω.If u is differentiable at the point aǫ=a1−ǫ,then u≡ξx inΩ.Therefore,the only smooth self-similar solution in S p(Ω) is the trivial solution u=ξx.Proof.Let f(x)=u(x)−ξx.Then,using u(y)=ǫ−1(u(a+ǫy)−ξa)for almost every y∈Ωand iterating(3.1),it is easy to verify that for k=1,2,...f(y)=ǫ−k f(aǫ+ǫk(y−aǫ)).From this and the fact that f is differentiable at aǫandǫ<1,we easily obtain by letting k→∞that f(y)=Df(aǫ)(y−aǫ)for almost every y∈Ω. Since f∈W1,p(Ω;R m)we must have Df(aǫ)=0and thus f≡0;this shows u≡ξx and completes the proof. Remark.Define“ ”by letting w v if and only if w≻v or w=v. The previous result shows that,if u∈S p(Ω)is a nontrivial solution,the relation“ ”is a partial ordering on the set[u]∩C1(Ω;R m).However,as we mentioned in the introduction,in applications,it may very well be possible that the set[u]∩C1(Ω;R m)is empty if u∈S p(Ω)is nontrivial.8BAISHENG YANThe following result shows that every nontrivial solution generates an equivalent(non smooth)self-similar solution.Proposition3.2.If u∈S p(Ω)is a nontrivial solution,then there exists a self-similar solution v∈[u].Proof.LetΩ1=Ωa,ǫ⊂⊂Ωfor some a∈R n,ǫ>0.As in the proof of Proposition2.1,using u∈S p(Ω)we construct a solution u1∈S p(G1),where G1=Ω\Ω1.Let f=u1−ξx∈W1,p(G0;R m).DefineΩk=a+ǫΩk−1and G k=Ωk−1\Ωk inductively for k=2,3,...and note that G k is the imageof G1under the map L k(x)=aǫ+ǫk(x−aǫ),where,as before,aǫ=a1−ǫ.We now define a map v onΩby letting v(x)=ξx+ǫk f(y)if x=L k(y)for some k=1,2,...and y∈G1.Then it can be verified that v∈S p(Ω),v∼u and v≻v. Remark.In some cases,we can construct a self-similar solution v as in the proof above such that v∈C1(Ω\{aǫ};R m).Therefore,the smoothness condition in Proposition3.1can not be dropped.3.2.Structure of a non-coarse solution.Suppose u∈S p(Ω)is not a coarse solution.Then,from the definition,the familyF={Ωa,ǫ⊂⊂Ω u∈S p(Ωa,ǫ), Ωa,ǫψ(Du)=ǫn Ωψ(Du),∀ψ∈C p(M)}is non-empty.Define a relation“≤”on F by letting U≤V if and only if U⊂⊂V or U=V.Then it is easily seen that(F,≤)is a partially ordered set(poset).Therefore,the HausdorffMaximal Principle asserts that there exists a maximal totally ordered subset M⊂F.Letσ=inf{|U| U∈M}. Lemma3.3.If there exists U∈M such that|U|=σ,then u∈S p(U)is a coarse solution on U.Proof.If u∈S p(U)is not a coarse solution,by definition,we have U1= U a,ǫ⊂⊂U such that u∈S p(U1)and U1ψ(Du)=ǫn Uψ(Du)for allψ∈C p(M).As U=Ωb,δ∈F,we easily see that U1∈F.We now show U1∈M and thus obtain the desired contradiction.Since U∈M and M is totally ordered,for any V∈M and V=U,we have either U⊂⊂V or V⊂⊂U; but the latter cannot happen since otherwise|V|<|U|=σ,contradicting the definition ofσ.Therefore,we have U⊂⊂V for all V∈M,V=U. Therefore U1≤V for all V∈M.This shows that the set M′={U1,M}is totally ordered by“≤”and thus by the maximality of M we have U1∈M and hence the contradiction.ON SELECTION OF SOLUTIONS 9Lemma 3.4.If |U |>σfor all U ∈M ,then σ=0.In this case,there exists a sequence {U k }⊂M such that U k +1⊂⊂U k for all k =1,2,...and ∩k U k ={a }for some a ∈U 1.Proof.Let {U k }⊂M be a sequence such that U k +1⊂⊂U k for all k =1,2,...and lim k →∞|U k |=σ.Let U ∞=∩k U k .It is easy to see U ∞=∩k U k is a compact set in U 1and |U ∞|=σ.Since each U k is of the form a k +ǫk Ω,it follows that U ∞=a +ǫΩfor some a ∈R n and ǫ≥0.The result will follow if ǫ=0and thus σ=0.Suppose for the contrary ǫ>0.Since U k ∈F we can also prove that Ωa,ǫ,the interior of U ∞,belongs to F .We claim Ωa,ǫ⊂⊂U for all U ∈M ,and therefore the set {Ωa,ǫ,M}is totally ordered by “≤”;this and the maximality of M would imply Ωa,ǫ∈M ,which contradicts with the assumption and the fact that |Ωa,ǫ|=σ.To prove our claim,we take an arbitrary U ∈M .By assumption,|U |>σ=lim k →∞|U k |,and hence |U |>|U k |for all sufficiently large k.Since M is totally ordered,this implies U k ⊂⊂U and hence Ωa,ǫ⊂⊂U k ⊂⊂U,proving the claim. Summarizing the above results,we have the following structural theorem for non-coarse solutions.In the sequel,we write Ωk ց{a }if Ωk +1⊂⊂Ωk and ∩k Ωk ={a }.Theorem 3.5.Let u ∈S p (Ω)be a non-coarse solution.Then,either (i )for some Ωa,ǫ⊂⊂Ω,u ∈S p (Ωa,ǫ)is a coarse solution on Ωa,ǫand Ωa,ǫψ(Du )=ǫn Ωψ(Du )for all ψ∈C p (M ),or(ii )there exist Ωk =Ωa k ,ǫk ⊂⊂Ωsuch that Ωk ց{a },u ∈S p (Ωk )and Ωkψ(Du )=ǫn k Ωψ(Du )for all ψ∈C p (M ).3.3.L p -maximal solutions.We now discuss another selection principle based on the L p -norm of u −ξx p .We say a solution u ∈S p (Ω)is L p -maximal provided that w −ξx L p (Ω)≥ v −ξx L p (Ω)for all v ∈[u ].If ξ∈K then the trivial solution ξx is L p -maximal since it is the only solution in [ξx ].In general,for a nontrivial solution u ,since [u ]is an infinite set,the existence of an L p -maximal solution in [u ]is not guaranteed.Let Φ(v )= v −ξx L p (Ω)and consider a Φ-maximizing sequence {u j }in [u ]:(3.2)lim j →∞Φ(u j )=ˆm ≡sup {Φ(v ) v ∈[u ]}.Since Du j −ξ p = Du −ξ p <∞is independent of j ,it follows that u j converges weakly (or weakly *if p =∞)to a map ¯u in W 1,p (Ω;R m )as j →∞and ¯u |∂Ω=ξx .From the Sobolev embedding theorem,u j →¯u in L p (Ω)and hence Φ(¯u )=ˆm.However,¯u may not be a solution.10BAISHENG YANFrom the weak lower semicontinuity of the norm,we have D¯u−ξ p≤ Du−ξ p.The following gives a sufficient condition for the weak limit¯u to be an L p-maximal solution.Proposition3.6.Let1<p<∞.Then the limit map¯u above belongs to[u] if and only if D¯u−ξ p= Du−ξ p.In this case,¯u is also an L p-maximal solution.Proof.If¯u∈[u],then D¯u−ξ p= Du−ξ p follows easily from Lemma 2.2.To prove the converse,suppose D¯u−ξ p= Du−ξ p.Since u j∈[u], we have Du j−ξ p= Du−ξ p= D¯u−ξ p for all j and hence Du j→D¯u strongly in L p(Ω),which impliesΩψ(D¯u(x))dx=lim j→∞ Ωψ(Du j(x))dx= Ωψ(Du(x))dxfor allψ∈C p(M).Using this identity withψ(η)=d K(η),the distance function to K,we obtain D¯u(x)∈K for a.e.x∈Ω.Since¯u∈W1,p(Ω;R m) and¯u|∂Ω=ξx,it follows that¯u∈S p(Ω)and¯u∼u,and hence¯u∈[u]. Moreover,by definition,¯u is also an L p-maximal solution.Remark.If it happens that[u]∈S p(Ω)satisfiesΨ([u])=min Sp(Ω)Ψ,thenthe result above shows that any limit map¯u obtained as above is either an L p-maximal solution in[u]or satisfies D¯u−ξ p< Dv−ξ p for all v∈S p(Ω).We now study the structure of the L p-maximal solutions.Lemma3.7.Let u∈S p(Ω)be L p-maximal andΩa,ǫ⊂⊂Ω.If u∈S p(Ωa,ǫ) and Ωa,ǫψ(Du)=ǫn Ωψ(Du)for allψ∈C p(M),then u−ξx L p(Ωa,ǫ)≤ǫ1+n p u−ξx L p(Ω).Proof.Define v(x)=ǫ−1(u(a+ǫx)−ξa)for x∈Ω.Then it is easy to seethat v∼u and u−ξx L p(Ωa,ǫ)=ǫ1+n p v−ξx L p(Ω).Hence the resultfollows from the L p-maximality of u. Combining this lemma with Theorem3.5,we have the following. Theorem3.8.Let u∈S p(Ω)be L p-maximal.Then,either (i)for someΩa,ǫ⊆Ω,u∈S p(Ωa,ǫ)is coarse onΩa,ǫ, Ωa,ǫψ(Du)=ǫn Ωψ(Du)for allψ∈C p(M)and u−ξx L p(Ωa,ǫ)≤ǫ1+n p u−ξx L p(Ω), or(ii)there existΩk=Ωak,ǫk⊂⊂Ωsuch thatΩkց{a}, Ωkψ(Du)=ǫn k Ωψ(Du)for allψ∈C p(M)and u−ξx L p(Ωk)≤ǫ1+n p k u−ξx L p(Ω).ON SELECTION OF SOLUTIONS 113.4.Directionally maximal solutions.In the following,we consider the special case when p =∞.In this case,a solution u ∈S ∞(Ω)can be viewed as a Lipschitz continuous map on ¯Ω.For any given Lipschitz map f :¯Ω→R m ,a unit vector h ∈R m is called a maximal direction of f on ¯Ωprovided f ∞=h ·f (¯x )for some ¯x ∈¯Ω.If f =0,then there exists at least one ¯x ∈¯Ωsuch that f ∞=|f (¯x )|>0,and hence the vector h =f (¯x )/|f (¯x )|is a maximal direction of f.Definition 3.2.Let u ∈S ∞(Ω),h ∈S m −1and u h (x )=h ·(u (x )−ξx ).We say u is h -directionally maximal provided that u h ∞≥ v h ∞for all v ∈[u ].Proposition 3.9.If u ∈S ∞(Ω)is L ∞-maximal and h ∈S m −1is a maximal direction then u is h -directionally maximal.Moreover,u ∈S ∞(Ω)is L ∞-maximal if it is h -directionally maximal for every h ∈S m −1.Proof.If u ∈S ∞(Ω)is L ∞-maximal and h is a maximal direction of u −ξx ,then(3.3) u h ∞= u −ξx ∞≥ v −ξx ∞≥ v h ′ ∞for any v ∈[u ]and h ′∈S m −1.Therefore,by definition,u is h -directionally maximal.On the other hand,if u h ∞≥ v h ∞for all h ∈S m −1and v ∈[u ],choosing h to be a maximal direction of v −ξx,we haveu −ξx ∞≥ u h ∞≥ v h ∞= v −ξx ∞,and hence u is L ∞-maximal.The proof is completed.4.Partial viscosity solutionsIn this section,we assume K ⊂M is a compact set and study the Lipschitz solutions u ∈S ∞(Ω)of problem (2.1).For any unit vector h ∈R m ,the function ϕ(x )=h ·u (x )is a Lipschitz solution of the problem(4.1)Dϕ(x )∈Γ a.e.x ∈Ω,ϕ|∂Ω=(h t ξ)x,where Γ=K h ={h t η|η∈K }is a subset of M 1×n ∼=R n .4.1.Partial viscosity solutions.We first review the definition of viscosity solutions introduced by Crandall and Lions [5](see also [4,8])for a special class of Hamilton-Jacobi equations relevant to the problem (4.1)above.Definition 4.1.Let H :R n →R and φ∈C (¯Ω)be given.Then,(a )φis called a viscosity super-solution of H (Dφ)=0if,for each w ∈C ∞(Ω)and for each ¯x ∈Ωat which φ−w has a local minimum,we have H (Dw (¯x ))≥0;12BAISHENG YAN(b)φis called a viscosity sub-solution of H(Dφ)=0if,for each w∈C∞(Ω)and for each¯x∈Ωat whichφ−w has a local maximum,we have H(Dw(¯x))≤0;(c)φis called a viscosity solution of H(Dφ)=0ifφis both viscosity super-solution and viscosity sub-solution of H(Dφ)=0.Remark.A viscosity solutionφto the problemH(Dφ(x))=0,φ|∂Ω=g(g given)can be studied as a certain limit of the solutionsφǫof the following regular-izing problem asǫ→0+(4.2)−ǫ∆φǫ+H(Dφǫ)=0,φǫ|∂Ω=g.The problem(4.2)makes no sense for the vector valued functionsφ:Ω→R m when m≥2.be the distance function to K h.We can write(4.1)asLet d Kh(Dϕ(x))=0 a.e.x∈Ω,ϕ|∂Ω=(h tξ)x.(4.3)d Kh,we may use other Of course,instead of using the distance function d KhHamiltonians to write the equation(4.1).For instance,if f:R n→R is any continuous function such that the zero set f−1(0)=K h then the equation Dϕ(x)∈K h can be written as f(Dϕ(x))=0.The class of Lipschitz solutions will not be affected by the choice of different Hamiltonians f. However,a different Hamiltonian f will give a different class of viscosity solutions to the problem(4.1).Definition4.2.We say u∈S∞(Ω)is a partial viscosity solution in direction h if the functionϕ(x)=h·u(x)is a viscosity solution of(4.3).Lemma 4.1.A Lipschitz continuous functionϕ:¯Ω→R withϕ|∂Ω= (h tξ)x is a viscosity solution of(4.3)if and only if D+ϕ(x)⊆K h for all x∈Ω,where(4.4)D+ϕ(x)≡ p∈R n lim sup y→x,y∈Ωϕ(y)−ϕ(x)−p·(y−x)≤0 .|y−x|≥0,any Lipschitz functionϕon¯Ωwithϕ|∂Ω=(h tξ)x Proof.Since d Khis automatically a viscosity super-solution of(4.3).Therefore,any such functionϕis a viscosity solution if and only if it is a viscosity sub-solution; the latter condition is equivalent to D+ϕ(x)⊆K h for all x∈Ω(see[4, 8]). Proposition4.2.Let u∈S∞(Ω)be a partial viscosity solution in direction h.Then either h tξ∈K h orϕ(x)=h·u(x)<(h tξ)x for all x∈Ω.ON SELECTION OF SOLUTIONS13 Proof.Let u h(x)=ϕ(x)−(h tξ)x and consider max¯Ωu h=ˆm.Then either (i)there exists a¯x∈Ωsuch that u h(¯x)=ˆm,or(ii)ˆm>u h(x)for all x∈Ω. In case(i),we have u h(y)≤u h(¯x)for all y∈¯Ωand henceϕ(y)−ϕ(¯x)−h tξ(y−¯x)≤0.This implies h tξ∈D+ϕ(¯x)and thus by the lemma above h tξ∈K h.In case(ii),we haveˆm=0,u h(x)<0and henceϕ(x)<(h tξ)x for all x∈Ω.The proof is completed.4.2.Geometric restrictions.We follow the paper[3]to study the rela-tionships between the boundary values and the domainΩfor a Lipschitz partial viscosity solution of problem(2.1).First of all,we need some defini-tions[1].Given a locally compact set E⊂R n and a point¯x∈E,a vectorθ∈R n is called a generalized tangent to E⊂R n at¯x provided that there exist sequences h k→0+and x k→¯x,x k∈E such that(x k−¯x)/h k→θas k→∞.The set of generalized normals of E at¯x,denoted by N E(¯x),is defined to be the set ofν∈R n such thatν·θ≤0for all generalized tangentsθof E at¯x.Obviously,N E(¯x)is a cone and may only consist of the single element0.The following theorem shows that the existence of Lipschitz partial vis-cosity solutions of(2.1)depends heavily on the set K,the boundary dataξ, h and the domainΩ.Theorem 4.3.If u∈S∞(Ω)is a Lipschitz partial viscosity solution in direction h,then for any x∈∂Ωand anyνx∈N R n\Ω(x)\{0},there exists a numberλ≥0such that h tξ+λνx∈K h.Proof.The result has been proved in[3]under the condition that h tξ∈int(conv(K h))(see Theorem3.4in[3]).However,in their proof,this condi-tion is not needed.Therefore,the theorem follows from the result of that paper.4.3.M¨u ller-ˇSver´a k’s solutions for the two-well problem.In this sub-section,we show that the Lipschitz solution constructed in M¨u ller and ˇSver´a k[9]for the two dimensional two-well problem([2,11])cannot bea partial viscosity solution in certain directions.In the following,let K=SO(2)∪SO(2)H be a two-well set,where SO(2) is the set of rotations and H=diag(λ,µ)with0<λ<λ−1<µ.In this case,the two-well K has rank-one connections;that is,for any A∈K there exist exactly two matrices B∈K such that rank(A−B)=1(see[2,11]). As in[9,11],it is convenient to identify the space M2×2with R2×R2using。
