数学建模习题-人口问题
数学建模实例人口预报问题

数学建模实例:人口预报问题1.问题人口问题是当前世界上人们最关心的问题之一.认识人口数量的变化规律,作出较准确的预报,是有效控制人口增长的前提.下面介绍两个最基本的人口模型,并利用表1给出的近两百年的美国人口统计数据,对模型做出检验,最后用它预报2000年、2010年美国人口.表1 美国人口统计数据2.指数增长模型(马尔萨斯人口模型)此模型由英国人口学家马尔萨斯(Malthus1766~1834)于1798年提出. [1] 假设:人口增长率r 是常数(或单位时间内人口的增长量与当时的人口成正比).[2] 建立模型: 记时刻t=0时人口数为x 0, 时刻t 的人口为()t x ,由于量大,()t x 可视为连续、可微函数.t 到t t ∆+时间内人口的增量为:()()()t rx tt x t t x =∆-∆+于是()t x 满足微分方程:()⎪⎩⎪⎨⎧==00x x rx d t d x(1)[3] 模型求解: 解微分方程(1)得()rt e x t x 0= (2)表明:∞→t 时,()∞→t x (r>0).[4] 模型的参数估计:要用模型的结果(2)来预报人口,必须对其中的参数r 进行估计,这可以用表1的数据通过拟合得到.拟合的具体方法见本书第16章或第18章.通过表中1790-1980的数据拟合得:r=0.307. [5] 模型检验:将x 0=3.9,r=0.307 代入公式(2),求出用指数增长模型预测的1810-1920的人口数,见表2.表2 美国实际人口与按指数增长模型计算的人口比较从表2可看出,1810-1870间的预测人口数与实际人口数吻合较好,但1880年以后的误差越来越大.分析原因,该模型的结果说明人口将以指数规律无限增长.而事实上,随着人口的增加,自然资源、环境条件等因素对人口增长的限制作用越来越显著.如果当人口较少时人口的自然增长率可以看作常数的话,那么当人口增加到一定数量以后,这个增长率就要随着人口增加而减少.于是应该对指数增长模型关于人口净增长率是常数的假设进行修改.下面的模型是在修改的模型中著名的一个.3. 阻滞增长模型(Logistic 模型)[1]假设:(a )人口增长率r 为人口()t x 的函数()x r (减函数),最简单假定()0, ,>-=s r sx r x r (线性函数),r 叫做固有增长率.(b )自然资源和环境条件年容纳的最大人口容量m x . [2]建立模型: 当mx x =时,增长率应为0,即()m x r =0,于是mx rs =,代入()sx r x r -=得:()⎪⎪⎭⎫⎝⎛-=m x x r x r 1 (3) 将(3)式代入(1)得:模型为: ()⎪⎩⎪⎨⎧=⎪⎪⎭⎫ ⎝⎛-=001xx x x x r dt dx m (4)[3] 模型的求解: 解方程组(4)得()rt m me x x x t x -⎪⎪⎭⎫ ⎝⎛-+=110 (5)根据方程(4)作出x dtdx~ 曲线图,见图1-1,由该图可看出人口增长率随人口数的变化规律.根据结果(5)作出x~t 曲线,见图1-2,由该图可看出人口数随时间的变化规律.[4] 模型的参数估计:利用表1中1790-1980的数据对r 和x m 拟合得:r=0.2072, x m =464. [5] 模型检验:将r=0.2072, x m =464代入公式(5),求出用指数增长模型预测的1800-1990的人口数,见表3第3、4列.也可将方程(4)离散化,得)())(1()()()1(t x x t x r t x x t x t x m-+=∆+=+ t=0,1,2,… (6) 用公式(6)预测1800-1990的人口数,结果见表3第5、6列.表3 美国实际人口与按阻滞增长模型计算的人口比较图1-2 x~t 曲线现应用该模型预测人口.用表1中1790-1990年的全部数据重新估计参数,可得r=0.2083, x m=457.6. 用公式(6)作预测得:x(2000)=275; x(2010)=297.9.也可用公式(5)进行预测.。
数学建模习题中国人口增长预测

中国人口增长预测本题是一个人口发展预测的问题。
人口发展与一般种群增长一样,是由自然增长率决定的。
然而,人类个体是一种社会的个体,所以人口发展有自己的特点。
想到人口的迁移,性别比例,城镇化等。
同时,人口发展受政策的影响,例如计划生育;也要受到人们意识的影响,像生育意识等。
但是从社会层面上看,生育意识在整个社会上体现为妇女的生育模式,进而可以特别地去考虑。
思考方法:首先,数据的处理。
在经过EXCEL分析和验证后,适当修正题中的个别有误数据后,利用有效数据进行建模求解,在此过程中,我们提取出死亡率、生育率等感念,且把人的一生按年龄分为青年期、衰老期等阶段。
这是求解人口增长模型的必要过程和方法。
其次,模型建立。
和一般的预测模型一样,本模型也是个预测模型,所以考虑到用题目所给的五年的信息,来推测今后几十年的人口的总数和结构情况。
对此,我们选用差分方程模型和数据参数拟合等方法。
同时,将死亡率与出生率分开分别计算和拟合,通过五年的实际数据拟合出相应函数的参数,再利用此函数进行评估和预测。
最后,利用已有信息以及上述所求出的对应函数和方程,对中短期与长期进行估计和预测,进而得出人口结构、人口比例、人口数量等一系列的相关数据。
以下是解答过程:1.数据说明:x:表示最大的年龄;mi=1,2,3,4,5,6 其中1表示市男性,2表示市女性,3表示镇男性,4表示镇女性,5表示乡男性,6表示乡女性;A :表示婴儿性别比例矩阵;* :表示点乘;P(x,t):表示t时刻年龄为x的人口数量;ibir(x,t):表示t时刻年龄为x的出生率;i)(,i dea x t:表示t时刻年龄为x的死亡率;)(i t k:表示t时刻婴儿的死亡率;tra(x,t):表示t时刻年龄为x的人口迁出率;i2.假设条件1. 假设国内社会环境稳定,无异常大量死亡或出生情况发生,人口比例,人口总数不会出现突变状况; 2. 假设只存在乡向城镇迁出,不存在其他迁移方式,且不同年龄段迁移率相同; 3. 假设不考虑国家之间的迁入与迁出,把中国内部看为一个封闭的模型; 4. 对于90岁以上的人都按照90岁处理; 5. 假设只存在乡向城镇迁出,不存在其他迁移方式,且不同年龄段迁出率相同,按照0.6%均匀增长。
6.2 人口增长模型 数学建模

一、粮食生产 19501950-1984 世界粮食产量的增幅超过人口增 长速度。但84年以后粮食产量增幅一直落后 长速度。但84年以后粮食产量增幅一直落后 于人口增长速度。 原因:缺少新垦土、灌溉量减少、土地生 产率的提高越来越难。
二、水资源的匮乏 国际水资源管理研究预测,到2050年, 国际水资源管理研究预测,到2050年, 约有10亿人口将面临缺水的状况。 约有10亿人口将面临缺水的状况。 三、海洋捕捞
2005年11月 世界人口状况报告》 2005年11月《世界人口状况报告》显示目 前世界总人口为64.647亿,我国占了约20% 前世界总人口为64.647亿,我国占了约20% 2050年世界人口将达77-112亿,若采取94 2050年世界人口将达77-112亿,若采取94 亿的预测值。会带来什么影响?
例题2齐次微分方程3一阶线性非线性微分方程其他模型malthusmalthus11模型假设模型假设33美国的实际人口数据美国的实际人口数据22模型建立模型建立33模型检验分析模型检验分析1人口预测人口预测22景区游客人数增长景区游客人数增长3城市人口增长城市人口增长
第六章鱼类减少
饲料
渔业养殖
四、森林覆盖率、生物多样性、能源危机等等
2、复习
1、微分方程:含有导数 或微分的方程 2、微分方程的类型:
(1)可分离变量的微分方程,形如 dy = f ( x) ⋅ g ( y ) dx
(2)齐次微分方程 (3)一阶线性、非线性微分方程 其他
例题 模型
2、模型建立
3、模型分析检验
美国的实际人口数据
二、阻滞增长模型
1、 模型假设 设人口增长率r是人口数N的线性递减函数, 记为r ( N ), K 是自然资源和环境条件的最大人 口容量,r 表示人口很少时的增长率(固有增 长率)
数学建模-人口统计模型

j
j
j 1
j
j
j
h(T ) P(0) h(T t1 )r (t1 )t h(T t2 )r (t2 )t
+ h(T tn )r (tn )t h(T ) P(0) h(T ti )r (ti )t.
i 1
n
当 n 无限增大时, P(T ) h(T ) P(0)
0 10
107 e1 / 4 e (10 t ) / 40 (5 104 105 t )dt
0
10 10 10 7 e 1 / 4 e 1 / 4 5 10 4 e t / 40 dt 10 5 tet / 40 dt 0 0
0
说明
4 人口统计模型(I)中两个人口密度 P(r ) 2 r 20 和 P(r ) 1.2e-0.2r 有一个共同特点 P' (r ) 0 ,即随着r
P(r ) 减少,这是符合实际的.另外,需要指 的增大, 出的是,当人口密度 P(r 选取不同的模式时,估算 ) 出的人口数可能会相差很大,因此,选择适当的人 口密度模式对于准确地估算人口数至关重要.
T
0
h(T t )r (t )dt
( 1)
解题过程
第五步: 4 5 t / 40 将 r (t ) 5 10 10 t, h(t ) e 及 T 10 , P(0) 107 代入(1)式得
P(10) h(10) P(0) h(10 t )r (t )dt
P(r ) 2πr r
j 1 j j
n
所以人口数
N P(r )2πrdr
0
2
.
数学建模-人口增长模型
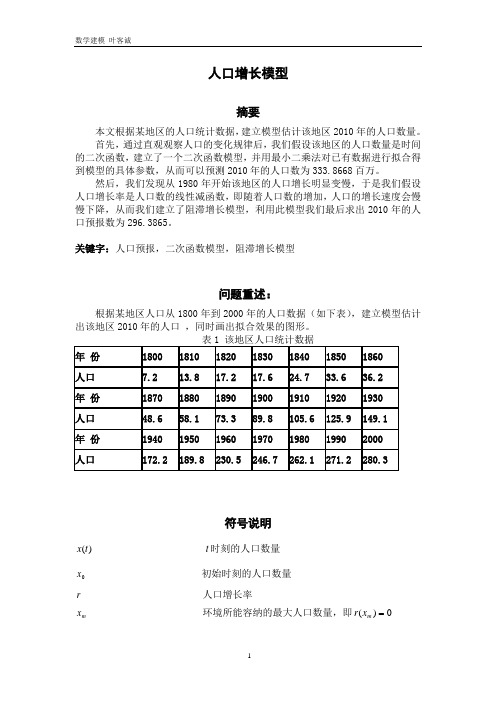
人口增长模型摘要本文根据某地区的人口统计数据,建立模型估计该地区2010年的人口数量。
首先,通过直观观察人口的变化规律后,我们假设该地区的人口数量是时间的二次函数,建立了一个二次函数模型,并用最小二乘法对已有数据进行拟合得到模型的具体参数,从而可以预测2010年的人口数为333.8668百万。
然后,我们发现从1980年开始该地区的人口增长明显变慢,于是我们假设人口增长率是人口数的线性减函数,即随着人口数的增加,人口的增长速度会慢慢下降,从而我们建立了阻滞增长模型,利用此模型我们最后求出2010年的人口预报数为296.3865。
关键字:人口预报,二次函数模型,阻滞增长模型问题重述:根据某地区人口从1800年到2000年的人口数据(如下表),建立模型估计出该地区2010年的人口 ,同时画出拟合效果的图形。
符号说明)(t x t 时刻的人口数量 0x 初始时刻的人口数量 r 人口增长率m x 环境所能容纳的最大人口数量,即0)( m x r问题分析首先,我们运用Matlab软件[1]编程(见附件1),绘制出1800年到2000年的人口数据图,如图1。
18001820184018601880190019201940196019802000图1 1800年到2000年的人口数据图从图1我们可以看出1800年到2000年的人口数是呈现增长的趋势的,而且类似二次函数增长。
所以我们可以建立了一个二次函数模型,并用最小二乘法对已有数据进行拟合得到模型的具体参数。
于是我们假设人口增长率是人口数的线性减函数,即随着人口数的增加,人口的增长速度会慢慢下降,从而我们可以建立一个阻滞增长模型。
模型建立模型一:二次函数模型我们假设该地区t时刻的人口数量的人口数量)(tx是时间t的二次函数,即:2()=++x t at bt c我们可以根据最小二乘法,利用已有数据拟合得到具体参数。
即,要求a、b和c,使得以下函数达到最小值:221(,,)()ni i i i E a b c at bt c x ==++-∑其中i x 是i t 时刻该地区的人口数,即有:2222)3.28020002000...)2.718001800(),,(-+⋅+⋅++-+⋅+⋅=c b a c b a c b a E令0,0,0E E E a b c∂∂∂===∂∂∂,可以得到三个关于a 、b 和c 的一次方程,从而可解得a 、b 和c 。
数学建模论文(人口预报问题)

数学建模论文人口预报问题实验组员:肖育鑫, 蒋忠炳,陈昶实验组长:陈昶实验指导:许志军老师2010年4月5日一、摘要 (3)二、问题重述 (3)三、模型假设 (4)四、分析与建立模型 (5)五、模型求解 (5)六、模型检验 (7)七、模型分析讨论及推广 (10)八、参考文献 (10)九、附录 (10)人口预报问题一、摘要人口是人类最为关心的问题之一,认识人口数量的变化规律,做出较为准确的预测,在现实社会有很大的作用,是帮住有效地控制人口增长的前提。
对于人口问题,我们可通过建立指数增长模型(马尔萨斯人口模型)和阻滞增长模型(logistic模型)分别对人口进行预算,据经验,建立logistic模型求解预测更加精确。
建立中国人口增长的数学模型,并由此对中国人口增长的中短期和长期趋势做出预测对未来的一段时期的人口结构作出总结性的结论,同时对两个模型作出一个总体的评价。
关键字指数增长阻滞增长模型人口模型二、问题重述表1-1 江苏省人口统计数据上表给出了江苏省1981年到2001年共21的人口数据,以1981 作为起始年,建立:(1)建立江苏省人口的指数增长模型(马尔萨斯人口模型),并 利用该模型进行人口预测,与上表的实际人口数据进行比较,并 计算其误差大小。
(2)建立江苏省人口的阻增长模型(logistic 模型),并利用 该模型进行人口预测,与上表的实际人口数据进行比较,并计算 其误差大小。
三、模型假设(1)对于问题一:①假设人口增长率r 是常数(或单位时间内人口增长量与当时人口呈正比);②假设人口平稳增长,无大型自然灾害、战争等因素影响; ③假设时刻t 的人口函数是连续可导的;④其中我们假设t 表示年份,r 表示人口增长率,x 表示人口数量。
(2)对于问题二:①假设人口增长率r 为人口x(t)的函数r(x)(减函数),最简单地可假设(),,0r x r sx r s =->(线性函数),r 叫做固有增长率; ②自然资源和环境条件年容纳的最大人口容量为m x ; ③假设在时刻t ,人口增长的速率与当时人口数成正比;④其中我们假设t 表示年份,r 表示人口增产率,x 表示人口数量。
数学建模模版之人口增长问题

“公平”分配方法
人数 席位 A方 B方 p1 p2 n1 n2
衡量公平分配的数量指标 当p1/n1= p2/n2 时,分配公平
若 p1/n1> p2/n2 ,对 A 不公平
p1/n1– p2/n2 ~ 对A的绝对不公平度
p1=150, n1=10, p1/n1=15 p2=100, n2=10, p2/n2=10 p1/n1– p2/n2=5 虽二者的绝对 不公平度相同
存贮模型
配件厂为装配线生产若干种产品,轮换产品时因更换设 备要付生产准备费,产量大于需求时要付贮存费。该厂 生产能力非常大,即所需数量可在很短时间内产出。 已知某产品日需求量100件,生产准备费5000元,贮存费 每日每件1元。试安排该产品的生产计划,即多少天生产 一次(生产周期),每次产量多少,使总费用最小。
一种确定参数的办法是测量或调查,请设计测量方法。
参数估计ቤተ መጻሕፍቲ ባይዱ
另一种确定参数的方法——测试分析
2
将模型改记作 t an bn ,
只需估计 a,b
理论上,已知t=184, n=6061, 再有一组(t, n)数据即可
实际上,由于测试有误差,最好用足够多的数据作拟合
现有一批测试数据: 用最小二乘法可得
存贮模型
生猪的出售时机 森林救火
3.4
最优价格
3.5 血管分支
3.6 消费者均衡
3.7 冰山运输
静 态 优 化 模 型
• 现实世界中普遍存在着优化问题
• 静态优化问题指最优解是数(不是函数) • 建立静态优化模型的关键之一是 根据建模目的确定恰当的目标函数 • 求解静态优化模型一般用微分法
问题
3.1
x(t ) x0 e
数学建模习题-人口问题

数学建模报告——浙江省人口增长预测模型的建立与分析问题综述:为了加快中国的经济建设进程,全面落实科学的发展观,按照构建社会主义和谐社会的要求,实现人口与经济社会资源环境的协调和可持续发展。
我们确定人口发展战略,必须既着眼于人口本身的问题,又处理好人口与经济社会资源环境之间的相互关系,构建社会主义和谐社会,统筹解决人口数量、素质、结构、分布等问题。
人口增长预测的研究是国家(地区)制定未来人口发展目标和生育政策等有关人口政策的基础,对于经济计划的制定和社会战略目标的决策具有重要参考价值。
一般的人口预测统计学模型,其预测精度难以保证。
所以选择一个好的人口预测模型,首先应符合人口基本理论和数学建模的要求,这是选择模型的关键,其次要保证模型数据可得一致性与可比性,在数据预测检验阶段应充分拟合原始数据。
浙江省是人口大省、地域小省(资源小省),虽然从“资源小省、经济小省(国家投入小省)、工业小省”迅速发展成为“经济大省”,但人口问题始终是制约浙江省发展的关键因素之一。
根据已有数据,运用数学建模的方法,对浙江省做出分析和预测是一个重要问题。
近年来浙江省的人口发展出现了一些新的特点,例如,老龄化进程加速、出生人口性别比持续升高,以及乡村人口城镇化等因素,这些都影响着浙江省人口的增长。
从浙江省的实际情况和人口增长的特点出发, 建立浙江省人口增长的数学模型,并由此对浙江省人口增长的中短期和长期趋势做出预测。
解:假设:不考虑特别年份的特殊性,例如特大自然灾害等对人口增长的影响;在研究 Logistic生物模型,假设其研究对象p(t) {p(t)表示在t时刻种群的大小}是连续的;不考虑男女出生比例对人口增长的影响。
模型建立:1.短期人口预测影响人口增长的因素有很多,有经济、政策、科学技术、自然环境等,这些众多的因素之间的关系难以准确描述出来, 它们对人口增长的作用不是用几个指标就能精确计算出来的。
人口系统具有明显的灰色性, 是一个部分信息已知而部分信息未知的系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模报告
——浙江省人口增长预测模型的建立与分析
问题综述:
为了加快中国的经济建设进程,全面落实科学的发展观,按照构建社会主义和谐社会的要求,实现人口与经济社会资源环境的协调和可持续发展。
我们确定人口发展战略,必须既着眼于人口本身的问题,又处理好人口与经济社会资源环境之间的相互关系,构建社会主义和谐社会,统筹解决人口数量、素质、结构、分布等问题。
人口增长预测的研究是国家(地区)制定未来人口发展目标和生育政策等有
关人口政策的基础,对于经济计划的制定和社会战略目标的决策具有重要参考价值。
一般的人口预测统计学模型,其预测精度难以保证。
所以选择一个好的人口预测模型,首先应符合人口基本理论和数学建模的要求,这是选择模型的关键,其次要保证模型数据可得一致性与可比性,在数据预测检验阶段应充分拟合原始数据。
浙江省是人口大省、地域小省(资源小省),虽然从“资源小省、经济小省(国家投入小省)、工业小省”迅速发展成为“经济大省”,但人口问题始终是制约浙江省发展的关键因素之一。
根据已有数据,运用数学建模的方法,对浙江省做出分析和预测是一个重要问题。
近年来浙江省的人口发展出现了一些新的特点,例如,老龄化进程加速、出生人口性别比持续升高,以及乡村人口城镇化等因素,这些都影响着浙江省人口的增长。
从浙江省的实际情况和人口增长的特点出发, 建立浙江省人口增长的数学模型,并由此对浙江省人口增长的中短期和长期趋势做出预测。
解:假设:不考虑特别年份的特殊性,例如特大自然灾害等对人口增长的影响;
在研究 Logistic生物模型,假设其研究对象p(t) {p(t)表示在t时刻种群的大小}是连续的;不考虑男女出生比例对人口增长的影响。
模型建立:1.短期人口预测
影响人口增长的因素有很多,有经济、政策、科学技术、自然环境等,这些众多的因素之间的关系难以准确描述出来, 它们对人口增长的作用不是用几个指标就能精确计算出来的。
人口系统具有明显的灰色性, 是一个部分信息已知而部分信息未知的系统。
灰色系统理论把这样受众多因素影响, 而又无法确定其复杂关系的量,称为灰色量。
灰色系统所要考察和研究的是对信息不完备的喜用,通过已知信息来研究和预测未知领域从而达到了解整个系统的目的。
本题采用了灰色系统预测方法进行短期人口预测
灰色系统模型建模是利用离散的时间序列数据建立近似连续的微分模型。
灰色模型预测的方法:
1.给定原始数据为
)()2(),1()0()0()0(n x x x ⋅⋅⋅⋅⋅⋅ (5) 2.将不同年份)0(x 累加得到新的数列)1(x 。
即
n i m x x
i
m ⋅⋅⋅⋅⋅⋅==∑=3,2,1,)(1
)0(1()
(6)
3.构造数据矩阵B 和)(n Y
)]2()1([21
)1()1(x x +- 1
B= )]3()2([2
1
)1()1(x x +- 1
(7)
……
)]()1([2
1
)1()1(n x n x +-- 1
T
n n x x Y )](3x 2[)0((0)0(⋅⋅⋅=),(),() (8) 根据)1(x 可以建立白化形式微分方程,解得GM (1,1)模型。
4.求解a 和u:
设a 和u 构成的待估参数向量
A=⎥⎦
⎤
⎢⎣⎡u a ,根据最小二乘法有:
A=n T T Y B B B ⋅⋅-1)( 。
(9) 5.GM (1,1)模型:
a
u e a u x k x ak +⋅-=+-∧]1[)1()
0()
1()(
(10) 6.求还原函数
ak a e a
u
x e k x --∧⋅--=+])1()[11()0()
0(() (11)
年份
1978
1979 1980 1981 1982 1983 1984 1985 1986 1987
设)0(x =[3750.96,3792.33,3826.58,3871.51, 3924.32, 3963.1, 3993.09, 4029.56, 4070.07, 4121.19, 4169.85, 4208.88, 4234.91,4261.37, 4285.91, 4313.3, 4341.2, 4369.63, 4400.09, 4422.28]
———浙江省1978至1997年的连续20 年的总人口数如上表1所示:
)1(x =[3750.96,7543.29,11369.87,15241.38,19165.7,23128.8,27121.89,31151
.45,35221.52,39342.71,43512.56,47721.44,51956.35,56217.72,60503.63,64816.93,69158.13,73527.76,77927.85,82350.13] A=[a;u]=[-0.0086;3777.265]
k)*exp(0.0086*0.0086))377.7265/(+(375.096*6))exp(-0.008-(11()
0(=+∧)k x 下面是由灰色模型预测的2007年到2020年的浙江省人口数
2.长期人口预测
用Logistic 模型对浙江省人口进行分析预测。
人口总数 3750.96
3792.33 3826.58 3871.51 3924.32 3963.1 3993.09 4029.56 4070.07 4121.19
年份 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 人口总数
4169.85
4208.88 4234.91 4261.37 4285.91 4313.3 4341.2 4369.63 4400.09 4422.28 年份 预测人口(万) 2007 4867.63 2014 5169.66 2008 4909.67 2015 5214.31 2009 4952.08 2016 5259.35 2010 4994.85 2017 5304.77 2011 5037.99 2018 5350.59 2012 5081.5 2019 5396.81 2013 5125.39 2020 5443.42
由0001()at
ap p bp a bp e -=
+- 可得0111at
b b e p a p a -⎡⎤=+-⎢⎥⎣⎦
由1 p2=
1(1)at ap bp a bp e -+- 可得1121at
b b e p a p a -⎡⎤=+-⎢⎥⎣⎦
所以01111[]121at
e p p p p --=-
, 011
11ln 1112
p p a t p p -
=- , 0(/11/)1at at
a e p p
b e -=- 选择1978,1992,2006间距相等的三个年份p(1978)=3750.96 ,p(1992)=4285.91,p(2006)= 4629.43,计算可得 a =0.0467 b =0.00921 令p(t)=
00()002()a t t ap a b bp a bp e --=+- 得(0)
00
a t t bp e a bp --=
- 0001ln bp t t a a bp =--,0000()()
()0000
//()()11a t t a t t a t t ap a b a b
p t a bp bp a bp e e e bp ------===
-+-++
将有关数据代入可求得
1956
t =
a/b =5.0706 ∴p(t)=0.0467()5.0706
()1t t p t e --=+
附录
#include<iostream>//灰色系统模型预测2007-2020人口数
#include<cmath>
using namespace std;
void main()
{ int i;
double x[15],y[15];
double
z[11]={0,3792.33,3826.58,3871.51,3924.32,3963.1,3993.09,4029.56,4070. 07,4121.19,4169.85};
for(i=1;i<=14;i++)
{ cin>>x[i];
y[i]=(1-exp(-0.0086))*(375.096+377.7265/(0.0086))*exp(0.0086*(x[i]));
}
for(i=1;i<=14;i++)
{ cout<<y[i]*10<<endl;
}
}
#include<iostream>//Logistic模型预测每年人口数
#include<cmath>
using namespace std;
void main()
{ double x,a;
for(int i=0;i<100;i++)
{ cin>>x;
a=5.0706/((1+1/exp(0.0467*(x-1956)))*1.0);
cout<<a<<endl;
}
}。
