2009考研试题
2009年全国考研数学一真题及答案.doc
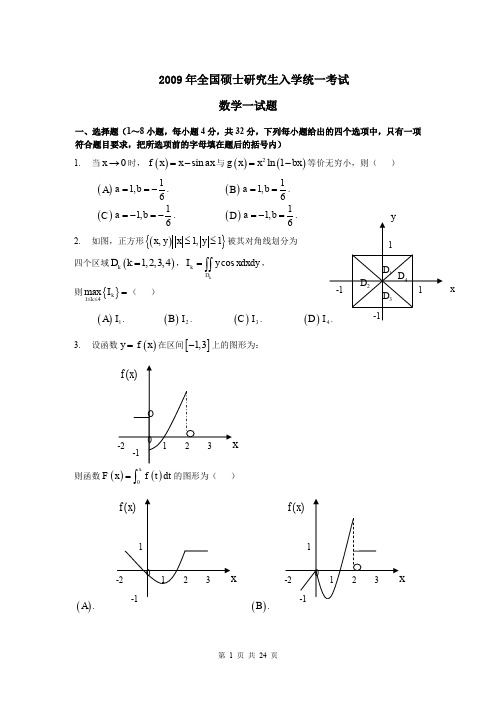
2009年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)1. 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.2. 如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=( )()A 1I .()B 2I . ()C 3I .()DI 3. 设函数()y f x =在区间[]1,3-上的图形为:则函数()()0x F x f t dt =⎰的图形为( )()A .()B .x()C .()D .4. 设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则( )()A 当1n n b ∞=∑收敛时,1n n n a b ∞=∑收敛.()B 当1n n b ∞=∑发散时,1n n n a b ∞=∑发散.()C 当1nn b∞=∑收敛时,221n nn a b∞=∑收敛.()D 当1nn b ∞=∑发散时,221n nn a b∞=∑发散.5. 设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基 122331,,αααααα+++的过渡矩阵为( )()A 101220033⎛⎫⎪⎪ ⎪⎝⎭. ()B 120023103⎛⎫⎪⎪ ⎪⎝⎭.()C 111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.()D 111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. 6. 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( )()A **32O B A O ⎛⎫ ⎪⎝⎭.()B **23OB A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫ ⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭.7. 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =( )()A 0.()B 0.3. ()C 0.7.()D 1.8. 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为( )()A 0.()B 1. ()C 2.()D 3.二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)9. 设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ 。
2009考研数二真题及解析

2009年全国硕士研究生入学统一考试数学二试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在答题纸指定位置上.(1) 函数()3sin x x f x xπ-=的可去间断点的个数为 ( )(A) 1.(B) 2. (C) 3.(D) 无穷多个.(2) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A) 11,6a b ==-. (B) 11,6a b ==. (C) 11,6a b =-=-. (D) 11,6a b =-=.(3) 设函数(),z f x y =的全微分为dz xdx ydy =+,则点()0,0 ( )(A) 不是(),f x y 的连续点.(B) 不是(),f x y 的极值点.(C) 是(),f x y 的极大值点. (D) 是(),f x y 的极小值点. (4) 设函数(),f x y 连续,则()()222411,,yxydx f x y dy dy f x y dx -+=⎰⎰⎰⎰( )(A) ()2411,xdx f x y dy -⎰⎰. (B) ()241,xxdx f x y dy -⎰⎰.(C)()2411,ydy f x y dx -⎰⎰. (D) ()221,ydy f x y dx ⎰⎰.(5) 若()f x ''不变号,且曲线()y f x =在点()1,1处的曲率圆为222x y +=,则函数()f x在区间()1,2内 ( ) (A) 有极值点,无零点. (B) 无极值点,有零点.(C) 有极值点,有零点. (D) 无极值点,无零点. (6) 设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为 ( )(A) (B)(C) (D)(7) 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为 ( ) (A) **32O B A O ⎛⎫⎪⎝⎭. (B) **23O B AO ⎛⎫⎪⎝⎭. (C) **32O A BO ⎛⎫⎪⎝⎭.(D) **23OA BO ⎛⎫⎪⎝⎭. (8) 设,A P 均为3阶矩阵,TP 为P 的转置矩阵,且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭.若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为 ( )(A) 210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B) 110120002⎛⎫⎪⎪ ⎪⎝⎭.(C) 200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D) 100020002⎛⎫⎪⎪ ⎪⎝⎭.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9) 曲线21022,ln(2)t u x e du y t t --⎧=⎪⎨⎪=-⎩⎰在点(0,0)处的切线方程为 .(10) 已知1k xe dx +∞-∞=⎰,则k = .(11) 1limsin x n e nxdx -→∞=⎰.(12) 设()y y x =是由方程1yxy e x +=+确定的隐函数,则22x d ydx== .(13) 函数2x y x =在区间(]01,上的最小值为 .(14) 设,αβ为3维列向量,T β为β的转置,若矩阵T αβ相似于200000000⎛⎫⎪⎪ ⎪⎝⎭,则T =βα_____________.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()[]401cos ln(1tan )limsin x x x x x→--+(16)(本题满分10 分)计算不定积分ln 1dx ⎛+ ⎝⎰ (0)x >. (17)(本题满分10分)设(),,z f x y x y xy =+-,其中f 具有二阶连续偏导数,求dz 与2z x y∂∂∂.(18)(本题满分10分)设非负函数()y y x = ()0x ≥满足微分方程20xy y '''-+=.当曲线()y y x = 过原点时,其与直线1x =及0y =围成的平面区域D 的面积为2,求D 绕y 轴旋转所得旋转体的体积.(19)(本题满分10分)计算二重积分()Dx y dxdy -⎰⎰,其中()()(){}22,112,D x y x y y x =-+-≤≥.(20)(本题满分12分)设()y y x =是区间(,)ππ-内过点(的光滑曲线,当0x π-<<时,曲线上任一点处的法线都过原点;当0x π≤<时,函数()y x 满足0y y x ''++=.求函数()y x 的表达式.(21)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(22)(本题满分11分)设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ; (Ⅱ)对(Ⅰ)中的任意向量23,ξξ,证明:123,,ξξξ线性无关. (23)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值.2009年全国硕士研究生入学统一考试数学二试题答案一、选择题:1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项是符合题目要求的.请将所选项前的字母填在答题纸指定位置上.(1)函数()3sin x x f x nx-=的可去间断点的个数为( )()A 1.()B 2. ()C 3.()D 无穷多个.【答案】C 【解析】()3sin x x f x xπ-=则当x 取任何整数时,()f x 均无意义故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±(2)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.【答案】A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C .另外201cos lim3x a axbx →--存在,蕴含了1cos 0a ax -→()0x →故 1.a =排除D .所以本题选A.(3)设函数(),z f x y =的全微分为dz xdx ydy =+,则点()0,0( )()A 不是(),f x y 的连续点. ()B 不是(),f x y 的极值点. ()C 是(),f x y 的极大值点. ()D 是(),f x y 的极小值点.【答案】 D【解析】因dz xdx ydy =+可得,z zx y x y∂∂==∂∂ 2222221,0,1z z z zA B C x x y y x y∂∂∂∂== === ==∂∂∂∂∂∂又在(0,0)处,0,0z zx y∂∂==∂∂ 210AC B -=>故(0,0)为函数(,)z f x y =的一个极小值点. (4)设函数(),f x y 连续,则()()222411,,yxydx f x y dy dy f x y dx -+=⎰⎰⎰⎰( )()A ()2411,xdx f x y dy -⎰⎰. ()B ()241,xxdx f x y dy -⎰⎰.()C ()2411,ydy f x y dx -⎰⎰.()D .()221,ydy f x y dx ⎰⎰【答案】C 【解析】222211(,)(,)xxdx f x y dy dy f x y dx +⎰⎰⎰⎰的积分区域为两部分:{}1(,)12,2D x y x x y =≤≤≤≤,{}2(,)12,4D x y y y x y =≤≤≤≤-将其写成一块{}(,)12,14D x y y x y =≤≤≤≤- 故二重积分可以表示为2411(,)ydy f x y dx -⎰⎰,故答案为C.(5)若()f x ''不变号,且曲线()y f x =在点()1,1上的曲率圆为222x y +=,则()f x 在区间()1,2内( )()A 有极值点,无零点. ()B 无极值点,有零点.()C 有极值点,有零点. ()D 无极值点,无零点.【答案】 B【解析】由题意可知,()f x 是一个凸函数,即''()0f x <,且在点(1,1)处的曲率322|''|2(1('))y y ρ==+,而'(1)1f =-,由此可得,''(1)2f =- 在[1,2] 上,'()'(1)10f x f ≤=-<,即()f x 单调减少,没有极值点. 对于(2)(1)'()1(1,2)f f f ζζ-=<- , ∈ , (拉格朗日中值定理)(2)0f ∴ <而 (1)10f =>由零点定理知,在[1,2] 上,()f x 有零点. 故应选(B ). (6)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为( )1 ()f x -2 0 2 3-1O()A .()B .()C .()D .【答案】D【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征:①[]0,1x ∈时,()0F x ≤,且单调递减. ②[]1,2x ∈时,()F x 单调递增. ③[]2,3x ∈时,()F x 为常函数.④[]1,0x ∈-时,()0F x ≤为线性函数,单调递增. ⑤由于F(x)为连续函数结合这些特点,可见正确选项为D .(7)设A ,B 均为2阶矩阵,**A B ,分别为A ,B 的伴随矩阵.若23A B ==,,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( ) ()A .**32O B A O ⎛⎫⎪⎝⎭()B .**23O B A O ⎛⎫⎪⎝⎭()C .**32O A BO ⎛⎫⎪⎝⎭()D .**23O A B O ⎛⎫⎪⎝⎭【答案】 B【解析】根据CC C E *=若111,C C C CC C*--*==分块矩阵00A B ⎛⎫⎪⎝⎭的行列式22012360A AB B ⨯=-=⨯=()即分块矩阵可逆 1111000066000100B BA A AB B BBAA A**---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫ ⎪=== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭10023613002B B AA ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭(8)设A P ,均为3阶矩阵,TP 为P 的转置矩阵,且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223P Q ααααααα==+(,,),(,,),则TQ AQ 为( ) ()A .210110002⎛⎫⎪⎪ ⎪⎝⎭()B .110120002⎛⎫⎪⎪ ⎪⎝⎭()C .200010002⎛⎫⎪⎪ ⎪⎝⎭()D .100020002⎛⎫⎪⎪ ⎪⎝⎭【答案】 A【解析】122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦,即:12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT T Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.(9)曲线2221-x=0ln(2)u t e du y t t -⎧⎪⎨⎪=-⎩⎰在(0,0)处的切线方程为 . 【答案】2y x =【解析】221222ln(2)22t dy t t t t dt t ==--⋅=--2(1)1(1)1t t dxe dt --==⋅-=- 所以 2dy dx= 所以 切线方程为2y x =.(10)已知+1k xe dx ∞=-∞⎰,则k = .【答案】2-【解析】1122lim bk xkx kxb e dx e dx e k +∞+∞-∞→+∞===⎰⎰因为极限存在所以0k <210k=-2k =-(11)1n lime sin x nxdx -→∞=⎰.【答案】0【解析】令sin sin cos x x xn I e nxdx e nx n e nxdx ---==-+⎰⎰2sin cos x x n e nx ne nx n I --=---所以2cos sin 1xn n nx nx I e C n -+=-++即11020cos sin lim sin lim()1xx n n n nx nx e nxdx e n --→∞→∞+=-+⎰ 122cos sin lim()110n n n n ne n n -→∞+=-+++= (12)设()y y x =是由方程xy 1ye x +=+确定的隐函数,则22x yx=∂=∂ .【答案】3-【解析】对方程xy 1y e x +=+两边关于x 求导有''1y y xy y e ++=,得'1yyy x e -=+ 对''1y y xy y e ++=再次求导可得''''''22()0y y y xy y e y e +++=,得''2''2()yyy y e y x e +=-+ (*)当0x =时,0y =,'(0)0101y e -==,代入(*)得 ''20''032(0)((0))(0)(21)3(0)y y e y e +=-=-+=-+(13)函数2x y x =在区间(]01,上的最小值为 . 【答案】2ee-【解析】因为()22ln 2x y x x '=+,令0y '=得驻点为1x e=. 又()22222ln 2xxy x x x x ''=++⋅,得21120e y e e -+⎛⎫''=> ⎪⎝⎭,故1x e=为2xy x =的极小值点,此时2e y e -=,又当10,x e ⎛⎫∈ ⎪⎝⎭时,()0y x '<;1,1x e ⎛⎤∈ ⎥⎝⎦时,()0y x '>,故y 在10,e ⎛⎫ ⎪⎝⎭上递减,在1,1e ⎛⎫ ⎪⎝⎭上递增.而()11y =,()()002022ln limlim 11lim 222ln 00lim lim 1x x x xx x xx xxx x x y x e e ee++→→+→++--+→→======,所以2xy x =在区间(]01,上的最小值为21ey e e -⎛⎫= ⎪⎝⎭.(14)设αβ,为3维列向量,T β为β的转置,若矩阵T αβ相似于200000000⎛⎫ ⎪⎪ ⎪⎝⎭,则T =βα .【答案】2【解析】因为T αβ相似于200000000⎛⎫⎪⎪ ⎪⎝⎭,根据相似矩阵有相同的特征值,得到T αβ得特征值是2,0,0而T βα是一个常数,是矩阵T αβ的对角元素之和,则T 2002βα=++= 三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()[]401cos ln(1tan )limsin x x x x x→--+.【解析】()[][]244001ln(1tan )1cos ln(1tan )2lim lim sin sin x x x x x x x x x x→→-+--+= 22201ln(1tan )lim 2sin sin x x x x x x→-+=201ln(1tan )1lim 2sin 4x x x x →-+== (16)(本题满分10 分)计算不定积分ln(1dx +⎰(0)x >. 【解析】t =得22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t +=+-+=---+⎰⎰⎰而22111112()11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以2ln(1)111ln(1ln 1412(1)1ln(1211ln(122t t dx C t t t x C x x C +++=+-+--+=++-+=+++⎰ (17)(本题满分10分)设(),,z f x y x y xy =+-,其中f 具有2阶连续偏导数,求dz 与2zx y∂∂∂.【解析】123123zf f yf x zf f xf y∂'''=++∂∂'''=-+∂1231232111213212223331323331122331323()()1(1)1(1)[1(1)]()()z z dz dx dy x yf f yf dx f f xf dyzf f f x f f f x f y f f f x x yf f f xyf x y f x y f ∂∂∴=+∂∂''''''=+++-+∂'''''''''''''''''''=⋅+⋅-+⋅+⋅+⋅-+⋅++⋅+⋅-+⋅∂∂'''''''''''=+-++++-(18)(本题满分10分)设非负函数()y y x = ()0x ≥满足微分方程20xy y '''-+=,当曲线()y y x = 过原点时,其与直线1x =及0y =围成平面区域D 的面积为2,求D 绕y 轴旋转所得旋转体体积. 【解析】解微分方程20xy y '''-+=得其通解212122,y C x C x C C =++其中,为任意常数 又因为()y y x =通过原点时与直线1x =及0y =围成平面区域的面积为2,于是可得10C =1112232220002()(2)()133C Cy x dx x C x dx x x ==+=+=+⎰⎰从而23C =于是,所求非负函数223(0)y x x x =+ ≥又由223y x x =+ 可得,在第一象限曲线()y f x =表示为11)3x =( 于是D 围绕y 轴旋转所得旋转体的体积为15V V π=-,其中55221005011)9(2393918V x dy dyy dyππππ==⋅=+-=⎰⎰⎰395117518186V ππππ=-==. (19)(本题满分10分)计算二重积分()Dx y dxdy-⎰⎰,其中()()(){}22,112,D x y x y y x =-+-≤≥.【解析】由22(1)(1)2x y -+-≤得2(sin cos )r θθ≤+,32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰ 2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-.(20)(本题满分12分)设()y y x =是区间-ππ(,)内过点(的光滑曲线,当-0x π<<时,曲线上任一点处的法线都过原点,当0x π≤<时,函数()y x 满足0y y x ''++=.求()y x 的表达式. 【解析】由题意,当0x π-<<时,'xy y =-,即ydy xdx =-,得22y x c =-+,又(y =代入22y x c =-+得2c π=,从而有222x y π+=当0x π≤<时,''0y y x ++=得 ''0y y += 的通解为*12cos sin y c x c x =+ 令解为1y Ax b =+,则有00Ax b x +++=,得1,0A b =-=, 故1y x =-,得''0y y x ++=的通解为12cos sin y c x c x x =+- 由于()y y x =是(,)ππ-内的光滑曲线,故y 在0x =处连续于是由1(0),(0)y y c π-=± += ,故1c π=±时,()y y x =在0x =处连续 又当 0x π-<<时,有22'0x y y +⋅=,得'(0)0xy y-=-=, 当0x π≤<时,有12'sin cos 1y c x c x =-+-,得2'(0)1y c +=- 由'(0)'(0)y y -+=得210c -=,即 21c =故 ()y y x =的表达式为0cos sin ,0x y x x x x πππ⎧-<<=⎨-+-≤<⎪⎩或0cos sin ,0x y x x x x πππ-<<=+-≤<⎪⎩,又过点,22ππ⎛⎫- ⎪⎝⎭,所以0cos sin ,0x y x x x x πππ-<<=+-≤<⎪⎩.(21)(本题满分11分)(Ⅰ)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(),a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-;(Ⅱ)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.【解析】(Ⅰ)作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----,易验证()x ϕ满足:()()a b ϕϕ=;()x ϕ在闭区间[],a b 上连续,在开区间(),a b 内可导,且''()()()()f b f a x f x b aϕ-=--.根据罗尔定理,可得在(),a b 内至少有一点ξ,使'()0ϕξ=,即'()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--(Ⅱ)任取0(0,)x δ∈,则函数()f x 满足;在闭区间[]00,x 上连续,开区间()00,x 内可导,从而有拉格朗日中值定理可得:存在()()000,0,x x ξδ∈⊂,使得()0'00()(0)x f x f f x ξ-=-……()*又由于()'lim x f x A +→=,对上式(*式)两边取00x +→时的极限可得:()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====- 故'(0)f +存在,且'(0)f A +=.(22)(本题满分11分设111111042A --⎛⎫ ⎪=- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭(Ⅰ)求满足22131,A A ξξξξ==的所有向量23,ξξ;(Ⅱ)对(Ⅰ)中的任一向量23,ξξ,证明:123,,ξξξ线性无关. 【解析】(Ⅰ)解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量,令32x =,由0Ax =解得,211,1x x =-= 求特解,令120x x ==,得31x =故21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,其中1k 为任意常数解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫⎪ ⎪=--→⎪ ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭故有两个自由变量,令21x =-,由20A x =得131,0x x ==求特解21200η⎛⎫ ⎪ ⎪= ⎪ ⎪⎪⎝⎭故 321121000k ξ⎛⎫⎪⎛⎫ ⎪⎪=-+ ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭ ,其中2k 为任意常数.(Ⅱ)证明:由于12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠ 故123,,ξξξ 线性无关.(23)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-(Ⅰ)求二次型f 的矩阵的所有特征值;(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. 【解析】(Ⅰ) 0101111a A aa ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+(Ⅱ) 若规范形为2212y y +,说明有两个特征值为正,一个为0.则 1) 若10a λ==,则 220λ=-< ,31λ= ,不符题意2) 若20λ= ,即2a =,则120λ=>,330λ=>,符合3) 若30λ= ,即1a =-,则110λ=-< ,230λ=-<,不符题意 综上所述,故2a =.。
2009年考研数学一真题及答案
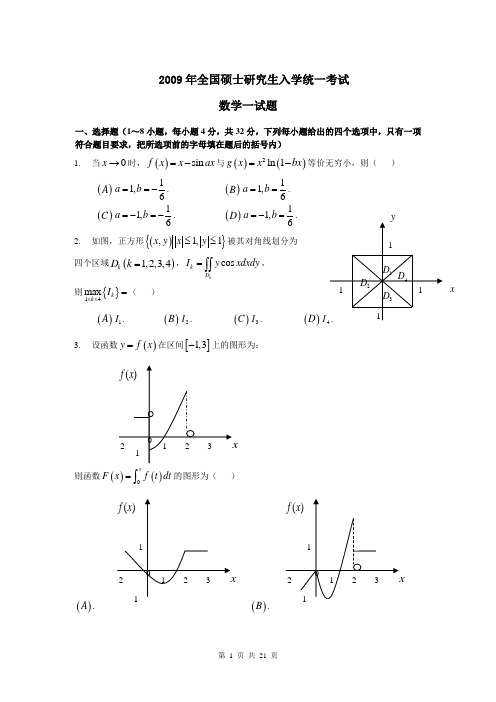
2009年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)1. 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则( )()A 11,6a b ==-. ()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.2. 如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=( )()A 1I .()B 2I . ()C 3I .()DI 3. 设函数()y f x =在区间[]1,3-上的图形为:则函数()()0x F x f t dt =⎰的图形为( )()A .()B .x()C .()D .4. 设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则( )()A 当1n n b ∞=∑收敛时,1n n n a b ∞=∑收敛.()B 当1n n b ∞=∑发散时,1n n n a b ∞=∑发散.()C 当1nn b∞=∑收敛时,221n nn a b∞=∑收敛.()D 当1nn b ∞=∑发散时,221n nn a b∞=∑发散.5. 设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基 122331,,αααααα+++的过渡矩阵为( )()A 101220033⎛⎫⎪⎪ ⎪⎝⎭. ()B 120023103⎛⎫⎪⎪ ⎪⎝⎭.()C 111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭.()D 111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭. 6. 设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为( )()A **32O B A O ⎛⎫ ⎪⎝⎭.()B **23OB A O ⎛⎫⎪⎝⎭. ()C **32O A BO ⎛⎫ ⎪⎝⎭.()D **23O A BO ⎛⎫⎪⎝⎭.7. 设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =( )()A 0.()B 0.3. ()C 0.7.()D 1.8. 设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为( )()A 0.()B 1. ()C 2.()D 3.二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)9. 设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ 。
2009考研试题及评分标准

2 A* O
(7)设随机变量 X 的分布函数为 F ( x ) 0.3 ( x ) 0.7 ( 分布的分布函数,则 EX = (A)0 (B)0.3 (C) 0.7
x 1 ) ,其中 ( x ) 为标准正态 2
(D)1
( 8 ) 设随机变量 X 与 Y 相互独立,且 X 服从标准正态分布 N (0,1) , Y 的概率分布为
L
.
2009 年(第 2 页)
(12) 设 ( x, y , z ) | x y z 1 ,则
2
2
2
z dxdydz =
2
.
(13) 设 3 维列向量 , 满足 T 2 ,其中 T 为 的转置,则矩阵 T 的非零特征值 为 . (14) 设 X 1 , X 2 , X m 为来自二项分布总体 B(n, p ) 的简单随机样本,X 和 S 2 分别为样本均 值和样本方差。若 X kS 2 为 np 2 的无偏估计量,则 k = .
2 2
2 xe x , 0,
x0
X1 , X 2 , , X n 是来自总体 X 的简单随机样本.
(Ⅰ) 求参数 的矩估计量; (Ⅱ) 求参数 的最大似然估计量.
其他,
,其中参数 ( 0)未知,
2009 年(第 4 页)
2009 年考研数学 ( 一 ) 试题
一.选择题 (1)A 二.填空题
'' '' (9) xf12 f 2' xyf 22
参考解答和评分标准
(2)A
(3)D
(4)C
(5)A
(6)B
(7)C
2009年考研数学二试题及答案解析

2009年全国硕士研究生入学统一考试数学二试题及答案解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1) 函数()3sin x x f x xπ-=的可去间断点的个数为()A 1 ()B 2 ()C 3 ()D 无穷多个 【答案】C【解析】由于()3sin x x f x xπ-=,则当x 取任何整数时,()f x 均无意义.故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±.320032113211131lim lim ,sin cos 132lim lim ,sin cos 132lim lim .sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±.(2) 当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则()A 11,6a b ==- ()B 11,6a b == ()C 11,6a b =-=- ()D 11,6a b =-= 【答案】A【解析】 22000()sin sin limlim lim ()ln(1)()x x x f x x ax x axg x x bx x bx →→→--==-⋅- 22002301cos sin lim lim 36sin lim 1,66x x x a ax a ax bx bxa ax ab b axa→→→---==-=-⋅洛洛 36a b ∴=-,故排除,B C .另外,201cos lim3x a axbx →--存在,蕴含了1cos 0a ax -→()0x →,故 1.a =排除D .所以本题选A .(3) 设函数(),z f x y =的全微分为dz xdx ydy =+,则点()0,0()A 不是(),f x y 的连续点 ()B 不是(),f x y 的极值点()C 是(),f x y 的极大值点 ()D 是(),f x y 的极小值点 【答案】D【解析】因dz xdx ydy =+可得,z zx y x y∂∂==∂∂. 2222221,0,1z z z zA B C x x y y x y∂∂∂∂== === ==∂∂∂∂∂∂,又在()0,0处,0,0z zx y∂∂==∂∂,210AC B -=>, 故()0,0为函数(,)z f x y =的一个极小值点. (4) 设函数(),f x y 连续,则()()222411,,yxydx f x y dy dy f x y dx -+=⎰⎰⎰⎰()A ()2411,xdx f x y dy -⎰⎰ ()B ()241,xxdx f x y dy -⎰⎰()C ()2411,ydy f x y dx -⎰⎰()D ()221,ydy f x y dx ⎰⎰ 【答案】C【解析】222211(,)(,)xxdx f x y dy dy f x y dx +⎰⎰⎰⎰的积分区域为两部分:{}1(,)12,2D x y x x y =≤≤≤≤,{}2(,)12,4D x y y y x y =≤≤≤≤-,将其写成一块{}(,)12,14D x y y x y =≤≤≤≤-, 故二重积分可以表示为2411(,)ydy f x y dx -⎰⎰,故答案为C .(5) 若()f x ''不变号,且曲线()y f x =在点()1,1上的曲率圆为222x y +=,则函数()f x 在区间()1,2内()A 有极值点,无零点 ()B 无极值点,有零点()C 有极值点,有零点()D 无极值点,无零点 【答案】B【解析】由题意可知,()f x 是一个凸函数,即()0f x ''<,且在点(1,1)处的曲率322||2(1())y y ρ''=='+,而(1)1f '=-,由此可得,(1)2f ''=-. 在[1,2] 上,()(1)10f x f ''≤=-<,即()f x 单调减少,没有极值点. 对于(2)(1)()1(1,2)f f f ξξ'-=<- , ∈ ,(拉格朗日中值定理)(2)0f ∴ <而(1)10f =>,由零点定理知,在[1,2] 上,()f x 有零点.故应选B .(6)设函数()y f x =在区间[]1,3-上的图形为:则函数()()0xF x f t dt =⎰的图形为()A ()B()C ()D【答案】D【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征:①[]0,1x ∈时,()0F x ≤,且单调递减。
2009年考研英语真题答案及解析

2009年全国硕士研究生招生考试英语(一)答案详解Section I Use of English一、文章总体分析本文是一个有关动物智力话题的文章。
文章第一段第一句就点名了文章中心,接着引用自然杂志上描述的实验论证这一观点。
从第二、三段作者从几个方面分析了产生这种情况的原因,最后一段从动物上升到对人的思考。
二、试题具体解析1.[A]Suppose假设猜想[B]Consider考虑[C]Observe观察[D]Imagine设想【答案】B【考点】固定搭配【解析】本题考查的是“consider+名词性词组”的用法,表示“以……为例”,显然与后面的试验搭配表示以该试验为例引出下文。
选项A、D同义,故排除。
选项C代入文中与上下文不合,故答案为B。
【补充】consider在这里等同于take…(as an example)。
2.[A]tended(to)倾向于……[B]feared害怕[C]happened(to)碰巧……[D]threatened(to)威胁要去做……【答案】A【考点】动词搭配【解析】从空格后面的to可首先排除B,因为fear不与to连用。
再结合文章题材看,文章是科技类,而科技类文章中通常为了表示说话客观性并避免绝对化,往往在主谓之间加一个tend to表示语气的弱化,故本题答案为A,其他两个代入文章语义不通。
3.[A]thinner较细的[B]stabler较稳定的[C]lighter更明亮的[D]dimmer较暗的【答案】D【考点】逻辑关系【解析】空前内容谈到聪明的果蝇寿命相对普通果蝇要短,这里拿灯泡做比喻,相对应的自然是光线的暗淡,即光线暗淡的灯泡使用时间更长。
下一句也有提示:no being too bright,故答案为D。
4.[A]tendency趋向[B]advantage优势[C]inclination倾向[D]priority优先【答案】B【考点】词汇辨析【解析】前文谈到暗淡的灯泡寿命更长,接着说“不太明亮也是”,对比四个选项,只有优势语义连贯,故答案为B。
2009考研数学一试题及答案解析

一、选择题:(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则()A 11,6a b ==-.()B 11,6a b ==. ()C 11,6a b =-=-. ()D 11,6a b =-=.【解析】2()sin ,()ln(1)f x x ax g x x bx =-=-为等价无穷小,则2222()sin sin 1cos sin limlimlimlimlim()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bxbx→→→→→---==-⋅---洛洛23sin lim166x a ax ab baxa →==-=-⋅ 36a b ∴=- 故排除,B C 。
另外21cos lim3x a ax bx→--存在,蕴含了1cos 0a ax -→()0x →故 1.a =排D 。
所以本题选A 。
(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为 四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14m ax kk I ≤≤=()A 1I .()B 2I .()C 3I .()D 4I .【解析】本题利用二重积分区域的对称性及被积函数的奇偶性。
24,D D 两区域关于x 轴对称,而(,)cos (,)f x y y x f x y -=-=-,即被积函数是关于y 的奇函数,所以240I I ==;13,D D 两区域关于y 轴对称,而(,)cos()cos (,)f x y y x y x f x y -=-==,即被积函数是关于x 的偶函数,所以{}1(,),012cos 0x y y x x I y xdxdy ≥≤≤=>⎰⎰;{}3(,),012cos 0x y y x x I y xdxdy ≤-≤≤=<⎰⎰.所以正确答案为A.(3)设函数()y f x =在区间[]1,3-上的图形为: 则函数()()0xF x f t dt =⎰的图形为x()A ()B()C ()D【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征: ①[]0,1x ∈时,()0F x ≤,且单调递减。
(完整word)2009年考研数学一试题及答案解析,推荐文档

令
故其最大似然估计量为
(4)设有两个数列 ,若 ,则
当 收敛时, 收敛. 当 发散时, 发散.
当 收敛时, 收敛. 当 发散时, 发散.
【答案】C
【解析】
方法一:
举反例A取
B取
D取
故答案为(C)
方法二:
因为 则由定义可知 使得 时,有
又因为 收敛,可得 则由定义可知 使得 时,有
从而,当 时,有 ,则由正项级数析】(I) 的方程为 ,
过点 与 的切线为 ,
所以 的方程为 。
(II)记 ,由 ,记 ,
则
(18)(本题满分11分)
(Ⅰ)证明拉格朗日中值定理:若函数 在 上连续,在 可导,则存在 ,使得
(Ⅱ)证明:若函数 在 处连续,在 内可导,且 ,则 存在,且 。
【解析】(Ⅰ)作辅助函数 ,易验证 满足:
的外侧。
【解析】 ,其中
①
②
③
①+②+③=
由于被积函数及其偏导数在点(0,0,0)处不连续,作封闭曲面(外侧)
有
(20)(本题满分11分)
设 ,
(Ⅰ)求满足 的所有向量 ,
(Ⅱ)对(Ⅰ)中的任一向量 ,证明: 线性无关。
【解析】(Ⅰ)解方程
故有一个自由变量,令 ,由 解得,
求特解,令 ,得
故 ,其中 为任意常数
; 在闭区间 上连续,在开区间 内可导,且 。
根据罗尔定理,可得在 内至少有一点 ,使 ,即
(Ⅱ)任取 ,则函数 满足;
在闭区间 上连续,开区间 内可导,从而有拉格朗日中值定理可得:存在 ,使得 ……
又由于 ,对上式(*式)两边取 时的极限可得:
故 存在,且 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年研究生入学考试西医综合科目试题 一、A型题:1~90小题,每小题1.5分;91~120小题,每小题2分:共195分。在每小题给出的A、B、C、D四个选项中,请选出一项最符合题目要求的答案。
1 、人体功能保持相对稳定依靠的调控系统是 A、 非自主控制系统 B 、负反馈控制系统 C 、正反馈控制系统 D 、前馈控制系统
2 、神经细胞中Na泵功能降低时,细胞的电位变化是: A、静息电位绝对值减小,动作电位幅度增大 B、静息电位绝对值增大,动作电位幅度减小 C、静息电位绝对值和动作电位均减小 D、静息电位绝对值和动作电位均增大
3 、骨骼肌 4、 M受体和乙酰胆碱活化的酶是 A、乙酰胆碱酯酶 5 、维持血浆平衡最主要的缓冲对是 B、NaHCO3/H2CO3 D、KHCO3/H2CO3
6、心房和心室收缩在时间不重叠,后者必定落后前者的原因 A、窦房结到心房距离近,而心室距离远 C 、心房细胞和心室细胞之间存在房室延迟
7、如果血管外周阻力不变,心脏每搏输出量增大,则血压变化是 A、收缩压不变, 舒张压增高 B、收缩压增高, 舒张压不变 C、收缩压升高比舒张压升高更明显 D、舒张压升高比收缩压升高更明显
8、某人潮气量为500ml,无效腔容积为150ML,功能残气量是2500ml,那么此人每次平静呼吸时肺泡更新气体量为: A 、1/10 B、 1/7 C、 1/5 D、1/3
9 、低氧时期呼吸活动增强的作用机制是 A、 兴奋外周化学感受器 B、 刺激中枢化学感受器 C、 刺激延髓呼吸中枢 D、 刺激脑桥
10、胃大部切除的患者易患贫血的原因是 A、壁细胞减小 B、内因子减小 C、蛋白酶原分泌减少
11、胆汁中与消化有关的成分是 A、消化酶 B、胆盐 C、卵磷脂 D、胆固醇
12、安静状态下,人体产热量最高的脏器或组织是? A、心脏 B、脑 C、肝脏 D、肾脏
13、循环系统实现体温调节的主要途径是? A、增加心脏输出量 B、 调节血管的弹性 C、 调节皮肤温度 D、 控制血流速度
14、葡萄糖几乎全部重吸收的主要部位是? A、近端小管 D、远曲小管和集合管
15、大量饮水后,尿量增多的主要原因是 A、血流量增加 B、醛固酮增多 C、抗利尿激素减小 D、 晶体渗透压降低 16、 视网膜中央凹外对光敏感性明显提高的主要原因是: A、 视杆细胞数量多 B、动作电位兴奋性高 C、 感光细胞色素含量多
17、听觉器官的感应装换装置——螺旋体所在的部位是? A、盖膜 B 、卵圆窗膜 C、基底膜 D、前庭膜
18、下列化学性突触传递特征叙述正确的是 A、 双向传播 B 、不衰减传播 D、 对内环境影响敏感 19、脑干结构当中网状上行激活 系统的主要功能? A、 形成模糊的感觉 B、维持大脑皮层的兴奋性 C 、唤醒作用 D、 躯体肢体平衡
20、生长激素增多的患者可出现? A、 血中氮含量降低 B、 血糖升高,尿糖升高 C 、血中脂肪酸含量降低 D、血中氨基酸含量降低
21、正常成年人调节血中钙磷的激素是 A 、 生长激素 B 、甲状旁腺激素 C 、甲状腺激素
22、下列那种激素能在排卵前一天左右诱发排卵所需的LH增高的激素是? A 、孕酮 B 、孕激素 C、雌激素 D、FSH
23、平静呼吸时,吸气的阻力主要来源于 A、 肺泡液气表面张力 B 、肺的弹性回缩力 D、胸廓弹性阻力
24 、血浆渗透压增高主要决定于 A 、血浆总蛋白 B、白蛋白含量 C、氯化钠浓度 D、氯化钾浓度
25、在蛋白质的组成中,不含天然的氨基酸是 A、瓜氨酸 B、半胱氨酸 C、脯氨酸
26、蛋白质变性后的主要表现是? A、分子量变小 B、粘度降低 C、溶解量降低 D 、不易被蛋白酶水解
27下列DNA分子中,可以使Tm值达到最高的是: A、 腺嘌呤和胸腺嘧啶含量为10% B 、腺嘌呤和胸腺嘧啶含量为20% C 、鸟嘌呤和胞嘧啶含量为30% D、鸟嘌呤和胞嘧啶含量为60%
28、下列关于辅酶与辅基叙述错误的是? D、一种辅酶或辅基只能与一种酶蛋白结合
29 、乙酰COA羧化酶的变构激活剂是 B、柠檬酸 C、AMP D、脂酰COA
30、下列氨基酸中,属于生糖兼生酮的是 A、瓜氨酸 B、半胱氨酸 C、色氨酸 D、苏氨酸 31、下列物质中,不是高能化合物的是 A 、ADP B、乙酰乙酸 C、三磷酸甘油酸 D、磷酸肌酸
33、下列核苷酸经核糖核苷酸还原酶催化能转化生成脱氧核苷酸的是 A、NMP B、NDP C、NTT D、DNTT
34、下列关于遗传酶叙述正确的是 催化合成的方向是3——5
35、催化HnRNA生成的酶是 B、RNA聚合酶2
36、对真核和原核生物反应过程均有干扰作用,故能用作抗菌药物的是? A、卡那霉素 B、 链霉素 C 、克拉霉素 D、嘌呤霉素
37、一个对5’UAG3’的可识别的密码是 B、5’CUA3’ D、3’CUA5’
38、基因表达调控的基本控制点是? A、MRNA从细胞核转移到细胞质 B、转录的起始
39、下列选项中不属于重组DNA的工具酶的是 A、拓扑异构酶 B、反转录酶 C、DNA连接酶 D、限制性核酸内切酶
40、血浆中能够转运胆红素和磺胺的蛋白质是 A、清蛋白 B、运铁蛋白 C、Y蛋白
42、下列选项中属于稳定细胞的是? A 表皮细胞 B 上皮细胞 C 心肌细胞 D肾移行细胞
43、VC缺乏常导致创伤愈合不良的主要原因是? A、表皮的再生困难 B、难以形成胶原物质 C、炎症难以控制 D、营养不良
44、溶酶体内出现弥散分布的,在胞浆内存在大量含铁血黄素的颗粒的巨噬细胞最常见于 A、 大叶性肺炎 B 、小叶性肺炎 C 、间质性肺炎 D、左心衰
45、血栓形成最主要的因素是? A、 血管内血流缓慢 B、 血流轴流消失 C 、内皮细胞损伤 D 、血小板增加
47、肿瘤的分级是指: A 、肿瘤的大小 B、肿瘤的侵润范围 C、肿瘤是否累计淋巴结 D 、肿瘤的分化程度
48 、中性粒细胞浸出过少的大叶性肺炎引发的 A、肺实质变 B 、肺脓肿 C、脓胸 D、败血症
49、肺癌中恶性程度最高的是? A、 鳞癌 B、腺癌 C、支气管癌 D、 小细胞癌 50、急性普通型肝炎的典型病变是? B、肝细胞水样变性和大片状点状坏死
52、出现浸润性小叶癌的主要病理学特征是? A、 癌细胞呈巢形分布, B、间质中有大量淋巴细胞浸润 C 、癌细胞呈线状分布,
53 、乙型脑炎的特征性病变是 A 、淋巴套形成 B、软化灶形成 C、卫星现象 D、胶质细胞增生
54、易发生贫血性梗死的脏器是? A、脾心肾 B、心脑肺 D、脾心肺
55、心内膜疣状物的实质是 A 、白色血栓 B、红色血栓 C、混合血栓 D 、透明血栓
56、下列肝硬化的病变中符合假小叶的是? A 、坏死细胞增生 B 、纤维包裹 D、 异型性细胞增生
57、剧烈呕吐时,患者呕出鲜血的常见病因是 A 、急性胃炎 B、 消化性溃疡 C 、食管贲门破裂 D、贲门撕裂综合征
58、患者进行性呼吸困难,肺部听诊出现VELO啰音,最可能是疾病是 A、 肺癌 C、 特发性肺纤维化 59、下列关于心力衰竭治疗的叙述正确的是? C 、Nacl的量应控制在3-5g/d之间 D、 严格限制盐的摄入量,不用控制液体数量
60、慢性心房颤动应用洋地黄的主要目的是? A 、控制心室率 D、 预防室性心率失常
61、患者,男、52岁,因 突发心悸,呼吸困难,咳嗽而入院,已往高血压,查体:HP 90-60mlHg。口唇紫绀,双肺布满中小水泡音,心率140次/分,心音不清,下列急症处理不正确的是? A 、高流量吸氧 B、 交感神经抑制剂 C 、服用长效B受体抑制剂 D、血管扩张剂
62、患者,男,40岁,发现血压增高半年, 最高达160/90mlHg,乏力,头痛,口渴,吸烟20年。查体:血压170/90 mlHg, 心脏不大,心律齐,心率60次/分,双下肢不肿,尿蛋白(±),比重1.008,血浆3.1mmol/l ,最可能的诊断是 A、 原发性醛固酮增高症 B、 原发性高血压 C、 肾性高血压 D 、肾血管性高血压
63、下列药物中属于治疗支气管哮喘患者的B2受体激动剂的是 A、氨茶碱 D、沙酊氨醇
64、下列那类人群中,ppt阳性对提示活动性结核病最有价值的是 A、肌肉多发结节伴纵隔淋巴节肿大的成年人 C、长期发热的患者 D、未接种卡介苗的婴幼儿
65、患者, 男,53岁,三小时前在投掷铅球转身后,突感左侧胸痛,随即出现胸闷气短,呼吸急促,后症状加重,伴出汗心悸,稍事休息后症状稍有缓解而来院, 既往有高血压,冠心病,肺结核病史,根据临床症状分析,应首先考虑下列那种疾病的可能性最大: A、 心绞痛 B、心肌梗死
