线段与角的计算-课件
合集下载
第1讲-线段与角度的相关计算
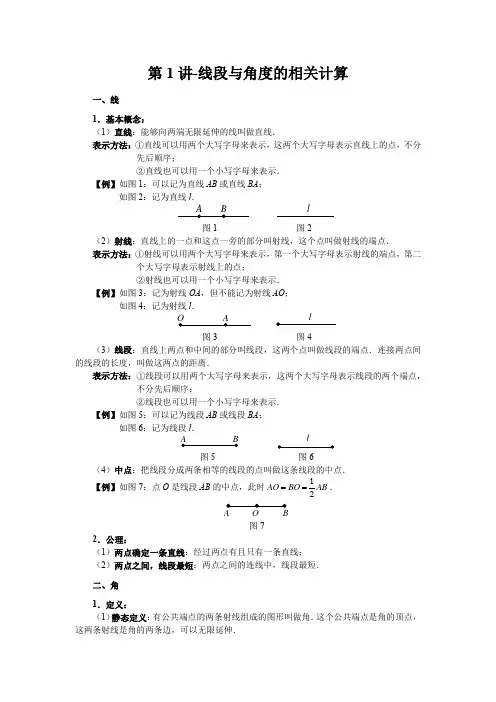
第1讲-线段与角度的相关计算一、线1．基本概念：（1）直线：能够向两端无限延伸的线叫做直线．表示方法：①直线可以用两个大写字母来表示，这两个大写字母表示直线上的点，不分先后顺序；②直线也可以用一个小写字母来表示．【例】如图1：可以记为直线AB 或直线BA ；如图2：记为直线l ．图1 图2（2）射线：直线上的一点和这点一旁的部分叫射线，这个点叫做射线的端点．表示方法：①射线可以用两个大写字母来表示，第一个大写字母表示射线的端点，第二个大写字母表示射线上的点；②射线也可以用一个小写字母来表示．【例】如图3：记为射线OA ，但不能记为射线AO ；如图4：记为射线l ．图3 图4（3）线段：直线上两点和中间的部分叫线段，这两个点叫做线段的端点．连接两点间的线段的长度，叫做这两点的距离．表示方法：①线段可以用两个大写字母来表示，这两个大写字母表示线段的两个端点，不分先后顺序；②线段也可以用一个小写字母来表示．【例】如图5：可以记为线段AB 或线段BA ；如图6：记为线段l ．图5 图6（4）中点：把线段分成两条相等的线段的点叫做这条线段的中点．【例】如图7：点O 是线段AB 的中点，此时AO BO AB 1==2．图72．公理：（1）两点确定一条直线：经过两点有且只有一条直线； （2）两点之间，线段最短：两点之间的连线中，线段最短． 二、角1．定义： （1）静态定义：有公共端点的两条射线组成的图形叫做角．这个公共端点是角的顶点，这两条射线是角的两条边，可以无限延伸．llA O (5) l A B(6)l（2）动态定义：由一条射线绕着它的端点旋转到另一个位置所成的图形叫做角．处于初始位置的那条射线叫做角的始边，终止位置的那条射线叫做角的终边．表示方法：①通常用三个字母表示：两条边上的点的字母写在两旁，顶点上的字母写在中间．②用一个大写字母来表示：这个大写字母一定要表示角的顶点，而且以它为顶点的角只有一个．③用数字或希腊字母来表示：可以用希腊字母（α，β，γ，θ，ϕ, ...）表示角的大小。
人教版七年级上数学《角》几何图形初步PPT教学课件
课堂练习：
练习
4．分别确定四个城市相应钟表上时针与分针所成的小于平角的角的度数， 并填在相应的横线上．
巴黎时间 30°
北京时间 120°
伦敦时间 0°
东京时间 90°
课堂练习：
练习
5．如图，一共有多少个小于平角东京时间的角？按图中字母把它们表示 出来，并指出哪些角可以用一个字母表示． 解：图中一共有14个小于平角的角，用字母表示为：
1°=60'
1′=60″
1''=
1 60
'
1'=
1 60
°
由此，我们可以得到度、分、秒是 60 进制的。
三、角的度量
角的度量工具：量角器 角的基本度量单位：
度、分、秒类比 时间单位
分、秒的定义：(60进制)
① 1 把 的角等分成60份，每一份就是1分,记作 1
② 把 1 的角等分成60份，每一份就是1秒,记作 1
O
A
(2) 如果∠AOD=100°，∠COD=20°，那么∠BOD 是多少度？
DC
解：因为 ∠COD = 20°，
B
所以 ∠AOC= ∠AOD－∠COD
= 100°－20°= 80°
又因为 OB 平分∠AOC，
O
A
1
1
所以∠AOB= 2∠AOC = 2 ×80°= 40°
所以∠BOD= ∠BOC+∠COD= 40°+ 20°= 60°
即：
1 ( 1 )
60
1 ( 1 ) 60
三、角的度量
角的基本度量单位：度、分、秒
1 ( 1 ) 60
1 ( 1 ) 60
1周角=360° 1平角 =180° 1直角=90 °
七年级数学上册4.6用尺规作线段与角习题课件(新版)沪科版
第十四页，共14页。
16．(8分)如图，已知线段(xiànduàn)a，b，用直尺和圆规作线段(xiànduàn)：
(1)AB＝b－a； (2)CD＝2a＋b.
解：略
第十二页，共14页。
17．(10分)如图，已知∠1，∠2，用尺规作∠AOB，使得：(不写作 (xiězuò)法，保留作图痕迹)
(1)∠AOB＝2∠1＋∠2；
第六页，共14页。
7．(4分)已知∠1和∠2，画一个角使它等于∠1＋∠2，画法如下： (1)画∠AOB＝_____∠__1__； (2)以O为顶点(dǐngdiǎn)，OB为始边在∠外AO部B(w的à_ib_ù_)____作∠BOC＝∠2， 则∠AOC就是所求作的角．
8．(8分)尺规作图：已知∠α和∠β，求作∠AOB，使∠AOB＝∠α＋ ∠β.
4.6 用尺规作线段(xiànduàn)与角
第一页，共14页。
1．几何中，通常用没__有__(_m__é_i _y_ǒ_u_)的刻直度尺(zhí chǐ)和圆规来画图，这种画图的
方法叫做尺规作图． 2．作一条线段等于已知线段时，射线画好后用__圆__规__(_y截uá取ng与uī)已知线段等长 的线段；作一个角等于已知角时，射线画好后第一次画弧的半径是任意长， 第二次画弧的圆心在角的一边上．
4．(4分)如图所示，已知a，b，c，BD＝_______c_－，bAC＝_______，aA＋Dc＝ _________a_＋__c．－b
第四页，共14页。
知识点2 作一个角等于(děngyú)已知角
5．(4分)下列尺规作图的语句错误的是( )
B
A．作∠AOB，使∠AOB＝3∠α
B．以点O为圆心(yuánxīn)作弧
第二页，共14页。
16．(8分)如图，已知线段(xiànduàn)a，b，用直尺和圆规作线段(xiànduàn)：
(1)AB＝b－a； (2)CD＝2a＋b.
解：略
第十二页，共14页。
17．(10分)如图，已知∠1，∠2，用尺规作∠AOB，使得：(不写作 (xiězuò)法，保留作图痕迹)
(1)∠AOB＝2∠1＋∠2；
第六页，共14页。
7．(4分)已知∠1和∠2，画一个角使它等于∠1＋∠2，画法如下： (1)画∠AOB＝_____∠__1__； (2)以O为顶点(dǐngdiǎn)，OB为始边在∠外AO部B(w的à_ib_ù_)____作∠BOC＝∠2， 则∠AOC就是所求作的角．
8．(8分)尺规作图：已知∠α和∠β，求作∠AOB，使∠AOB＝∠α＋ ∠β.
4.6 用尺规作线段(xiànduàn)与角
第一页，共14页。
1．几何中，通常用没__有__(_m__é_i _y_ǒ_u_)的刻直度尺(zhí chǐ)和圆规来画图，这种画图的
方法叫做尺规作图． 2．作一条线段等于已知线段时，射线画好后用__圆__规__(_y截uá取ng与uī)已知线段等长 的线段；作一个角等于已知角时，射线画好后第一次画弧的半径是任意长， 第二次画弧的圆心在角的一边上．
4．(4分)如图所示，已知a，b，c，BD＝_______c_－，bAC＝_______，aA＋Dc＝ _________a_＋__c．－b
第四页，共14页。
知识点2 作一个角等于(děngyú)已知角
5．(4分)下列尺规作图的语句错误的是( )
B
A．作∠AOB，使∠AOB＝3∠α
B．以点O为圆心(yuánxīn)作弧
第二页，共14页。
人教版中考备战策略课件第16讲线段、角、相交线与平行线
答案：55°
三、解答题(共 4 3 分) 18．(8 分)如图，直线 a∥b，点 B 在直线 b 上， 且 AB⊥BC，∠1＝55°，求∠2 的度数．
解：如图，∵AB⊥BC，∴∠1＋∠3＝90°. ∵∠1＝55°，∴∠3＝35°. ∵a∥b，∴∠2＝∠3＝35°.
19．(10 分)如图，已知直线 AB，CD 相交于点 O， OE，OF 为射线，∠AOE＝90°，OF 平分∠AOC，∠AOF ＋∠BOD＝51°，求∠EOD 的度数．
【答案】 B
考点二 余角、补角的定义 例 2 (2015·崇左)下列各图中，∠1与∠2互为余 角的是( )
【点拨】A 中，∠1 的对顶角与∠2 是同位角关系， 只能说明∠1＝∠2；B 中，∠1 和∠2 是对顶角，∠1 ＝∠2；C 中，∠1＋∠2＝90°，∠1 与∠2 互余；D 中， ∠1＋∠2＝180°，∠1 与∠2 互补．综上所述，选 C.
3．平行线的判定 (1)定义：在同一平面内不相交的两条直线，叫做 平行线； (2)同位角相等，两直线平行； (3)内错角相等，两直线平行； (4)同旁内角互补，两直线平行．
温馨提示： 除上述平行线的判定方法外，还有“在同一平面 内垂直于同一条直线的两条直线平行”及“平行于同 一条直线的两条直线平行”的判定方法.
【解析】∵∠ECA＝α°，∴ ∠ECB＝180°－∠ECA＝
180°－ α°.∵CD
平
分
∠ECB
，
∴∠DCB
＝
1 2
∠ECB
＝
12×(180°－ α°)＝90－α2 °.∵FG∥CD，∴∠GFB＝∠DCB
＝90－α2 °.
答案：90－α2
16．(2015·泰州)如图，直线 l1∥l2，∠α＝∠β， ∠1 ＝40°，则∠2＝ .
三、解答题(共 4 3 分) 18．(8 分)如图，直线 a∥b，点 B 在直线 b 上， 且 AB⊥BC，∠1＝55°，求∠2 的度数．
解：如图，∵AB⊥BC，∴∠1＋∠3＝90°. ∵∠1＝55°，∴∠3＝35°. ∵a∥b，∴∠2＝∠3＝35°.
19．(10 分)如图，已知直线 AB，CD 相交于点 O， OE，OF 为射线，∠AOE＝90°，OF 平分∠AOC，∠AOF ＋∠BOD＝51°，求∠EOD 的度数．
【答案】 B
考点二 余角、补角的定义 例 2 (2015·崇左)下列各图中，∠1与∠2互为余 角的是( )
【点拨】A 中，∠1 的对顶角与∠2 是同位角关系， 只能说明∠1＝∠2；B 中，∠1 和∠2 是对顶角，∠1 ＝∠2；C 中，∠1＋∠2＝90°，∠1 与∠2 互余；D 中， ∠1＋∠2＝180°，∠1 与∠2 互补．综上所述，选 C.
3．平行线的判定 (1)定义：在同一平面内不相交的两条直线，叫做 平行线； (2)同位角相等，两直线平行； (3)内错角相等，两直线平行； (4)同旁内角互补，两直线平行．
温馨提示： 除上述平行线的判定方法外，还有“在同一平面 内垂直于同一条直线的两条直线平行”及“平行于同 一条直线的两条直线平行”的判定方法.
【解析】∵∠ECA＝α°，∴ ∠ECB＝180°－∠ECA＝
180°－ α°.∵CD
平
分
∠ECB
，
∴∠DCB
＝
1 2
∠ECB
＝
12×(180°－ α°)＝90－α2 °.∵FG∥CD，∴∠GFB＝∠DCB
＝90－α2 °.
答案：90－α2
16．(2015·泰州)如图，直线 l1∥l2，∠α＝∠β， ∠1 ＝40°，则∠2＝ .
尺规作图.作一条线段等于已知线段;.作一个角等于已知角 大赛获奖教学课件
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
活动2
教材导学
理解尺规作图 完成下列填空，想一想直尺和圆规有什么用途？ 无数条直线，需要的工具是 (1)已知点 A，经过点 A 可以画____ ____ 直尺； (2)已知不同的两点 A， B， 经过点 A， B 可以画____ 一 条直线， 具体画法是用 ____的边缘靠紧 A，B 两点画线； 直尺 (3)已知线段 A，要求不用刻度尺画一条线段 AB，使 AB＝ A.其画法是先用直尺 ____画射线 AC， 再用圆规 ____在射线 AC 上截取 AB ＝A. 你知道只用直尺和圆规还可以画出哪些图形？ ◆ 知识链接——[新知梳理]知识点一
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
►
知识点二
尺规作图的步骤及作图语言的规范
1．尺规作图的步骤 (1)已知：当作图题是用文字语言叙述的，要根据文字语言用数学语言 写出题目中的条件； (2)求作：根据题目写出要求作出的图形及此图形应满足的条件； (3)作法：根据作图的过程写出每一步的操作过程．当不要求写作法时 ，要保留作图痕迹．对于较复杂的作图，可先画出草图，使它同所要作的 图形大致相同，然后借助草图寻找作法． 2．作图语言的规范叙述 用直尺作图时的规范语言主要有：(1)过点×作直线××，作线段×× ，以点×为端点作射线××；(2)连结××，以点×为端点作线段××，延 长线段××到点×；延长线段××到点×，使××＝××. 用圆规作图时的规范语言主要有：(1)以点×为圆心，××为半径作圆；(2) 以点×为圆心，××为半径作弧交××于点×；(3)在××上截取一点×， 使××＝××.
探究问题二
作一个角等于已知角
例 2 如图 13－4－4 所示，已知线段 A 和∠α，∠β ， 求作△ABC，使 AB＝A，∠A＝∠α，∠B＝∠β.
2020春青岛版五年制数学三年级下册-第5单元 线和角-单元课件
过一点画两条射线，形成的是什么图形？ 从一点引出两条射线所组成的图形叫作角。
角通常用符号“∠”表示。
记作：∠1
1
读作：角一
课堂练习
1.下图中哪些是直线？哪些是射线？哪些是线段？
① 射线
② 线段
③ 直线
④×
⑤ 直线
⑥ 射线
2.数一数，下列图形中各有几个角？请标出来。
1 23
1
2ห้องสมุดไป่ตู้
5
34
14 23
课后作业
1.从教材课后习题中选取； 2.从课时练中选取。
青岛版五年制 数学 三年级 下册
5 线和角
角的度量
情境导入
探究新知
课堂练习
课堂小结
课后作业
情境导入
你能提出什么 问题？
铲斗臂上的角 能大能小。
工地上有这么 多挖掘机啊！
铲斗臂形成的角有多大？
探究新知
铲斗臂形成的角有多大？
﹒﹒ 用 —— 可以计量线段的长度。
为了准确测量角的大小，要有统一的计 量单位和度量工具。
常用的量角工具是量角器。
量角器上有两圈刻度线。
角的计量单位是“度”， 用符号“°”表示。
0°刻度线
1°
把半圆平均分成180份， 每一份所对的角就是1度
的角，记作1°。
怎样用量角器量角呢？
60°
另一条边在量角器 上所对的刻度是60， 这个角就是60°。
3.下图中有几条射线？组成了几个角？
3条射线 3个角
∟
4.下图中一共有几条线段？
A
BC D
一共有 6 条线段。
课堂小结
这节课你们都学会了哪些知识？
线段有两个端点,不能延长;射线有一 个端点,可以向一端无限延长;直线没有端 点,可以向两端无限延长。
北师大版四年级数学上册《线与角——线的认识》教学PPT课件(3篇)
A
B
C
直线有3条:直线AC或直线CA，直线AB或
直线BA，直线BC或直线CB； 射线有6条:射线AC，射线CA，射线AB，
射线 BA，射线BC，射线CB； 线段有3条:线段AB或线段BA，线段BC或
线段CB，线段AC或线段CA。
教材第17页第3题。
可以 无数条 不可以 1条
教材第17页第4题。 一样长。
(2)用两个图钉把一张硬纸条钉在木板上，硬纸条可以转动吗？ 过两点可以画出多少条直线？
A
Ｂ
过两点可以画 出一条直线
2.蚂蚁到洞口的距离是多少？画一画，量一量。
6.狐狸从家到小树林的距离是多少？画一画，量一量。
通过本节课的学习，你有什么收获呢？
北师大版数学四年级上册
第2单元 线与角
线的认识
学习目标
教材第17页第5题。 5.蚂蚁到洞口的距离是多少？画一画，量
一量。
教材第17页第6题。 6.狐狸从家到小树林距离是多少？画一画，量
一量。
返回作业设计
作业2
思维创新 提升培优 基础巩固
返回作业设计
1.(基础题)找出下面哪些是直线,哪些 是射线,哪些是线段。
BD
FH
AC
2.(基础题) 填一填。
今天我们认识了三种线，都是哪三种？ 这三种线的共北师]
学习新知
随堂练习
作业设计
学习新知 从图中你们获得了哪些信息?
“线”有什么相同 和不同？
A
B
线段A 或BA B
A
B
射线B
A
AB
直线A B
说一说,从老虎山到狐狸洞有哪几条路?描 出最短的路线，你发现了什么？
C.无数
线段的长度与角度
线段的长度与角度在几何学中，线段的长度与角度是两个重要的概念。
线段是指两个点之间的直线部分，长度是描述线段的大小，而角度则是两条线段之间的夹角大小。
本文将从理论和实际应用的角度分别讨论线段长度与角度的相关性。
一、线段长度线段长度是指两个点之间的距离，可以用数值表示。
在平面几何学中，我们可以通过两点之间的坐标计算线段的长度。
假设有两个点A(x₁, y₁)和B(x₂, y₂)，则线段AB的长度可以通过以下公式计算：AB = √((x₂ - x₁)² + (y₂ - y₁)²)这个公式被称为勾股定理，也是线段长度的计算公式。
通过这个公式，我们可以得到线段的精确长度，无论线段是水平、垂直还是倾斜的。
线段长度的计算在实际中有广泛的应用。
例如，在建筑设计中，需要计算建筑物的各个模块的尺寸，包括线段的长度。
在工程测量中，也常常需要测量线段的长度来确定地块的大小或测绘地形图。
线段长度的准确计算对于这些应用非常重要。
二、线段角度线段的角度是指两个线段之间的夹角大小。
角度可以用弧度或度数来表示。
在平面几何学中，我们通常使用度数来表示角度。
360度是一个完整的圆，而角度的单位可以是任意的。
例如，直角是90度，平分一个直角则是45度。
要计算线段的角度，我们需要明确两个线段之间关系的性质和角度的计算方法。
例如，两条直线相交时，相交处形成的角度叫做相交角。
相交角的计算可以使用数学中的三角函数。
通过三角函数的计算，我们可以得到线段之间的夹角大小。
线段角度的计算在实际中也有广泛的应用。
例如，在导航系统中，我们需要知道两条线段之间的角度，以确定行驶方向或路径选择。
在机器人技术中，精确计算线段角度可以帮助机器人进行路径规划和避障。
总结：线段的长度与角度是几何学中重要的概念。
线段长度可以通过勾股定理计算，而线段角度可以通过三角函数计算。
线段长度与角度的准确计算在实际应用中有广泛的应用，包括建筑设计、工程测量、导航系统和机器人技术等领域。
四年级上册数学课件《认识线与角》︳青岛版(共20张PPT)
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
直线线段
把线段的两端无限延长，就得到一条直线。
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
画一画
作图要求：
1.独立画图，怎样画能一眼判断出它是哪种线。 2.小组交流，看看谁画的更合适。 3.准备汇报，找出小组作品代表。
过一点能画无数条直线
过一点能画无数条射线 过两点只能画1数条直线
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
巩固练习
1.辨一辨：下面的说法对吗？
（1）一条线段长6厘米，一条直线长6千米。（×） （2）线段是直线的一部分。（√ ） （3）过一点只能画一条射线。（×）
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
对比发现
线段、射线、直线三者之间有什么区别？
线段
端点
2个端点
射线
1个端点
直线
0个端点
长度
可测
不可测
（无限长）
不可测
（无限长）
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
巩固练习 2.数一数：
下图中有几条射线？组成了几个角？各是什么角？
四年级上册数学课件-2.1 《认识线与角》 ︳青岛版 (共20张PPT)
平面几何中的线段与角度计算
平面几何中的线段与角度计算在平面几何学中，线段和角度是两个基本的概念。
线段是一个有两个端点的直线部分，它可以通过测量长度来确定。
而角度是由两条交叉的线段形成的空间区域，用于描述物体之间的方位关系。
在本文中，我们将讨论线段的计算和测量，以及角度的计算方法。
一、线段的计算和测量方法1. 直尺法直尺法是一种常用的线段计算和测量方法。
首先，我们需要一把直尺，将其边与线段的一端对齐，然后沿着直尺的边缘延伸，直到达到线段的另一端。
通过读取直尺上的刻度，我们可以得到线段的长度。
2. 钢尺法钢尺法也是一种常用的线段计算和测量方法。
与直尺法类似，我们需要一把刻有刻度的钢尺。
将钢尺的一端对齐线段的一端，然后延伸钢尺直到达到线段的另一端。
通过读取钢尺上的刻度，我们可以得到线段的长度。
相比直尺法，钢尺法的精度更高。
3. 割线法割线法是一种通过几何原理计算线段长度的方法。
首先，我们需要一块刻有刻度的长直板。
将直板上的一条边与线段的一端对齐，并用手指按住与线段相切的另一条边。
然后，将直板沿着手指的位置移动，直到与线段的另一端相切。
通过读取直板上的刻度，我们可以得到线段的长度。
二、角度的计算方法1. 量角器法量角器是一种用于测量和计算角度的工具。
将量角器的一个端点对齐于角的顶点，然后将量角器的另一条边与角的一条边对齐。
通过读取量角器上的刻度，我们可以得到角的度数。
2. 三角函数法三角函数是一种用于计算角度的数学工具。
在平面几何中，常用的三角函数有正弦、余弦和正切等。
通过使用三角函数的定义和性质，我们可以计算某些特定角度的值。
3. 直观估计法在某些情况下，我们可以通过直观估计的方式得到角度的近似值。
例如，对于钝角或锐角，我们可以根据视觉判断来估计其大致值。
这种方法通常用于大致的角度计算，不适用于精确的测量。
结论通过直尺法、钢尺法和割线法，我们可以计算和测量线段的长度。
而借助量角器法、三角函数法和直观估计法，我们可以计算角度的大小。
初一上数学课件(沪科版)-用尺规作线段与角
11．已知∠AOB＝22.5°，分别以射线 OA、OB 为始边，在∠AOB 的外部作 ∠AOC＝∠AOB，∠BOD＝2∠AOB，则∠COD 的度数是 90°.
11．已知∠AOB＝22.5°，分别以射线 OA、OB 为始边，在∠AOB 的外部作 ∠AOC＝∠AOB，∠BOD＝2∠AOB，则∠COD 的度数是 90° . 12．在作 2∠α－∠β 时，作图的步骤为：①作∠AOB＝ ∠α ；②以点 O 为 顶点，以 OA 为一边，在∠AOB 的外部作∠AOC＝ ∠α ；③以点 O 为顶点， 以 OC 为一边，在∠COB 的内部作∠COD＝∠β .则 ∠BOD ＝2∠α－∠β. 13．如图，已知线段 a、b、c，用尺规作一条线段，使它等于 3a－b＋2c.
9．下列说法正确的是( D ) ①用尺规作图能作一条线段等于两条线段的差；
②用尺规作图能作一个角等于已知两个角的和；
③利用尺规作图能作一个角等于已知角的 3 倍；
④利用尺规作图能作一个角等于已知两个角的差．
A．1 个
B．2 个
C．3 个
D．4 个
10．如图所示，已知线段 a、b、c(a＞b＋c)，求作线段 AB，使 AB＝a－b －c.下面利用尺规作图正确的是( D )
知识点一：尺规作图 通常用没有 刻度 的直尺和圆规来画图，这种画图的方法叫做尺规作图． 1．下列各题中，只用没有刻度的直尺就能作出的是( B ) A．作线段 AB＝a B．过点 O、P 作射线 OP C．在直线上取线段 AB＝a D．在射线 OA 上截取线段 OB＝a
2．如图，点 C 在∠AOB 的 OB 边上，用尺规作出了∠NCE，使∠NCE＝∠ AOB，作图痕迹中，弧 FG 是( D )
【规范解答】(1)作∠AOC＝α；(2)以 OC 为一边，在∠AOC 的边 OA 同侧， 再作∠BOC＝β.∠AOB 就是所求作的角．
四年级上册数学课件-4.1线和角：线-线段.射线和直线 ▎冀教版(2014秋)(共19张PPT)
否
（2）总结线段、直线和射线的特点。
（课件出示歌谣：直线、射线和线段，为人正直腰不弯。直 线本领大，身体无限长；射线向一方，也是无限长；线段最 乖巧，只在两点之间跑。）
（3）火眼金睛：完成33页“试一试”。
（这一环节，先让学生讨论交流，总结线段、直线和射线有 什么共同点和不同点，整理成形象直观的表格，再用充满童 趣的歌谣进行深化，既再次激起学生的兴趣，又强化了学生
3、认识射线。
（1）启发想象：把线段的一端无限延伸会怎么样？（学生 想象交流）教师画图展示，说明：这样的线我们就叫做射线。
（2）看看射线长得什么样？（直直的，只有一个端点，向 一方延伸，不能度量）
（3）你能说说生活中还有哪些可以近似地看作射线吗？ （学生举例，教师用课件展示，如：太阳照射的光线，手电 筒射出的光线，枪的弹道，探照灯光，等等）
学习指南一
直观认识线段有两个端点；在认识线段 的基础上再认识直线和射线。教学直线 时，采用的是想象、描述相结合的方式 （即先想象把一条线段向两端无限延伸 会怎么样？再描述“把一条线段向两端 无限延伸就得到一条直线” ）
学习指南二
教学射线时，采用的是想象、描述、举 例相结合的方式进行（即先想象把一条 线段向一端无限延伸会怎么样？再描述 “把一条线段向一个方向无限延伸就得 到一条射线” 最后举出探照灯射出的光 线、太阳射出的光线，帮助学生强化对 射线的认识。）
总之，整节课始终坚持以学生为课堂活动的主体，密 切结合学生的生活实际，时时处处注意激发学生的学 习兴趣，相信，能够比较圆满地完成了教学任务。
在深入学习新课标精神，透彻理 解教材编写意图的基础上，结合 四年级学生的认知特点，我确定 本节课的教学目标如下：
尺规作图.作一条线段等于已知线段;.作一个角等于已知角 大赛获奖教学课件
图 13－4－5
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
[归纳总结] 注意：(1)求作两角和或差时，一定要注明“外 部”或“内部”；
(2)求作三角形，一般情况下先作线段再作角，并结合全等 三角形的判定方法作图；
(3)本题实质是已知两角及其夹边作三角形．由“角边角” 定理，在此条件下所作的三角形是唯一的．一般情况下先作线 段，再作两个角，必须指明在线段的同侧，否则不会相交．基 本作图的“作法”不必再详说，如作线段 AB 的步骤，作∠BAM ＝∠α 的步骤，但必须保留作图痕迹．
13.2.5 边边边
[归纳总结] 证明三角形全等的步骤： 第一步：从已知出发，探究要证明的相等的线段或角分别 在哪两个全等三角形中； 第二步：分解图形——将所证全等三角形从“复合”图形 中分离出来； 第三步：“移植”条件——将已知条件转移到图形中，再 根据已知条件及隐含条件寻求恰当的证明方法．
可以确定△ABC 与△A′B′C′的关系是
全等
．
你能用一句话概括出三角形全等的这种判定方法吗？
◆知识链接——[新知梳理]知识点一
13.2.5 边边边
新知梳理
► 知识点一 “S.S.S.”基本事实及运用 基本事实：三__边__分别相等的两个三角形全等．简记为 S.S.S.(或边边边)．
13.2.5 边边边
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
► 知识点二 尺规作图的步骤及作图语言的规范
1．尺规作图的步骤 (1)已知：当作图题是用文字语言叙述的，要根据文字语言用数学语言 写出题目中的条件； (2)求作：根据题目写出要求作出的图形及此图形应满足的条件； (3)作法：根据作图的过程写出每一步的操作过程．当不要求写作法时 ，要保留作图痕迹．对于较复杂的作图，可先画出草图，使它同所要作的 图形大致相同，然后借助草图寻找作法． 2．作图语言的规范叙述 用直尺作图时的规范语言主要有：(1)过点×作直线××，作线段×× ，以点×为端点作射线××；(2)连结××，以点×为端点作线段××，延 长线段××到点×；延长线段××到点×，使××＝××. 用圆规作图时的规范语言主要有：(1)以点×为圆心，××为半径作圆；(2) 以点×为圆心，××为半径作弧交××于点×；(3)在××上截取一点×， 使××＝××.
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
[归纳总结] 注意：(1)求作两角和或差时，一定要注明“外 部”或“内部”；
(2)求作三角形，一般情况下先作线段再作角，并结合全等 三角形的判定方法作图；
(3)本题实质是已知两角及其夹边作三角形．由“角边角” 定理，在此条件下所作的三角形是唯一的．一般情况下先作线 段，再作两个角，必须指明在线段的同侧，否则不会相交．基 本作图的“作法”不必再详说，如作线段 AB 的步骤，作∠BAM ＝∠α 的步骤，但必须保留作图痕迹．
13.2.5 边边边
[归纳总结] 证明三角形全等的步骤： 第一步：从已知出发，探究要证明的相等的线段或角分别 在哪两个全等三角形中； 第二步：分解图形——将所证全等三角形从“复合”图形 中分离出来； 第三步：“移植”条件——将已知条件转移到图形中，再 根据已知条件及隐含条件寻求恰当的证明方法．
可以确定△ABC 与△A′B′C′的关系是
全等
．
你能用一句话概括出三角形全等的这种判定方法吗？
◆知识链接——[新知梳理]知识点一
13.2.5 边边边
新知梳理
► 知识点一 “S.S.S.”基本事实及运用 基本事实：三__边__分别相等的两个三角形全等．简记为 S.S.S.(或边边边)．
13.2.5 边边边
13.4.1 作一条线段等于已知线段 13.4.2 作一个角等于已知角
► 知识点二 尺规作图的步骤及作图语言的规范
1．尺规作图的步骤 (1)已知：当作图题是用文字语言叙述的，要根据文字语言用数学语言 写出题目中的条件； (2)求作：根据题目写出要求作出的图形及此图形应满足的条件； (3)作法：根据作图的过程写出每一步的操作过程．当不要求写作法时 ，要保留作图痕迹．对于较复杂的作图，可先画出草图，使它同所要作的 图形大致相同，然后借助草图寻找作法． 2．作图语言的规范叙述 用直尺作图时的规范语言主要有：(1)过点×作直线××，作线段×× ，以点×为端点作射线××；(2)连结××，以点×为端点作线段××，延 长线段××到点×；延长线段××到点×，使××＝××. 用圆规作图时的规范语言主要有：(1)以点×为圆心，××为半径作圆；(2) 以点×为圆心，××为半径作弧交××于点×；(3)在××上截取一点×， 使××＝××.
第14节线段、角、相交线与平行线-中考数学一轮知识复习课件
☞命题点3 平行线的性质与判定(必考) 7.(2019·广东 12 题 4 分)如图，已知 a∥b，∠1＝
75°，则∠2＝___1_0_5_°__.
8．(2020·郴州)如图，直线 a，b 被直线 c， d 所截，下列条件能判定 a∥b 的是( D )
A.∠1＝∠3 B．∠2＋∠4＝180° C．∠4＝∠5 D．∠1＝∠2
O，OA 平分∠EOC，∠EOC＝100°，则∠BOD 的度数
是( C )
A．20°
B．40°
C．50°
D．80°
2．(2020·吉林)如图，某单位要在河岸 l 上建一个 水泵房引水到 C 处，他们的做法是：过点 C 作 CD⊥l 于点 D，将水泵房建在了 D 处．这样做最节省水管长 度，其数学道理是_垂__线__段__最__短___.
针对训练 9．(2020·常德)如图，已知 AB∥DE，∠1 ＝30°，∠2＝35°，则∠BCE 的度数为( B )
A．70° C．30°
B．65° D．5°
10．(2020·武汉)如图，直线 EF 分别与直线 AB，
CD 交于点 E，F.EM 平分∠BEF，FN 平分∠
CFE，且 EM∥FN.求证：AB∥CD.
第四章 三角形
第十四节 线ห้องสมุดไป่ตู้、角、相交线与平行线
课标解读
1.点、线、面、角 (1)会比较线段的长短，理解线段的和、差，以及线 段中点的意义． (2)能运用基本事实：两点确定一条直线和两点之间 线段最短解决相关问题． (3)能比较角的大小，并会计算角的和、差．
2．相交线与平行线 (1)能运用对顶角相等，同角(等角)的余角相等，同 角(等角)的补角相等进行计算或证明． (2)能过一点画已知直线的垂线；能度量点到直线的 距离；掌握基本事实：过一点有且只有一条直线与已 知直线垂直． (3)会辨认同位角、内错角、同旁内角，能运用平行 线的性质定理和判定定理进行计算或证明；能用三角 尺和直尺过已知直线外一点画这条直线的平行线． (4)会用平行于同一条直线的两条直线平行进行推理 证明．
小学数学四年级下册冀教 第四单元 线和角 第1课时--线 课件
第1课时 线
JJ 四年级上册
四 线和角
1 课堂探究点
（1）认识线段、直线和射线 （2）画指定长度的线段
2 课时流程
探索 新知
课堂 小结
当堂 检测
课后 作业
仔细观察路灯的光线，你发现了什么？
探究点1 认识线段、直线和射线
绷紧的弓弦、人行横道线都可以近似地看作线段。 把一条线段向两端无限延伸就得到一条直线。
把一条线段向一个方向无限延伸就形成了射线。
线段、直线和射线有什么共同点和不同点？
生活中，有哪些事物可以近似地看作线段或射线？
探究点2 画指定长度的线段
画出的线段可以记作：AB=4厘米。
小试牛刀
2．画一条比3厘米长2厘米的线段。
Hale Waihona Puke 归纳总结：1．线段、射线、直线都是直的。直线、射线无限 长，只有线段能量出长度。
4. 下面分别给出了 3个点、4个点和5个点。在每相邻
的两个点 之间画线段。
. ..
.. ..
. ..
..
三角形
长方形
五边形
易错辨析
3．填空。 下图中有( 6 )条射线。
辨析：数射线时不要遗漏中间的点。
2．过一点能画无数条直线，过两点只能画一条直 线和一条线段，但能画两条射线。
3．画线段要画两个端点，还要标明线段的长度。
夯实基础
1.说出下面各条线的名称。
①射线 ②直线 ③曲线 ④线段
2. 自己画一条线段，标明线段的长度。
3. 量一量下面线段的长。
AB=________ AC=_________ AD= ________ BD=________ BC=_________ CD= ________
JJ 四年级上册
四 线和角
1 课堂探究点
（1）认识线段、直线和射线 （2）画指定长度的线段
2 课时流程
探索 新知
课堂 小结
当堂 检测
课后 作业
仔细观察路灯的光线，你发现了什么？
探究点1 认识线段、直线和射线
绷紧的弓弦、人行横道线都可以近似地看作线段。 把一条线段向两端无限延伸就得到一条直线。
把一条线段向一个方向无限延伸就形成了射线。
线段、直线和射线有什么共同点和不同点？
生活中，有哪些事物可以近似地看作线段或射线？
探究点2 画指定长度的线段
画出的线段可以记作：AB=4厘米。
小试牛刀
2．画一条比3厘米长2厘米的线段。
Hale Waihona Puke 归纳总结：1．线段、射线、直线都是直的。直线、射线无限 长，只有线段能量出长度。
4. 下面分别给出了 3个点、4个点和5个点。在每相邻
的两个点 之间画线段。
. ..
.. ..
. ..
..
三角形
长方形
五边形
易错辨析
3．填空。 下图中有( 6 )条射线。
辨析：数射线时不要遗漏中间的点。
2．过一点能画无数条直线，过两点只能画一条直 线和一条线段，但能画两条射线。
3．画线段要画两个端点，还要标明线段的长度。
夯实基础
1.说出下面各条线的名称。
①射线 ②直线 ③曲线 ④线段
2. 自己画一条线段，标明线段的长度。
3. 量一量下面线段的长。
AB=________ AC=_________ AD= ________ BD=________ BC=_________ CD= ________
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：因为∠COF＋∠BOE＝∠EOF－∠BOC＝60°－20°＝40°， 因为OE平分∠AOB，所以∠AOB＝2∠BOE，因为OF平分∠COD， 所以∠COD＝2∠COF，所以∠COD＋∠AOB＝2(∠COF＋∠BOE) ＝2×40°＝80°，所以∠AOD＝∠COD＋∠AOB＋∠BOC＝80° ＋20°＝100°
8．如图，将一块直角三角板的直角顶点放在直线AB上，若∠1＝ 40°，则∠2＝_5_0__°. 9．如图，点C是线段AB上的一点，点D是AC的中点，若AB＝8 cm， BC＝2 cm，则AC＝__6__cm，BD＝___5_cm.
10．延长线段 AB 到 C，使 BC＝21AB，点 D 是 AC 的中点，点 E 是
BC 的中点，若 CE＝2 cm，则 DE＝_4___cm. 11．如图，∠AOC＝15°，∠BOC＝45°，OD 平分∠AOB，则∠COD ＝__1_5_°___．
12．如图，直线 AB 和 CD 相交于点 O，OE 平分∠DOB，∠AOC＝ 40°，则∠DOE＝_2_0__度． 13．如图，点 C，D 是线段 AB 上的两点，AC＝7 cm，BD＝5 cm，E
谢谢观赏
You made my day!
我们，还在路上……
5．如图，C，D是线段AB的三等分点，E是线段CD的中点，则下列 结论错误的是( D )
A．AC＝CD＝BD B．AE＝BE C．AD＝4DE D．CE＝15AB
6．一轮船A观测灯塔B在其北偏西50°，灯塔C在其南偏西40°，试问 此时∠BAC＝( B ) A．80° B．90° C．40° D．不能确定 7．如图，OM平分∠AOB，ON平分∠COD，若∠AOD＝84°， ∠MON＝68°，则∠BOC的度数为( C ) A．48° B．50° C．52° D．54°
•
15、最具挑战性的挑战莫过于提升自 我。。2021年3月2021/3/52021/3/52021/3/53/5/2021
•
16、业余生活要有意义，不要越轨。2021/3/52021/3/5Marc h 5, 2021
•
17、一个人即使已登上顶峰，也仍要 自强不 息。2021/3/52021/3/52021/3/52021/3/5
•
12、越是无能的人，越喜欢挑剔别人 的错儿 。2021/3/52021/3/52021/3/5Fr iday, March 05, 2021
•
13、知人者智，自知者明。胜人者有 力，自 胜者强 。2021/3/52021/3/52021/3/52021/3/53/5/2021
•
14、意志坚强的人能把世界放在手中 像泥块 一样任 意揉捏 。2021年3月5日星期 五2021/3/52021/3/52021/3/5
•
9、有时候读书是一种巧妙地避开思考 的方法 。2021/3/52021/3/5Fr iday, March 05, 2021
•
10、阅读一切好书如同和过去最杰出 的人谈 话。2021/3/52021/3/52021/3/53/5/2021 9:33:56 AM
•
11、越是没有本领的就越加自命不凡 。2021/3/52021/3/52021/3/5M ar-215- Mar-21
A．10
B．9
C．6
D．5
3．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD ＝25°，则∠AOB等于( B ) A．120° B．100° C．75° D．50°
4．已知，O是直线AB上的一点，∠AOC＝40°，∠COD是直角，
OE平分∠BOC，则∠DOE的度数为( B ) A．10° B．20° C．25° D．30°
综合训练 线段与角的计算
1．如图，点C是线段AB的中点，点D是线段BC的中点，若AB＝ 10 cm，则线段CD的长为( B )
A．1.5 cm C．3 cm
B．2.5 cm D．5 cm
2．如图，点 C 是线段 AB 上的一点，AC＝15AB，点 D 是线段 BC 的 中点，若 AB＝15，则 AD 的长为( B )
16．如图，E是线段AB的一个三等分点，F是线段AB的中点，若 EF＝1，求线段BF的长．
解：设线段 AB 的长为 x，因为 E 为线段 AB 的一个三等分点，所 以 AE＝31AB＝13x，因为 F 为线段 AB 的中点，所以 AF＝12AB＝12x， 所以 EF＝AF－AE＝12x－13x＝61x＝1，所以 x＝6，即 AB＝6，所以 BF＝12AB＝12×6＝3
∠COE＝∠COD＋∠DOE＝90°－32x＋x＝72°，解得 x＝36°，即 ∠DOE＝36°，所以∠BOD＝3∠DOE＝108°，所以∠EOB＝∠BOD －∠DOE＝108°－36°＝72°
18．如图，OE平分∠AOB，OF平分∠COD，若∠EOF＝60°， ∠BOC＝20°，求∠AOD的度数．
是 CD 的中点，若 CD＝15AB，则 CE＝__1__cm，AD＝__5__cm.
14．如图，点 M 是线段 AB 的中点，点 N 在线段 BM 上，MN＝35AM， 若 MN＝3 cm，求线段 AB，BN 的长．
解：因为 MN＝35AM，且 MN＝3，所以35AM＝3，则 AM＝5.因为 M 为线段 AB 的中点，所以 AB＝2AM＝2×5＝10，BM＝AM＝5，所 以 BN＝BM－MN＝5－3＝2.即 AB 的长为 10 cm，BN 的长为 2 cm
15．如图，线段AB＝8 cm，M为线AB的中点，点C为线段MB上的 一点，且MC＝2 cm，点N为线段AC的中点，求线段MN的长．
解：因为 M 为 AB 的中点，所以 AM＝12AB＝12×8＝4，所以 AC ＝AM＋MC＝4＋2＝6.因为 N 为 AC 的中点，所以 AN＝12AC＝12 ×6＝3，所以 MN＝AM－AN＝4－3＝1(cm)
∠COE
，
所
以
∠3
＝
1 2
∠COE
＝
1 2
×46
°
＝
23°
(2) 因 为 ∠AOD ＝
∠AOC＋∠3＝40°＋23°＝63°，OA 为正东方向，所以有 90°－63°
＝27°，所以 OD 在北偏东 27°的位置 (3)设此时为 3 点过 x 分钟，
依题意，得21x＋90－6x＝63，解得 x＝41110，即此时为 3 点过 41110分
17．如图，点 O 在直线 AB 上，OC 是∠AOD 的平分线，OE 在∠BOD 内，∠DOE＝31∠BOD，∠COE＝72°，求∠EOB 的度数．
解：设∠DOE＝x，因为∠DOE＝13∠BOD，所以∠BOD＝3∠DOE ＝3x，所以∠AOD＝180°－∠BOD＝180°－3x，因为 OC 是∠AOD 的平分线，所以∠COD＝12∠AOD＝12(180°－3x)＝90°－32x，所以
19．如图，已知∠1＝20°，∠AOE＝86°，OB平分∠AOC，OD 平分∠COE. (1)求∠3的度数； (2)若以O为观察中心，OA为正东方向，射线OD在什么位置？ (3)若以OA为钟面上的时针，OD为分针，且OA正好在“3”的下方 不远，你知道此时的时刻吗？
解：(1)因为 OB 平分∠AOC，所以∠AOC＝2∠1＝2×20°＝40°， 所以∠COE＝∠AOE－∠AOC＝86°－40°＝46°，因为 OD 平分
8．如图，将一块直角三角板的直角顶点放在直线AB上，若∠1＝ 40°，则∠2＝_5_0__°. 9．如图，点C是线段AB上的一点，点D是AC的中点，若AB＝8 cm， BC＝2 cm，则AC＝__6__cm，BD＝___5_cm.
10．延长线段 AB 到 C，使 BC＝21AB，点 D 是 AC 的中点，点 E 是
BC 的中点，若 CE＝2 cm，则 DE＝_4___cm. 11．如图，∠AOC＝15°，∠BOC＝45°，OD 平分∠AOB，则∠COD ＝__1_5_°___．
12．如图，直线 AB 和 CD 相交于点 O，OE 平分∠DOB，∠AOC＝ 40°，则∠DOE＝_2_0__度． 13．如图，点 C，D 是线段 AB 上的两点，AC＝7 cm，BD＝5 cm，E
谢谢观赏
You made my day!
我们，还在路上……
5．如图，C，D是线段AB的三等分点，E是线段CD的中点，则下列 结论错误的是( D )
A．AC＝CD＝BD B．AE＝BE C．AD＝4DE D．CE＝15AB
6．一轮船A观测灯塔B在其北偏西50°，灯塔C在其南偏西40°，试问 此时∠BAC＝( B ) A．80° B．90° C．40° D．不能确定 7．如图，OM平分∠AOB，ON平分∠COD，若∠AOD＝84°， ∠MON＝68°，则∠BOC的度数为( C ) A．48° B．50° C．52° D．54°
•
15、最具挑战性的挑战莫过于提升自 我。。2021年3月2021/3/52021/3/52021/3/53/5/2021
•
16、业余生活要有意义，不要越轨。2021/3/52021/3/5Marc h 5, 2021
•
17、一个人即使已登上顶峰，也仍要 自强不 息。2021/3/52021/3/52021/3/52021/3/5
•
12、越是无能的人，越喜欢挑剔别人 的错儿 。2021/3/52021/3/52021/3/5Fr iday, March 05, 2021
•
13、知人者智，自知者明。胜人者有 力，自 胜者强 。2021/3/52021/3/52021/3/52021/3/53/5/2021
•
14、意志坚强的人能把世界放在手中 像泥块 一样任 意揉捏 。2021年3月5日星期 五2021/3/52021/3/52021/3/5
•
9、有时候读书是一种巧妙地避开思考 的方法 。2021/3/52021/3/5Fr iday, March 05, 2021
•
10、阅读一切好书如同和过去最杰出 的人谈 话。2021/3/52021/3/52021/3/53/5/2021 9:33:56 AM
•
11、越是没有本领的就越加自命不凡 。2021/3/52021/3/52021/3/5M ar-215- Mar-21
A．10
B．9
C．6
D．5
3．如图，OC是∠AOB的平分线，OD是∠AOC的平分线，且∠COD ＝25°，则∠AOB等于( B ) A．120° B．100° C．75° D．50°
4．已知，O是直线AB上的一点，∠AOC＝40°，∠COD是直角，
OE平分∠BOC，则∠DOE的度数为( B ) A．10° B．20° C．25° D．30°
综合训练 线段与角的计算
1．如图，点C是线段AB的中点，点D是线段BC的中点，若AB＝ 10 cm，则线段CD的长为( B )
A．1.5 cm C．3 cm
B．2.5 cm D．5 cm
2．如图，点 C 是线段 AB 上的一点，AC＝15AB，点 D 是线段 BC 的 中点，若 AB＝15，则 AD 的长为( B )
16．如图，E是线段AB的一个三等分点，F是线段AB的中点，若 EF＝1，求线段BF的长．
解：设线段 AB 的长为 x，因为 E 为线段 AB 的一个三等分点，所 以 AE＝31AB＝13x，因为 F 为线段 AB 的中点，所以 AF＝12AB＝12x， 所以 EF＝AF－AE＝12x－13x＝61x＝1，所以 x＝6，即 AB＝6，所以 BF＝12AB＝12×6＝3
∠COE＝∠COD＋∠DOE＝90°－32x＋x＝72°，解得 x＝36°，即 ∠DOE＝36°，所以∠BOD＝3∠DOE＝108°，所以∠EOB＝∠BOD －∠DOE＝108°－36°＝72°
18．如图，OE平分∠AOB，OF平分∠COD，若∠EOF＝60°， ∠BOC＝20°，求∠AOD的度数．
是 CD 的中点，若 CD＝15AB，则 CE＝__1__cm，AD＝__5__cm.
14．如图，点 M 是线段 AB 的中点，点 N 在线段 BM 上，MN＝35AM， 若 MN＝3 cm，求线段 AB，BN 的长．
解：因为 MN＝35AM，且 MN＝3，所以35AM＝3，则 AM＝5.因为 M 为线段 AB 的中点，所以 AB＝2AM＝2×5＝10，BM＝AM＝5，所 以 BN＝BM－MN＝5－3＝2.即 AB 的长为 10 cm，BN 的长为 2 cm
15．如图，线段AB＝8 cm，M为线AB的中点，点C为线段MB上的 一点，且MC＝2 cm，点N为线段AC的中点，求线段MN的长．
解：因为 M 为 AB 的中点，所以 AM＝12AB＝12×8＝4，所以 AC ＝AM＋MC＝4＋2＝6.因为 N 为 AC 的中点，所以 AN＝12AC＝12 ×6＝3，所以 MN＝AM－AN＝4－3＝1(cm)
∠COE
，
所
以
∠3
＝
1 2
∠COE
＝
1 2
×46
°
＝
23°
(2) 因 为 ∠AOD ＝
∠AOC＋∠3＝40°＋23°＝63°，OA 为正东方向，所以有 90°－63°
＝27°，所以 OD 在北偏东 27°的位置 (3)设此时为 3 点过 x 分钟，
依题意，得21x＋90－6x＝63，解得 x＝41110，即此时为 3 点过 41110分
17．如图，点 O 在直线 AB 上，OC 是∠AOD 的平分线，OE 在∠BOD 内，∠DOE＝31∠BOD，∠COE＝72°，求∠EOB 的度数．
解：设∠DOE＝x，因为∠DOE＝13∠BOD，所以∠BOD＝3∠DOE ＝3x，所以∠AOD＝180°－∠BOD＝180°－3x，因为 OC 是∠AOD 的平分线，所以∠COD＝12∠AOD＝12(180°－3x)＝90°－32x，所以
19．如图，已知∠1＝20°，∠AOE＝86°，OB平分∠AOC，OD 平分∠COE. (1)求∠3的度数； (2)若以O为观察中心，OA为正东方向，射线OD在什么位置？ (3)若以OA为钟面上的时针，OD为分针，且OA正好在“3”的下方 不远，你知道此时的时刻吗？
解：(1)因为 OB 平分∠AOC，所以∠AOC＝2∠1＝2×20°＝40°， 所以∠COE＝∠AOE－∠AOC＝86°－40°＝46°，因为 OD 平分