中南大学系统可靠性分析与评价作业答案(课堂PPT)
系统可靠性分析方法ppt课件
任务剖面、任务阶段
分析明确系统中的产品在完成不同的任务时所应具备 的功能、工作方式及工作时间等
功能描述
确定故障判据
制定系统及产品的故障判据。选择FMECA方法等
故障判据 分析方法
13
②故障模式影响分析FMEA
依据。
依据。
10
FMECA的步骤
1 系统定义
2 FMEA
3CA
明 确 分 析 范 围
产 品 功 能 与 任 务 分 析
确 定 故 障 判 据
故 障 模 式 分 析
故 障 原 因 分 析
故 障 影 响 分 析
故 障 检 测 方 法 分 析
补 偿 措 施 分 析
危 害 性 分 析
得 出 分 析 结 果
25
实施FMECA应注意的问题
重视FMECA的策划
实施FMECA前，应对所需进行的FMECA活动进行完整、全面、 系统地策划，尤其是对复杂大系统，更应强调FMECA的重要性。 其必要性体现在以下几方面：
结合产品研制工作，运用并行工程的原理，对所需的FMECA进行完 整、全面、系统地策划，将有助于保证FMECA分析的目的性、有效 性，以确保FMECA工作与研制工作同步协调，避免事后补做的现象。
保证FMECA的实时性、规范性、有效性
实时性。FMECA工作应纳入研制工作计划、做到目的明确、 管理务实；FMECA工作与设计工作应同步进行，将FMECA 结果及时反馈给设计过程。
FMECA的发展 设计阶段发现对系统造成重大影响的元部件故
障 设计更改、可靠性补偿
是可靠性、维修性、保障性和安全性设计 分析的基础
系统工程导论第十章系统可靠性.ppt
❖
1994年版ISO 9000把R．M．S．T．不叫广义可靠性，而是取了一个
名词Depend Ability(可信性)。可信性是用于表述可用性及其影响因素
(可靠性、维修性和保障性)的综合术语，仅用于非定量的总体描述。这
个概念是随着科学技术的发展，尤其是军事技术的发展而发展起来的。
❖
可信性的概念更加体现了系统可靠性的思想，其目标是：提高产品
❖ 对于电子元器件而言，随着环境变化、电源电 压变化等，不仅有漂移性变化，还伴随着储存和使 用时间在进行着不可逆的特性参数值退化的变化。
❖ 4．环境防护设计
❖ 环境条件就是指产品在储存、运输和工作过程 中可能遇到的一切外界影响。环境条件对产品的可 靠性有着重大的影响。如：温度、湿度、霉菌、盐 雾、尘埃、电磁干扰等。所以要进行抗干扰设计、 “三防”设计等。
❖ 2．降额设计
❖ 电子设备可靠性降额设计，主要是指构 成电子设备的元器件使用中所承受的应力(主 要是电应力和温度应力)低于其设计的额定值， 以达到延缓参数退化，延长工作寿命，提高 使用可靠性的目的。
❖ 施加在电子元器件上的电应力、热应力 大小直接影响电子元件的失效率高低。
❖ 3．动态设计
第十章 系统可靠性 10．1 引言 10．2 系统可靠性的基本 概念 10．3 系统可靠性模型 10．4 系统可靠性设计 10．5 系统可靠性分配
❖ 10．1 引言
❖
本章介绍系统可靠性(system reliability )，目的在于加深理解
系统概念。我们将会看到，同样的几个元件，组成不同结构的系统，其
造、使用和维修的整个过程之中。可靠性技术是一门综合性的工程技术，
是系统工程的一个重要组成部分。
❖ 10．2．2 系统可靠性的含义
系统可靠性原理习题及答案
系统可靠性原理习题及答案1、 元件可靠性的定义是什么？规定条件、规定时间、规定功能各是什么含义？ 解：元件的可靠性：元件在规定的吋间内、规定条件下完成规定功能的能力。
规定时间：指保修期、使用期和贮存期。
规定条件：即使用条件，主要包括：环境条件、包装条件、贮存条件、维 修条件，操作人员条件等。
规定功能：指元件/系统的用途。
2、 元件的可靠度、故障率和平均寿命各是怎么定义的？解：元件的可靠度：在规定条件下，在时刻t 以前正常工作的概率。
元件故障率：即故障率函数，元件在t 时刻以前正常工作，在t 时刻后单 位时间内发生故障的(条件)概率。
平均寿命：即平均无故障工作时间，也称做首次故障平均时间，是寿命的 期望值。
3、 设某种元件的X=0.001/h,试求解：(1)由这种元件组成的二元件并联系统、两元件串联、2/3 (G)系统的平 均寿命。
解:由题意可知,单个元件的可靠度为Rj(t)=e'M , i=l, 2, 3。
A 、二元件并联： 系统的可靠度为： R p (t)=l-(l-R 1(t))(l-R 2(t))=2e At -e-2At 此时系统的平均寿命为由于 1=0.001/h,故 MITF=1500(h)B 、二元件串联： 系统的可靠度为： Rs(t)=Ri(t)R 2(t)=e 2M此时系统的平均寿命为由于 X=0.001/h,故 MTTF=500(h)C 、2/3 (G)系统： 系统的可靠度为：RG("Rdt)R2(t)R3(t)+⑴ Rdt))R2(t)R3(t)+R 丄⑴⑴ R2(t))R3(t)+R"t)R2(t)⑴也⑴)=3严2严此时系统的平均寿命为由于 D ・001/h,故 MTTF=2500/3 (h)(2) t=100h, 500h,1000h时，由这种元件组成的二元件并联系统、两元件串MTTF= R G (t)dt53e"2Xt 一 2e"3At dt =—32e"At _ e _2At dt =—Z联、2/3 （G ）系统的可靠度分别是多少？ 解：将各t 值代入⑴中的各可靠度R （t ）即可得结果。
系统可靠性模型和可靠度计算ppt课件
19
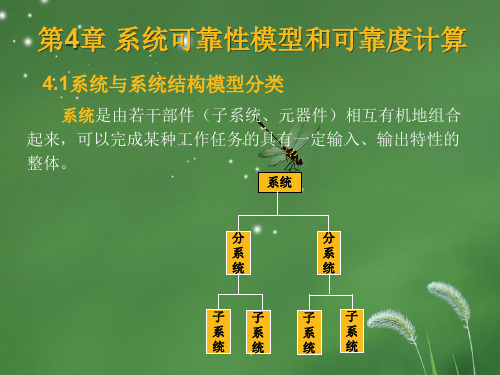
第4章 系统可靠性模型和可靠度计算
（2）n-r/n表决系统 n个单元并联，只允r个单元失效的系统，当各个单元的
可靠度相同时，系统的可靠度为
Rs Rn nRn1F Cn2 Rn2 F 2 Cnr Rnr F r
20
第4章 系统可靠性模型和可靠度计算
3、混联系统可靠度计算 把若干个串联系统或并联系统重复地加以串联或并联，就得
弹药系统可靠性模型
一般弹药系统的可靠 性指标分为安全性、 作用可靠性与贮存可 靠性。
第4章 系统可靠性模型和可靠度计算
可靠性模型：是为预计或估算产品的可靠性所建立的数学 模型和可靠性框图。
基本可靠性：产品在规定条件下无故障的持续时间和概率。 基本可靠性模型是用来估计产品及组成元件引起的维修及保障 要求。它是一个串联模型，即使存在冗余单元，也按串联处理。 系统中任一单元发生故障都需要维修或更换。储备元件越多， 系统的基本可靠性越低。
狭义的定义：弹药是装有火炸药或化学战剂,能投射到敌方达到杀伤、破 坏或其他战术目的的物体的总称。
按此定义弹药的范围较窄：它不包括地雷、水雷、地雷以及爆破筒、爆 破罐、炸药包等使用时不需要投射的爆炸物。
本书所研究的弹药可靠性，主要指狭义的弹药。
28
第4章 系统可靠性模型和可靠度计算
弹药的一般组成
弹药系统一般由战斗部分和投射部分组成。
隔爆机构
隔爆机构A
隔爆机构B
引信隔爆机构结构框图
隔爆机构A
隔爆机构B 引信保险状态的可靠性框图 两套保险有一套正常工作
隔爆机构正常
隔爆机构A 隔爆机构B
引信解除状态的可靠性框图 两套保险机构都解除保险 机构正常工作
11
第4章 系统可靠性模型和可靠度计算
【高质量】可靠性评估与故障分析PPT文档
表示无故障工作时间T的期望E (T) 。
分析可知，可靠度函数 、失效率函数之间的关系为：
用户平均停电分钟数SAIDI : 用户持续停电的总分钟数除以用户总数，单位是分钟/(用户年)
(t) dr(t)
Ns (t)dt 式中 (t) ——故障率；
dr (t ) ——t 时刻后，dt时间内故障的产品数；
N s (t) —残存产品数，即到t 时刻尚未故障的产品数。
分析可知，可靠度函数 、失效率函数之间的关系为：
R(t) e0t(t)dt
大多数产品的故障率随时间的变化曲线形似浴盆，称之
如何对这些故障进行归纳和组织，以便更清晰地反映 设备故障与生产工艺和运行环境密切相关，由于不同时期设计的设备结构不同，所以引发设备事故的主要故障类型也在逐渐变化 。
表示无故障工作时间T的期望E (T) 。
可靠度及可靠度函数
故障间的因果关系。成为进一步研究的重点。 设备故障与生产工艺和运行环境密切相关，由于不同时期设计的设备结构不同，所以引发设备事故的主要故障类型也在逐渐变化 。
3.2 电气设备故障调查
电气设备的可靠性评估，不仅要对可靠性指标评估，更重 要的是找到提高可靠性的途径。因而要对故障或者失效的 模式、机理和失效原因进行分析。失效模式分析就包括故 障调查，电气设备失效分析最常用的是故障树方法。失效 模式、机理、原因的分析也是设备状态监测、故障诊断的 主要内容。
故障＝设备的“病”
或门
为了提高设备故障诊断的水平，需要对设备故障有一个系统的认识，这不仅有助于预防自然发生的故障，同时也有利于阻止人们可能 引发故障的过失行为。
割集代表了系统故障发生的一种可能模式。
其意义在于它能描述系统故障时所必须要修理的基本故障，代表系统中的薄弱环节。
《系统可靠性分析》PPT课件
d t
0
假设n(t)表示t时刻失效的产品数，△n(t)表示在(t, t+△t)时间内失效的产品数。
累 积 失 效 概 率 为 ： F ˆ(t)= 到 t时 试 刻 验 失 产 效 品 的 总 产 数 品 数 = n N (t)
失效概率密度为:
3、失效率
(1)失效率定义
失效率(瞬时失效率)是：“工作到t时刻尚未 失效的产品，在该时刻t后的单位时间内发生失效 的概率”，也称为失效率函数，记为λ(t)。由失 效率的定义可知，在t时刻完好的产品，在(t， t+△t)时间内失效的概率为：
5、寿命方差与标准差
平均寿命能够说明一批产品寿命的平均 水平，而寿命方差和寿命标准差则能够反映 产品寿命的离散程度。产品寿命方差的定义 为：
2 ( t -) 2f(t)d t t2f(t)d t2
0
0
如果n个产品抽样测试的寿命分别为t1，t2，…， tn，产品寿命平均值与方差分别为：
可修产品平均寿命MTBF估计值为：
MTTF
1
n
nj
tij
N i1 j1
式中：N为测试产品所有的故障数； ni为第i个测试产品的故障数；
如果仅考虑首次失效 前的一段工作时间，
tij为第i个产品第j-1次故障到第j次故障 的工作时间，单位为h。
两者平均寿命θ估
计值为：
所 有 产 总 品 的 总 故 的 障 工 数 作 时 间 N 1iN 1ti
P(t)=P(T>t) P(t)具有下面三条性质： (1)P(t)为时间的递减函数； (2)0≤ P(t) ≤ 1； (3)P(t=0)=1；P(t=∞)=0 系统或设备的可靠性是一个与时间有密切关系的 量，使用时间越长，系统越不可靠。
3 系统可靠性分析
当λ=0.001时
Rij (t ) e t 服从指数分布，此时，串 并联系统可靠度为： R (t ) 1 [1 e-mt ]n
(2) 并---串联系统
并---串联系统是由一部 分单元先并联组成一些子系 统，再由这些子系统组成一 个串联系统，如右图。
当λ=0.001时
可靠性框图
使水流出系统属串联系统，使水关闭系统属并联系统。 并—串联系统框图
串--并联系统框图
2、串联系统
由n个单元组成的串联系统表示当这n个单元都 正常工作时，系统才正常工作，换句话说，当系统任 一单元失效时，就引起系统失效。 串联系统可靠度计算如下
R串联 (t ) P( X t ) P( X1 t X 2 t X n t ) P( X i t ) Ri (t )
第三章 系统可靠性分析
第三章 系统可靠性分析
所谓系统，是为了完成某一特定功能，由 若干个彼此有联系而且又能相互协调工作的单 元所组成的综合体。系统可以是机器、设备、 部件和零件；单元也可以是机器、设备、部件 和零件。系统和单元的含义是相对而言的，由 研究的对象而定。 系统可以分为可修复系统与不可修复系 统两类。
习题19:
系统的可靠性框图如下图所示，R1=R2=0.9， R3=R4=0.8，R5=R6=0.7，R7=R8=0.6 求系统的可靠度。
1 2
3 5 4 6 7 8
习题18:设各单元可靠度相同，均为R0=0.99
(1)四个单元串联构成的串联系统 R4个串联 (t ) Ri (t ) R04 0.9606
可修复系统
技术上不能修 经济上不值得修
不可修复系统
一次性使用不必修复
3.1 不可修复系统可靠性分析
可靠性习题(答案)
答案……10页系统可靠性习题学号___________ 姓名___________第一章习题1—1如图所示，有三个阀门连在一起。
阀门如发生故障，水便不能通过。
设三个阀门发生故障的概率均为p。
求水能流过a、c的概率。
图1—11-2判断系统是否正常工作,采用“多数表决”,即有两个或三个单元正常工作,系统就可正常工作。
如各单元的可靠工作概率为R，表决器可靠工作概率为1，求系统的可靠工作概率。
工作单元图1—2 2/3多数表决系统1—3信号机灯泡使用时数在1000小时以上概率为0.2，求三显示信号机三个灯泡在使用1000小时后最多有一个坏了的概率.1—4在某个车站电气集中设备中有800个继电器.设在某段时间里每个继电器的故障率为0。
005。
求在这段时间内不多于10个继电器故障的概率。
1—5某产品先后通过A、B、C三种机器加工,这些机器的偶然故障及人为原因将影响产品质量.产品是否合格只有在生产全过程终了时才能检查出来。
根据统计资料，三种产品的合格率分别为30%，40％和20％。
假设机器独立运转，求产品的合格率。
1-6计算机内第K个元件在时间T内发生故障的概率等于P K(K=1,2……n)。
所有元件的工作是相互独立的，如果任何一个元件发生故障计算机就不能正常工作。
求在时间T内计算机正常工作的概率。
1-7电路由电池Ⅰ与两个并联的电池Ⅱ、Ⅲ串联而成。
设电池Ⅰ、Ⅱ、Ⅲ损坏的概率分别为0.3、0.2和0.2，各个电池损坏与否是独立的。
求电路由于电池损坏而发生故障的概率。
1-8 电路由五个元件联接而成，设各个元件发生故障是独立的，已知元件1、2发生断路故障的概率各为0.2，元件3、4、5发生断路故障的概率为0。
5，求：⑴由于元件1或2发生断路故障而电路断路的概率；⑵由于元件3、4、5都发生断路故障而电路断路的概率；⑶由于任何元件发生断路故障而电路断路的概率.第二章习题2—1有两种零件,一种寿命分布呈指数型,平均寿命为1000小时；另一种寿命分布呈正态型，平均寿命为900小时,标准离差为400小时。
系统评价习题答案
系统评价习题答案系统评价习题答案随着教育的发展，习题作为一种常见的教学形式，被广泛应用于各个学科的教学中。
而对于学生来说，习题答案的准确性和科学性是他们学习的重要保障。
因此，对习题答案进行系统评价显得尤为重要。
本文将探讨系统评价习题答案的意义、方法以及存在的问题。
一、系统评价习题答案的意义1.提高教学质量系统评价习题答案可以帮助教师及时发现和纠正教学中存在的问题，提高教学质量。
通过对习题答案进行评价，教师可以了解学生对知识点的掌握情况，及时调整教学内容和方法，使教学更加精准有效。
2.促进学生学习系统评价习题答案可以帮助学生更好地理解和掌握知识点。
通过对习题答案的分析，学生可以了解自己的答题情况，找出错误和不足之处，从而更好地改进学习方法，提高学习效果。
3.提高教学评价的科学性系统评价习题答案可以为教学评价提供科学的依据。
通过对习题答案的评价，可以客观地反映学生的学习水平和教学效果，为教学评价提供参考依据，确保评价结果的公正、准确。
二、系统评价习题答案的方法1.准确性评价准确性评价是对习题答案正确与否的评价。
评价者可以通过对习题答案进行对比，检查答案的正确性。
同时，还可以参考教材和相关参考书的答案，确保评价的准确性。
2.完整性评价完整性评价是对习题答案是否包含所有必要内容的评价。
评价者可以检查习题答案是否涵盖了所有关键知识点，并且答案是否清晰明了，没有遗漏或模糊之处。
3.科学性评价科学性评价是对习题答案解题思路和方法的评价。
评价者可以分析习题答案的解题过程，看是否科学合理。
同时，还可以评价答案的解题方法是否简洁明了，是否符合教学要求。
三、系统评价习题答案存在的问题1.答案标准不一致不同教材、不同教师对于同一道题的答案标准可能存在差异，这就导致了习题答案的评价标准不一致。
这对于学生来说是一种困扰，他们需要适应不同的答案标准，这可能会对他们的学习造成困惑。
2.评价方式单一目前，对习题答案的评价方式主要以文字形式为主，这种方式存在着评价内容有限、表达不够准确等问题。
第二章-第三节-系统的可靠性分析课件
(2) 当阀1与阀2处于闭合状态时，(图中虚线所示)两个 阀的功能是截流，不能截流为系统失败，其中包括阀 门泄漏。若阀1与阀2这两个单元功能是相互独立的， 这两上单元至少有一个正常(闭合)，系统就能实现其截 流功能，因此该系统的可靠性框图如图3.4(b)所示，为
R (t)R 1(t)R 2(t)F 3(t)R 1(t)F 2(t)R 3(t)(3-1-16) F 1(t)R 2(t)R 3(t)R 1(t)R 2(t)R 3(t)
如单元的寿命服从指数分布，即 Ri(t) ei t ，则 有
R ( t ) e (1 2 ) t e (2 3 ) t e (1 3 ) t 2 e (1 2 3 ) t
由计算可靠寿命的公式 t(r) R1(r) 可以算
出可靠水平r分别为0.99、0.90、0.70、0.50、0.20时一 个单元与2/3(G)系统的可靠寿命t(r)，见表3.1。
表3.1中第2列数据10与61分别表示一个单元能工作到 10h的概率为0.99,2/3(G)系统能工作到61h的概率为0.99。 其余类似。
(3-1-17)
当三个单元都属于同一类型，它们的可靠度相同为 ，
则2/3G系统的可靠度和平均寿命分别为 Ro (t)
R(t)3R 0 2(t)2R 0 3(t)
(3-1-18)
(3-1-19)
1 1221 31 131 1 2 3
特别，当各单元失效率都为时，有源自F(t)12e3t 3e2t
可靠性工程基础习题答案PPT课件
第32页/共34页
(3) 直径为
Z 3.091
r 3.382, r 0.017 d 2 r 6.764 , d 0.034
0.9312
② 图（B)为并串联系统，其可靠性为
RS / Fx (t) 1 (1 R1R4) (1 R5R3)
1 (1 0.7 0.8)(1 0.9 0.8) 0.8768
RS Rx (t)RS / Rx (t) Fx (t)RS / Fx (t)
0.7 0.9312 0.3 0.8768 0.91488
14 (1 14)35 4512313(13)245 141351435 4512313245
第9页/共34页
③ 系统可靠度 RS P(系统工作) P(141351435 4512313245)
R1R4 (1 R1)R3R5 R1(1 R4)R3R5 (1 R4)(1 R5)R1R2R3 (1 R1)(1 R3)R2R4R5
3. (1) 并串联 ： RS1 Rn (2 Rn ) (2) 串并联 ： RS2 Rn (2 R)n
(3) 比较 RS1和RS2大小：
由于 0 ＜R＜ 1 n ＞ 1的自然数
第4页/共34页
当 R → 1 时 ( 2 – Rn ) → 1 ( 2 – R )n → 1
当 R → 0 时 ( 2 – Rn ) → 2
( 2 - R )n → ∝
可见0 ＜R＜ 1 ， n 为 2，3···时
( 2 – R )n ＞( 2 – Rn ) RS2= Rn ( 2 - R )n ＞ RS1= Rn ( 2 - Rn )
4. n 6, k 3, 40106 h-1。
《系统可靠性模型》课件
1 可能存在误差
系统可靠性模型在实际应用中可能存在一定的误差，需要注意评估和修正。
2
对于一些极端情况不适用
3
需要不断地更新和改进
总结
系统可靠性模型是描述系统可靠性的重要数学模型。不同的可靠性模型适用于不同的系统结构和情况。在实际 应用中需要不断改进和更新系统可靠性模型。
可靠性连通模型
可靠性冗余模型
动态可靠性/X模型
一种常用的系统可靠性模型。
2
Weibull模型
3
Rayleigh模型
系统可靠性模型在实际应用中的应用
可靠性的分析与设计
通过系统可靠性模型进行系统 的可靠性分析和设计，提高系 统的可靠性。
风险管理
故障检测与诊断
系统可靠性模型的局限性和改进
系统可靠性模型
系统可靠性模型是一种描述系统在一定时间内正常运行的可能性的数学模型。 它是研究系统可靠性的重要工具。
什么是系统可靠性模型
系统可靠性模型用于描述系统在一定时间内正常运行的可能性。它包括可靠 性、失效率、寿命分布等核心概念。
系统可靠性模型的分类
按系统结构
可靠性均衡模型
按时间
静态可靠性模型
中南大学系统可靠性分析与评价作业答案(课堂PPT)
4
3
28 31
仍旧工作数N-n(t) 46 44 41 34 29
26
22 19
求：(1)零件在100h和400h的可靠度；(2)100h和400h的累积失效概率； (3)求10h和25h时的失效概率密度；(4)求t=25h和t=100h的失效率。
解： Rˆ (1 0 0 ) N n (t1 0 0 ) 3 4 0 .6 8
求X的分布律。
习题9
一架飞机有三个着陆轮胎，如果不多于一个轮胎爆破， 飞机能安全着陆。试验表明，每一千次着陆发生一次轮 胎爆破。用二项分布求飞机安全着陆的概率。
习题10
某一大型网络系统的平均故障是每三个月一次，设系统
故障服从泊松分布，求一年发生5次以上故障的概率。
12
习题8
已 知 离 散 型 随 机 变 量 X的 分 布 函 数 为 ：
16
解得r1=2.243年(r2=13.66 年>8年舍去)。
R0.368为特征寿命，即：
10.25t0.25t2 0 16
解得t1=t2=8年，表明8年后元件将 全部失效
0.368=1-0.25r+0.25r2 16
解得r1=3.147年(r2=12.85 年>8舍去)。
4
习题2：已知某产品的失效率为常数， λ(t)=λ=0.25×10-4/h。
16
习题12
已 知 随 机 变 量 X的 服 从 N(5,102)的 正 态 分 布 。
(1)写 出 该 随 机 变 量 的 分 布 密 度 函 数 ， 可 靠 度 函 数 和 失 效 率 函 数 ；
(2)计 算 P(0X20)
正 交 表 ： (0.5)=0.6915； (1.5)=0.9332
中南大学《安全系统工程》课程作业一及参考答案
(一) 单选题1. 事故和隐患的关系是（）(A) 完全相同的(B) 后者是前者的可能性(C) 后者是前者的必然条件(D) 前者是后者的必然条件参考答案：(C)2. 以下特征表述不属于安全系统特点的是（）(A) 突变性(B) 有序与无序的统一体(C) 渐变性(D) 开放性参考答案：(C)3. 安全是（）(A) 没有危险的状态(B) 没有事故的状态(C) 达到可接受的伤亡和损失的状态(D) 舒适的状态参考答案：(C)4. 以下不属于系统安全分析方法的是（）(A) 预先危害分析(B) 事故树分析(C) 危险与可操作性研究(D) 安全经济效益分析参考答案：(D)5. 系统安全分析是使用系统工程的原理和方法，辨别、分析系统存在的（）(A) 安全因素(B) 危险系数(C) 危险指数(D) 危险因素参考答案：(D)6. 故障类型及影响分析（FMEA）方法对辨识和分析工业系统中的潜在危险有良好效果，以下概念在该方法表格构建中基本没被应用的是（）(A) 故障类型(B) 检查标准(C) 故障原因 (D) 校正措施参考答案： (B)7. ( )是系统安全的主要观点(A) 安全是绝对的(B) 安全只是系统运行阶段要考虑的工作(C) 在系统各个阶段都要进行危险源的辨识、评价和控制 (D) 事故是系统的危险源参考答案： (C)8. 以下关于安全检查表方法的叙述，正确的是（）(A) 按查隐患要求列出检查项目，同类性质的问题不需要列在一起。
(B) 安全检查表应列举需查明的所有能导致工伤或事故的不安全状态或行为。
(C) 各类检查表都有其适用对象，虽内容各有侧重，但可以通用。
(D) 安全检查表格式有统一规定，不同要求都可采用相同的安全检查表。
参考答案： (B)9. 以下不适用于方案设计阶段的系统安全方法是（）(A) 预先危险性分析(B) 因果分析(C) 安全检查表法(D) 事故树分析参考答案：(C)10. 系统的安全性评价是运用( )的方法对系统中存在的危险进行评价和预测的过程(A) 卫生工程(B) 系统工程(C) 人机工程(D) 安全工程参考答案：(B)11. 根据安全系统科学理论的分析，事故的直接原因是（）(A) 生产效益不好，安全投入无保障(B) 不安全行为、不安全状态和环境不良(C) 人的情绪不佳(D) 操作规程不健全，无章可循参考答案：(B)12. 事故隐患泛指生产系统中导致事故发生的（）(A) 潜藏着的祸患(B) 各种危险物品以及管理上的缺陷(C) 人、机、环境的危险性(D) 人的不安全行为、物的不安全状态和管理上的缺陷参考答案：(D)13. 运用安全检查表分析（）(A) 既能得出定性的结果，又能得出定量的结果(B) 既不能得出定性的结果，又不能得出定量的结果(C) 仅能得出定量的结果，不能得出定性的结果(D) 仅能得出定性的结果，不能得出定量的结果参考答案：(D)14. 系统是指由相互作用、相互联系和相互影响的若干部分结合成具有（）的有机整体(A) 特定功能(B) 很多功能(C) 一般功能(D) 一定功能参考答案：(A)15. 预先危险性分析法（PHA）可以用于工程活动的（）(A) 方案设计阶段(B) 建造投产阶段(C) 事故调查期间(D) 日常运行阶段参考答案：(A)16. 预先危害分析中的第3级危险源划为（）(A) 安全的(B) 临界的(C) 危险的(D) 灾害的参考答案：(C)17. 系统按起源分为（）(A) 实体系统和概念系统(B) 自然系统和社会系统(C) 开放性系统和封闭性系统(D) 静态系统和动态系统参考答案：(B)18. 在工业领域引进安全系统工程方法有很多优越性，对其特点叙述正确的是（）(A) 通过安全系统分析，可了解系统薄弱环节及可能导致事故的条件，从而采取措施防止事故的发生(B) 通过安全系统评价和优化决策，可以用较大的投资去获得基本的安全效果(C) 安全系统工程的方法仅适用于工程技术优化，不适用于安全管理(D) 安全系统工程与安全标准的制定无关，不需要特意收集任何可靠性数据参考答案： (A)19. 预先危险性分析的分析步骤可分为三个主要环节，它们分别是：危险性（），危险性（）和危险性控制对策。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4
3
28 31
仍旧工作数N-n(t) 46 44 41 34 29
26
22 19
求：(1)零件在100h和400h的可靠度；(2)100h和400h的累积失效概率； (3)求10h和25h时的失效概率密度；(4)求t=25h和t=100h的失效率。
解： Rˆ (1 0 0 ) N n (t1 0 0 ) 3 4 0 .6 8
0
1 6
R(t) 1 F (t) 1 0.25t 0.25 t2 16
(t)
f (t) R (t )
82 0.25t 2t 0.15t2R(t)dt (1 0 .2 5t 0 .2 5 t 2 )d t
0
0
16
上式中不知道∞是多少，但有R(∞)=0，即：
R 0.5为中位寿命，即： 0.5=1-0.25r+0.25r2
习题1：一组元件的故障密度函数为：
f (t) 0.25(0.25)t 8
式中：t为年。 求：累积失效概率F(t)，可靠度函数 R(t)，失效率λ(t)，平均寿命MTTF， 中位寿命T(0.5)和特征寿命T(e-1)。
1
习题2：已知某产品的失效率为常数， λ(t)=λ=0.25×10-4/h。
求：可靠度R=99%的可靠寿命，平均 寿命MTTF，中位寿命T(0.5)和特征寿 命T(e-1)。
fˆ(25) Vn(25) 3 2.4103 / h NVt 50(50 25)
ˆ(25) Vn(25) 3 2.7103 / h (N Vn(25))Vt 44(50 25)
ˆ(100) Vn(100)
5
2.9103 / h
(N Vn(100))Vt 34(150 100)
要点：f(t)、 λ(t)是研究t时间后单位时间的失效产品数， f(t) 是除以试验
1 0.25104
ln(0.368)
40000h
平均寿命：
R(t)dt
etdt 1 40000h
0
0
5
习题3：50个在恒定载荷运行的零件，运行记录如下表：
时间h
10 25 50 100 150 250
失效数△n(t)
42 37
5
3
累积失效数n(t) 4 6 9 16 21
24
400 3000
R(5)=exp(- λt)=exp(-5/20)=0.779
R(15)=exp(- λt)= exp(-15/20)=0.472 (2)A= μ/(μ+λ)=0.909或A=MTBF/(MTBF+MTT稳R态)=2有0/2效2=度0.9定09义
A ( ) A 可 工 作 时 可 间 工 作 不 时 能 间 工 作 时 间 U U D M T B M F T B M F T T R 8
2
习题3：50个在恒定载荷运行的零件， 运行记录如下表：
时间h
10 25 50 100 150 250 400 3000
失效数△n(t)
42 37 5
3
4
3
累积失效数n(t) 4 6 9 16 21 24 28 31
仍旧工作数N-n(t) 46 44 41 34 29 26 22 19
求：(1)零件在100h和400h的可靠度；(2)100h和 400h的累积失效概率；(3)求10h和25h时的失效 概率密度；(4)求t=25h和t=100h的失效率。
产品总数，λ(t)是除以t时仍正常工作的产品数。注意单位。
6
习题4：一设备从以往的经验知道，平均无故障时 间为20天，如果出了故障需2天方能修复，假定该 设备发生故障时间及修复时间服从指数分布。 求：(1)该设备5天和15天的可靠度各为多少?； (2)该设备的稳态有效度为多少?
提示：
如果维修时间服从指数分布，有 如果R(t)et,服从指数分布
习题6
设离散型随机变量X的分布律为P(X=k)=pkbk k=1,2,3,L，则b,必须满足什么条件？
提示：等比级数：(
aqnaaqn)
n=0
1q
习题7
设随机变量X的分布律为：
P(X k) p(1p)k1,k 1,2,3L ,(0 p1)
求：可靠度R=99%的可靠寿命，平均寿命θ ，中 位寿命T(0.5)和特征寿命T(e-1)。
t
解：
R(t)
(t)dt
e 0
et
t 1 ln R(t)
可靠性寿命t(0.99)
1 0.25104
ln(0.99)
402h
中位寿命t(0.5)
1 0.25104
ln(0.5)
27725.6h
特征寿命t(e1)
N
50
Rˆ ( 4 0 0 ) N n (t 4 0 0 ) 2 2 0 .4 4
N
50
Fˆ (1 0 0 ) n (1 0 0 ) 1 6 / 5 0 0 .3 2 N
Fˆ ( 4 0 0 ) n ( 4 0 0 ) 2 8 / 5 0 0 .5 6 N
fˆ(10) Vn(10) 2 2.67103 / h NVt 50(2510)
3
答案 习题1：一组元件的故障密度函数为：f(t)0.25(0.25)t 8
式中：t为年。求：累积失效概率F(t)，可靠度函数R(t)，失效率
λ(t)，平均寿命θ ，中位寿命T(0.5)和特征寿命T(e-1)。
解：F (t)
t f (x)dx 0.25t ( 0.25 )t2
0
16
8(1 0 .2 5 t0 .2 5t2)d t2 .6 6 7 年
16
解得r1=2.243年(r2=13.66 年>8年舍去)。
R0.368为特征寿命，即：
10.25t0.25t2 0 16
解得t1=t2=8年，表明8年后元件将 全部失效
0.368=1-0.25r+0.25r2 16
解得r1=3.147年(r2=12.85 年>8舍去)。
4
习题2：已知某产品的失效率为常数， λ(t)=λ=0.25×10-4/h。
MTTR1
MTBF
R(t)dt
1
0
7
习题4答案：一设备从以往的经验知道，平均无故障时间 为20天，如果出了故障需2天方能修复，假定该设备发生 故障时间及修复时间服从指数分布。 求：(1)该设备5天和15天的可靠度各为多少?；(2)该设备 的稳态有效度为多少?
解： (1)该设备平均无故障时间时间为20天，即MTBF=20 因MTBF=1/λ，λ=1/20； 同理平均修复时间为2天，MTTR=1/μ，μ=1/2