习题解答将线性规划问题化为标准形式.doc
线性规划化为标准型

线性规划化为标准型线性规划是一种数学优化方法,用于在给定约束条件下寻找最优解。
在实际应用中,线性规划问题往往需要转化为标准型,以便使用现有的优化算法进行求解。
本文将介绍线性规划如何转化为标准型,并给出详细的步骤和示例。
首先,让我们来看一个简单的线性规划问题:Maximize 3x + 5y。
Subject to:2x + y ≤ 20。
-4x + 5y ≥ 10。
x, y ≥ 0。
这是一个典型的线性规划问题,我们需要将其转化为标准型。
标准型的线性规划问题具有以下形式:Maximize c^T x。
Subject to:Ax = b。
x ≥ 0。
其中,c是一个n维向量,x是一个n维变量向量,A是一个m×n的矩阵,b 是一个m维向量。
转化为标准型的关键在于将所有的约束条件转化为等式,并引入松弛变量。
对于小于等于形式的约束条件,我们引入一个松弛变量,对于大于等于形式的约束条件,我们引入一个人工变量。
同时,我们将目标函数转化为标准的形式。
在上面的例子中,我们可以将第一个约束条件转化为等式,并引入一个松弛变量:2x + y + s1 = 20。
其中,s1 ≥ 0。
将第二个约束条件转化为等式,并引入一个人工变量:-4x + 5y s2 = 10。
其中,s2 ≥ 0。
然后,我们将目标函数转化为标准的形式:Maximize 3x + 5y + 0s1 + 0s2。
现在,我们的线性规划问题已经转化为标准型,具体形式如下:Maximize c^T x。
Subject to:Ax = b。
x ≥ 0。
其中,。
c = [3, 5, 0, 0]x = [x, y, s1, s2]A = [[2, 1, 1, 0],。
[-4, 5, 0, -1]]b = [20, 10]通过上面的转化过程,我们成功将原始的线性规划问题转化为标准型。
现在,我们可以使用标准的线性规划算法对其进行求解,得到最优解x,y,s1,s2。
这样,我们就可以得到原始线性规划问题的最优解了。
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
习题解答将线性规划问题化为标准形式.doc
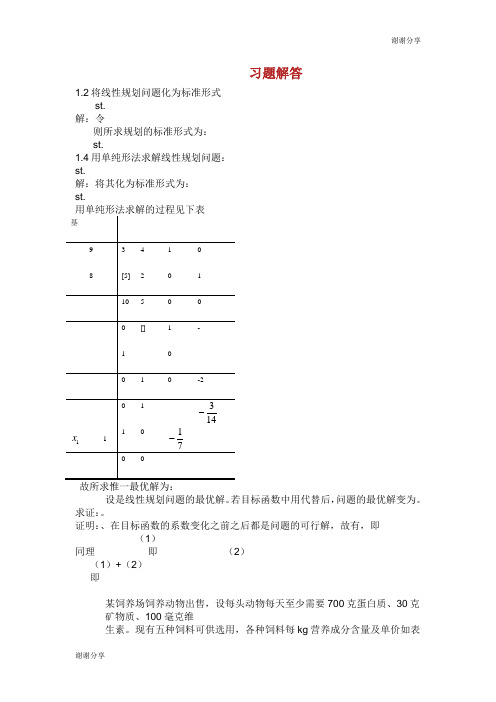
习题解答
1.2将线性规划问题化为标准形式
st.
解:令
则所求规划的标准形式为:
st.
1.4用单纯形法求解线性规划问题:
st.
解:将其化为标准形式为:
st.
设是线性规划问题的最优解。
若目标函数中用代替后,问题的最优解变为。
求证:。
证明:、在目标函数的系数变化之前之后都是问题的可行解,故有,即
(1)
同理即(2)
(1)+(2)
即
某饲养场饲养动物出售,设每头动物每天至少需要700克蛋白质、30克
矿物质、100毫克维
生素。
现有五种饲料可供选用,各种饲料每kg营养成分含量及单价如表
所示:
饲料蛋白质(g) 矿物质(g) 维生素(mg) 价格(元/kg)
1 3 1 0.5 0.2
2 2 0.5 1.0 0.7
3 1 0.2 0.2 0.4
4 6 2 2 0.3
5 18 0.5 0.8 0.8
要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
(仅建模型)
解:设分别代表5种饲料的采购数,则模型为:
st.。
《运筹学》习题集

第一章线性规划1.1将下述线性规划问题化成标准形式1)min z=-3x1+4x2-2x3+5 x4-x2+2x3-x4=-24xst. x1+x2-x3+2 x4 ≤14-2x1+3x2+x3-x4 ≥ 2x1,x2,x3≥0,x4无约束2)min z =2x1-2x2+3x3+x2+x3=4-xst. -2x1+x2-x3≤6x1≤0 ,x2≥0,x3无约束1.2用图解法求解LP问题,并指出问题具有唯一最优解、无穷多最优解、无界解还是无可行解。
1)min z=2x1+3x24x1+6x2≥6st2x1+2x2≥4x1,x2≥02)max z=3x1+2x22x1+x2≤2st3x1+4x2≥12x1,x2≥03)max z=3x1+5x26x1+10x2≤120st5≤x1≤103≤x2≤84)max z=5x1+6x22x1-x2≥2st-2x1+3x2≤2x1,x2≥01.3找出下述LP问题所有基解,指出哪些是基可行解,并确定最优解(1)min z=5x1-2x2+3x3+2x4x1+2x2+3x3+4x4=7st2x1+2x2+x3 +2x4=3x1,x2,x3,x4≥01.4 分别用图解法与单纯形法求解下列LP 问题,并对照指出最优解所对应的顶点。
1) maxz =10x 1+5x 23x 1+4x 2≤9 st 5x 1+2x 2≤8 x 1,x 2≥02) maxz =2x 1+x 2 3x 1+5x 2≤15 st 6x 1+2x 2≤24x 1,x 2≥01.5 分别用大M 法与两阶段法求解下列LP 问题。
1) minz =2x 1+3x 2+x 3 x 1+4x 2+2x 3≥8 st 3x 1+2x 2 ≥6x 1,x 2 ,x 3≥02) max z =4x 1+5x 2+ x 3. 3x 1+2x 2+ x 3≥18St. 2x 1+ x 2 ≤4x 1+ x 2- x 3=53) maxz = 5x 1+3x 2 +6x 3 x 1+2x 2 -x 3 ≤ 18 st 2x 1+x 2 -3 x 3 ≤ 16 x 1+x 2 -x 3=10 x 1,x 2 ,x 3≥01231231231231234)m ax 101512539561515.25,,0z x x x x x x x x x st x x x x x x =++++≤⎧⎪-++≤⎪⎨++≥⎪⎪≥⎩1.61.7某班有男生30人,女生20人,周日去植树。
运筹学教程(第二版)(胡运权)课后答案(清华大学出版社)

运筹学教程(第⼆版)(胡运权)课后答案(清华⼤学出版社)运筹学教程(第⼆版)习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。
并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。
1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解,1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解, x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。
习题解答将线性规划问题化为标准形式.doc

习题解答1.2将线性规划问题化为标准形式st.⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=0,0624322min 21321321321x x x x x x x x x x x z解:令,'11x x -='"3'33,z z x x x -=-= 则所求规划的标准形式为:st.⎪⎩⎪⎨⎧≥≥≥≥≥≥=++-+=+-++⋅+⋅-+-+=0,0,0,0,0,062403322max 54"3'32'15"3'32'14"3'32'154"3'32'1'x x x x x x x x x x x x x x x x x x M x x x x z1.4用单纯形法求解线性规划问题:st.⎪⎩⎪⎨⎧≥≥≤+≤++=0,0825943510max 21212121x x x x x x x x z解:将其化为标准形式为:st.⎪⎩⎪⎨⎧≥≥≥≥=++=+++=0,0,0,08259532max 432142132121x x x x x x x x x x x x z用单纯形法求解的过程见下表故所求惟一最优解为:.2117max ,2,121===z x x10.1 设0X 是线性规划问题0,,max ≥==X b AX CX z 的最优解。
若目标函数中用*C 代替C 后,问题的最优解变为*X 。
求证:0))((0≥--**X X C C 。
证明:0X 、*X 在目标函数的系数变化之前之后都是问题的可行解,故有*≥CX CX 0,即0)(,0)(00≥--≥-**X X C X X C (1)同理,0X C X C ***≥ 即 0)(0≥-**X X C (2)(1)+(2)0)()(00≥---***X X C X X C 即 .0))((0≥--**X X C C13.1某饲养场饲养动物出售,设每头动物每天至少需要700克蛋白质、30克矿物质、100毫克维生素。
线性规划化为标准型

线性规划化为标准型线性规划是运筹学中的一种重要方法,用于在给定约束条件下寻找最优解。
而将线性规划问题转化为标准型是解决线性规划问题的第一步,本文将介绍线性规划如何转化为标准型。
首先,让我们来了解一下线性规划的基本形式。
线性规划问题通常包括一个目标函数和一组约束条件。
目标函数是需要最大化或最小化的线性函数,约束条件则是一组线性不等式或等式。
一般来说,线性规划问题可以表示为:Maximize (or Minimize) Z = c1x1 + c2x2 + ... + cnxn。
Subject to:a11x1 + a12x2 + ... + a1nxn ≤ b1。
a21x1 + a22x2 + ... + a2nxn ≤ b2。
...am1x1 + am2x2 + ... + amnxn ≤ bm。
xi ≥ 0,i = 1,2,...,n。
其中,c1,c2,...,cn为目标函数的系数,aij为约束条件的系数,bi为约束条件的右端常数,xi为决策变量。
接下来,我们将介绍如何将一般形式的线性规划问题转化为标准型。
标准型的线性规划问题具有以下形式:Maximize Z = c1x1 + c2x2 + ... + cnxn。
Subject to:a11x1 + a12x2 + ... + a1nxn = b1。
a21x1 + a22x2 + ... + a2nxn = b2。
...am1x1 + am2x2 + ... + amnxn = bm。
xi ≥ 0,i = 1,2,...,n。
为了将一般形式的线性规划问题转化为标准型,我们需要进行如下步骤:1. 将不等式约束转化为等式约束。
对于每个不等式约束ai1x1 + ai2x2 + ... + ainxn ≤ bi,我们引入一个新的非负松弛变量si,使得不等式约束转化为等式约束,ai1x1 + ai2x2 + ... + ainxn + si = bi,si ≥ 0。
将以下线性规划问题转化为标准形式...

第二章 线性规划(LP ) §2.1 线性规划数学模型的建立LP 问题提出:苏联:康德洛维奇 1939 一、线性规划数学模型的三要素:1.决策变量(decision variable):决策问题待定的量值。
用字母(例如X1,X2,···,Xn )来表示可控制的因素。
每一组决策变量的实际值就表示一个具体方案。
2.目标函数(objective function ):MaxZ=CX 或 MinZ=CX ;(衡量决策优劣的准则) 特点:(1)单一目标;(2)关于决策变量的线性函数。
(定义:课本P20)3.约束条件(constraint conditions):s.t. (subject to) 受制于约束;AX ≤(≥,=)b 特点:若干关于决策变量的线性函数。
二、LP 数学模型的一般形式(1)繁写形式目标函数:Max (Min )z = c1 x1 + c2 x2 + … + cn xn 约束条件:a 11 x1 + a 12 x2 + … + a 1n xn ≤ ( =, ≥ )b1 a 21 x1 + a 22 x2 + … + a 2n xn ≤ ( =, ≥ )b2 s.t. …… …… a m1 x1 + a m2 x2 + … + a mn xn ≤ ( =, ≥ )bm x1 ,x2 ,… ,xn ≥ 0 (2)向量形式目标函数:Max (Min ) z = CX≤(≥,=)bXj ≥ 0 (j=1,2, …,n)其中,C=(c1 , c2 , … , cn )(价值向量) X= (x1 , x2 , … , xn )T(决策变量向量) b=(b1 , b2 , … , bm )T (限定向量)pj= (a 1j , a 2j … a mj ) T (约束条件系数列向量) 注:矩阵相乘条件:左列=右行 (3)矩阵形式★目标函数:Max (Min ) z = CX 约束条件:∑=nj jjx p1AX ≤(=, ≥)bX≥0其中,C=(c1 , c2 , … , cn )(价值向量)X= (x1 , x2 , … , xn )T(决策变量向量)b=(b1 , b2 , … , bm )T (限定向量、资源向量)a11 a12 (1)a21 a22 … a2n (系数矩阵)A= ……a m1 a m2 … a mn三、建模的一般步骤前提假设:假设模型中有n个决策变量,m个约束条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南省衡阳县2018-2019学年高一上学期期末质量检测数学试题)(解析版)一、选择题(本大题共10小题,共30.0分)1.已知集合A={x|x<1},B={x|3x<1},则()A. A∩B={x|x<0}B. A∪B=RC. A∪B={x|x>1}D. A∩B=⌀【答案】A【解析】解:∵集合A={x|x<1},B={x|3x<1}={x|x<0},∴A∩B={x|x<0},故A正确,D错误;A∪B={x|x<1},故B和C都错误.故选:A.先分别求出集合A和B,再求出A∩B和A∪B,由此能求出结果.本题考查交集和并集求法及应用,是基础题,解题时要认真审题,注意交集、并集定义的合理运用.2.下列四组函数,表示同一函数的是()A. f(x)=x2,g(x)=xB. f(x)=x,g(x)=x2xC. f(x)=x2−4,g(x)=x−2⋅x+2D. f(x)=x,g(x)=3x3【答案】D【解析】解:A.f(x)=x2=|x|,g(x)=x,所以两个函数的对应法则不一致,所以A不是同一函数.B.f(x)的定义域为R,而g(x)的定义域为(−∞,0)∪(0,+∞),所以定义域不同,所以B 不是同一函数.C.由x2−4≥0,解得x≥2或x≤−2,由x+2≥0x−2≥0,解得x≥2,两个函数的定义域不一致,所以C不是同一函数.D.f(x)的定义域为R,而g(x)的定义域为R,且g(x)=3x3=x,所以定义域和对应法则相同,所以D是同一函数.故选:D.分别判断两个函数的定义域和对应法则是否一致,否则不是同一函数.本题主要考查判断两个函数是否为同一函数,判断的标准就是判断两个函数的定义域和对应法则是否一致,否则不是同一函数.3.下列函数中,既是奇函数又在区间(0,+∞)上单调递増的函数为()A. y=1xB. y=lnxC. y=x3D. y=x2【答案】C【解析】解:由于y=1x在区间(0,+∞)上单调递减,故排除A;由于y=lnx不是奇函数,故排除B;由于y=x3既是奇函数又在区间(0,+∞)上单调递増,故它满足条件;由于y=x2是偶函数,不是奇函数,故排除D,故选:C.由题意利用函数的奇偶性和单调性,得出结论.本题主要考查函数的奇偶性和单调性,属于基础题.4.如图所示,观察四个几何体,其中判断正确的是()A. 如图是棱台B. 如图是圆台C. 如图是棱锥D. 如图不是棱柱【答案】C【解析】解:对于学习A,不是由棱锥截来的,所以A不是棱台,故A错误;对于学习B,上、下两个面不平行,所以不是圆台;对于学习C,是棱锥.对于学习D,前、后两个面平行,其他面是平行四边形,且每相邻两个四边形的公共边平行,所以D是棱柱.故选:C.利用几何体的结构特征进行分析判断.本题考查几何体的结构特征,解题时要认真审题,注意熟练掌握几何体的基本概念和性质.5.函数y=loga(x+2)+1的图象过定点()A. (1,2)B. (2,1)C. (−2,1)D. (−1,1)【答案】D【解析】解:由函数图象的平移公式,我们可得:将函数y=logax(a>0,a≠1)的图象向左平移2个单位,再向上平移1个单位,即可得到函数y=loga(x+2)+1(a>0,a≠1)的图象.又∵函数y=logax(a>0,a≠1)的图象恒过(1,0)点,由平移向量公式,易得函数y=loga(x+2)+1(a>0,a≠1)的图象恒过(−1,1)点,故选:D.由对数函数恒过定点(1,0),再根据函数平移变换的公式,结合平移向量公式即可得到到正确结论.本题考查对数函数的单调性与特殊点,记住结论:函数y=loga(x+m)+n(a>0,a≠1)的图象恒过(1−m,n)点6.经过点(−1,0),且与直线x+2y−3=0垂直的直线方程是()A. 2x−y+2=0B. 2x+y+2=0C. 2x−y−2=0D. x−2y+1=0【答案】A【解析】解:∵直线x+2y−3=0的斜率为−12,∴与之垂直的直线斜率为2,∴所求直线方程为y−0=2(x+1),化为一般式可得2x−y+2=0故选:A.由垂直关系可得直线的斜率,进而可得点斜式方程,化为一般式即可.第2页,共9页本题考查直线的一般式方程和垂直关系,属基础题.7.在四面体P−ABC的四个面中,是直角三角形的面至多有()个.A. 0个B. 1个C. 3个D. 4个【答案】D【解析】解:如图,PA⊥底面ABC,△ABC是∠ABC为直角的直角三角形,则四面体P−ABC的四个面中,是直角三角形的面最多,有4个.故选:D.由题意画出图形得答案.本题考查棱锥的结构特征,正确画出图形是关键,是中档题.8.直线x−3y+1=0的倾斜角为()A. π3B. π6C. 2π3D. 5π6【答案】B【解析】解:直线x−3y+1=0的斜率为k=33,设倾斜角为α,可得tanα=33,由0≤α<π,且α≠π2,可得α=π6,故选:B.求出直线的斜率,由直线的倾斜角与斜率的关系,计算即可得到所求值.本题考查直线的斜率和倾斜角的关系,考查运算能力,属于基础题.9.函数f(x)=ln(x2+1)的图象大致是()A. B.C. D.【答案】A【解析】解:∵x2+1≥1,又y=lnx在(0,+∞)单调递增,∴y=ln(x2+1)≥ln1=0,∴函数的图象应在x轴的上方,又f(0)=ln(0+1)=ln1=0,∴图象过原点,综上只有A符合.故选:A.∵x2+1≥1,又y=lnx在(0,+∞)单调递增,∴y=ln(x2+1)≥ln1=0,函数的图象应在x轴的上方,在令x取特殊值,选出答案.对于函数的选择题,从特殊值、函数的性质入手,往往事半功倍,本题属于低档题.10.已知函数f(x)是R上的奇函数,且满足f(x+2)=−f(x),当x∈(0,1]时,f(x)=2x−1,则方程f(x)=log7|x−2|解的个数是()A. 8B. 7C. 6D. 5【答案】B【解析】解:函数f(x)是R上的奇函数,f(0)=0,由f(x+2)=−f(x),可得f(x+4)=f(x),∴f(x)的周期T=4.作出在同一坐标系中画y=2x−1和y=log7|x−2|图象,从图象不难看出,其交点个数7个,故选:B.根据函数f(x)是R上的奇函数,f(0)=0,且满足f(x+2)=−f(x),求解f(x)的周期T=4,当x∈(0,1]时,f(x)=2x−1,作出图象,f(x)=log7|x−2|解的个数,即为2x−1=log7|x−2|图象的交点个数.数形结合可得答案.本题考查了指数和对数的图象画法和交点个数问题.属于基础题.二、填空题(本大题共5小题,共20.0分)11.已知幂函数y=f(x)的图象过点(2,2),则这个函数解析式为______.【答案】y=x12(x≥0)【解析】解:设f(x)=xα,∵幂函数y=f(x)的图象过点(2,2),∴2α=2∴α=12.这个函数解析式为y=x12(x≥0).故答案为:y=x12(x≥0).根据幂函数的概念设f(x)=xα,将点的坐标代入即可求得α值,从而求得函数解析式.本题主要考查了待定系数法求幂函数解析式、指数方程的解法等知识,属于基础题.12.已知正方体ABCD−A1B1C1D1中,直线AB1与DD1所成的角是______,【答案】45∘第4页,共9页【解析】解:∵BB1//DD1,∴∠BB1A是直线AB1与DD1所成的角,∵AB⊥BB1,AB=BB1,∴∠AB1B=45∘,∴直线AB1与DD1所成的角是45∘.故答案为:45∘.由BB1//DD1,得∠BB1A是直线AB1与DD1所成的角,由此能求出直线AB1与DD1所成的角.本题考查异面直线所成角的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是基础题.13.已知△ABC的三个顶点A(1,3),B(3,1),C(−1,0),则△ABC的面积为______.【答案】5【解析】解:由A(1,3),B(3,1),设AB的直线方程为y=kx+b,则1=3k+b3=k+b,解得:k=−1,b=4.AB的直线方程为x+y−4=0.C(−1,0)到直线AB的距离h=|−1−4|2=52.AB的距离d=(3−1)2+(3−1)2=22.则△ABC的面积S=12×52×22=5.故答案为:5.根据A(1,3),B(3,1),求出AB的直线方程,和AB的距离,利用点到直线的距离就是AB为底的高,即可得△ABC的面积.本题此解法用了点与直线的性质,两点之间的距离公式.属于基础题.14.已知一个正方形的所有项点在一个球面上,若这个正方体的表面积为24,则这个球的表面积为______,【答案】12π【解析】解:设正方体的棱长为a,球的半径为R,则正方体的表面积为6a2=24,得a=2,所以,2R=3a=23,则R=3,因此,这个球的表面积为4πR2=12π.故答案为:12π.先由正方体的表面积计算出正方体的棱长a,然后利用2R=3a求出球体的半径R,最后利用球体的表面积公式可得出答案.本题考查球体的表面积的计算,解本题的关键在于弄清楚正方体的外接球的半径为棱长之间的关系,考查了计算能力,属于中等题.15.已知函数f(x)=2x−1,若x∈[2,6],则该函数的最大值为______.【答案】2【解析】解:画出函数f(x)的图象,如图示:,∴函数f(x)在[2,6]递减,∴函数f(x)最大值=f(2)=2,故答案为:2.先求出函数的图象,得到函数的单调性,从而求出函数的最大值.本题考查了函数的单调性问题,考查了函数的最值问题,是一道基础题.三、解答题(本大题共6小题,共50.0分)16.计算下列各式的值(1)(827)−13−(π−1)0+214(2)log327+lg25−lg4.【答案】解:(1)原式=(23)3×(−13)−1+(32)2=32−1+32=2.(2)原式=log3332+lg25×4=32−1=12.【解析】(1)利用指数运算法则即可得出;(2)利用对数的运算法则即可得出.本题考查了指数与对数运算法则,属于基础题.17.已知直线l1:x+2y+1=0,l2:−2x+y+2=0,它们相交于点A.(1)判断直线l1和l2是否垂直?请给出理由;(2)求过点A且与直线l3:3x+y+4=0平行的直线方程.【答案】解:(1)直线l1的斜率k1=−12,直线l2的斜率k2=2,∵k1k2=−12×2=−1∴l1⊥l2(2)由方程组−2x+y+2=0x+2y+1=0解得点A坐标为(35,−45),直线l3的斜率为−3,所求直线方程为:y−(−45)=−3(x−35)化为一般式得:3x+y−1=0.【解析】(1)先求出两直线的斜率,发现斜率之积等于−1,故可得两直线垂直.(2)先求出交点A的坐标,再根据斜率等于直线l3的斜率,点斜式写出直线的方程,并化为一般式.本题考查判断两直线垂直的方法,当两直线平行时,它们的斜率间的关系;用点斜式求直线方程.18.已知函数f(x)=x2−2|x|−3.(1)作出函数f(x)的大致图象,并根据图象写出函数f(x)的单调区间;(2)求函数f(x)在[−2,4]上的最大值与最小值.【答案】解:(1)f(x)=x2−2|x|−3=x2+2x−3,x<0x2−2x−3,x≥0.图象如图:第6页,共9页由图象知函数的单调减区间是(−∞,−1],(0,1].单调增区间是(−1,0],(1,+∞);(2)结合图象可知最小值为f(1)=f(−1)=−4,最大值为f(4)=5.【解析】(1)写出分段函数解析式,结合二次函数的图象作图,由图象得函数的单调区间;(2)直接由图象得到函数f(x)在[−2,4]上的最大值与最小值.本题考查了分段函数的图象,考查了由图象判断函数的单调性,并由函数单调性求函数的最值,是基础题.19.直线l过点(−1,0),圆C的圆心为C(2,0).(Ⅰ)若圆C的半径为2,直线l截圆C所得的弦长也为2,求直线l的方程;(Ⅱ)若直线l的斜率为1,且直线l与圆C相切;若圆C的方程.【答案】解:(Ⅰ)设直线l的方程为y=k(x+1),则∵圆C的半径为2,直线l截圆C所得的弦长为2,∴圆心到直线l的距离为3,即|3k|k2+1=3,解得k=±22,即直线l的方程为y═±22(x+1);(Ⅱ)∵直线l的斜率为1,∴直线l的方程为y=x+1,∵直线l与圆C相切,∴r=31+1=322,∴圆C的方程为(x−2)2+y2=92.【解析】(Ⅰ)设直线l的方程为y=k(x+1),根据圆C的半径为2,直线l截圆C所得的弦长为2,利用点到直线的距离公式,建立方程,即可求直线l的方程;(Ⅱ)根据直线l与圆C相切,利用点到直线的距离公式,可得圆C的半径r,从而可得圆C的方程.本题考查直线与圆的位置关系,考查点到直线的距离公式,考查圆的性质,属于中档题.20.四棱锥P−ABCD中,底面ABCD是正方形,PA⊥面ABCD垂足为点A,PA=AB=4,点M是PD的中点(1)求证:PB//平面ACM(2)求证:BD⊥平面PAC:(3)求四面体A−MBC的体积.∵点O,M分别是BD,PD的中点,∴MO//PB.又PB⊄面ACM,MO⊂面ACM,∴PB//面ACM…(3分)(2)∵PA⊥面ABCD,∴PA⊥BD,∵底面ABCD是正方形,∴AC⊥BD,又∵PA∩AC=A,∴BD⊥面PAC…(6分)(3)∵VA−MBC=VM−ABC=13⋅S△ABC⋅h,且h=12PA,∴VA−MBC=13⋅(12⋅AB⋅AD)⋅(12⋅PA)=23…(9分)【解析】(1)连接AC,BD,记AC与BD的交点为O,连接MO.证明MO//PB,然后证明PB//面ACM.(2)证明PA⊥BD,AC⊥BD,然后证明BD⊥面PAC.(3)通过VA−MBC=VM−ABC=13⋅S△ABC⋅h,然后求解即可.本题考查直线与平面垂直以及直线与平面平行的判定定理的应用,几何体的他就的求法,考查计算能力.21.已知f(x)是定义在[−1,1]上的奇函数,且f(1)=1,若a,b∈[−1,1],a+b≠0时,有f(a)+f(b)a+b>0成立.(1)判断f(x)在[−1,1]上的单调性(2)解不等式f(log2(x+2))≤f(12)(3)若f(x)≤m2−2am+11对所有的a∈[−1,1]恒成立,求实数m的取值范围.【答案】解:(1)f(x)在[−1,1]上单调递增…(1分)任取x1,x2∈[−1,1],且x1<x2,则−x2∈[−1,1].∵f(x)为奇函数,∴f(x1)−f(x2)=f(x1)+f(−x2)=f(x1)+f(−x2)x1+(−x2)⋅(x1−x2).由已知得f(x1)+f(−x2)x1+(−x2)>0,又x1−x2<0,∴f(x1)−f(x2)<0,即f(x1)<f(x2),∴f(x)在[−1,1]上单调递增…(3分)(2)不等式f(log2(x+2))≤f(12),由(1)可得:−1≤log2(x+2)≤1log2(x+2)≤12,解得12−2≤x≤0,不等式的解集为:{x|12−2≤x≤0}…(5分)(3)∵f(1)=1,且f(x)在[−1,1]上单调递增,∴在[−1,1]上,f(x)≤1.问题转化为m2−2am+1≥1,即m2−2am≥0,对a∈[−1,1]成立…(6分)第8页,共9页设g(a)=−2m⋅a+m2,①若m=0,则g(a)=0≥0,对a∈[−1,1]恒成立②若m≠0,则g(a)为关于a的一次函数,若g(a)≥0对a∈[−1,1]恒成立,必须有g(−1)≥0,且g(1)≥0,即m2−2m≥0m2+2m≥0,结合相应各函数图象,得m≤−2或m≥2…(8分)综上所述,实数m的取值范围是(−∞,−2]∪{0}∪[2,+∞)…(9分)【解析】(1)利用函数的单调性的定义以及函数的奇偶性,判断证明即可.(2)利用函数的单调性以及函数的定义域,列出不等式组,求解即可.(3))通过f(1)=1,且f(x)在[−1,1]上单调递增,问题转化为m2−2am+1≥1,即m2−2am≥0,对a∈[−1,1]成立,设g(a)=−2m⋅a+m2,通过①若m=0,②若m≠0,若g(a)≥0对a∈[−1,1]恒成立,列出不等式组求解即可.本题考查函数恒成立体积的应用,考查分类讨论思想以及转化思想的应用,考查计算能力.。
