行测资料分析:年均增长量的求法
【行测资料分析】速算年均增长率必杀技!!!

【行测资料分析】速算年均增长率必杀技!!!
年均增长率,在求解的时候,涉及到多次方,相对比较复杂。
很多考生在计算年均增长率的时候,会花费较多时间,有些考生干脆直接放弃了。
但其实,掌握了估算年均增长率的必杀技,是可以快速得出答案。
另外,这种题型的选项一般不会太难,还是比较容易排除的。
做这类题,核心思想是:代入排除法!是可以秒杀的!!!是不用开方的!!!
因为讲得比较细节,文章有点长,希望可以认真看完,一定要看完例题和解题过程,相信会有收获的!
一、代入的公式:
因为代入的公式是解这类题的关键,所以放在前面先说。
假设,基期为A,现期为B,A到B共有N年(N的计算方法是,直接用B 减去A。
比如,A是2013年,B是2017年,那么N=2017-2013=4年),A到B的增长率为R(即首尾增长率),年均增长率为r,则有下列公式(近似公式):
真题考试中,考得最多的是5年之内的年均增长率,所以,3~5年的公式必须记住,必须记住,必须记住。
重要的事情说三遍,说三遍,说三遍!
2008-2012年,公立医院次均门诊费用的年均增长率与下列哪个最接近?(A)
A. 8.6%
B. 9.2%
C. 9.7%
D. 10.2%
第一步,计算首尾增长率:第二步,用
第一步,计算首尾增长率:
第二步,用
上图是SCI收录中国科技论文情况,则2003—2007年间,SCI收录中国科技论文数的年均增长率约为(C)
A、6%
B、10%
C、16%
D、25%
第一步,计算首尾增长率:第二步,用。
行测资料分析之年均增长率解题技巧分析

一、年均增长率的概念分析我们首先必须区分开年增长率、年均增长率以及年平均增长率这三个概念,年增长率是我们最常见的,是考试的重点,它指的是末期增加值与基期的比值,表示的是相邻年份的增长情况,通常针对的是某一年,如2006年某省地区生产总值的年增长率,对应的公式就是年增长率=增加量/基期=(末期-基期)/基期。
年平均增长率与年均增长率在近几年行测考试中的区分性已经很小,在这里我们也就不做区分了,免得更加混乱,在下面的讲解我们就将这两者统一为年均增长率。
年均增长率,表示的是一段时间的某个指标的增长情况,我们用专业术语表达的话应该是这样的,如果第1年为M,第n+1年为N,且N/M=(1+r)n,则称r为第1~n+1年的年均增长率,如2006~2011年某省地区生产总值的年平均增长率,对应的公式就是年均增长率=。
我们先看个例题。
【例题】2001年以来,中央重点新闻网站的访问量,以平均每月递增12%的速度上升。
目前中国互联网产业对GDP的贡献达到7%,而未来三年有可能达到15%。
求:2001年以来,中央重点新闻网站访问量的年平均递增速度是()。
A.1.1212 B.1.1212-1 C.0.1212 D.0.12【分析】这个试题就是考察的年均增长率,题目变化一下就是2001~2002年的年均增长率。
假设2000年12月的访问量为1,那么2001年12月就是1×(1+12%)12,那么年均增长率就1×(1+12%)12÷1-1=1.1212-1。
二、年均增长率解题技巧年均增长率,在求解的时候,涉及到多次方数,相对比较复杂,在解题时,如果没有什么思路,可以选择放弃,否则肯定会浪费时间,但是对于年均增长率,并不是没有方法解答,下面我们讲解几种比较常用的解题方法。
(一)二项式定理的应用什么是二项式定理呢,它就是我们高中学到的多次方的展开式,我们先看看这个展开式是什么样的,。
一般年均增长率有(1+r)n=N/M,计算式和二项式定理很相似吧,那好,我们就用这个来分析,也就是a=1,b=r,此时二项式就可以化为,当r很小,在10%以内的时候,r2,r3,…,r n无限趋近于0,此时,有(1+r)n≈1+n×r。
年平均增长率计算方法

年平均增长率计算方法在经济学中,年平均增长率是一个非常重要的概念。
它用来衡量某个指标在一定时间内的平均增长率,可以帮助我们了解经济的发展趋势及其稳定性。
计算年平均增长率有多种方法,本文将介绍其中几种常用的方法。
方法一:简单平均法简单平均法是一种比较基础和直观的计算年平均增长率的方法。
其公式为:年平均增长率 = (末值 - 初始值) ÷ (初始值) × 100%例如,按照这个方法计算中国GDP从2010年到2019年的年平均增长率,公式如下:年平均增长率 = (90.03万亿元 - 40.15万亿元) ÷ (40.15万亿元) ×100% = 124.28%这个结果看起来有些不合理,因为这意味着GDP每年都会增长124.28%,这显然是不可能的。
因此,这种方法只适用于数据的增长率比较稳定的情况下,一旦出现波动,结果就会失去可靠性。
方法二:复合增长率法复合增长率法是一种更加稳妥和科学的计算年平均增长率的方法。
其公式为:年平均增长率 = [(末值 ÷初始值) ^ (1÷n) - 1] × 100%其中,n代表时间段的年数,例如,如果要计算中国GDP从2010年到2019年的年平均增长率,n=9。
年平均增长率 = [(90.03 ÷ 40.15) ^ (1÷9) - 1] × 100% = 8.49%这个结果相对来说比较合理,符合中国GDP近年来的增长情况。
复合增长率法的优点在于其可以反映出一个数据在不同时间段内的增长变化,相对比较准确。
方法三:加权平均法加权平均法是一种考虑不同时间段内数据权重的计算年平均增长率的方法。
当某一时间段的数据比较重要时,可以用这种方法更加准确地计算年平均增长率。
其公式为:年平均增长率= Σ(wi × gi) ÷ Σ(wi) ×100%其中,wi表示时间段i内数据的权重,gi表示时间段i内数据的年平均增长率,时间段i的数量为n。
资料分析中年均增长量的求法

资料分析中年均增长量的求法年均增长量:就是假设每一年较之前的年份都以相同的增长量在增长,这就是所谓的年均增长量。
年均增长量在考试中主要有三种题型:1.已知初期量a,年均增长量x,增长年份n,求末期量。
末期量=初期量+nx其中n代表的是增长的年份,具体计算就是两个年份之差。
2.已知末期量b,年均增长量x,增长年份n,求初期量。
通过计算可以求解:初期量=末期量-nx这个求解过程是一个逆向的求解过程,所以这时候用的是一个减法。
3.已知初期量和末期量,还有已知增长年份,求年均增长量。
年均增长量=末期量-初期量/年份差易错点:1.年份差算成年份数。
例:2021年的棉花产量是23412吨,2021年的棉花产量是67893吨,求从2021年到2021年的年均增长量?错误的解法:67893-23412/6错误认为从09年到14年之间总共有6个年份,所以最后除以6对于年均增长量或年均增长率的问题都是除以两个年份直接做差所以正确的答案为67893-23412/52.年均增长量的初期量算错。
年份 2000 2001 2002 2021 2021 2021棉花产量 1234 4576 6571 7213 9521 10384求十一五期间棉花产量的年均增长量。
其实这道题的算法没有绝对的正确,只不过针对历年的考试主要有两种求法,两种求法都是正确的。
第一种解法:10384-4576/5这种解法主要是把起点定在2001年,因为十一五的起点就是2001年。
第二种解法:10384-1234/6这种解法是把起点定在2000年,这种解法相对第一种解法就是把2001年的增长情况也考虑在内,也有其合理性。
以上两种方法都可以运用,至于在考试过程中如何选择操作方法,233网校教育专家建议面临国考的同学可以用第一种方法来求解。
感谢您的阅读,祝您生活愉快。
年均增长率公式简便算法
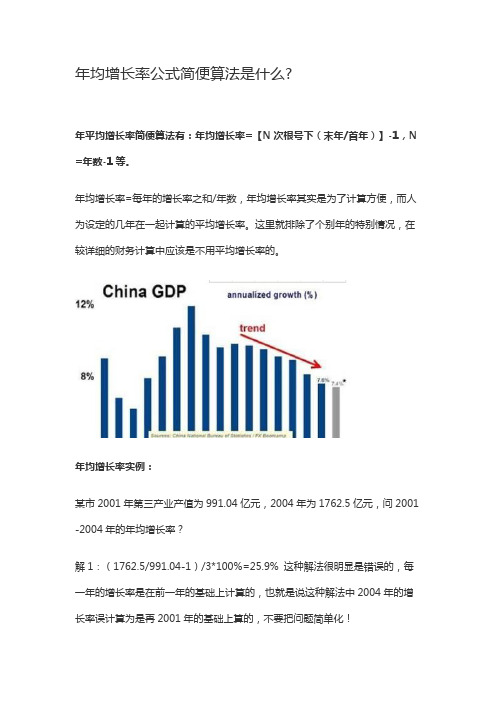
年均增长率公式简便算法是什么?
年平均增长率简便算法有:年均增长率=【N次根号下(末年/首年)】-1,N =年数-1等。
年均增长率=每年的增长率之和/年数,年均增长率其实是为了计算方便,而人为设定的几年在一起计算的平均增长率。
这里就排除了个别年的特别情况,在较详细的财务计算中应该是不用平均增长率的。
年均增长率实例:
某市2001年第三产业产值为991.04亿元,2004年为1762.5亿元,问2001 -2004年的年均增长率?
解1:(1762.5/991.04-1)/3*100%=25.9% 这种解法很明显是错误的,每一年的增长率是在前一年的基础上计算的,也就是说这种解法中2004年的增长率误计算为是再2001年的基础上算的,不要把问题简单化!
解2:{[(1762.5/991.04)^1/3]-1}*100%=21.1% 解法2是正确的,符合定义的公式!。
资料分析公式汇总

资料分析公式汇总在进行资料分析时,掌握一些关键的公式可以帮助我们更高效、准确地处理数据和得出结论。
下面就为大家汇总一些常用的资料分析公式。
一、增长类公式1、增长量=现期量基期量增长量是指现期量相对于基期量的增加量。
2、增长量=基期量 ×增长率这个公式用于在已知基期量和增长率的情况下,计算增长量。
3、增长率=(现期量基期量)÷基期量 × 100%增长率反映了数据的增长速度。
4、年均增长量=(末期量初期量)÷间隔年份用于计算一段时间内平均每年的增长量。
5、年均增长率=\(\sqrtn{\frac{末期量}{初期量}} 1 \)(n 为间隔年份)用来衡量在若干年中平均每年的增长幅度。
二、比重类公式1、比重=部分量÷整体量 × 100%比重表示部分在整体中所占的比例。
2、整体量=部分量÷比重通过已知部分量和比重,求出整体量。
3、部分量=整体量×比重已知整体量和比重,计算部分量。
三、平均数类公式1、平均数=总数÷个数这是最基本的平均数计算方式。
2、平均增长量=(末期平均数初期平均数)÷间隔年份用于计算一段时间内平均每年的增长情况。
3、平均增长率=\(\sqrtn{\frac{末期平均数}{初期平均数}}1 \)(n 为间隔年份)衡量平均数在若干年中的平均增长幅度。
四、倍数类公式1、倍数= A÷BA 是B 的多少倍,用 A 除以 B 即可得出。
2、基期倍数=\(\frac{A}{B} ×\frac{1 + b\%}{1 +a\%}\)A、B 分别为现期量,a%、b%分别为对应的增长率。
五、隔年增长类公式1、隔年增长率=当年增长率+上年增长率+当年增长率×上年增长率用于计算间隔一年的增长率。
2、隔年基期量=现期量÷(1 +隔年增长率)通过现期量和隔年增长率,求出隔年的基期量。
年均增长率计算公式文

年均增长率计算公式文年均增长率计算公式。
年均增长率是一个用来衡量某一指标在一定时间内平均增长速度的指标。
它可以帮助我们了解某一指标的增长趋势,对于投资、经济发展等方面都具有重要的意义。
在本文中,我们将介绍年均增长率的计算公式,并且讨论一些实际应用的案例。
年均增长率的计算公式如下:年均增长率 = (终值 / 初值)^(1/年数) 1。
其中,终值代表某一指标在结束时的数值,初值代表某一指标在开始时的数值,年数代表所观察的时间段的年数。
通过这个公式,我们可以计算出某一指标在一定时间内的平均增长率。
为了更好地理解这个公式,我们可以通过一个实际的例子来进行说明。
假设某公司在2015年的销售额为1000万元,在2020年的销售额为1500万元,我们可以使用年均增长率的公式来计算出这五年间的销售额的平均增长率。
首先,我们可以将初值和终值代入公式中:初值 = 1000万元。
终值 = 1500万元。
年数 = 2020 2015 = 5年。
然后,我们可以将这些值代入年均增长率的公式中进行计算:年均增长率 = (1500 / 1000)^(1/5) 1。
= (1.5)^(1/5) 1。
≈ 0.086。
通过这个计算,我们可以得出该公司在这五年间的年均增长率约为8.6%。
这个数字可以帮助我们更好地了解该公司销售额的增长趋势,对于投资者来说也具有重要的参考价值。
除了上面的例子之外,年均增长率还可以在很多其他方面进行应用。
比如在经济学中,我们可以使用年均增长率来衡量一个国家的经济增长速度;在投资中,我们可以使用年均增长率来评估某一投资组合的表现等等。
总的来说,年均增长率是一个非常有用的指标,它可以帮助我们更好地了解某一指标的增长趋势,并且可以在很多领域进行应用。
通过年均增长率的计算公式,我们可以更加准确地评估某一指标的增长情况,为决策提供更加科学的依据。
年均增长量的计算方法

年均增长量的计算方法嘿,朋友们!今天咱就来唠唠年均增长量的计算方法。
这可是个挺重要的玩意儿呢,就好像你要去一个目的地,得知道走哪条路最近最靠谱。
咱先打个比方哈,比如说你有一笔钱,每年都在增加,你想知道平均每年增加了多少,这就是年均增长量啦。
那怎么算呢?其实很简单啦,就是用总的增长量除以年数。
就好比你跑一段路,总的距离就是增长量,跑的年数就是时间,用距离除以时间不就得到速度了嘛,这里的速度就相当于年均增长量。
比如说,从第一年到第五年,某个数值从 100 变成了 150,那总的增长量就是 150 减去 100 等于 50 呀。
然后除以年数 5 减 1 等于 4 年,那年均增长量不就是 50 除以 4 嘛。
这有啥难的呀,对吧?可别小看这年均增长量,它用处可大了去了。
比如说你想看看一个公司这几年发展得咋样,看看它的某个指标的年均增长量,就能大概心里有个数啦。
再比如说,你想知道自己的财富增长速度,也可以用这个方法呀。
每年记记账,看看自己的资产增加了多少,再除以年数,不就知道自己平均每年能多赚多少钱啦。
而且啊,学会了这个方法,你还能跟别人吹吹牛呢,“嘿,你知道年均增长量咋算不?我可会呢!”多牛气呀!咱再举个例子哈,有个城市的人口,十年前是 100 万,现在是 130 万,那这十年的增长量就是 130 万减去 100 万等于 30 万呀。
那年均增长量就是 30 万除以 10 年等于 3 万每年。
你看,这不就清楚明白啦。
所以啊,朋友们,年均增长量的计算方法真的不难,就是那么简单的几步。
只要你稍微用点心,肯定能学会。
学会了它,你就能在很多方面派上用场,就像你有了一把万能钥匙,能打开很多知识的大门呢!别犹豫啦,赶紧去试试吧!看看你身边的各种数据,算算它们的年均增长量,说不定会有很多有趣的发现哦!这多有意思呀,对吧?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
官方网站: 给人改变未来的力量
强烈推荐!!!中公教育.公务员考试第一品牌!
/(中公官网)
公考社区:/公考伤我千百遍,我待公考如初恋!公务员考试经验交流,考碗族聚集地。
加入公考QQ群,/zg/2014qqhz/全国公考的学霸都在这,找自己得小伙伴一起学习吧!
公务员考试行测资料分析题型中有一类求增长量的题目,考生普遍感觉比较混乱,这一类的题型就是求年均增长量,下面中公教育专家就年均增长量谈谈该如何求解。
年均增长量:就是假设每一年较之前的年份都以相同的增长量在增长,这就是所谓的年均增长量。
年均增长量在考试中主要有三种题型:
1.已知初期量a,年均增长量x,增长年份n,求末期量。
末期量=初期量+nx
其中n代表的是增长的年份,具体计算就是两个年份之差。
2.已知末期量b,年均增长量x,增长年份n,求初期量。
公考咨询交流、公考资讯早知道、公考资料获取,尽在中公网
官方网站: 给人改变未来的力量通过计算可以求解:初期量=末期量-nx
这个求解过程是一个逆向的求解过程,所以这时候用的是一个减法。
3.已知初期量和末期量,还有已知增长年份,求年均增长量。
年均增长量=(末期量-初期量)/年份差
易错点:
1.年份差算成年份数。
例:2009年的棉花产量是23412吨,2014年的棉花产量是67893吨,求从2009年到2014年的年均增长量?
错误的解法:(67893-23412)/6
错误认为从09年到14年之间总共有6个年份,所以最后除以6
对于年均增长量或年均增长率的问题都是除以两个年份直接做差
所以正确的答案为(67893-23412)/5
2.年均增长量的初期量算错。
年份 2000 2001 2002 2003 2004 2005
棉花产量 1234 4576 6571 7213 9521 10384
公考咨询交流、公考资讯早知道、公考资料获取,尽在中公网
官方网站: 给人改变未来的力量求十一五期间棉花产量的年均增长量。
其实这道题的算法没有绝对的正确,只不过针对历年的考试主要有两种求法,两种求法都是正确的。
第一种解法:
(10384-4576)/5
这种解法主要是把起点定在2001年,因为十一五的起点就是2001年。
第二种解法:
(10384-1234)/6
这种解法是把起点定在2000年,这种解法相对第一种解法就是把2001年的增长情况也考虑在内,也有其合理性。
以上两种方法都可以运用,至于在考试过程中如何选择操作方法,中公教育专家建议面临国考的同学可以用第一种方法来求解。
公考咨询交流、公考资讯早知道、公考资料获取,尽在中公网。
