(最新最全)全等三角形练习题综合拔高题
(完整)全等三角形证明之能力拔高(经典题目)

全等三角形能力拔高题姓名:一、角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4.如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l 的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.二、二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF.3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.MF E CBA5、已知:如图,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F ,DB=DC , 求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB ,AB ∥CD. 求证:△ADC 是等腰三角形。
2、如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MCG FEDC BA3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE= 。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
(完整word版)全等三角形拔高题目附附答案解析

全等三角形提高练习1. 如图所示,△ABC ≌△ADE ,BC 的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF 的度数。
2. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB 交于点C (A ′不在OB 上),则∠A ′CO 的度数为多少?3. 如图所示,在△ABC 中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△C 的度数是多少?4.如图所示,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C,A ′B′交AC 于点D ,若∠A ′DC=90°,则∠A=5. 已知,如图所示,AB=AC ,AD ⊥BC 于D ,且AB+AC+BC=50cm ,而,则AD是多少?AB'CA6. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE,垂足分别为D 、E ,若BD=3,CE=2,则DE=7. 如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、G ,AD 与EF 垂直吗?证明你的结论.8. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,DE ⊥AB 于E,DF ⊥AC 于F,△ABC 的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
9. 已知,如图:AB=AE ,∠B=∠E ,∠BAC=∠EAD ,∠CAF=∠DAF ,求证:10. 如图,AD=BD ,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点BCB11. 如图所示,已知,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于F ,且有BF=AC ,FD=CD ,求证:BE ⊥AC12. △DAC 、△EBC 均是等边三角形,AF 、BD 分别与CD 、CE 交于点M 、N,求证:(1)AE=BD (2)CM=CN (3)△CMN 为等边三角形 (4)MN ∥BC13. 已知:如图1,点C 为线段AB 上一点,△ACM 、△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN于点F(1) 求证:AN=BM(2) 求证:△CEF 为等边三角形14. 如图所示,已知△ABC 和△BDE 都是等边三角形,下列结论:①AE=CDAHD ;④∠AHC=60°;⑤△BFG 是等边三角形;⑥FG ∥AD ,其中正确的有(A .3个B 。
(最新最全)全等三角形练习题综合拔高题
全等三角形拔高题如图,在厶ABC 中,D 是边BC 上一点,AD 平分/ BAC 在AB 上截取AE=AC 连结DE 已知DE=2cmBD=3cm 求线段BC 的长2. BD = CE, AD 与BE 相交于点P,求ZAPE 的大小。
3. A已知等边三角形ABC 中, 若/ BAE 的平分线AF 交BE 于F , AC=8求DC 的长已知:如图所示,BD 为/ ABC 的平分线,AB=BC 点P 在BD 上 ,PMLAD 于 M ?PN1 CD 于 N , 5. 判断PM 与PN 的关系.4. 如图所示,P 为/ AOB 的平分线上一点,PCI OA 于 C, ?/ OAP+Z OBP=180° , 若 OC=4cm 求 AO+B (的值.如图所示,A , E , F , C 在一 条直线上,AE=CF 过E , F 分别作DE?LAC,BF 丄AC,若 EF,为什么?若将△DEC 的边EC 沿 AB=CD 可以得到BD 平分AC 方向移动,变为如图所示时,其余条件不变,上述结论是否 成立?请说明理由.6.如图,△ ABC 中 , D 是BC 的中点,过D 点的直线GF 交AC于F ,交AC 的平行线BG 于G 点, DE 丄DF,交AB 于点E,连结EG EF. 求证:BG=CF;请你判断BE+CF 与 EF 的大小关系,并说明理由。
7.已知:如图 E 在厶ABC 的边AC 上,且/ AEB= / ABC ⑴求证:/ ABE " C; FD// BC 交 AC 于 D ,设AB=5 0(1)(2) 于点N ,试判断线段BN 与CN 的数量关系, 并证明你的结论.9.已知:如C8.如图,在厶ABC 和厶DCB中,AB= DC AC= DB AC 与 DB 交于点M求证:△ ABC^A DCB ;过点C 作CN// BD,过点B 作BN// AC CN 与BN 交 且DOAE, E 为AB 的中点,1.10.14. (1)(2)求证:△ AED^A EBC观看图前,的三角形.A11.E、DE如c A如图①,AF=CE,MBD在不添辅助线的情况下,除厶EBC外,请再写出两个与厶AED的面积相等(直接写出结果,不要求证明):F分别为线段AC上的两个动点,且DEL AC于E, BF L AC于F,若AB=CDBD交AC于点M.(1) 求证:MB=MD ME=MF2)当E、F两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.EF M图,已知在厶ABC中,/BAC为直角,AB=AC D为上一点,CEL BD于E.(1) 若BD平分/1ABC 求证CE=2(2) 若D为AC上一动点,/ AED如何变化,若变化,求它的变化范围;若不变,求出它的度数,并说明理由12.在厶ABC中, ,AB=AC取点E,使CE=BD,在AB边上取点D,在AC延长线上了连接DE交BC于点F,求证DF=EF .“也”表示出BE中线,过C作CF L AE,垂足为F,过(1) 求证:(1)AE=CD;(2)若A、o如图,取一张长方形纸片,用点,将其折叠,使点D与点B重合形,如果有,请先用13.如图△ABC^A A 'E' C , /ACB900, /A=25°,点B 在A'B' 上,求/ ACA'的度数。
全等三角形的练习题(100题)

1、如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC.2、如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.(1)求证:△ABE≌DCE;(2)当∠AEB=50°,求∠EBC的度数?3、如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF4、如图,点E、F在BC上,BE=FC,AB=DC,∠B=∠C.求证:∠A=∠D.5、如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l 于点C,BD⊥l交l于点D.求证:AC=OD.6、如图,已知AD是△ABC的中线,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:BE=CF.7、如图,已知点B、E、C、F在同一条直线上,BE=CF,AB∥DE,∠A=∠D.求证:AB=DE.8、如图,CD=CA,∠1=∠2,EC=BC,求证:DE=AB9、如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.求证:AD=CF10、如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.(1)求证:CF=DG;(2)求出∠FHG的度数.11、如图,C是AB的中点,AD=BE,CD=CE.求证:∠A=∠B.12、已知:如图,D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.13、已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证:BC=ED.14、如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.(1)求证:△ADE≌△BFE;(2)连接EG,判断EG与DF的位置关系并说明理由.15、在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:;结论:。
(完整版)全等三角形练习题及答案

全等三角形练习题及答案1、下列判定直角三角形全等的方法,不正确的是()A、两条直角边对应相等。
B、斜边和一锐角对应相等。
C、斜边和一条直角边对应相等。
D、两锐角相等。
2、在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是()A.∠AB.∠BC.∠CD.∠B或∠C3、下列各条件中,不能作出唯一三角形的是()A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角 D.已知三边4、在△ABC与△DEF中,已知AB=DE;∠A=∠D;再加一个条件,却不能判断△ABC与△DEF全等的是().A. BC=EF B.AC=DFC.∠B=∠E D.∠C=∠F5、使两个直角三角形全等的条件是()A.一锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条直角边对应相等6、在△ABC和△A'B'C'中有①AB=A'B',②BC=B'C',③AC=A'C',④∠A=∠A',⑤∠B=∠B',⑥∠C=∠C',则下列各组条件中不能保证△ABC≌△A'B'C'的是()A、①②③B、①②⑤C、①②④D、②⑤⑥7、如图,已知∠1=∠2,欲得到△ABD≌△ACD,还须从下列条件中补选一个,错误的选法是()A、∠ADB=∠ADCB、∠B=∠CC、DB=DCD、AB=AC8、如图,△ABC≌△ADE,若∠BAE=120°,∠BAD=40°,则∠BAC的度数为A. 40°B. 80°C.120°D. 不能确定9、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=600,∠B=250,则∠EOB的度数为()A.600 B.700C.750D.85010、如图,已知AB=DC,AD=BC,E.F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )A. 150°B.40°C.80°D. 90°11、①两角及一边对应相等②两边及其夹角对应相等③两边及一边所对的角对应相等④两角及其夹边对应相等,以上条件能判断两个三角形全等的是( )A.①③ B.②④ C.②③④ D.①②④12、下列条件中,不能判定两个三角形全等的是()A.三条边对应相等 B.两边和一角对应相等C.两角及其一角的对边对应相等 D.两角和它们的夹边对应相等13、如图,已知,,下列条件中不能判定⊿≌⊿的是()(A)(B)(C)(D)∥14、如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠B=30°,则∠D的度数为().A.50° B.30° C.80° D.100°15、如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于点F,若BF=AC,则∠ABC的度数是.16、在△ABC和△中,∠A=44°,∠B=67°,∠=69°,∠=44°,且AC=则这两个三角形全等(填“一定”或“不一定”)17、如图,,,,在同一直线上,,,若要使,则还需要补充一个条件:或.18、(只需填写一个你认为适合的条件)如图,已知∠CAB=∠DBA,要使△ABC≌△BAD,需增加的一个条件是。
全等三角形练习题及答案

全等三角形练习题及答案1、下列判定直角三角形全等的方法,不正确的是()A 、两条直角边对应相等。
B 、斜边和一锐角对应相等。
C 、斜边和一条直角边对应相等。
D 、两锐角相等。
C. / CD. / B 或/ C3、下列各条件中,不能作岀唯一三角形的是( )A.已知两边和夹角B.已知两角和夹边C.已知两边和其中一边的对角 D.已知三边4、在△ DEF 中,已知AB=DE / A =Z D;再加一个条件,却不能判断△ ABC WA DEF 全等的是(A. BC=EF B . AC=DFC.Z B=Z E D ./ C=Z F5、使两个直角三角形全等 的条件是A . —锐角对应相等 D.两条直角边对应相等6、在△ ABC ^A ABC 中有① ABA ' B ,② BC =B C ,③ AC=A C ,④/ A =Z A ,⑤/ B =Z B ,⑥/ C =Z C ,则下列各组条件中不能保证厶 AB9A ABC 的是 ()2、在△ ABC 中,/ B = Z 0与厶ABC 全等的三角形有一个角是100 °,那么在厶ABC 中与这100 °角对应相等的角是B.两锐角对应相等C . 一条边对应相等A、①②③B、①②⑤C、①②④D、②⑤⑥7、如图,已知/ 仁/2,欲得到△ ABD^A ACD 还须从下列条件中补选一个,错误的选法是8、如图,△ ABC^A ADE 若/ BAE =120°,/ BAt =40°,则/ BAC 的度数为9、如图,AE = AF , AB= AC EC 与 BF 交于点 O, / A = 600,/ B = 25°,则/ EOB 的度数为()10、 如图,已知 AB= DC AD= BC,在 DB 上两点且 BF = DE,若/ AEB= 12°°, / ADB= 3°°,则/ BCF= ( )D. 90应相等,以上条件能判断两个三角形全等的是 ( )A 、/ ADB=/ ADCB 、/ B=/C C 、DB=DCD 、 AB=ACA. 40B. 8 0 D.不能确定A . 60°B . 70° C. 75° D. 85°A. 150 11、①两角及一边对应相等②两边及其夹角对应相等 ③两边及一边所对的角对应相等 ④两角及其夹边对A .①③B •②④C •②③④D •①②④B •两边和一角对应相等C .两角及其一角的对边对应相等D •两角和它们的夹边对应相等13、如图,已知…二八二,二归七=4■.二厂,下列条件中不能判定/ 「上工幻/ f 「的是( )15、如图,△ ABC 中,AD 丄BC 于D, BE 丄AC 于E ,AD 与BE 相交于点F ,若BF = AC,则/ ABC 的度数是 _____________________16、在厶 ABC 和△」-'-•中,/ A=44°,Z B=67°,/ -=69 °,/丄=44 °,且 AC='则这两个三角形 ___________________ 全等(填“一定”或“不一定”)17、如图,止,L',丄-在同一直线上,-匚|',若要使一-,则还需要补充个条件: _________________ 或 ______________A .三条边对应相等 (C)--V(B)二二i =-—(D )匚If II -14、如图,AB 与 CD 交于点 O, 0¥OC OD= OB, / A=50°,Z B= 30° ,则/D 的度数为( ).r第上题A . 50B . 30°C . 80°D .10018、(只需填写一个你认为适合的条件)如图,已知/ CABN DBA 要使△ AB3A BAD,需增加的一个条件F21、如图,△ ABD △ ACE都是正三角形,BE和CD交于0点,则/ BOC= ________________ :22、已知:如图,/ ABC=Z DEF,,AB= DE 要说明△ ABC^A DEF,(1)若以“ SAS'为依据,还须添加的一个条件为 _____________________(2)若以“ ASA'为依据,还须添加的一个条件为 _____________________(3)若以“ AAS'为依据,还须添加的一个条件为 _____________________23、如图4,如果AB= AC, ______________________ ,即可判定△ ABD^A AC吕A24、如图2, Z仁/2,由AAS判定△ ABD^A ACD,则需添加的条件是__________________25、如图,已知 / ACBM BDA 只要再添加一个条件: ________________ ,就能使△ ACB^A BDA (填一个即可)26、已知,如图 2:Z ABCK DEF, AB=DE 要说明△ ABC^A DEF⑴ 若以“ SAS'为依据,还要添加的条件为 ___________________(2) 若以“ ASA ”为依据,还要添加的条件为 __________________27、如图9所示,BC=EC /仁/ 2,要使△ ABC^A DEC 则应添加的一个条件为 ________________________________ [答案不唯一,只需填一个]。
人教版八年级上数学全等三角形经典拔高题型汇总50题(后附答案详解)

人教版八年级上数学全等三角形经典拔高题型汇总50题(后附答案详解)一、单选题(共8题;共16分)1.如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC 于F,已知:AD:DB=1:3,BC=4√6,则PE+PF的长是()A. 4√6B. 4√2C. 6D. 2√62.如图,△ACB和△DCE均为等腰直角三角形,且∠ACB=∠DCE=90°,点A、D、E在同一条直线上,CM平分∠DCE,连接BE.以下结论:① AD=CE;② CM⊥AE;③ AE=BE+ 2CM;④ CM//BE,正确的有()A. 1个B. 2个C. 3个D. 4个3.如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点∠C;②当∠C=60°时,AF+BE=AB;③若OD=O作OD⊥BC于D,下列四个结论:①∠AOB=90°+ 12a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是()A. ①②B. ②③C. ①②③D. ①③4.如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边的中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,则以下结论;①∠DBM=∠CDE;②BN=DN;③AC=2DF;④S ΔBDE﹤S 四边形BMFE其中正确的结论是()A. ①②③B. ②③④C. ①②④D. ①③5.如图,在Rt△ABC中,CA=CB,D为斜边AB的中点,Rt∠EDF在△ABC内绕点D转动,分别交边AC,BC于点E,F(点E不与点A,C重合),下列说法正确的是()① ∠DEF=45°;② BF2+AE2=EF2;③ CD<EF≤√2CDA. ①②B. ①③C. ②③D. ①②③6.如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是()① BF=CF;②若BE⊥AC,则CF=DF;③若BE平分∠ABC,则FG=3;④连结EF,若2BE⊥AC,则∠DFE=2∠ABE.A. ①②③B. ③④C. ①②④D. ①②③④7.如图,已知直线AB:y=√55x+√55分别交x轴、y轴于点B、A两点,C(3,0),D、E分别为线段3AO和线段AC上一动点,BE交y轴于点H,且AD=CE.当BD+BE的值最小时,则H点的坐标为()A. (0,√55) B. (0,5) C. (0,4) D. (0,√55) 28.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中:①AC=BD;②∠AMB=30°;③△OEM≌△OFM;④MO平分∠BMC.正确的个数有()A. 4个B. 3个C. 2个D. 1个二、填空题(共6题;共7分)9.如图所示是一个3×3的正方形,则∠1+∠2+∠3+⋯+∠9=________.10.如图,△ABC中(AB>BC),G在CB的延长线上,边AC的垂直平分线DE与∠ABG的角平分线交于点M,与AB交于点D,与AC相交于E,MN⊥AB于N.已知AB=13,BC=9,MN=3,则△BMN的面积是________.11.如图,在锐角三角形ABC中,∠B=45°,ABAC =65,点D为边AB的中点,点E在边AC上,将△ADE沿DE折叠得到△FDE.若FE⊥AC,则AEEC 的值为________;DEAF的值为________.12.如图,在平面直角坐标系中,点A,B的坐标分别为(−1,0),(0,2),点C是反比例函数y=k x (x>0)图象上一点,∠ABC=135°,AC交y轴于点D,ADDC=23,则k的值为________.13.如图,矩形ABCD中,点E,F分别在边AD,CD上,且EF⊥BE,EF=BE,△DEF的外接圆⊙O恰好切BC于点G,BF交⊙O于点H,连结DH.若AB=4,则DH=________ .14.如图,点P在正方形ABCD的BC边上,连接AP,作AP的垂直平分线,交AD延长线于点E,连接PE,交CD于点F.若点F是CD的中点,则tan∠BAP=________.三、综合题(共36题;共441分)15.有公共顶点A的△ABD,△ACE都是等边三角形.(1)如图1,将△ACE绕顶点A旋转,当E,C,B共线时,求∠BCD的度数;(2)如图2,将△ACE绕顶点A旋转,当∠ACD=90°时,延长EC角BD于F,①求证:∠DCF=∠BEF;②写出线段BF与DF的数量关系,并说明理由.16.如图,一次函数y=﹣2x+b的图象与x轴、y轴分别交于点A、B,线段AB的中点为D(3,32).将△AOB沿直线CD折叠,使点A与点B重合,直线CD与x轴交于点C.(1)求此一次函数的解析式;(2)求点C的坐标;(3)在坐标平面内存在点P(除点C外),使得以A、D、P为顶点的三角形与△ACD全等,请直接写出点P的坐标.17.已知△ABC是等边三角形,D是BC边上的一动点,连结AD.(1)如图1所示,若BD = 2,DC = 4,求AD的长.(2)如图2所示,以AD为边作∠ADE =∠ADF =60°,分别交AB,AC于点E,F.①小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE = AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的两种想法.想法1:利用AD是∠EDF的平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.想法2:利用AD是∠EDF的平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证请你参考上面的想法,帮助小明证明AE =AF(一种方法即可).②小聪在小明的基础上继续进行思考,发现:四边形AEDF的面积与AD的长存在一定的关系.若用S表示四边形AEDF的面积,x表示AD的长,请你直接写出S与x之间的函数表达式.18.在直线上顺次取A,B,C三点,分别以AB,BC为边在直线的同侧作等边三角形,作得的两个等边三角形的另一顶点分别为D,E两点.连结DE.(1)如图1所示,连结CD,AE,求证:CD = AE.(2)如图2所示,若AB = 1,BC = 2,求证:∠BDE = 90°.(3)如图3所示,将图2中的等边三角形BEC绕点B作适当的旋转,连结AE,若有DE 2 + BE 2 = AE2,试求∠DEB的度数.19.如图,在△ABC中.(1)如图①,分别以AB、AC为边作等边△ABD和等边△ACE,连接BE,CD;①猜想BE与CD的数量关系是▲;②若点M,N分别是BE和CD的中点,求∠AMN的度数;(2)如图②,若分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE=α,DC、BE交于点P,连接AP,请直请接写出∠APC与α的数量关系20.已知△ABC中,AC=BC;△DEC中,DC=EC;∠ACB=∠DCE=α,点A.D.E在同一直线上,AE与BC相交于点F,连接BE.(1)如图1,当α=60°时,①请直接写出△ABC和△DEC的形状;②求证:AD=BE;③请求出∠AEB的度数.(2)如图2,当α=90°时,请直接写出:① ∠AEB的度数;②若∠CAF=∠BAF,BE=2,线段AF的长.21.已知△ABC是等腰直角三角形,∠ACB=90°,BC=AC.直角顶点C在x轴上,锐角顶点B在y轴上,过点A作AD⊥x轴,垂足为点D.当点B不动,点C在x轴上滑动的过程中.(1)如图1,当点C的坐标是(−1,0),点A的坐标是(−3,1)时,请求出点B的坐标;(2)如图2,当点C的坐标是(1,0)时,请写出点A的坐标;(3)如图3,过点A作直线AE⊥y轴,交y轴于点E,交BC延长线于点F.AC与y轴交于点G.当y轴恰好平分∠ABC时,请写出AE与BG的数量关系.22.如图①,在△ABC中,AC=BC,∠ACB=90°,点D是AC的中点,连接BD,过点C作CE 平分∠ACB交BD于点E,点F在AB上,且∠ACF=∠CBD(1)求证:CF=BE;(2)如图②,过点A作AG⊥AB交BD的延长线于点G,①若DG=2,求CF;②设CF交BD于H,求HE的值.AG23.已知:如图,在平面直角坐标系中,∠OAC=∠OCA=60°,OC=CB(1)如图①,若OB=8,求点A的坐标(2)点E为线段AB上一动点,点E的横坐标为t,∠EOF=60°,EO=FO,连接BF,①如图②在(1)的条件下,设△OFB的面积为S,请用含t的式子表示S,②如图③,连接EF,EF交射线AC于点N,若∠ENA=45°,EN=3√2,求点E的坐标.24.如图(1)问题发现:如图1,如果△ABC和△ADE均为等边三角形(等边三角形的三条边都相等,三个角都是60°),点B、E、D三点在同一直线上,连接CD.则CD与BE的数量关系为________;∠BDC 的度数为________度.(2)探究:如图2,若△ABC为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出∠BOD的度数?25.已知△ABC是等边三角形,点D是AC的中点,点E在射线BC上,点F在射线BA上,∠EDF= 120°.(1)如图1,若点F与B点重合,求证:DB=DE;(2)如图2,若点E在线段BC上,点F在线段BA上,求BE+BF的值;AC(3)如图3,若AF+CE=BD,直接写出∠EDC的度数为________.26.已知△ABC和△DEF为等腰三角形,AB=AC,DE=DF,∠BAC=∠EDF,点E在AB 上,点F在射线AC上.(1)如图1,若∠BAC=60°,点F与点C重合,①求证:AF=AE+AD;②求证:AD//BC.(2)如图2,若AD=AB,那么线段AF,AE,BC之间存在怎样的数量关系.27.如图①在平面直角坐标系中,已知点A(a,0),B(0,−b)的坐标满足|a+b−8|+a2−2ab+b2=0.连接AB.点C在x轴负半轴上,作AH垂直BC交BC于点H,交OB于点P,且OC=OP.(1)直接写出点A与点B的坐标:(2)如图②,在题(1)的条件下,连接OH,求证:2∠OHP=∠AHB;(3)如图③,E为AB的中点,动点G在y轴上,连接GE,作EF⊥GE交x轴于F,猜想GB,OB,AF 三条线段之间的数量关系,并说明理由.28.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AB于点E,以点O为圆心,OE为半径作半圆,交AO于点F.(1)求证:AC是⊙O的切线;(2)若点F是OA的中点,OE=3,求图中阴影部分的面积;(3)在(2)的条件下,点P是BC边上的动点,当PE+PF取最小值时,直接写出BP的长.29.(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.(1)(材料理解)在图1中证明小明的发现.(2)(深入探究)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有________.(将所有正确的序号填在横线上).(3)(延伸应用)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.30.如图,∠CAD与∠CBD的角平分线交于点P.(1)若∠C=35°,∠D=29°,求∠P的度数;(2)猜想∠D,∠C,∠P的等量关系.31.如图,在平面直角坐标系中,O为坐标原点,AD为等腰△AOC底边OC上的高,直线OA的解析式为y=x,抛物线y=a(x−4)2+k的顶点为点A,且经过坐标原点.(1)求该抛物线的解析式;(2)有一动点P从点O出发,沿射线OA方向以每秒√2个单位长度的速度运动,连接PD,设△APD的面积为S,点P的运动时间为t秒,求S与t的关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,过点D做PD的垂线交射线AC于点E,过点E作OC的垂线交抛物线于点F,直接写出当t为何值时,CE的长为√2,并写出此时点F的坐标.32.在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx−3交x轴负半轴于点A,交xOA.轴正半轴于点B,交y轴于点C,OB=OC=32(1)如图1,求抛物线的解析式;(2)如图2,点D在抛物线上,且点D在第二象限,连接DB交y轴于点E,若tan∠EBA=1,求点D的坐标;2(3)如图3,在(2)的条件下,点P在抛物线上,且点P在第三象限,点F在PB上,FC= FB,过点F作x轴的垂线,点G为垂足,连接DG并延长交BF于点H,若∠DHP=∠CEB,求BP的长.33.如图,在平面直角坐标系中,点A、B分别在x、y轴上,已知点B的坐标为(0,1),且∠BOA=30∘.(1)求AB的长度;(2)以AB为一边作等边,过点A作AD⊥AB,交OA的垂直平分线MN于点D.求证:BD= OE;(3)在(2)的条件下,连接DE交AB于F,求证:F为DE的中点.34.如图,A,B,C,D四点都在OO上,弧AC=弧BC,连接AB,CD、AD,∠ADC=45°.(1)如图1,AB是⊙O的直径;(2)如图2,过点B作BE⊥CD于点E,点F在弧AC上,连接BF交CD于点G,∠FGC=2∠BAD,求证:BA平分∠FBE;(3)如图3,在(2)的条件下,MN与⊙O相切于点M,交EB的延长线于点N,连接AM,若AB,EN=26,求线段CD的长.2∠MAD+∠FBA=135°,MN=101335.如图:已知点A(0,1),点B在第一象限,△OAB是等边三角形,点C是X轴上的动点,以AC为边作等边三角形△ACD(A、C、D三点按逆时针排列),直线BD交Y轴于点E(1)求证:△CAO≌△DAB;(2)点C运动时,点E是动点还是定点?若是动点,指出其运动路径;若是定点,求其坐标;(3)连接CE,若∠ACD=25°,求∠CED的度数.36.如图,已知△ABC中,BE平分∠ABC,且BE=BA,点F是BE延长线上一点,且BF= BC,过点F作FD⊥BC于点D.(1)若∠ABC=72°,求等腰三角形BFC与等腰三角形ABE的底角的度数;(2)求证:∠BEC=∠BAF;(3)判断△AFC的形状并说明理由.37.在Rt△ABC中,∠ACB=90°,AC=BC,D为BC上一点,连接AD,过点C作CE上AD于点E.(1)如图,过点B作BF⊥BC交CE的延长线于点F,求证△ACD≌△CBF;(2)如图,若D为BC的中点,CE交AB于点M,连接DM,求证:∠BDM=ADC;(3)在(2)的条件下,若AE=4,CE=2,直接写出CM的长.38.在△ABC中,AB=AC=10,AD是BC边上的高,点E在边BC上,连接AE.(1)当AD=6时,①求△ABC的面积.②若AE平分∠BAD,求CE的长.(2)探求三条线段AE,BE,CE之间的等量关系.x+1与x轴、y轴分别交于点A、B.39.如图,直线y=−√33(1)求点A、B的坐标;(2)以线段AB为直角边作等腰直角△ABC,点C在第一象限内,∠BAC=90°,求点C的坐标;(3)若以Q、A、C为顶点的三角形和△ABC全等,求点Q的坐标.40.如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,如图1,等腰△ABC与等腰△ADE中,∠BAC=∠DAE=α,AB=AC,AD=AE.我们把它们构成的这个图形叫做“手拉手模型”.(1)【探究模型】如图1,线段BD与线段CE存在怎样的数量关系?请证明你的结论;(2)【应用模型】如图2,等腰直角三角形ABC中,∠BAC=90°,BC=4 √3,点P是BC边的中点,直线MN经过点P,且与直线BC的夹角为30°,点D是直线MN上的动点,将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE.①如图3,当点E落在BC边上时,求C,E两点之间的距离.②直接写出在点D运动过程中,点C和点E之间的最短距离.41.如图1,已知一次函数y=kx+6的图象分别交y轴正半轴于点A,x轴正半轴于点B,且△AOB的面积是24,P是线段OB上一动点.(1)求一次函数解析式;(2)如图1,将△AOP沿AP翻折得到△AO'P,当点O'正好落在直线AB上时,①求点P的坐标;②将直线AP绕点P顺时针旋转45°得到直线A'P,求直线A'P的表达式;(3)如图2,上题②中的直线A'P与线段AB相交于点M,将△PBM沿着射线PA'向上平移,平移后对应的三角形为△P'B'M',当△APB'是以AP为直角边的直角三角形时,请求出点P'的坐标.42.在矩形ABCD中,点E在边BC上,连接AE.(1)如图①,当矩形ABCD为正方形时,将△ABE沿AE翻折得到△AFE,连接EF并延长交边CD 于点G,连接AG.求证:GE=BE+DG;(2)如图②,在矩形ABCD的边CD上取一点G,连接AG,使∠EAG=45°.①若AB=3,AD=4,DG=1,则BE=________(直接填空);②过点G作GH//BC,交AE于点H,如图③,若AD=mAB(m>1),请直接写出线段GH、BE、DG之间的数量关系.________43.在等腰△ABC中,∠BAC=90°,作∠ABC的平分线交AC于点D,∠MDN=135°,将∠MDN绕点D旋转,使∠MDN的两边交直线BA于点E,交直线BC于点F.(1)当∠MDN绕点D旋转到如图①的位置时,请直接写出三条线段AE,CF,AD的数量关系;(2)当∠MDN绕点D旋转到如图②的位置时,(1)中结论是否成立,若成立,请证明;若不成立,请写出正确的结论,并说明理由;(3)若BC=2+ √2,当∠CDF=15°时,请直接写出线段CF的长度.44.如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与AB的垂直平分线DE相交于点E。
全等三角形拔高题目附带标准答案

全等三角形提高练习1. 如图所示,△AB C ≌△AD E,BC 的延长线过点E ,∠ACB =∠AE D=105°,∠CA D=10°,∠B=50°,求∠D EF的度数。
2. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A′OB′,边A ′B ′与边O B交于点C(A ′不在OB 上),则∠A ′CO 的度数为多少?3. 如图所示,在△AB C中,∠A=90°,D 、E 分别是AC 、BC 上的点,若△ADB ≌△EDB ≌△EDC,则∠C 的度数是多少?4. 如图所示,把△ABC 绕点C 顺时针旋转35°,得到△A′B ′C ,A ′B′交AC 于点D,若∠A ′DC=90°,则∠A=5. 已知,如图所示,A B=AC ,A D⊥BC 于D ,且AB +AC+B C=50cm ,而AB+BD +AD=40cm ,则AD 是多少?6. 如图,R t△A BC中,∠BAC=90°,AB=AC ,分别过点B 、C作过点A 的垂线BC 、CE ,垂足分别为D 、E,若BD=3,CE=2,则DE=AB'CA7. 如图,AD 是△A BC 的角平分线,D E⊥AB ,D F⊥AC,垂足分别是E、F,连接EF,交AD于G,AD 与EF 垂直吗?证明你的结论。
8. 如图所示,在△AB C中,AD 为∠BAC 的角平分线,D E ⊥AB 于E,DF ⊥AC 于F ,△ABC 的面积是28cm2,AB=20cm ,AC=8cm ,求DE 的长。
9. 已知,如图:AB =AE ,∠B=∠E ,∠BAC=∠EAD ,∠CAF =∠DAF,求证:AF ⊥CD10. 如图,A D=BD ,A D ⊥BC 于D,BE ⊥AC 于E ,AD 与BE相交于点H ,则BH 与A C相等吗?为什么?11. 如图所示,已知,AD 为△AB C的高,E 为A C上一点,BE 交AD 于F ,且有BF=AC ,FD=CD,求证:BE⊥AC12. △DAC 、△E BC均是等边三角形,A F、BD 分别与CD 、CE 交于点M、N,求证:(1)A E=BD (2)CM=CN (3)△CMN 为等边三角形 (4)M N∥BCBCBBA B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形拔高题
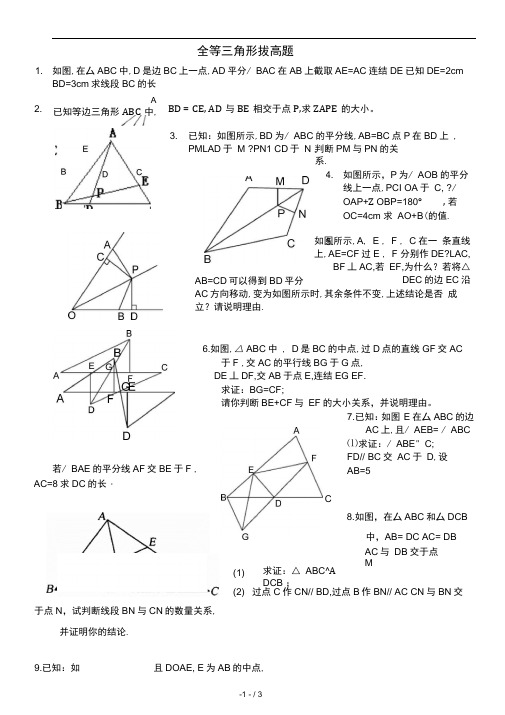
1. 如图,在ΔABC 中,D 是边BC 上一点,AD 平分∠BAC ,在AB 上截取AE=AC ,连结DE ,已知DE=2cm ,
BD=3cm ,求线段BC 的长。
2. 已知等边三角形ABC中,BD=CE,AD与BE相交于点P,求∠APE的大小。
3. 已知:如图所示,BD 为∠ABC 的平分线,AB=BC ,点P 在BD 上,
PM ⊥AD 于M ,•PN ⊥CD 于N ,判断PM 与PN 的关系.
4. 如图所示,P 为∠AOB 的平分线上一点,PC ⊥OA 于C ,•∠OAP+
∠OBP=180°,若OC=4cm ,求AO+BO 的值.
A B C D
E P D A
C
B
M N
P
A C
5.如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE•⊥AC,BF⊥AC,若AB=CD,
可以得到BD平分EF,为什么?若将△DEC的边EC沿AC方向移动,变为如图所示时,其余条件不变,上述结论是否成立?请说明理由.
6.如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,
交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由。
7.已知:如图E在△ABC的边AC上,且∠AEB=∠ABC。
(1)求证:∠ABE=∠C;
(2)若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长。
G
D F
A
C B
E
G
D F
A
C
B
E
F
E
D C
B
A
G
8. 如图,在△ABC 和△DCB 中,AB = DC ,AC = DB ,AC 与DB 交于点M .
(1) 求证:△ABC ≌△DCB ;(2)过点C 作CN ∥BD ,过点B 作BN ∥AC ,CN 与BN 交于点N ,试判断线段BN 与CN 的数量关系,并证明你的结论.
9. 已知:如图,DC ∥AB ,且DC =AE ,E 为AB 的中点,
(1) 求证:△AED ≌△EBC .
(2) 观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等
的三角形.(直接写出结果,不要求证明):
10. 如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,
BD 交AC 于点M .
(1) 求证:MB =MD ,ME =MF
(2) 当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请
给予证明;若不成立请说明理由.
B
C
A D
M
N
O E
D C B A
11. 如图,已知在△ABC 中,∠BAC 为直角,AB=AC ,D 为AC 上一点,CE ⊥BD 于E .
(1) 若BD 平分∠ABC ,求证CE=1
2
BD ;
(2) 若D 为AC 上一动点,∠AED 如何变化,若变化,求它的变化范围;若不变,求出它
的度数,并说明理由。
12. 在△ABC 中,,AB=AC , 在AB 边上取点D ,在AC 延长线上了取点E ,使CE=BD , 连接DE 交
BC 于点F ,求证DF=EF .
13. 如图△ABC ≌△A `B`C,∠ACB=90°,∠A=25°,点B 在A `B`上,求∠ACA `的度数。
14. 如图,取一张长方形纸片,用A 、B 、C 、D 表示其四个顶点,将其折叠,使点D 与点B 重合。
图中有没有全等的三角形,如果有,请先用“≌”表示出来,再说明理由。
E
D
C B A
B
A`B
15. 如图:四边形ABCD 中,AD ∥BC ,AB=AD+BC ,E 是CD 的中
点,求证:AE ⊥BE 。
16. 如图所示,△ABC 中,∠ACB=90°,AC=BC,AE 是BC 边上的中线,过C 作CF ⊥AE, 垂足为F,过B 作
BD ⊥BC 交CF 的延长线于D.
(1) 求证:(1)AE=CD;(2)若AC=12cm,求BD 的长.
2.
E
D
C
B
A
F
17. 在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF=BE 。
(1) 求证:CE=CF 。
(2) 在图中,若G 点在AD 上,且∠GCE=45° ,则GE=BE+GD
成立吗?为什么?
18. 如图(1), 已知△ABC 中, ∠BAC=900, AB=AC, AE 是过A 的一条直线, 且B 、C 在A 、E 的异侧, BD
⊥AE 于D, CE ⊥AE 于E (1) 试说明: BD=DE+CE.
B E
E
(2) 若直线AE 绕A 点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD 与DE 、CE 的关系如何? 为什么?
(3) 若直线AE 绕A 点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD 与DE 、CE 的关系如何? 请直接写出结果, 不需说明.
(4)归纳前二个问得出BD 、DE 、CE 关系。
用简洁的语言加以说明。
19. 如图所示,已知D 是等腰△ABC 底边BC 上的一点,它到两腰AB 、AC 的距离分别为DE 、DF,CM ⊥
AB,垂足为M,请你探索一下线段DE 、DF 、CM 三者之间的数量关系, 并给予证明.
E D C
B
A
M
F
20. 在Rt △ABC 中,AB=AC ,∠BAC=90°,O 为BC 的中点.
(1) 写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系,并说明理由. (2) 若点M 、N 分别是AB 、AC 上的点,且BM=AN ,试判断△OMN 形状,并证明你的
(3)。
