中考数学复习专题五一次函数、反比例函数与实际应用

合集下载

专题五一次函数、反比例函数的综合运用

专题五一次函数、反比例函数与实际应用教学目标：知识技能：进一步理解掌握一次函数、反比例函数的图象与性质，并能熟练运用其解决一次函数、反比例函数有关的综合题；过程方法：结合图象，分析题意，从函数的图象中获取解题信息解决实际问题，掌握解题方法技巧；情感价值：引导学生分析题意，构建函数模型，运用数形结合思想解决问题，提高学生的综合运用能力。

教学重点：运用数形结合思想从图象中获取解题信息教学难点：根据题意构建函数模型教学过程：解题策略此专题内容多出在中档题中，主要有以下三种题型：(1)待定系数法求表达式；(2)应用题找等量关系建立函数模型；(3)两种函数的混搭．,重难点突破)一次函数与反比例函数综合题【例1】一次函数y ＝mx ＋5的图像与反比例函数y ＝k x(k≠0)在第一象限的图像交于A(1，n)和B(4，1)两点，过点A 作y 轴的垂线，垂足为M.(1)求一次函数和反比例函数的表达式；(2)求△OAM 的面积S ；(3)在y 轴上求一点P ，使PA ＋PB 最小．【解析】(1)根据待定系数法分别求出反比例函数与一次函数表达式即可；(2)根据反比例函数的性质，直接求出面积即可；(3)作点A 关于y 轴的对称点N ，连接BN 交y 轴于点P ，则点P 即为所求．【答案】解：(1)将B(4，1)代入y ＝k x ，得1＝k 4.∴k ＝4，∴y ＝4x.将B(4，1)代入y ＝mx ＋5，得1＝4m ＋5，∴m ＝－1，∴y ＝－x ＋5；(2)在y ＝4x 中，令x ＝1，解得y ＝4，∴A(1，4)，∴S ＝12×1×4＝2；(3)作点A 关于y 轴的对称点N ，则N(－1，4)，连接BN 交y 轴于点P ，点P 即为所求．设直线BN 的关系式为y ＝kx ＋b ，由⎩⎪⎨⎪⎧4k ＋b ＝1，－k ＋b ＝4，解得⎩⎪⎨⎪⎧k ＝－35，b ＝175，y ＝－35x ＋175，∴P ⎝ ⎛⎭⎪⎪⎫0，175. 1、一次函数y ＝kx ＋b 与反比例函数y ＝m x的图像相交于A(－1，4)，B(2，n)两点，直线AB 交x 轴于点D.(1)求一次函数与反比例函数的表达式；(2)过点B 作BC⊥y 轴，垂足为C ，连接AC 交x 轴于点E ，求△AED 的面积S.解：(1)将A(－1，4)代入y ＝m x ，得4＝m －1，∴m ＝－4，∴y ＝－4x. 将x ＝2代入y ＝－4x，得y ＝－2， ∴B(2，－2)．将A(－1，4)，B(2，－2)代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧－k ＋b ＝4，2k ＋b ＝－2，解得：⎩⎪⎨⎪⎧k ＝－2，b ＝2， ∴y ＝－2x ＋2；(2)∵△AED 的高为4，△ACB 的高为：4＋2＝6.∵ED∥BC，∴△AED ∽△ACB ，∴S △AED S △ACB ＝(46)2＝49，∴S △AED ＝49×12×2×6＝83. 【方法指导】先综合考虑两者之间的联系，再利用待定系数法求一次函数及反比例函数的表达式．一次函数的实际应用【例2】山地自行车越来越受到中学生的喜爱，各种品牌相继投入市场，某车行经营的A型车去年销售总额为5万元，今年每辆售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%。

2020年中考复习数学课件：一次函数与反比例函数的应用 (共30张PPT)

(2)“ 一元一次不等式 ” 实际上是指一次函数的函数值 “y>0 ， y<0 或 y≥0，y≤0”，从图象上看是指抛物线在x轴上方或x轴下方的情况． 5.应用反比例函数解题的注意事项 (1)要注意自变量取值范围符合实际意义； (2)确定反比例函数之前一定要考察两个变量与定值之间的关系，若k未知时，应首先由已知条件求出k值． (3)求“至少”，“最多”时可根据函数性质得到．
∵A(2,1)，∴B(－2，－1)，
∵由函数图象可知，当0＜x＜2或x＜－2时函数y1的图象在y2的上方， ∴使y1＞y2的x的取值范围是x＜－2或0＜x＜2.
123
3.一辆慢车与一辆快车分别从甲、乙两地同时出发，匀速相向而行，两
车在途中相遇后分别按原速同时驶往甲地，两车之间的距离S(km)与
慢车行驶时间t(h)之间的函数图象如图所示，下列说法：
一次函数与反比例函数的应用
知识梳理
1.一次函数的应用利用一次函数并与方程(组)、不等式(组)联系在一起解决实际生活中的利率、利润、租金、生产方案的设计问题． 2.应用一次函数解决实际问题的步骤 (1)认真审题，准确理解题意，领悟其数学实质； (2)舍弃与解题无关的非本质因素，将问题简单化； (3)抽象、归纳其中的数量关系，建立一次函数数学模型； (4)根据所建立的数学模型，解出模型的数学结果； (5)“翻译”回到实际问题，得到实际问题的答案．
3.一次函数y＝kx＋b(b≠0)的自变量x的取值范围一次函数y＝kx＋b(b≠0)的自变量x的取值范围是全体实数，图象是一条直线，因此没有最大值与最小值，但在实际问题中得到的一次函数解析式自变量的取值范围一般受到限制，则图象为线段或射线，根据一次函数的性质，此时就存在最大值或最小值范围． 4.一次函数与一次方程、一次不等式间的关系 (1)已知一次函数y＝kx＋b的函数值为，求自变量x的值，就是解一元一次方程kx＋b＝h；反过来，解一元一次方程kx＋b＝h，就是把一次函数y＝kx＋b－h的函数值看做0，求自变量x的值．

【中考数学复习】一次函数与反比例函数知识

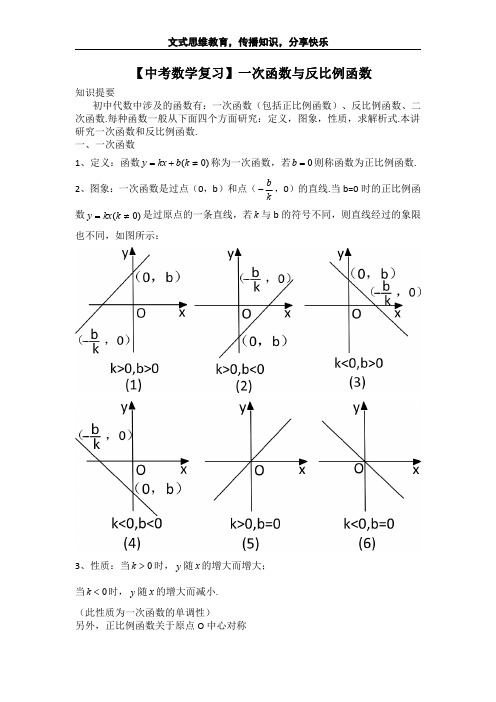
【中考数学复习】一次函数与反比例函数知识提要初中代数中涉及的函数有：一次函数（包括正比例函数）、反比例函数、二次函数.每种函数一般从下面四个方面研究：定义，图象，性质，求解析式.本讲研究一次函数和反比例函数.一、一次函数1、定义：函数)0(≠+=k b kx y 称为一次函数，若0=b 则称函数为正比例函数.2、图象：一次函数是过点（0，b ）和点（kb -，0）的直线.当b=0时的正比例函数)0(≠=k kx y 是过原点的一条直线，若k 与b 的符号不同，则直线经过的象限也不同，如图所示：3、性质：当0>k 时，y 随x 的增大而增大；当0<k 时，y 随x 的增大而减小.（此性质为一次函数的单调性）另外，正比例函数关于原点O 中心对称4、求解析式：求一次函数的解析式，一般需要两个条件，求出表达式b kx y +=中的k 及b 的值，常用待定系数法来求一次函数.而正比例函数的解析式只需要一个条件.二、反比例函数1、定义：形如)0(≠=k x k y 形式称为反比例函数，定义域为0≠x 的所有实数.2、图象：反比例图象为双曲线，如图所示：3、性质：反比例函数x k y =在0>k 且0>x 时，函数值y 随x 的增大而减小；在0>k 且0<x 时，函数值y 随x 的增大而减小.即：当0>k 时，反比例函数x k y =分布在一、三象限，在每个象限内，y 随x 的增大而减小，如图（1）所示.当0<k 时，反比例函数xk y =分布在二、四象限，在每个象限内，y 随x 的增大而增大，如图（2）所示.反比例函数x k y =图象上的点关于原点O 成中心对称的.当0>k 时，函数的图象关于直线x y =成轴对称；当0<k 时，函数的图象关于直线x y -=成轴对称.4、求解析式：反比例函数的解析式，只需要一个条件，求出xk y =)0(≠k 中的k 即可.在解决有关一次函数及反比例函数的问题时，常运用数形结合及分类讨论的思想方法.待定系数法是研究函数表达式的基本方法，同时紧密结合图象寻求思路，是处理这类问题的重要方法.例1、已知正比例函数x y =和)0(>=a ax y 的图象与反比例函数xky =（k>0）的图象在第一象限内分别相交于A 、B 两点，过A 、B 作x 轴的垂线，垂足分别为C 、D ，设△AOC 和△BOD 的面积分别为1S 、2S ，则1S 与2S 的大小关系怎样？例2、两个反比例函数x y 3=，x y 6=在第一象限内的图象如图所示，点1P ，2P ，3P ，…2005P 在反比例函数x y 6=图象上，它们的横坐标分别是1x ，2x ，3x ，…2005x ，纵坐标分别是1，3，5，…，共2005个连续奇数，过点1P ，2P ，3P ，…2005P 分别作y 轴的平行线，与xy 3=的图象交点依次是)(111y x Q ，，)(222y x Q ，，)(333y x Q ，，…)(200520052005y x Q ，，则_________2005=y .例3、平面直角坐标系内有A （2，－1）、B （3，3）两点，点P 是y 轴上一动点，求P 到A 、B 距离之和最小时的坐标.例4、已知一次函数的图象经过点（2，2），它与两坐标轴所围成的三角形的面积等于1，求这个一次函数的解析式.例5、已知A （-2，0）、B （4，0），点P 在直线221+=x y 上，若△PAB 是直角三角形，求点P 的坐标.例6、已知两人连续6年对某县农村甲鱼养殖业的规模（产量）进行调查，提供两个方面的信息，如图所示，请根据图中提供的信息，求：（1）第2年全县生产甲鱼的只数及甲鱼池的个数；（2）到第6年，这个县的甲鱼养殖规模比第1年是扩大了还是缩小了，请说明理由.例7、如图，已知C 、D 是双曲线xm y =在第一象限内的分支上的两点，直线CD 分别交x 轴、y 轴于A 、B 两点，设C 、D 的坐标分别是（11y x ，）、（22y x ，），连接OC 、OD.（1）求证：111y m y OC y +<<；（2）若α=∠=∠AOD BOC ，31tan =α，10=OC ，求直线CD 的解析式.（3）在（2）的条件下，双曲线是否存在一点P ，使POD POC S S ∆∆=？若存在，求出P 点坐标；若不存在，请说明理由.例8、有一个附有进、出水管的容器，每单位时间进、出的水量都是一定的，设从某时刻开始5分钟内只进水不出水，在随后的15分钟内既进水又出水，得到时间x （分）与水量y （升）之间的关系如图所示，若20分钟后只放水不进水，求多长时间能将水放完？例9、为了预防流感，某学校对教室用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y （毫克）与时间x （分钟）成正比例，药物燃烧后，y 与x 成反比例（如图），观测得药物8分钟燃毕，此时室内空气中每立方米的含药量为6毫克，请根据题中提供的信息解答下列问题：（1）药物燃烧时，y 关于x 的函数关系式为__________，自变量x 的取值范围是___________；药物燃烧后y 关于x 的函数关系式为____________.（2）研究表明，当空气中的每立方米含药量低于1.6毫克时，学生方可进教室，那么从消毒开始，至少需要经过多少分钟后，学生才能回到教室.（3）研究表示，当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？例10、某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按120个工时计算）生产空调器、彩电、冰箱共360台，且冰箱至少生产60台，已知生产这些家电产品每台所需工时和每台产值如下表所示：家电名称空调器彩电冰箱工时/个213141产值/千元432问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？（以千元为单位）练习1、已知0≠abc 并且p b a c a c b c b a =+=+=+而直线p px y +=一定通过（）A 第一、二象限B 第二、三象限C 第三、四象限D 第一、四象限2、函数kx y =和)0(<=k x k y 在同一坐标系中的图象是（）3、一次函数b kx y +=过点)(11y x ，和)(22y x ，，且0>k ，b<0，当210x x <<时，有（）A 21y b y >>B 21y b y <<C b y y <<<210D 012<<<y b y 4、若点（-2，1y ），（1，2y ），（2，3y ）在反比例函数x y 21=的图象上，则下列结论正确的是（）A 123y y y >>B 312y y y >>C 132y y y >>D 321y y y >>5、反比例函数x k y =的图象是轴对称图形，它的一条对称轴是下列正比例函数图象中的（）A kxy -=B x k y =C x k k y =D kxy =6、一个一次函数图象与直线49545+=x y 平行，与x 轴、y 轴的交点分别为A 、B ，并且过点（-1，-25），则在线段AB 上（包括端点A 、B ），横、纵坐标都是整数的点有（）A 4个B 5个C 6个D 7个7、如图，正比例函数x y 3=的图象与反比例函数xk y =（0>k ）的图象交于点A ，若取k 为1，2，3，…，20，对应的Rt △AOB 的面积分别为1S ，2S ，…20S ，则__________2021=+++S S S .8、不论k 为何值，解析式0)11()3()12(=--+--k y k x k 表示函数的图象都经过一定点，则这个定点是_________.9、如图所示，直线l 和双曲线x k y =（0>k ）交于A 、B 两点，P 是线段AB 上的点（不与A 、B 重合），过点A 、B 、P 分别向x轴作垂线，垂足分别为C 、D 、E ，连接OA 、OB 、OP.设△AOC 的面积为1S ，△BOD 的面积为2S ，△POE 的面积为3S ，则321S S S 、、的大小关系是______________.10、甲、乙两车出发后再同一条公路行驶，行驶路程与时间的关系如图所示，那么可以知道：（1）出发行驶在前面的车是_________，此时两车相隔_________；（2）两车的速度分别为甲：___________千米/小时，乙：_________千米/小时，经过___________小时，快车追上慢车；（3）甲、乙两车均行驶600千米时各用的时间分别是：甲用_________小时，乙用__________小时.11、如图，函数221+-=x y 的图象交y 轴于M ，交x 轴于N ，MN 上两点A ，B 在x 轴上射影分别为11B A 、，若411>+OB OA ，则A OA 1∆的面积1S 与B OB 1∆的面积2S 的大小关系是_____________.12、已知非负数x 、y 、z 满足323=++z y x ，433=++z y x ，则z y x w 423+-=的最大值为_________，最小值为__________.13、在直角坐标系中，有四个点：A （-8，3），B （-4，5），C （0，n ），D （m ，0）,当四边形ABCD 的周长最短时，求nm 的值.14、设直线1)1(=++y k kx （k 是自然数）与两坐标轴所围成的图形的面积为1S ，2S ，…，2000S .求200021S S S +++ 的值.15、如图（1），已知直线m x y +-=21与反比例函数xk y =的图象在第一象限内交于A 、B 两点（点A 在点B 的左侧），分别于x 、y 轴交于C 、D ，AE ⊥x 轴于E.（1）若OE·CE=12，求k 的值；（2）如图（2），作BF ⊥y 轴于F ，求证：EF ∥CD ；（3）在（1）（2）的条件下，5=EF ,52=AB ，P 是x 轴正半轴上一点，且△PAB 是以P 为直角顶点的等腰直角三角形，求P 点的坐标.（1）（2）16、已知直线62+-=-k y x 和143+=+k y x ，若它们的交点在第四象限内.（1）求k 的取值范围；（2）若k 为非负整数，点A 的坐标为（2，0），点P 在直线62+-=-k y x 上，求使△PAO 为等腰三角形的点P 的坐标.17、A 市、B 市和C 市分别有某种机器10台、10台和8台，现决定把这些机器支援给D 市18台，E 市10台.已知从A 市调运一台机器到D 市、E 市的运费分别为200元和800元，从B 市调运一台机器到D 市、E 市的运费分别为300元和700元，从C 市调运一台机器到D 市、E 市的运费分别为400元和500元.（1）设从A 市、B 市各调x 台到D 市，当28台机器全部调运完毕后，求总运费w （元）关于x （台）的函数式，并求w 的最大值和最小值；（2）设从A 市调x 台到D 市，从B 市调y 台到D 市，当28台机器全部调运完毕后，用x ，y 表示总运费w （元），并求w 的最大值和最小值.18、直线133+-=x y 与x 轴、y 轴分别交于点A 、B ，以线段AB 为直角边在第一象限内作等腰直角三角形ABC ，其中∠BAC=90°.如果第二象限内有一点P （a ，21），使△ABP 的面积和△ABC 的面积相等，求a 的值.文式思维教育，传播知识，分享快乐19、如图，在直角坐标系中，点1O 的坐标为（1，0），⊙1O 与x 轴交于原点O 和点A ，又点B 、C 的坐标分别为（-1，0），（0，b ），且30<<b ，直线l 是过B 、C 点的直线.（1）当点C 在线段OC 上移动时，过点1O 作l D O 直线⊥1，交l 于D ，若a S S CBO BOC=∆∆1，试求b a 与的函数关系式及a 的取值范围.20、某仓储系统有20条输入传送带、20条输出传送带.某日，控制室的电脑显示，每条输入传送带每小时进库的货物流量如图（a ），每条输出传送带每小时出库的货物流量如图（b ）,而该日仓库中原有货物8吨，在0时至5时，仓库中货物存量变化情况如图（c ），则在0时至2时有多少条输入传送带在工作？在4至5时有多少条输入传送带和输出传送带在工作？。

一次函数与反比例函数综合应用教案

一次函数与反比例函数综合应用教案一、教学目标1. 让学生掌握一次函数和反比例函数的基本概念和性质。

2. 培养学生运用一次函数和反比例函数解决实际问题的能力。

3. 引导学生通过合作交流，提高解决问题的策略和思维能力。

二、教学内容1. 一次函数的基本概念和性质。

2. 反比例函数的基本概念和性质。

3. 一次函数和反比例函数的综合应用。

三、教学重点与难点1. 教学重点：一次函数和反比例函数的基本概念、性质和综合应用。

2. 教学难点：一次函数和反比例函数的综合应用。

四、教学方法1. 采用问题驱动法，引导学生主动探究一次函数和反比例函数的性质。

2. 利用案例分析法，让学生通过实际问题体会一次函数和反比例函数的应用价值。

3. 采用合作交流法，培养学生团队协作和沟通能力。

五、教学过程1. 导入新课：通过生活实例引入一次函数和反比例函数的概念。

2. 自主学习：让学生自主探究一次函数和反比例函数的性质。

3. 案例分析：分析实际问题，引导学生运用一次函数和反比例函数解决问题。

4. 合作交流：分组讨论，让学生分享解题策略和心得。

5. 总结提升：总结一次函数和反比例函数的性质及应用，提高学生解决问题的能力。

6. 课后作业：布置相关练习题，巩固所学知识。

六、教学活动设计1. 活动一：引入概念通过展示实际生活中的线性关系图片，如直线轨道上列车的运动，引导学生思考线性关系的表现形式。

引导学生提出一次函数的表达式，并解释其含义。

2. 活动二：探索性质学生通过绘制一次函数图像，观察并总结其在坐标系中的性质。

通过实际例子，让学生理解一次函数的斜率和截距对图像的影响。

3. 活动三：反比例函数的引入引导学生从比例关系出发，思考反比例函数的概念。

通过实际问题，如在固定面积内，距离与面积的关系，引入反比例函数。

七、教学评价设计1. 评价目标：学生能理解并应用一次函数和反比例函数解决实际问题。

通过设计具有挑战性的问题，如购物预算问题，让学生应用所学的函数知识。

中考复习_一次函数与反比例函数的综合应用

一次函数与反比例函数的综合应用一、选择题1. （2011四川凉山，12，4分）二次函数2y ax bx c =++的图象如图所示，反比列函数a y x =与正比列函数y bx =在同一坐标系内的大致图象是（）考点：二次函数的图象；正比例函数的图象；反比例函数的图象．专题：数形结合．分析：由已知二次函数y ＝ax 2＋bx ＋c 的图象开口方向可以知道a 的取值范围，对称轴可以确定b 的取值范围，然后就可以确定反比例函数xa y =与正比例函数y ＝bx 在同一坐标系内的大致图象．解答：解：∵二次函数y ＝ax 2＋bx ＋c 的图象开口方向向下，∴a ＜0，对称轴在y 轴的左边，∴x ＝－a b 2＜0，∴b ＜0， ∴反比例函数xa y =的图象在第二四象限，正比例函数y ＝bx 的图象在第二四象限．故选B ．点评：此题主要考查了从图象上把握有用的条件，准确选择数量关系解得a 的值，简单的图象最少能反映出2个条件：开口向下a ＜0；对称轴的位置即可确定b 的值．2. （2011•青海）一次函数y=﹣2x+1和反比例函数y=错误!未找到引用源。

的大致图象是（）A 、B 、Ox yO y x A O y x B O y xD O y x CC、D、考点：反比例函数的图象；一次函数的图象。

分析：根据一次函数的性质，判断出直线经过的象限；再根据反比例函数的性质，判断出反比例函数所在的象限即可．解答：解：根据题意：一次函数y=﹣2x+1的图象过一、二、四象限；反比例函数y=错误!未找到引用源。

过一、三象限．故选：D．点评：此题主要考查了一次函数的图象及反比例函数的图象，重点是注意y=k1x+b中k1、b 及y=错误!未找到引用源。

中k2的取值．3.（2011山东青岛，8，3分）已知一次函数y1=kx+b与反比例函数y2=kx错误!未找到引用源。

在同一直角坐标系中的图象如图所示，则当y1＜y2时，x的取值范围是（）A．x＜﹣1或0＜x＜3 B．﹣1＜x＜0或x＞3 C．﹣1＜x＜0 D．x＞3 考点：反比例函数与一次函数的交点问题。

一次函数与反比例涵数的专题复习

一次函数与反比例函数专题复习第一部分知识梳理考点一、平面直角坐标系（3分） 1、平面直角坐标系在平面内画两条互相垂直且有公共原点的数轴，就组成了平面直角坐标系。

其中，水平的数轴叫做x 轴或横轴，取向右为正方向；铅直的数轴叫做y 轴或纵轴，取向上为正方向；两轴的交点O （即公共的原点）叫做直角坐标系的原点；建立了直角坐标系的平面，叫做坐标平面。

为了便于描述坐标平面内点的位置，把坐标平面被x 轴和y 轴分割而成的四个部分，分别叫做第一象限、第二象限、第三象限、第四象限。

注意：x 轴和y 轴上的点，不属于任何象限。

2、点的坐标的概念点的坐标用（a ，b ）表示，其顺序是横坐标在前，纵坐标在后，中间有“，”分开，横、纵坐标的位置不能颠倒。

平面内点的坐标是有序实数对，当b a ≠时，（a ，b ）和（b ，a ）是两个不同点的坐标。

考点二、不同位置的点的坐标的特征（3分） 1、各象限内点的坐标的特征（1）点P(x,y)在第一象限0,0>>⇔y x（2）点P(x,y)在第二象限0,0><⇔y x （3）点P(x,y)在第三象限0,0<<⇔y x （4）点P(x,y)在第四象限0,0<>⇔y x 2、坐标轴上的点的特征（1）点P(x,y)在x 轴上0=⇔y ，x 为任意实数（2）点P(x,y)在y 轴上0=⇔x ，y 为任意实数（3）点P(x,y)既在x 轴上，又在y 轴上⇔x ，y 同时为零，即点P 坐标为（0，0） 3、两条坐标轴夹角平分线上点的坐标的特征（1）点P(x,y)在第一、三象限夹角平分线上⇔x 与y 相等（2）点P(x,y)在第二、四象限夹角平分线上⇔x 与y 互为相反数 4、和坐标轴平行的直线上点的坐标的特征（1）位于平行于x 轴的直线上的各点的纵坐标相同。

（2）位于平行于y 轴的直线上的各点的横坐标相同。

5、关于x 轴、y 轴或远点对称的点的坐标的特征（1）点P 与点p ’关于x 轴对称⇔横坐标相等，纵坐标互为相反数（2）点P 与点p ’关于y 轴对称⇔纵坐标相等，横坐标互为相反数（3）点P 与点p ’关于原点对称⇔横、纵坐标均互为相反数 6、点到坐标轴及原点的距离（1）点P(x,y)到x 轴的距离等于y （2）点P(x,y)到y 轴的距离等于x （3）点P(x,y)到原点的距离等于22y x +考点三、函数及其相关概念（3~8分） 1、变量与常量在某一变化过程中，可以取不同数值的量叫做变量，数值保持不变的量叫做常量。

中考数学专题复习反比例函数及其应用

上一页返回导航下一页
(教材母题链接：北师九上 P162T11)
上一页返回导航下一页
反比例函数与几何图形的综合 9．(2020 滨州)如图，点 A 在双曲线 y＝4x上，点 B 在双曲线 y＝1x2上，且 AB∥x 轴，点 C，D 在 x 轴上，若四边形 ABCD 为矩形，则它的面积为 (C )
(C ) A．k＝2 B．函数图象分布在第一、三象限
C．当 x＞0 时，y 随 x 的增大而增大
D．当 x＞0 时，y 随 x 的增大而减小
上一页返回导航下一页
2．(2020 河南)若点 A(－1，y1)，B(2，y2)，C(3，y3)在反比例函数 y＝－6x的图象上，则 y1，y2，y3 的大小关系是( C )
上一页返回导航下一页
2．关于反比例函数 y＝－3x，下列说法不正确的是( D ) A．图象经过点(1，－3) B．图象位于第二、四象限 C．图象关于直线 y＝x 对称 D．y 随 x 的增大而增大
上一页返回导航下一页
三、反比例函数解析式的确定待定系数法： (1)设所求的反比例函数的解析式为 y＝kx(k≠0)； (2)将图象上的一点坐标代入 y＝kx中，求出 k； (3)把 k 代入解析式 y＝kx中，写出解析式.
第一部分夯实基础
第三章函数
第3节反比例函数及其应用
上一页返回导航下一页
课标导航 ·结合具体情境体会反比例函数的意义，能根据已知条件确定反比例函数的表达式． ·能画出反比例函数的图象，根据图象和表达式 y＝kx(k≠0)．探索并理解 k＞0 和 k＜0 时，图象的变化情况． ·能用反比例函数解决简单实际问题．
上一页返回导航下一页
(2)若一次函数图象与 y 轴交于点 C，点 D 为点 C 关于原点 O 的对称点，求△ACD 的面积．

中考复习——平面直角坐标系、一次函数、反比例函数及其图象知识点汇总及典例分析

中考复习——平面直角坐标系、一次函数、反比例函数【知识梳理】一、平面直角坐标系1. 坐标平面上的点与有序实数对构成一一对应；2. 各象限点的坐标的符号；3. 坐标轴上的点的坐标特征．4. 点P （a ，b ）关于x 轴对称的点的坐标为；关于y 轴对称的点的坐标为；关于原点对称的点的坐标为5.两点之间的距离二、函数的概念1.概念：在一个变化过程中有两个变量x 与y ，如果对于x 的每一个值，y 都有的值与它对应，那么就说x 是自变量，y 是x 的函数.2.自变量的取值范围：（1）使解析式（2）实际问题具有意义3.函数的表示方法；（1）（2）（3）三、一次函数的概念、图象、性质1．正比例函数的一般形式是（），一次函数的一般形式是 (k≠0). 2. 一次函数y kx b =+的图象是经过（，）和（，）两点的一条直线.4.若两个一次函数解析式中，k 相等，表示两直线；若两直线垂直，则。

5.的大小决定直线的倾斜程度，越大，直线越；四、反比例函数的概念、图象、性质1．反比例函数：一般地，如果两个变量x 、y 之间的关系可以表示成y ＝或或（k 为常数，k≠0）的形式，那么称y 是x 的反比例函数． 2. 反比例函数的图象和性质k ＞0，b ＞0k ＞0，b ＜0k ＜0，b ＞0k ＜0，21212211P P )0()0()2(y y y P y P -＝，　，，，21212211P P )0()0()1(x x x P x P -＝，　，　，，　3．k 的几何含义：反比例函数y ＝k x(k≠0)中比例系数k 的几何意义，即过双曲线y ＝k x(k≠0)上任意一点P 作x 轴、y 轴垂线，设垂足分别为A 、B ，则所得矩形OAPB 的面积为。

【例题精讲】例1.函数22y x =-中自变量x 的取值范围是 ;函数y =x 的取值范围是．例2.已知点(13)A m -，与点(21)B n +，关于x 轴对称，则m = ，n = ．例3.如图，在平面直角坐标系中，点A 的坐标是（10，0），点B 的坐标为（8，0）,点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形，点C 的坐标为例4．一次函数y=(3a+2)x －(4－b),求满足下列条件的a 、b 的取值范围。

中考数学《一次函数》《二次函数》《反比例函数》考点分析及专题训练

中考数学《一次函数》《二次函数》《反比例函数》考点分析及专题训练函数及其图象1、坐标与象限定义1：我们把有顺序的两个数a与b所组成的数对，叫做有序数对，记作（a，b）。

定义2：平面直角坐标系即在平面内画互相垂直，原点重合的两条数轴。

水平的数轴称为x轴或横轴，取向右方向为正方向；竖直的数轴称为y轴或纵轴，取向上方向为正方向。

两坐标轴的交点为平面直角坐标系的原点。

建立平面直角坐标系后，坐标平面被两条坐标轴分成了四个部分，每个部分称为象限，分别叫做第一象限、第二象限、第三象限、第四象限，坐标轴上的点不属于任何象限。

2、函数与图象定义1：在一个变化过程中，我们称数值发生变化的量为变量，数值始终不变的量为常量。

定义2：一般地，在一个变化过程中，如果有两个变量x和y，并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数。

如果当x=a时，y=b，那么b叫做当自变量的值为a时的函数值。

定义3：一般地，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象。

定义4：用关于自变量的数学式子表示函数与自变量之间的关系，是描述函数的常用方法。

这种式子叫做函数的解析式。

表示函数的方法：解析式法、列表法和图象法。

解析式法可以明显地表示对应规律；列表法直接给出部分函数值；图象法能直观地表示变化趋势。

画函数图象的方法——描点法：第1步，列表。

表中给出一些自变量的值及其对应的函数值；第2步，描点。

在直角坐标系中，以自变量的值为横坐标、相应的函数值为纵坐标，描出表格中数值对应的各点；第3步，连线。

按照横坐标由小到大的顺序，把所描出的各点用平滑曲线连接起来。

1、结合实例进一步体会用有序数对可以表示物体的位置。

2、理解平面直角坐标系的有关概念，能画出直角坐标系；在给定的直角坐标系中，能根据坐标描出点的位置、由点的位置写出它的坐标。

中考数学专题复习《一次函数与反比例函数的综合》经典题型讲解

中考数学专题复习《一次函数与反比例函数的综合》经典题型讲解【经典母题】如图Z6－1是一个光学仪器上用的曲面横截面示意图，图中的曲线是一段反比例函数的图象，端点A的纵坐标为80，另一端点B的坐标为B(80，10)．求这段图象的函数表达式和自变量的取值范围．【解析】利用待定系数法设出反比例函数的表达式后，代入点B的坐标即可求得反比例函数的表达式．解：设反比例函数的表达式为y＝k x ，∵一个端点B的坐标为(80，10)，∴k＝80×10＝800，∴反比例函数的表达式为y＝800x.∵端点A的纵坐标为80，∴80＝800x，x＝10，∴点A的横坐标为10，∴自变量的取值范围为10≤x≤80.【思想方法】求反比例函数的表达式宜用待定系数法，设y＝kx，把已知一点代入函数表达式求出k的值即可．【中考变形】1．已知正比例函数y＝ax与反比例函数y＝bx的图象有一个公共点A(1，2)．(1)求这两个函数的表达式；图Z6－1(2)在图Z6－2中画出草图，根据图象写出正比例函数值大于反比例函数值时x 的取值范围．图Z6－2中考变形1答图解：(1)把A (1，2)代入y ＝ax ，得2＝a ，即y ＝2x ；把A (1，2)代入y ＝b x ，得b ＝2，即y ＝2x ； (2)画草图如答图所示．由图象可知，当x ＞1或－1＜x ＜0时，正比例函数值大于反比例函数值． 2．如图Z6－3，已知一次函数y ＝k 1x ＋b 与反比例函数y ＝k 2x 的图象交于第一象限内P ⎝ ⎛⎭⎪⎫12，8，Q (4，m )两点，与x 轴交于A 点．(1)分别求出这两个函数的表达式； (2)写出点P 关于原点的对称点P ′的坐标； (3)求∠P ′AO 的正弦值．图Z6－3【解析】①将P 点坐标代入反比例函数关系式，即可求出反比例函数表达式；将Q 点代入反比例函数关系式，即可求出m 的值；将P ，Q 两个点的坐标分别代入一次函数关系式，即可求出一次函数的表达式．②根据平面直角坐标系中，两点关于原点对称，则横、纵坐标互为相反数，可以直接写出点P ′的坐标；③过点P ′作P ′D ⊥x 轴，垂足为D ，可构造出′AD ，又∵点A 在一次函数的图象上，∴可求出点A 坐标，得到OA 长度，利用P ′ 点坐标，可以求出P ′D ，P ′A ，即可得到∠P ′AO 的正弦值．解：(1)∵点P 在反比例函数的图象上，∴把点P ⎝ ⎛⎭⎪⎫12，8代入y ＝k 2x ，得k 2＝4，∴反比例函数的表达式为y ＝4x ，∴Q 点坐标为(4，1)．把P ⎝ ⎛⎭⎪⎫12，8，Q (4，1)分别代入y ＝k 1x ＋b 中，得⎩⎨⎧8＝12k 1＋b ，1＝4k 1＋b ，解得⎩⎪⎨⎪⎧k 1＝－2，b ＝9.∴一次函数的表达式为y ＝－2x ＋9； (2)P ′⎝ ⎛⎭⎪⎫－12，－8；(3)如答图，过点P ′作P ′D ⊥x 轴，垂足为D . ∵P ′⎝ ⎛⎭⎪⎫－12，－8，中考变形2答图∴OD ＝12，P ′D ＝8.∵点A 在y ＝－2x ＋9的图象上，∴点A 坐标为⎝ ⎛⎭⎪⎫92，0，即OA ＝92，∴DA ＝5，∴P ′A ＝P ′D 2＋DA 2＝89. ∴sin ∠P ′AD ＝P ′D P ′A ＝889＝88989.∴sin ∠P ′AO ＝88989.3．[2017·成都]如图Z6－4，在平面直角坐标系xOy 中，已知正比例函数y ＝12x与反比例函数y ＝kx 的图象交于A (a ，－2)，B 两点． (1)求反比例函数表达式和点B 的坐标；(2)P 是第一象限内反比例函数图象上一点，过点P 作y 轴的平行线，交直线AB 于点C ，连结PO ，若△POC 的面积为3，求点P 的坐标．图Z6－4 中考变形3答图解：(1)∵点A (a ，－2)在正比例函数y ＝12x 图象上， ∴－2＝12a ，∴a ＝－4， ∴点A 坐标为(－4，－2)．又∵点A 在反比例函数y ＝kx 的图象上， ∴k ＝xy ＝－4×(－2)＝8， ∴反比例函数的表达式为y ＝8x .∵A ，B 既在正比例函数图象上，又在反比例函数图象上， ∴A ，B 两点关于原点O 中心对称， ∴点B 的坐标为(4，2)；(2)如答图，设点P 坐标为⎝ ⎛⎭⎪⎫a ，8a (a ＞0)，∵PC ∥y 轴，点C 在直线y ＝12x 上，∴点C 的坐标为⎝ ⎛⎭⎪⎫a ，12a ，∴PC ＝⎪⎪⎪⎪⎪⎪12a －8a ＝⎪⎪⎪⎪⎪⎪a 2－162a ， ∴S △POC ＝12PC ·a ＝12⎪⎪⎪⎪⎪⎪a 2－162a ·a ＝⎪⎪⎪⎪⎪⎪a 2－164＝3，当a 2－164＝3时，解得a ＝28＝27， ∴P ⎝⎛⎭⎪⎫27，477. 当a 2－164＝－3时，解得a ＝2，∴P (2，4)．综上所述，符合条件的点P 的坐标为⎝⎛⎭⎪⎫27，477，(2，4)． 4．如图Z6－5，一次函数y ＝kx ＋b 与反比例函数y ＝mx 的图象交于A (1，4)，B (4，n )两点．(1)求反比例函数的表达式； (2)求一次函数的表达式；(3)P 是x 轴上的一个动点，试确定点P 并求出它的坐标，使得P A ＋PB 最小．图Z6－5解：(1)∵点A (1，4)在函数y ＝mx 上， ∴m ＝xy ＝4，∴反比例函数的表达式为y ＝4x ； (2)把B (4，n )代入y ＝4x ，4＝xy ＝4n ，得n ＝1， ∴B (4，1)，∵直线y ＝kx ＋b 经过A ，B ， ∴⎩⎪⎨⎪⎧4＝k ＋b ，1＝4k ＋b ，解得⎩⎪⎨⎪⎧k ＝－1，b ＝5， ∴一次函数的表达式为y ＝－x ＋5； (3)点B 关于x 轴的对称点为B ′(4，－1)，设直线AB ′的表达式为y ＝ax ＋q ， ∴⎩⎪⎨⎪⎧4＝a ＋q ，－1＝4a ＋q ，解得⎩⎪⎨⎪⎧a ＝－53，q ＝173，∴直线AB ′的表达式为y ＝－53x ＋173，令y ＝0，解得x ＝175，∴当点P 的坐标为⎝ ⎛⎭⎪⎫175，0时，P A ＋PB 最小．5．[2017·广安]如图Z6－6，一次函数y ＝kx ＋b 的图象与反比例函数y ＝mx 的图象在第一象限交于点A (4，2)，与y 轴的负半轴交于点B ，图Z6－6且OB ＝6.(1)求函数y ＝mx 和y ＝kx ＋b 的表达式．(2)已知直线AB 与x 轴相交于点C .在第一象限内，求反比例函数y ＝mx 的图象上一点P ，使得S △POC ＝9.解：(1)∵点A (4，2)在反比例函数y ＝mx 的图象上， ∴m ＝4×2＝8，∴反比例函数的表达式为y ＝8x . ∵点B 在y 轴的负半轴上，且OB ＝6， ∴点B 的坐标为(0，－6)，把点A (4，2)和点B (0，－6)代入y ＝kx ＋b 中，得⎩⎪⎨⎪⎧4k ＋b ＝2，b ＝－6，解得⎩⎪⎨⎪⎧k ＝2，b ＝－6. ∴一次函数的表达式为y ＝2x －6； (2)设点P 的坐标为⎝ ⎛⎭⎪⎫n ，8n (n ＞0)．在直线y ＝2x －6上，当y ＝0时，x ＝3， ∴点C 的坐标为(3，0)，即OC ＝3， ∴S △POC ＝12×3×8n ＝9，解得n ＝43. ∴点P 的坐标为⎝ ⎛⎭⎪⎫43，6.6．[2017·黄冈]如图Z6－7，一次函数y ＝－2x ＋1与反比例函数y ＝kx 的图象有两个交点A (－1，m )和B ，过点A 作AE ⊥x 轴，垂足为E ；过点B 作BD ⊥y 轴，垂足为D ，且点D 的坐标为(0，－2)，连结DE . (1)求k 的值；(2)求四边形AEDB 的面积．图Z6－7 中考变形6答图解：(1)将点A (－1，m )代入一次函数y ＝－2x ＋1，得－2×(－1)＋1＝m ，解得m ＝3.∴A 点的坐标为(－1，3)．将A (－1，3)代入y ＝kx ，得k ＝(－1)×3＝－3；(2)如答图，设直线AB 与y 轴相交于点M ，则点M 的坐标为(0，1)， ∵D (0，－2)，则点B 的纵坐标为－2，代入反比例函数，得DB ＝32， ∴MD ＝3.又∵A (－1，3)，AE ∥y 轴， ∴E (－1，0)，AE ＝3. ∴AE ∥MD ，AE ＝MD .∴四边形AEDM 为平行四边形． ∴S 四边形AEDB ＝S ▱AEDM ＋S △MDB ＝3×1＋12×32×3＝214.7．[2016·金华]如图Z6－8，直线y ＝33x －3与x ，y 轴分别交于点A ，B ，与反比例函数y ＝kx (k ＞0)的图象交于点C ，D ，过点A 作x 轴的垂线交该反比例函数图象于点E . (1)求点A 的坐标；(2)若AE ＝AC ，①求k 的值；②试判断点E 与点D 是否关于原点O 成中心对称？并说明理由．图Z6－8中考变形7答图解：(1)当y ＝0时，得0＝33x －3，解得x ＝3. ∴点A 的坐标为(3，0)；(2)①如答图，过点C 作CF ⊥x 轴于点F .设AE ＝AC ＝t ，点E 的坐标是(3，t )，则反比例函数y ＝k x 可表示为y ＝3tx . ∵直线y ＝33x －3交y 轴于点B ， ∴B (0，－3)．在Rt △AOB 中，tan ∠OAB ＝OB OA ＝33， ∴∠OAB ＝30°.在Rt △ACF 中，∠CAF ＝30°， ∴CF ＝12t ，AF ＝AC ·cos30°＝32t ，∴点C 的坐标是⎝⎛⎭⎪⎫3＋32t ，12t .∴⎝⎛⎭⎪⎫3＋32t ×12t ＝3t ，解得t 1＝0(舍去)，t 2＝2 3. ∴k ＝3t ＝6 3.②点E 的坐标为()3，23，设点D 的坐标是⎝ ⎛⎭⎪⎫x ，33x －3，∴x ⎝ ⎛⎭⎪⎫33x －3＝63，解得x 1＝6(舍去)，x 2＝－3， ∴点D 的坐标是()－3，－23， ∴点E 与点D 关于原点O 成中心对称．【中考预测】如图Z6－9，一次函数y ＝kx ＋b (k ，b 为常数，k ≠0)的图象与x 轴，y 轴分别交于A ，B 两点，且与反比例函数y ＝nx (n 为常数且n ≠0)的图象在第二象限交于点C ，CD ⊥x 轴，垂足为D ，若OB ＝2OA ＝3OD ＝6. (1)求一次函数与反比例函数的表达式； (2)求两函数图象的另一个交点的坐标；(3)直接写出不等式kx ＋b ≤nx 的解集．图Z6－9解：(1)∵OB ＝2OA ＝3OD ＝6， ∴OB ＝6，OA ＝3，OD ＝2， ∵CD ⊥DA ，∴DC ∥OB ， ∴OB DC ＝AO AD ，∴6DC ＝35， ∴DC ＝10，∴C (－2，10)，B (0，6)，A (3，0)，代入一次函数y ＝kx ＋b ，得⎩⎪⎨⎪⎧b ＝6，3k ＋b ＝0，解得⎩⎪⎨⎪⎧k ＝－2，b ＝6， ∴一次函数的表达式为y ＝－2x ＋6. ∵反比例函数y ＝nx 经过点C (－2，10)， ∴n ＝－20，∴反比例函数的表达式为y ＝－20x ；(2)由⎩⎨⎧y ＝－2x ＋6，y ＝－20x ，解得⎩⎪⎨⎪⎧x ＝－2，y ＝10或⎩⎪⎨⎪⎧x ＝5，y ＝－4， ∴另一个交点坐标为(5，－4)；(3)由图象可知kx ＋b ≤nx 的解集为－2≤x ＜0或x ≥5.。

中考数学复习----《反比例函数之综合应用》知识点总结与练习题(含答案解析)

中考数学复习----《反比例函数之综合应用》知识点总结与练习题（含答案解析）知识点总结1. 反比例函数k 的集合意义：①过反比例函数图像上任意一点作坐标轴的垂线，两垂线与坐标轴构成一个矩形，矩形的面积等于k 。

②过反比例函数图像上任意一点作其中一条坐标轴的垂线，并连接这个点与原点，则构成一个三角形。

这个三角形的面积等于2k 。

2. 待定系数法求反比例函数解析式：在反比例函数中只有一个系数k ，所以只需要在图像上找一个对应的点即可求出k 的值，从而求出反比例函数解析式。

3. 反比例函数与一次函数的不等式问题：若反比例函数()0≠=k x ky 与一次函数()0≠+=k b kx y 有交点，则不等式b kx xk +＞的解集取反比例函数图像在一次函数图像上方的部分所对应的自变量取值范围；等式b kx xk+＜的解集取反比例函数图像在一次函数图像下方的部分所对应的自变量取值范围。

反比例函数与一次函数的交点把自变量分成三部分。

练习题1、（2022•日照）如图，矩形OABC 与反比例函数y 1＝xk1（k 1是非零常数，x ＞0）的图像交于点M ，N ，与反比例函数y 2＝xk2（k 2是非零常数，x ＞0）的图像交于点B ，连接OM ，ON ．若四边形OMBN 的面积为3，则k 1﹣k 2＝（）A ．3B ．﹣3C ．23 D ．﹣23【分析】根据矩形的性质以及反比例函数系数k 的几何意义即可得出结论．【解答】解：∵y 1、y 2的图像均在第一象限， ∴k 1＞0，k 2＞0，∵点M 、N 均在反比例函数y 1＝（k 1是非零常数，x ＞0）的图像上，∴S △OAM ＝S △OCN ＝k 1，∵矩形OABC 的顶点B 在反比例函数y 2＝（k 2是非零常数，x ＞0）的图像上，∴S 矩形OABC ＝k 2，∴S 四边形OMBN ＝S 矩形OABC ﹣S △OAM ﹣S △OCN ＝3， ∴k 2﹣k 1＝3， ∴k 1﹣k 2＝﹣3，故选：B ．2、（2022•牡丹江）如图，等边三角形OAB ，点B 在x 轴正半轴上，S △OAB ＝43，若反比例函数y ＝xk（k ≠0）图像的一支经过点A ，则k 的值是（）A ．233 B ．23C ．433 D ．43【分析】根据正三角形的性质以及反比例函数系数k 的几何意义，得出S △AOC ＝S △AOB ＝2＝|k |，即可求出k 的值．【解答】解：如图，过点A 作AC ⊥OB 于点C ， ∵△OAB 是正三角形， ∴OC ＝BC ，∴S △AOC ＝S △AOB ＝2＝|k |，又∵k ＞0， ∴k ＝4，故选：D ．3、（2022•郴州）如图，在函数y ＝x2（x ＞0）的图像上任取一点A ，过点A 作y 轴的垂线交函数y ＝﹣x8（x ＜0）的图像于点B ，连接OA ，OB ，则△AOB 的面积是（）A ．3B ．5C ．6D ．10【分析】根据反比例函数系数k 的几何意义进行计算即可．【解答】解：∵点A 在函数y ＝（x ＞0）的图像上， ∴S △AOC ＝×2＝1，又∵点B 在反比例函数y ＝﹣（x ＜0）的图像上， ∴S △BOC ＝×8＝4， ∴S △AOB ＝S △AOC +S △BOC ＝1+4 ＝5，故选：B ．4、（2022•黑龙江）如图，在平面直角坐标系中，点O 为坐标原点，平行四边形OBAD 的顶点B 在反比例函数y ＝x 3的图像上，顶点A 在反比例函数y ＝xk的图像上，顶点D 在x 轴的负半轴上．若平行四边形OBAD 的面积是5，则k 的值是（）A ．2B ．1C ．﹣1D ．﹣2【分析】设B （a ，），根据四边形OBAD 是平行四边形，推出AB ∥DO ，表示出A 点的坐标，求出AB ＝a ﹣，再根据平行四边形面积公式列方程，解出即可．【解答】解：设B （a ，）， ∵四边形OBAD 是平行四边形， ∴AB ∥DO ， ∴A （，），∴AB ＝a ﹣，∵平行四边形OBAD 的面积是5， ∴（a ﹣）＝5，解得k ＝﹣2，故选：D ．5、（2022•十堰）如图，正方形ABCD 的顶点分别在反比例函数y ＝xk 1（k 1＞0）和y ＝xk 2（k 2＞0）的图像上．若BD ∥y 轴，点D 的横坐标为3，则k 1+k 2＝（）A ．36B ．18C ．12D ．9【分析】连接AC交BD于E，延长BD交x轴于F，连接OD、OB，设AE＝BE＝CE＝DE ＝m，D（3，a），根据BD∥y轴，可得B（3，a+2m），A（3+m，a+m），即知k1＝3（a+2m）＝（3+m）（a+m），从而m＝3﹣a，B（3，6﹣a），由B（3，6﹣a）在反比例函数y＝（k1＞0）的图像上，D（3，a）在y＝（k2＞0）的图像上，得k1＝3（6﹣a）＝18﹣3a，k2＝3a，即得k1+k2＝18﹣3a+3a＝18．【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D（3，a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图像上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图像上，D（3，a）在y＝（k2＞0）的图像上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B ．6、（2022•邵阳）如图是反比例函数y ＝x1的图像，点A （x ，y ）是反比例函数图像上任意一点，过点A 作AB ⊥x 轴于点B ，连接OA ，则△AOB 的面积是（）A ．1B ．C ．2D ．【分析】由反比例函数的几何意义可知，k ＝1，也就是△AOB 的面积的2倍是1，求出△AOB 的面积是．【解答】解：∵A （x ，y ）， ∴OB ＝x ，AB ＝y ，∵A 为反比例函数y ＝图像上一点， ∴xy ＝1，∴S △ABO ＝AB •OB ＝xy ＝1＝，故选：B ．7、（2022•内江）如图，在平面直角坐标系中，点M 为x 轴正半轴上一点，过点M 的直线l ∥y 轴，且直线l 分别与反比例函数y ＝x 8和y ＝xk的图像交于P 、Q 两点．若S △POQ ＝15，则k 的值为（）A ．38B ．22C ．﹣7D ．﹣22【分析】利用k 的几何意义解题即可．【解答】解：∵直线l ∥y 轴， ∴∠OMP ＝∠OMQ ＝90°，∴S △OMP ＝×8＝4，S △OMQ ＝﹣k ．又S △POQ ＝15， ∴4﹣k ＝15，即k ＝11，∴k ＝﹣22．故选：D ．8、（2022•东营）如图，△OAB 是等腰直角三角形，直角顶点与坐标原点重合，若点B 在反比例函数y ＝x1（x ＞0）的图像上，则经过点A 的函数图像表达式为．【分析】作AD ⊥x 轴于D ，BC ⊥x 轴于C ，根据△OAB 是等腰直角三角形，可证明△BOC ≌△OAD ，利用反比例函数k 的几何意义得到S △OBC ＝，则S △OAD ＝，所以|k |＝，然后求出k 得到经过点A 的反比例函数解析式．【解答】解：如图，作AD ⊥x 轴于D ，BC ⊥x 轴于C ， ∴∠ADO ＝∠BCO ＝90°，∵∠AOB ＝90°， ∴∠AOD +∠BOC ＝90°， ∴∠AOD +∠DAO ＝90°， ∴∠BOC ＝∠DAO ， ∵OB ＝OA ，∴△BOC ≌△OAD （AAS ），∵点B 在反比例函数y ＝（x ＞0）的图像上， ∴S △OBC ＝， ∴S △OAD ＝， ∴k ＝﹣1，∴经过点A 的反比例函数解析式为y ＝﹣．故答案为：y ＝﹣．9、（2022•盐城）已知反比例函数的图像经过点（2，3），则该函数表达式为．【分析】利用反比例函数的定义列函数的解析式，运用待定系数法求出函数的解析式即可．【解答】解：令反比例函数为y ＝（k ≠0）， ∵反比例函数的图像经过点（2，3）， ∴3＝， k ＝6，∴反比例函数的解析式为y ＝．故答案为：y ＝．10、（2022•湖北）在反比例函数y ＝xk 1−的图像的每一支上，y 都随x 的增大而减小，且整式x 2﹣kx +4是一个完全平方式，则该反比例函数的解析式为．【分析】由整式x 2﹣kx +4是一个完全平方式，可得k ＝±4，由反比例函y ＝的图像的每一支上，y 都随x 的增大而减小，可得k ﹣1＞0，解得k ＞1，则k ＝4，即可得反比例函数的解析式．【解答】解：∵整式x 2﹣kx +4是一个完全平方式，∴k ＝±4， ∵反比例函数y ＝的图像的每一支上，y 都随x 的增大而减小，∴k ﹣1＞0，解得k ＞1， ∴k ＝4，∴反比例函数的解析式为y ＝．故答案为：y ＝．35．（2022•陕西）已知点A （﹣2，m ）在一个反比例函数的图像上，点A '与点A 关于y 轴对称．若点A '在正比例函数y ＝21x 的图像上，则这个反比例函数的表达式为．【分析】根据轴对称的性质得出点A '（2，m ），代入y ＝x 求得m ＝1，由点A （﹣2，1）在一个反比例函数的图像上，从而求得反比例函数的解析式．【解答】解：∵点A '与点A 关于y 轴对称，点A （﹣2，m ）， ∴点A '（2，m ），∵点A '在正比例函数y ＝x 的图像上， ∴m ＝＝1，∴A （﹣2，1），∵点A （﹣2，1）在一个反比例函数的图像上， ∴反比例函数的表达式为y ＝﹣，故答案为：y ＝﹣．11、（2022•攀枝花）如图，正比例函数y ＝k 1x 与反比例函数y ＝xk 2的图像交于A （1，m ）、B 两点，当k 1x ≤xk2时，x 的取值范围是（）A ．﹣1≤x ＜0或x ≥1B ．x ≤﹣1或0＜x ≤1C ．x ≤﹣1或x ≥1D ．﹣1≤x ＜0或0＜x ≤1【分析】根据反比例函数的对称性求得B 点的坐标，然后根据图像即可求得．【解答】解：∵正比例函数y ＝k 1x 与反比例函数y ＝的图像交于A （1，m ）、B 两点，∴B （﹣1，﹣m ），由图像可知，当k 1x ≤时，x 的取值范围是﹣1≤x ＜0或x ≥1，故选：A ．37．（2022•东营）如图，一次函数y 1＝k 1x +b 与反比例函数y 2＝xk 2的图像相交于A ，B 两点，点A 的横坐标为2，点B 的横坐标为﹣1，则不等式k 1x +b ＜xk2的解集是（）A ．﹣1＜x ＜0或x ＞2B ．x ＜﹣1或0＜x ＜2C ．x ＜﹣1或x ＞2D ．﹣1＜x ＜2【分析】根据两函数图像的上下位置关系结合交点横坐标，即可得出不等式k 1x +b ＜的解集，此题得解．【解答】解：观察函数图像可知，当﹣1＜x ＜0或x ＞2时，一次函数y 1＝k 1x +b 的图像在反比例函数y 2＝的图像的下方，∴不等式k 1x +b ＜的解集为：﹣1＜x ＜0或x ＞2，故选：A ．12、（2022•朝阳）如图，正比例函数y ＝ax （a 为常数，且a ≠0）和反比例函数y ＝xk（k 为常数，且k ≠0）的图像相交于A （﹣2，m ）和B 两点，则不等式ax ＞xk的解集为（）A ．x ＜﹣2或x ＞2B ．﹣2＜x ＜2C ．﹣2＜x ＜0或x ＞2D ．x ＜﹣2或0＜x ＜2【分析】根据关于原点对称的点的坐标特征求得B （2，﹣m ），然后根据函数的图像的交点坐标即可得到结论．【解答】解：∵正比例函数y ＝ax （a 为常数，且a ≠0）和反比例函数y ＝（k 为常数，且k ≠0）的图像相交于A （﹣2，m ）和B 两点， ∴B （2，﹣m ），∴不等式ax ＞的解集为x ＜﹣2或0＜x ＜2，故选：D ．13、（2022•无锡）一次函数y ＝mx +n 的图像与反比例函数y ＝xm的图像交于点A 、B ，其中点A 、B 的坐标为A （﹣m1，﹣2m ）、B （m ，1），则△OAB 的面积是（） A ．3B ．413C ．27D ．415【分析】根据反比例函数图像上点的坐标特征求出m ，进而求出点A 、B 的坐标，根据三角形的面积公式计算即可．【解答】解：∵点A （﹣，﹣2m ）在反比例函数y ＝上， ∴﹣2m ＝，解得：m ＝2，∴点A 的坐标为：（﹣，﹣4），点B 的坐标为（2，1）， ∴S △OAB ＝××5﹣××4﹣×2×1﹣×1＝，故选：D ．14、（2022•荆州）如图是同一直角坐标系中函数y 1＝2x 和y 2＝x2的图像．观察图像可得不等式2x ＞x2的解集为（）A ．﹣1＜x ＜1B ．x ＜﹣1或x ＞1C ．x ＜﹣1或0＜x ＜1D ．﹣1＜x ＜0或x ＞1【分析】结合图像，数形结合分析判断．【解答】解：由图像，函数y 1＝2x 和y 2＝的交点横坐标为﹣1，1， ∴当﹣1＜x ＜0或x ＞1时，y 1＞y 2，即2x ＞，故选：D ．15、（2022•怀化）如图，直线AB 交x 轴于点C ，交反比例函数y ＝xa 1−（a ＞1）的图像于A 、B 两点，过点B 作BD ⊥y 轴，垂足为点D ，若S △BCD ＝5，则a 的值为（）A．8B．9C．10D．11【分析】设点B的坐标为（m，），然后根据三角形面积公式列方程求解．【解答】解：设点B的坐标为（m，），∵S△BCD＝5，且a＞1，∴×m×＝5，解得：a＝11，故选：D．16、（2022•宁夏）在显示汽车油箱内油量的装置模拟示意图中，电压U一定时，油箱中浮子随油面下降而落下，带动滑杆使滑动变阻器滑片向上移动，从而改变电路中的电流，电流表的示数对应油量体积，把电流表刻度改为相应油量体积数，由此知道油箱里剩余油量．在不考虑其他因素的条件下，油箱中油的体积V与电路中总电阻R总（R总＝R+R0）是反比例关系，电流I与R总也是反比例关系，则I与V的函数关系是（）A．反比例函数B．正比例函数C．二次函数D．以上答案都不对【分析】由油箱中油的体积V与电路中总电阻R总是反比例关系，电流I与R总是反比例关系，可得V＝I（为常数），即可得到答案．【解答】解：由油箱中油的体积V与电路中总电阻R总是反比例关系，设V•R总＝k（k为常数），由电流I与R总是反比例关系，设I•R总＝k'（k为常数），∴＝，∴V＝I（为常数），∴I与V的函数关系是正比例函数，故选：B．17、（2022•宜昌）已知经过闭合电路的电流I（单位：A）与电路的电阻R（单位：Ω）是反比例函数关系．根据下表判断a和b的大小关系为（）A．a＞b B．a≥b C．a＜b D．a≤b【分析】根据等量关系“电流＝”，即可求解．【解答】解：∵闭合电路的电流I（单位：A）与电路的电阻R（单位：Ω）是反比例函数关系，∴40a＝80b，∴a＝2b，∴a＞b，故选：A．18、（2022•丽水）已知电灯电路两端的电压U为220V，通过灯泡的电流强度I（A）的最大限度不得超过0.11A．设选用灯泡的电阻为R（Ω），下列说法正确的是（）A．R至少2000ΩB．R至多2000ΩC．R至少24.2ΩD．R至多24.2Ω【分析】利用已知条件列出不等式，解不等式即可得出结论．【解答】解：∵电压U一定时，电流强度I（A）与灯泡的电阻为R（Ω）成反比例，∴I＝．∵已知电灯电路两端的电压U为220V，∴I＝．∵通过灯泡的电流强度I（A）的最大限度不得超过0.11A，∴≤0.11，∴R≥2000．故选：A．19、（2022•郴州）科技小组为了验证某电路的电压U（V）、电流I（A）、电阻R（Ω）三者之间的关系：I＝U，测得数据如下：那么，当电阻R＝55Ω时，电流I＝A．【分析】由表格数据求出反比例函数的解析式，再将R＝55Ω代入即可求出答案．【解答】解：把R＝220，I＝1代入I＝得：1＝，解得U＝220，∴I＝，把R＝55代入I＝得：I＝＝4，故答案为：4．20、（2022•山西）根据物理学知识，在压力不变的情况下，某物体承受的压强p（Pa）是它的受力面积S（m2）的反比例函数，其函数图像如图所示．当S＝0.25m2时，该物体承受的压强p的值为Pa．【分析】设p＝，把（0.1，1000）代入得到反比例函数的解析式，再把S＝0.25代入解析式即可解决问题．【解答】解：设p＝，∵函数图像经过（0.1，1000），∴k＝100，∴p＝，当S＝0.25m2时，物体所受的压强p＝＝400（Pa），故答案为：400．。

2025年中考数学高频考点专题练习-一次函数与反比例函数的实际应用

2025年中考数学高频考点专题练习一次函数与反比例函数的实际应用一、解答题1．某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培蔬菜．某天恒温系统从开启到关闭及关闭后，大棚内温度y （℃）与时间x （h ）之间的函数关系如图所示，其中BC 段是恒温阶段，CD 段是某反比例函数图象的一部分，请根据图中信息解答下列问题：(1)求CD 段反比例函数图象的关系式，并写出自变量x 的取值范围； (2)恒温阶段保持的时间有多少小时？(3)大棚里栽培的一种蔬菜在温度为12℃到20℃的条件下最适合生长，若某天恒温系统开启前的温度是10℃，那么这种蔬菜一天内最适合生长的时间有多长？ 2．如图直线y x m =-+与双曲线ky x=交于A ，B 两点，点A 的坐标为(1,2)．(1)求一次函数和反比例函数的表达式； (2)求AOB 的面积．3．在平面直角坐标系xOy 中，一次函数()0y kx b k =+≠经过点，()0,1A -，()3,2B ．(1)求这个一次函数的解析式； (2)①当双曲线()0my m x=≠经过点B 时，求m 的值； ①当3x >时，对于x 的每一个值，永远有()10mkx b k x+->≠成立，直接写出m 的取值范围． 4．数学兴趣小组了解到一款如图1所示的电子托盘秤，它是通过所称重物调节可变电阻R 的大小，从而改变电路中的电流I ，最终通过显示器显示物体质量．已知可变电阻R (单位①k Ω)与物体质量m (单位①kg )之间的关系如图2所示，电流I (单位①mA )与可变电阻 R 之间关系为 ()603I R R =≥+．(1)该小组先探究函数 ()60I R =≥的图像与性质，并根据I 与R 之间关系得到如下表格：①表格中的p = ；①请在图3 中画出 ()603I R R =≥+对应的函数图像； (2)该小组综合图2和图3发现，I 随着m 的增大而；(填“增大”或“减小”)(3)若将该款电子秤中的电路电流范围设定为0.20.4I <≤(单位：mA )，判断该电子托盘秤能否称出质量为2kg 的物体的质量？请说明理由． 5．如图，一次函数y ＝x ＋4的图象与反比例函数ky x=（k ≠0）的图象交于A （－1，a ），B 两点，与x 轴交于点C ．(1)直接写出结果：k ＝，点B 的坐标为；(2)若点P 在x 轴上，且3ACP BOC S S ∆∆=，求点P 的坐标．6．如图，一次函数y x b =+的图像和反比例函数()0k y x x=>的图像交于()2,4A ．(1)求一次函数的解析式和反比例函数的解析式；(2)设点()0,P m ，过点P 作平行于x 轴的直线与直线2y x =+和反比例函数()0ky x x=>的图像分别交于点C ，D ，当4CD ≤时，直接写出m 的取值范围．7．实验研究发现：初中生在数学课上听课注意力指标随上课时间的变化而变化，上课开始时，学生兴趣激增，中间一段时间，学生的兴趣保持平稳状态，随后开始分散．学生注意力指标y 随时间x （分钟）变化的函数图象如图所示，其中当2045x ≤≤时，图象是反比例函数的一部分．(1)求点C ，D 所在反比例函数的表达式和直线AB 的表达式；(2)张老师想在数学课上讲解一道数学综合题，希望学生注意力指标不低于36，那么她最多可以讲______分钟．8．已知某消毒药物燃烧时，室内每立方米空气中的含药量y （微克）与时间x （小时）成正比例，药物熄灭后，y （微克）与x （小时）成反比例，如图所示，现测得药物4小时燃毕，此时室内空气每立方米的含药量为6微克，请你根据题中提供的信息，解答下列问题：(1)分别求出药物燃烧时和药物熄灭后y 关于x 的函数关系式；(2)研究表明，当空气中每立方米的含药量不低于3微克且持续时间不低于10小时时，才能杀灭空气中的毒，那么这次消毒是否有效？为什么？ 9．如图，一次函数1y kx b =+的图像与反比例函数()20my x x=>的图像交于点(4,1)A 和点(2,)B n ．(1)求一次函数和反比例函数解析式；(2)过点B 作BC y ⊥轴于点C ，连接OA ，求四边形OABC 的面积；(3)根据图像直接写出使mkx b x+<成立的x 的取值范围． 10．如图，在平面直角坐标系xOy 中，直线2y x =与双曲线ky x=与相交于A ，B 两点（点A 在点B 的左侧）．(1)当5AB =k 的值；(2)点B 关于y 轴的对称点为C ，连接AC BC ，； ①判断ABC 的形状，并说明理由；①当ABC 的面积等于16时，双曲线上是否存在一点P ，连接AP BP ，，使PAB 的面积等于ABC 面积？若存在，求出点P 的坐标，若不存在，请说明理由．11．如图，已知点A 在正比例函数2y x =-图像上，过点A 作AB x ⊥轴于点B ，四边形ABCD 是正方形，点D 在反比例函数ky x=图像上．(1)若点A 的横坐标为−2，求k 的值；(2)若设正方形的边长为m ，试用含m 的代数式表示k 值．12．如图，直线1y x =+与y 轴交于A 点，与反比例函数(0)k y x x=>的图像交于点M ，过M 作MH x ⊥轴于点H ，且1tan 2AHO ∠=．(1)请直接写出k 的值；(2)设点()1,N a 是反比例函数()0k y x x=>图像上的点，在y 轴上是否存在点P ，使得PM PN +最小？若存在，求出点P 的坐标；若不存在，请说明理由．13．如图，已知直线1：y =x +4与反比例函数y =kx(x <0)的图象交于点A (−1，n )，直线l ′经过点A ，且与l 关于直线x =−1对称．(1)求反比例函数的解析式； (2)求图中阴影部分的面积．14．如图，在平面直角坐标系xOy 中，正比例函数1y k x =与反比例函数ky x=的图象相交于A ，B 两点，其中点A 的坐标为()14，．(1)直接写出点B 的坐标为_______________；(2)过点A 作直线AC ，交反比例函数图象于另一点C ，连接BC ，当线段AC 被y 轴分成长度比为1:2的两部分时，求BC 的长．15．如图，平面直角坐标系中，四边形AOBC 为平行四边形，11y k x b =+与双曲线22(0)k y x x=>交于点()1,3A 和点()3,E m ．(1)求1k ，2k 和b 的值；(2)直接写出120y y -<时x 的取值范围；(3)如果平行四边形AOBC 的对角线OC 交双曲线于点P ，求点P 的坐标．。

中考数学复习基本过关训练综合训练5。正比例函数,一次函数,反比例函数

卷5 ：正比例函数一次函数反比例函数班级：姓名：分数：一、选择题（8⨯3′=2 4′ ）1. 在正比例函数y=kx 中，如果 y 随x 的增大而增大，那么应满足的条件是-（）（A ）0<k （B ）0>k （C ）0≥k （D ）0≤k 2．对于函数y =xk ，下列说法正确的是--------------------------------------------（）（A ）当k =2时，y 随x 的增大而增大；（B ）当k = 一2时，在每一象限内，y 随x 的增大而增大；（C ）当k =2时，图象位于第二四象限；（D ）当k = 一2时，图象位于第一三象限．3．一次函数y =3一4x 的图象不经过---------------------------------------------（）（A ）第一象限（B ）第二象限（C ）第三象限（ D ）第四象限 4．已知函数y =ax 和反比例函数y =xb ，它们的图象在同一坐标系内没有交点，则a 与b 的关系是 -----------------------------------------------------------------（）（ A ）同号（B ）异号（C ）互为倒数（D ）互为相反数5．在函数y = 一3x +2的图象上的点是-----------------------------------------（）（A ）（1，0）（B ）（1，2）（C ）（一1，3）（D ）（一1，5）6．下列命题中，正确的是--------------------------------------------------------（）（A ） xy =2中，y 与x 不成正比例函数，也不成反比例；（B ）正比例函数y =kx ，y 随x 的增大而增大；（C ）反比例函数xy 4-=中，y 随x 的增大而增小；（D ）圆面积公式A =πR 2中，A 与R 2成比例．7．下列问题中，两个变量成正比例的是---------------------------- --------（）（A ）等腰三角形的面积一定，它的底边和底边上的高；（B ）等边三角形的面积和它的边长；（C ）长方形的一边长确定，它的周长与另一边长；（D ）长方形的一边长确定，它的面积与另一边长． 8．如果点A （1x ，1y ）、B （2x ，2y ）在反比例函数y =xk （k <0）的图象上，若1x ﹥2x ﹥0，则1y 与2y 的大小关系是-------------------------------（）（A ）1y ﹥2y （B ）1y ﹤2y （C ）1y =2y （D ）不能确定二、填空题（16⨯4′=64′）9．正比例函数的图象过点（一2，6），则此正比例函数的解析式为． 10．反比例函数xm y -=2的图象过点（1，一3），则m= ．11．正比例函数)0(≠=k kx y ，当图象（除原点外）在第象限时，y 随x的增大而增大． 12．反比例函数)0(≠=k xk y ，在每一象限内时y 随x 的增大而增大时，图象在第象限．13．一次函数y =kx+b 的图象位于第一二四象限时，那么y 的值随x 的增大而． 14．直线b x y +=2不经过第二象限，那么b o ．15．一次函数的图象在y 轴上截距为4，且平行于直线y = 一3x ，则一次函数解析式为． 16．直线2x+y+m =0在y 轴上截距为6，则m = ．17．y 与x 2成正比例且当x =1时，y =2，则当y =32，x = ．18．y 一1与x 成反比例，若当x=1时，y=3，则当y=8，x= ． 19．若()1023--=mx m y 是反比例函数，则m= ．20．当a ，b 时，函数3)5(++-=b x a y 是正比例函数．21．已知y 与x 成正比例，x 与 z 成反比例，则y 与z 成比例关系．22．直线y =2x +1沿y 轴向上平移4个单位得到，再沿x 轴向右平移3 个单位得到直线解析式为．23．等腰三角形的周长为12cm ，腰长为xcm ，其底边长y = cm ，其中x 的取值范围为．24．正比例函数图象过点A （4，一2）和B （m ，3），则线段AB 的长等于．三．解答题（25～31题，4⨯8′+3⨯10′=62′）25．已知一次函数y=kx+b 平行于直线y= 一6x ，且与双曲线 y= 一x2 的一个交点为A （2，m ），求此函数解析式．x26．已知A 城与B 城相距200千米，一列火车以每小时60千米的速度从A城驶向B 城，求：（1）火车与B 城的距离S （千米）与行驶的时间t （小时）的函数关系式；（2）t （小时）的取值范围；（3）画出函数的图象．27．已知△ABC 中，BD 平分∠ABC ，过D 作AB 平行线交BC 于E ，BC =6，BE =x ，AB=y ，求y 关于x 的函数并写出自变量x 的取值范围．28．已知一次函数图象经过点（一1，2），图象与y 轴的交点到原点的距离等于4，求这个一次函数解析式．29．如图平行四边形ABCD 中，CD =8，BC =7，E 是AB 边上不与点B 重合的一动点，AE =x ，DE 的延长线交CB 的延长线于 F ，设CF =y ，求y 关于x 的函数解析式．30．已知函数y =y 1+y 2，y 1与x 成正比例，y 2与（x 一2）成反比例，当x =1时，1-=y ；当x =3时y =5，求此函数解析式．31．反比例函数xy 4=的图象上两点M 、N 的坐标分别为M （1，m ），N （n ，一1）经过点M 、N 作直线b kx y +=，求（1）k ，b 的值；（2）O 为坐标原点，求△MNO 的面积．（ 10分）FEDCA卷5参考答案：一、选择题（1）B （2）B （3）C （4）B （5）D （6）D （7）D （8） A 二填空题（9）x y 3-=；（ 10）5 ；（11）一、三；（12）二、四；（13）减小；（14） b ≤0；（15）y= 一3x+4 ；（16）一6；（17）4±；（18）72 ；（19）一3 ；（20）a ≠5，b= 一3；（21）反；（22）y=2x+5， y=2x —1；（23）y=12—2x ， 63<<x ；（24）55三．解答题25、解： ∵一次函数y=kx+b 平行于直线y= 一6x ， ∴k= 一6∵双曲线 y= 一x2 过点A （2，m ）∴m= 一1 ∴A （2，一1） ∵y= 一6x+b 过点A （2，一1）， ∴b=11 ∴一次函数解析式为y= 一6x+11．26、（1）t S 60200-=；（2）3100≤≤t ；（3）图略．27、解：∵BD 平分∠ABC∴∠ABD=∠DBE∵AB ∥DE ， ∴∠ABD=∠BDE ∴∠BDE=∠DBE ， ∴BE=DE=x ∵DE ∥AB ， ∴ABDE = BC EC∴yx = 66x -， ∴y= xx -66∴x 取值范围为60<<x ．28、解：设一次函数解析式y=kx+b则它的图象与Y 轴的交点为（0，b ），交点到原点的距离为∣b ∣由已知得∣b ∣=4 ∴b=4，或b= 一4∵函数图象过点（一1，2）∴一k+b=2∴当b=4时，k=2 ；当b= 一4时，k= 一6 ∴所求一次函数解析式为y=2x+4或y= 一6x 一4．29、解：∵平行四边形ABCD ∴AD ∥FC ，∠A=∠C∴∠ADF=∠F ∴△AED ∽△CDF ∴CFAD =CDAE∵AD=BC=7，AE=x ，CF=y ，CD=8， ∴y7=8x ， ∴y=x56 （80<<x ）．30、22-+=x x y ；31、解：（1）反比例函数y= x4 的图象上两点分别为M （1，m ），N （n ，一1）∴m=4，n= 一4∴M （1，4） N （一4，一1）∵过点M ，N 作直线y=kx+bk+b=4∴ 解得 k=1 一4k+b= 一1b=3（2）215=∆MNO S ．。

中考《第五讲：一次函数与反比例函数》专题复习含答案

中考数学专题辅导第五讲应用题（一次函数与反比例函数专题）选讲此部分内容包括：函数的应用（主要是一次函数与反比例函数），则属于中档题。

真题再现：1．(2008年苏州•本题8分)如图，帆船A和帆船B在太湖湖面上训练，O为湖面上的一个定点，教练船静候于O点．训练时要求A、B两船始终关于O点对称．以O为原点．建立如图所示的坐标系，轴、y 轴的正方向分别表示正东、正北方向．设A、B两船可近似看成在双曲线上运动，湖面风平浪静，双帆远影优美．训练中当教练船与A、B两船恰好在直线上时，三船同时发现湖面上有一遇险的C船，此时教练船测得C船在东南45°方向上，A船测得AC与AB的夹角为60°，B船也同时测得C船的位置（假设C船位置不再改变，A、B、C三船可分别用A、B、C三点表示)．(1)发现C船时，A、B、C三船所在位置的坐标分别为A( ，)、B( ，)和C( ，)；(2)发现C船，三船立即停止训练，并分别从A、O、B三点出发沿最短路线同时前往救援，设A、B两船的速度相等，教练船与A船的速度之比为3：4，问教练船是否最先赶到?请说明理由。

2．(2010年苏州•本题8分) 如图，四边形OABC是面积为4的正方形，函数(x＞0)的图象经过点B．(1)求k的值；(2)将正方形OABC分别沿直线AB、BC翻折，得到正方形MABC′、MA′BC．设线段MC′、NA′分别与函数(x＞0)的图象交于点E、F，求线段EF所在直线的解析式．3．（2014年•苏州•本题7分）如图，已知函数y＝－x＋b的图象与x轴、y轴分别交于点A，B，与函数y＝x的图象交于点M，点M的横坐标为2．在x轴上有一点P (a，0)（其中a>2），过点P作x轴垂线，分别交函数y＝－x＋b和y＝x的图象于点C，D．(1)求点A的坐标；(2)若OB＝CD，求a的值．x4yx=y x=kyx=kyx=12124．（2014年•苏州• 8分）如图，已知函数y＝（x>0）的图象经过点A ，B ，点A 的坐标为(1，2)．过点A 作AC ∥y 轴，AC ＝1（点C 位于点A 的下方），过点C 作CD ∥x 轴，与函数的图象交于点D ，过点B 作BE ⊥CD ，垂足E 在线段CD 上，连接OC ，OD ． (1)求△OCD 的面积； (2)当BE ＝AC 时，求CE 的长．5．（2015年苏州•本题满分8分）如图，已知函数（x ＞0）的图像经过点A 、B ，点B 的坐标为（2，2）．过点A 作AC ⊥x 轴，垂足为C ，过点B 作BD ⊥y 轴，垂足为D ，AC 与BD 交于点F ．一次函数y=ax +b 的图像经过点A 、D ，与x 轴的负半轴交于点E ．（1）若AC =OD ，求a 、b 的值；（2）若BC ∥AE ，求BC 的长．6．（2016年苏州•本题满分8分）如图一次函数的图像与轴交于点A ，与反比例函数的图像交干点B (2,n)．过点B 作轴于点P ，P 是该反比例函数图像上的一点，且∠PBC=∠ABC ．求反比例函数和一次函数的表达式．7．（2017年苏州•本题满分8分）如图，在中，，轴，垂足为．反比例函数（）的图像经过点，交于点．已知，． kx12ky x=326y kx =+x (0)my x x=>BC x ⊥(34,1)n -C ∆AB C C A =B x AB ⊥A k y x =0x >C AB D 4AB =5C 2B =（1）若，求的值；（2）连接，若，求的长．8. （2017年南京市•本题满分3分）如图，已知点A 是一次函数y =x (x ≥0)图像上一点，过点A 作x 轴的垂线l ，B 是l 上一点(B 在A 上方)，在AB 的右侧以AB 为斜边作等腰直角三角形ABC ，反比例函数(k )0)的图像过点B 、C ，若△OAB 的面积为6,求△ABC 的面积.9．（2017年南京市•本题满分8分）如图，已知一次函数y =kx +b 的图像与x 轴交于点A ，与反比例函数y =(x <0)的图像交于点B (-2,n )，过点B 作BC ⊥x 轴于点C ，点D (3-3n ,1)是该反比例函数图像上一点. (1)求m 的值；(2)若∠DBC =∠ABC ，求一次函数y =kx +b 的表达式.10．（2017年无锡市•本题满分12分）操作：“如图1，P 是平面直角坐标系中一点（x 轴上的点除外），过点P 作PC ⊥x 轴于点C ，点C 绕点P 逆时针旋转60°得到点Q ．”我们将此由点P 得到点Q 的操作称为点的T 变换．（1）点P （a ，b ）经过T 变换后得到的点Q的坐标为；若点M 经过T 变换后得到点N （6，﹣），则点M 的坐标为．（2）A 是函数y =x 图象上异于原点O 的任意一点，经过T 变换后得到点B ．①求经过点O ，点B 的直线的函数表达式；②如图2，直线AB 交y 轴于点D ，求△OAB 的面积与△OAD 的面积之比．11．（2017年泰州市•本题满分12分）阅读理解：如图①，图形l 外一点P 与图形l 上各点连接的所有线段中，若线段PA 1最短，则线段PA 1的长度称为点P 到图形l 的距离．4OA =k C O D C B =B C O 12ky x=mx例如：图②中，线段P1A的长度是点P1到线段AB的距离；线段P2H的长度是点P2到线段AB的距离．解决问题：如图③，平面直角坐标系xOy中，点A、B的坐标分别为（8，4），（12，7），点P从原点O出发，以每秒1个单位长度的速度向x轴正方向运动了t秒．（1）当t=4时，求点P到线段AB的距离；（2）t为何值时，点P到线段AB的距离为5？（3）t满足什么条件时，点P到线段AB的距离不超过6？（直接写出此小题的结果）模拟训练：1．(2017年常熟市•本题满分8分)如图，点、分别在轴和轴上， (点和点在直线的两侧)，点的坐标为(4,).过点的反比例函数的图像交边于点. (1)求反比例函数的表达式; (2)求点的坐标.2．（2018年蔡老师预测•本题满分8分如图，正比例函数y=2x 的图象与反比例函数y=的图象交于点A 、B ，AB=2，（1）求k 的值；（2）若反比例函数y=的图象上存在一点C ，则当△ABC 为直角三角形，请直接写出点C 的坐标．3．( 2017年张家港•本题满分8分) 货车和轿车分别从甲、乙两地同时出发，沿同一公路相向而行.轿车出发3h 后休息，直至与货车相遇后，以原速度继续行驶.设货车出发h 后，货车、轿车分别到达离甲地km 和km 的地方，图中的线段、折线分别表示、与之间的函数关系.(1)求点的坐标，并解释点的实际意义;(2)求线段所在直线的函数表达式; (3)当货车出发 h 时，两车相距50km.4．(2017年苏州市区•本题满分8分)如图，在平面直角坐标系中，函数（，是常数）的图像经过，，其中．过点作轴垂线，垂足为，过点作轴垂线，垂足为，AC 与BD 交于点E ，连结，，．A B y x BC AB ⊥C O AB C n C (0)m y x x =>AC 1(,3)3D n +B x 1y 2y OA BCDE 1y 2y x D D DE ky x=0x >k (26)A ，(,)B m n 2m >A x C B y D AD DC CB（1）若的面积为3，求的值和直线的解析式；（2）求证：；（3）若∥ ，求点B 的坐标．5．(2017年昆山市•吴江区••本题满分7分)如图，在平面直角坐标系中，矩形的对角线相交于点，且，(1)求证:四边形是菱形;(2)如果，求出经过点的反比例函数解析式.6．(2017年高新区•本题满分8分) 如图，反比例函数y ＝的图象与一次函数y ＝kx +b 的图象交于A ，B 两点，点A 的坐标为(2，6)，点B 的坐标为(n ，1)．(1)求反比例函数与一次函数的表达式；(2)点E 为y 轴上一个动点，若S △AEB ＝10，求点E 的坐标．7．(2017年吴中区•本题满分8分)如图，一次函数的图象与反比例(为常数，且)的图象交于，两点。

专题5 一次函数、反比例函数与实际应用

第三十三页，编辑于星期三：五点五十分。
第三十四页，编辑于星期三：五点五十分。
第三十五页，编辑于星期三：五点五十分。
第一页，编辑于星期三：五点五十分。
第二页，编辑于星期三：五点五十分。
第三页，编辑于星期三：五点五十分。
第四页，编辑于星期三：五点五十分。
第五页，编辑于星期三：五点五十分。
第六页，编辑于星期三：五点五十分。
第七页，编辑于星期三：五点五十分。
第八页，编辑于星期三：五点五十分。
第九页，编辑于星期三：五点五十分。
第十页，编辑于星期三：五点五十分。
第十一页，编辑于星期三：五点五十分。
第十二页，编辑于星期三：五点五十分。
第十三页，编辑于星期三：五点五十分。
第十四页，编辑于星期三：五点五十分。
第十五页，编辑于星期三：五点五十分。
第十六页，编辑于星期三：五点五十分。
第二十五页，编辑于星期三：五点五十分。
第二十六页，编辑于星期三：五点五十分。
第二十七页，编辑于星期三：五点五十分。
第二十八页，编辑于星期三：五点五十分。
第二十九页，编辑于星期三：五点五十分。
第三十页，编辑于星期三：五点五十分。
第三十一页，编辑于星期三：五点五十分。
第三十二页，编辑于星期三：五点五十分。
第十七页，编辑于星期三：五点五十分。
第十八页，编辑于星期三：五点五十分。
第十九页，编辑于星期三：五点五十分。
第二十页，编辑于星期三：五点五十分。
第二十一页，编辑于星期三：五点五十分。
第二十二页，编辑于星期三：五点五十分。
第二十三页，编辑于星期三：五点五十分。

2023年中考数学专项突破之函数的实际应用课件(共50张PPT)

要防止轻易放弃.
方法点拨
解决这类问题一般遵循这样的方法：
返回主目录
三
二次函数的实际应用
(1)运用转化的思想.由于函数与几何结合的问题都具有较强的综合性,因此在解决这
类问题时,要善于把“新知识”转化为“旧知识”,把“未知”转化为“已知”,把
“抽象”的问题转化为“具体”的问题,把“复杂”的问题转化为“简单”的问题.
返回主目录
三
二次函数的实际应用
题型讲解
二次函数在中考数学中常常作为压轴题,具有一定的综合性和较大的难度,学生往往
因缺乏思路,感到无从下手,难以拿到分数.事实上,我们只要理清思路,方法得当,稳步
推进,力争少失分、多得分,同时需要心态平和,切忌急躁,当思维受阻时,要及时调整
思路和方法,并重新审视题意,注意挖掘隐蔽的条件和内在联系,既要防止钻牛角尖,又
解：∵a=0.1时,s=500,
k
∴500= ,解得k=50.
0.1
则该轿车可行驶的总路程s与平均耗油量a之间的函数解析式是s=
50
.a返回主目录源自(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米？
50
50
解：将a=0.08代入s= ,得s=
=625.
a
0.08
答：当平均耗油量为0.08升/千米时,该轿车可以行驶625千米.
提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔
记本的价格都提高x元,在不考虑其他因素的条件下,当x定为多少元时,才能使该文具
若y是x的反比例函数,其图象如图所示：
(1)求y与x的函数解析式；
分析：用待定系数法确定反比例函数解析式.
k
解析：设y与x的函数关系式为y= (k≠0),

2021年九年级数学中考复习——函数专题：反比例函数实际应用【有答案】

2021年九年级数学中考复习——函数专题：反比例函数实际应用（五）1．已知蓄电池的电压为定值．使用此蓄电池作为电源时，电流Ⅰ（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．（1）求这个反比例函数的表达式；（2）如果以此蓄电池为电源的用电器的电流不能超过8A，那么该用电器的可变电阻至少是多少？2．某游泳池有900立方米水，每次换水前后水的体积保持不变．设放水的平均速度为v立方米/小时，将池内的水放完需t小时，（1）求v关于t的函数表达式，并写出自变量t的取值范围；（2）若要求在2.5小时至3小时内（包括2.5小时与3小时）把游泳池内的水放完，求放水速度的范围．3．某气球内充满了一定量的气体，当温度不变时，气球内气体的气压P（kPa）是气球体积V（m3）的反比例函数，且当V＝0.8m3时，P＝120kPa．（1）求P与V之间的函数表达式；（2）当气球内的气压大于100kPa时，气球将爆炸，为确保气球不爆炸，气球的体积应不小于多少？4．我们知道函数y＝a（x﹣m）2+n（a≠0，m＞0，n＞0）的图象是由二次函数y＝ax2的图象向右平移m个单位，再向上平移n个单位得到：类似地，函数y＝+n（k≠0，m＞0，n＞0）的图象是由反比例函数y＝的图象向右平移m个单位，再向上平移n个单位得到，其对称中心坐标为（m，n）．例如：函数y＝+1的图象可由函数y＝的图象向右平移3个单位，再向上平移1个单位得到，其对称中心坐标（3，1），请根据以上材料解决下列问题：（1）函数y＝﹣2的对称中心是，在平面直角坐标系xOy中，请根据所给的y＝的图象画出函数y＝﹣2的图象，并根据图象指出，x在什么范围内变化时，y≥﹣1？（2）某老师对一位学生的学习情况进行跟踪研究，假设刚学完新知识时的记忆存留量为1，新知识学习后经过的时间为x，发现该生的记忆存留量随x变化的函数关系为y 1＝；若该生在某一时刻进行了第一次复习，发现他复习后的记忆存留量是复习前的2倍（复习的时间忽略不计），且复习后的记忆存留量随x变化的函数关系为y 2＝，如果记忆存留量为时是复习的“最佳时机点”，且他第一次复习是在“最佳时机点”进行的，那么当x为何值时，是他第二次复习的“最佳时机点”？5．教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃停止加热，水温开始下降，此时水温y（℃）与开机后用时x（min）成反比例关系，直至水温降至30℃，饮水机关机，饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时接通电源，水温y（℃）与时间x（min）的关系如图所示：（1）分别写出水温上升和下降阶段y与x之间的函数关系式；（2）怡萱同学想喝高于50℃的水，请问她最多需要等待多长时间？6．某厂今年1月的利润为600万元，从2月初开始适当限产，并投入资金进行设备更新升级，升级期间利润明显下降．设今年1月为第1个月，第x个月的利润为y万元，从1月到5月，y与x满足反比例关系，到5月底，设备更新升级完成，从这时起，y与x满足一次函数关系，如图所示．（1）分别求该厂设备更新升级期间及升级完成后y与x之间的函数关系式；（2）问该厂今年有几个月的利润低于200万元？7．老李想利用一段5米长的墙（图中EF），建一个面积为32平方米的矩形养猪圈，另外三面（图中AB，BC，CD）需要自己建筑．老李准备了可以修建20米墙的材料（可以不用完）．（1）设AB＝y，BC＝x，求y关于x的函数关系式．（2）对于（1）中的函数y的值能否取到8.5？请说明理由．8．据报道，从2018年8月以来，“非洲猪瘟”给生猪养殖户带来了不可估量的损失．某养殖户为了预防“非洲猪瘟”的侵袭，每天对猪场进行药熏消毒．一瓶药物在释放过程中，一个圈舍内每立方米空气中含药量y（毫克）与时间x（分钟）之间满足正比例函数关系；已知一个圈舍内一瓶药物打开后10分钟释放完毕，此时圈舍内每立方米的空气中含药量为30毫克，药物释放完后，y与x之间满足反比例函数关系．（1）分别求当0≤x≤10和x＞10时，y与x之间满足的函数关系式；（2）请补全函数图象；（3）据测定，当空气中每立方米的含药量不低于15毫克时，消毒才有效．根据函数图象，你知道这次熏药的有效消毒时间大约是多少分钟？9．为了做好校园疫情防控工作，校医每天早上对全校办公室和教室进行药物喷洒消毒，她。