山西省临汾市曲沃中学2015-2016学年高二数学上学期期末试卷 文(含解析)
山西省临汾市曲沃县中学高二数学理联考试卷含解析

山西省临汾市曲沃县中学高二数学理联考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知点是椭圆的两个焦点,点P是该椭圆上一个动点,那么的最小值为A.0 B.1 C.2 D.参考答案:C2. 函数的定义域为()A. B. C. D.参考答案:A3. 某个命题与正整数有关,若当时该命题成立,那么可推得当时该命题也成立,现已知当时该命题不成立,那么可推得( )A.当时,该命题不成立B.当时,该命题成立C.当时,该命题成立D.当时,该命题不成立参考答案:D4. 一个命题与他们的逆命题、否命题、逆否命题这4个命题中()A真命题与假命题的个数相同 B真命题的个数一定是奇数C真命题的个数一定是偶数 D真命题的个数一定是可能是奇数,也可能是偶数参考答案:C略5. 过抛物线的焦点作倾斜角为的直线交抛物线于两点,若线段的中点坐标为,则的值为A. B. C.D.4参考答案:C略6. 个连续自然数按规律排成下表,根据规律,2011到2013,箭头的方向依次为()A.↓→B.→↓C.↑→D.→↑参考答案:B略7. 若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的母线与轴所成的角为( )A. 30°B. 45°C. 60°D. 90°参考答案:A设圆锥侧面展开图的半径为,则圆锥底面周长为,设底面半径为,则,圆锥的母线长为侧面展开图的半径,设该圆锥的母线与轴所成的角为,则.本题选择A选项.8. 若函数f(x)=2x2-lnx在其定义域内的一个子区间 (k-1,k+1)内不是单调函数,则实数k的取值范围是( )A.[1,+∞)B.[1,) C.[1,2) D.,2)参考答案:B9. 经过抛物线y2 = 4x的焦点弦的中点轨迹方程是()A.y2=x-1 B.y2=2(x-1) C.y2=x- D.y2=2x-1参考答案:B10. 如图是一个算法的程序框图,该算法所输出的结果是()A. B. C. D.参考答案:C运行第一次的结果为n=0+=;第二次n=+=;第三次n=+=.此时i=4程序终止,即输出n=.二、填空题:本大题共7小题,每小题4分,共28分11. 如果圆(x-2a)2+(y-a-3)2=4上总存在两个点到原点的距离为1,则实数a的取值范围是________.参考答案:-<a<012. 定义:如果对于实数,使得命题“曲线,点到直线的距离”为真命题,就把满足条件的的最小值对称为曲线到直线的距离.已知曲线到直线的距离等于曲线到直线的距离,则实数___________.参考答案:圆的圆心为,半径为,圆心到直线的距离为,∴曲线到直线的距离为,则曲线到直线的距离等于.令解得,故切点为,切点到直线的距离为,即,解得或.∵当时,直线与曲线相交,故不符合题意.综上所述,.13. 曲线在点处的切线的斜率为.参考答案:略14. 命题,的否定命题参考答案:,15. 若, 则从小到大的排列顺序是____________.参考答案:3y, 2x, 5z16. 如图所示的算法中, , , , 其中是圆周率, 是自然对数的底数, 则输出的结果是 .参考答案:17. 若双曲线的离心率为,则两条渐近线的方程为____参考答案:略三、解答题:本大题共5小题,共72分。
山西省临汾市赵曲高级中学高二数学文上学期期末试卷含解析

山西省临汾市赵曲高级中学高二数学文上学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 若方程C:(是常数)则下列结论正确的是()A.,方程C表示椭圆 w. B.,方程C表示双曲线C.,方程C表示椭圆 D.,方程C表示抛物线参考答案:B2. 的值为()A. B. C. D.1参考答案:A略3. 不等式-6x2-x+2≤0的解集是()A. B.C. D.参考答案:B试题分析:.故选B.考点:解一元二次不等式.4. 正方体ABCD—A1B1C1D1中直线与平面夹角的余弦值是()A. B. C. D.参考答案:C略5. 某四面体三视图如图所示,该四面体四个面的面积中最大的是A. B. C. D.参考答案:C略6. 某几何体的三视图如下图所示,它的体积为( )A. B. C. D.参考答案:C7. 如图是把二进制数11111(2)化为十进制数的一个程序框图,则判断框内应填入的条件是()A.i>4 B.i≤4C.i>5 D.i≤5参考答案:B【考点】程序框图.【分析】因为11111(2)=31(10),故执行程序框图,当i=4时满足条件,有S=31,i=5时此时应该不满足条件,退出执行循环体,输出S的值为31.【解答】解:因为11111(2)=31(10)执行程序框图,有S=1,i=1满足条件,有S=3,i=2;满足条件,有S=7,i=3;满足条件,有S=15,i=4;满足条件,有S=31,i=5;此时应该不满足条件,退出执行循环体,输出S的值为31.故选:B.8. 过抛物线的焦点F的直线交抛物线于A、B两点,且A、B在直线上的射影分别M、N,则∠MFN等于()A.45°B.60°C.90° D.以上都不对参考答案:C9. 已知函数是定义在R上的奇函数,且当时不等式成立,若,,则的大小关系是A. B. C. D.参考答案:A试题分析:令函数F(x)=xf(x),则F′(x)=f(x)+xf′(x)∵f(x)+xf′(x)<0,∴F(x)=xf(x),x∈(-∞,0)单调递减,∵y=f(x)是定义在R上的奇函数,∴F(x)=xf(x),在(-∞,0)上为减函数,可知F(x)=xf(x),(0,+∞)上为增函数∵,∴a=F(-3),b=F(-2),c=F(1)F(-3)>F(-2)>F(-1),即考点:函数的单调性与导数的关系;奇偶性与单调性的综合10. 已知,则的值为()A. 1 B.2 C. 3D.4参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 已知△ABC的顶点B、C在椭圆+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是.参考答案:A【考点】椭圆的简单性质.【分析】设另一个焦点为F,根据椭圆的定义可知|AB|+|BF|=2a,|AC|+|FC|=2a最后把这四段线段相加求得△ABC的周长.【解答】解:椭圆+y 2=1的a=.设另一个焦点为F ,则根据椭圆的定义可知 |AB|+|BF|=2a=2,|AC|+|FC|=2a=2.∴三角形的周长为:|AB|+|BF|+|AC|+|FC|=4.故答案为:4.12. 设,则的值为参考答案: -213. 已知向量,,若,则m=.参考答案:3【考点】平面向量数量积的运算.【分析】直接利用向量的数量积运算法则求解即可. 【解答】解:向量,,若,则1?m ﹣3×1=0 解得m=3. 故答案为:3.14. 设满足约束条件,则的最大值是 .参考答案: 515. 某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为 .参考答案:2【考点】由三视图求面积、体积. 【专题】立体几何.【分析】由主视图知CD⊥平面ABC 、B 点在AC 上的射影为AC 中点及AC 长,由左视图可知CD 长及△ABC 中变AC 的高,利用勾股定理即可求出最长棱BD 的长.【解答】解:由主视图知CD⊥平面ABC ,设AC 中点为E ,则BE⊥AC,且AE=CE=1; 由主视图知CD=2,由左视图知BE=1, 在Rt△BCE 中,BC=, 在Rt△BCD 中,BD=, 在Rt△ACD 中,AD=2.则三棱锥中最长棱的长为2.故答案为:2.【点评】本题考查点、线、面间的距离计算,考查空间图形的三视图,考查学生的空间想象能力,考查学生分析解决问题的能力.16. 设的最小值为,则参考答案:17.已知函数f (x )=2ax 2-bx +1,若a 是从区间[0,2]上任取的一个数,b 是从区间[0,2]上任取的一个数,则此函数在[1,+∞)递增的概率为________. 参考答案:略三、 解答题:本大题共5小题,共72分。
2015-2016学年高二上学期期末考试数学(文)试题

高二数学(文史类)2016.1 本试卷共4页,分第卷(选择题)和第卷(非选择题)两部分,共150分,考试时间120分钟。
第I 卷(选择题 共50分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试证号、考试科目涂写在答题卡上.2.每小题选出答案后,用2B 铅笔把答题卡上对应的答案标号涂黑,如需改动,用想橡皮擦干净后,再选涂其他答案标号. 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.已知,a b 为非零实数,且a b <,则下列结论一定成立的是A. 22a b <B.33a b <C. 11a b> D.22ac bc < 2.命题:3"[0,),20"x x x ∀∈+∞+≥的否定是A. 3(,0),20x x x ∀∈-∞+<B. 3[0,),20x x x ∃∈+∞+<C. 3(,0),20x x x ∀∈-∞+≥D.3[0,),20x x x ∃∈+∞+≥3."0"x <是的"0"1x x <+ A. 充分不必要条件 B.必要不充分条件C. 充要条件D.既不充分也不必要条件 4.已知焦点在x 轴上的椭圆2219x y m +=的离心率12e =,则m = A.12 B.-4 C.-6 D.-85.已知等差数列{}n a 的公差为2,若134,,a a a 成等比数列,则2a =A. 12B. 4-C. 6-D.8- 6.在ABC 中,内角A,B,C 的对边分别为,,a b c ,且满足cos b C a =,则ABC 的形状是A. 等边三角形B.锐角三角形C. 直角三角形D.钝角三角形7.已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线平行于直线:43200l x y -+=,且双曲线的一个焦点在直线l 上,,则双曲线方程为A. 221916x y -= B. 221169x y -= C. 22551916x y -= D.22551169x y -= 8.我国古代数学巨著《九章算术》中,有如下问题:“今女子善织,日自倍,五日织五尺,问日织几何?”这个问题用今天的白话叙述为:一位善于织布的女子,每天织的布都是前一天的2倍,她5天共织布5尺,问这位女子每天分别织布多少?根据上题已知条件,可求得该女子第四天所织布的尺数为 A. 815 B. 1615 C.2031 D.40319.对任意实数x ,若不等式4210x x m -⋅+>恒成立,则实数m 的取值范围是A. 2m <B. 22m -<<C. 2m ≤D.22m -≤≤10.已知抛物线2:12C y x =的焦点为F ,准线为l ,P 为l 上一点,Q 是直线PF 与抛物线C 的一个交点,若230FP FQ += ,则||QF =A.5B.152C.10D.15第II 卷(非选择题 共90分)注意事项:1.将第卷答案用0.5mm 的黑色签字笔答在答题卡的相应位置上.2.答卷前将密封线内的项目填写清楚.二、填空题(本大题共5小题,每小题5分,共25分)11.已知函数()cos f x x =,则'()______.6f π= 12.设实数,x y 满足条件101020x x y x y +≥⎧⎪-+≤⎨⎪+-≤⎩,则2z y x =-的最大值为______.13..在ABC 中,内角A,B,C 的对边分别为,,a b c ,若,,b c a 成等比数列,且2a b =,则cos A =_____.14.过抛物线2:8C y x =的焦点F 作直线l 交抛物线C 于,A B 两点,若A 到抛物线的准线的距离为6,则||_____.AB =15.给出下列四个命题:①命题”若3πθ=-则tan 3θ=-”的否命题是”若3πθ≠-则tan 3θ≠-”; ②在ABC 中,”A>B ”是”sin sin A B >”的充分不必要条件;③定义:12...nn p p p +++为n 个数12...n p p p +++的”均倒数”,已知数列{}n a 的前n 项的”均倒数”为12n +,则数列{}n a 的通项公式为21;n a n =+ ④在ABC 中,2,6,BC AC AB ==边上的中线长为2,则22AB =. 以上命题正确的为_______.(写出所以正确命题的序号)三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.16.(本小题满分12分)已知二次函数2()2f x ax ax b =+-,其图像过点(2,-4),且(1) 3.f =-()I 求,a b 的值;()II 设函数()ln (),h x x x f x =+求曲线()h x 在1x =处的切线方程.17.(本小题满分12分)在ABC 中,内角A,B,C 的对边分别为,,a b c ,且22()13a b c ab+-=. ()I 求C ∠.()II 若3,2c b ==,求B ∠及ABC 的面积.18.(本小题满分12分)已知:p 方程22112x y m m+=--表示焦点在y 轴上的椭圆;q :实数m 满足22(21)0m a a a -+++<且q ⌝是p ⌝的充分不必要条件,求实数a 的取值范围.19.(本小题满分12分)中国海警缉私船对一般走私船进行定位:以走私船的当前位置为原点,以正北方向为y 轴正方向建立平面直角坐标系(以1海里为单位长度),中国海警缉私船恰在走私船的正南方向18海里A 处,现假设:①走私船的移动路径可视为抛物线29;28y x =②定位后中国海警缉私船即刻沿直线匀速前往追捕;③中国海警缉私船出发t 小时后,走私船所在位置的横坐标为27.t()I 当1t =时,写出走私船所在位置P 的纵坐标,若此时两船恰好相遇,求中国海警缉私船速度的大小;()II 问中国海警缉私船的时速是多少海里能追上走私船?20.(本小题满分13分)已知数列{}n a 是等差数列,其前n 项和为n S ,且满足15410,16;a a S +==数列{}n b 满足:2112333....3()3n n n b b b b n N -+++++=∈ ()I 求数列{}n a ,{}n b 的通项公式;()II 设11n n n n n c a b a a +=+,求数列{}n c 的前项和n T . 21.(本小题满分14分) 已知椭圆2222:1(0)x y E a b a b +=>>经过点(0,2),离心率为63,点O 为坐标原点. ()I 求椭圆E 的标准方程;()II 过左焦点F 任作一直线l ,交椭圆E 于P 、Q 两点,()i 求OP OQ 的取值范围;()ii 若直线l 不垂直于坐标轴,记弦PQ 的中点为M ,过F 作PQ的垂线FN 交直线于点N 。
2015-2016年山西省太原市高二上学期期末数学试卷(文科)与解析
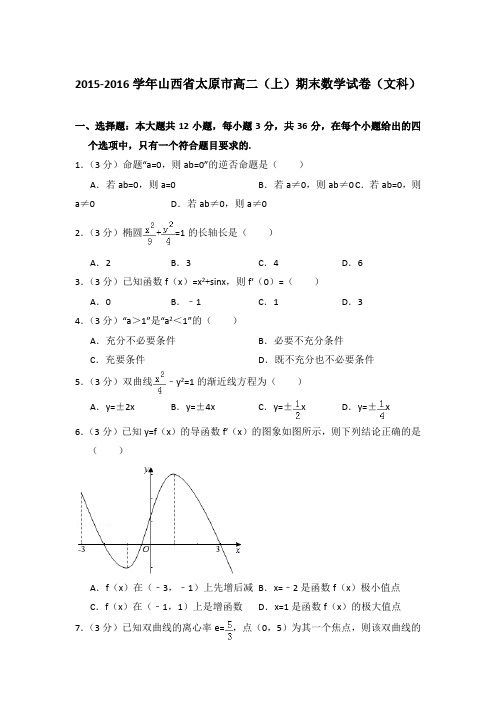
2015-2016学年山西省太原市高二(上)期末数学试卷(文科)一、选择题:本大题共12小题,每小题3分,共36分,在每个小题给出的四个选项中,只有一个符合题目要求的.1.(3分)命题“a=0,则ab=0”的逆否命题是()A.若ab=0,则a=0B.若a≠0,则ab≠0C.若ab=0,则a≠0D.若ab≠0,则a≠02.(3分)椭圆+=1的长轴长是()A.2B.3C.4D.63.(3分)已知函数f(x)=x2+sinx,则f′(0)=()A.0B.﹣1C.1D.34.(3分)“a>1”是“a2<1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.(3分)双曲线﹣y2=1的渐近线方程为()A.y=±2x B.y=±4x C.y=±x D.y=±x 6.(3分)已知y=f(x)的导函数f′(x)的图象如图所示,则下列结论正确的是()A.f(x)在(﹣3,﹣1)上先增后减B.x=﹣2是函数f(x)极小值点C.f(x)在(﹣1,1)上是增函数D.x=1是函数f(x)的极大值点7.(3分)已知双曲线的离心率e=,点(0,5)为其一个焦点,则该双曲线的标准方程为()A.﹣=1B.﹣=1C.﹣=1D.﹣=18.(3分)函数f(x)=xlnx的单调递减区间为()A.(﹣∞,)B.(0,)C.(﹣∞,e)D.(e,+∞)9.(3分)若方程+=1表示焦点在y轴上的椭圆,则实数m的取值范围为()A.(﹣∞,1)B.(1,2)C.(2,3)D.(3,+∞)10.(3分)已知命题p:∀x∈(0,+∞),2x>3x,命题q:∃x0∈(0,+∞),x>x,则下列命题中的真命题是()A.p∧q B.p∨(¬q)C.(¬p)∧(¬q)D.(¬p)∧q11.(3分)f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是()A.(﹣∞,﹣3)∪(0,3)B.(﹣∞,﹣3)∪(3,+∞)C.(﹣3,0)∪(3,+∞)D.(﹣3,0)∪(0,3)12.(3分)过点M(2,﹣1)作斜率为的直线与椭圆+=1(a>b>0)相交于A,B两个不同点,若M是AB的中点,则该椭圆的离心率e=()A.B.C.D.二、填空题:本大题共4个小题,每小题4分.、共16分.13.(4分)抛物线x2=4y的焦点坐标为.14.(4分)已知命题p:∃x0∈R,3=5,则¬p为.15.(4分)已知曲线f(x)=xe x在点P(x0,f(x0))处的切线与直线y=x+1平行,则点P的坐标为.16.(4分)已知f(x)=ax3+3x2﹣1存在唯一的零点x0,且x0<0,则实数a的取值范围是.三、解答题:本大题共7小题,共48分,解答应写出文字说明、证明过程或演算步骤.17.(8分)已知命题p:函数y=kx是增函数,q:方程+y2=1表示焦点在x轴上的椭圆,若p∧(¬q)为真命题,求实数k的取值范围.18.(10分)已知函数f(x)=2x3﹣6x2+m在[﹣2,2]上的最大值为3,求f(x)在[﹣2,2]上的最小值.19.(10分)已知点P(1,﹣2)在抛物线C:y2=2px(p>0)上.(1)求抛物线C的方程及其准线方程;(2)若过抛物线C焦点F的直线l与抛物线C相交于A,B两个不同点,求|AB|的最小值.20.(10分)已知函数f(x)=x﹣﹣2alnx(a∈R).(1)若函数f(x)在x=处取得极值,求实数a的值;(2)求证:当a≤1时,不等式f(x)≥0在[1,+∞)恒成立.21.已知函数f(x)=x﹣﹣2alnx(a∈R).(1)若函数f(x)在x=处取得极值,求实数a的值;(2)若不等式f(x)≥0在[1,+∞)恒成立,求实数a的取值范围.22.(10分)已知椭圆C:+=1(a>b>0)的离心率e=,点P(﹣,1)在该椭圆上.(1)求椭圆C的方程;(2)若点A,B是椭圆C上关于直线y=kx+1对称的两点,求实数k的取值范围.23.已知椭圆C:+=1(a>b>0)的离心率e=,原点到直线+=1的距离为.(1)求椭圆C的方程;(2)若点A,B是椭圆C上关于直线y=kx+1对称的两点,求实数k的取值范围.2015-2016学年山西省太原市高二(上)期末数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题3分,共36分,在每个小题给出的四个选项中,只有一个符合题目要求的.1.(3分)命题“a=0,则ab=0”的逆否命题是()A.若ab=0,则a=0B.若a≠0,则ab≠0C.若ab=0,则a≠0D.若ab≠0,则a≠0【解答】解:因为原命题是“a=0,则ab=0”,所以其逆否命题为“若ab≠0,则a≠0”,故选:D.2.(3分)椭圆+=1的长轴长是()A.2B.3C.4D.6【解答】解:椭圆+=1的实轴长是:2a=6.故选:D.3.(3分)已知函数f(x)=x2+sinx,则f′(0)=()A.0B.﹣1C.1D.3【解答】解:函数的导数f′(x)=2x+cosx,则f′(0)=cos0=1,故选:C.4.(3分)“a>1”是“a2<1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:由a2<1解得﹣1<a<1,∴“a>1”是“a2<1”的既不充分也不必要条件.故选:D.5.(3分)双曲线﹣y2=1的渐近线方程为()A.y=±2x B.y=±4x C.y=±x D.y=±x【解答】解:双曲线=1的渐近线方为,整理,得y=.故选:C.6.(3分)已知y=f(x)的导函数f′(x)的图象如图所示,则下列结论正确的是()A.f(x)在(﹣3,﹣1)上先增后减B.x=﹣2是函数f(x)极小值点C.f(x)在(﹣1,1)上是增函数D.x=1是函数f(x)的极大值点【解答】解:由图象得:﹣3<x<﹣2时,f′(x)>0,﹣2<x<﹣1时,f′(x)<0,∴f(x)在(﹣3,﹣2)递增,在(﹣2,﹣1)递减,故选:A.7.(3分)已知双曲线的离心率e=,点(0,5)为其一个焦点,则该双曲线的标准方程为()A.﹣=1B.﹣=1C.﹣=1D.﹣=1【解答】解:设双曲线的方程为﹣=1(a,b>0),由题意可得e==,c=5,可得a=3,b==4,即有双曲线的标准方程为﹣=1.故选:D.8.(3分)函数f(x)=xlnx的单调递减区间为()A.(﹣∞,)B.(0,)C.(﹣∞,e)D.(e,+∞)【解答】解:函数的定义域为x>0∵y′=lnx+1令lnx+1<0得0<x<,∴函数y=xlnx的单调递减区间是(0,),故选:B.9.(3分)若方程+=1表示焦点在y轴上的椭圆,则实数m的取值范围为()A.(﹣∞,1)B.(1,2)C.(2,3)D.(3,+∞)【解答】解:方程+=1表示焦点在y轴上的椭圆,可得m﹣1>3﹣m>0,解得2<m<3.故选:C.10.(3分)已知命题p:∀x∈(0,+∞),2x>3x,命题q:∃x0∈(0,+∞),x>x,则下列命题中的真命题是()A.p∧q B.p∨(¬q)C.(¬p)∧(¬q)D.(¬p)∧q【解答】解:命题p:∀x∈(0,+∞),2x>3x,是假命题,例如取x=2不成立;命题q:∵∀x∈(0,+∞),2x<3x,因此命题q是假命题,∴只有(¬p)∧(¬q)是真命题.故选:C.11.(3分)f(x),g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)g(x)+f(x)g′(x)>0,且g(﹣3)=0,则不等式f(x)g(x)<0的解集是()A.(﹣∞,﹣3)∪(0,3)B.(﹣∞,﹣3)∪(3,+∞)C.(﹣3,0)∪(3,+∞)D.(﹣3,0)∪(0,3)【解答】解:令h(x)=f(x)g(x),则h(﹣x)=f(﹣x)g(﹣x)=﹣f(x)g (x)=﹣h(x),因此函数h(x)在R上是奇函数.①∵当x<0时,h′(x)=f′(x)g(x)+f(x)g′(x)>0,∴h(x)在x<0时单调递增,故函数h(x)在R上单调递增.∵h(﹣3)=f(﹣3)g(﹣3)=0,∴h(x)=f(x)g(x)<0=h(﹣3),∴x<﹣3.②当x>0时,函数h(x)在R上是奇函数,可知:h(x)在(0,+∞)上单调递增,且h(3)=﹣h(﹣3)=0,∴h(x)<0,的解集为(0,3).∴不等式f(x)g(x)<0的解集是(﹣∞,﹣3)∪(0,3).故选:A.12.(3分)过点M(2,﹣1)作斜率为的直线与椭圆+=1(a>b>0)相交于A,B两个不同点,若M是AB的中点,则该椭圆的离心率e=()A.B.C.D.【解答】解:设A(x1,y1),B(x2,y2),则x1+x2=4,y1+y2=﹣2,A,B两个不同点代入椭圆方程,可得+=1,+=1,作差整理可得+=0,∵斜率为==,∴a=2b,∴c==b,∴e==.故选:C.二、填空题:本大题共4个小题,每小题4分.、共16分.13.(4分)抛物线x2=4y的焦点坐标为(0,1).【解答】解:抛物线x2=4y的焦点在y轴上,开口向上,且2p=4,∴∴抛物线x2=4y的焦点坐标为(0,1)故答案为:(0,1)14.(4分)已知命题p:∃x0∈R,3=5,则¬p为∀x∈R,3x≠5.【解答】解:由特称命题的否定可知:¬p:∀x∈R,3x≠5,故答案为:∀x∈R,3x≠5.15.(4分)已知曲线f(x)=xe x在点P(x0,f(x0))处的切线与直线y=x+1平行,则点P的坐标为(0,0).【解答】解:f(x)=xe x的导数为f′(x)=(x+1)e x,可得切线的斜率为(x0+1)e x0,由切线与直线y=x+1平行,可得(x0+1)e x0=1,即有x0为x+1=e﹣x的解,由y=x+1﹣e﹣x,在R上递增,且x=0时,y=0.即有x0=0,则P的坐标为(0,0).故答案为:(0,0).16.(4分)已知f(x)=ax3+3x2﹣1存在唯一的零点x0,且x0<0,则实数a的取值范围是(﹣∞,﹣2).【解答】解:(i)当a=0时,f(x)=﹣3x2+1,令f(x)=0,解得x=,函数f(x)有两个零点,舍去.(ii)当a≠0时,f′(x)=3ax2+6x=3ax(x+),令f′(x)=0,解得x=0或﹣.①当a<0时,﹣>0,当x>﹣或x<0,f′(x)<0,此时函数f(x)单调递减;当0<x<﹣时,f′(x)>0,此时函数f(x)单调递增.∴故x=﹣是函数f(x)的极大值点,0是函数f(x)的极小值点.∵函数f(x)=ax3+3x2﹣1存在唯一的零点x0,且x0<0,则f(﹣)=﹣+﹣1=﹣1<0,即a2>4得a>2(舍)或a<﹣2.②当a>0时,﹣<0,当x<﹣或x>0时,f′(x)>0,此时函数f(x)单调递增;当﹣<x<0时,f′(x)<0,此时函数f(x)单调递减.∴x=﹣是函数f(x)的极大值点,0是函数f(x)的极小值点.∵f(0)=﹣1<0,∴函数f(x)在(0,+∞)上存在一个零点,此时不满足条件.综上可得:实数a的取值范围是(﹣∞,﹣2).故答案为:(﹣∞,﹣2).三、解答题:本大题共7小题,共48分,解答应写出文字说明、证明过程或演算步骤.17.(8分)已知命题p:函数y=kx是增函数,q:方程+y2=1表示焦点在x轴上的椭圆,若p∧(¬q)为真命题,求实数k的取值范围.【解答】解:命题p:函数y=kx是增函数,∴k>0.命题q:方程+y2=1表示焦点在x轴上的椭圆,∴k>1.∵p∧(¬q)为真命题,∴p为真命题,q为假命题.∴,解得0<k≤1.∴实数k的取值范围是0<k≤1.18.(10分)已知函数f(x)=2x3﹣6x2+m在[﹣2,2]上的最大值为3,求f(x)在[﹣2,2]上的最小值.【解答】解:f′(x)=6x2﹣12x,令f′(x)=0,则x=0或x=2,∴f(x)在[﹣2,0]上单调递增,在(0,2]上单调递减,∴f(x)max=f(0)=m=3,即f(x)=2x3﹣6x2+3,又∵f(﹣2)=﹣37,f(2)=﹣5,∴f(x)min=f(﹣2)=﹣37.19.(10分)已知点P(1,﹣2)在抛物线C:y2=2px(p>0)上.(1)求抛物线C的方程及其准线方程;(2)若过抛物线C焦点F的直线l与抛物线C相交于A,B两个不同点,求|AB|的最小值.【解答】解:∵点P(1,﹣2)在抛物线C:y2=2px(p>0)上,∴2p=4,解得:p=2,∴抛物线C的方程为y2=4x,准线方程为x=﹣1;(2)设直线l的方程为:x+my﹣1=0,代入y2=4x,整理得,y2+4my﹣4=0设A(x1,y1),B(x2,y2),则y1,y2是上述关于y的方程的两个不同实根,所以y1+y2=﹣4m根据抛物线的定义知:|AB|=x1+x2+2=(1﹣my1)+(1﹣my2)=4(m2+1)∴|AB|=4(m2+1)≥4,当且仅当m=0时,|AB|有最小值4.20.(10分)已知函数f(x)=x﹣﹣2alnx(a∈R).(1)若函数f(x)在x=处取得极值,求实数a的值;(2)求证:当a≤1时,不等式f(x)≥0在[1,+∞)恒成立.【解答】解:(1)f(x)的定义域是(0,+∞),f′(x)=1+﹣,∴f′()=1+4(2a﹣1)﹣4a=0,解得:a=,∴a=时,f′(x)=,∴f(x)在(0,)递增,在(,1)递减,f(x)在x=处取得极值,故a=符合题意;(2)f′(x)=1+﹣=,当a≤1时,则2a﹣1≤1,∴f′(x)>0在(1,+∞)恒成立,函数f(x)递增,∴f(x)≥f(1)=2(1﹣a)≥0.21.已知函数f(x)=x﹣﹣2alnx(a∈R).(1)若函数f(x)在x=处取得极值,求实数a的值;(2)若不等式f(x)≥0在[1,+∞)恒成立,求实数a的取值范围.【解答】解:(1)f(x)的定义域是(0,+∞),f′(x)=1+﹣,∴f′()=1+4(2a﹣1)﹣4a=0,解得:a=,∴a=时,f′(x)=,∴f(x)在(0,)递增,在(,1)递减,f(x)在x=处取得极值,故a=符合题意;(2)依题意有:f min(x,)≥0f′(x)=,令f′(x)=0,得:x1=2a﹣1,x2=1,①当2a﹣1≤1即a≤1时,函数f'(x)≥0在[1,+∞)恒成立,则f(x)在[1,+∞)单调递增,于是f min(x)=f(1)=2﹣2a≥0,解得:a≤1;②当2a﹣1>1即a>1时,函数f(x)在[1,2a﹣1]单调递减,在[2a﹣1,+∞)单调递增,于是f min(x)=f(2a﹣1)<f(1)=2﹣2a<0,不合题意,综上所述:实数a的取值范围是a≤1.22.(10分)已知椭圆C:+=1(a>b>0)的离心率e=,点P(﹣,1)在该椭圆上.(1)求椭圆C的方程;(2)若点A,B是椭圆C上关于直线y=kx+1对称的两点,求实数k的取值范围.【解答】解:(1)由已知e==,即c2=a2,b2=a2﹣c2=a2,将P(﹣,1)代入椭圆方程,可得+=1,∴a=2,b=,∴a2=4,∴b2=2,∴椭圆C的方程为:+=1;(2)椭圆C上存在点B,A关于直线y=kx+1对称,设A(x1,y1),B(x2,y2),y1≠y2AB的中点(x0,y0),直线y=kx+1且k≠0,恒过(0,1),则x12+(y1﹣1)2=x22+(y2﹣1)2,点B,A在椭圆上,∴x12=4﹣2y12,x22=4﹣2y22,∴4﹣2y12+(y1﹣1)2=4﹣2y22+(y2﹣1)2,化简可得:y12﹣y22=﹣2(y1﹣y2),即y1+y2=﹣2,∴y0==﹣1,又因为AB的中点在y=kx+1上,所以y0=kx0+1,x0=﹣,由,可得x=±,∴0<﹣<,或﹣<﹣<0,即k<﹣或k>.则k的取值范围是(﹣∞,﹣)∪(,+∞).23.已知椭圆C:+=1(a>b>0)的离心率e=,原点到直线+=1的距离为.(1)求椭圆C的方程;(2)若点A,B是椭圆C上关于直线y=kx+1对称的两点,求实数k的取值范围.【解答】解:(1)由已知e==,即c2=a2,b2=a2﹣c2=a2,原点到直线+=1的距离为,即有=,∴a=2,b=,∴a2=4,∴b2=2,∴椭圆C的方程为:+=1;(2)椭圆C上存在点B,A关于直线y=kx+1对称,设A(x1,y1),B(x2,y2),y1≠y2AB的中点(x0,y0),直线y=kx+1且k≠0,恒过(0,1),则x12+(y1﹣1)2=x22+(y2﹣1)2,点B,A在椭圆上,∴x12=4﹣2y12,x22=4﹣2y22,∴4﹣2y12+(y1﹣1)2=4﹣2y22+(y2﹣1)2,化简可得:y 12﹣y22=﹣2(y1﹣y2),即y1+y2=﹣2,∴y 0==﹣1,又因为AB 的中点在y=kx +1上,所以y 0=kx 0+1,x 0=﹣, 由,可得x=±,∴0<﹣<,或﹣<﹣<0,即k <﹣或k>.则k 的取值范围是(﹣∞,﹣)∪(,+∞)赠送—高中数学知识点【1.3.1】单调性与最大(小)值 (1)函数的单调性②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数.③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为yxo减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()u g x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减.(2)打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数,分别在[,0)a -、]a 上为减函数.(3)最大(小)值定义①一般地,设函数()y f x =的定义域为I ,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M ≤;(2)存在0x I ∈,使得0()f x M =.那么,我们称M 是函数()f x 的最大值,记作max ()f x M =.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y轴两侧相对称的区间增减性相同,偶函数在y轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.。
山西省曲沃二中2015-2016学年高二数学上册期末测试题2

曲沃二中2015-2016学年(上)期末考试试题数学(文科)一、选择题(本大题共12小题,共60.0分)1.命题“”的否定是()A. B.C.D.2.下列说法正确的是()A. 命题“”为真命题,则命题“”和命题“”均为真命题B. 已知,则“”是“”的充分不必要条件C. 命题“”的否定是:“”D. 命题“若,则”的逆命题是真命题3.命题:“若,则”的逆否命题是()A. 若或,则B. 若,则C. 若或,则D. 若,则或4.“”是“”的()A. 必要不充分条件B. 既不充分也不必要条件C. 充分必要条件D. 充分不必要条件5.如果方程表示焦点在y轴上的椭圆,则m的取值范围是( )A. 3<m<4B.C.D.6.椭圆x2+4y2=1的离心率为( )A.B.C.D.7.在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线的通径为4,则P=()知识改变命运A. 1B. 4C. 2D. 88.若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能为( )A.B.C.D.9.曲线在点处的切线方程为()A.B.C.D.10.设,若,则()A. B.C.D.11.若点的坐标为,是抛物线的焦点,点在抛物线上移动时,取得最小值的的坐标为()知识改变命运A.B.C.D.12.已知双曲线的左、右焦点分别是,若双曲线的左支上有一点M 到右焦点的距离为18,N 是的中点,则等于( )A. B. 1 C. 4 D. 2二、填空题(本大题共4小题,共20.0分)13.命题:“若则”的逆否命题为.14.经过点的抛物线的标准方程为.15.椭圆=1的两焦点为F1、F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为________.16.若曲线在点处的切线平行于轴,则______.三、解答题(本大题共6小题,共70.0分)17.(本小题满分10分)命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2-4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.18.(本小题满分12分)已知,q:1-m≤x≤1+m,若非P是非q的必要不充分条件,求实数m的取值范围.19.(本小题满分12分)已知双曲线经过M(1,1),N(-2,5)两点,求双曲线的标准方程.20.(本小题满分12分)已知函数f(x)=x3+x-16.求曲线y=f(x)在点(2,-6)处的切线的方程21.(本小题满分12分)知识改变命运知识改变命运已知函数,当时,有极大值1.(Ⅰ)求 ,的值;(Ⅱ)求函数在区间上的最大值和最小值.22.(本小题满分12分)已知椭圆的离心率为,短轴一个端点到右焦点的距离为。
2015-2016年山西省临汾市曲沃中学高二上学期期末数学试卷(文科)与解析

2015-2016学年山西省临汾市曲沃中学高二(上)期末数学试卷(文科)一、选择题(本大题共12小题,共60分)1.(5分)已知命题p::“∀x∈R,x2>0”,则¬p是()A.∀x∈R,x2≤0B.∃x∈R,x2>0C.∃x∈R,x2<0D.∃x∈R,x2≤02.(5分)下列说法正确的是()A.命题“p∨q”为真命题,则命题“p”和命题“q”均为真命题B.已知x∈R,则“x>1”是“x>2”的充分不必要条件C.命题“∃x∈R,x2﹣x>0”的否定是:“∀x∈R,x2﹣x≤0”D.命题“若am2<bm2,则a<b”的逆命题是真命题3.(5分)命题:“若x2<1,则﹣1<x<1”的逆否命题是()A.若x≥1或x≤﹣1,则x2≥1B.若﹣1<x<1,则x2<1C.若x>1或x<﹣1,则x2>1D.若x2≥1,则x≥1或x≤﹣1 4.(5分)“x>3”是“x2>9”的()A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件5.(5分)如果方程表示焦点在y轴上的椭圆,则m的取值范围是()A.3<m<4B.C.D.6.(5分)椭圆x2+4y2=1的离心率为()A.B.C.D.7.(5分)在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px 的通径为4,则P=()A.1B.4C.2D.88.(5分)若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能()A.B.C.D.9.(5分)曲线y=在点(﹣1,1)处的切线方程为()A.y=2x+3B.y=2x+1C.y=﹣2x﹣1D.y=﹣2x 10.(5分)设f(x)=xlnx,若f′(x0)=2,则x0=()A.e2B.ln2C.D.e11.(5分)若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为()A.(0,0)B.C.D.(2,2)12.(5分)已知曲线左、右焦点分别为F1、F2,若双曲线的左支上有一点M到右焦点F2的距离为18,N是MF2的中点,O为坐标原点,则|NO|等于()A.3B.1C.2D.4二、填空题(本大题共4小题,共20分)13.(5分)命题:“若a≥b,则2a≥2b”的逆否命题为.14.(5分)经过点P(4,﹣2)的抛物线的标准方程是.15.(5分)椭圆的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为.16.(5分)若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=.三、解答题(本大题共6小题,共70.0分)17.(10分)命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2﹣4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.18.(12分)已知,q:1﹣m≤x≤1+m,若非P是非q的必要不充分条件,求实数m的取值范围.19.(12分)已知双曲线经过M(1,1),N(﹣2,5)两点,求双曲线的标准方程.20.(12分)已知函数f(x)=x3+x﹣16,求曲线y=f(x)在点(2,﹣6)处的切线的方程.21.(12分)已知函数f(x)=ax3+bx2,当x=1时,f(x)有极大值1.(Ⅰ)求a,b的值;(Ⅱ)求函数f(x)在区间上的最大值和最小值.22.(12分)已知椭圆C:+=1(a>b>0)的离心率为,短轴一个端点到右焦点F的距离为2.(Ⅰ)求椭圆C的方程;(Ⅱ)设点P(,),过点F的直线l与椭圆C交于A,B两点,与直线x=m (m>a)交于M点,若直线PA,PM,PB的斜率成等差数列,求m的值.2015-2016学年山西省临汾市曲沃中学高二(上)期末数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,共60分)1.(5分)已知命题p::“∀x∈R,x2>0”,则¬p是()A.∀x∈R,x2≤0B.∃x∈R,x2>0C.∃x∈R,x2<0D.∃x∈R,x2≤0【解答】解:命题:∀x∈R,x2>0的否定是:∃x∈R,x2≤0.故选:D.2.(5分)下列说法正确的是()A.命题“p∨q”为真命题,则命题“p”和命题“q”均为真命题B.已知x∈R,则“x>1”是“x>2”的充分不必要条件C.命题“∃x∈R,x2﹣x>0”的否定是:“∀x∈R,x2﹣x≤0”D.命题“若am2<bm2,则a<b”的逆命题是真命题【解答】解:命题“p∨q”为真命题,则命题“p”和命题“q”至少有1个为真命题,故A错误;已知x∈R,则“x>1”是“x>2”的必要不充分条件,故B错误;命题“∃x∈R,x2﹣x>0”的否定是:“∀x∈R,x2﹣x≤0”,故C正确;命题“若am2<bm2,则a<b”的逆命题是假命题,故D错误;故选:C.3.(5分)命题:“若x2<1,则﹣1<x<1”的逆否命题是()A.若x≥1或x≤﹣1,则x2≥1B.若﹣1<x<1,则x2<1C.若x>1或x<﹣1,则x2>1D.若x2≥1,则x≥1或x≤﹣1【解答】解:∵“x2<1”的否定为“x2≥1”.“﹣1<x<1”的否定是“x≤﹣1或x≥1”.∴命题“若x2<1,则﹣1<x<1”的逆否命题是:“若x≥1或x≤﹣1,则x2≥1”.故选:A.4.(5分)“x>3”是“x2>9”的()A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件【解答】解:由x2>9得x>3或x<﹣3,则“x>3”是“x2>9”的充分不必要条件,故选:B.5.(5分)如果方程表示焦点在y轴上的椭圆,则m的取值范围是()A.3<m<4B.C.D.【解答】解:由题意可得:方程表示焦点在y轴上的椭圆,所以4﹣m>0,m﹣3>0并且m﹣3>4﹣m,解得:.故选:D.6.(5分)椭圆x2+4y2=1的离心率为()A.B.C.D.【解答】解:把椭圆方程化为标准方程得:x2+=1,得到a=1,b=,则c==,所以椭圆的离心率e==.故选:A.7.(5分)在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px 的通径为4,则P=()A.1B.4C.2D.8【解答】解:由题意,2p=4,∴p=2.故选:C.8.(5分)若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能()A.B.C.D.【解答】解:由y=f′(x)可得y=f′(x)有两个零点,x1,x2,且0<x1<x2,当x<x1,或x>x2时,f′(x)<0,即函数为减函数,当x1<x<x2,时,f′(x)>0,函数为增函数,即当x=x1,函数取得极小值,当x=x2,函数取得极大值,9.(5分)曲线y=在点(﹣1,1)处的切线方程为()A.y=2x+3B.y=2x+1C.y=﹣2x﹣1D.y=﹣2x【解答】解:y′===2∴y′|x=﹣1而切点的坐标为(﹣1,1)∴曲线y=在点(﹣1,1)处的切线方程为y=2x+3.故选:A.10.(5分)设f(x)=xlnx,若f′(x0)=2,则x0=()A.e2B.ln2C.D.e【解答】解:∵f′(x)=lnx+1;故f′(x0)=2可化为lnx0+1=2;故x0=e;故选:D.11.(5分)若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为()A.(0,0)B.C.D.(2,2)【解答】解:由题意得F(,0),准线方程为x=﹣,设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3﹣(﹣)=.把y=2代入抛物线y2=2x 得x=2,故点M的坐标是(2,2),12.(5分)已知曲线左、右焦点分别为F1、F2,若双曲线的左支上有一点M到右焦点F2的距离为18,N是MF2的中点,O为坐标原点,则|NO|等于()A.3B.1C.2D.4【解答】解:∵曲线左、右焦点分别为F1、F2,左支上有一点M到右焦点F2的距离为18,N是MF2的中点,连接MF1,ON是△MF1F2的中位线,∴ON∥MF1,ON=MF1,∵由双曲线的定义知,MF2﹣MF1=2×5,∴MF1=8.ON=4,故选:D.二、填空题(本大题共4小题,共20分)13.(5分)命题:“若a≥b,则2a≥2b”的逆否命题为若2a<2b,则a<b.【解答】解:命题:“若a≥b,则2a≥2b”的逆否命题为:若2a<2b,则a<b,故答案为:若2a<2b,则a<b14.(5分)经过点P(4,﹣2)的抛物线的标准方程是y2=x或x2=﹣8y.【解答】解:设抛物线方程为y2=2px或x2=2py(p>0),∵抛物线过点(4,﹣2)∴2p×4=4或2p×(﹣2)=16∴2p=1或﹣8∴抛物线的标准方程为y2=x或x2=﹣8y故答案为:y2=x或x2=﹣8y.15.(5分)椭圆的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为20.【解答】解:∵a=5,由椭圆第一定义可知△PQF2的周长=4a.∴△PQF2的周长=20.,故答案为20.16.(5分)若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=﹣1.【解答】解:由题意得,y′=k+,∵在点(1,k)处的切线平行于x轴,∴k+1=0,得k=﹣1,故答案为:﹣1.三、解答题(本大题共6小题,共70.0分)17.(10分)命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2﹣4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.【解答】解:逆命题:已知a、b为实数,若a2﹣4b≥0,则x2+ax+b≤0有非空解集.否命题:已知a、b为实数,若x2+ax+b≤0没有非空解集,则a2﹣4b<0.逆否命题:已知a、b为实数,若a2﹣4b<0,则x2+ax+b≤0没有非空解集.原命题、逆命题、否命题、逆否命题均为真命题.18.(12分)已知,q:1﹣m≤x≤1+m,若非P是非q的必要不充分条件,求实数m的取值范围.【解答】解:由题意得p:﹣2≤x≤10.∵非p是非q的必要不充分条件,∴q是p的必要不充分条件,∴p⇒q,q推不出p,∴p不属于q∴∴m≥9;∴实数m的取值范围是{m|m≥9}.19.(12分)已知双曲线经过M(1,1),N(﹣2,5)两点,求双曲线的标准方程.【解答】解:设所求双曲线方程为mx2﹣ny2=1(mn>0),∵M(1,1),N(﹣2,5)两点在双曲线上,∴,解得:,∴双曲线方程是:x2﹣y2=1.20.(12分)已知函数f(x)=x3+x﹣16,求曲线y=f(x)在点(2,﹣6)处的切线的方程.【解答】解:函数f(x)=x3+x﹣16的导数为f′(x)=3x2+1,即有f(x)在点(2,﹣6)处的切线斜率为k=3×4+1=13,则曲线y=f(x)在点(2,﹣6)处的切线的方程为y+6=13(x﹣2),即为13x﹣y﹣32=0.21.(12分)已知函数f(x)=ax3+bx2,当x=1时,f(x)有极大值1.(Ⅰ)求a,b的值;(Ⅱ)求函数f(x)在区间上的最大值和最小值.【解答】解:(Ⅰ)∵f(x)=ax3+bx2,∴f′(x)=3ax2+2bx,由题意可知,解得a=﹣2,b=3;(Ⅱ)由(Ⅰ)知,f(x)=﹣2x3+3x2,∴f′(x)=﹣6ax2+6x=﹣6x(x﹣1),令f′(x)=﹣6ax2+6x=﹣6x(x﹣1)=0可解得,x=0或x=1;∵f(﹣)=1,f(0)=0,f(1)=1,f(2)=﹣4;故函数f(x)在区间上的最大值是1,最小值为﹣4.22.(12分)已知椭圆C:+=1(a>b>0)的离心率为,短轴一个端点到右焦点F的距离为2.(Ⅰ)求椭圆C的方程;(Ⅱ)设点P(,),过点F的直线l与椭圆C交于A,B两点,与直线x=m(m>a)交于M点,若直线PA,PM,PB的斜率成等差数列,求m的值.【解答】解:(Ⅰ)由题意可得e==,a==2,可得c=,b=1,即有椭圆的方程为+y2=1;(Ⅱ)由F(,0),设直线AB的方程为y=k(x﹣),代入椭圆方程x2+4y2=4,可得(1+4k2)x2﹣8k2x+12k2﹣4=0,设A(x1,y1),B(x2,y2),可得x1+x2=,x1x2=,设M(m,k(m﹣)),由直线PA,PM,PB的斜率成等差数列,可得2•=+=+即为2k ﹣=2k ﹣•,代入韦达定理,可得=,解得m=.赠送—高中数学知识点【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数.③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()u g x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减. (2)打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数,分别在[,0)a -、]a 上为减函数.(3)最大(小)值定义①一般地,设函数()y f x =的定义域为I ,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M ≤; (2)存在0x I ∈,使得0()f x M =.那么,我们称M 是函数()f x 的最大值,记作max ()f x M =.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法yxo②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.。
山西省临汾市曲沃中学2015-2016学年高二上学期期末化学试卷 含解析

2015—2016学年山西省临汾市曲沃中学高二(上)期末化学试卷一、单选题(本大题共16小题,共48分)1.下列设备工作时,将化学能转化为热能的是()A.太阳能生热器B.硅太阳能电池C.燃气灶D.锂离子电池2.某反应过程能量变化如图所示,下列说法正确的是()A.改变催化剂,可改变该反应的活化能B.该反应为放热反应,热效应等于E 1﹣E 2C.反应过程a 有催化剂参与D.有催化剂条件下,反应的活化能等于E 1+E 23.标准状态下,气态分子断开1mol化学键的焓变称为键焓.已知H﹣H、H﹣O和O═O 键的键焓△H分别为436kJ•mol ﹣1、463kJ•mol ﹣1和495kJ•mol ﹣1.下列热化学方程式正确的是()A.H 2O(g)═H 2(g)+O 2(g)△H=﹣485 kJ•mol ﹣1B.H 2O(g)═H 2(g)+O 2(g)△H=+485 kJ•mol ﹣1C.2H 2(g)+O 2(g)═2H 2O(g)△H=+485 kJ•mol ﹣1D.2H 2(g)+O 2(g)═2H 2O(g)△H=﹣485 kJ•mol ﹣14.根据下列热化学方程式(1)C(s)+O2(g)=CO2(g)△H1=﹣393。
5kJ/mol(2)H2(g)+O2(g)=H2O(l)△H2=﹣285.8kJ/mol(3)CH3COOH(l)+2O2(g)=2CO2(g)+2H2O(l)△H3=﹣870。
3kJ/mol可以计算出2C(s)+2H2(g)+O2(g)=CH3COOH(l)的反应热为()A.△H=244。
1kJ/mol B.△H=﹣488。
3kJ/molC.△H=﹣996.6kJ/mol D.△H=996.6kJ/mol5.下列事实中,能用勒沙特列原理来解释的是()A.由H 2(g)、I 2(g)、HI(g)组成的混合气体平衡体系加压后颜色加深B.久置的氯水变成了稀盐酸C.在FeCl 3溶液中加入铁粉防止氧化变质D.加入催化剂有利于SO 2与O 2反应制SO 36.将固体NH 4I置于密闭容器中,在某温度下发生下列反应:①NH 4I(s)⇌NH 3(g)+HI(g),②2HI(g)⇌H 2(g)+I 2(g),当反应达到平衡时,测得c(H 2)=0.5mol/L,c(HI)=4mol/L,则反应①的平衡常数为()A.4(mol/L) 2B.16(mol/L)2C.20(mol/L) 2D.25(mol/L) 27.下列有关化学反应速率的说法中,正确的是()A.100 mL 1 mol/L 的稀硫酸与锌反应时,加入适量的氯化钠溶液,生成氢气的速率不变B.合成氨的反应是一个放热反应,所以升高温度,反应速率减慢C.用铁片和稀硫酸反应制取氢气时,改用铁片和浓硫酸可以加快产生氢气的速率D.汽车尾气中的CO 和NO 可以缓慢反应生成N2和CO2,减小压强,反应速率减慢8.下列事实能说明亚硝酸是弱电解质的是()A.pH=4的亚硝酸溶液c(H+)=1×10﹣4mol/LB.用亚硝酸溶液作导电实验,灯泡很暗C.将Vml pH=4的亚硝酸稀释成pH=5的溶液,所需加入的水量大于10VmlD.10mL 1mol/L的亚硝酸恰好与10mL 1mol/L NaOH溶液完全中和9.在室温下,等体积的酸和碱溶液混合后pH一定小于7的是()A.pH=3的HNO 3与pH=11的KOH溶液B.pH=3的HNO 3与pH=11的氨水C.pH=3的H 2SO 4与pH=11的NaOH溶液D.pH=3的CH 3COOH与pH=11的Ba(OH)2溶液10.在0.1mol/L的CH3COOH溶液中,要促进醋酸电离,且氢离子浓度增大,应采取的措施是()A.升温 B.降温 C.加入NaOH溶液D.加入稀HCl11.下列有关AgCl沉淀的溶解平衡状态的说法中,正确的是()A.AgCl沉淀的生成和溶解不断进行,但速率相等B.AgCl难溶于水,溶液中没有Ag +和Cl ﹣C.升高温度,AgCl的溶解度不变D.向AgCl沉淀的溶解平衡体系中加入NaCl固体,AgCl的溶解度不变12.下列有关金属腐蚀与防护的说法正确的是()A.在酸性环境下,钢铁只能发生析氢腐蚀B.金属腐蚀的实质是金属失去电子被还原的过程C.轮船的船壳水线以下常装有一些锌块,这是利用了牺牲阳极的阴极保护法D.铜铁交接处,在潮湿的空气中直接发生反应:Fe﹣3e﹣═Fe3+,继而形成铁锈13.如图是锌、铜和稀硫酸形成的原电池,下列叙述不合理的是()A.溶液中H+向Zn电极移动B.外电路中电流方向为:Cu→ZnC.负极上的电极反应:Zn﹣2e﹣═Zn2+D.有1 mol电子流过导线,则Cu电极上产生的H2为11。
山西省临汾市曲沃中学2016届高三上学期10月段考数学试卷(文科) 含解析

2015—2016学年山西省临汾市曲沃中学高三(上)10月段考数学试卷(文科)一、选择题(每题5分,共60分)1.已知集合A={x|x2+x﹣2<0},B={x|x>0},则集合A∩B等于()A.{x|x>﹣2} B.{x|0<x<1}C.{x|x<1}D.{x|﹣2<x<1}2.已知命题p:∃n∈N,n+<4,则¬p为()A.∃n∈N,n+<4 B.∀n∈N,n+>4 C.∃n∈N,n+≤4 D.∀n∈N,n+≥4 3.已知函数f(x)是奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=()A.﹣2 B.0 C.1 D.24.已知α为第二象限角,且,则tan(π+α)的值是()A.B.C. D.5.已知a<b<0,则下列不等式一定成立的是()A.a2<ab B.|a|<|b|C.D.6.已知向量=(1,),=(3,m),若向量,的夹角为,则实数m=()A.2B.C.0 D.﹣7.已知等差数列{a n}中,a1+a5=6,则a1+a2+a3+a4+a5=()A.10B.5C.30 D.158.已知α为第二象限角,,则sin2α=()A.B.C.D.9.如果实数x、y满足条件,则2x+y的最大值为()A.1 B.C.2 D.310.如果函数f(x)=a x+b﹣1(a>0且a≠1)的图象经过第一、二、四象限,不经过第三象限,那么一定有()A.0<a<1且b>0 B.0<a<1且0<b<1 C.a>1且b<0 D.a>1且b>0 11.曲线y=2x3﹣3x+1在点(1,0)处的切线方程为()A.y=4x﹣5 B.y=﹣3x+2 C.y=﹣4x+4 D.y=3x﹣312.设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内任意一点,则等于()A.B.2C.3D.4二、填空题(每题5分,共20分)13.函数f(x)=的定义域是.14.复数z=,则|z|=.15.若正数x,y满足x+3y=5xy,则3x+4y的最小值是.16.如图是函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<)的图象,则其解析式是.三、解答题(共70分)17.曲线y=xln x在点(e,e)处的切线与直线x+ay=1垂直,求实数a的值.18.在平面直角坐标系中,A、B两点的坐标分别为(1,2),(3,8),向量=(x,3).(Ⅰ)若,求x的值;(Ⅱ)若,求x的值.19.在△ABC中,内角A、B、C的对边分别是a、b、c,且b2+c2﹣a2=bc.(1)求A;(2)若a=,cosB=,求b.20.已知函数f(x)=x3﹣3x(1)求函数f(x)的极值(2)求函数f(x)在[﹣3,]上的最大值和最小值.21.已知函数f(x)=2cosx(sinx+cosx),x∈R.(1)求函数f(x)的单调递增区间;(2)求函数f(x)在区间上的最大值和最小值.22.已知数列{a n}是首项为a1=,公比q=的等比数列,设b n+2=3log a n(n∈N*),数列{c n}满足c n=a n•b n(1)求证:{b n}是等差数列;(2)求数列{c n}的前n项和S n.2015-2016学年山西省临汾市曲沃中学高三(上)10月段考数学试卷(文科)参考答案与试题解析一、选择题(每题5分,共60分)1.已知集合A={x|x2+x﹣2<0},B={x|x>0},则集合A∩B等于()A.{x|x>﹣2} B.{x|0<x<1} C.{x|x<1}D.{x|﹣2<x<1}【考点】交集及其运算.【分析】求出A中不等式的解集确定出A,找出A与B的交集即可.【解答】解:由A中不等式变形得:(x﹣1)(x+2)<0,解得:﹣2<x<1,即A={x|﹣2<x<1},∵B={x|x>0},∴A∩B={x|0<x<1},故选:B.2.已知命题p:∃n∈N,n+<4,则¬p为()A.∃n∈N,n+<4 B.∀n∈N,n+>4 C.∃n∈N,n+≤4 D.∀n∈N,n+≥4【考点】命题的否定.【分析】根据特称命题的否定是全称命题进行判断即可.【解答】解:命题为特称命题,根据特称命题的否定是全称命题得命题的否定为:∀n∈N,n+≥4,故选:D.3.已知函数f(x)是奇函数,且当x>0时,f(x)=x2+,则f(﹣1)=()A.﹣2 B.0 C.1 D.2【考点】函数奇偶性的性质.【分析】由奇函数定义得,f(﹣1)=﹣f(1),根据x>0的解析式,求出f(1),从而得到f(﹣1).【解答】解:∵f(x)是定义在R上的奇函数,∴f(﹣x)=﹣f(x),f(﹣1)=﹣f(1),又当x>0时,f(x)=x2+,∴f(1)=12+1=2,∴f(﹣1)=﹣2,故选:A.4.已知α为第二象限角,且,则tan(π+α)的值是()A.B.C. D.【考点】诱导公式的作用;同角三角函数间的基本关系.【分析】由α为第二象限角,根据sinα的值,利用同角三角函数间的基本关系求出cosα的值,进而求出tanα的值,原式利用诱导公式化简,将tanα的值代入计算即可求出值.【解答】解:∵α为第二象限角,sinα=,∴cosα=﹣=﹣,∴tanα==﹣,则tan(π+α)=tanα=﹣.故选D5.已知a<b<0,则下列不等式一定成立的是()A.a2<ab B.|a|<|b|C.D.【考点】不等关系与不等式.【分析】令a=﹣2,b=﹣1,可得A、B、D都不正确,只有C正确,从而得出结论.【解答】解:令a=﹣2,b=﹣1,可得A、B、D都不正确,只有C正确,故选:C.6.已知向量=(1,),=(3,m),若向量,的夹角为,则实数m=()A.2B.C.0 D.﹣【考点】数量积表示两个向量的夹角.【分析】由条件利用两个向量的夹角公式、两个向量的数量积公式,求得m的值.【解答】解:由题意可得cos===,解得m=,故选:B.7.已知等差数列{a n}中,a1+a5=6,则a1+a2+a3+a4+a5=()A.10B.5C.30 D.15【考点】等差数列的性质.【分析】根据题意和等差数列的性质求出a3的值,代入所求的式子化简求值即可.【解答】解:由等差数列的性质得,a1+a5=a2+a4=2a3=6,则a3=3,∴a1+a2+a3+a4+a5=5a3=15,故选:D.8.已知α为第二象限角,,则sin2α=()A.B.C.D.【考点】二倍角的正弦;同角三角函数间的基本关系.【分析】直接利用同角三角函数的基本关系式,求出cosα,然后利用二倍角公式求解即可.【解答】解:因为α为第二象限角,,所以cosα=﹣=﹣.所以sin2α=2sinαcosα==.故选A.9.如果实数x、y满足条件,则2x+y的最大值为()A.1 B.C.2 D.3【考点】简单线性规划.【分析】由约束条件作出可行域,数形结合得到最优解,联立方程组求出最优解的坐标,代入目标函数得答案.【解答】解:由约束条件作出可行域如图,联立,解得B(1,1),令z=2x+y,得y=﹣2x+z,由图可知,当直线y=﹣2x+z过B时直线在y轴上的截距最大,z最大为2×1+1=3.故选:D.10.如果函数f(x)=a x+b﹣1(a>0且a≠1)的图象经过第一、二、四象限,不经过第三象限,那么一定有()A.0<a<1且b>0 B.0<a<1且0<b<1 C.a>1且b<0 D.a>1且b>0【考点】指数函数的图象变换.【分析】利用指数函数的图象判断a,b的取值范围.【解答】解:因为函数f(x)=a x+b﹣1(a>0且a≠1)的图象经过第一、二、四象限,不经过第三象限,则根据指数函数的图象可知,0<a<1,当x=0时,0<y<1,即0<1+b﹣1<1,解得0<b<1.故选B.11.曲线y=2x3﹣3x+1在点(1,0)处的切线方程为()A.y=4x﹣5 B.y=﹣3x+2 C.y=﹣4x+4 D.y=3x﹣3【考点】利用导数研究曲线上某点切线方程.【分析】求出函数的导数,求得切线的斜率,由点斜式方程,即可得到切线方程.【解答】解:y=2x3﹣3x+1的导数为y′=6x2﹣3,在点(1,0)处的切线斜率为k=3,则在点(1,0)处的切线方程为y﹣0=3(x﹣1),即为y=3x﹣3.故选D.12.设M为平行四边形ABCD对角线的交点,O为平行四边形ABCD所在平面内任意一点,则等于()A.B.2C.3D.4【考点】向量在几何中的应用.【分析】虑用特殊值法去做,因为O为任意一点,不妨把O看成是特殊点,再代入计算,结果满足哪一个选项,就选哪一个.【解答】解:∵O为任意一点,不妨把A点看成O点,则=,∵M是平行四边形ABCD的对角线的交点,∴=2=4故选:D.二、填空题(每题5分,共20分)13.函数f(x)=的定义域是(0,1].【考点】函数的定义域及其求法.【分析】根据函数成立的条件,即可求出函数的定义域.【解答】解:要使函数f(x)有意义,则,即0<2x﹣1≤1,则1<2x≤2,解得0<x≤1,故函数的定义域为(0,1],故答案为:(0,1].14.复数z=,则|z|=.【考点】复数代数形式的乘除运算;复数求模.【分析】利用复数的运算法则和模的计算公式即可得出.【解答】解:∵复数===1﹣i.∴|z|==.故答案为:.15.若正数x,y满足x+3y=5xy,则3x+4y的最小值是5.【考点】基本不等式.【分析】将方程变形,代入可得3x+4y=(3x+4y)()=×3,然后利用基本不等式即可求解.【解答】解:∵x+3y=5xy,x>0,y>0∴∴3x+4y=(3x+4y)()=×3=5当且仅当即x=2y=1时取等号故答案为:516.如图是函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|<)的图象,则其解析式是f (x)=3sin(2x+).【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【分析】由图知A=3,T=π,从而可求ω,再由ω+φ=2kπ+π(k∈Z)求得φ,即可得其解析式.【解答】解:由图知,A=3,T=﹣(﹣)=π,∴ω==2,又ω+φ=2kπ+π(k∈Z),即×2+φ=2kπ+π(k∈Z),∴φ=2kπ+(k∈Z),∴f(x)=3sin(2x+),故答案为:f(x)=3sin(2x+).三、解答题(共70分)17.曲线y=xln x在点(e,e)处的切线与直线x+ay=1垂直,求实数a的值.【考点】利用导数研究曲线上某点切线方程.【分析】利用导数求出曲线y=xlnx在点(e,e)处的切线斜率,根据切线与直线x+ay=1垂直的关系,求出a的值.【解答】解:∵y=xlnx,x>0;∴y′=lnx+1,当x=e时,y′=lne+1=2;∴曲线y=xlnx在点(e,e)处的切线斜率为k=2,又该切线与直线x+ay=1垂直,∴﹣•2=﹣1,解得a=2.故答案为:2.18.在平面直角坐标系中,A、B两点的坐标分别为(1,2),(3,8),向量=(x,3).(Ⅰ)若,求x的值;(Ⅱ)若,求x的值.【考点】数量积判断两个平面向量的垂直关系;平面向量共线(平行)的坐标表示.【分析】(Ⅰ)先求出的坐标,再根据,利用两个向量共线的性质得到2×3﹣6x=0,解方程求出x的值.(Ⅱ)根据两个向量的坐标及两个向量垂直的性质,得到2x+6×3=0,解方程求得x的值.【解答】解:(Ⅰ)依题意得,,…∵,∴2×3﹣6x=0…∴x=1.…(Ⅱ)∵,,∴2x+6×3=0…∴x=﹣9.…19.在△ABC中,内角A、B、C的对边分别是a、b、c,且b2+c2﹣a2=bc.(1)求A;(2)若a=,cosB=,求b.【考点】余弦定理;正弦定理.【分析】(1)由余弦定理求得角A的余弦值,结合特殊角的三角函数值和甲A的取值范围可以求得角A的大小;(2)利用(1)的结论和正弦定理进行解答.【解答】解:(1)由余弦定理有,∵0<A<π,∴;(2)由,有,∵,则.20.已知函数f(x)=x3﹣3x(1)求函数f(x)的极值(2)求函数f(x)在[﹣3,]上的最大值和最小值.【考点】函数在某点取得极值的条件;利用导数求闭区间上函数的最值.【分析】(1)求导函数,进而可得函数的单调区间,由此可求函数的极值;(2)求出端点函数值,与极值比较,可求函数在区间上的最值.【解答】解:(1)f'(x)=3(x+1)(x﹣1),令f’(x)>0,可得x<﹣1或x>1,∴(﹣∞,﹣1),(1,+∞)为函数f(x)的单调增区间令f’(x)<0,可得﹣1<x<1,∴(﹣1,1)为函数f(x)的单调减区间∴x=﹣1时,函数取得极大值为f(﹣1)=2;x=1时,函数取得极小值为f(1)=﹣2;(2)因为f(﹣3)=﹣18,f(﹣1)=2,f(1)=﹣2,f()=﹣,所以当x=﹣3时,f(x)min=﹣18,当x=﹣1时,f(x)max=221.已知函数f(x)=2cosx(sinx+cosx),x∈R.(1)求函数f(x)的单调递增区间;(2)求函数f(x)在区间上的最大值和最小值.【考点】两角和与差的正弦函数;正弦函数的单调性;三角函数的最值.【分析】(1)由三角函数恒等变换的应用化简解析式可得f(x)=,由,解得函数单调递增区间.(2)由可求,利用正弦函数的图象和性质即可得解.【解答】解:(1)f(x)=2cosx(sinx+cosx)=2sinxcosx+2cos2x=sin2x+cos2x+1=…由,解得所以函数f(x)单调递增区间为…(2)当时,所以当即时,函数f(x)取得最大值,当即时,函数f(x)取得最小值0…22.已知数列{a n}是首项为a1=,公比q=的等比数列,设b n+2=3log a n(n∈N*),数列{c n}满足c n=a n•b n(1)求证:{b n}是等差数列;(2)求数列{c n}的前n项和S n.【考点】等差关系的确定;数列的求和.【分析】(1)由题意知,,所以数列{b n}是首项b1=1,公差d=3的等差数列.(2)由题设条件知,,运用错位相减法可求出数列{c n}的前n项和S n.【解答】解:(1)由题意知,∵∴∴数列{b n}是首项b1=1,公差d=3的等差数列(2)由(1)知,∴∴,于是两式相减得=.∴2016年11月2日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015-2016学年某某省某某市曲沃中学高二(上)期末数学试卷(文科)一、选择题(本大题共12小题,共60分)1.全称命题:∀x∈R,x2>0的否定是()A.∀x∈R,x2≤0B.∃x∈R,x2>0C.∃x∈R,x2<0D.∃x∈R,x2≤02.下列说法正确的是()A.命题“p∨q”为真命题,则命题“p”和命题“q”均为真命题B.已知x∈R,则“x>1”是“x>2”的充分不必要条件C.命题“∃x∈R,x2﹣x>0”的否定是:“∀x∈R,x2﹣x≤0”D.命题“若am2<bm2,则a<b”的逆命题是真命题3.命题:“若x2<1,则﹣1<x<1”的逆否命题是()A.若x≥1或x≤﹣1,则x2≥1B.若﹣1<x<1,则x2<1C.若x>1或x<﹣1,则x2>1D.若x2≥1,则x≥1或x≤﹣14.“x>3”是“x2>9”的.()A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件5.如果方程表示焦点在y轴上的椭圆,则m的取值X围是()A.3<m<4B.C.D.6.椭圆x2+4y2=1的离心率为()A.B.C.D.7.在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px的通径为4,则P=()A.1B.4C.2D.88.若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能()A.B.C.D.9.曲线y=在点(﹣1,1)处的切线方程为()A.y=2x+3B.y=2x+1C.y=﹣2x﹣1D.y=﹣2x10.设f(x)=xlnx,若f′(x0)=2,则x0=()A.e2B.ln2C.D.e11.若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为()A.(0,0)B.C.D.(2,2)12.已知曲线左、右焦点分别为F1、F2,若双曲线的左支上有一点M到右焦点F2的距离为18,N是MF2的中点,O为坐标原点,则|NO|等于()A.3B.1C.2D.4二、填空题(本大题共4小题,共20分)13.命题:“若a≥b,则2a≥2b”的逆否命题为.14.经过点P(4,﹣2)的抛物线的标准方程是.15.椭圆的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为.16.若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=.三、解答题(本大题共6小题,共70.0分)17.命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2﹣4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.18.已知,q:1﹣m≤x≤1+m,若非P是非q的必要不充分条件,某某数m的取值X围.19.已知双曲线经过M(1,1),N(﹣2,5)两点,求双曲线的标准方程.20.已知函数f(x)=x3+x﹣16,求曲线y=f(x)在点(2,﹣6)处的切线的方程.21.已知函数f(x)=ax3+bx2,当x=1时,f(x)有极大值1.(Ⅰ)求a,b的值;(Ⅱ)求函数f(x)在区间上的最大值和最小值.22.已知椭圆C:+=1(a>b>0)的离心率为,短轴一个端点到右焦点F的距离为2.(Ⅰ)求椭圆C的方程;(Ⅱ)设点P(,),过点F的直线l与椭圆C交于A,B两点,与直线x=m(m>a)交于M点,若直线PA,PM,PB的斜率成等差数列,求m的值.2015-2016学年某某省某某市曲沃中学高二(上)期末数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,共60分)1.全称命题:∀x∈R,x2>0的否定是()A.∀x∈R,x2≤0B.∃x∈R,x2>0C.∃x∈R,x2<0D.∃x∈R,x2≤0【考点】命题的否定.【专题】阅读型.【分析】欲写出命题的否定,必须同时改变两个地方:①:“∀”;②:“>”即可,据此分析选项可得答案.【解答】解:命题:∀x∈R,x2>0的否定是:∃x∈R,x2≤0.故选D.【点评】这类问题的常见错误是没有把全称量词改为存在量词,或者对于“>”的否定用“<”了.这里就有注意量词的否定形式.如“都是”的否定是“不都是”,而不是“都不是”.特称命题的否定是全称命题,“存在”对应“任意”.2.下列说法正确的是()A.命题“p∨q”为真命题,则命题“p”和命题“q”均为真命题B.已知x∈R,则“x>1”是“x>2”的充分不必要条件C.命题“∃x∈R,x2﹣x>0”的否定是:“∀x∈R,x2﹣x≤0”D.命题“若am2<bm2,则a<b”的逆命题是真命题【考点】四种命题.【专题】对应思想;综合法;简易逻辑.【分析】根据复合命题判断A,根据结合的包含关系判断B,根据命题的否定判断C,根据不等式的性质判断D,从而得到答案.【解答】解:命题“p∨q”为真命题,则命题“p”和命题“q”至少有1个为真命题,故A 错误;已知x∈R,则“x>1”是“x>2”的必要不充分条件,故B错误;命题“∃x∈R,x2﹣x>0”的否定是:“∀x∈R,x2﹣x≤0”,故C正确;命题“若am2<bm2,则a<b”的逆命题是假命题,故D错误;故选:C.【点评】本题考查了复合命题的判断,考查集合的包含关系,考查不等式的性质以及集合的包含关系,是一道基础题.3.命题:“若x2<1,则﹣1<x<1”的逆否命题是()A.若x≥1或x≤﹣1,则x2≥1B.若﹣1<x<1,则x2<1C.若x>1或x<﹣1,则x2>1D.若x2≥1,则x≥1或x≤﹣1【考点】四种命题.【专题】对应思想;综合法;简易逻辑.【分析】先否定原命题的题设做结论,再否定原命题的结论做题设,就得到原命题的逆否命题.【解答】解:∵“x2<1”的否定为“x2≥1”.“﹣1<x<1”的否定是“x≤﹣1或x≥1”.∴命题“若x2<1,则﹣1<x<1”的逆否命题是:“若x≥1或x≤﹣1,则x2≥1”.故选:A.【点评】本题考查四种命题的相互转化,解题时要认真审题,注意.“﹣1<x<1”的否定是“x≤﹣1或x≥1”.4.“x>3”是“x2>9”的.()A.必要不充分条件B.充分不必要条件C.充分必要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【专题】简易逻辑.【分析】根据充分条件和必要条件的定义结合不等式的解法,进行判断即可.【解答】解:由x2>9得x>3或x<﹣3,则“x>3”是“x2>9”的充分不必要条件,故选:B【点评】本题主要考查充分条件和必要条件的应用,根据不等式的性质结合充分条件和必要条件的定义是解决本题的关键.5.如果方程表示焦点在y轴上的椭圆,则m的取值X围是()A.3<m<4B.C.D.【考点】椭圆的定义.【专题】计算题.【分析】进而根据焦点在y轴推断出4﹣m>0,m﹣3>0并且m﹣3>4﹣m,求得m的X 围.【解答】解:由题意可得:方程表示焦点在y轴上的椭圆,所以4﹣m>0,m﹣3>0并且m﹣3>4﹣m,解得:.故选D.【点评】本题主要考查了椭圆的标准方程,解题时注意看焦点在x轴还是在y轴.6.椭圆x2+4y2=1的离心率为()A.B.C.D.【考点】椭圆的简单性质.【专题】综合题.【分析】把椭圆的方程化为标准方程后,找出a与b的值,然后根据a2=b2+c2求出c的值,利用离心率公式e=,把a与c的值代入即可求出值.【解答】解:把椭圆方程化为标准方程得:x2+=1,得到a=1,b=,则c==,所以椭圆的离心率e==.故选A【点评】此题考查学生掌握椭圆的离心率的求法,灵活运用椭圆的简单性质化简求值,是一道综合题.7.在圆锥曲线中,我们把过焦点最短的弦称为通径,那么抛物线y2=2px的通径为4,则P=()A.1B.4C.2D.8【考点】抛物线的简单性质.【专题】计算题;方程思想;综合法;圆锥曲线的定义、性质与方程.【分析】利用么抛物线y2=2px的通径为4,即可得出结论.【解答】解:由题意,2p=4,∴p=2.故选:C.【点评】本题考查抛物线的简单的性质,考查抛物线的弦长,是一个圆锥曲线的基础题.8.若函数y=f(x)的导函数y=f′(x)的图象如图所示,则y=f(x)的图象可能()A.B.C.D.【考点】利用导数研究函数的单调性.【专题】数形结合;转化思想;转化法;导数的概念及应用.【分析】根据函数单调性和导数之间的关系判断函数的单调性即可.【解答】解:由y=f′(x)可得y=f′(x)有两个零点,x1,x2,且0<x1<x2,当x<x1,或x>x2时,f′(x)<0,即函数为减函数,当x1<x<x2,时,f′(x)>0,函数为增函数,即当x=x1,函数取得极小值,当x=x2,函数取得极大值,故选:C【点评】本题主要考查函数图象的判断,结合函数单调性,极值和导数之间的关系是解决本题的关键.9.曲线y=在点(﹣1,1)处的切线方程为()A.y=2x+3B.y=2x+1C.y=﹣2x﹣1D.y=﹣2x【考点】利用导数研究曲线上某点切线方程.【专题】计算题;导数的概念及应用.【分析】根据导数的几何意义求出函数在x=﹣1处的导数,从而得到切线的斜率,再利用点斜式方程写出切线方程即可.【解答】解:y′==∴y′|x=﹣1=2而切点的坐标为(﹣1,1)∴曲线y=在点(﹣1,1)处的切线方程为y=2x+3.故选:A.【点评】本题主要考查了利用导数研究曲线上某点切线方程,考查运算求解能力,属于基础题.10.设f(x)=xlnx,若f′(x0)=2,则x0=()A.e2B.ln2C.D.e【考点】导数的运算;函数的零点.【专题】计算题;导数的概念及应用.【分析】由题意求导f′(x)=lnx+1,从而得lnx0+1=2;从而解得.【解答】解:∵f′(x)=lnx+1;故f′(x0)=2可化为lnx0+1=2;故x0=e;故选D.【点评】本题考查了导数的求法及应用,属于基础题.11.若点A的坐标为(3,2),F是抛物线y2=2x的焦点,点M在抛物线上移动时,使|MF|+|MA|取得最小值的M的坐标为()A.(0,0)B.C.D.(2,2)【考点】抛物线的定义.【专题】计算题.【分析】求出焦点坐标和准线方程,把|MF|+|MA|转化为|MA|+|PM|,利用当P、A、M三点共线时,|MA|+|PM|取得最小值,把y=2代入抛物线y2=2x 解得x值,即得M的坐标.【解答】解:由题意得F(,0),准线方程为x=﹣,设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3﹣(﹣)=.把y=2代入抛物线y2=2x 得x=2,故点M的坐标是(2,2),故选D.【点评】本题考查抛物线的定义和性质得应用,解答的关键利用是抛物线定义,体现了转化的数学思想.12.已知曲线左、右焦点分别为F1、F2,若双曲线的左支上有一点M到右焦点F2的距离为18,N是MF2的中点,O为坐标原点,则|NO|等于()A.3B.1C.2D.4【考点】双曲线的简单性质.【专题】计算题.【分析】利用ON是△MF1F2的中位线,ON=MF1,再由双曲线的定义求出MF1,进而得到ON的值.【解答】解:∵曲线左、右焦点分别为F1、F2,左支上有一点M到右焦点F2的距离为18,N是MF2的中点,连接MF1,ON是△MF1F2的中位线,∴ON∥MF1,ON=MF1,∵由双曲线的定义知,MF2﹣MF1=2×5,∴MF1=8.ON=4,故答案选D.【点评】本题考查双曲线的定义和性质.二、填空题(本大题共4小题,共20分)13.命题:“若a≥b,则2a≥2b”的逆否命题为若2a<2b,则a<b .【考点】四种命题.【专题】整体思想;定义法;简易逻辑.【分析】根据逆否命题的定义进行求解即可.【解答】解:命题:“若a≥b,则2a≥2b”的逆否命题为:若2a<2b,则a<b,故答案为:若2a<2b,则a<b【点评】本题主要考查四种命题的关系,根据逆否命题的定义是解决本题的关键.比较基础.14.经过点P(4,﹣2)的抛物线的标准方程是y2=x或x2=﹣8y .【考点】抛物线的标准方程.【专题】计算题.【分析】先设处抛物线的标准方程,把点P坐标代入,即可求得p,则抛物线方程可得.【解答】解:设抛物线方程为y2=2px或x2=2py(p>0),∵抛物线过点(4,﹣2)∴2p×4=4或2p×(﹣2)=16∴2p=1或﹣8∴抛物线的标准方程为y2=x或x2=﹣8y故答案为:y2=x或x2=﹣8y.【点评】本题主要考查了抛物线的简单性质.注意讨论焦点在x轴和y轴两种情况.15.椭圆的两焦点为F1,F2,一直线过F1交椭圆于P、Q,则△PQF2的周长为20 .【考点】椭圆的应用.【专题】计算题.【分析】由椭圆第一定义可知△PQF2的周长=4a,由此能够求出△PQF2的周长.【解答】解:∵a=5,由椭圆第一定义可知△PQF2的周长=4a.∴△PQF2的周长=20.,故答案为20.【点评】作出草图,结合图形求解事半功倍.16.若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=﹣1 .【考点】利用导数研究曲线上某点切线方程.【专题】导数的概念及应用.【分析】先求出函数的导数,再由题意知在1处的导数值为0,列出方程求出k的值.【解答】解:由题意得,y′=k+,∵在点(1,k)处的切线平行于x轴,∴k+1=0,得k=﹣1,故答案为:﹣1.【点评】本题考查了函数导数的几何意义应用,难度不大.三、解答题(本大题共6小题,共70.0分)17.命题:已知a、b为实数,若x2+ax+b≤0有非空解集,则a2﹣4b≥0,写出该命题的逆命题、否命题、逆否命题,并判断这些命题的真假.【考点】复合命题的真假.【分析】原命题中,a、b为实数是前提,条件是x2+ax+b≤0有非空解集(即不等式有解),结论是a2﹣4b≥0,由四种命题的关系可得出其他三种命题.【解答】解:逆命题:已知a、b为实数,若a2﹣4b≥0,则x2+ax+b≤0有非空解集.否命题:已知a、b为实数,若x2+ax+b≤0没有非空解集,则a2﹣4b<0.逆否命题:已知a、b为实数,若a2﹣4b<0,则x2+ax+b≤0没有非空解集.原命题、逆命题、否命题、逆否命题均为真命题.【点评】本题以复合命题的真假为载体考查二次方程的解的问题.熟练掌握四种命题的定义,复合命题的真值表,特称命题的否定的方法是解答本题的关键.18.已知,q:1﹣m≤x≤1+m,若非P是非q的必要不充分条件,某某数m的取值X围.【考点】必要条件、充分条件与充要条件的判断;逻辑联结词“非”.【专题】计算题.【分析】由题意得p:﹣2≤x≤10,.由此可知实数m的取值X围是{m|m≥9}.【解答】解:由题意得p:﹣2≤x≤10.∵非p是非q的必要不充分条件,∴q是p的必要不充分条件,∴p⇒q,q推不出p,∴p不属于q∴∴m≥9;∴实数m的取值X围是{m|m≥9}.【点评】本题考查不等式的基本性质和应用,解题时要认真审题,仔细解答.19.已知双曲线经过M(1,1),N(﹣2,5)两点,求双曲线的标准方程.【考点】双曲线的简单性质.【专题】方程思想;综合法;圆锥曲线的定义、性质与方程.【分析】双曲线的焦点不知在哪个轴上时,设双曲线方程为mx2﹣ny2=1(mn>0),结合点M,N在双曲线上,可得关于m与n的方程组,求出m与n的值即可得到答案.【解答】解:设所求双曲线方程为mx2﹣ny2=1(mn>0),∵M(1,1),N(﹣2,5)两点在双曲线上,∴,解得:,∴双曲线方程是:x2﹣y2=1.【点评】本题主要考查用待定系数法求双曲线的标准方程的方法,解题的关键将所求双曲线设成mx2﹣ny2=1(mn>0),属于基础题.20.已知函数f(x)=x3+x﹣16,求曲线y=f(x)在点(2,﹣6)处的切线的方程.【考点】利用导数研究曲线上某点切线方程.【专题】计算题;导数的概念及应用;直线与圆.【分析】求出函数的导数,求得切线的斜率,由点斜式方程即可得到切线方程.【解答】解:函数f(x)=x3+x﹣16的导数为f′(x)=3x2+1,即有f(x)在点(2,﹣6)处的切线斜率为k=3×4+1=13,则曲线y=f(x)在点(2,﹣6)处的切线的方程为y+6=13(x﹣2),即为13x﹣y﹣32=0.【点评】本题考查导数的运用:求切线方程,主要考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,正确求导和运用点斜式方程是解题的关键.21.已知函数f(x)=ax3+bx2,当x=1时,f(x)有极大值1.(Ⅰ)求a,b的值;(Ⅱ)求函数f(x)在区间上的最大值和最小值.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的极值.【专题】计算题;导数的综合应用.【分析】(Ⅰ)求导,由题意可知,从而求a,b的值;(Ⅱ)代入a,b的值,求极值处的极值及端点值,从而求函数f(x)在区间上的最大值和最小值.【解答】解:(Ⅰ)∵f(x)=ax3+bx2,∴f′(x)=3ax2+2bx,由题意可知,解得a=﹣2,b=3;(Ⅱ)由(Ⅰ)知,f(x)=﹣2x3+3x2,∴f′(x)=﹣6ax2+6x=﹣6x(x﹣1),令f′(x)=﹣6ax2+6x=﹣6x(x﹣1)=0可解得,x=0或x=1;∵f(﹣)=1,f(0)=0,f(1)=1,f(2)=﹣4;故函数f(x)在区间上的最大值是1,最小值为﹣4.【点评】本题考查了导数的综合应用及闭区间上的最值,属于中档题.22.已知椭圆C:+=1(a>b>0)的离心率为,短轴一个端点到右焦点F的距离为2.(Ⅰ)求椭圆C的方程;(Ⅱ)设点P(,),过点F的直线l与椭圆C交于A,B两点,与直线x=m(m>a)交于M点,若直线PA,PM,PB的斜率成等差数列,求m的值.【考点】椭圆的简单性质.【专题】综合题;方程思想;分析法;等差数列与等比数列;圆锥曲线的定义、性质与方程.【分析】(Ⅰ)运用离心率公式和a,b,c的关系,解得a=2,b=1,即可得到所求椭圆方程;(Ⅱ)由F(,0),设直线AB的方程为y=k(x﹣),代入椭圆方程,运用韦达定理,以及等差数列的中项性质,和直线的斜率公式,计算化简即可得到所求值.【解答】解:(Ⅰ)由题意可得e==,a==2,可得c=,b=1,即有椭圆的方程为+y2=1;(Ⅱ)由F(,0),设直线AB的方程为y=k(x﹣),代入椭圆方程x2+4y2=4,可得(1+4k2)x2﹣8k2x+12k2﹣4=0,设A(x1,y1),B(x2,y2),可得x1+x2=,x1x2=,设M(m,k(m﹣)),由直线PA,PM,PB的斜率成等差数列,可得2=+=+即为2k﹣=2k﹣,代入韦达定理,可得=。
