单图三维重构方法
三维重建综述

三维重建综述
三维重建是利用二维图像重构出三维模型的一种技术,也称三维照相术,是运
动机器人、虚拟现实等技术的重要基础。
三维重建开发技术可以利用机器视觉技术、激光扫描技术以及计算机处理技术之间的结合来计算出单一或多个图像绘制出三维空间中对象的图形,如图像等。
机器视觉技术在三维重建中的应用非常普遍,其主要原理是基于摄像机实时拍
摄到的图像和知识信息之间的结合,根据图像的特征与物体形状之间的关系来构建三维空间模型。
激光扫描技术是三维重建中应用得比较广泛的技术之一,原理是通过精确测量
激光点来重建物体的三维模型,它的优势是能更准确的模拟出物体的实际形状,而且扫描比较快,效率高。
计算机处理技术是三维重建中的重要组成部分,一般是利用数字图像编辑技术
来构建三维模型,以软件运算和处理技术模拟出三维模型,再把这些数据通过算法来彻底处理和改善。
未来,随着技术发展,三维重建技术会朝着更为精准,更为高效的方向发展,
其在工业生产、虚拟现实、机器人研究以及医疗应用等方面的应用也会更加广泛,可以给人类带来更多的便利。
三维CAD模型重构方法、过程及实例

特征的定义及表达
几何特征是几何造型的关键,他们对控制几何形体的形状 有极为重要作用,同时几何特征之间还具有确定的几何约束 关系。
因此,在产品模型的重构过程中,一个重要的目标就是 还原这些特征以及他们之间的约束,得到一个优化的CAD模型, 使孤立的曲面片转化成一个整体的几何模型。
三维CAD模型重构方法、 过程和实例
输出匹配的 文件格式
自动将点云 数据转换为
多边形
Geomagic Studio
主要功能
快速减少 多边形数目
(Decimate)
曲面分析 (公差分析等)
把多边形 转换为曲面
三维CAD模型重构方法、 过程和实例
Geomagic Studio软件工作流程如下图所示:
这和多数工业产品的设计意图相符合。可有效解决产品 的装配对齐、造型的对称等问题,进而减小误差,提高产品 质量。
三维CAD模型重构方法、 过程和实例
约束的定义、分类及表达
逆向工程中的曲面重构不是对数据的简单拟合,而是 要满足几何约束下的重构。
三维CAD模型重构方法、 过程和实例
Imageware 软件
• 应用曲线拟合造型的典型商用软件 • 广泛应用于汽车、航天、消费家电、模具、计算机零部
件等设计与制造领域。 • 软件包括以下几个模块:基础模块、点处理模块、曲线、
曲面模块、多边形造型模块、检验模块和评估模块。
三维CAD模型重构方法、 过程和实例
曲
面
模
模
型
型
评
重
价
建
实 体 模 型
下 游 应 用
三维CAD模型重构方法、 过程和实例
➢ 应用这种三边域曲面重构方法的典型商用软件是 Geomagic Studio软件。该软件可轻易地从扫描所得的 点云数据创建出完美的多边形模型和网格,并可自动 转换为 NURBS 曲面。
三维重构
三维重构三维重构(一)(2007-08-29 11:00:26)标签:知识/探索(一)空间的三维重构问题按照不同的实际情况来看算法的种类非常多,但核心的思想还是利用三角形来覆盖待重构区域的表面。
传统的算法将“覆盖”的思想体现的并不是非常形象,通常只是将待重构区域利用各种方法撒一些点,然后利用三角形来连接这些节点。
如:假如已知某物体的空间的三个剖面,那么如何重建这个物体呢?第一步:将每个剖面的轮廓线提取出来。
第二步:从每条轮廓线中取出拐点和端点。
第三步:利用这些点和三角形来实现物体的重构。
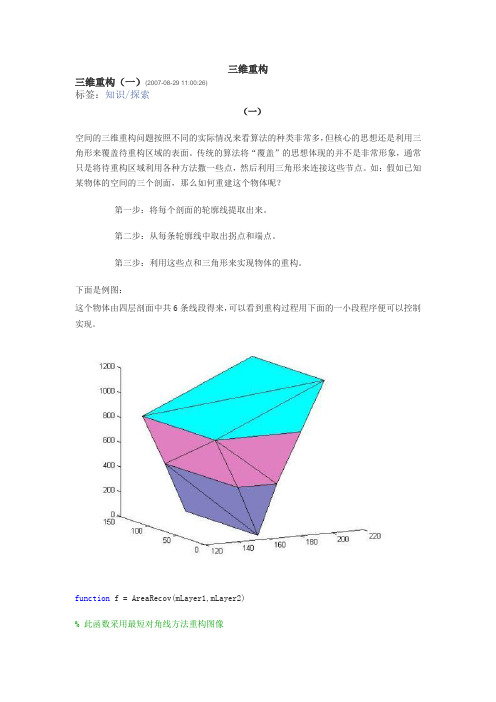
下面是例图:这个物体由四层剖面中共6条线段得来,可以看到重构过程用下面的一小段程序便可以控制实现。
function f = AreaRecov(mLayer1,mLayer2)% 此函数采用最短对角线方法重构图像% 输入:% mLayer1 第一层的点坐标集 n*3% mLayer2 第二层的点坐标集 m*3% 输出:% f 输出的三角形顶点集 max(n,m)*3*3 max(n,m)*三个顶点*三维坐标% 注: 原对角线的重构方法只适用于两层点数相同的情况,% 现在的算法对原算法进行了一些改动。
[Len1,vTemp2,vTemp3] = size(mLayer1) ;[Len2,vTemp2,vTemp3] = size(mLayer2) ;mMaxNum = max([Len1,Len2]) ;f = zeros(mMaxNum,3,3) ;if mMaxNum == Len1vLayer1 = mLayer1 ;vLayer2 = mLayer2 ;elsevLayer1 = mLayer2 ;vLayer2 = mLayer1 ;Len2 = Len1 ; % 用Len2存储小长度endfor counter = 1:mMaxNum-1f(counter,1,:) = vLayer1(counter,:) ;[f(counter,2,:),mIndexTemp] = NearPoint(vLayer1(counter,:),vLayer2) ;% 寻找三角形的第三个顶点if mIndexTemp<=Len2-1 %如果点少的一层还有剩余点vTemp2 = DistanJudg( vLayer1(counter,1:2),vLayer1(counter+1,1:2),...vLayer2(mIndexTemp,1:2),vLayer2(mIndexTemp+1,1:2) ) ;f(counter,3,:) = vLayer2(mIndexTemp+1,:) ;if vTemp2 == -1f(counter,3,:) = vLayer1(counter+1,:) ;endelse% 如果点少的一层没有剩余点,则直接取临点作为第三个顶点f(counter,3,:) = vLayer1(counter+1,:) ;endend对于这个简单的例子来说实现的很完美,但实际中的问题有如下几点:1,寻找物体表层的点时会有很复杂的判断问题,即选择哪几个点作为小三角形的定点来连接。
切片式三维重构的原理

切片式三维重构的原理三维重构是计算机视觉、图像处理和计算机图形学领域中的一个重要研究方向。
它涉及到从一系列二维图像或点云数据中重建出三维场景的几何结构和纹理信息。
其中,切片式三维重构是一种常见的方法,其原理基于对三维场景的不同切片进行分析和重建。
切片式三维重构的核心思想是将三维场景从不同视角拍摄得到的二维图像或点云数据,按照一定顺序进行切片,然后分析每个切片并根据其特征进行三维重建。
具体而言,切片式三维重构包括以下几个步骤:第一步,图像获取和预处理。
通过摄像机或激光扫描器等设备获取一系列二维图像或点云数据,并对其进行去噪、纠偏等预处理工作,以提高后续重建的准确性和稳定性。
第二步,相机标定和对齐。
对于二维图像,需要进行相机标定以确定其内外参数,然后对齐各个视角的图像,使其在同一个坐标系统下进行重建。
对于点云数据,需要进行点云对齐,以确保各个切片对应的点云在同一坐标系统下进行处理。
第三步,切片选择和分析。
在这个步骤中,根据需求选择适当数量和精度的切片,并对每个切片进行分析和处理。
具体分析方法包括特征提取、图像配准、点云配准等。
通过分析每个切片的特征和关系,可以得到场景的几何结构和纹理信息。
第四步,三维重建和表面重构。
根据切片的分析结果,可以进行三维重建和表面重构工作。
其中,三维重建可以根据切片中的特征点或处理后的点云数据,通过三角剖分、体素填充等方法,生成三维场景的几何结构。
表面重构则可以通过融合切片的纹理信息,生成真实场景的表面模型。
第五步,优化和修正。
在得到初步的三维重建结果后,可以进行优化和修正工作,以提高重建的精度和完整性。
优化方法包括图像拼接、点云融合、去除误差等。
对于表面模型,还可以进行网格重构、去噪等操作,以获得最终的三维重建结果。
切片式三维重构的原理非常灵活,适用于各种不同场景的三维重建需求。
它可以克服单一视角无法获取完整信息的局限性,有效提高重建的准确性和稳定性。
同时,切片式三维重构还可以通过调整切片的数量和精度,灵活平衡重建的效率和精度。
TEM三维重构技术ppt课件

实例2:表征材料显微组织之间的相对位置
在纳米管中填充金属颗粒相对改 善纳米管的性能有明显的作用。但 金属颗粒是否被真正填充到纳米管 中,还是附着在纳米管的表面,从 TEM 的形貌观察中无法确认。利用 三维重构,可以从不同角度观察金 属颗粒的位置,确定是否真正完成 了在纳米管中的填充。
通过合成的录像( movie) 可以明 显的判定金属颗粒包裹在碳纳米管 内部。
样品为具有孔道结构、直径约 为150 nm 的二氧化硅球,经三 维重构后Amira 软件模拟出二氧 化硅球内部的孔道信息,如图7e, 二氧化硅球是空心的,孔道分布 呈现发散状,但不规则
TEM 模式下分别倾转( a) - 62°,( b) 0°,( c) +60°Xplore 软件采集的二维图像6 ;d: 重构得到的三维模型; e: 二氧化硅球内部孔道示意图Bar = 100 nm
1
精选ppt2021最新
TEM 三维重构的基本原理示意图
2
精选ppt2021最新
TEM 三维重构操作步骤
3
精选ppt2021最新
在纳米材料领域应用实例
实例1:表征材料的立体空间形貌- 纳米球包裹纳米纤维
当合成纳米球并包裹纳米纤维 时,无法从TEM 的二维图片直观 地判断纳米纤维是否均匀的分布 在纳米球上,利用三维重构可以 从立体空间形貌上判断合成后材 料的均匀程度;
任何实空间的三维物体沿电子束方向投影的傅立叶变换是该物体所对应的傅立叶空间中通过中心且垂直于投影方向的一个截面换言之只要收集样品在不同方向的投影或同一样品在不同角度的投影对每张投影图进行傅立叶变换按照投影方向填充到三维傅里叶空间对应的切面再进行反傅立叶变换就可得到实空间的三维结构
精选ppt2021最新
由单幅图像重构三轴试样三维变形

由单 幅 图像 重 构三 轴试 样 三维 变形
・ 5・ 7
由单 幅 图像 重 构 三 轴 试 样 三 维 变 形
刘 永禄 ,陈 志 军 苏 轼 鹏 邵 龙 潭 , ,
(1 .海 大连舰艇学 院 事海洋系 , 辽宁 大连 16 1 ; .大连市气象局 , 10 8 2 辽宁 大连
1Hale Waihona Puke 1 ) 0 8 1a n w D e o tuci n me h d b s d o i g e i g — in — tu t r t d i o o e Be a e t e p i t e 3 r c nsr to t o a e n sn l ma e sg s sr c u e meho spr p s d. c us h o n s
Absr c : mi tp o lmso he t r e di nso a a u e n n s i s mp e r— x a eo main t s, t a t Ai ng a r b e ft h e — me in lme s r me ti ol a l stia ild f r to e t
Blender中的模型修复和重构教程

Blender中的模型修复和重构教程Blender是一款强大的三维建模软件,广泛用于游戏开发、动画制作和设计等领域。
然而,在使用Blender进行建模时,我们经常会遇到一些模型不完整或破损的情况。
本教程将向大家介绍一些在Blender中修复和重构模型的技巧和方法。
1. 寻找模型问题在进行模型修复之前,我们首先需要找出模型存在的问题。
常见的问题包括缺失的面、裂缝、非封闭的边和顶点错误等。
在Blender中,我们可以使用编辑模式下的选择工具来检查模型细节,并使用渲染模式下的快速预览来查看模型的完整性。
2. 移除不需要的几何体修复模型的第一步是移除不需要的几何体。
这些几何体可能是重叠的、重复的或者与整体模型不相连的。
使用Blender的选择工具,选中这些几何体并按下Delete键将其删除。
3. 修复缺失的面缺失的面是一个常见的问题,它会导致模型出现空洞或不真实的外观。
在Blender中,我们可以使用填充工具来修复这些面。
在编辑模式下,选中缺失的边并按下F键,Blender会自动创建一个新的面。
4. 修复裂缝裂缝是模型中常见的问题,它会导致模型的表面不平滑或者无法完全封闭。
在Blender中,我们可以使用修补工具来修复这些裂缝。
在编辑模式下,选中裂缝周围的边并按下Ctrl + E,在弹出的菜单中选择“桥接边”或“连接边”选项,Blender会自动填补裂缝。
5. 修复非封闭的边非封闭的边会导致模型无法完全封闭,使其无法进行后续的操作或者导出。
在Blender中,我们可以使用合并工具来修复这些非封闭的边。
在编辑模式下,选中非封闭的边并按下Ctrl + M,在弹出的菜单中选择“合并边”选项,Blender会自动将这些非封闭的边合并起来。
6. 修复顶点错误顶点错误是模型中另一个常见的问题,它会导致模型的形状不正确或者无法进行平滑处理。
在Blender中,我们可以使用顶点合并工具来修复这些顶点错误。
在编辑模式下,选中需要合并的顶点并按下Alt + M,在弹出的菜单中选择合适的选项,Blender会自动将这些顶点合并起来。
三维重建过程ppt课件

稠密点云的网格化
通过上面的步骤可以得到基于图像的三维点云,但要对空间物体的 表面信息进行重构,需要对三维点云进行三角剖分。
三角剖分的方法:
(1)平面投影法方法
采用投影映射的方法,将三维点云投影到二维平面上,接着对投影后的 二维点进行三角剖分,然后将二维剖分关系传递给三维点云的三角剖分。。
(2)直接剖分法方法 三角剖分所给点集R,保留原始点云的拓扑结构,实际上是
特征点匹配方法:
(1)NCC特征匹配
归一化互相关(normalizes cross correlation)方法的优点是它可以抵抗 全局的亮度变化和对比度变化,并且速度快。
缺点是:(a)不抗图像缩放。(b)不抗大的视角的变化。(c)当初始匹配点的 错误匹配率高于 40%的时候以上两种方法失效。
(2)SIFT特征匹配
相机标定
相机标定就是求出相机的内部参数,最终得到内参数矩阵K。
相机标定的方法:
(1)Tsai的两步标定方法
其主要思想是首先利用透视变换原理线性求解出一些相机参数,接着把 求得的这些参数作为非线性优化算法的初始值,只考虑相机的径向畸变,通 过优化算法求解其余参数,从而相对于线性标定方法提高了标定的精度。
主要思想是用特征点的 16×16 的邻域计算该邻域的每个点的梯度。然 后将 16×16 的区域划分为 4×4 的小区域,每个小区域的点向 8 个方向投影。 这样总共可以得到 4×4×8=128 维的特征向量描述符。特征点的匹配首先需 要将特征点旋转到它的主方向上,然后计算匹配点的 128 维特征描述符的欧 式距离。距离最小的匹配点为正确匹配点。
椒盐噪声过滤算法:GA-BP神经网络噪声检测的自适应滤波算法。 遗传算法:Genetic Algorithm GA 反向传播神经网络:Back BP BP
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第36卷 第19期
VoL36
No.19
·图形图像处理·
计算机工程
Computer Engineering 文tttllqt 1000----3428(2010)19--0227---02
文献标识码;A
2010年10月
October 2010
中围分类号t TP391.41
单图三维重构方法
吴教,方向虑,董皓远 (上海交通大学图像通信与信息处理研究所,上海200240)
[Key words]multi-viewpoim image;distortion;depth information;3D reconstruction
1概述 图像本质上是一种三维场景的二维投射,其中空间点到
平面像素的映射关系是由成像系统的几何特性决定的。最常 见的成像系统是基于透视投射的传统相机,在这样的系统中, 所有的入射光线汇聚于一点(焦点),然后投射到成像平面上。 由于人眼习惯于透视场景…,透视成像系统所获得的图像通 常被认为是未失真的,任何非透视的图像都被看作是失真的 (或扭曲的)。透视成像系统虽然不会引入失真,但由于物理 焦距的限制,其视野范围相当有限。
万方数据
全已知,图像也不可能脱离深度信息而转化成透视视角,即 显现出失真,这样的失真称为焦散失真【4J。
如上所述,在深度信息未知的情况下,单幅多视点图像 的焦散失真是无法消除的。这种失真的程度恰恰是由物体所 在位置的深度决定的。本文通过提取多视点单图中所包含的 场景深度信息,实现对已知函数形式的_:般空间曲线的三维 几何结构重建,如直线、圆、二次曲线。
定曲线C等价于确定C所在的平面:
17:血+缈+Q+D=0
(2)
平面曲线的重构方法,本节推导一种线性方案直接由单幅多 视点图像计算出其中直线的空间三维位置。简单起见,假定 成像系统是中心对称的。在这样的系统中,视点可以被认为 处于系统的对称轴上,称为视线轴,如图2所示。空间直线£ 由一中心对称系统成像,可以将视线束看作是从视线轴出发 的,这为直线的线性三维重构提供了简便的数学论证方法。
圈1室同曲铸
如果是光束共面,则交任意平面于一条直线,因此,是
不能霞构的。由式(1)、式(2),可以将深度五或点列Q表示为 平面参数{彳,B,C,D}的函数。现在将点列Q旋转至XOY平面
(这样的旋转并不改变Q的约束条件,如作为直线、圆),得
到相应的二维坐标Q2。(一,B,C,D)。由于曲线C在XOY平面
因此,此处可以忽略视点的轨迹而近似为单个视点,利 用视线束与某个平面的交点列拟合一个椭圆,并由此椭圆计 算得出空间圆所在场景平面的法向量,由对称性可知将得到 2个可能的结果。分别以这2个法向量作为起始点按式(4)对 平面参数{爿,B,C。D)进行全局最小值的非线性搜索,从而重 构出空间圆的三维位置。这种方法比直接搜索更快速准确。
2多视点图像及图像失真
为了增大视角,相机不再局限于透视投射模型,却仍保 持单个的有效视点。典型的单视点成像系统包括基于透镜的 折射式相机,如广角相机、鱼眼相机12j。由于仍是单个视点, 因此,这类相机所产生的图像失真可以简单地通过图像变 形131消除。然而,这类单视点成像系统对器件及其装配的精 确性有极高的要求,否则,系统将偏离单个的视点。
假定成像系统的几何特性可以通过校准获知【j“,则对于
多视点图像中的任意像素qt,可以计算出它处于焦散面上的 视点位置Sc(吼)=【&,疋,,&】及其视线方向K(吼)= 【‰,K,,%】一J,于是该像素所对应的场景点可表示为:
Q=足(qt)+五·K(吼)=
【置搿+五‰,疋r+五Kr,scz+兄%】(五>点Q之间的距离,即深度。
基金项目:上海市科委基金资助项目“无线高清数字电视基础研发”
(08dzl 500803)
作者倚介:吴敖(1985--)。男,硕士研究生,主研方向:图像处理;
方向忠,教授、博士生导师;董皓远,硕士研究生
收稿日捆:2010—03-27
E—mail:beibei8056@hotmail.corn
IAbs订actl Without knowing scene sU'uctttre,caustic distortions due to multi—viewpoint imaging call not be removed.Based on the skewed light rays in multi-viewpoint imaging,this paper extracts depth information from structured features in distorted images,and performs 3D Euclidean
方便起见,将视线轴定为z轴,则任意空间直线可以被 定义为以下2个平面的交线:
/70:墙工+Boy+z=0
z乙:易x+易J,+l=0
(6)
其中,%表示经过原点而不平行于z轴的平面;Hz表示平 行于z轴而不经过原点的平面。注意既经过原点又平行于z 轴,即经过z轴的平面,对应于3.1节提到的共面情形,这 种情况下任何平面曲线都不能蕾构。
的二维方程形式描述包括椭圆、抛物线和双曲线在内的所有
圆锥曲线:
F{Q叫l:ax2+丘秒+钞2+出+秒+,=0
(5)
这种二维模型并不需要已知曲线在平面中的方向,而事 实上也包含了直线和圆。 3.3圈的三维重构
圆是一类特殊的圆锥曲线。在对圆所在平面的4个参数 {爿,B,c,D}进行非线性搜索之前,本文介绍一种数学方法估 计出其中的3个参数{爿,B,C),即平面的方向(或法向量)。这
image.The reconstruction from a single multi-viewpoint
reconstructing principle includes all curves of known functional form,and provides
specially designed mathematical approaches for features such as space lines and circles.
理,本节用渲染的场景进行仿真实验,进一步描述整个三维 重构中的交互过程。采用渲染场景便于对比重构结果与原始 场景位置。
4.1曲线识羽 首先用PovRay渲染一个大约6 m×6 m×3.5 m的室内场
景,使用一个仿真的相机以l m为半径绕房间的中心轴水平 旋转一周,将每一帧图像的中间列像素拼接得到图3所示的 全景图像。由于像素的视点都不同,因此得到的图像显然是 多视点的。用户通过标注采样点指定待重构曲线,通过线性
足的限制条件:
4‰+Boy,r—Azscz%一BzS,zKr=一吃
(8)
对于直线上的点列,可以写成如下矩阵形式:
,
【‰%屯%屯%¨4 Bo幺易】=一% (9)
其中,&、珞、%、吃是对应于直线上点列(远多于4个)
的列向量。由这个矩阵方程可以计算出凡、风、如、易, 即场景直线的空间三维位置。
4渲染场景的实验仿真 上一节论述了单幅多视点图像中平面曲线的三维重构原
3.4直线的三维重构 直线是生活中最常见的图形,除了3.1节中介绍的一般
—-228一
万方数据
圈2视线轴
定理空间中给定4条不同的直线,存在0条、1条、 2条或无穷多条直线与之相交【5。。
在本文的例子中,存在2条直线与视线束(远多于4条) 相交,其中一条是视线轴,另一条是待重构的场景直线。因 此,采用下述空间直线的表示方法,排除了视线轴,从而使 场景直线成为唯一满足条件的结果。
上的函数形式:
r(a2D1=o
(3)
是已知的,因此可通过非线性搜索平面参数{丘最G斟使表达式:
NI
.一.I
argmin xlrl Q尸)I
(4)
,7{』口,c.D}I=l‘
。。
的值最小,其中,Ⅳ为视线束与场景平面的交点个数。注意
此重构方法并不要求已知曲线在场景平面中的方向。
3.2圈锥曲线的三维重构
圆锥曲线是生活中常见的一类平面曲线,可以采用统一
(下转第23l页)
可以看出,1SBWA算法存在非常严重的过分割现象,尤 其是对噪声污染比较严重的图像,过分割使分水岭算法几乎 失效;NMBWA算法比ISBWA算法有较大的改进,很大程 度J二解决了过分割问题,但NMBWA算法在保留微弱边缘与 消除噪声和纹理细节之间存在不可调和的矛盾。
如图3~图6左面一组分割结果,原始图像的背景含有大 量纹理细节,NMBWA算法仅仅利j}l极小值深度信息并没有 完全消除纹理细节的影响,增大深度阈值町以加强对纹理细 节的抑制作用,但同时会丢失许多真实的微弱边缘,如空中 的乒乓球以及运动员手掌的下部都没能与背景很好地分割开 来。此外,NMBWA算法对噪声比较敏感,在噪声污染严重 的情况下产生了大量虚假边缘,边缘定位能力比较弱。而本 文算法结合了极小值深度信息和汇水盆地尺度信息两方面特 征,有效地解决了保留微弱边缘和消除噪声两者之间的矛盾, 分割效果最好。表l给出了各算法在AMD Athlon 2800+ 1.8 GHz处理器、512 MB内存微机上的区域数及运行时间。
