2012北京中考二模试题22题汇总包含09,10,11中考22题
2012北京海淀区中考二模数学和答案(word版)

海淀区九年级第二学期期末练习数学2012. 6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的.1. -5的倒数是A.15B.15-C.5-D.52. 2012年4月22日是第43个世界地球日,中国国土资源报社联合腾讯网发起“世界地球日”微话题,共有18 891 511人次参与了这次活动,将18 891 511用科学记数法表示(保留三个有效数字)约为A. 18.9⨯106B. 0.189⨯108C. 1.89⨯107D. 18.8⨯1063. 把2x2− 4x + 2分解因式,结果正确的是A.2(x− 1)2B.2x(x− 2) C.2(x2− 2x + 1) D.(2x−2)24. 右图是由七个相同的小正方体堆砌而成的几何体,则这个几何体的俯视图是A BCD5.从1, -2, 3这三个数中,随机抽取两个数相乘,积为正数的概率是A.0 B.13C.23D.16. 如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为A.21 B. 3 C. 2D. 1C. 中位数是51.5D. 众数是588.如图,在梯形ABCD 中,AD //BC ,∠ABC =60°,AB = DC =2, AD =1, R 、P 分别是BC 、CD 边上的动点(点R 、B 不重合, 点P 、C 不 重合),E 、F 分别是AP 、RP 的中点,设BR=x ,EF=y ,则下列 图象中,能表示y 与x 的函数关系的图象大致是A B C D 二、填空题(本题共16分,每小题4分)9. 若二次根式23-x 有意义,则 x 的取值范围是 .10.若一个多边形的内角和等于540︒,则这个多边形的边数是 . 11. 如图,在平面直角坐标系xOy 中,已知点A 、B 、C 在双 曲线xy 6=上,BD ⊥x 轴于D , CE ⊥ y 轴于E ,点F 在x 轴上, 且AO =AF , 则图中阴影部分的面积之和为 .A'ED ABCF E RP B CDA12.小东玩一种“挪珠子”游戏,根据挪动珠子的难度不同而得分不同,规定每次挪动珠子的颗数与所得分数的对应关系如下表所示:按表中规律,当所得分数为71分时,则挪动的珠子数为 颗; 当挪动n 颗 珠子时(n 为大于1的整数), 所得分数为 (用含n 的代数式表示). 三、解答题(本题共30分,每小题5分) 1311|5|()3tan604---+︒. 14.解方程:6123x x x +=-+.15. 如图,AC //EG , BC //EF , 直线GE 分别交BC 、BA 于P 、D ,且AC=GE , BC=FE . 求证:∠A =∠G .16.已知2220a a --=,求代数式221111121a a a a a --÷--++的值.17. 如图,一次函数的图象与x 轴、y 轴分别交于点A (-2, 0)、B (0, 2). (1)求一次函数的解析式;(2)若点C 在x 轴上,且OC =23, 请直接写出∠ABC 的度数.18. 如图,在四边形ABCD 中,∠ADB =∠CBD =90︒,BE//CD 交AD 于E , 且EA=EB .若AB=54,DB =4, 求四边形ABCD 的面积.GFEDC BAP EDCA四、解答题(本题共20分,第19题、第20题各5分,第21题6分,第22题4分) 19. 某街道办事处需印制主题为“做文明有礼的北京人,垃圾减量垃圾分类从我做起”的宣传单. 街道办事处附近的甲、乙两家图文社印制此种宣传单的收费标准如下: 甲图文社收费s (元)与印制数t (张)的函数关系如下表:乙图文社的收费方式为:印制2 000张以内(含2 000张),按每张0.13元收费;超过 2 000张,均按每张0.09元收费.(1)根据表中给出的对应规律,写出甲图文社收费s (元)与印制数t (张)的函数关系式; (2)由于马上要用宣传单,街道办事处同时在甲、乙两家图文社共印制了1 500张宣传单,印制费共179元,问街道办事处在甲、乙两家图文社各印制了多少张宣传单?(3)若在下周的宣传活动中,街道办事处还需要加印5 000张宣传单,在甲、乙两家图文社中选择 图文社更省钱.20.如图,AC 、BC 是⊙O 的弦, BC //AO , AO 的延长线与过点C 的射线交于点D , 且∠D =90︒-2∠A .(1)求证:直线CD 是⊙O 的切线;(2)若BC=4,1tan 2D =,求CD 和AD 的长.21. 李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了 为期半个月的跟踪调查,他将调查结果分为四类,A :很好;B :较好;C :一般;D : 较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:类别50%25%15%D CB A(1)李老师一共调查了多少名同学?(2)C 类女生有 名,D 类男生有 名,将上面条形统计图补充完整; (3)为了共同进步,李老师想从被调查的A 类和D 类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位 男同学和一位女同学的概率. 22.阅读下面材料:小明遇到这样一个问题:我们定义: 如果一个图形绕着某定点旋转一定的角度α (0︒ <α <360︒) 后所得的图形与原图形重合,则称此图形是旋转对称图形. 如等边三角形就是一个旋转角为120︒的旋转对称图形. 如图1,点O 是等边三角形△ABC 的中心, D 、E 、F 分别为AB 、BC 、 CA 的中点, 请你将△ABC 分割并拼补成一个与△ABC 面积相等的新的旋转对称图形.图1 图2小明利用旋转解决了这个问题,图2中阴影部分所示的图形即是与△ABC 面积相等的新的旋转对称图形.请你参考小明同学解决问题的方法,利用图形变换解决下列问题: 如图3,在等边△ABC 中, E 1、E 2、E 3分别为AB 、BC 、CA 的中点,P 1、P 2, M 1、M 2, N 1、N 2分别为AB 、BC 、CA 的三等分点. (1)在图3中画出一个和△ABC 面积相等的新的旋转 对称图形,并用阴影表示(保留画图痕迹);(2)若△ABC 的面积为a ,则图3中△FGH 的面积为 .五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知抛物线 2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点. (1)求m 的取值范围;E 3 E 12 P 1 P 2N 1N 2 2M 1BA 图3G FH(2)若m >1, 且点A 在点B 的左侧,OA : OB =1 : 3, 试确定抛物线的解析式; (3)设(2)中抛物线与y 轴的交点为C ,过点C 作直线l //x 轴, 将抛物线在y 轴左侧的部分沿直线 l 翻折, 抛物线的其余部分保持不变,得到一个新图象. 请你结合新图象回答: 当直线13y x b =+与新图象只有一个公共点P (x 0, y 0)且 y 0≤7时, 求b 的取值范围.24. 如图, 在平面直角坐标系xOy 中,抛物线x x my 222-=与x 轴负半轴交于点A , 顶点为B , 且对称轴与x 轴交于点C .(1)求点B 的坐标 (用含m 的代数式表示);(2)D 为BO 中点,直线AD 交y 轴于E ,若点E 的坐标为(0, 2), 求抛物线的解析式; (3)在(2)的条件下,点M 在直线BO 上,且使得△AMC 的周长最小,P 在抛物线上,Q 在直线 BC 上,若以A 、M 、P 、Q 为顶点的四边形是平行四边形,求点P 的坐 标.25. 在矩形ABCD 中, 点F 在AD 延长线上,且DF = DC , M 为AB 边上一点, N 为MD 的中 点, 点E 在直线CF 上(点E 、C 不重合).(1)如图1, 若AB =BC , 点M 、A 重合, E 为CF 的中点,试探究BN 与NE 的位置关系及BMCE的值, 并证明你的结论; (2)如图2,且若AB =BC , 点M 、A 不重合, BN =NE ,你在(1)中得到的两个结论是否成立, 若成立,加以证明; 若不成立, 请说明理由;(3)如图3,若点M 、A 不重合,BN =NE ,你在(1)中得到的结论两个是否成立, 请直接写出你的结论.图1 图2 图3FA ( M) DNDCENM B FECBFNMECBA海淀区九年级第二学期期末练习数学试卷答案及评分参考 2012. 6说明: 与参考答案不同, 但解答正确相应给分. 一、选择题(本题共32分,每小题4分)1. B2. C3. A4. C5. B6. D7. D8. C 二、填空题(本题共16分,每小题4分)9.23x ≥10. 5 11. 12 12.8; 21n n +- (每空各 2分) 三、解答题(本题共30分,每小题5分)13115()3tan604---+︒=54-+ …………………………………………………4分=1. …………………………………………………5分14.解:去分母,得 ()()()()63223x x x x x ++-=-+. ………………………………2分2261826x x x x x ++-=+-. ……………………………………………………3分 整理,得 324x =-. 解得 8x =-. ………………………………………………………………4分 经检验,8x =-是原方程的解. 所以原方程的解是8x =-. ……………………………………………………5分15.证明:∵ AC //EG ,∴ C CPG ∠=∠. …………1分 ∵ BC //EF ,∴ CPG FEG ∠=∠.∴ C FEG ∠=∠. …………………………………………2分在△ABC 和△GFE 中,,,,AC GE C FEG BC FE =⎧⎪∠=∠⎨=⎪⎩ ∴ △ABC ≌△GFE . …………………………………………………4分∴A G ∠=∠. …………………………………………………5分16. 解:原式=()()()21111111a a a a a +-⋅-+-- ……………………………………………2分 =()21111a a a +--- …………………………………………………3分 =22.(1)a -- …………………………………………………4分 由2220a a --=,得 2(1)3a -=.∴ 原式=23-. …………………………………………………5分GFEDC AP17.解:(1)依题意设一次函数解析式为2y kx =+. …………………………………1分∵ 点A (2,0-)在一次函数图象上, ∴022k =-+. ∴ k =1. ……………………………………………………2分 ∴ 一次函数的解析式为2y x =+. …………………………………3分 (2)ABC ∠的度数为15︒或105︒. (每解各1分) ……………………5分18.解: ∵∠ADB =∠CBD =90︒,∴ DE ∥CB . ∵ BE ∥CD , ∴ 四边形BEDC 是平行四边形. ………1分 ∴ BC=DE .在Rt △ABD 中,由勾股定理得8AD ===. ………2分设DE x =,则8EA x =-. ∴8EB EA x ==-.在Rt △BDE 中,由勾股定理得 222DE BD EB +=.∴ 22248x x +=-(). ……………………………………………………3分 ∴ 3x =.∴ 3BC DE ==. ……………………………………………………4分∴1116622.22ABD BDC ABCD S S S BD AD BD BC ∆∆=+=⋅+⋅=+=四边形 ………… 5分 四、解答题(本题共20分,第19题、第20题各5分,第21题6分, 第22题4分) 19.解:(1)甲图文社收费s (元)与印制数t (张)的函数关系式为0.11s t =. ……1分(2)设在甲、乙两家图文社各印制了x 张、y 张宣传单, 依题意得{1500,0.110.13179.x y x y +=+= ………………………………………… 2分解得800,700.x y =⎧⎨=⎩……………………………………………… 3分答:在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分(3) 乙 . ……………………………………………………… 5分20.(1)证明:连结OC .∴ ∠DOC =2∠A . …………1分 ∵∠D = 90°2A -∠, ∴∠D +∠DOC =90°. ∴ ∠OCD =90°.∵ OC 是⊙O 的半径,∴ 直线CD 是⊙O 的切线. ………………………………………………2分 (2)解: 过点O 作OE ⊥BC 于E , 则∠OEC =90︒.∵ BC =4,∴ CE =12BC =2.∵ BC //AO ,∴ ∠OCE =∠DOC .D EC BA∵∠COE +∠OCE =90︒, ∠D +∠DOC =90︒,∴ ∠COE =∠D . ……………………………………………………3分 ∵tan D =12, ∴tan COE ∠=12. ∵∠OEC =90︒, CE =2,∴4tan CEOE COE==∠.在Rt △OEC 中, 由勾股定理可得OC ==在Rt △ODC 中, 由1tan 2OC D CD ==,得CD =, ……………………4分由勾股定理可得 10.OD =∴10.AD OA OD OC OD =+=+= …………………………………5分 21.解:(1)(64)50%20+÷=. 所以李老师一共调查了20名学生. …………………1分 (2)C 类女生有 3 名,D 类男生有 1 名;补充条形统计图略.说明:其中每空1分,条形统计图1分. ……………………………………4分 (3)解法一:由题意画树形图如下:………………………5分从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分 解法二:由题意列表如下:………………………5分由上表得出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选 两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P (所选两位同学恰好是一位男同学和一位女同学)=3162=. ………………6分 22.解:(1)画图如下:(答案不唯一) …………………………………2分图3从D 类中选取从A 类中选取女女男男女女男女男(2)图3中△FGH 的面积为7a. …………………………………4分 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 解:(1)∵ 抛物线2(1)(2)1y m x m x =-+--与x 轴交于A 、B 两点,∴210,(2)4(1)0.m m m ì-?ïïíïD =-+->ïî由①得1m ¹, 由②得0m ¹,∴ m 的取值范围是0m ¹且1m ¹. ……………………………………………2分 (2)∵ 点A 、B 是抛物线2(1)(2)1y m x m x =-+--与x 轴的交点,∴ 令0y =,即 2(1)(2)10m x m x -+--=. 解得 11x =-,211x m =-. ∵1m >,∴10 1.1m >>-- ∵ 点A 在点B 左侧,∴ 点A 的坐标为(1,0)-,点B 的坐标为1(,0)1m -. …………………………3分 ∴ OA=1,OB =11m -. ∵ OA : OB =1 : 3,∴ 131m =-.∴ 43m =.∴ 抛物线的解析式为212133y x x =--. ………………………………………4分 (3)∵ 点C 是抛物线212133y x x =--与y 轴的交点,∴ 点C 的坐标为(0,1)-.依题意翻折后的图象如图所示.令7y =,即2121733x x --=. 解得16x =, 24x =-.∴ 新图象经过点D (6,7). 当直线13y x b =+经过D 点时,可得5b =.① ② …………………………………………1分当直线13y x b =+经过C 点时,可得1b =-.当直线1(1)3y x b b =+<-与函数2121(33y x x x =-->的图象仅有一个公共点P (x 0, y 0)时,得20001121333x b x x +=--.整理得 203330.x x b ---= 由2(3)4(33)12210b b D =----=+=,得74b =-结合图象可知,符合题意的b 的取值范围为15b -<≤或4b <-. ……………7分 说明:15b -<≤ (2分),每边不等式正确各1分;74b <-(1分) 24.解:(1)∵22222221212112()()4422y x x x mx m m x m m m m m m =-=-+-⋅=--,∴抛物线的顶点B 的坐标为11(,)22m m -. ……………………………1分(2)令2220x x m-=,解得10x =, 2x m =.∵ 抛物线x x my 222-=与x 轴负半轴交于点A ,∴ A (m , 0), 且m <0. …………………………………………………2分过点D 作DF ⊥x 轴于F .由 D 为BO 中点,DF //BC , 可得CF =FO =1.2CO ∴ DF =1.2BC由抛物线的对称性得 AC = OC . ∴ AF : AO =3 : 4. ∵ DF //EO ,∴ △AFD ∽△AOE .∴ .FD AF OE AO=由E (0, 2),B 11(,)22m m -,得OE =2, DF =14m -.∴134.24m-=∴ m = -6.∴ 抛物线的解析式为2123y x x =--. ………………………………………3分(3)依题意,得A (-6,0)、B (-3, 3)、C (-3, 0).可得直线OB 的解析式为x y -=,直线BC 为3x =-. 作点C 关于直线BO 的对称点C '(0,3),连接AC '交BO 于M ,则M 即为所求. 由A (-6,0),C ' (0, 3),可得直线AC '的解析式为321+=x y .由13,2y x y x⎧=+⎪⎨⎪=-⎩ 解得2,2.x y =-⎧⎨=⎩ ∴ 点M 的坐标为(-2, 2). ……………4分由点P 在抛物线2123y x x =--上,设P (t ,213t - (ⅰ)当AM 为所求平行四边形的一边时. 如右图,过M 作MG ⊥ x 轴于G ,过P 1作P1H ⊥ BC 于H , 则x G = x M =-2, x H = x B =-3.由四边形AM P 1Q 1为平行四边形, 可证△AMG ≌△P 1Q 1H . 可得P 1H = AG =4. ∴ t -(-3)=4. ∴ t =1.∴17(1,)3P -. ……………………5分 如右图,同 方法可得 P 2H=AG =4. ∴ -3- t =4. ∴ t =-7.∴27(7,)3P --. ……………………6分(ⅱ)当AM 为所求平行四边形的对角线时, 如右图,过M 作MH ⊥BC 于H , 过P 3作P 3G ⊥ x 轴于G ,则x H = x B =-3,x G =3P x =t . 由四边形AP 3MQ 3为平行四边形, 可证△A P 3G ≌△MQ 3H . 可得AG = MH =1. ∴ t -(-6)=1. ∴ t =-5. ∴35(5,)3P -. ……………………………………………………7分 综上,点P 的坐标为17(1,)3P -、27(7,)3P --、35(5,)3P -.25. 解:(1)BN 与NE 的位置关系是BN ⊥NE ;CE BM.证明:如图,过点E 作EG ⊥AF 于G , 则∠EGN =90°.∵ 矩形ABCD 中, AB =BC , ∴ 矩形ABCD 为正方形.∴ AB =AD =CD , ∠A =∠ADC =∠DCB =90°. ∴ EG//CD , ∠EGN =∠A , ∠CDF =90°. ………………………………1分 ∵ E 为CF 的中点,EG//CD ,∴ GF =DG =11.22DF CD =∴ 1.2GE CD =∵ N 为MD (AD )的中点, ∴ AN =ND =11.22AD CD = ∴ GE =AN , NG=ND+DG=ND+AN=AD=AB . ……………………………2分 ∴ △NGE ≌△BAN . ∴ ∠1=∠2. ∵ ∠2+∠3=90°, ∴ ∠1+∠3=90°. ∴ ∠BNE =90°. ∴ BN ⊥NE . ……………………………………………………………3分 ∵ ∠CDF =90°, CD =DF , 可得 ∠F =∠FCD =45°,CFCD= .于是12CFCE CE CE BM BA CD CD ==== ……………………………………4分 (2)在(1)中得到的两个结论均成立.证明:如图,延长BN 交CD 的延长线于点G ,连结BE 、GE ,过E 作EH ⊥CE ,交CD 于点H .∵ 四边形ABCD 是矩形,∴ AB ∥CG .∴ ∠MBN =∠DGN ,∠BMN =∠GDN . ∵ N 为MD 的中点,∴ MN =DN .∴ △BMN ≌△GDN .∴ MB =DG ,BN =GN . ∵ BN =NE ,∴ BN =NE =GN . ∴ ∠BEG =90°. ……………………………………………5分 ∵ EH ⊥CE , ∴ ∠CEH =90°. ∴ ∠BEG =∠CEH .HGA BC DEM N F 321GFEA (M )CD NB∴ ∠BEC =∠GEH . 由(1)得∠DCF =45°. ∴ ∠CHE =∠HCE =45°. ∴ EC=EH , ∠EHG =135°.∵∠ECB =∠DCB +∠HCE =135°, ∴ ∠ECB =∠EHG . ∴ △ECB ≌△EHG . ∴ EB =EG ,CB =HG . ∵ BN =NG ,∴ BN ⊥NE. ……………………………………………6分∵ BM =DG= HG -HD= BC -HD =CD -CE ,∴CE BM. ……………………………………………7分(3)BN ⊥NE ;CEBM.………………………………………………8分。
北京2012中考英语二模试卷(附答案)

北京2012中考英语二模试卷(附答案)北京2012年中考英语二模试卷(附答案)知识运用(共25分)四、单项填空。
(共13分,每小题1分)22. Taylor Swift is very popular now, and she is ____ favorite singer.A. weB. usC. ourD. ours23. The Spring Festival is coming. It comes ____ January 23 this year. A. in B. onC. atD. for24. The film was so____that the children couldn't stop laughing.A. funnyB. funnierC. funniestD. the funniest25. I like cartoons,____ I didn't go to watch The Adventures of Tintin last week because of the test.A. soB. andC. butD. or26. Although she added salt, it stillwasn't____.A. enouugh saltB. salt enoughC. enough saltyD. salty enough27. Jimmy is a kindboy.He____others fix up the bikes for ten years.A. helpsB. will helpC. helpedD. has helped 28. —When____you____reading the book Steve Jobs?—It's hard to say. Maybe next week.A. did; finishB. have;finishedC. will;finishD. do;finish29. The microwave oven is usedfor____food.A. heatB. heatingC. heatedD. heats30. We like making friends with the people____like helping others.A. whenB. whereC. whoD. what31. By the time I got into theclassroom, the teacher____the test papers.A. had handed outB. handed outC. has handed outD. hands out32. They hope____to London during the Olympics this summer.A. to goB. goC. goingD. gone33. The mobile phone____by Martin Cooper in 1973.A. inventsB. inventedC. is inventedD. was invented34. —Can you tell me____the old people's home?—Last Sunday.A. when they will visitB. when they visitedC. when did they visitD. when will they visit五、阅读下面的短文,掌握其大意,然后从短文后各题所给的A、B、C、D四个选项中,选择最佳选项。
2012年北京各区县二模试题分实验操作题解析版
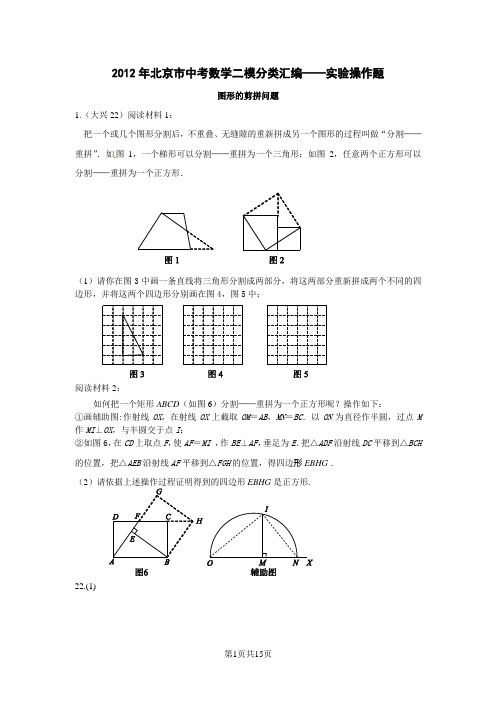
2012年北京市中考数学二模分类汇编——实验操作题图形的剪拼问题1.(大兴22)阅读材料1:把一个或几个图形分割后,不重叠、无缝隙的重新拼成另一个图形的过程叫做“分割——重拼”.如图1,一个梯形可以分割——重拼为一个三角形;如图2,任意两个正方形可以分割——重拼为一个正方形.(1)请你在图3中画一条直线将三角形分割成两部分,将这两部分重新拼成两个不同的四边形,并将这两个四边形分别画在图4,图5中;阅读材料2:如何把一个矩形ABCD(如图6)分割——重拼为一个正方形呢?操作如下:①画辅助图:作射线OX,在射线OX上截取OM=AB,MN=BC.以ON为直径作半圆,过点M 作MI⊥OX,与半圆交于点I;②如图6,在CD上取点F,使AF=MI,作BE⊥AF,垂足为E.把△ADF沿射线DC平移到△BCH 的位置,把△AEB沿射线AF平移到△FGH的位置,得四边形EBHG.(2EBHG是正方形.22.(1)2分 (2)证明:在辅助图中,连接∵ON 是所作半圆的直径,∴∠OIN =90°.∵M I ⊥ON , ∴∠OMI =∠IMN =90°且∠∴△OIM ∽△INM .∴OM IM =IM NM .即IM 2=OM ·NM .………………3分 ∵OM=AB ,MN=BC ∴IM 2 = AB ·BC∵AF=IM ∴AF 2=AB ·BC=AB ·AD .∵四边形ABCD 是矩形,BE ⊥AF ,∴DC ∥AB ,∠ADF =∠BEA =90°. ∴∠DFA =∠EAB .∴△DFA ∽△EAB . ∴AD BE =AFAB .即AF ·BE =AB ·AD=AF 2.∴AF =BE .……………………4分∵AF=BH ∴BH =BE . 由操作方法知BE ∥GH ,BE =GH .∴四边形EBHG 是平行四边形. ∵∠GEB =90°,∴四边形EBHG 是正方形.………………………5分2.(怀柔22)阅读下面材料:在数学课上,李老师给同学们提出两个问题:①“谁能将下面的任意三角形分割后,再拼成一个矩形”;②“谁能将下面的任意四边形分割后,再拼成一个平行四边形”.图⑤ 图⑥图⑦图⑧ 图⑨图① 图② 图③ 图④. 经过小组同学动手合作,第3案,如图1和图2所示;请你参考小亮同学的做法,解决下列问题:(1)“请你将图3再设计一种分割方法,沿分割线剪开后所得的几块图形恰好也能拼成一个矩形”;(2)“请你设计一种方法,将图4分割后,再拼成一个矩形”.22.答案:(说明:本题分割方法不唯一)(1)…………………2分方法一、方法二、方法三、方法四、(2)……5分方法一、方法二、图形的面积问题3.(房山22)⑴阅读下面材料并完成问题:已知:直线AD与△ABC的边BC交于点D,①如图1,当BD=DC时,则S△ABD________S△ADC.(填“=”或“<”或“>”)图3图4DBCADBCABCAD图1 图2 图3②如图2,当BD =21DC 时,则=∆ABD S A D C S ∆ .③如图3,若AD ∥BC ,则有S ∆DBC S ∆ .(填“=”或“<”或“>”)⑵请你根据上述材料提供的信息,解决下列问题:过四边形ABCD 的一个顶点画一条直线,把四边形ABCD 的面积分成1︰2的两部分.(保留画图痕迹)22.①=--------------------------------------1分②21--------------------------------------2分③=--------------------------------------3分⑵BDE ∥AC 交BC 延长线于点E F 为BE 三等分点 过E 作F G ∥BD 交DC 于点E ,BC 于G 则直线AF 为所求 则直线DG 为所求 --------------------------------------5分BCADlN4.(西城区22) 阅读下列材料小华在学习中发现如下结论:如图1,点A ,A 1,A 2在直线l 上,当直线l ∥BC 时,BCABC A ABC S S S 21∆∆∆==.请你参考小华的学习经验画图(保留画图痕迹):(1)如图2,已知△ABC ,画出一个..等腰△DBC ,使其面积与△ABC 面积相等; (2)如图3,已知△ABC ,画出两个..Rt △DBC ,使其面积与△ABC 面积相等(要求:所画的两个三角形不全等...); (3)如图4,已知等腰△ABC 中,AB=AC ,画出一个..四边形ABDE ,使其面积与△ABC 面积相等,且一组对边DE=AB ,另一组对边BD ≠AE ,对角∠E =∠B .图2 图3 图422.解:(1) 如图所示,答案不唯一. 画出△D 1BC ,△D 2BC ,△D 3BC ,△D 4BC ,△D 5BC 中的一个即可.(将BC 的平行线l 画在直线BC 下方对称位置所画出的三角形亦可)﹍﹍ 2分符合要求的点,或将BC 的平行线画在直线BC 下方对称位置所画出的三角形亦可) ﹍﹍﹍﹍﹍﹍﹍﹍﹍4分(3) 如图所示(答案不唯一).﹍﹍﹍ 5分如上图所示的四边形ABDE 的画法说明:(1)在线段BC 上任取一点D (D 不为BC 的中点),连结AD ;(2)画出线段AD 的垂直平分线MN ;(3)画出点C 关于直线MN 的对称点E ,连结DE ,AE . 则四边形ABDE 即为所求.B5.(平谷22)在数学活动课上,老师请同学们在一张长为18cm ,宽为14cm 的长方形纸上剪下一个腰为12cm 的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上).小明同学按老师要求画出了如图(1)的设计方案示意图,请你画出与小明的设计方案不同的所有满足老师要求的示意图,并通过计算说明哪种情况下剪下的等腰三角形的面积最小(含小明的设计方案示意图).22.正确画出图形2分图(1)272AEF S cm ∆=;..........................................................3分图(2)2AEF S ∆=;..................................................4分 图(3)2AEF S ∆=.比较上述计算结果可知,图(3)剪下的三角形面积最小. ...............5分图形变换操作题6.(延庆22)阅读下面材料:阅读下面材料:小伟遇到这样一个问题:如图1,在△ABC (其中∠BAC 是一个可以变化的角)中,AB=2,AC=4,以BC 为边在BC 的下方作等边△PBC ,求AP 的最大值。
北京市中考数学二模试题汇编 人教新课标版

北京2012年数学中考二模试题汇编目录丰台区2012年初三统一练习石景山2012年初三统一练习顺义区2012年初三统一练习大兴区2012年初三统一练习通州区2012年初三统一练习门头沟2012年初三统一练习房山区2012年初三统一练习延庆县2012年初三统一练习密云县2012年初三统一练习海淀区2012年初三统一练习丰台区2012年初三统一练习(二)数学试卷学校姓名准考证号一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的.1.2-的绝对值是A.12- B.12C.2 D.2-2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 002 5米,把0.000 002 5用科学记数法表示为A .62.510⨯B .50.2510-⨯C . 62.510-⨯D .72510-⨯ 3.如图,在△ABC 中, DE ∥BC ,如果AD =1, BD =2,那么DEBC的值为 A .12 B .13 C .14 D .194.在4张完全相同的卡片上分别画有等边三角形、矩形、菱形和圆,在看不见图形的情况下随机抽取1张,卡片上的图形是中心对称图形的概率是 A .14 B .12C .34D .1 5.若20x +=则 y x 的值为A .-8B .-6C .6D .8 6.下列运算正确的是 A .222()a b a b +=+ B .235a b ab +=C .632a a a ÷=D .325a a a ⋅=7.小张每天骑自行车或步行上学,他上学的路程为2 800米,骑自行车的平均速度是步行 的平均速度的4倍,骑自行车上学比步行上学少用30分钟.设步行的平均速度为x 米/分.根据题意,下面列出的方程正确的是A .30428002800=-xx B .30280042800=-x xC .30528002800=-x xD .30280052800=-xx8.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上..一面的字是 A .北 B .京C .精D .神二、填空题(本题共16分,每小题4分)9x 的取值范围是 .DOCBA EDCBA10.分解因式:=+-b ab b a 25102.11.如图, ⊙O 的半径为2,点A 为⊙O 上一点,OD ⊥弦BC 于点D ,如果1OD =,那么BAC ∠=________︒.12.符号“f ”表示一种运算,它对一些数的运算如下:2(1)11f =+,2(2)12f =+,2(3)13f =+, 2(4)14f =+,…,利用以上运算的规律写出()f n = (n 为正整数) ;(1)(2)(3)(100)f f f f ⋅⋅⋅= .三、解答题(本题共30分,每小题5分)13.计算: ()︒⎪⎭⎫ ⎝⎛+45sin 4-211-3-272-03 .14.已知2230a a --=,求代数式2(1)(2)(2)a a a a --+-的值.15.解分式方程:21124x x x -=--.16.如图,在△ABC 与△ABD 中, BC 与AD 相交于点O ,∠1=∠2,CO = DO .求证:∠C =∠D .17.已知:如图,在平面直角坐标系xOy 中,一次函数y =-x 的图象与反比例函数ky x=的图象交于A 、B 两点. (1)求k 的值;(2)如果点P 在y 轴上,且满足以点A 、B 、P 为顶点的三角形是直角三角形,直接写出点P 的坐标.18.为了增强居民的节约用电意识,某市拟出台居民阶梯电价政策:每户每月用电量不超过230千瓦时的部分为第一档,按每千瓦时0.49元收费;超过230千瓦时且不超过400千瓦时的部分为第二档,超过的部分按每千瓦时0.54元收费;超过400千瓦时的部分为第三档,超过的部分按每千瓦时0.79元收费.(1)将按阶梯电价计算得以下各家4月份应交的电费填入下表:21DOCBA(2)设一户家庭某月用电量为x 千瓦时,写出该户此月应缴电费y (元)与用电量x (千瓦时)之间的函数关系式.四、解答题(本题共20分,每小题5分)19.已知:如图,菱形ABCD 中,过AD 的中点E 作AC 的垂线EF ,交AB 于点M ,交CB 的延长线于点F .如果FB 的长是2,求菱形ABCD 的周长.20.已知:如图,点A 、B 在⊙O 上,直线AC 是⊙O 的切线,联结AB 交O C 于点D ,AC =CD . (1)求证:OC ⊥OB ;MFEBCDA(2)可以估计这所学校八年级的学生中,每学期参加社会实践活动的时间不少于8小时的学生大约有多少人?22.小杰遇到这样一个问题:如图1,在□ABCD 中,AE ⊥BC 于点E ,AF ⊥CD 于点F ,连结EF ,△AEF的三条高线交于点H ,如果AC =4,EF =3,求AH 的长.小杰是这样思考的:要想解决这个问题,应想办法将题目中的已知线段与所求线段尽可能集中到同一个三角形中.他先后尝试了翻折、旋转、平移的方法,发现可以通过将△AEH 平移至△GCF 的位置(如图2),可以解决这个问题.请你参考小杰同学的思路回答: (1)图2中AH 的长等于 .(2)如果AC =a ,EF =b ,那么AH 的长等于 .BA D CEFHG HFECDA B图1 图2五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的一元二次方程242(1)0x x k -+-=有两个不相等的实数根. (1)求k 的取值范围;(2)如果抛物线242(1)y x x k =-+-与x 轴的两个交点的横坐标为整数,求正整数k 的值;(3)直线y =x 与(2)中的抛物线在第一象限内的交点为点C ,点P 是射线OC 上的一个动点(点P 不与点O 、点C 重合),过点P 作垂直于x 轴的直线,交抛物线于点M ,点Q 在直线PC 上,距离点P 个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.24.在△ABC 中,D 为BC 边的中点,在三角形内部取一点P ,使得∠ABP =∠ACP .过点P 作PE ⊥AC 于点E ,PF ⊥AB 于点F .(1)如图1,当AB =AC 时,判断的DE 与DF 的数量关系,直接写出你的结论;(2)如图2,当AB ≠AC ,其它条件不变时,(1)中的结论是否发生改变?请说明理由.图1 图225.如图,将矩形OABC 置于平面直角坐标系xOy 中,A (32,0),C (0,2). (1) 抛物线2y x bx c =-++经过点B 、C ,求该抛物线的解析式;(2)将矩形OABC 绕原点顺时针旋转一个角度α(0°<α<90°),在旋转过程中,当矩形的顶点落在(1)中的抛物线的对称轴上时,求此时这个顶点的坐标; (3)如图(2),将矩形OABC 绕原点顺时针旋转一个角度θ(0°<θ<180°),将得到矩形OA’B’C’,设A’C’的中点为点E ,联结CE ,当θ= °时,线段CE 的长度最大,最大值为 .AEFPD E BAD F P北京市丰台区2011_2012学年第二学期初三综合练习(二)参考答案13.解:原式=3-1+4-422⨯……4分 =6-22….5分14.解:2(1)(2)(2)a a a a --+-=22224a a a --+……1分. =224a a -+. ……2分2230a a --=, ∴223a a -=.…3分∴原式=224347a a -+=+=.….….5分 15.21124x x x -=-- 解:2(2)(4)1x x x +--=.……1分 22241x x x +-+=.……2分23x =-.…… 3分32x =-.…….4分 检验:经检验,32x =-是原方程的解.∴原方程的解是32x =-.……5分16.证明:∠1=∠2, ∴OA=OB .…1分在△COA 和△DOB 中 ,OA=OB ,∠AOC =∠BOD ,CO=DO .∴△COA ≌△DOB .……….4分∴∠C =∠D . …………….5分 17.解: (1)反比例函数ky x=的图象经过点A (-1,1) , ∴-11-1k =⨯=.…………1分(2)P 1(0)、 P 2(0,)、P 3(0,2)、 P 4(0,-2) ……5分18.解:(1)……2分(2)当0230x ≤≤时,0.49y x =;……3分 当230400x <≤时,0.54-11.5y x =;……4分当400x >时,0.79-111.5y x =.……5分 四、解答题(本题共20分,每小题5分)19.解:联结BD . ∵在菱形ABCD 中,∴AD ∥BC ,AC ⊥BD .……1分 又∵EF ⊥AC , ∴BD ∥EF .∴四边形EFBD 为平行四边形.……2分 ∴FB = ED =2.……3分 ∵E 是AD 的中点. ∴AD =2ED =4.……4分 ∴菱形ABCD 的周长为4416⨯=.……5分(2)700⨯(1-0.04)=672.……5分答:这所学校每学期参加社会实践活动的时间不少于23.解:(1)由题意得△>0. ∴△=2(4)4[2(1)]8240k k ---=-+>.……1分 ∴解得3<k .……2分(2)∵3<k 且k 为正整数,∴1=k 或2.……3分当1=k 时,x x y 42-=,与x 轴交于点(0,0)、(4,0),符合题意; 当2=k 时,242+-=x x y ,与x 轴的交点不是整数点,故舍去. 综上所述,1=k .……4分(3)∵2,4y x y x x =⎧⎨=-⎩,∴点C 的坐标是(5,5).∴OC 与x 轴的夹角为45°.过点Q 作QN ⊥PM 于点N ,(注:点Q 在射线PC 上时,结果一样,所以只写一种情况即可)∴∠NQP =45°,NQ PM S ⋅=21.∵PQ ,∴NQ =1.∵P (t t ,),则M (t t t 4,2-),∴PM =t t t t t 5)4(22+-=--.……5分 ∴t t S 5212+-=. ∴当50<<t 时,t t S 25212+-=;……6分 当5>t 时,t t S 25212-=.……7分24.解:(1)DE =DF .……1分(2)DE =DF 不发生改变.……2分理由如下:分别取BP 、CP 的中点M 、N ,联结EM 、DM 、FN 、DN .∵D 为BC 的中点,∴BP DN BP DN //,21=.……3分∵,AB PE ⊥∴BP BM EM 21==.∴21,∠=∠=EM DN .∴12213∠=∠+∠=∠.…4分同理,524,//DM FN MD PC =∠=∠. ∴四边形MDNP 为平行四边形.……5分∴67∠=∠.∵,41∠=∠∴35∠=∠. ∴EMD DNF ∠=∠.……6分 ∴△EMD ≌△DNF . ∴DE =DF .……7分25.解:(1)∵矩形OABC ,A (32,0),C (0,2),∴B (32,2).∴抛物线的对称轴为x =3.∴b =3.……1分∴二次函数的解析式为:22y x =-++.……2分(2)①当顶点A 落在对称轴上时,设点A 的对应点为点A ’,联结OA ’,设对称轴x =3与x 轴交于点D ,∴OD =3. ∴OA ’ = OA =32.在Rt △OA ’D 中,根据勾股定理A ’D =3. ∴A ’(3,-3) . ……4分 ②当顶点落C 对称轴上时(图略),设点C 的对应点为点C ’,联结OC ’, 在Rt △OC ’D 中,根据勾股定理C ’D =1. ∴C ’(3, 1).……6分 (3) 120°,4.……8分石景山区2012年初三第二次统一练习数 学 试 卷7654321NMCD BPFEA第Ⅰ卷(共32分)一、选择题(本题共32分,每小题4分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母填在题后的括号内.1.2的算术平方根是( ) A .21B .2C .2-D .2±2.2012年2月,国务院同意发布新修订的《环境空气质量标准》增加了PM2.5监测指标.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000 001 米,那么数据0.000 002 5用科学记数法可以表示为( ) A .6105.2-⨯ B .5105.2-⨯ C .5105.2⨯- D .6105.2-⨯-3.如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120︒ 的菱形,剪口与折痕所成的角α 的度数应为( )A .15︒或30︒B .30︒或45︒C .45︒或60︒D .30︒或60︒ 4年星级饭店客房出租率(%A .61、62B .62、62C .61.5、62D .60.5、625.如图,有6张形状、大小、质地均相同的卡片,正面分别印有北京精神——“爱国、创新、包容、厚德”的字样.背面完全相同,现将这6张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片恰好是“创新”的概率是( ) A .31 B .32 C .61 D .41 6.若一个多边形的内角和是900°,则这个多边形的边数是( )第3题图A .5B .6C .7D .87.将二次函数2x y =的图象如何平移可得到342++=x x y 的图象( )A .向右平移2个单位,向上平移一个单位B .向右平移2个单位,向下平移一个单位C .向左平移2个单位,向下平移一个单位D .向左平移2个单位,向上平移一个单位8.已知正方形纸片的边长为18,若将它按下图所示方法折成一个正方体纸盒,则纸盒的边(棱)长是( ) A .6B .23C .29D .32第Ⅱ卷(共88分)二、填空题(本题共16分,每小题4分) 9.分式3-x x有意义的条件为 . 10.分解因式:=-339ab b a ______ ________. 11.已知:如图是斜边为10的一个等腰直角三角形与两个半径为5的扇形的重叠情形,其中等腰直角三角形顶角平分线与两扇形相切,则图中阴影部分面积的和是 .12.如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n ,则电子跳蚤连续跳(2-3n )步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳12-13=⨯步到标有数字2的圆圈内,完成一次跳跃,第二次则要连续跳42-23=⨯步到达标有数字6的圆圈,…依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字为 ;第2012次电子跳蚤能跳到的圆圈内所标的数字为 .三、解答题(本题共30分,每小题5分)第8题图 111210987654321第12题图13.()22145cos 314.38-⎪⎭⎫⎝⎛+︒---π.解:14.解分式方程123482---=-xxx .解:15.已知,如图,点D 在边BC 上,点E 在△ABC 外部,DE 交AC 于F ,若AD =AB ,∠1=∠2=∠3. 求证:BC=DE . 证明:16.已知:0162=-+x x ,求代数式()()()()3312122+-+--+x x x x x 的值.解:17.已知一次函数y kx b =+的图象与直线y =平行且经过点()3,2-,与x 轴、y轴分别交于 A 、 B 两点. (1)求此一次函数的解析式;(2)点C 是坐标轴上一点,若△ABC 是底角为︒30的等腰三角形,求点C 的坐标. 解:18.列方程(组)解应用题:如图是一块长、宽分别为60 m 、50 m 的矩形草坪,草坪中有宽度均为x m 的一横两纵的甬道.(1)用含x 的代数式表示草坪的总面积S ;(2)当甬道总面积为矩形总面积的4.10%时,求甬道的宽. 解:四、解答题(本题共20分,每小题5分)19.如图,梯形纸片ABCD 中,AD //BC ,∠B =30º.折叠纸片使BC 经过点A ,点B 落在点B’处,EF 是折痕,且BE =EF =4,AF ∥CD . (1)求∠BAF 的度数; (2)当梯形的上底AD 多长时,线段DF 恰为该梯形的高? 解:20.以下是根据全国 2011年国民经济和社会发展统计公报中的相关数据,绘制的统计图的一部分. 请根据以上信息,解答下列问题:(产量相关数据精确到1万吨)(1)请补全扇形统计图;(2)通过计算说明全国的粮食产量与上一年相比,增长最多的是 年; (3)2011年早稻的产量为 万吨;(4)2008-2011这三年间,比上一年增长的粮食产量的平均数为多少万吨,若按此平均数增长,请你估计2012年的粮食产量为多少万吨.(结果保留到整数位) 解:21.已知:如图,M 是⊙O 的直径AB 上任意一点,过点M 作AB 的垂线MP ,D 是MPA BD E C B 'F 6%22%%早稻夏粮秋粮2011年各类粮食占全体 粮食的百分比分组统计图的延长线上一点,联结AD 交⊙O 于点C ,且PC PD =. (1)判断直线PC 与⊙O 的位置关系,并证明你的结论; (2)若22tan =D ,3=OA ,过点A 作PC 的平行线AN 交⊙O 于点N .求弦AN 的长.解:22.阅读下面材料:小阳遇到这样一个问题:如图(1),O 为等边△ABC 内部一点,且3:2:1::=OC OB OA ,求AOB ∠的度数.小阳是这样思考的:图(1)中有一个等边三角形,若将图形中一部分绕着等边三角形的某个顶点旋转60°,会得到新的等边三角形,且能达到转移线段的目的.他的作法是:如图(2),把△CO A 绕点A 逆时针旋转60°,使点C 与点B 重合,得到△O AB ',连结O O '. 则△O AO '是等边三角形,故OA O O =',至此,通过旋转将线段OA 、OB 、OC 转移到同一个三角形B O O '中. (1)请你回答:︒=∠AOB . (2)参考小阳思考问题的方法,解决下列问题: 已知:如图(3),四边形ABCD 中,AB=AD ,∠DAB =60°,∠DCB =30°,AC =5,CD =4.求四边形ABCD 的面积. 解:五、解答题(本题满分22分,第23题7分,第24题7分,第25题8分) 23.已知:直线122y x =+分别与 x 轴、y 轴交于点A 、点B ,点P (a ,b )在直线AB 上,点P 关于y 轴的对称点P ′ 在反比例函数xky =图象上.(1) 当a =1时,求反比例函数xky =的解析式;DCBA图⑴ 图⑵ 图⑶OCBA(2) 设直线AB 与线段P'O 的交点为C .当P'C =2CO 时,求b 的值;(3) 过点A 作AD //y 轴交反比例函数图象于点D ,若AD =2b,求△P ’DO 的面积.解:24.在△ABC 中,AC AB =,D 是底边BC 上一点,E 是线段AD 上一点,且∠BAC CED BED ∠=∠=2.(1) 如图1,若∠︒=90BAC ,猜想DB 与DC 的数量关系为 ; (2) 如图2,若∠︒=60BAC ,猜想DB 与DC 的数量关系,并证明你的结论; (3)若∠︒=αBAC ,请直接写出DB 与DC 的数量关系.A B C D E AE B C D图1 图2备用图解:25.已知:抛物线y=-x2+2x+m-2交y轴于点A(0,2m-7).与直线y=2x交于点B、C(B在右、C在左).(1)求抛物线的解析式;∠=∠,(2)设抛物线的顶点为E,在抛物线的对称轴上是否存在一点F,使得BFE CFE 若存在,求出点F的坐标,若不存在,说明理由;(3)射线OC上有两个动点P、Q同时从原点出发,分别以每秒5个单位长度、每秒25个单位长度的速度沿射线OC运动,以PQ为斜边在直线BC的上方作直角三角形PMQ (直角边分别平行于坐标轴),设运动时间为t秒,若△PMQ与抛物线y=-x2+2x+m-2有公共点,求t的取值范围.解:备用图草稿纸石景山区2012初三第二次统一练习数学参考答案阅卷须知:1.一律用红钢笔或红圆珠笔批阅.2.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共8道小题,每小题4分,共32分)9.3≠x ; 10.()()b a b a ab 33-+; 11.225-225π; 12.10;6. 三、解答题(本题共6道小题,每小题5分,共30分)13.解:()22145cos 3--14.38-⎪⎭⎫⎝⎛+︒-π=4223122+⨯-- ……………………………4分 =322+…………………………………………………5分 14. 123482---=-xxx解:()()123228---=-+x x x x ……………………………1分 ()()()42382--+-=x x x ……………………………3分46822+---=x x x ……………………………4分∴10-=x经检验:10-=x 是原方程的根.………………………5分15.证明:∵∠1=∠2=∠3∴DAE BAC ∠=∠…………………………… 1分 又∵AFE DFC ∠=∠∴E C ∠=∠ …………………………… 2分 在△ABC 和△ADE 中⎪⎩⎪⎨⎧=∠=∠∠=∠AD AB EC DAE BAC (3)分 ∴△ABC ≌△ADE ……………………………………………………… 4分∴BC=DE . ……………………………………………………… 5分16.解:原式222922144x x x x x -++-++= …………………………………2分1062++=x x ………………………………… 3分当0162=-+x x 时,162=+x x ………………………………… 4分 原式11=. …………………………………5分17.解:(1)∵一次函数y kx b =+的图象与直线y =平行且经过点()3,2-∴⎩⎨⎧-=+-=323b k k 解得⎩⎨⎧=-=33b k∴一次函数解析式为33+-=x y …………………………………1分(2)令0=y ,则1=x ;令0=x 则3=y∴()()3,0,0,1B A∵1=OA ,3=OB …………………………2分 ∴2=AB ∴︒=∠30ABO若AC AB =,可求得点C 的坐标为()0,31C 或()3,02-C ………………………4分 若CA CB =如图︒=︒-︒=∠3030603OAC ,3330tan 3=︒=OA OC ∴⎪⎪⎭⎫ ⎝⎛33,03C …………………………………………5分 ∴()0,31C ,()3,02-C ,⎪⎪⎭⎫ ⎝⎛33,03C 18.解:(1)S = 6050⨯-(60 x + 2×50 x -2×x 2 )=3000 + 2x 2-160x .………2分(2)由题意得:-2x 2+160x =60501000104⨯⨯, ………………3分解得 x = 2 或 x = 78. …………………………………4分 又0<x <50,所以x = 2,答:甬道的宽是2米. ……………………………………5分 19. 解:(1)∵BE =EF ∴∠EFB =∠B ,由题意,△EF B '≌△BEF∴∠EFB ’ =∠EFB =∠B=30° ∴△BFA 中,︒=︒-︒-︒-︒=∠90303030180BAF ……………………………………2分 (2)联结DF ,∵AD //BC ,AF ∥CD∴四边形AFCD 是平行四边形 ……………………………………3分 ∴∠C =∠A FB =60°∴CD =AF =3230cos =︒EF ……………………………………4分 若BC DF ⊥,则360cos =︒=CD FC此时3=AD . ……………………………………5分 20.(1)72%;(2)2011;(3)3427; ……………………每空1分,共3分(4)(57121-52871)÷3≈=1417 ………………………………………4分57121+1417=58538. ………………………………………5分21.(1)联结CO , … …………………………………1分∵DM ⊥AB∴∠D+∠A=90° ∵PC PD = ∴∠D=∠PCD ∵OC=OA ∴∠A=∠OCA∴∠OCA+∠PCD=90° ∴PC ⊥OC∴直线PC 是⊙O 的切线 …………………………………2分 (2)过点A 作PC 的平行线AN 交⊙O 于点N . ∴∠NAC=∠PCD=∠D, AN ⊥OC,设垂足是Q ∴Rt △CQA 中 ∴22tanD QAC tan ==∠ ∴设CQ=x ,AQ=x 2 ∴OQ=x -3∵222AQ OQ OA +=∴222)3()2(3x x -+=解得2=x …………………………………4分 ∴22=AQ∴242==AQ AN …………………………………5分22. 解:(1)150° ………………………1分(2) 如图,将△ADC 绕点A 顺时针旋转60°,使点D 与点B 重合,………2分 得到△O AB ',连结O C '. 则△O AC '是等边三角形,可知4,5'===='DC BO CA O C ,ADC ABO ∠=∠'……………………3分在四边形ABCD 中,︒=∠-∠-︒=∠+∠270360DCB DAB ABC ADC ,)(360''ABO ABC BC O ∠+∠-︒=∠∴︒=︒-︒=90270360. ……………………4分34522=-=∴BC 6432543215432''-=⨯⨯-⨯=-=∴∆∆BCO ACO ABCD S S S 四边形.………………5分23.(1)∵点P 在直线AB 上, 1=a 时,2121+⨯=b =25………………………1分 ∴)25,1(P ,∴)25,1(-'P ,代入x k y = 得25-=k ,∴x y 25-= …………………………2分 (2)联结'PP∵点P 和点P '关于y 轴对称 ∴'PP ∥x 轴 ∴OCA C PP ∽△△'O 'DCBA∴'PP ∶=OA C P '∶CO …………3分 ∵CO C P 2'= ∴'PP =OA 2∵221+=x y 与x 轴交于点A 、点B ∴)0,4(-A ,)2,0(B 可得4=OA∴8'=PP ∴a =4∴42421=+⨯=b ………………………5分 (3)当点P 在第一象限时:∵点P 和点P '关于y 轴对称且),(b a P∴),('b a P -∵y AD ∥∴)24-(b D , ∵D P 、点点'在xk y =上 ∴b a b⨯-=⨯-24 ∴2=a∴32221=+⨯=b ∵),23,4(-D )3,2('-P∴29'=DO P S △ …………6分当点P 在第二象限时:)24-(bD -,∴b a b⨯-=-⨯-24∴2-=a∴12)2(21=+-⨯=b∵),21,4(--D )1,2('P∴23'=DO P S △ …………7分24.解:(1)DC DB 2= (2) DC DB 2=证明:过点C 作CF ∥BE 交AD 的延长线于点F , 在 AD 上取点G 使得CF CG = ∴76∠=∠=∠F7654321AEBCG D∵︒=∠=∠=∠602BAC CED BED ∴︒=∠=∠606F ,︒=∠30CED ∴41205∠=︒=∠∵︒=∠+∠=∠=∠+∠6021713 ∴23∠=∠ ∵AC AB = ∴△ABE ≌△CAG ∴AG BE AE CG ==, ∵︒=∠-∠=∠306CED GCE ∴EG CG =∴BE AG CG CF 2121=== 由△DBE ∽△DCF 得2==FCBEDC BD∴DC DB 2=(3) 结论:DC DB 2=.25.解:(1)点A (0,2m -7)代入y =-x 2+2x +m -2,得m =5∴抛物线的解析式为y =-x 2+2x +3 ………………………2分(2)由⎩⎨⎧=++-=x y x x y 2322得⎪⎩⎪⎨⎧==323y x ,⎪⎩⎪⎨⎧=-=323y x∴B (32,3),C (32,3--)B (32,3)关于抛物线对称轴1=x 的对称点为)32,32('-B可得直线C B '的解析式为32632-+=x y , 由⎩⎨⎧=-+=132632y x y ,可得⎩⎨⎧==61y x∴)6,1(F ………………………5分(3)当)2,2(t t M --在抛物线上时,可得03242=-+t t ,4131±-=t , 当)2,(t t P --在抛物线上时,可得32=t ,3±=t ,舍去负值,所以t 的取值范围是34131≤≤+-t .………………8分顺义区2012届初三第二次统一练习F图(2)F E B AO 数学试卷一、选择题(本题共32分,每小题4分) 下面各题均有四个选项,其中只有一个..是符合题意的. 1.9的平方根是A .3B .-3C .3±D .132.据人民网报道,“十一五”我国铁路营业里程达9.1万公里.请把9.1万用科学记数法表示应为A .59.110⨯B .49.110⨯C .49110⨯D . 39.110⨯ 3.如图,下列选项中不是..正六棱柱三视图的是( )A B C D4.把2416a b b -分解因式,结果正确的是A .2(24)b a - B . (22)(22)b a a +-C .24(2)b a -D .4(2)(2)b a a +-5.北京是严重缺水的城市,市政府号召居民节约用水,为了解居民用水情况,小敏在某小区随机抽查了10户家庭的5月份用水量,结果如下(单位:立方米):5,6,6,2,5,6,7,10,7,6,则关于这10户家庭的5月份用水量,下列说法错误的是 A.众数是6 B.极差是8C.平均数是6D.方差是46.如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA 、OB 在O 点钉在一起,并使它们保持互相垂直.在测直径时,把O 点靠在圆周上,读得刻度OE=4个单位, OF=3个单位,则圆的直径为A .7个单位B .6个单位C .5个单位D .4个单位7.从1,-2, 3,-4四个数中,随机抽取两个数相乘,积是正数的概率是A .14 B .13 C .12D .238.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去右上方的小三角形.将纸片展开,得到的图形是DC BA二、填空题(本题共16分,每小题4分) 9.若分式261x x --的值为0,则x 的值等于 . 10.如图,□ABCD 中,E 是边BC 上一点,AE 交BD 于F ,若2BE =,3EC =,则BFDF的值为 . 11.将方程2410x x --=化为2()x m n -=的形式,其中m ,n 是常数,则m n += . 12.如图,△ABC 中,AB =AC=2 ,若P 为BC的中点,则2AP BP PC +的值为 ; 若BC 边上有100个不同的点1P ,2P ,…,100P , 记i i i i m AP BP PC =+(1i =,2,…,100), 则12m m ++…100m +的值为 .三、解答题(本题共30分,每小题5分)13.计算:101()2sin 45(34---+︒-.14.解不等式2(2)x +≤4(1)6x -+,并把它的解集在数轴上表示出来. 15.已知:如图,E ,F 在BC 上,且AE ∥DF ,AB ∥CD ,AB =CD .求证:BF = CE .F EDCBAP iPCBAFEDCBA16.解分式方程:32322x x x -=+-.17.已知2x -3=0,求代数式5(2)(2)(4)1x x x x ---++的值.18.某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y (万吨)随着时间x (年)逐年成直线上升,y 与x 之间的关系如图所示.(1)求y 与x 之间的关系式;(2)请你估计,该市2011年因实施“限塑令”而减少的塑料消耗量为多少?四、解答题(本题共20分,每小题5分) 19.如图,在矩形ABCD 中,E 是边CB 延长线上的点,且EB=AB ,DE 与AB 相交于点F ,AD=2,CD=1,求AE 及DF 的长.20.已知:如图,P 是⊙O 外一点,PA 切⊙O 于点A ,AB 是⊙O 的直径,BC ∥OP 交⊙O 于点C .(1)判断直线PC 与⊙O 的位置关系,并证明你的结论; (2)若BC=2,11sin23APC ∠=,求PC 的长及点C 到PA 的距离.21.阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”.某校倡导学生读书,下面的表格是学生阅读课外书籍情况统计表,图1是该校初中三个年级学生人数分布的扇形统计图,其中八年级FEDC B AOCBAP学生人数为204人,请你根据图表中提供的信息,解答下列问题:(1)求该校八年级学生的人数占全校学生总人数的百分比; (2)求表中a ,b 的值;(3)求该校学生平均每人读多少本课外书?22.阅读下列材料:问题:如图1,P 为正方形ABCD 内一点,且PA ∶PB ∶PC =1∶2∶3,求∠APB 的度数.小娜同学的想法是:不妨设PA=1, PB=2,PC=3,设法把PA 、PB 、PC 相对集中,于是他将△BCP 绕点B 顺时针旋转90°得到△BAE (如图2),然后连结PE ,问题得以解决.请你回答:图2中∠APB 的度数为 . 请你参考小娜同学的思路,解决下列问题:如图3,P 是等边三角形ABC 内一点,已知∠APB=115°,∠BPC=125°.(1)在图3中画出并指明以PA 、PB 、PC 的长度为三边长的一个三角形(保留画图痕迹);(2)求出以PA 、PB 、PC 的长度为三边长的三角形的各内角的度数分别等于 .EDDPPPCCCBBBAAA图1 图2 图3五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.如图,直线AB 经过第一象限,分别与x 轴、y 轴交于A 、B 两点,P为线段AB 上任意一点(不与A 、B 重合),过点P 分别向x 轴、y 轴作垂线,垂足分别为C 、D .设OC=x ,四边形OCPD 的面积为S .PyxB A DCO(1)若已知A (4,0),B (0,6),求S 与x 之间的函数关系式; (2)若已知A (a ,0),B (0,b ),且当x=34时,S 有最大值98,求直线AB 的解析式; (3)在(2)的条件下,在直线AB 上有一点M ,且点M 到x 轴、y 轴的距离相等,点N在过M 点的反比例函数图象上,且△OAN 是直角三角形,求点N 的坐标. 24.已知:如图,D 为线段AB 上一点(不与点A 、B 重合),CD ⊥AB ,且CD=AB ,AE ⊥AB ,BF ⊥AB ,且AE=BD ,BF=AD .(1)如图1,当点D 恰是AB 的中点时,请你猜想并证明∠ACE 与∠BCF 的数量关系; (2)如图2,当点D 不是AB 的中点时,你在(1)中所得的结论是否发生变化,写出你的猜想并证明;(3)若∠ACB=α,直接写出∠ECF 的度数(用含α的式子表示).图1 图225.如图,在平面直角坐标系xOy 中,二次函数212y x bx c =++的图象经过点A (-3,6),并与x 轴交于点B (-1,0)和点C ,顶点为P .(1)求二次函数的解析式;(2)设D 为线段OC 上的一点,若DPC BAC ∠=∠,求点D 的坐标;FED CBAFE D C B A(3)在(2)的条件下,若点M 在抛物线212y x bx c =++上,点N 在y 轴上,要使以M 、N 、B 、D 为顶点的四边形是平行四边形,这样的点M 、N 是否存在,若存在,求出所有满足条件的点M 的坐标;若不存在,说明理由.顺义区2012届初三第二次统一练习 数学学科参考答案及评分细则9.3; 10.25; 11.7; 12.4,400.三、解答题(本题共30分,每小题5分)13.解:101()2sin 45(34---+︒--4212=-⨯- …………………………………………………… 4分3=-…………………………………………………………………… 5分14.解:去括号,得 24x +≤446x -+.…………………………………………… 1分移项,得 24x x -≤464-+-.…………………………………………… 2分 合并,得 2x -≤-2 . ………………………………………… 3分 系数化为1,得 x ≥1 . ……………………………………………… 4分 不等式的解集在数轴上表示如下:……………………………………… 5分15.证明:∵AE ∥DF ,∴∠1=∠2. ………………………… 1分∵ AB ∥CD , ∴ ∠B =∠C .………………………… 2分 在△ABE 和 △DCF 中, 12,,,B C AB DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ △ABE ≌△DCF .…………………………………………………… 4分∴ BE =CF .∴BE -EF =CF -EF .即BF =CE .……………………………………………………………… 5分16.解:去分母,得 3(2)2(2)3(2)(2)x x x x x --+=+-.…………………… 1分去括号,得 223624312x x x x ---=-. ………………………… 2分 整理,得 88x -=-.…………………………………………………… 3分解得 1x =. ……………………………………………………………… 4分经检验,1x =是原方程的解.……………………………………………… 5分 ∴ 原方程的解是1x =.17.解:5(2)(2)(4)1x x x x ---++ 22510(28)1x x x x =--+-+ ……………………………………………… 2分 22510281x x x x =---++24129x x =-+ ………………………………………………………………… 3分 (23)(23)x x =+- …………………………………………………………… 4分 当2x -3=0时,原式(23)(23)0x x =+-=.………………………………… 5分18.解:(1)设y 与x 之间的关系式为y=kx+b .……………………………………… 1分由题意,得20084,2010 6.k b k b +=⎧⎨+=⎩ 解得1,2004.k b =⎧⎨=-⎩…………………… 3分 21F EDC BA∴y 与x 之间的关系式为y =x -2004(2008≤x ≤2012). …………… 4分(2)当x =2012时,y =2012-2004=8.∴该市2012年因“限塑令”而减少的塑料消耗量约为8万吨.……… 5分19.解:∵四边形ABCD 是矩形,且AD=2,CD=1,∴BC=AD=2,AB=CD=1,∠ABC =∠C= 90°,AB ∥DC .∴EB=AB=1. ………………………………………………………………… 1分 在Rt △ABE中,AE =2分 在Rt △DCE 中,DE == 3分∵AB ∥DC , ∴12EF EB DF BC ==. …………………………………………………………… 4分设EF x =,则2DF x =. ∵EFDF DE +=,∴2x x +=.∴3x =. ∴2DF x == 5分 20.解:(1)直线PC 与⊙O 相切.证明:连结OC , ∵BC ∥OP ,∴∠1 =∠2,∠3=∠4. ∵OB=OC ,∴∠1=∠3.∴∠2=∠4.又∵OC=OA ,OP=OP ,∴△POC ≌△POA . ……………………………………………… 1分∴∠PCO =∠PAO .∵PA 切⊙O 于点A ,∴∠PAO =90°.∴∠PCO =90°. ∴PC 与⊙O 相切. ……………………………………………… 2分(2)解:∵△POC ≌△POA ,∴∠5=∠6=12APC ∠. ∴11sin 5sin 23APC ∠=∠=. ∵∠PCO =90°,∴∠2+∠5=90°. ∴1cos 2sin 53∠=∠=. ∵∠3=∠1 =∠2,∴1cos 33∠=. 4321O C B A P图3M P C B A D 85674321O C B A P 连结AC ,∵AB 是⊙O 的直径,∴∠ACB =90°. ∴261cos 33BC AB ===∠.………………………………………… 3分 ∴OA=OB=OC=3,AC ==.∴在Rt △POC 中,9sin 5OC OP ==∠.∴PC ==.…………………………………… 4分 过点C 作CD ⊥PA 于D ,∵∠ACB =∠PAO =90°,∴∠3+∠7 =90°,∠7+∠8 =90°.∴∠3=∠8. ∴1cos 8cos 33∠=∠=. 在Rt △CAD中,1cos 83AD AC =∠==∴163CD ==.……………………………………… 5分 21.解:(1)∵1-28%-38%=34%.∴该校八年级学生的人数占全校学生总人数的百分比为34%.……… 1分(2)∵1440.062400÷=,∴24000.25600a =⨯=, ……………………………………………… 2分 84024000.35b =÷=. ……………………………………………… 3分(3)∵八年级学生人数为204人,占全校学生总人数的百分比为34%,∴全校学生总人数为20434%600÷=. ……………………………… 4分 ∴该校学生平均每人读课外书:24006004÷=.答:该校学生平均每人读4本课外书. ………………………………… 5分22.解:图2中∠APB 的度数为 135° .……………… 1分(1)如图3,以PA 、PB 、PC 的长度为三边长的一个三角形是 △APM .(含画图)………… 2分(2)以PA 、PB 、PC 的长度为三边长的三角形的各内角的度数分别等于60°、65°、55° .……………… 5分 23.解:(1)设直线AB 的解析式为y kx b =+,由A (4,0),B (0,6),得40,6.k b b +=⎧⎨=⎩ 解得3,26.k b ⎧=-⎪⎨⎪=⎩ ∴直线AB 的解析式为362y x =-+.……………………………… 1分 ∵OC=x ,∴3(,6)2P x x -+. ∴3(6)2S x x =-+. 即2362S x x =-+(0< x <4). …………………………………… 2分 (2)设直线AB 的解析式为y mx n =+,∵OC=x ,∴(,)P x mx n +.∴2S mx nx =+.∵当x=34时,S 有最大值98, ∴3,24939.1648n m m n ⎧-=⎪⎪⎨⎪+=⎪⎩ 解得2,3.m n =-⎧⎨=⎩∴直线AB 的解析式为23y x =-+.………………………………… 3分∴A (32,0),B (0,3). 即32a =,3b =.……………………………………………………… 5分 (3)设点M 的坐标为(M x ,M y ), 由点M 在(2)中的直线AB 上,∴23M M y x =-+.∵点M 到x 轴、y 轴的距离相等,∴M M x y =或M M x y =-.当M M x y =时,M 点的坐标为(1,1).过M 点的反比例函数的解析式为1y x =. ∵点N 在1y x=的图象上,OA 在x 轴上,且△OAN 是直角三角形, ∴点N 的坐标为32,23⎛⎫⎪⎝⎭.……………………………………………… 6分 当M M x y =-时,M 点的坐标为(3,-3),B DC F E A 过M 点的反比例函数的解析式为9y x =-. ∵点N 在9y x=-的图象上,OA 在x 轴上,且△OAN 是直角三角形, ∴点N 的坐标为3,62⎛⎫- ⎪⎝⎭.……………………………………………… 7分 综上,点N 的坐标为32,23⎛⎫⎪⎝⎭或3,62⎛⎫- ⎪⎝⎭. 24.解:(1)猜想:∠ACE=∠BCF .证明:∵D 是AB 中点,∴AD=BD ,又∵AE=BD ,BF=AD ,∴AE=BF .∵CD ⊥AB ,AD=BD ,∴CA=CB .∴∠1 =∠2. ∵AE ⊥AB ,BF ⊥AB ,∴∠3 =∠4=90°.∴∠1+∠3 =∠2+∠4.即∠CAE=∠CBF .∴△CAE ≌△CBF .∴∠ACE=∠BCF .……………………………………………… 2分(2)∠ACE=∠BCF 仍然成立.证明:连结BE 、AF .∵CD ⊥AB ,AE ⊥AB ,∴∠CDB=∠BAE=90°.又∵BD = AE ,CD = AB ,△CDB ≌△BAE .……………… 3分 ∴CB=BE ,∠BCD=∠EBA .在Rt △CDB 中,∵∠CDB =90°, ∴∠BCD+∠CBD =90°.∴∠EBA+∠CBD =90°. 即∠CBE =90°.∴△BCE 是等腰直角三角形.∴∠BCE=45°. ……………………………………………… 4分 同理可证:△ACF 是等腰直角三角形.∴∠ACF=45°. ……………………………………………… 5分 ∴∠ACF=∠BCE .∴∠ACF -∠ECF =∠BCE -∠ECF .即∠ACE=∠BCF .……………………………………………… 6分(3)∠ECF 的度数为90°-α.……………………………………………… 7分4321F E D C B A25.解:(1)将点A (-3,6),B (-1,0)代入212y x bx c =++中,得 936,210.2b c b c ⎧-+=⎪⎪⎨⎪-+=⎪⎩ 解得 1,3.2b c =-⎧⎪⎨=-⎪⎩ ∴二次函数的解析式为21322y x x =--.…………………………… 2分 (2)令0y =,得213022x x --=,解得 11x =-,23x =. ∴点C 的坐标为(3,0). ∵22131(1)2222y x x x =--=--, ∴顶点P 的坐标为(1,-2).…………………………………………… 3分 过点A 作AE ⊥x 轴,过点P 作PF ⊥x 轴,垂足分别为E ,F .易得 45ACB PCD ∠=∠=︒.AC ==,PC ==.又DPC BAC ∠=∠,∴△ACB ∽△PCD .…………………… 4分 ∴BC AC CD PC=. ∵3(1)4BC =--=, ∴43BC PC CD AC ==. ∴45333OD OC CD =-=-=. ∴点D 的坐标为5(,0)3.……………………………………………… 5分 (3)当BD 为一边时,由于83BD =, ∴点M 的坐标为885(,)318-或811(,)318-. ………………………… 7分 当BD 为对角线时,点M 的坐标为235(,)318-. …………………… 8分大兴区2011~2012学年度第二学期模拟试卷(二)初三数学参考答案及评分标准第Ⅰ卷 (机读卷 共32分)一、选择题(共8道小题,每小题4分,共32分)第Ⅱ卷 (非机读卷 共88分)二、填空题(共4道小题,每小题4分,共16分)三、解答题(本题共30分,每小题5分)13.解:原式=412222441-⨯+--……………………4分 =2421-………………………………5分 14.解:方程的两边同乘)4(+x x ,得x x 54=+……………………2分解得:1=x ……………………3分检验:把1=x 代入)4(+x x 05≠= ……………………4分∴原方程的解为:1=x . ……………………5分15.证明:(1)BE CF =,∴BE EF +CF EF =+,BF CE =即.……………………………1分∠ABC=90°,DC ⊥BC∴∠ABC=∠DCE=90°………………3分在ABF △和DCE △中,⎪⎩⎪⎨⎧=∠=∠=CE BF DCE ABC DC ABABF DCE ∴△≌△.…………………………5分16.解:原式=2244(441)3x x x x x ---++………………………………………………2分=22444413x x x x x --+-+ (3)分=31x - (4)分 当13x =-时,原式=312x -=-.………………5分 17.解:(1)∵ 点A (1,)n -在一次函数2y x =-的图象上,∴ 2(1)2n =-⨯-=.∴ 点A 的坐标为12-(,).………………1分 ∵ 点A 在反比例函数k y x=的图象上, ∴ 2k =-. ∴反比例函数的解析式为2y x =-. ………………3分 (2)点P 的坐标为(2,0)(0,4)-或.………………5分18.解:设第一批购进水果x 千克,则第二批购进水果2.5x 千克,…………………………1分依据题意得:,12005.2550=-xx ……………………………………3分 解得x=20,经检验x=20是原方程的解,且符合题意……………………………4分答:第一批购进水果20千克;…………………………5分四、解答题(本题共20分,每小题5分)19.解:过A 作BC AD ⊥交BC 于D ,则︒=∠30BAD ,︒=∠45CAD∵BC AD ⊥∴︒=∠90ADB ,︒=∠90ADC∵︒=∠30BAD ,︒=∠90ADB ,6001060=⨯=AB ∴3006002121=⨯==AB BD ………………………………………………………2分 DAB AB AD ∠=cos ︒⨯=30cos 6003300=……………………………………3分∵︒=∠90ADC ,︒=∠45CAD ,3300=AD∴3300==AD CD …………………………………………………………………4分∵BD CD BC += ∴3003300+=BC …………………………………………………………………5分 答:甲乙两人之间的距离是)3003300(+米20.解:(1)50.9;…………………………….…………………………………………….2分(2)①……………………………………………………………………………….5分21. 解:(1)连接OD .∵OA=OD∴∠OAD =∠ODA .∵AD 平分∠BAC∴∠OAD =∠CAD ,∴∠ODA =∠CAD .∴OD ∥AC .………………………………………………1分∵DE ⊥AC ,∴∠DEA =∠FDO=90°∴EF ⊥OD .∴EF 是⊙O 的切线. ……………………………………2分(2)设BF 为x .∵OD ∥AE ,∴△ODF ∽△AEF . ……………………………………3分∴OD OF AE AF =,即2234x x +=+. 解得 x =2∴BF 的长为2. ……………………………………5分 22.(1)分割正确,且画出的相应图形正确……………………………………………………2分(2)证明:在辅助图中,连接OI 、NI .∵ON 是所作半圆的直径,∴∠OIN =90°.∵MI ⊥ON ,∴∠OMI =∠IMN =90°且∠OIM =∠INM .∴△OIM ∽△INM .∴OM IM =IM NM .即IM 2=OM ·NM .…………………………………………………3分 ∵OM=AB ,MN=BC∴IM 2 = AB ·BC∵AF=IM∴AF 2=AB ·BC=AB ·AD .∵四边形ABCD 是矩形,BE ⊥AF ,∴DC ∥AB ,∠ADF =∠BEA =90°.∴∠DFA =∠EAB .∴△DFA ∽△EAB .∴AD BE =AF AB .即AF ·BE =AB ·AD=AF 2.∴AF =BE .………………………………………………………………………4分∵AF=BH∴BH =BE .由操作方法知BE ∥GH ,BE =GH .∴四边形EBHG 是平行四边形.∵∠GEB =90°,∴四边形EBHG 是正方形.……………………………………………………5分 图⑤ 图⑥ 图⑦图⑧ 图⑨ 图① 图② 图③ 图④。
2012年北京市中考试题及答案汇总

2012年北京市中考试题及答案汇总目录2012年北京市中考数学试卷 (2)2012年北京市中考数学答案 (8)2012年北京市中考语文试卷 (14)2012年北京市中考语文答案 (21)2012年北京市中考英语试卷 (23)2012年北京市中考英语答案 (32)2012年北京市中考化学试卷 (33)2012年北京市中考化学答案 (40)2012年北京市中考物理试卷 (42)2012年北京市中考物理答案 (49)2012年北京市高级中等学校招生考试数 学 试 卷学校 姓名 准考证号一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1. 9-的相反数是A .19-B .19C .9-D .92. 首届中国(北京)国际服务贸易交易会(京交会)于2012年6月1日闭幕,本届京交会期间签订的项目成交总金额达60 110 000 000美元,将60 110 000 000用科学记数法表示应为 A .96.01110⨯B .960.1110⨯C .106.01110⨯D .110.601110⨯3. 正十边形的每个外角等于A .18︒B .36︒C .45︒D .60︒4. 右图是某个几何体的三视图,该几何体是A .长方体B .正方体C .圆柱D .三棱柱5. 班主任王老师将6份奖品分别放在6个完全相同的不透明礼盒中,准备将它们奖给小英等6位获“爱集体标兵”称号的同学.这些奖品中3份是学习文具,2份是科普读物,1份是科技馆通票.小英同学从中随机取一份奖品,恰好取到科普读物的概率是 A .16B .13C .12D .236. 如图,直线AB ,C D 交于点O ,射线O M 平分A O C ∠,若76BO D ∠=︒,则BO M ∠等于 A .38︒ B .104︒C .142︒D .144︒7. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如下表所示:A .180,160B .160,180C .160,160D .180,1808. 小翔在如图1所示的场地上匀速跑步,他从点A 出发,沿箭头所示方向经过点B 跑到点C ,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为t (单位:秒),他与教练的距离为y (单位:米),表示y 与t 的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的 A .点MB .点NC .点PD .点Q二、填空题(本题共16分,每小题4分) 9. 分解因式:269mn mn m ++= .10.若关于x 的方程220x x m --=有两个相等的实数根,则m 的值是 . 11.如图,小明同学用自制的直角三角形纸板D EF 测量树的高度AB ,他调整自己的位置,设法使斜边D F 保持水平,并且边D E与点B 在同一直线上.已知纸板的两条直角边40c m D E =,20cm EF =,测得边D F 离地面的高度1.5mAC =,8m C D =,则树高AB = m .12.在平面直角坐标系xOy 中,我们把横 、纵坐标都是整数的点叫做整点.已知点()04A ,,点B 是x 轴正半轴上的整点,记AO B △内部(不包括边界)的整点个数为m .当3m =时,点B 的横坐标的所有可能值是 ;当点B 的横坐标为4n (n 为正整数)时,m = (用含n 的代数式表示.)三、解答题(本题共30分,每小题5分)13.计算:()11π32sin 458-⎛⎫-+︒- ⎪⎝⎭.14.解不等式组:4342 1.x x x x ->⎧⎨+<-⎩,15.已知023a b =≠,求代数式()225224a b a b a b-⋅--的值.16.已知:如图,点E A C ,,在同一条直线上,AB C D ∥,AB CE AC CD ==,.求证:B C E D =.17.如图,在平面直角坐标系xOy 中,函数()40y x x=>的图象与一次函数y kx k =-的图象的交点为()2A m ,.(1)求一次函数的解析式;(2)设一次函数y kx k =-的图象与y 轴交于点B ,若P 是x 轴上一点,且满足P A B △的面积是4,直接写出点P 的坐标.18.列方程或方程组解应用题:据林业专家分析,树叶在光合作用后产生的分泌物能够吸附空气中的一些悬浮颗粒物,具有滞尘净化空气的作用.已知一片银杏树叶一年的平均滞尘量比一片国槐树叶一年的平均滞尘量的2倍少4毫克,若一年滞尘1000毫克所需的银杏树叶的片数与一年滞尘550毫克所需的国槐树叶的片数相同,求一片国槐树叶一年的平均滞尘量.四、解答题(本题共20分,每小题5分)19.如图,在四边形ABC D 中,对角线AC BD ,交于点E ,904530BAC CED D CE D E ∠=︒∠=︒∠=︒=,,,BE =.求C D 的长和四边形ABC D 的面积.20.已知:如图,AB 是O ⊙的直径,C 是O ⊙上一点,O D BC ⊥于点D ,过点C 作O ⊙的切线,交O D 的延长线于点E ,连结BE . (1)求证:BE 与O ⊙相切;(2)连结AD 并延长交BE 于点F ,若9OB =,2s i n 3ABC ∠=,求BF的长.21.近年来,北京市大力发展轨道交通,轨道运营里程大幅增加,2011年北京市又调整修订了2010至2020年轨道交通线网的发展规划.以下是根据北京市轨道交通指挥中心发布的有关数据制作的统计图表的一部分.请根据以上信息解答下列问题:(1)补全条形统计图并在图中标明相应数据;(2)按照2011年规划方案,预计2020年北京市轨道交通运营里程将达到多少千米?(3)要按时完成截至2015年的轨道交通规划任务,从2011到2015这4年中,平均每年需新增运营里程多少千米?22.操作与探究:(1)对数轴上的点P 进行如下操作:先把点P 表示的数乘以13,再把所得数对应的点向右平移1个单位,得到点P 的对应点P '.点A B ,在数轴上,对线段AB 上的每个点进行上述操作后得到线段A B '',其中点A B ,的对应点分别为A B '',.如图1,若点A 表示的数是3-,则点A '表示的数是 ;若点B '表示的数是2,则点B 表示的数是 ;已知线段AB 上的点E 经过上述操作后得到的对应点E '与点E 重合,则点E 表示的数是 ;北京市轨道交通已开通线路相关数据统计表(截至2010年底)(2)如图2,在平面直角坐标系xOy 中,对正方形ABC D 及其内部的每个点进行如下操作:把每 个点的横、纵坐标都乘以同一种实数a ,将得到的点先向右平移m 个单位,再向上平移n 个单位(00m n >>,),得到正方形A B C D ''''及其内部的点,其中点A B ,的对应点分别为A B '',。
北京市海淀区2012年九年级中考二模数学试题及答案

海淀区九年级第二学期期末练习数学试卷答案及评分参考2012. 6说明: 与参考答案不同, 但解答正确相应给分.一、选择题(本题共32分,每小题4分)1. B2. C3. A4. C5. B6. D7. D8. C二、填空题(本题共16分,每小题4分)9. 10. 5 11. 12 12.8; (每空各2分)三、解答题(本题共30分,每小题5分)13.解:= …………………………………………………4分= . …………………………………………………5分14.解:去分母,得.………………………………2分. ……………………………………………………3分整理,得.解得.………………………………………………………………4分经检验,是原方程的解.所以原方程的解是.……………………………………………………5分15.证明:∵AC //EG,∴.…………1分∵BC //EF,∴.∴.…………………………………………2分在△ABC和△GFE中,∴△ABC≌△GFE.…………………………………………………4分∴.…………………………………………………5分16. 解:原式= ……………………………………………2分= …………………………………………………3分= …………………………………………………4分由,得.∴原式= . …………………………………………………5分17.解:(1)依题意设一次函数解析式为. …………………………………1分∵点A( )在一次函数图象上,∴.∴k=1. ……………………………………………………2分∴一次函数的解析式为. …………………………………3分(2)的度数为15︒或105︒.(每解各1分)……………………5分18.解: ∵∠ADB=∠CBD =90︒,∴DE∥CB.∵BE∥CD,∴四边形BEDC是平行四边形. ………1分∴BC=DE.在Rt△ABD中,由勾股定理得. ………2分设,则.∴.在Rt△BDE中,由勾股定理得.∴.……………………………………………………3分∴.∴.……………………………………………………4分∴………… 5分四、解答题(本题共20分,第19题、第20题各5分,第21题6分, 第22题4分)19.解:(1)甲图文社收费(元)与印制数(张)的函数关系式为. ……1分(2)设在甲、乙两家图文社各印制了张、张宣传单,依题意得………………………………………… 2分解得……………………………………………… 3分答:在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分(3)乙. ……………………………………………………… 5分20.(1)证明:连结OC.∴∠DOC =2∠A. …………1分∵∠D = 90°,∴∠D+∠DOC =90°.∴∠OCD=90°.∵OC是⊙O的半径,∴直线CD是⊙O的切线. ………………………………………………2分(2)解: 过点O作OE⊥BC于E, 则∠OEC=90︒.∵BC=4,∴CE= BC=2.∵BC//AO,∴∠OCE=∠DOC.∵∠COE+∠OCE=90︒, ∠D+∠DOC=90︒,∴∠COE=∠D. ……………………………………………………3分∵= ,∴.∵∠OEC =90︒, CE=2,∴.在Rt △OEC中, 由勾股定理可得在Rt △ODC中, 由,得, ……………………4分由勾股定理可得∴…………………………………5分21.解:(1). 所以李老师一共调查了20名学生. …………………1分(2)C类女生有 3 名,D类男生有1 名;补充条形统计图略.说明:其中每空1分,条形统计图1分. ……………………………………4分(3)解法一:由题意画树形图如下:………………………5分从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选两位同学恰好是一位男同学和一位女同学的结果共有3种.所以P(所选两位同学恰好是一位男同学和一位女同学)= . ………………6分解法二:由题意列表如下:A类D类男女女男(男,男)(女,男)(女,男)女(男,女)(女,女)(女,女)………………………5分由上表得出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选两位同学恰好是一位男同学和一位女同学的结果共有3种.所以P(所选两位同学恰好是一位男同学和一位女同学)= . ………………6分22.解:(1)画图如下:(答案不唯一)…………………………………2分图3(2)图3中△FGH的面积为. …………………………………4分五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23. 解:(1)∵抛物线与x轴交于A、B两点,∴由①得,由②得,∴m的取值范围是且.……………………………………………2分(2)∵点A、B是抛物线与x轴的交点,∴令,即.解得,.∵,∴∵点A在点B左侧,∴点A的坐标为,点B的坐标为. …………………………3分∴OA=1,OB= .∵OA : OB=1 : 3,∴.∴.∴抛物线的解析式为.………………………………………4分(3)∵点C是抛物线与y轴的交点,∴点C的坐标为.依题意翻折后的图象如图所示.令,即.解得, .∴新图象经过点D .当直线经过D点时,可得.当直线经过C点时,可得.当直线与函数的图象仅有一个公共点P(x0, y0)时,得.整理得由,得.结合图象可知,符合题意的b的取值范围为或.……………7分说明:(2分),每边不等式正确各1分;(1分)24.解:(1)∵,∴抛物线的顶点B的坐标为. ……………………………1分(2)令,解得, .∵抛物线与x轴负半轴交于点A,∴A (m, 0), 且m<0. …………………………………………………2分过点D作DF⊥x轴于F.由D为BO中点,DF//BC, 可得CF=FO=∴DF =由抛物线的对称性得AC = OC.∴AF : AO=3 : 4.∵DF //EO,∴△AFD∽△AOE.∴由E (0, 2),B ,得OE=2, DF= .∴∴m = -6.∴抛物线的解析式为. ………………………………………3分(3)依题意,得A(-6,0)、B (-3, 3)、C (-3, 0).可得直线OB的解析式为, 直线BC为. 作点C关于直线BO的对称点C '(0,3),连接AC '交BO于M,则M即为所求.由A(-6,0),C' (0, 3),可得直线AC'的解析式为.由解得∴点M的坐标为(-2, 2). ……………4分由点P在抛物线上,设P (t,).(ⅰ)当AM为所求平行四边形的一边时.ϕ如右图,过M作MG⊥ x轴于G,过P1作P1H⊥ BC于H,则xG= xM =-2, xH= xB =-3.由四边形AM P1Q1为平行四边形,可证△AMG≌△P1Q1H .可得P1H= AG=4.∴t -(-3)=4.∴t=1.∴. ……………………5分κ如右图,同ϕ方法可得P2H=AG=4.∴-3- t =4.∴t=-7.∴. ……………………6分(ⅱ)当AM为所求平行四边形的对角线时,如右图,过M作MH⊥BC于H,过P3作P3G⊥ x轴于G,则xH= xB =-3,xG= =t.由四边形AP3MQ3为平行四边形,可证△A P3G≌△MQ3H .可得AG= MH =1.∴t -(-6)=1.∴t=-5.∴. ……………………………………………………7分综上,点P的坐标为、、.25. 解:(1)BN与NE的位置关系是BN⊥NE;= .证明:如图,过点E作EG⊥AF于G, 则∠EGN=90°.∵矩形ABCD中, AB=BC,∴矩形ABCD为正方形.∴AB =AD =CD, ∠A=∠ADC =∠DCB =90°.∴EG//CD, ∠EGN =∠A, ∠CDF =90°.………………………………1分∵E为CF的中点,EG//CD,∴GF=DG =∴∵N为MD(AD)的中点,∴AN=ND=∴GE=AN, NG=ND+DG=ND+AN=AD=AB. ……………………………2分∴△NGE≌△BAN.∴∠1=∠2.∵∠2+∠3=90°,∴∠1+∠3=90°.∴∠BNE =90°.∴BN⊥NE.……………………………………………………………3分∵∠CDF =90°, CD=DF,可得∠F =∠FCD =45°, .于是……………………………………4分(2)在(1)中得到的两个结论均成立.证明:如图,延长BN交CD的延长线于点G,连结BE、GE,过E作EH⊥CE,交CD于点H.∵四边形ABCD是矩形,∴AB∥CG.∴∠MBN=∠DGN,∠BMN=∠GDN.∵N为MD的中点,∴MN=DN.∴△BMN≌△GDN.∴MB=DG,BN=GN.∵BN=NE,∴BN=NE=GN.∴∠BEG=90°.……………………………………………5分∵EH⊥CE,∴∠CEH =90°.∴∠BEG=∠CEH.∴∠BEC=∠GEH.由(1)得∠DCF =45°.∴∠CHE=∠HCE =45°.∴EC=EH, ∠EHG =135°.∵∠ECB =∠DCB +∠HCE =135°,∴∠ECB =∠EHG.∴△ECB≌△EHG.∴EB=EG,CB=HG.∵BN=NG,∴BN⊥NE. ……………………………………………6分∵BM =DG= HG-HD= BC-HD =CD-HD =CH= CE,∴= . ……………………………………………7分(3)BN⊥NE;不一定等于. ………………………………………………8分。
北京市2012年中考二模试题汇编.

北京市2012年中考二模试题汇编—综合实验题【东城】32.(6分下面三个实验采用的是对比实验方法进行的有关探究。
(1用实验一所示装置进行二氧化性质的探究。
当长颈漏斗中的稀盐酸与锥形瓶中的大理石接触后,有大量气泡产生,该反应的化学方程式是 ;C 中观察到的现象是。
(2用实验二进行石灰石性质的探究。
用两支坩埚钳分别夹持大小相同的石灰石固体d 、e ,向 E 中酒精灯的火焰通氧气,受热相同时间后冷却,将固体d 、e 固体分别放入盛有酚酞溶液的烧杯中,前者溶液不变色,后者溶液变为红色。
则向酒精灯火焰通氧气的目的是。
通过上述实验对比分析,可得出的结论是。
(3用实验三所示装置进行活性炭吸附能力的实验探究。
实验开始时,在常温常压条件下,烧瓶1内为氮气,烧瓶2内为相同体积的氯气,将相同质量的活性炭装入两支烧瓶后,F 侧导管中的液面与烧杯内水的液面基本一致,G 侧导管中的液面高于烧杯内水的液面。
当将两只烧瓶放入冰水混合物中,观察到两侧导管中液面都有所上升,且G 侧上升的高度比F 侧明显。
通过该对比实验可以得出的结论是。
答案:(1CaCO 3 + 2HCl = CaCl 2 + H 2O + CO 2↑干燥的试纸不变色,湿润的试纸变色(2提高酒精灯火焰的温度石灰石在加热时不能分解,在高温时能分解(3活性炭对不同气体的吸附能力不同、活性炭对气体的吸附能力随温度降低而增强(2分【西城】32.(5分某小组同学用下图所示的装置进行了两组兴趣实验(a 、b 管的体积相等,夹持装置已略去。
图1a b K 白磷红磷铜铜 a b 图2 K 1 2 1 2【资料】(1白磷的着火点为40℃,红磷的着火点为240℃(22NaOH + MgCl 2 = Mg(OH2↓ + 2NaCl(1如图1所示进行实验。
关闭K ,向烧杯中注入一定量的90℃的热水至图中虚线处。
一段时间后,观察到a 管中的现象是。
其中发生反应的化学方程式是。
对比a 、b 管中的实验现象,可得出燃烧的条件是。
2012北京市东城区中考二模数学试题及答案(真题)

北京市东城区2011--2012学年第二学期初三综合练习(二)数 学 试 卷 2012.6一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的. 1. 9的算术平方根是A .-9B .9C .3D .±3 2. 如图,由几个小正方体组成的立体图形的俯视图是3. 下列运算正确的是A .532a a a =+B .532a a a =⋅C .3332)(b a ab =D .5210a a a =÷4. 抛掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得朝上一面的点数为奇数的概率为 A .16B .14C .13D .125. 如果一个多边形的内角和是其外角和的2倍,那么这个多边形是 A .六边形B .五边形C .四边形D .三角形6. 在社会实践活动中,某同学对甲、乙、丙、丁四个城市一至五月份的香蕉价格进行调查.四个城市5个月香蕉价格的平均值均为3.50元,方差分别为2S 甲=18.3,2S 乙=17.4,2S 丙=20.1,2S 丁=12.5.一至五月份香蕉价格最稳定的城市是 A .甲B .乙C .丙D .丁7. 如图,在平行四边形ABCD 中,E 为AD 的中点,DEF △的周长为1,则BCF △的周长为A .1B .2C .3D .48. 如右图,正方形ABCD 的顶点A ,B ,顶点C D 、位于第一象限,直线:(0l x t t =≤将正方形ABCD 分成两部分,记位于直线l 左侧阴影部分的面积为S ,则S 关于t 的函数图象大致是二、填空题(本题共16分,每小题4分)9.x 的取值范围是 .10. 一个扇形的圆心角为120°,半径为1,则这个扇形的弧长为 . 11. 观察下列等式: 1=1,2+3+4=9, 3+4+5+6+7=25, 4+5+6+7+8+9+10=49,……照此规律,第5个等式为 . 12. 如图,正方形ABCD 内接于⊙O ,⊙O 的半径为2,以圆心O 为顶点作 ∠MON ,使∠MON =90°,OM 、ON 分别与⊙O 交于点E 、F ,与正方形ABCD 的边交于点G 、H , 则由OE 、OF 、EF ⌒及正方形ABCD 的边围成的图形(阴影部分)的面积S= .三、解答题(本题共30分,每小题5分) 13.0(4)6cos302-π-+-.14. 解方程组212x y x y +=⎧⎨-=⎩,.15. 已知:如图,∠ABC =∠DCB ,BD 、CA 分别是∠ABC 、∠DCB 的平分线.求证:AB =DC .16. 先化简,再求值:2212111x x x x -+⎛⎫-÷ ⎪-⎝⎭,其中2x =-.17. 列方程或方程组解应用题:小明家有一块长8m 、宽6m 的矩形空地,现准备在该空地上建造一个十字花园(图中阴影部分),并使花园面积为空地面积的一半,小明设计了如图的方案,请你帮小明求出图中的x 值.18. 如图,在平面直角坐标系xOy 中,直线AB 与反比例函数ky x =的图像交于点A(-3,4),AC ⊥x 轴于点C.(1)求此反比例函数的解析式;(2)当直线AB 绕着点A 转动时,与x 轴的交点为B(a,0),并与反比例函数ky x=图象的另一支还有一个交点的情形下,求△ABC 的面积S 与a 之间的函数关系式.并写出自变量a 的取值范围.四、解答题(本题共20分,每小题5分)19.在母亲节来临之际,某校团委组织了以“学会生存,感恩父母”为主题的教育活动,在学校随机调查了若干名同学平均每周在家做家务的时间,统计并制作了如下的频数分布表和扇形统计图:根据上述信息回答下列问题:(1)a= ,b= ;(2)在扇形统计图中,B 组所占圆心角的度数为 ;(3)全校共有1000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?20. 如图,在平行四边形ABCD 中,5AB =,8BC =,AE BC ⊥于点E ,53cos =B ,求tan CDE ∠的值.21.如图,在矩形ABCD 中,点O 在对角线AC 上,以OA 长为 半径的O ⊙与AD ,AC 分别交于点E ,F ,∠ACB =∠DCE .(1)请判断直线CE 与O ⊙的位置关系,并证明你的结论;(2)若 DE:EC=1 2BC =,求⊙O 的半径.22. 阅读并回答问题:小亮是一位刻苦学习、勤于思考、勇于创新的同学.一天他在解方程21x =-时,突发奇想:21x =-在实数范围内无解,如果存在一个数i ,使21i =-,那么当21x =-时,有x =±i ,从而x =±i 是方程21x =-的两个根.据此可知:(1) i 可以运算,例如:i 3=i 2·i =-1×i =-i ,则i 4= , i 2011=______________,i 2012=__________________;(2)方程2220x x -+=的两根为 (根用i 表示).五.解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 已知关于x 的方程2(1)(4)30m x m x -+-+=. (1) 若方程有两个不相等的实数根,求m 的取值范围;(2) 若正整数m 满足822m ->,设二次函数2(1)(4)3y m x m x =-+-+的图象与x 轴交于A B 、两点,将此图象在x 轴下方的部分沿x 轴翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当直线3y kx =+与此图象恰好有三个公共点时,求出k 的值(只需要求出两个满足题意的k 值即可).24. 已知:等边ABC ∆中,点O 是边AC,BC 的垂直平分线的交点,M,N 分别在直线AC , BC上,且60MON ∠=.(1) 如图1,当CM=CN 时, M 、N 分别在边AC 、BC 上时,请写出AM 、CN 、MN 三者之间的数量关系;(2) 如图2,当CM ≠CN 时,M 、N 分别在边AC 、BC 上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;(3) 如图3,当点M 在边AC 上,点N 在BC 的延长线上时,请直接写出线段AM 、CN 、MN 三者之间的数量关系.25.如图,在平面直角坐标系xOy 中,已知二次函数2+2y ax ax c =+的图像与y 轴交于点(0,3)C ,与x轴交于A 、B 两点,点B 的坐标为(-3,0) (1) 求二次函数的解析式及顶点D 的坐标;(2) 点M 是第二象限内抛物线上的一动点,若直线OM 把四边形ACDB 分成面积为1:2的两部分,求出此时点M 的坐标;(3) 点P 是第二象限内抛物线上的一动点,问:点P 在何处时△CPB 的面积最大?最大面积是多少?并求出 此时点P 的坐标.2012北京市东城区中考二模数学试题及答案11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012中考二模试题22题
昌平22.有一种亮度可以调节的小台灯,其电路图如图
5甲所示。
电源电压保持不变,通过灯泡L 的电流跟其两端电压的关系如图5乙所示。
调节滑动变阻器,当灯泡两端电压为额定电压12V 时,滑动变阻器接入电路的电阻为R 1,此时灯泡L 电阻与R 1的比值为4:1;调节滑动变阻器R ,使灯泡L 的功率为3.6W ,此时滑动变阻器
R 连入电路的阻值为 Ω。
顺义22.在图9所示的电路中,电源电压保持不变,电阻Ω=601R 。
闭合开关S ,移动
滑动变阻器的滑片P ,当电流表的示数为0.2A 时,滑动变阻器消耗的电功率为3.6W ;当电流表的示数为0.3A 时,滑动变阻器在20s 的内产生的热量是 J 。
石景山
23.灯泡L 1标有“6V 9W ”,灯泡L 2标有“?V 1W ”,灯泡L 2的额定电压模糊不清。
将两灯泡并联在3V 的电
源上,灯泡L 1比灯泡L 2亮;将两灯泡串联在5V 的电源上,灯泡L 2恰好正常发光,此时灯泡L 1消耗的电功率为 W 。
0.25
门头沟22.阻值为R 1的电阻丝接入电压为U 的电路中,通电10min ,电流产生的热量为Q 。
阻值为R 2的电阻丝
接入电压为2U 的电路中,通电5min ,电流产生的热量是4Q 。
如果将电阻丝R 1、R 2串联接入电压为U 的电路中,为使电阻丝R 1、R 2产生的总热量为Q ,则需要通电的时间是 min 。
15
丰台22. 有两台电炉,其电热丝的电阻分别为R 1和R 2,把R 1单独接在电压为U 的某一电源上给初温为t o ,质量
为m 的一壶冷水加热至沸腾需要时间为t 1,把R 2单独接在此电源上给同样这壶水加热至沸腾,需要时间为t 2,如果把它们串联在此电源上仍给这壶水加热至沸腾,需要时间t 为 ________ 。
2(t 1+t 2)
西城22.如图9所示电路电源两端电压不变。
只闭合开关S 1时,电流表的示数为I 1;只闭合开关S 2时,电流表
的示数为I 2。
通过先后闭合开关S 2和S 3,使两个电阻各自的通电时间分别为t 和t '。
若I 1∶I 2=2∶3,t ∶t '=3∶2,则电流通过电阻R 1和R 2做功之比W 1∶W 2=________。
4∶3
图5
东城23.如图11所示电路,滑动变阻器的最大阻值为R 2=30Ω,灯上标有“3V
3W ”字样,电源电压及灯L 的电阻保持不变。
当S 1、S 2闭合S 3断开、且滑片
滑到a 端时,电流表A 1、A 2的示数之比是3:1;当S 1、S 2断开S 3闭合,且滑片P 置于变阻器的中点时,灯刚好正常发光。
通过调节开关的通断和变阻器滑片
的位置,可使整个电路消耗的电功
率最小,此最小电功率值是 W 。
(保留两位小数)4.5×107
1. 小芳家里的电饭锅铭牌上标有“220V 1100W ”的字样,电热水壶的铭牌上标有“220V 550W ”的字样。
有
一天,在家庭电路的用电高峰期间,小芳同时使用电饭锅煮粥和电热水壶烧水,电饭锅和电热水壶的实际工作电压是200V ,煮粥和烧水各用了11min ,则电饭锅和电热水壶共放出__________J 的热量。
(电饭锅和电热水壶工作时的电阻保持不变)。
海淀22.有甲、乙两根电阻丝和一个输出电压不变的电源。
如果将甲、乙两根电阻丝串联后接在这个电源两端,
甲、乙两根电阻丝在时间t 内产生的热量分别为Q 1、Q 2;将乙电阻丝单独接在这个电源两端,若不计电阻丝电阻随温度的变化,则乙电阻丝在时间t 内产生的热量为 。
2009年22.图7所示的电路中,电阻R 1的阻值为10Ω。
闭合开关S ,电流表A 1的示数为2A ,电流表A 2的
示数为0.8A ,则电阻R 2的阻值为 Ω。
2010年22.如图9所示,电源两端电压不变,电阻R 1的阻值为2Ω。
闭合开关S ,当
滑动变阻器的滑片P 位于A 点时,电压表V 1的示数为4V ,电压表V 2的示数为10V 。
当滑动变阻器的滑片P 位于B 点时,电压表V 1的示数为8V ,电压表V 2的示数为11V 。
则电阻R 2的阻值是 Ω。
2011年22.有两根电阻丝R 1、R 2和一个电源E ,且电源E 两端电压保持不变。
如果只将电阻丝R 1接在电源E
两端,电阻丝R 1在120s 内产生的热量为12Q ;如果将电阻丝R 1、R 2并联接在电源E 两端,电阻丝R 1、R 2在60s 内产生的总热量为8Q ;如果将电阻丝R 1、R 2串联接在电源E 两端,为使电阻丝R 1、R 2产生的总热量为3Q ,则需要通电的时间是 s 。
图11
图9。
