北京市第 届迎春杯小学数学竞赛决赛试题
北京市第10届迎春杯小学数学竞赛决赛试题.doc

北京市第10届迎春杯小学数学竞赛决赛试题1.计算:(×1.65-+×)×47.5×0.8×2.52.计算:(-)÷[+(4-)÷1.35]3.用一个杯子盛满水向一个空罐里倒水。
如果倒进2杯水,连罐共重0.6千克;如果倒进5杯水,连灌共重0.975千克。
这个空罐重________千克。
4.一个直角梯形,它的上底是下底的60%。
如果上底增加24米,可变成正方形。
原来直角梯形的面积是________平方米。
5.如果按一定规律排出的加法算式是:3+4,5+9,7+14,9+19,11+2 4,…。
那么,把各个算式中前后两个加数分别排到第10个就是________和_ _______;第80个算式就是________。
6.甲乙二人共同加工一批零件,8小时可完成任务。
如果甲单独加工,便需要12小时完成。
现在甲、乙二人共同生产了小时后,甲被调出做其他工作,由乙继续生产了420个零件才完成任务。
乙一共加工零件________个。
7.把一个长25厘米,宽10厘米,高4厘米的长方体木块锯成若干个大小相等的正方体,然后拼成一个大的正方体。
这个大正方体的表面积是______ __平方厘米。
8.有5000多根牙签,可按六种规格分成小包。
如果10根一包,那么最后还剩9根。
如果9根一包,那么最后还剩8根。
第三、四、五、六种的规格是,分别以8、7、6、5根为一包,那么最后也分别剩7、6、5、4根。
原来一共有牙签________根。
9.用红、黄、蓝、黑、白、绿六种颜色分别涂在正方体的各面上(每个面只涂一种颜色),现在涂色方式完全一样的相同的四块小正方体,把它们拼成一长方体,如图所示。
试回答:每个小正方体红色面的对面涂的是______ __色,黄色面的对面涂的是________色,黑色面的对面涂的是________色。
10.李刚给军属王奶奶运蜂窝煤,第一次运了全部的,第二次运了50块。
2022年1月1日迎春杯数学竞赛决赛小高组真题及解析

小学高年级组决赛试卷C一.填空题Ⅰ(每小题8分,共32分)1. 算式+⨯÷−⨯20 4.5 4.522 4.5 4.5)()( 的计算结果是__________.〖答案〗23〖解析〗+⨯÷−⨯=⨯+⨯÷⨯−⨯=÷=20 4.5 4.522 4.5 4.52049922499161723)()()()(2. 右图中,有一个以AB 为直径的半圆,和一个以C 为圆心的扇形.如果AB 长20厘米,那么整个图形的面积是__________平方厘米.(π取3.14) 〖答案〗214〖解析〗S =S 半圆+S 扇形-S △ABC =π×10²÷2+π×(20²÷2)÷4-20²÷4 =50π+50π-100=100π-100≈214 (平方厘米)3. 在2021年8月8日闭幕的东京奥运会上,中国获金、银、铜牌共88枚.其中金牌、铜牌枚数和比银牌枚数多75%,金牌枚数是银牌、铜牌枚数和的76%.那么,中国在这届奥运会上共获铜牌__________枚. 〖答案〗18 〖解析〗银牌枚数=88÷(1+75%+1)=32;金牌枚数=88÷(1+76%)×76%=38; ∴ 铜牌枚数=88-32-38=184. 如图,乘法算式中已经填出了“2022”和“9”,那么算式的乘积是__________. 〖答案〗87957 〖解析〗2022=2×3×337,故竖式中做加法时的两个三位数只能选自337或674. 337或674中最大数字为7,从而做加法时十位向百位不进位.再看做加法时的百位,□+2+□=9,两个方块对应337或674中的个位或百位,只有337的百位3与674的个位4满足.从而第一个乘数为337,第2个乘数为261,337×261=87957二.填空题Ⅱ(每小题10分,共40分)5.甲,乙,丙,丁,戊五人在参加数学测评前,预测如下:甲说:“如果戊进了前三名,那我就能得第二.”乙说:“如果甲得了第二,那我就能得第一.”丙说:“第一名肯定是我.”丁说:“估计戊的名次高于我.”戊说:“我想这次测评应能如期进行.”结果这五人恰好获得了这次测评的前五名(无并列),且他们的预测全都正确.如果甲,乙,丙,丁,戊获得的名次依次是A,B,C,D,E,那么五位数ABCDE是__________.〖答案〗32154〖解析〗据丙所说知丙第1,结合乙所说知甲不是第2,再结合甲所说知戊没进了前三,从而戊得第4或第5,又据丁所说知戊第4且丁第5.甲不是第2,那甲只能是第3,余下乙只能为第2.∴五位数ABCDE=32154.6.将0~9分别填入到右图的10个圆圈中,使得各条直线上圆圈中所填数的和都相等.现已将1填入,那么圆圈A、B、C、D中所填数字依次组成的四位数是__________.〖答案〗2480〖解析〗共6条直线,除了F只在1条直线上,其余圆圈都恰好在2条直线上.设每条直线上圆圈中所填数的和为S,则6S=(0+1+2+…+9)×2-F.由6|F得F为0或6.若F=0,则S=15,E=14,矛盾!∴F=6,从而S=14,E=7.若9在A~D中,则14=9+5=9+0+2+3,而C≥14-1-9=4,只能C=9,从而I=4,H≤14-7-2=5,8只能在G,D=14-8-4=2,余下5在H,B =14-7-5=2,矛盾!∴9不在A~D中,G=9或I=9.若I=9,8不能与7或9同直线,只能A=8,从而B+D=14-8-4=2=2+0,B=2,D=0,得H=14-7-2=5,G=14-9-0=5,矛盾!I≠9∴G=9.8不能与7或9同直线,只能C=8.从而I=14-1-8=5,D=14-9-5=0,A=45-14×2-6-9-0=2,B=14-2-8-0=4,H=14-7-4=3,如右图.∴圆圈A、B、C、D中所填数字依次组成的四位数是2480.7. 圣诞老人的袋子里有一百多块糖.有10个小朋友排着队等待圣诞老人依次发糖.圣诞老人给每个小朋友发糖之前都会问:“你猜我现在袋子里糖的块数是质数还是合数?如果猜对了就给你3块糖,如果猜错了就只能给1块糖咯!”结果10个小朋友全都猜“是合数”,那么这10个小朋友得到的糖果块数总和至少是__________. 〖答案〗26 〖解析〗假设开始时袋子里糖数为N ,如果N 是3的倍数,那么10个人都猜对了. 如果N 除以3余1,那么有1个小朋友猜错后,糖数就会变为3的倍数,剩余的小朋友都能猜对. 如果N 除以3余2,那么有2个小朋友猜错后,糖数就会变为3的倍数,剩余的小朋友都能猜对. ∴ 10个小朋友中最多只有2个人猜错了,至少得到⨯+⨯=218326块糖. 下面举例说明存在2个小朋友猜错的情况: 比如N =140,那么①140√,②137×,③136√,④133√,⑤130√,⑥127×,⑦126√,从第7个小朋友开始,糖数均为3的倍数,都能猜对. ∴ 综上所述,本题答案为26.8. 2022除了自身以外,最大的3个约数分别是1011、674、337,这三个数之和恰好是2022本身;那么像2022这样,除了自身以外最大3个约数之和等于自身的数,叫做“和谐数”.那么,小于2022的“和谐数”共有__________个. 〖答案〗134 〖解析〗设N 除了自身以外,最大的三个约数是A >B >C ,那么D =N ÷A 、E =N ÷B 、F =N ÷C 全是N 的约数,且D <E <F .由A +B +C =N ,有++=N N N A B C 1即++=D E F1111,有唯一解:D =2、E =3、F =6.∴ N 是“和谐数” 即 2|N 且3|N 但N 不能是4的倍数或5的倍数1~2021中6的倍数有⎣⎦⎢⎥⎡⎤62021=336个;其中,4的倍数有⎣⎦⎢⎥⎡⎤122021=168个,5的倍数有⎣⎦⎢⎥⎡⎤302021=67个,既是4的倍数又是5的倍数有⎣⎦⎢⎥⎡⎤602021=33个.∴ 小于2022的“和谐数”共有336-168-67+33=134个.AB C D E三.填空题Ⅲ(每小题12分,共48分)9. A 、B 两地之间有四段山路,其中AC 段和DE 段路程相等,CD 段与EB 段路程相等.甲、乙两人分别从A 、B 两地同时出发相向而行,两人上山速度相同,下山速度也相同,并且下山速度均为上山速度的1.5倍.当甲到C 点时,乙已经到E 点并向下走了180米;乙比甲早1分钟到达D 点;甲比乙早10分钟到达C 点;那么A 、B 两地之间的路程为__________米. 〖答案〗1296 〖解析〗AC 段比BE 段多180÷1.5=120米;从而当乙到达D 时,甲差180-120=60米到D ,则下山速度为60米/分,上山速度40米/分;当甲到C 时,乙在E 下行180米处(设为F 点),乙F →D →C 共用10分钟,FD 段比DC 段短60米,那么C →D →C 共用10+60÷60=11分钟,时间比为1:1.5=2:3,从而C →D 用11÷(2+3)×2=4.4分钟.∴ CD 段长60×4.4=264米. ∴ A 、B 两地之间的路程为(264×2+120)×2=1296米.10. 一个自然数共有18个因数,其中恰好有6个一位数,6个两位数,6个三位数;那么这个自然数是__________. 〖答案〗972 〖解析〗设这个自然数为M ,则M 必定为三位数.18=2×3×3,故M 分解质因数后有3类可能:⨯⨯A B C 221、⨯A B 81、⨯A B 52,(1)若=⨯⨯M A B C 221,由于因数中不存在3次方,故8不是M 的因数,2和3必定是M 的因数.如果A =2,B =3,此时M 已经有了6个一位因数(1、2、3、4、6、9)和3个两位因数(12、18、36);如果要有6个两位因数,C 必须满足4C ≥100,而M 是个三位数,所以有36C <1000,因为不存在同时满足两个条件的质数,所以A =2,B =3不成立.如果B =3,C =2,此时M 已有了5个一位因数(1、2、3、6、9)和一个两位因数(18);如果要有6个一位因数,A 必须等于5或者7,此时两位因数已有7个(18、2A 、3A 、6A 、9A 、A ²、2A ²),矛盾!所以B =3,C =2不成立;同理B =2,C =3也不成立.(2)若=⨯M A B 81,为了确保M 是三位数,必定有A =2,B =3,容易发现此时M 有7个一位因数(1、2、3、4、6、8、9),故此种情况不成立.(3)若=⨯M A B 52,为了确保M 是三位数,只能A =2,B =3或A =3,B =2.当A =2,B =3时M 有7个一位因数(1、2、3、4、6、8、9),矛盾!当A =3,B =2时M =972恰好有6个一位因数(1、2、3、4、6、9),6个两位因数(12、18、27、36、54、81),6个三位因数(108、162、243、324、486、972) ∴ 综上所述,M =972.11. 5对兄弟,分成5组,每组2人,要求每人都不与自己的兄弟同组,共有__________种不同的分组方式. 〖答案〗544〖解析〗设这5对兄弟分别是A 1,A 2,B 1,B 2,C 1,C 2,D 1,D 2,E 1,E 2,用“B →E →C →…→B ”来表示B 组中的哥哥与E 组中的某人同组,E 组中的另一人与C 组中的某人同组,…,最后必然有人与B 组的弟弟同组,形成循环.形成循环的关系只有右图中的2种.(1)若5对兄弟形成5边形的循环:⨯=A 2384444(2)若3对兄弟形成3边形的循环和另2对兄弟的循环:⨯⨯⨯⨯=C A A 2216052122211)()(∴ 综上所述,同的分组方式共有:384+160=544种. 〖注〗本题还可用容斥原理或递推方法解答.12. (投票题)四.填空题Ⅳ(每小题15分,共30分)13. 如图,每个正六边形都有三个顶点在长方形ABCD 的边上;大正六边形的顶点O 恰为AB 中点,小正六边形的面积为60.(1)DECD的值是__________.(6分) (2)长方形ABCD 的面积是__________.(9分) 〖答案〗(1)9 (2)315〖解析〗(1)设大,小正六边形的边长分别为a ,b ,据右图的分割知:AO =1.5b +0.5a ,BO =1.5a ,由AO =BO 得a =1.5b . CD =AB =1.5a ×2=3a =4.5b ,DE =0.5b . ∴ CD ÷DE =4.5b ÷0.5b =9.(2)设EF =c ,则OG =1.5c ,则BC =OG +2c =1.5c +2c =3.5c ,∴ 长方形面积为4.5b ×3.5c =15.75bc . 而小正六边形的面积为b ×c ÷2×6=3bc .∴ 小正六边形和长方形的面积比是3bc : 15.75bc =4 : 21 ∴ 长方形的面积是60÷4×21=315.14. 在右图5×5的表格中,微型机器人任选一小格为出发格,任选上、下、左、右中的一个方向为出发方向,走到前方相邻的小格;新到小格编号若为奇数则往左拐,为偶数则往右拐,再走到前方相邻的小格;若前方走到了5×5表格外面或前方相邻小格已经到过则停止.如选择编号为17的小格出发向右,则只能如图17→18(右拐)→23(左拐)→24(右拐,出界,停止).(1)如果每个小格编号如右图,那么微型机器人到过的小格(含出发格)编号总和的最大值为__________.(5分) (2)如果对图中25个小格任意编号为1~25,那么微型机器人到过的小格(含出发格)编号总和的最大值为__________.(10分)〖答案〗(1)129 (2)304 〖解析〗(1)任意相邻两格编号的奇偶性不同,从而微型机器人前进构成中,左拐、右拐相间,∴ 机器人行进路线(或旋转翻转后)必为图中阶梯箭头状,最多能到9格.对角线上5数的和为13×5=65,另4数选10+14+18+22=64最大,9数和为65+64=129,如右图.而选7格时最大为64+15+19+23=121<129.∴ 小格编号如右图时,微型机器人到过的小格编号总和的最大值为129.(2)如图,对5×5的表格中每个小格标上1、2、3、4中的1个,微型机器人连续经过的4个小格必是标有1、2、3、4的各1个;而标4的有4个,从而机器人至多经过4×4+3=19格,1~25中最大的19个不同数的和是:7+8+9+…+25=304.而右图中机器人依次经过标有25,24,23,…,7的小格.∴ 综上所述,对小格任意编号为1~25时,机器人到过的小格编号总和的最大值为304.。
“迎春杯”数学竞赛训练题

“迎春杯”数学竞赛训练题1.计算:11112481024++++ = . 2.计算:17911131582131220304256⎛⎫-+-+-⨯⨯ ⎪⎝⎭= . 3.已知:()2,220m n m m m n ++=--=那么mn = .4.方程0.30.80.020.30.80.410.50.33x x x ++---=的解是x = . 5.三位数中至少有1位是9的一共有 个. 6.已知关于x 的方程5514228x x a -=+中, x 和a 都是正整数,那么a 最小为 . 7.一堆彩色球,有红、兰两种颜色.第一次拿出50个球,其中49个是红球,以后每次拿出8个球,都有7个红球,一直拿到最后恰好拿完.如果在所有拿出的球中红球不少于90%,那么这堆球最多有 个.8.已知一列数:1121123211,,,,,,,,,,1222333334 ,那么710是第 个数,第400个数是 . 9.一个盒子里有7个球,标有1、2、3、…、7号,每次取出一个,记下它的号后,再放回,共记录4次.那么记录下的数字最大数恰好是5的取法数是 .10.从1、3、4、5、7、8、9中任选四个数(无重复)组成四位数,把它们从小到大排列起来,那么从小开始第117个数是 .11.如果方程组5311x y m x y +=⎧⎨+=⎩的解是正整数,那么整数m = .12.有一个工程,甲单独做a 天完成,乙单独做b 天完成(a 、b 都是正整数),现在甲先作4天,余下的由甲、乙合作3天完成,那么a = ,b = .13.已知520,2530m n ≤≤≤≤,那么m n的最大值为 ,最小值为 . 14.如果1x =-是方程20x ax b ++=的一个根,且17a b a b -=+,那么ab = . 15.一个六位数是4的倍数,被11除余5,中间的四位数是1527,那么首位与末位的和为 .16.如图,每个圆的面积是30, A 与B 、B 与C 、C 与A 的重合部分面积分别为6、8、5, 三个圆总覆盖面积为73,那么阴影部分的面积为 .17.图中的五角星共有线段 条.18.如果m 为整数,244m m --是完全平方数,那么m = .19. 甲、乙二人进行400米竞走,当甲到达终点时,乙距终点还差m 米.如果甲、乙二个速度不变,甲从()400m +米处开始,那么比赛结果是 先到.20.如图,长方形ABCD 的面积为64, EC =2BE , CF =2FD ,那么三角形AEF 的面积为 .21.如图,P 为三角形ABC 内一点, AP 、BP 、CP 分别与对边交于D 、E 、F , 把三角形ABC 分成六个小三角形,其中四个小三角形的面积已在图中给出,那么三角形ABC 的面积为 .22.有A 、B 、C 、D 、E 、F 、G 、H 8名学生,参加某项比赛,赛后他们猜测比赛的第一名: A : F 或H 是第一名;B : 我是第一名;C : G 是第一名;D : B 不是第一名;E : A 说的不对;F : 我不是第一名,H 也不是第一名;G : C 不是第一名;H: 我同意A 的意见.老师指出:有三个人猜对了,那么第一名是 .23.若关于x 的方程()()3223512a x b x x ++-+=+有无穷多个解,那么a = ,b .24.平面上有2003个点,以这些点为端点连线段,且不能以这些点为顶点构成三角形, 那么最多可连线段 条.25. A 、B 两地相距20千米, 甲、乙两人分别从A 、B 两地同时相向而行,两小时后在途中相遇;然后甲回A 地,乙仍继续前行,当甲回到A 地时,乙离A 地还有两千米,那么甲的速度为 ,乙的速度为 .26.已知1x 、2x …n x 的值只能取0、1、2-其中的一个,且1x +2x +…+n x =5-,2221219n x x x +++= ,那么55512n x x x +++=.A F EB27.某工程队修建一条铁路,第一周铺了全长的30%,第二周的进度是第一周的89,第三周铺完剩余的路段.如果第三周比第二周多铺75米,那么这条铁路全长为 米.28. A 种原料的价格为50元/千克, B 种原料的价格为40元/千克, 以x 千克A 种原料和y 千克B 种原料混合.如果A 种原料价格增加10%,B 种原料价格减少15%,那么混合后原料价格不变, 则:x y = .29.某人乘船由甲地顺流到乙地,再从乙地逆流回到甲地.如果水流速度和船速保持不变,请你思考,在静水时用的时间多,还是在有流速时用的时间多?30.某项工程,由甲、乙两队承包,125天可以完工,需1800元;由乙、丙两队承包,154天可以完工,需1500元;由丙、甲两队承包,207天可以完工,需1600元.如果工程必须在一周内完成,只请一队,请你思考,请哪队完成工程,较为合算.31.代数式111213x x x ++-++的最小值为 .32,某种商品的原价为100元,现有四种调价方案:(1)先涨价m %,再降价n %;(2)先涨价n %,再降价m %;(3)先涨价2m n -%,再降价2m n -%; (4)先涨价2m n +%,再降价2m n +%; 其中0100n m <<<,那么调价后售价最高的方案是 . (只需填1、2、3、4中之一即可).33.如图,DE 、FG 、HI 、BC 分别平行,图中梯形的个数一共有 个.34.某校初中一年级有书法、舞蹈、足球、数学四个课外小组,一班学生共有46名,每人至少参加一个小组,至多参加三个小组,那么,其中至少有 个同学参加的课外小组相同.35.已知1x ,2x , ,n x 是一些互不相等的正整数,如果222122003n x x x +++= ,那么1x ,2x , ,n x 这些互不相等的正整数最多有 个.B C C E36.小王在一年中去少年宫学习56次.如图所示,小王家在P点,他去少年宫都是走最近的路且每次所走的路线是互不相同的,那么少年宫在点处.(A点代码1, B点代码2, C点代码3, D点代码4, E点代码5,只需填入代码即可)37.有A、B、C、D四位女同学在演唱会上表演三重唱,即每唱一首歌只出场三人.已知D唱了7首歌,比其他任何人都多,A唱了4首歌,比其他任何人都少,那么在三重唱中B唱了首歌.38.某个篮球运动员共参加了十场比赛,他在第六、七、八、九场比赛中分别得了23、14、11和20分,他的前九场比赛的平均分比前五场比赛的平均分要高,如果他的十场比赛的平均得分超过18分,那么他在第十场比赛中至少得了分.39.某校同学在一块直角三角形土地上植树(如图),以B为起点,在直角边上每隔1米取1点,如图纵横平行画出网格,要求在每个纵横交汇点(包括三角形的顶点和边上的点)处植一棵树.那么,一共可植树棵.40.有五个相同的小正方形纸片,将它们拼接成不同的图形,要求每两个相邻小正方形纸片的两边必须完全重合,并且不重叠,五个纸片连在一起(经过翻折或旋转后,形状相同的图形视为同一种).那么一共可拼接成不同图形的种数是.。
北京市第11届迎春杯小学数学竞赛决赛试题.doc

北京市第11届迎春杯小学数学竞赛决赛试题1.计算:0.625×(+)+÷―2.计算:[(-×)-÷3.6]÷3.某单位举行迎春茶话会,买来4箱同样重的苹果,从每箱取出24千克后,结果各箱所剩下的苹果重量的和,恰好等于原来一箱的重量。
那么原来每箱苹果重________千克。
4.游泳池有甲、乙、丙三个注水管。
如果单开甲管需要20小时注满水池;甲、乙两管合开需要8小时注满水池;乙、丙两管合开需要6小时注满水池。
那么,单开丙管需要________小时注满水池。
5.如图是由18个大小相同的小正三角形拼成的四边形。
其中某些相邻的小正三角形可以拼成较大的正三角形若干个。
那么,图中包含“*”号的大、小正三角形一共有________个。
6.如图,点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点。
那么,阴影部分的面积与三角形ABC的面积比是。
7.五个小朋友A、B、C、D、E围坐一圈(如下图)。
老师分别给A、B、C、D、E发2、4、6、8、10个球。
然后,从A开始,按顺时针方向顺序做游戏:如果左邻小朋友的球的个数比自己少,则送给左邻小朋友2个球;如果左邻小朋友的球的个数比自己多或者同样多,就不送了。
如此依次做下去,到第四圈为止,他们每人手中的球的个数分别是________。
8.一个分数,把它的分母减去2,即,约分以后等于;如果原来的分数的分母加上9,即,约分以后等于。
那么,=________。
9.某学生将1.2乘以一个数α时,把1.2误看成1.23,使乘积比正确结果减少0.3。
则正确结果应该是________。
10.某校师生为贫困地区捐款1995元,这个学校共有35名教师,14个教学班。
各班学生人数相同且多余30人不超过45人。
如果平均每人捐款的钱数是整数,那么平均每人捐款________元。
11.已知:[13.5÷(11+)-1÷7]×=1。
2017年迎春杯五年级竞赛决赛数学试卷二试(答案解析)

解析 A、A+1、B、B+1均不为质数;也不能是质数的n次方.所以,B只能是14.(B为6、10
时,B+1都是质数),此时B+1为15,B(B+1)含有质因数2、3、5、7;最小符合条件的A
为20,所以,A+ B最小值为34 .
在空格里填入数字1~6,使得每行、每列和每宫数字都不重复,每个灰格里的数,在它周
解答
如图,0为三角形ABC内一点.三角形OAC、三角形OAB、三角形OBC的面积分别为30、
60、120 .如果AD= 1.5DB,AE=2EC,求∶
(1) OM: MB.
(2)三角形OMN的面积 .
学而思培优
(1) 1:2.
(2) 16.
(1)方法一∶延长BO交AC于K,
由左图得,BO∶OK=60∶10=6∶1,BO=号BK;
学而思培优
2017年迎春杯五年级竞赛决赛数学试卷二试
填空 将一个正四面体的6条棱中的3条染成黑色,另外3条染成白色,有_种不同的染色方
法.(旋转后相同的染色方法视为同一种染色方法)
如果两个正整数A和ຫໍສະໝຸດ 满足以下条件 ∶①A(A+ 1)是B(B+ 1)的倍数; ②A和(A+ 1)都不是B或者(B+ 1)的倍数; 那么,A+ B的最小值是_
店的编号居然还是a2,此时,甲刚好走到一个编号为三位完全平方数的加油站.
那么,AB两地相距多少千米 ?
840.
从出发到甲、丙相遇为第一阶段,从甲丙相遇到乙、丙相遇为第二阶段,乙第一阶段走了52
,第二阶段走了72,所以∶
t:ta=5:2,
8,8,=1∶(号×台
{(P-1)=b-1,可得P=97,B2= 121; (S-5P+5d): s=5:2
号加油站开始,依次是1号、2号、3号……;每隔7千米,有一个便利店,从A地的1号便利
第1-29届历届小学“迎春杯”真题word版

目录第1届“迎春杯”数学竞赛刊赛试题... .............................................................. . 1 第2届“迎春杯”数学竞赛决赛试题... .............................................................. . 5 第3届“迎春杯”数学竞赛决赛试题... .............................................................. . 8 第4届“迎春杯”数学竞赛决赛试题... ............................................................ .. 10 第5届“迎春杯”数学竞赛决赛试题... ............................................................ .. 11 第6届“迎春杯”数学竞赛决赛试题... ............................................................ .. 13 第7届“迎春杯”数学竞赛决赛试题... ............................................................ .. 16 第8届“迎春杯”数学竞赛决赛试题... ............................................................ .. 18 第9届“迎春杯”数学竞赛决赛试题... ............................................................ .. 20 第10 届“迎春杯”数学竞赛决赛试题... .......................................................... (23)第11 届“迎春杯”数学竞赛初赛试题... ........................................................... (25)第11 届“迎春杯”数学竞赛决赛试题... ........................................................... (27)第12 届“迎春杯”数学竞赛决赛试题... .......................................................... (29)第12 届“迎春杯”数学竞赛决赛试题... .......................................................... (31)第13 届“迎春杯”数学竞赛初赛试题... .......................................................... (33)第13 届“迎春杯”数学竞赛决赛试题... .......................................................... (35)第14 届“迎春杯”数学竞赛决赛试题... .......................................................... (37)第14 届“迎春杯”数学竞赛决赛试题... .......................................................... (39)第15 届“迎春杯”数学竞赛初赛试题... .......................................................... (41)第15 届“迎春杯”数学竞赛决赛试题... .......................................................... (43)第16 届“迎春杯”数学科普活动日区县邀请赛试题... .................................. (45)第17 届“迎春杯”数学科普活动日队际交流试题... ....................................... . 47 第18 届“迎春杯”数学科普活动日队际交流试题... ....................................... . 50 第19 届“迎春杯”数学科普活动日计机交流试题... ....................................... . 52 第19 届“迎春杯”数学科普活动日队际交流试题... ....................................... . 54 第20 届“迎春杯”数学科普活动日试题... ....................................................... .. 55 第21 届“迎春杯”数学科普活动日解题能力展示初赛试题... ...................... (57)第21 届“迎春杯”数学解题能力展示读者评选活动复试计算机交流试题... (58)第22 届“迎春杯”数学解题能力展示读者评选活动中年级初试试题... ..... .. 60 第22 届“迎春杯”数学解题能力展示读者评选活动中年级复试试题... ..... .. 62 第22 届“迎春杯”数学解题能力展示评选活动高年级初试试题... .............. . 64第22 届“迎春杯”数学解题能力展示评选活动高年级复试试题... .............. . 66第23 届“迎春杯”数学解题能力展示评选活动中年级初试试题... .............. . 69第23 届“迎春杯”数学解题能力展示评选活动中年级复试试题... .............. . 71第23 届“迎春杯”数学解题能力展示评选活动高年级初试试题... .............. . 73第23 届“迎春杯”数学解题能力展示评选活动高年级复试试题... .............. . 75第24 届“迎春杯”数学解题能力展示评选活动三年级初试试题... .............. . 77第24 届“迎春杯”数学解题能力展示评选活动四年级初试试题... .............. . 79第24 届“迎春杯”数学解题能力展示评选活动中年级复试试题... .............. . 81第24 届“迎春杯”数学解题能力展示评选活动五年级初试试题... .............. . 83第24 届“迎春杯”数学解题能力展示评选活动六年级初试试题... .............. . 85第24 届“迎春杯”数学解题能力展示评选活动高年级复试试题... .............. . 88第25 届“迎春杯”数学解题能力展示评选活动三年级初试试题... .............. . 90第25 届“迎春杯”数学解题能力展示评选活动四年级初试试题... .............. . 92第25 届“迎春杯”数学解题能力展示评选活动中年级复试试题... .............. . 94第25 届“迎春杯”数学解题能力展示评选活动五年级初试试题... .............. . 96第25 届“迎春杯”数学解题能力展示评选活动六年级初试试题... .............. . 98第25 届“迎春杯”数学解题能力展示评选活动高年级复试试题... ........... .. 100 第26 届“迎春杯”数学解题能力展示评选活动三年级初试试题... ........... .. 102 第26 届“迎春杯”数学解题能力展示评选活动四年级初试试题... ........... .. 104 第26 届“迎春杯”数学解题能力展示评选活动中年级复试试题... ........... .. 106 第26 届“迎春杯”数学解题能力展示评选活动五年级初试试题... ........... .. 108 第26 届“迎春杯”数学解题能力展示评选活动六年级初试试题... ........... .. 110 第26 届“迎春杯”数学解题能力展示评选活动高年级复试试题... ........... .. 112 第27 届“迎春杯”数学解题能力展示评选活动三年级初试试题... ........... .. 114 第27 届“迎春杯”数学解题能力展示评选活动四年级初试试题... ........... .. 116 第27 届“迎春杯”数学解题能力展示评选活动中年级复试试题... ........... .. 118第 27届“迎春杯”数学解题能力展示评选活动六年级初试试题... .......... .. 122 第 27届“迎春杯”数学解题能力展示评选活动高年级复试试题... .......... .. 124 第 28届“迎春杯”数学解题能力展示评选活动三年级初试试题... .......... .. 126 第 28届“迎春杯”数学解题能力展示评选活动四年级初试试题... .......... .. 128 第 28届“迎春杯”数学解题能力展示评选活动中年级复试试题... .......... .. 130 第 28届“迎春杯”数学解题能力展示评选活动五年级初试试题... .......... .. 132 第 28届“迎春杯”数学解题能力展示评选活动六年级初试试题... .......... .. 134 第 28届“迎春杯”数学解题能力展示评选活动高年级复试试题... .......... .. 136 第 29届“迎春杯”数学解题能力展示评选活动三年级初试试题... .......... .. 138 第 29届“迎春杯”数学解题能力展示评选活动四年级初试试题... .......... .. 140 第 29届“迎春杯”数学解题能力展示评选活动中年级复试试题... .......... .. 141 第 29届“迎春杯”数学解题能力展示评选活动五年级初试试题... .......... .. 143 第 29届“迎春杯”数学解题能力展示评选活动六年级初试试题... .......... .. 144 第 29届“迎春杯”数学解题能力展示评选活动高年级复试试题... .......... .. 145第 1 届“迎春杯”数学竞赛刊赛试题1.天安门广场是世界上最大的广场,面积约44万平方米,合____亩。
2022-2023学年度第一学期迎春杯系列竞赛一年级数学试题
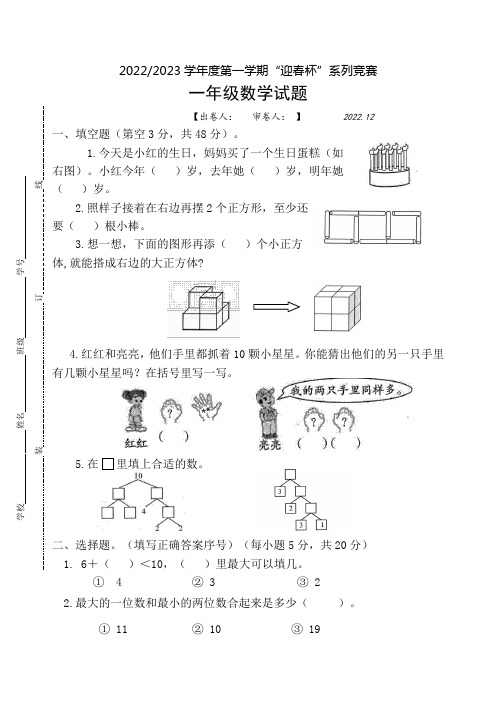
2022/2023学年度第一学期“迎春杯”系列竞赛一年级数学试题【出卷人: 审卷人: 】 2022.12 一、填空题(第空3分,共48分)。
1.今天是小红的生日,妈妈买了一个生日蛋糕(如右图)。
小红今年( )岁,去年她( )岁,明年她( )岁。
2.照样子接着在右边再摆2个正方形,至少还要( )根小棒。
3.想一想,下面的图形再添( )个小正方体,就能搭成右边的大正方体? 4.红红和亮亮,他们手里都抓着10颗小星星。
你能猜出他们的另一只手里有几颗小星星吗?在括号里写一写。
5.在 里填上合适的数。
二、选择题。
(填写正确答案序号)(每小题5分,共20分) 1. 6+( )<10,( )里最大可以填几。
① 4 ② 3 ③ 2 2.最大的一位数和最小的两位数合起来是多少( )。
① 11 ② 10 ③ 19学校 姓名 班级 学号 装 订 线3. 10位女同学,每人发一朵花,买下面哪两束比较合适?()① 4+5 ② 4+6 ③ 5+64.明明在计数器上拨了5个珠子表示一个数。
这个数比10大,比15小。
这个数是多少()。
① 5 ② 15 ③ 14三、解决问题。
(7+7+6+6+6=32分)1.王老师带着9个小朋友在玩老鹰抓小鸡游戏,已经抓住了6个小朋友,还剩几个人在做游戏?=(人)2.停车场一共有8辆小汽车,先开走4辆,接着又开走2辆,停车场现在还有多少辆小汽车?=(辆)3.(1)美术组和围棋组一共有多少人?=(人)(2)舞蹈组比美术组多多少人?=(人)(3)舞蹈组男生有6人,女生有多少人?=(人)。
北京市第10届迎春杯小学数学竞赛决赛试题

北京市第10届迎春杯小学数学竞赛决赛试题1. 计算:(×1.65-+×)×47.5×0.8×2.52.计算:(-)÷[+(4-)÷1.35]3.用一个杯子盛满水向一个空罐里倒水。
如果倒进2杯水,连罐共重0.6千克;如果倒进5杯水,连灌共重0.975千克。
这个空罐重________千克。
4.一个直角梯形,它的上底是下底的60%。
如果上底增加24米,可变成正方形。
原来直角梯形的面积是________平方米。
5.如果按一定规律排出的加法算式是:3+4,5+9,7+14,9+19,11+24,…。
那么,把各个算式中前后两个加数分别排到第10个就是________和________;第80个算式就是________。
6.甲乙二人共同加工一批零件,8小时可完成任务。
如果甲单独加工,便需要12小时完成。
现在甲、乙二人共同生产了2.4小时后,甲被调出做其他工作,由乙继续生产了420个零件才完成任务。
乙一共加工零件________个。
7.把一个长25厘米,宽10厘米,高4厘米的长方体木块锯成若干个大小相等的正方体,然后拼成一个大的正方体。
这个大正方体的表面积是________平方厘米。
8.有5000多根牙签,可按六种规格分成小包。
如果10根一包,那么最后还剩9根。
如果9根一包,那么最后还剩8根。
第三、四、五、六种的规格是,分别以8、7、6、5根为一包,那么最后也分别剩7、6、5、4根。
原来一共有牙签________根。
9.用红、黄、蓝、黑、白、绿六种颜色分别涂在正方体的各面上(每个面只涂一种颜色),现在涂色方式完全一样的相同的四块小正方体,把它们拼成一长方体,如图所示。
试回答:每个小正方体红色面的对面涂的是________色,黄色面的对面涂的是________色,黑色面的对面涂的是________色。
10.李刚给军属王奶奶运蜂窝煤,第一次运了全部的,第二次运了50块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市第11届迎春杯小学数学竞赛决赛试题
1. 计算:0.625×(+)+÷―
2. 计算:[(-×)-÷3.6]÷
3. 某单位举行迎春茶话会,买来4箱同样重的苹果,从每箱取出24千克后,结果各箱所剩下的苹
果重量的和,恰好等于原来一箱的重量。那么原来每箱苹果重________千克。
4. 游泳池有甲、乙、丙三个注水管。如果单开甲管需要20小时注满水池;甲、乙两管合开需要8
小时注满水池;乙、丙两管合开需要6小时注满水池。那么,单开丙管需要________小时注满水
池。
5. 如图是由18个大小相同的小正三角形拼成的四边形。其中某些相邻的小正三角形可以拼成较大
的正三角形若干个。那么,图中包含“*”号的大、小正三角形一共有________个。
6. 如图,点D、E、F与点G、H、N分别是三角形ABC与三角形DEF各边的中点。那么,阴影部分
的面积与三角形ABC的面积比是。
7. 五个小朋友A、B、C、D、E围坐一圈(如下图)。老师分别给A、B、C、D、E发2、4、6、8、1
0个球。然后,从A开始,按顺时针方向顺序做游戏:如果左邻小朋友的球的个数比自己少,则
送给左邻小朋友2个球;如果左邻小朋友的球的个数比自己多或者同样多,就不送了。如此依次
做下去,到第四圈为止,他们每人手中的球的个数分别是________。
8. 一个分数,把它的分母减去2,即,约分以后等于;如果原来的分数的分母加上9,即
,约分以后等于。那么,=________。
9. 某学生将1.2乘以一个数α时,把1.2误看成1.23,使乘积比正确结果减少0.3。则正确结
果应该是________。
10. 某校师生为贫困地区捐款1995元,这个学校共有35名教师,14个教学班。各班学生人数相同
且多余30人不超过45人。如果平均每人捐款的钱数是整数,那么平均每人捐款________元。
11. 已知:[13.5÷(11+)-1÷7]×=1。那么,О=________。
12. 两个自然数a与b,它们的最小公倍数是60。那么,这两个自然数的差有________种可能的数值。
13. 少年歌手大奖赛的裁判小组由若干人组成。每名裁判员给歌手的最高分不超过10分。第一名歌
手演唱后的得分情况是:全体裁判员所给分数的平均分是9.64分;如果只去掉一个最高分,则其
余裁判员所给分数的平均分是9.60分;如果只去掉一个最低分,则其余裁判员所给分数的平均分
是9.68分。那么,所有裁判员所给分数中的最低分最少可以是________分,这次大奖赛的裁判员
共有________名。
14. 有一座时钟现在显示10时整,那么,经过________分钟,分针与时针第一次重合;再经过____
____分钟,分针与时针第二次重合。
15. 有甲、乙、丙三种大小不同的正方体木块,其中甲的棱长是乙的棱长的,乙的棱长是丙的棱长
的。如果用甲、乙、丙三种木块拼成一个体积尽可能小的大正方体(每种至少用一块)。那么
最少需要这三种木块一共________块。
16. 为举办春节拥军优属联欢会,第一居委会买了9千克桔子和10千克苹果,一共用了73.8元;第
二居委会买了17千克鸭梨和6千克香蕉,一共用了69.8元。如果桔子和鸭梨的单价相同,苹果
和香蕉的单价也相同。那么桔子每千克________元,香蕉每千克________元。
17. 如图,九个小正方形内各有一个两位数,而且每行、每列及两条对角线上的三个整数的和相等。
那么Χ=________。
18. 小明从家到学校时,前一半路程步行,后一半路程乘车;他从学校回家时,前时间乘车,后
时间步行。结果去学校的时间比回家所用的时间多2小时。已知小明步行每小时行5千米,乘车
每小时行15千米。那么,小明从家到学校的路程是________千米。
19. 甲有桌子若干张,乙有椅子若干把。如果乙用全部椅子换回数量同样多的桌子,则需补给甲320
元;如果乙不补钱,就要少换回5张桌子。已知3张桌子比5把椅子的价钱少48元,那么乙原有
椅子多少把?
20. 请将1,2,3,…,99,100这一百个自然数中既是奇数又是合数的自然数排成一行,使每两个
相邻的数都不互质(若一行写不下,可移至第二行接着写,若第二行仍写不下,可移至第三行接
着写)。
