10 平行四边形性质及判定练习题
平行四边形判定专项练习30题

平行四边形的判定专项练习30 题(有答案)1.如图,四边形ABCD 中, AD ∥BC, ED∥ BF , AF=CE ,求证: ABCD 是平行四边形.2.如图,四边形ABCD 中,∠ BAC=90 °, AB=11 ﹣ x, BC=5 , CD=x ﹣ 5, AD=x ﹣ 3, AC=4 .求证:四边形ABCD 为平行四边形.3.已知四边形ABCD 的对角线AC 与 BD 交于点 O,现给出四个条件:① OA=OC ;② AB=CD ;③∠ BAD= ∠DCB ;④ AD ∥ BC.请你从中选择两个,推出四边形ABCD 为平行四边形,并写出你的推理过程.( 1)从以上 4 个条件中任意选取 2 个条件,能推出四边形ABCD 是平行四边形的有(用序号表示)_________.( 2)从( 1)中选出一种情况,写出你的推理过程.4.如图,已知:点 B 、 E、 F、D 在一条直线上,DF=BE , AE=CF .请从下列三个条件中选择一个合适的条件,添加到已知条件中,使四边形ABCD 是平行四边形,并说明理由,供选择的三个条件(请从其中选择一个):①AB=DC ;② BC=AD ;③ ∠ AED= ∠ CFB .5.如图,在 ?ABCD 中, AC 交 BD 于点 O,点 E,点 F 分别是 OA ,OC 的中点,请判断线段 BE , DF 的位置关系和数量关系,并说明你的结论.6.如图所示,以△ABC 的三边为边在 BC 的同侧分别作三个等边三角形△ ABD 、△ BCE、△ ACF ,猜想:四边形ADEF 是什么四边形,试证明你的结论.7.如图,已知BE ⊥ AD , CF⊥ AD ,且 BE=CF .求证:( 1)AD 是△ ABC 的中线;( 2)请连接BF、 CE,试判断四边形BECF 是何种特殊四边形,并说明理由.8.如图,矩形 ABCD 的两条对角线 AC 和 BD 相交于点 O, E、 F 是 BD 上的两点,且∠ AEB= ∠CFD .求证:四边形AECF 是平行四边形.9.如图:在四边形ABCD 中, AD ∥BC , AB=CD ,E 是 BC 上一点, DE=AB .求证:四边形ABED 是平行四边形.10.如图,已知AB ∥DC, E 是 BC 的中点, AE , DC 的延长线交于点F;(1)求证:△ ABE ≌△ FCE ;(2)连接 AC , BF.则四边形 ABFC 是什么特殊的四边形?请说明理由.11.等边△ ABC 中,点 D 在 BC 上,点 E 在 AB 上,且 CD=BE ,以 AD 为边作等边△ADF ,如图.求证:四边形CDFE 是平行四边形.12.如图,分别以 Rt△ ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD 、等边△ ABE .若∠ BAC=30 °, EF⊥ AB ,垂足为 F,连结 DF.求证:( 1)△ ABC ≌△ EAF ;( 2)四边形ADFE 是平行四边形.13.已知:如图,在△ ABC 中,中线 BE ,CD 交于点 O, F, G 分别是 OB ,OC 的中点.求证:四边形 DFGE 是平行四边形.14.如图所示:在四边形A、C 同时出发,点 P以(1)几秒钟后,四边形(2)几秒钟后,四边形ABCD 中, AD ∥BC、 BC=18cm , CD=15cm ,AD=10cm , AB=12cm ,动点 P、Q 分别从2cm/秒的速度由 A 向 D 运动,点 Q 以 3cm/秒的速度由 C 向 B 运动.ABQP 为平行四边形?并求出此时四边形ABQP 的周长PDCQ 为平行四边形?并求出此时四边形PDCQ 的周长.15.求证:顺次连接四边形各边中点所得的四边形是平行四边形.16.△ ABC 中,中线 BE 、 CF 相交于 O, M 是 BO 的中点, N 是 CO 的中点,求证:四边形 MNEF 是平行四边形.17.如图, AD=DB , AE=EC ,FG∥ AB , AG ∥BC .(1)证明:△ AGE ≌△ CFE;(2)说明四边形 ABFG 是平行四边形;(3)研究图中的线段 DE, BF , FC 之间有怎样的位置关系和数量关系.18.如图,△ ABC 和△ ADE 都是等边三角形,点 D 在 BC 边上, AB 边上有一点F,且 BF=DC ,连接 EF、 EB .(1)求证:△ ABE ≌△ ACD ;(2)求证:四边形 EFCD 是平行四边形.19.已知在△ ABC 中, D、 E 分别是 AB 、AC 的中点,点 F 在 DE 的延长线上,且 EF=DE ,图中有几个平行四边形?请说明你的理由.20.如图,在△ ABC 中,AD 是中线,点 E 是 AD 的中点,过 A 点作 BC 的平行线交CE 的延长线于点F,连接 BF.求证:四边形AFBD 是平行四边形.21.如图:在四边形 ABCD 中, AD ∥ BC, E 是 BC 的中点, BC=2AD .找出图中所有的平行四边形,并选择一个说明它是平行四边形的理由.22.求证:两组对角分别相等的四边形是平行四边形.23.已知:如图,A、 B、 C、D 在同一条直线上,且AB=CD , AE ∥ DF,AE=DF .求证:四边形EBFC 是平行四边形.24.如图,在△ ABC 中, D 是 BC 边的中点, E、 F 分别在 AD 及其延长线上, CE∥ BF ,连接 BE、 CF.图中的四边形BFCE 是平行四边形吗?为什么?25.已知点 E、 F、 G、H 分别为四边形ABCD 四边的中点,试问四边形EFGH 的形状并说明理由.26.如图,已知四边形 ABCD 中 AD=BC ,点 A 、 B、 E 在同一条直线上,且∠ B=∠ EAD ,试说明四边形 ABCD 是平行四边形.27.如图, AD ∥ BC, ED∥ BF ,且 AE=CF ,求证:四边形ABCD 是平行四边形.28.已知:△ ABC 的中线 BD、 CE 交于点 O, F、 G 分别是 OB 、 OC 的中点.求证:四边形DEFG 是平行四边形.29.如图,△ACD 、△ ABE 、△ BCF 均为直线 BC 同侧的等边三角形.当 AB ≠AC 时,求证:四边形 ADFE 为平行四边形.30.已知:在四边形ABCD 中, AD ∥ BC,且 AB=DC=5 , AC=4 , BC=3 .求证:四边形ABCD 为平行四边形.平行四边形的判定30 题参考答案:1.∵ AD ∥BC ,∴∠ DAE= ∠ BCF ,∵ED∥ BF,∴∠ DEF= ∠ BFE,∴∠ AED= ∠ CFB ,又∵ AF=CE ,∴AE=CF ,在△ADE 和△ CBF 中:∵∠ DAE= ∠ BCF ,∠AED= ∠CFB ,AE=CF ,∴△ ADE ≌△ CBF (AAS ),∴AD=CB ,即: AD ∥ CB,AD=CB ,∴四边形 ABCD 是平行四边形,2.∵∠ BAC=90 °, AB=11 ﹣ x, BC=5 , AC=4 .222∴( 11﹣ x) +4 =5 ,解得: x1=8, x2=14 >11(舍去),当x=8 时, BC=AD=5 ,AB=CD=3 ,∴四边形 ABCD 为平行四边形.3.( 1)解:能推出四边形 ABCD 是平行四边形的有①④ 、③④ ;故答案是:①④、③④;( 2)以①④为例进行证明.如图,在四边形ABCD 中, OA=OC , AD ∥ BC .证明:∵ AD ∥ BC,∴∠ DAO= ∠ BCO.∴在△ AOD 与△COB 中,,∴四边形ABCD 是平行四边形.5. BE=DF , BE∥ DF因为 ABCD 是平行四边形,所以 OA=OC , OB=OD ,因为 E, F 分别是 OA ,OC 的中点,所以 OE=OF ,所以BFDE 是平行四边形,所以 BE=DF , BE ∥ DF6.四边形ADEF 是平行四边形.连接 ED 、EF,∵△ ABD 、△BCE 、△ACF 分别是等边三角形,∴AB=BD , BC=BE ,∠ DBA= ∠EBC=60 °.∴∠ DBE= ∠ ABC .∴△ ABC ≌△ DBE .同理可证△ ABC ≌△ FEC,∴AB=EF , AC=DE .∵AB=AD , AC=AF ,∴AD=EF , DE=AF .∴四边形 ADEF 是平行四边形7.( 1)∵ BE ⊥ AD ,CF⊥ AD ,∴∠ BED= ∠ CFD.∵∠ BDE= ∠ CDF, BE=CF ,∴△ BED ≌△ CFD.∴BD=CD .∴AD 是△ ABC 的中线.(2)四边形 BECF 是平行四边形,由( 1)得: BD=CD , ED=FD .∴四边形 BECF 是平行四边形8.∵四边形ABCD 是矩形∴ AB ∥CD , AB=CD ,∴△ AOD ≌△ COB ( ASA ),∴AD=BC ,∴在四边形ABCD 中, AD BC ,∴四边形 ABCD 为平行四边形.∴∠ ABE= ∠ CDF,又∵∠ AEB= ∠ CFD,∴△ ABE ≌△ CDF,∴BE=DF ,又∵四边形ABCD 是矩形,∴OA=OC , OB=OD ,∴OB ﹣BE=OD ﹣ DF,∴OE=OF ,∴四边形AECF 是平行四边形4.选择①,9.∵ AD ∥ BC, AB=CD ,∵ DF=BE ,AE=CF , AB=CD ,∴四边形ABCD 是等腰梯形,∴△ ABE ≌△ CDF (sss),∴∠ B=∠ C,∴∠ DEC= ∠B ,∴AB ∥DE,∴四边形 ABED 是平行四边形.10.( 1)证明:∵ AB ∥ DC ,∴∠ 1=∠ 2,∠ FCE= ∠EBA ,∵E 为 BC 中点,∴CE=BE ,∵在△ ABE 和△ FCE 中,∠ 1=∠ 2,∠ FCE= ∠EBA ,CE=BE ,∴△ ABE ≌△ FCE;(2)四边形ABFC 是平行四边形;理由:由( 1)知:△ ABE ≌△ FCE,∴ EF=AE ,∵CE=BE ,∴四边形 ABFC 是平行四边形11.连接 BF ,∵△ ADF 和△ ABC 是等边三角形,∴AF=AD=DF , AB=AC=BC ,∠ABC= ∠ACD= ∠CAB= ∠ FAD=60 °,∴∠ FAD ﹣∠ EAD= ∠ CAB ﹣∠ EAD ,∴∠ FAB= ∠CAD ,在△FAB 和△DAC 中,∴△ FAB ≌△ DAC ( SAS),∴BF=DC ,∠ ABF= ∠ ACD=60 °,∵ BE=CD ,∴BF=BE ,∴△ BFE 是等边三角形,∴EF=BE=CD ,在△ACD 和△CBE 中∵,∴△ ACD ≌△ CBE ( SAS),∴AD=CE=DF ,∵EF=CD ,∴四边形 CDFE 是平行四边形.∴∠ FEA= ∠ BAC ,在△ ABC 和△EAF 中,,∴△ ABC ≌△ EAF ( AAS );(2)∵∠BAC=30 °,∠DAC=60 °,∴∠ DAB=90 °,即 DA ⊥ AB ,∵EF⊥AB ,∴ AD ∥EF,∵△ABC ≌△EAF ,∴ EF=AC=AD ,∴四边形 ADFE 是平行四边形13.在△ ABC 中,∵AD=BD , AE=CE ,∴DE∥BC 且 DE=BC .在△ OBC 中,∵ OF=FB , OG=GC ,∴FG∥ BC 且 FG= BC .∴DE ∥ FG, DE=FG .∴四边形 DFGE 为平行四边形14.(1)x 秒后,四边形 ABQP 为平行四边形.则 2x=18﹣3x,解得 x=3.6 .3.6 秒钟后,四边形 ABQP 为平行四边形,此时四边形ABQP 的周长是 3.6×2×2+12 ×2=38.4cm .(2)y 秒后,四边形 PDCQ 为平行四边形. 10﹣ 2y=3y ,解得 y=2.2 秒钟后,四边形 PDCQ 为平行四边形,此时四边形 PDCQ 的周长是 3.6×2×2+15×2=43.2cm .15.:连接 BD ,∵E、F 为 AD ,AB 中点,∴ FE BD .又∵ G、H 为 BC,CD 中点,∴GH BD ,故GH FE.同理可证, EH FG.∴四边形FGHE 是平行四边形16.∵ BE ,CF 是△ ABC 的中线,∴EF∥ BC 且 EF= BC,∴MN ∥BC 且 MN= BC,∴EF∥MN 且 EF=MN ,∴四边形 MNEF 是平行四边形.17.( 1)证明:∵ AG∥ BC (已知)∴∠ G=∠ EFC(两直线平行,内错角相等)∵∠AEG= ∠FEC(对顶角相等),又AE=EC (已知)∴△ AGE ≌△ CFE( AAS );( 2)说明:∵ FG∥ AB ,AG ∥ BC (已知)∴四边形 ABFG 是平行四边形(平行四边形的定义);∵EF=BF ,BF=DC ,∴ EF=DC ,∴四边形 EFCD 是平行四边形19.平行四边形ADCF 和平行四边形DBCF .理由:( 1)∵ D 、E 分别是 AB 、 AC 边的中点,∴DE∥BC,.又∵ EF=DE ,∴DF=BC ,∴四边形DBCF 是平行四边形;( 2)在四边形 ADCF 中,( 3)解:线段 DE ,BF,FC 之间的位置关系是DE ∥ BF,∵ EF=DE ,DE ∥FC ,数量关系是 DE=BF=FC ,又∵ E 是 AC 边的中点,理由:由( 1)可知△ AGE ≌△ CFE∴ EA=EC ,∴ AG=FC , FE=EG (全等三角形的对应边相等),∴四边形 ADCF 是平行四边形∴ E 是 FG 的中点,又∵ AD=DB (已知)20.∵ E 为 AD 中点,∴ DE 为三角形 ABC 的中位线,∴ AE=DE ,∴ DE= BC,DE ∥ BC,∵AF ∥BC,∴∠ AFE= ∠ DCE ,即 DE∥ BF, DE ∥ FC,在△AEF 和△CED 中由( 2)可知四边形 ABFG 是平行四边形∴ AG=BF ,∵,∴ BF=FC= BC ,∴△ AEF ≌△ CED( AAS ),∴ DE=BF=FC ,∴ AF=DC ,即线段 DE , BF, FC 之间的位置关系是 DE∥BF ,∵ AD 是△ ABC 的中线,DE ∥FC ,数量关系是 DE=BF=FC .∴ BD=DC ,∴ AF=BD ,即 AF∥ BD ,AF=BD ,故四边形 AFBD 是平行四边形21.图中有两个平行四边形: ?ABED 、 ?AECD .18.( 1)∵△ ABC 和△ ADE 都是等边三角形,∵,∴ AE=AD , AB=AC ,∠ EAD= ∠ BAC=60 °,∴∠ EAD ﹣∠ BAD= ∠ BAC ﹣∠ BAD ,∴ AD=BE ,∵ AD ∥ BC ,即:∠ EAB= ∠ DAC ,∴四边形 ABED 是平行四边形.∴△ ABE ≌△ ACD ( SAS);22.已知:四边形ABCD ,∠ A= ∠C,∠ B= ∠D ,( 2)证明:∵△ ABE ≌△ ACD ,∴ BE=DC ,∠ EBA= ∠ DCA ,又∵ BF=DC ,∴ BE=BF .∵△ ABC 是等边三角形,求证:四边形 ABCD 是平行四边形,∴∠ DCA=60 °,证明:∵∠ A= ∠ C,∠ B=∠ D,∴△ BEF 为等边三角形.∠ A+ ∠ B+∠ C+∠ D=360 °,∴∠ EFB=60 °, EF=BF∴ 2∠A+2 ∠B=360 °,∵△ ABC 是等边三角形,∴∠ A+ ∠ B=180 °,23.∵ AE ∥ DF,∴∠ A=∠D,在△ABE 和△ DCF 中∴△ ABE ≌△ DCF (SAS),∴EB=FC ,∠ ABE= ∠DCF ,∵∠ ABE+ ∠EBC=180 °,∠ DCF+ ∠ FCB=180 °,∴∠ EBC= ∠FCB ,∴BE ∥FC,∵ BE=FC ,∴四边形 EBFC 是平行四边形24.∵ CE∥ BF , BD=CD ,∴△ BDF ≌△ CDE ,∴BF=CE ,∴四边形 BFCE 是平行四边形.25.四边形 EFGH 是平行四边形证明:连接 AC 、 BD∵ E、 F、 G、H 分别为四边形ABCD 四边的中点∴ EH= BD ,FG= BD , HG= AC , EF= AC∴EH=FG , EF=HG∴四边形 EFGH 是平行四边形.26.∵∠ B=∠ EAD ,∴AD ∥BC,∵ AD=BC ,∴四边形 ABCD 是平行四边形.27.∵ AD ∥BC,∴∠ EAD= ∠ FCB ,又ED∥ BF,∴∠FED= ∠ EFB,∠ AED=180 °﹣∠ FED ,∠ CFB=180 °﹣∠ EFB,∴∠ AED= ∠ CFB,又已知 AE=CF ,∴△ AED ≌△ CFB ,∴AD=BC ,∴四边形ABCD 是平行四边形.28.∵AD ∥BC ,∴∠ EAD= ∠ FCB,又ED∥ BF,∴∠FED= ∠ EFB ,∠ AED=180 °﹣∠ FED,∠ CFB=180 °﹣∠ EFB ,∴∠ AED= ∠ CFB,又已知 AE=CF ,∴△AED ≌△CFB ,∴ AD=BC ,∴四边形 ABCD 是平行四边形.29.∵△ ABE 、△ BCF 为等边三角形,∴AB=BE=AE ,BC=CF=FB ,∠ ABE= ∠CBF=60 °.∴∠ FBE= ∠ CBA ,在△FBE 和△CBA 中,,∴△ FBE ≌△ CBA ( SAS).∴EF=AC .又∵△ ADC 为等边三角形,∴CD=AD=AC .∴EF=AD .同理可得 AE=DF .∴四边形 AEFD 是平行四边形30.∵ AB=5 , AC=4 , BC=3222∴ AB =AC +BC∴∠ BCA=90 °∵AD ∥BC∴∠ DAC= ∠BCA=90 °∵DC=5 ,AC=4 ,222∴AD =DC ﹣AC =9∴ AD=BC=3∴四边形ABCD 为平行四边形.。
平行四边形的判定与性质专项训练题

平行四边形的判定与性质专项训练题1.如图,在▱ABCD中,∠C=60°,M、N分别是AD、BC的中点.(1)求证:四边形MNCD是平行四边形;(2)若BC=2CD,MN=1,求BD的长.2.如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.(1)求证:四边形DEFB是平行四边形:(2)若∠ACB=90°,AC=6cm,DE=2cm,求四边形DEFB的面积.3.已知:如图,在四边形ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F,延长DE、BF,分别交AB于点H,交BC于点G,若AD∥BC,AE=CF.(1)求证:四边形ABCD为平行四边形;(2)若∠DAH=∠GBA,GF=2,CF=4,求AD的长.4.如图,在▱ABCD中,点E、F分别是AD、BC边的中点,求证:BE∥DF.5.如图,四边形ABCD中,BD垂直平分AC,垂足为点F、E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.(1)求证:四边形ABDE是平行四边形;(2)如果DA平分∠BDE,AB=3,AD=4,求AC的长.6.如图,已知∠AOB,P、F是OA、OB上一点.(1)用尺规作图法作▱OPEF;(2)若∠AOB=30°,OP=4,OF=5,求OP与EF的距离.7.在Rt△ABC中,∠ACB=90°,D是斜边AB上的一点,作DE⊥BC,垂足为E,延长DE到F,连结CF,使∠A=∠F.(1)求证:四边形ADFC是平行四边形.(2)连接CD,若CD平分∠ADE,CF=10,CD=12,求四边形ADFC的面积.8.如图,在▱ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.(1)求证:四边形ABFC是平行四边形;(2)若AF平分∠BAD,∠D=60°,AD=8,求▱ABCD的面积.9.已知:如图,四边形ABCD中,AB∥CD,AB=CD.求证:(1)AD=BC;(2)AD与BC的位置关系为:.10.如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.(1)求证:四边形BEFD是平行四边形;(2)若∠AFB=90°,AB=6,求四边形BEFD的周长.11.如图,四边形ABCD是平行四边形AE⊥BD于点E,CF⊥BD于点F,连接AF和CE.(1)证明:四边形AECF是平行四边形;(2)已知BD=6,DF=2,BC=5,求CE的长.12.如图,BC∥AD,AB∥CD.(1)求证:△ABC≌△CDA;(2)若AB=3,BC=5,求四边形ABCD的周长.13.▱ABCD中,BD是对角线,CE⊥CD交BD于E点,AF⊥AB交BD于F点,连接AE、CF.求证:四边形AECF是平行四边形.14.如图,已知四边形ABCD是平行四边形,延长BA至点E,使AE=AB,连接DE,AC.(1)求证:四边形ACDE为平行四边形;(2)连接CE交AD于点O.若AC=AB=6.5,BC=5,求线段CE的长.15.如图,已知点A,C在线段EF上,且AE=CF.作AD∥BC,DE∥BF.(1)求证:四边形ABCD是平行四边形;(2)直接写出图中所有相等的线段(AE=CF除外).16.如图,在平行四边形ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.(1)求证:四边形AFCE是平行四边形.(2)若AD=13cm,AE=12cm,AB=20cm,求四边形AFCE的面积.17.已知,如图,在▱ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.18.如图,在▱ABCD中,E、F分别为边BC、AD的中点,连接AE、CF.(1)求证:四边形AECF是平行四边形.(2)当∠B=60°,AB=6时,求AD与BC之间的距离.19.如图,在平行四边形ABCD中,点O是AD的中点,连接BO并延长交CD的延长线于点E,连接BD,AE.(1)求证:四边形ABDE是平行四边形;(2)若BD=CD,判断四边形ABDE的形状,并说明理由.20.如图,在△ABC中,D是边AC的中点,连结BD并延长至点E,使DE=BD,延长BC 至点F,使CF=BC,连结AE、EF.(1)求证:四边形ACFE是平行四边形.(2)连结AF,交线段BE于点G.若△ABC的面积为2,则△ADG的面积为.21.如图,在四边形ABCD中,AB=CD,AD=BC,直线MN交BD于点O,求证:∠1=∠2.22.如图,在▱ABCD中,E,F是对角线BD上的两点(点E在点F左侧),且∠AEB=∠CFD=90°,求证:四边形AECF是平行四边形.23.已知,如图,在▱ABCD中,点E、F分别在AD、BC上,且∠BAF=∠DCE.求证:(1)△ABF≌△CDE.(2)四边形AECF是平行四边形.24.如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,若∠AED=∠CFB,求证:四边形DEBF是平行四边形.25.如图,在等边△ABC中,D、E两点分别在边BC、AC上,BD=CE,以AD为边作等边△ADF,连接EF,CF.(1)求证:△CEF为等边三角形;(2)求证:四边形BDFE为平行四边形;(3)若AE=2,EF=4,求四边形BDFE的面积.26.如图,▱ABCD的对角线AC与BD相交于点O,点E,F分别在OB和OD上,且∠AEB =∠CFD.(1)求证:四边形AECF是平行四边形;(2)若∠AEB=90°,AE=EF=2,求线段AC的长.27.如图,在平行四边形ABCD中,对角线AC,BD交于点O,分别过点B,D作BE⊥AC,DF⊥AC,垂足分别为点E、F.(1)求证:四边形BEDF是平行四边形;(2)若DF=EF,CE=7,AB=13,求平行四边形ABCD的面积.28.(1)如图,以线段AB,BC为邻边,用尺规作图画出平行四边形ABCD(保留作图痕迹),并说明它是平行四边形的判定方法?(2)连接AC,BD,若AB=6,BC=8,求AC2+BD2的值(要有必要的过程).。
(完整版)平行四边形的性质判定练习题

第一部分 平行四边形的性质练习题 例题1、平行四边形得周长为50cm ,两邻边之差为5cm,求各边长。
变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长。
例题2.平行四边形ABCD 中,∠A-∠B=20°,求平行四边形各内角的度数。
变题3.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图,在平行四边形ABCD 中,∠BAC=34°, ∠ACB=26°,求∠DAC 与∠D 的度数。
例题3.如图,在平行四边形ABCD 中,CE ⊥AD,CF ⊥BA 交BA 的延长线于F ,∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。
变题5.如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
1、如图,四边形ABCD 是平行四边形,AB=6cm,BC=8cm ,∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________.3、平行四边形得周长为50cm ,两邻边之差为5cm,则长边是________ ,短边是__________.4、平行四边形ABCD 中,∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中,∠A+∠C=200°.则:∠A= _______,∠B= _________ .7、如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
(完整版)平行四边形性质和判定习题(答案详细)(可编辑修改word版)
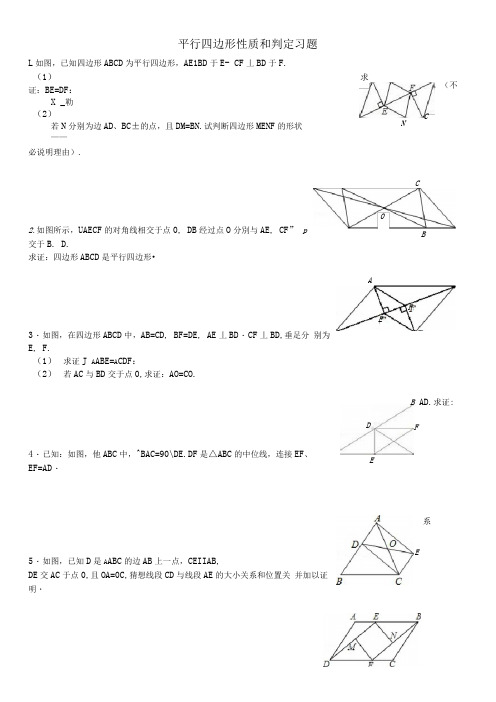
平行四边形性质和判定习题L如图,已知四边形ABCD为平行四边形,AE1BD于E- CF丄BD于F.(1)求证:BE=DF:X _勒(2)若N分别为边AD、BC±的点,且DM=BN.试判断四边形MENF的形状——必说明理由).2.如图所示,UAECF的对角线相交于点0, DB经过点O分別与AE, CF” p交于B. D.求证:四边形ABCD是平行四边形•3・如图,在四边形ABCD中,AB=CD, BF=DE, AE丄BD・CF丄BD,垂足分别为E, F.(1)求证J A ABE=A CDF:(2)若AC与BD交于点0,求证:AO=CO.4・已知:如图,他ABC中,^BAC=90\DE.DF是△ABC的中位线,连接EF、EF=AD・5・如图,已知D是A ABC的边AB上一点,CEIIAB,DE交AC于点0,且OA=0C,猜想线段CD与线段AE的大小关系和位置关并加以证明・B AD.求证:。
(不CNCBAFED FE系E6・如图,已知,UABCD中,AE=CF, M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形•7・如图,平行四边形ABCD, E 、F 两点在对角线BD 上,且BE=DF,连接AE. EG CF, FA ・求证:四边形AECF 是平行四边形•& 在UABCD 中,分别以AD 、BC 为边向内作等边△ADE 和等边△BCF,连接BE. DF ・求证:四边形BEDF 是平 行四边形・DBIIAC,且DB 丄AC. E 是AC 的中点,求证:BC=DE ・2如图,在梯形ABCD 中,ADIIBC, AD=24cm. BC=30cm,点P 自点A 向D 以IcmZs 的速度运动,到D 点Q 自点C 向B 以2cm/s 的速度运动,到B点即停止,直线PQ 截梯形为两个四边形•问当P. Q同时10. 已知脣 点即停止. 出发,几秒后其中一个四边形为平行四边形?IL 如图:已知D 、E 、F 分别是A ABC 各边的中点, 求证:AE 仃DF 互相平分.如图所示, 9・ED13.如图,已知四边形ABCD中,点E, F. G, H分别是AB、CD、AC. BD的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分・14.如图J oABCD 中,MNIIAC.试说明MQ=NP.15.已知:如图所示「平行四边形ABCD的对角线AC, BD柑交于点6 EF经过点0并且分别和AB. CD相交于点E, F,点G, H分别为OA, 0C的中点.求证:四边形EHFG是平行四边形.-46 如制已知的ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH. 连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,尖余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在A ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证J AF=CE:(2)如果AC=EF,且ZACB=135\试判断四边形AFCE是什么样的四边形,并证明你的结论・18,如图平行四边形ABCD 中.mBC=6(几 点E 、F 分別在CD.BC 的延长线上,AE||BD ・ EEhBB 垂足为点F, DF=2 (1) 求证:D 是EC 中点; (2) 求FC 的长.19.如图,已知A ABC 是等边三角形,点D 、F 分别在线段BC 、AB 匕 厶EFB=60。
平行四边形的性质与判定经典例题练习

平行四边形的性质与判定经典例题练习一、平行四边形的性质1. 定义:平行四边形是一种具有两对对边平行的四边形。
定义:平行四边形是一种具有两对对边平行的四边形。
2. 性质1:平行四边形的对边相等。
性质1:平行四边形的对边相等。
3. 性质2:平行四边形的对角线相等。
性质2:平行四边形的对角线相等。
4. 性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
5. 性质4:平行四边形的两组对边分别互相平行并且相互等长。
性质4:平行四边形的两组对边分别互相平行并且相互等长。
二、平行四边形的判定1. 判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
2. 判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
三、经典例题练1. 例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
2. 例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
3. 例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
- (a)根据对边平行和相等的判定方法,若AB = CD且AD与BC互相垂直,则四边形ABCD是平行四边形。
平行四边形的性质与判定(练习)

E DCBA 平行四边形的性质与判定(练习)【知识点】:1. 平行四边形的定义:2.平行四边形性质:⑴边: ;⑵角: ; ⑶对角线: ;(3)对称性:___________________________. 3.平行四边形判定:边:①___________________ ___②_____________ ___________③ ; 角: ; 对角线: ; 【基础训练】一.填空题 (3分×10 = 30分)1.在□ABCD 中,如果∠A +∠C =120°,那么∠B = °.2.已知平行四边形的周长为56㎝,两邻边之比为3:1,则四边形较长的边长为 . 3.已知□ABCD 中,AB = 6,BC 、AB 边上的高分别为6、4,则BC 边长为 . 4.已知□ABCD 中,∠A =60°,AB = 4㎝,AD = 6㎝,则□ABCD 的面积为 . 5.已知□ABCD 中,若∠B 的2倍与∠A 的补角的和为90°,则∠B = 度.6.已知□ABCD 的周长为20cm ,对角线相交于点O ,且△BOC 的周长比△AOB 的周长多2cm ,则AB = cm .7.如图1,已知□ABCD 中,AE =CF ,则图中有 对全等三角形.8.如图2,已知□ABCD 中,BC =12,AB =10,AE ⊥BC 于点E ,且AE =8,则AB 与CD 两边之间的距离为 .9.如图3,已知□ABCD 中,AB =6,AD =8,AE 平分∠BAD 交BC 于E ,则EC = .图1 图2 图310.在四边形ABCD 中,AB =CD ,要使这个四边形成为平行四边形,则可添加的一个条件可以是 . 二.选择题 (3分×6 = 18分)E DCB A1.平行四边形是 ( )(A )轴对称图形 (B )既是轴对称图形,又是中心对称图形 (C )中心对称图形 (D )既不是轴对称图形,也不是中心对称图形2.用两个全等的三角形(三边互不相等)拼成不同的四边形,其中不同的平行四边形的个数是 ( ) (A )1个 (B )2个 (C )3 个 (D )4个 3.下列条件中,能判断四边形是平行四边形的条件是( ) (A )一组对边平行 (B )四条边相等 (C )一组对边平行,另一组对边相等 (D )两条对角线相等4.已知□ABCD 的周长为40cm ,△ABC 的周长为25cm ,则对角线AC 长为( ) (A )5cm (B )15cm (C )6cm (D )16cm 5.如图4,已知四边形ABCD 和CEFG 都是平行四边形, 则下列等式中正确的是( )(A )∠1+∠8=1800(B )∠1+∠5=180° (C )∠4+∠6=180° (D )∠2+∠8=180°6.已知P 为□ABCD 的边AB 上的任一点,则△PCD 与 图4□ABCD 的面积的比S △PCD :S □ABCD 为( )(A )1:2 (B )1:3 (C )1:4 (D )不能确定 三、几何证明1.已知:如图,D 、F 分别是ΔABC 的边BC 、AC 的中点,点E 在线段DF 的延长线上,FE =DF 。
平行四边形10道经典例题

平行四边形经典例题一、已知平行四边形的性质求角度例题:在平行四边形ABCD 中,∠A 的度数比∠B 的度数小40°,求∠A 和∠B 的度数。
解析:因为平行四边形的邻角互补,即∠A + ∠B = 180°。
又已知∠A 比∠B 小40°,即∠B - ∠A = 40°。
联立这两个方程可得:∠A = 70°,∠B = 110°。
二、利用平行四边形的性质求边长例题:平行四边形ABCD 的周长为40,AB = 6,求BC 的长。
解析:平行四边形的对边相等,所以AB = CD = 6,BC = AD。
周长为40,则2(AB + BC) = 40,即2×(6 + BC) = 40,解得BC = 14。
三、判断四边形是否为平行四边形例题:已知四边形ABCD 中,AB∠CD,AB = CD,判断四边形ABCD 是否为平行四边形。
解析:一组对边平行且相等的四边形是平行四边形,所以四边形ABCD 是平行四边形。
四、根据平行四边形的性质求线段长度例题:在平行四边形ABCD 中,AC、BD 是对角线,AC = 10,BD = 8,且AC 与BD 的夹角为60°,求AB 的长度。
解析:过 A 作AE∠BD 于E。
设O 为AC 与BD 的交点,则AO = 5,BO = 4。
在直角三角形AOE 中,因为∠AOE = 60°,所以OE = AO×cos60° = 5×1/2 = 2.5,AE = AO×sin60° = 5×√3/2。
在直角三角形ABE 中,根据勾股定理可得AB = √(AE² + BE²) = √[(5×√3/2)²+(4 + 2.5)²]。
五、利用平行四边形的性质证明线段相等例题:在平行四边形ABCD 中,E、F 分别是AB、CD 的中点,连接DE、BF。
初中数学专训:平行四边形性质和判定
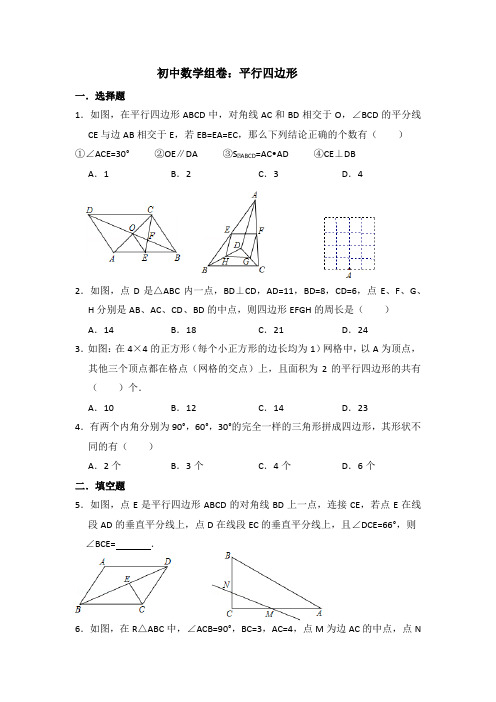
初中数学组卷:平行四边形一.选择题1.如图,在平行四边形ABCD中,对角线AC和BD相交于O,∠BCD的平分线CE与边AB相交于E,若EB=EA=EC,那么下列结论正确的个数有()①∠ACE=30° ②OE∥DA ③S▱ABCD=AC•AD ④CE⊥DBA.1B.2C.3D.42.如图,点D是△ABC内一点,BD⊥CD,AD=11,BD=8,CD=6,点E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是()A.14B.18C.21D.243.如图:在4×4的正方形(每个小正方形的边长均为1)网格中,以A为顶点,其他三个顶点都在格点(网格的交点)上,且面积为2的平行四边形的共有()个.A.10B.12C.14D.234.有两个内角分别为90°,60°,30°的完全一样的三角形拼成四边形,其形状不同的有()A.2个B.3个C.4个D.6个二.填空题5.如图,点E是平行四边形ABCD的对角线BD上一点,连接CE,若点E在线段AD的垂直平分线上,点D在线段EC的垂直平分线上,且∠DCE=66°,则∠BCE=.6.如图,在R△ABC中,∠ACB=90°,BC=3,AC=4,点M为边AC的中点,点N为边BC上任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为.7.如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为.8.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,AB=1,点P为BC上任意一点,连接PA,以PA、PC为邻边作▱PAQC,连接PQ,则PQ的最小值为.9.如图,顺次连结△ABC三边的中点D,E,F得到的三角形面积为S1,顺次连结△CEF三边的中点M,G,H得到的三角形面积为S2,顺次连结△CGH三边的中点得到的三角形面积为S3.设△ABC的面积为S,则S1+S2+S3=.10.如图,在平行四边形ABCD中,AC与BD交于点M,点F在AD上,AF=6cm,BF=12cm,∠FBM=∠CBM,点E是BC的中点,若点P以1cm/秒的速度从点A 出发,沿AD向点F运动;点Q同时以2cm/秒的速度从点C出发,沿CB向点B运动.点P运动到F点时停止运动,点Q也同时停止运动.当点P运动__________秒时,以点P、Q、E、F为顶点的四边形是平行四边形.11.如图,平行四边形ABCD中,∠A是它的外角的,延长CB到E,使CE=CD,过E作EF⊥CD于F,若EF=1,则DF的长等于.12.如图在平行四边形ABCD中,PQ、MN分别平行DC、AD、PQ、MN交于O点,其中S四边形AMOP=3,S四边形MBQO=4,S四边形NCQO=10,则△DMQ的面积=.三.解答题13.如图,在四边形ABCD中,∠ADC=90°,AB=AC,E,F分别为AC,BC的中点,连接EF,ED,FD.(1)求证:ED=EF;(2)若∠BAD=60°,AC平分∠BAD,AC=6,求DF的长.14.如图:在平行四边形ABCD中,∠BAD=45°,∠BDA=60°,点E为线段BD边上一动点,连接AE,将△AED剪下平移到△BGC,将△ABE剪下平移到△DCF.(1)试证明点G、C、F在一条直线上.(2)判断四边形BDFG的形状,并加以证明.15.已知:如图,在Rt△ABC中,∠C=90°,CD平分∠ACB,AD⊥CD,垂足为点D,M是边AB的中点,AB=20,AC=10,求线段DM的长.16.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=10,AC=6,求DF的长.17.如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F.求证:(1)△ABE是等边三角形;(2)△ABC≌△AED;(3)S△ABE =S△CEF.18.如图,在平面直角坐标系中,点A,B的坐标分别是(﹣3,0),(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C 从点B出发,沿射线BO方向以每秒2个单位的速度运动.以CP,CO为邻边构造□PCOD.在线段OP延长线上一动点E,且满足PE=AO.(1)当点C在线段OB上运动时,求证:四边形ADEC为平行四边形;(2)当点P运动的时间为秒时,求此时四边形ADEC的周长是多少?19.如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=8,DC=6,AD=10.动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒).(1)若四边形ABQP为平行四边形,求运动时间t.(2)当t为何值时,三角形BPQ是以BQ或BP为底边的等腰三角形?20.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,∠ADC的平分线交AB于点M,交AE于点N,连接DE(1)求证:BC=CE;(2)若BC=2,∠ABC=120°,求DE的长.21.在△ABC中,BD是角平分线,点E、F分别在BC、AB边上,DE∥AB,BE=AF,EF交BD于点G.(1)如图1,求证:四边形ADEF是平行四边形;(2)如图2,若∠ABC=30°,D为AC边中点,请直接写出图中所有与BE长相等的线段.22.如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.(1)求∠FGH度数;(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.23.在△ABC中,AB=AC,点P为△ABC所在平面内的一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.(1)如图1,若点P在BC边上,此时PD=0,猜想并写出PD、PE、PF与AB满足的数量关系,然后证明你的猜想;(2)请直接利用(1)中的结论解答下列问题:(a)如图2,当点P在△ABC内,猜想并写出PD、PE、PF与AB满足的数量关系,然后证明你的猜想;(b)如图3,当点P在△ABC外,猜想并写出PD、PE、PF与AB满足的数量关系.(不用说明理由)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B E C F D O A B D C 平行四边形性质及判定练习题
班级: 姓名:
一、耐心填一填!
1、ABCD 中,∠B-∠A =40°,则∠D =__。
2、ABCD 的周长是44cm ,AB 比A D大2cm ,则AB=__cm,AD=__c m。
3、平行四边形的两个相邻内角的平分线相交所成的角的度数是__。
4、平行四边形的两条邻边的比为2∶1,周长为60cm ,则这个四边形较短的边长为__。
5、如图所示,在AB CD 中,AE ⊥BC 于E,AF ⊥CD 于F , ∠BA D=120°,BE=2,FD=3,则∠EA F=___,
AB CD 的周长为__。
6.若平行四边形的两邻边的长分别为16和20,两长边间的距离为8,
则两短边间的距离为_____________.
7、ABCD ,AB=6c m,BC=8c m,∠B=70°,则AD=________,CD=______, ∠D=__________,∠A=_________,∠C=__________.
8、平行四边形周长为50cm,两邻边之差为5cm,各边长为 。
9.如图,平行四边形AB CD 的周长为30cm,它的对角线AC 和BD 相交于O, 且△AO B的周长比△BOC 的周长大5cm ,AB= 、BC= 。
10.平行四边形ABCD 的对角线A C和BD 相交于O ,则其中全等的三角形有___对。
二、精心选一选!
11、下面各条件中,能判定四边形是平行四边形的是 ( )
A 、对角线互相垂直 B、对角线互相平分 C 、一组对角相等 D 、一组对边相等
12、已知下列四个命题:
①一组对边平行且相等的四边形;②两组对角分别相等的四边形;
③对角线相等的四边形; ④对角线互相平分的四边形。
其中能判定平行四边形的命题的个数为 ( )
E D C O
F B A A 、1个 B 、2个 C 、3个 D 、4个
13、平行四边形的两条对角线及一边的长可依次取 ( )
A 、6、6、6 B、6、4、3 C 、6、4、6 D 、3、4、5
14、以不共线三点为三个顶点作平行四边形,一共可作平行四边形的个数是 ( )
A 、2个
B 、3个
C 、4个
D 、5个
15、四边形ABCD 的四个角∠A ∶∠B ∶∠C ∶∠D 满足下列哪一条件时,四边形AB CD 是
平行四边形?( )
A 、1∶2∶2∶1
B 、2∶1∶1∶1 C、1∶2∶3∶4 D 、2∶1∶2∶1
16、如图所示,在ABC D中,EF 过对角线的交点,若AB =4,BC =7,OE =3,
则四边形EF DC的周长是( )
A 、14
B 、11
C 、10
D 、17
17、四边形ABCD 中,A D∥B C,要判定四边形AB CD 是平行四边形,还应满足( )
A 、∠A+∠C=180° B、∠B+∠D=180° C 、∠A +∠B=180° D 、∠A+∠D =180°
18、根据下列条件,得不到平行四边形的是( )
A 、A B=CD,AD=BC
B 、AB ∥CD,A B=CD
C 、AB=CD,AD∥BC
D 、AB ∥CD,A D∥BC
19、若ABCD 的周长为40cm,ΔABC 的周长为27cm ,则AC 的长是( )
A 、13cm
B 、3cm C、7cm D、11.5cm
20、平行四边形的对角线长分别是x 和y,一边长为12,则下列各组数据可能是
x 与y 的值的是( )
A、8与14 B、10与14 C 、18与20 D、10与36
21、
中 ,则 和 的度数分别为( ) A . , B . , C .
, D . , 三、说理与简答
22、在ABCD 中,E、F 分别在DC 、AB 上,且DE=BF 。
A B E C F D
B E D A B F O
C
D
E 求证:四边形A FCE 是平行四边形。
23、如图所示,四边形ABCD 是平行四边形,且∠EAD =∠BAF 。
① 求证:ΔCEF 是等腰三角形;
②观察图形,ΔCE F的哪两边之和恰好等于ABC D的周长?并说明理由。
24、如图所示,AB CD 中的对角线A C、B D相交于O ,EF 经过点O 与AD 延长线交于
E,与CB 延长线交于F 。
求证:OE=OF
25、如图所示,在ΔABC 中,AE平分∠BA C交BC 于E,DE∥AC 交AB 于D ,过D 作DF
∥BC交AC 于F 。
求证: AD=F C
P A B C D H G E D C F B A
26.如图, ABCD 中,G 是CD 上一点,BG 交A D延长线于E ,AF=CG , 100=∠DGE .
(1) 求证:D F=BG; (2)求AFD ∠的度数.
27、如图所示,在ABCD 中,P 是AC 上任意一点,求证:APD ABP S S ∆∆=
28、如图所示,ABCD 中,E 、F 分别为AD 、B C的中点,AF 与BE 相交于G ,D F与CE
相交于H,连结EF 、GH 。
求证:EF 、GH 互相平分。
29、如图,在□A BCD 中,E、F 、G 、H分别是四条边上的点,且满足BE=DF,CG=AH,
连接EF 、G H。
求证:EF 与GH 互相平分。
A B C D F E G
A
B C D
F
O
G H。
