洛伦兹力的大小和方向
《洛伦兹力的应用》 知识清单

《洛伦兹力的应用》知识清单一、洛伦兹力的基本概念洛伦兹力是指运动电荷在磁场中所受到的力。
当电荷以速度 v 在磁感应强度为 B 的磁场中运动时,所受到的洛伦兹力 F 的大小为 F =qvBsinθ,其中 q 为电荷的电荷量,θ 为速度方向与磁场方向的夹角。
洛伦兹力的方向始终与电荷的运动方向和磁场方向垂直,遵循左手定则。
二、洛伦兹力的特点1、洛伦兹力永不做功由于洛伦兹力始终与电荷的运动方向垂直,所以它对电荷不做功,只改变电荷的运动方向,而不改变电荷的速度大小。
2、洛伦兹力与电荷的运动状态相关电荷的速度大小、方向以及磁场的强度和方向都会影响洛伦兹力的大小和方向。
三、洛伦兹力在现代科技中的应用1、质谱仪质谱仪是一种用于测量带电粒子质量和比荷的仪器。
其工作原理是利用电场对带电粒子进行加速,然后让粒子进入磁场,通过测量粒子在磁场中的偏转半径来计算粒子的质量和比荷。
在质谱仪中,洛伦兹力起到了使粒子偏转的关键作用。
假设一个电荷量为 q、质量为 m 的粒子,经过加速电压 U 加速后,获得的速度为 v。
根据动能定理,有 qU = 1/2mv²,解得 v =√(2qU/m)。
当粒子进入磁感应强度为 B 的磁场中时,受到洛伦兹力 F = qvB,粒子做圆周运动,其半径 r = mv/qB。
通过测量偏转半径 r 和已知的磁场强度 B、加速电压 U 以及电荷量 q,就可以计算出粒子的质量 m。
2、回旋加速器回旋加速器是一种利用电场加速和磁场偏转来使带电粒子获得高能量的装置。
在回旋加速器中,带电粒子在两个半圆形的金属盒之间被电场加速,然后在磁场中做圆周运动。
由于洛伦兹力的作用,粒子的运动轨迹是一个不断增大半径的螺旋线。
当粒子的速度增加时,其在磁场中的偏转半径也会增大。
通过不断调整电场的频率,使得粒子在每次通过电场时都能被加速。
经过多次加速,粒子可以获得很高的能量。
3、磁流体发电机磁流体发电机是一种新型的高效发电装置。
运动电荷在磁场中受到的力

一、洛伦兹力
1、运动电荷在磁场中受到的力称为洛伦兹力.
洛伦兹,荷兰物理学家, 首先提出磁场对运动电 荷有作用力的观点。 洛 伦兹创立了经典电子论, 提出了洛伦兹变换公式, 1902年与其学生塞曼共 同获得诺贝尔物理学奖。 为纪念洛伦兹的卓著功 勋,荷兰政府决定从 1945年起,把他的生日 定为“洛伦兹节”。
洛伦兹力的大小
如图所示,设有一段长度为L,横截面 积为S的导线,导线单位体积内含有的自由 电荷数为n,每个自由电荷的电荷量为q,定 向移动速率为v,将这段通电导线垂直磁场 方向放入磁感应强度为B的磁场中。
洛伦兹力的大小 1、运动电荷在磁场中受到的力称为洛伦兹力.
洛伦兹创立了经典电子论,提出了洛伦兹变换公式,1902年与其学生塞曼共同获得诺贝尔物理学奖。
每个电子受的磁场力为F = F /N 通过导体的电子数:N=nsL
洛 为纪念洛伦兹的卓著功勋,荷兰政府决定从1945年起,把他的生日定为“洛伦兹节”。
四指指向负电荷运动的反方向即可。
安
每个电子受的磁场力为F洛 = F安/N
1、试判断带电粒子在磁场中受到的洛伦兹力
V2 V1
洛仑兹力的大小
(1)当速度方向与磁感应强度方向垂直(v⊥B)
通过导体的电子数:N=nsL
通过导体的电子数:N=nsL (1)当速度方向与磁感应强度方向垂直(v⊥B)
每个电子受的磁场力为F洛 = F安/N 若为负电荷,应如何判断?
洛伦兹创立了经典电子论,提出了洛伦兹变换公式,1902年与其学生塞曼共同获得诺贝尔物理学奖。
2、电子的速率v=3×106 m/s,垂直射入B=0.
电流的微观表达式为 I=nqsv 伸开左手,使拇指与其余四个手指垂直,并且都与手掌在同一个平面内;
洛伦兹力
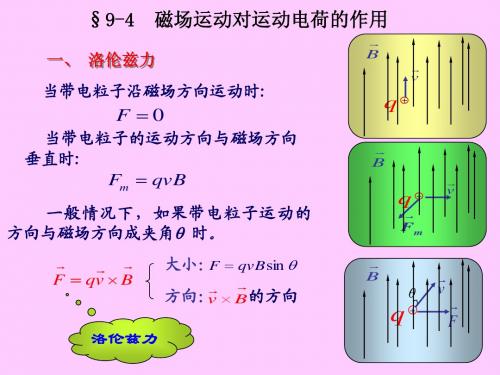
9.0×103 -3 n = 6.0×1023 × m = 8.4 ×1028 m-3 0.064
霍耳电势差
IB 200 ×1.5 V1- 2 = - V = V 28 −19 ned 8.4 ×10 ×1.6×10 × 0.001 = −2.2 ×10−5V = −22µV
铜片中电流为200A时 霍耳电势差只有22μV, 铜片中电流为200A时,霍耳电势差只有22μV,可见在通常情况下铜片 200A 22μV 中的霍尔效应是很弱的。 中的霍尔效应是很弱的。 在半导体中, 远小于单位金属中自由电子的浓度, 在半导体中,载流子浓度n远小于单位金属中自由电子的浓度,因此可 得到较大的霍耳电势差。在这些材料中能产生电流的数量级约为1mA 1mA, 得到较大的霍耳电势差。在这些材料中能产生电流的数量级约为1mA,如果 选用和例中铜片大小相同的材料, =0.1mA, 选用和例中铜片大小相同的材料,取I=0.1mA,n=1020 m-3 ,则可算出其霍 耳电势差约为9.4mV 用一般的毫伏表就能测量出来。 9.4mV, 耳电势差约为9.4mV,用一般的毫伏表就能测量出来。
把一宽为2 cm, cm的铜片 放在B= 的铜片, B=1 的磁场中, 例2 把一宽为2.0cm,厚1.0cm的铜片,放在B=1.5T的磁场中,磁场垂直 通过铜片。如果铜片载有电流200 200A 通过铜片。如果铜片载有电流200A,求呈现在铜片上下两侧间的霍耳电势差 有多大? 有多大?
解 每个铜原子中只有一个自由电子,故单位体积内的自由电 每个铜原子中只有一个自由电子, 子数n即等于单位体积内的原子数 已知铜的相对原子质量为64, 即等于单位体积内的原子数。 子数 即等于单位体积内的原子数 。 已知铜的相对原子质量为 , 1mol铜( 0.064kg)有 6.0×1023个原子( 阿伏加得罗常数) , 铜 个原子(阿伏加得罗常数) 铜 ) × 的密度为9.0× 的密度为 ×103 kg/m3,所以铜片中自由电子的密度
洛伦兹力
洛伦兹力带电粒子在磁场中的运动一、洛伦兹力1.定义:______________在磁场中所受的力.2.与安培力的关系:通电导线在磁场中所受的安培力是洛伦兹力的______________,而洛伦兹力是安培力的微观本质.二、洛伦兹力的方向和大小1.洛伦兹力的方向(1)左手定则:伸开左手,使拇指与其余四个手指垂直,并且都与手掌在同一平面内.让______从掌心进入,并使四指指向____________,这时拇指所指的方向就是运动的正电荷在磁场中所受_____的方向.负电荷受力的方向与正电荷受力的方向______.(2)特点:洛伦兹力的方向与电荷运动方向和磁场方向都______________,即洛伦兹力垂直于速度方向、磁感应强度方向所构成的平面洛伦兹力,只改变带电粒子的速度,不改变速度,对电荷做功.2.洛伦兹力的大小(1)一般公式:F=qvB sinθ,其中θ为________方向与________方向的夹角.(2)当________时,F=qvB. (3)当________时,F=0.注意:1.洛伦兹力方向的特点(1)洛伦兹力的方向与电荷运动的方向和磁场方向都垂直,即洛伦兹力的方向总是垂直于运动电荷的速度方向和磁场方向确定的平面.(2)当电荷运动方向发生变化时,洛伦兹力的方向也随之变化.特别提醒洛伦兹力对电荷不做功;安培力对通电导线可做正功,可做负功,也可不做功;电场力对电荷可做正功,可做负功,也可不做功.思考:带电粒子在电场中一定受力吗?带电导线在磁场中一定受力吗?带电粒子在磁场中运动一定受力吗?假设受的话方向如何确定? 三、带电粒子在匀强磁场中的运动试画出图3中几种情况下带电粒子的运动轨迹.1.若v ∥B ,带电粒子不受洛伦兹力,在匀强磁场中做____________运动.2.若v ⊥B ,带电粒子仅受洛伦兹力作用,在垂直于磁感线的平面内以入射速度v 做__________运动. (1)向心力由洛伦兹力提供:qvB =__________=__________;(2)轨道半径公式:R =mvqB;(3)周期:T =2πR v =2πmqB (周期T 与速度v 、轨道半径R 无关);(4)频率:f =1T =qB 2πm ; (5)角速度:ω=2πT=__________.思考:根据公式T =2πRv,能说T 与v 成反比吗?注意:带电粒子在分区域匀强电场、磁场中运动问题 “磁偏转”和“电偏转”的区别电偏转磁偏转偏转条件 带电粒子以v⊥E 进入匀强电场带电粒子以v⊥B 进入匀强磁场 受力情况 只受恒定的电场力只受大小恒定的洛伦兹力运动轨迹 抛物线圆弧物理规律类平抛知识、牛顿第二定律牛顿第二定律、向心力公式基本公式L =vt y =12at 2 a =qE mtan θ=at/vqvB =m v 2rr =mv/(qB) T =2πm/(qB) t =θT/(2π) sin θ=L/r做功情况电场力既改变速度方向,也改变速度的大小,对电荷要做功洛伦兹力只改变速度方向,不改变速度的大小,对电荷永不做功物理图象1.圆心的确定:如图甲、乙所示,试确定两种情况下圆弧轨道的圆心,并总结此类问题的分析方法.图2 图3 图4总结:两种情况下圆心的确定分别采用以下方法:(1)已知入射方向和出射方向时,可通过入射点和出射点分别作垂直于入射方向和出射方向的直线,两条直线的交点就是圆弧轨道的圆心(如图3所示,图中P 为入射点,M 为出射点).(2)已知入射点和出射点的位置时,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨道的圆心(如图4所示,P 为入射点,M 为出射点). 2 根据以上总结的结论可以分析下面几种常见的不同边界磁场中的运动规律:①直线边界(进出磁场具有对称性,如图5(a)、(b)、(c)所示)②平行边界(存在临界条件,如图6(a)、(b)、(c)所示)图6 图7③圆形边界(沿径向射入必沿径向射出,如图7所示) 3.半径的确定用几何知识(勾股定理、三角函数等)求出半径的大小. 4.动时间的确定粒子在磁场中运动一周的时间为T ,当粒子运动的圆弧所对应的圆心角为α时,其运动时间表示为:t =α360°T(或t =α2πT).五:典例剖析例1,在y <0的区域内存在匀强磁场,磁场方向垂直于xy 平面并指向纸面外,磁感应强度为B 。
洛仑兹力

据题意,小球P在球面上做水平的匀速圆周运动 在球面上做水平的匀速圆周运动, 解: 据题意,小球 在球面上做水平的匀速圆周运动 该圆周的圆心为O' 受到向下的重力mg、 该圆周的圆心为 。P受到向下的重力 、球面对它 受到向下的重力 方向的支持力N和磁场的洛仑兹力 f=qvB 沿OP方向的支持力 和磁场的洛仑兹力 方向的支持力 和磁场的洛仑兹力f = 式中v为小球运动的速率, 的方向指向O′, 式中 为小球运动的速率,洛仑兹力 f 的方向指向 为小球运动的速率 根据牛顿第二定律: 根据牛顿第二定律:
2m B≥ q g R cosθ
可见,为了使小球能够在该圆周上运动, 可见,为了使小球能够在该圆周上运动,磁感应强度 大小的最小值为
Bmin 2m = q g R cosθ
此时,带电小球做匀速圆周运动的速率为n R sinθ
v= 2a = 2m
N cosθ mg = 0
v2 f N sinθ = m R sinθ 由前面三式得: 由前面三式得: qBR sinθ gR sin2 θ v2 v+ =0 m cosθ
N P mg f R θ O O'
由于v是实数,必须满足: 由于 是实数,必须满足: 是实数 qBR sinθ 2 4 gR sin2 θ =( ) ≥0 m cosθ 由此得: 由此得:
若小球带负电, 解: 若小球带负电,带电小球受到的洛仑兹力向 试管底,不能从试管口处飞出, 错 试管底,不能从试管口处飞出,A错。 洛仑兹力与运动方向垂直,不做功, 错 洛仑兹力与运动方向垂直,不做功,C错。 小球带正电,受到洛仑兹向试管口作匀加速运动 小球带正电,受到洛仑兹向试管口作匀加速运动, 同时随试管向右匀速运动,合运动的轨迹是一条 同时随试管向右匀速运动, 抛物线, 正确 正确。 抛物线,B正确。 小球受到洛仑兹向试管口作匀加速 运动时,又受到洛仑兹力, 运动时,又受到洛仑兹力,方向向 且逐渐增大, 左,且逐渐增大,所以维持试管匀 速运动的拉力F应逐渐增大 正确. 应逐渐增大,D正确 速运动的拉力 应逐渐增大 正确
第15天 洛伦兹力-2023年高二物理(人教版2019)(解析版)

第15天洛伦兹力(预习篇)1.知道什么是洛伦兹力,会用左手定则判断洛伦兹力的方向.2.掌握洛伦兹力公式的推导过程,会计算洛伦兹力的大小.3.知道电视显像管的基本构造及工作的基本原理.一、洛伦兹力的方向和大小1.洛伦兹力(1)定义:运动电荷在磁场中受到的力.(2)与安培力的关系:通电导线在磁场中受到的安培力是洛伦兹力的宏观表现.2.洛伦兹力的方向左手定则:伸开左手,使拇指与其余四个手指垂直,并且都与手掌在同一个平面内,让磁感线从掌心垂直进入,并使四指指向正电荷运动的方向,这时拇指所指的方向就是运动的正电荷在磁场中所受洛伦兹力的方向.负电荷受力的方向与正电荷受力的方向相反.3.洛伦兹力的大小(1)当v与B成θ角时,F=q v B sin θ.(2)当v⊥B时,F=q v B.(3)当v∥B时,F=0.二、电子束的磁偏转1.显像管的构造:如图所示,由电子枪、偏转线圈和荧光屏组成.2.显像管的原理(1)电子枪发射高速电子.(2)电子束在磁场中偏转.(3)荧光屏被电子束撞击时发光.3.扫描:在偏转区的水平方向和竖直方向都有偏转磁场,其方向、强弱都在不断变化,使得电子束打在荧光屏上的光点从上向下、从左向右不断移动.一、洛伦兹力的方向例题1.试判断下列图中的带电粒子刚进入磁场时所受的洛伦兹力的方向,其中垂直于纸面指向纸里的是()答案D解析根据左手定则可以判断,选项A中的带电粒子所受的洛伦兹力方向向下;选项B中的带电粒子所受的洛伦兹力方向向上;选项C中的带电粒子所受的洛伦兹力方向垂直纸面指向纸外;选项D中的带电粒子所受的洛伦兹力方向垂直于纸面指向纸里,D正确.解题归纳:1.洛伦兹力的方向总是与电荷运动的方向及磁场方向垂直,即洛伦兹力的方向总是垂直于运动电荷速度方向和磁场方向确定的平面.即F、B、v三个量的方向关系是:F⊥B,F⊥v,但B与v不一定垂直,如图甲、乙所示.2.在用左手定则判断运动的电荷在磁场中所受洛伦兹力的方向时,对于正电荷,四指指向电荷的运动方向;但对于负电荷,四指应指向电荷运动的反方向.二、洛伦兹力的大小例题2.如图所示,各图中的匀强磁场的磁感应强度均为B,带电粒子的速率均为v,带电荷量均为q.试求出图中带电粒子所受洛伦兹力的大小,并指出洛伦兹力的方向.答案 (1)q v B 垂直于v 指向左上方 (2)12q v B 垂直纸面向里 (3)q v B 垂直纸面向里 (4)q v B 垂直于v 指向左上方解析 (1)因v ⊥B ,所以F =q v B ,方向垂直于v 指向左上方.(2)v 与B 的夹角为30°,将v 分解成垂直磁场的分量和平行磁场的分量,v ⊥=v sin 30°,F =q v B sin 30°=12q v B ,方向垂直纸面向里.(3)因v ⊥B ,所以F =q v B ,由左手定则判断出洛伦兹力的方向垂直纸面向里. (4)因v ⊥B ,所以F =q v B ,方向垂直于v 指向左上方. 解题归纳:1.洛伦兹力与安培力的关系(1)安培力是导体中所有定向移动的自由电荷受到的洛伦兹力的宏观表现,而洛伦兹力是安培力的微观本质.(2)洛伦兹力对电荷不做功,但安培力却可以对导体做功.2.洛伦兹力的大小:F =q v B sin θ,θ为电荷运动的方向与磁感应强度方向的夹角. (1)当θ=90°时,v ⊥B ,sin θ=1,F =q v B ,即运动方向与磁场垂直时,洛伦兹力最大. (2)当v ∥B 时,θ=0°,sin θ=0,F =0,即运动方向与磁场平行时,不受洛伦兹力.1. 在下列四个选项中,正确标明了带正电粒子所受洛伦兹力F 方向的是( )答案 D解析 根据左手定则可知,A 项中洛伦兹力方向应该垂直纸面向里,故A 错误;B 项中洛伦兹力方向应该是垂直纸面向外,故B 错误;C 项中洛伦兹力方向应该竖直向下,故C 错误;D 项中洛伦兹力方向应该竖直向上,故D 正确.2.两个带电粒子以相同的速度垂直磁感线方向进入同一匀强磁场,两粒子质量之比为1∶4,电荷量之比为1∶2,则刚进入磁场时两带电粒子所受洛伦兹力之比为()A.2∶1 B.1∶1 C.1∶2 D.1∶4答案C解析带电粒子的速度方向与磁感线方向垂直时,洛伦兹力F=q v B,与电荷量成正比,与质量无关,C项正确.(建议用时:30分钟)一、单选题1.铁环上绕有绝缘的通电导线,电流方向如图所示,一束电子沿过铁环中心O点的轴线垂直纸面向里射入,则该束粒子偏转方向()A.向左B.向右C.向上D.向下【答案】B【解析】右手螺旋定则可知,铁环左右两侧相当于两个N极在上端的条形磁铁,O点在两条形磁铁之间磁场方向竖直向下,再根据左手定则可知电子受到向右方向的洛伦兹力,故选B。
洛伦兹力问题及解题策略

判断洛伦兹力的方向可以使用左 手定则,即伸开左手,让大拇指 与四指在同一平面内且互相垂直, 将磁感应强度穿过掌心,四指指 向正电荷的运动方向,大拇指所 指方向即为洛伦兹力的方向。
在解决洛伦兹力问题时,需要对 带电粒子进行受力分析,特别是 分析洛伦兹力的方向和大小,以 便进一步求解问题。
03 解题策略
2
在解题过程中,应注意逻辑的严密性和物理量的 单位统一,避免出现计算错误和单位不统一的情 况。
3
在解题过程中,应注意对题目中的隐含条件进行 挖掘和分析,如磁场方向、粒子的电性等。
THANKS FOR WATCHING
感谢您的观看
洛伦兹力公式F=qvB只在非匀 强磁场中成立,在匀强磁场中,
洛伦兹力应为F=qvBsinθ。
当带电粒子在磁场中做匀速 圆周运动时,洛伦兹力提供
向心力,即F=mv²/r。
在处理带电粒子在磁场中的运 动问题时,应先分析粒子的受 力情况,再根据牛顿第二定律
列方程求解。
注意解题的逻辑性和严密性
1
在解题过程中,应先明确已知条件和待求量,再 根据物理规律建立方程,最后求解方程得出结果。
洛伦兹力的大小和方向
洛伦兹力的大小公式为:F=qvBsinθ,其中q为粒子电量,v为粒子速度,B为磁感应强度,θ为粒子运动方向与磁场方向的夹角。
洛伦兹力的方向由左手定则确定,伸开左手,让大拇指与其余四指垂直,将左手放入磁场中,让磁感线垂直穿过手心,四指 指向粒子的运动方向,则大拇指所指方向即为洛伦兹力的方向。
05 解题技巧与注意事项
掌握洛伦兹力的基本性质
01
洛伦兹力始终垂直于运动方向,不会改变速度的大小,只改变 速度的方向。
02
洛伦兹力的大小与磁感应强度、电荷量以及速度大小有关,方
第二讲 洛伦兹力

.
必考部分 选修3-1 第八章 磁场
栏目导引
二、带电粒子在匀强磁场中的运动 匀速直线 运 1.若v∥B,带电粒子不受洛伦兹力,在匀强磁场中做 . ∥ ,带电粒子不受洛伦兹力, 动. 2.若v⊥B,带电粒子仅受洛伦兹力作用,在垂直于磁感线的平面 . ⊥ ,带电粒子仅受洛伦兹力作用, 内以入射速度v做 内以入射速度 做 (1)基本公式 基本公式
3.运动时间的确定 . 粒子在磁场中运动一周的时间为T, 粒子在磁场中运动一周的时间为 ,当粒子运动的圆弧所对应的圆 α α 心角为α时 其运动时间由下式表示: = T(或t= T). 心角为 时,其运动时间由下式表示:t= 或= . 360° 2π
工具
必考部分 选修3-1 第八章 磁场
栏目导引
4.带电粒子在不同边界磁场中的运动 . (1)直线边界 进出磁场具有对称性, 如下图 直线边界(进出磁场具有对称性 如下图) 直线边界 进出磁场具有对称性,
mv 2 向心力公式: ①向心力公式:Bqv= r . = mv 轨道半径公式: = ②轨道半径公式:r= qB .
匀速圆周
运动. 运动.
工具
必考部分 选修3-1 第八章 磁场
栏目导引
③周期、频率和角速度公式: 周期、频率和角速度公式:
2πr 2πm T= = = v qB qB 1 . f= = = 2πm T 2π qB . ω= =2πf= = = T m
工具
必考部分 选修3-1 第八章 磁场
栏目导引
2.如右图所示,在一矩形区域内,不加磁场时,不计重力的带电粒 如右图所示,在一矩形区域内,不加磁场时, 如右图所示 子以某一初速度垂直左边界射入,穿过此区域的时间为t.若加上磁感应 子以某一初速度垂直左边界射入 ,穿过此区域的时间为 若加上磁感应 强度为B水平向外的匀强磁场,带电粒子仍以原来的初速度入射,粒子 强度为 水平向外的匀强磁场,带电粒子仍以原来的初速度入射, 水平向外的匀强磁场 飞出时偏离原方向60° 利用以上数据可求出下列物理量中的 飞出时偏离原方向 °,利用以上数据可求出下列物理量中的( A.带电粒子的比荷 . B.带电粒子在磁场中运动的周期 . C.带电粒子的初速度 . D.带电粒子在磁场中运动的半径 . )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
洛伦兹力的大小、方向及公式
一、单项选择题
1.(09年广东理科基础)带电粒子垂直匀强磁场方向运动时,会受到洛伦兹力的作用。
下列表述正确的是 ( ) A .洛伦兹力对带电粒子做功 B .洛伦兹力不改变带电粒子的动能 C .洛伦兹力的大小与速度无关 D .洛伦兹力不改变带电粒子的速度方向
2.有一束电子流沿x 轴正方向高速运动,如图所示,电子流在z 轴上的P 点处所产生的磁场方向是( ) A 、y 轴正方向 B 、y 轴负方向 C 、z 轴正方向 D 、z 轴负方向
3.(泰州市2008届第二学期期初联考)“月球勘探者号”
进行了近距离勘探,在月球重力分布、磁场分布及元素测定方面取得了新的成果。
月球上的磁场极其微弱,通过探测器拍摄电子在月球磁场中的运动轨迹,可分析月球磁场的强弱分布情况。
如图是探测器通过月球表面①、②、③、④四个位置时,拍摄到的电子运动轨迹照片(尺寸比例相同),设电子速率相同,且与磁场方向垂直,则可知磁场从强到弱的位置排列正确的是( )
A. ①②③④
B. ①④②③
C. ④③②①
D. ③④②①
4.在匀强磁场中有一带电粒子做匀速圆周运动,当它运动到M 点,突然与一不带电的静止粒子碰撞合为一体,碰撞后的运动轨迹应是图中的哪一个?(实线为原轨迹,虚线为碰后轨迹,不计粒子的重力) ( )
二、双向选择题
5.海南省海口市2010届高三调研测试如图所示,一束电子以大小不同的速率沿图示方向
飞入横截面为一正方形的匀强磁场区,在从ab 边离开磁场的电子中,下列判断正确的是 ( )
A.从b 点离开的电子速度最大
B.从b 点离开的电子在磁场中运动时间最长
C.从b 点离开的电子速度偏转角最大
D.在磁场中运动时间相同的电子,其轨迹线一定重合
6.(烟台市2008届第一学期期末考)如图所示,在x 轴上方存在磁感应强度为B 的匀强磁场,一个电子(质量为m ,电荷量为q )从x 轴上的O 点以速度v 斜向上射入磁场中,速度方向与x 轴的夹角为45°并与磁场方向垂直.电子在磁场中运动一段时间后,从x 轴上的P 点射出磁场. 则
( )
A .电了在磁场中运动的时间为q
B m
2π
B .电子在磁场中运动的时间为qB
m π
C .OP 两点间的距离为
qB
mv 2
D .OP 两点间的距离为
qB
mv 2
7.如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a 、
b 、
c ,以不同的速率对准圆心O 沿着AO 方向射入磁场,
其运动轨迹如右图。
若带电粒子只受磁场力作用,下列说法正确的是
A .a 粒子动能最大
B .c 粒子速率最大
C .c 粒子在磁场中运动时间最长
D .它们做圆周运动的周期 8.(青岛市2008届第一次质检)一带电粒子以垂直于磁场方向的初速度飞入匀强磁场后做圆周运动,磁场方向和运动轨迹如图所示,下列情况可能的是( )
A .粒子带正电,沿逆时针方向运动
B .粒子带正电,沿顺时针方向运动 C
.粒子带负电,沿逆时针方向运动 D .粒子带负电,沿顺时针方向运动
•
B
c
b a T T T ==
9.(山东嘉祥一中2008年5月高考模拟)如图所示,在一匀强磁场中有三个带电粒子,其中1和2为质子、3为α粒子的径迹.它们在同一平面内沿逆时针方向作匀速圆周运动,三者轨道半径r 1>r 2>r 3,并相切于P 点.设T 、v 、a 、t 分别表示它们作圆周运动的周期、线速度、向心加速度以及各自从经过P 点算起到第一次通过图中虚线MN 所经历的时间,则( ) A .3
21T T T <= B .
3
21v v v >=
C .3
21a a a >> D .321t t t >>
三、非选择题
10、如图所示,在第一象限的区域加一个垂直于XY 平面向外,磁感强度为B 的匀强磁场,一个带正电的质点,质量为m ,电荷量为q ,(不计重力),从Y 轴上A 点(OA=a )以垂直于Y 轴的速度射入磁场区域后,恰好从X 轴上B 点(OB=b ),射出,试求质点的速度大小和出射方向。
11、(山东嘉祥一中2008年5月高考模拟)如图所示,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B = 0.60T 。
磁场内有一块足够大的平面感光平板ab ,板面与磁场方向平行。
在距ab 的距离为l = 10cm 处,有一个点状的α放射源S ,它仅在纸平面内向各个方向均匀地发射α粒子。
设放射源每秒发射n = 3.0×104
个α粒子,每个α粒子的速度都是v = 6.0×106
m/s 。
已知α粒子的电荷与质
量之比7
10
0.5⨯=m q
C/kg 。
求每分钟有多少个α粒子打中ab 感光平
板?
x
12.湖南省长沙市一中·雅礼中学2010届高三三月联考如图(a )所示,在以直角坐标系xOy 的坐标原点O 为圆心、半径为r 的圆形区域内,存在磁感应强度大小为B 、方向垂直xOy 所在平面的匀强磁场。
一带电粒子由磁场边界与x 轴的交点A 处,以速度v 0沿x 轴负方向射入磁场,粒子恰好能从磁场边界与y 轴的交点C 处,沿y 轴正方向飞出磁场,不计带电粒子所受重力。
(1)求粒子的荷质比
q m。
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B ′,该粒子仍从A 处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b )所示,求磁感应强度B ′的大小。
图(b )
图(a )
参考答案
10.解析:设质点速度为V ,轨道半径为R ,B 点的出射速度与X 轴夹角为θ,在Rt ΔBOO ,
中:有 R 2
=(R -a )2
+b 2
R=mV/qB (
)
ma
b
a
qB m
qBR V 22
2
+=
=
cos θ=(R -a )/R=(b 2
-a 2
)/(a 2
+b 2
)
⎪⎪⎭
⎫
⎝⎛+-=2
22
2arccos b
a a
b θ (0<θ<π) 答案:(
)
ma
b
a
qB 22
2
+,⎪
⎪⎭
⎫
⎝⎛+-=2222arccos b a a b θ(0<θ<π)
11.解析:α粒子磁场中沿逆时针方向做匀速圆周运动,用R 表示轨道半径,有
R
mv qvB 2
=
, 由此得 qB
mv R =
,
R = 20cm ,
因朝不同方向发射的α粒子的圆轨迹都过S ,由此可知,某一圆轨迹以O 圆心在图中N 的左端与ab 相切于P 1点,由此O 点为能打到感光平板上的α粒子圆轨迹圆心左侧最低位置,设此时α粒子从S 射出的方向与SN 的夹角为θ, 由几何关系可得 2/1/)(sin =-=R l R θ, θ = 30° , 同理O′为圆心在图中N 的右侧与ab 相切
于P 2点,则此O′点为能打到感光平板上的α粒子圆轨迹圆心右侧最低位置,设此时α粒子从S 射出的方向与SN 的夹角为θ′, 由上图几何关系可得θ′= 30°, 分析可知∠cSd = 120°方向的α粒子不能打到ab 感光平板上,则每分钟能打到ab 感光平板上的α粒子数为:
6
10
2.13/2)60(⨯=⨯=n x
个。
12.
解析:(1
)由几何关系可知,粒子的运动轨迹如图,其半径R =r ,
洛伦兹力等于向心力,即 2
0v q v B
m
R
= 得
0v q m
B r
=
(2)粒子的运动轨迹如图,设其半径为R ′,洛伦兹力提供向心力,即
2
00''m v q v B R =
又因为 tan 2
'
r R θ
=
解得 'tan
2
B B θ
=。
