高考总复习知识点总结(一)
高考数学知识点总结(全而精-一轮复习必备)

高中数学第一章-集合考试内容:集合、子集、补集、交集、并集.逻辑联结词.四种命题.充分条件和必要条件.考试要求: (1)理解集合、子集、补集、交集、并集的概念;了解空集和全集的意义;了解属于、包含、相等关系的意义;掌握有关的术语和符号,并会用它们正确表示一些简单的集合.(2)理解逻辑联结词“或”、“且”、“非”的含义理解四种命题及其相互关系;掌握充分条件、必要条件及充要条件的意义.§01. 集合与简易逻辑 知识要点一、知识结构:本章知识主要分为集合、简单不等式的解法(集合化简)、简易逻辑三部分:二、知识回顾:(一)集合1.基本概念:集合、元素;有限集、无限集;空集、全集;符号的使用.2.集合的表示法:列举法、描述法、图形表示法.集合元素的特征:确定性、互异性、无序性. 集合的性质:①任何一个集合是它本身的子集,记为;②空集是任何集合的子集,记为;③空集是任何非空集合的真子集;如果,同时,那么A = B.如果.[注]:①Z = {整数}(√) Z ={全体整数} (×)②已知集合S 中A 的补集是一个有限集,则集合A 也是有限集.(×)(例:S=N ; A=,则C s A= {0})A A ⊆A ⊆φB A ⊆A B ⊆C A C B B A ⊆⊆⊆,那么,+N③空集的补集是全集.④若集合A=集合B,则C B A=,C A B =C S(C A B)=D(注:C A B =).3. ①{(x,y)|xy =0,x∈R,y∈R}坐标轴上的点集.②{(x,y)|xy<0,x∈R,y∈R二、四象限的点集.③{(x,y)|xy>0,x∈R,y∈R} 一、三象限的点集.[注]:①对方程组解的集合应是点集.例:解的集合{(2,1)}.②点集与数集的交集是. (例:A ={(x,y)| y =x+1} B={y|y =x2+1} 则A∩B =)4. ①n个元素的子集有2n个. ②n个元素的真子集有2n-1个. ③n个元素的非空真子集有2n-2个.5. ⑴①一个命题的否命题为真,它的逆命题一定为真. 否命题逆命题.②一个命题为真,则它的逆否命题一定为真. 原命题逆否命题.例:①若应是真命题.,则a+b = 5,成立,所以此命题为真.②.1或y = 2.,故是的既不是充分,又不是必要条件.⑵小范围推出大范围;大范围推不出小范围.3.例:若.4.集合运算:交、并、补.5.主要性质和运算律(1)包含关系:(2)等价关系:(3)集合的运算律:交换律:结合律:分配律:.∅∅∅}⎩⎨⎧=-=+1323yxyxφ∅⇔⇔325≠≠≠+baba或,则且1≠x3≠y1≠∴yx且3≠+yx21≠≠yx且255xxx或,⇒{|,}{|}{,}A B x x A x BA B x x A x BA x U x A⇔∈∈⇔∈∈⇔∈∉U交:且并:或补:且C,,,,,;,;,.UA A A A U A UA B B C A C A B A A B B A B A A B B⊆Φ⊆⊆⊆⊆⊆⇒⊆⊆⊆⊇⊇CUA B A B A A B B A B U⊆⇔=⇔=⇔=C.;ABBAABBA==)()();()(CBACBACBACBA==)()()();()()(CABACBACABACBA==0-1律:等幂律:求补律:A∩C U A=φA∪C U A=U C U U=φ C Uφ=U反演律:C U(A∩B)= (C U A)∪(C U B) C U(A∪B)= (C U A)∩(C U B)6.有限集的元素个数定义:有限集A的元素的个数叫做集合A的基数,记为card( A)规定 card(φ) =0.基本公式:(3) card( U A)= card(U)- card(A)(二)含绝对值不等式、一元二次不等式的解法及延伸1.整式不等式的解法根轴法(零点分段法)①将不等式化为a0(x-x1)(x-x2)…(x-x m)>0(<0)形式,并将各因式x的系数化“+”;(为了统一方便)②求根,并在数轴上表示出来;③由右上方穿线,经过数轴上表示各根的点(为什么?);④若不等式(x的系数化“+”后)是“>0”,则找“线”在x轴上方的区间;若不等式是“<0”,则找“线”在x轴下方的区间.(自右向左正负相间)则不等式的解可以根据各区间的符号确定.特例①一元一次不等式ax>b解的讨论;②一元二次不等式ax2+box>0(a>0)解的讨论.>∆0=∆0<∆二次函数cbxaxy++=2(0>a)的图象,,,A A A U A A U A UΦ=ΦΦ===.,AAAAAA==(1)()()()()(2)()()()()()()()()card A B card A card B card A Bcard A B C card A card B card Ccard A B card B C card C Acard A B C=+-=++---+x)0)((002211><>++++--aaxaxaxa nnnn原命题若p 则q否命题若┐p 则┐q 逆命题若q 则p 逆否命题若┐q 则┐p 互为逆否互逆否互为逆否互互逆否互一元二次方程()的根002>=++a c bx ax 有两相异实根)(,2121x x x x <有两相等实根ab x x 221-== 无实根的解集)0(02>>++a c bx ax {}21x x x x x ><或⎭⎬⎫⎩⎨⎧-≠a b x x 2R 的解集)0(02><++a c bx ax {}21x x x x << ∅∅2.分式不等式的解法(1)标准化:移项通分化为>0(或<0); ≥0(或≤0)的形式,(2)转化为整式不等式(组)3.含绝对值不等式的解法(1)公式法:,与型的不等式的解法.(2)定义法:用“零点分区间法”分类讨论.(3)几何法:根据绝对值的几何意义用数形结合思想方法解题.4.一元二次方程根的分布一元二次方程ax 2+bx+c=0(a≠0)(1)根的“零分布”:根据判别式和韦达定理分析列式解之.(2)根的“非零分布”:作二次函数图象,用数形结合思想分析列式解之.(三)简易逻辑1、命题的定义:可以判断真假的语句叫做命题。
高考知识点归纳总结(汇总5篇)

高考知识点归纳总结第1篇1.整理公式数学的内容更加灵活一些,不需要去背诵,只是会应用就可以了。
首先可以把,这段时间学习到的公式整理一下,对于知识点有大概的了解。
考试也是针对这些知识点进行出题考查的,了解了这些公式,才能更加快速、精确地答题。
2.复习错题这个是数学科目复习的重点,拿出自己的错题本,可以把自己错的题再做一遍,重新巩固自己所学的知识点。
并且,达到能够解这一类型的题目,避免在期中考试中再犯相同的错误。
错题本重在理解。
3.多做练习数学考查的还是同学们运用的能力。
平常多刷题(可以重复刷自己会做错的题,直到做对为止),能够提高自己的做题速度,并且可以见到更多不同题型的考查方法,能够真正地提高自己的数学成绩。
“题海战术”虽然古老,但是一直很好用!高考数学答题注意事项答题时应遵循“先易后难勿恋战”的原则。
高考试题编制上一般都有先易后难的特点,这样比较符合心理学原理。
刚进考场时,绝大部分考生都会感到情绪比较紧张,其感知、记忆、思维等心理过程都还未完全适应考场的紧张氛围,没有达到思维的最佳状态。
解答了几道比较容易的试题后,心情渐趋稳定,智力活动恢复常态,思维的灵活性和批判性大大提高,解题速度明显加快。
而且,容易题做得越多,拿到的分数就越高,底气越足,自信心大大增强。
遭遇难题时,若屡试不爽,则干脆跳过去,千万不能纠缠不休。
试想想,一道15分的题目,你花了半个多小时才解答出来,即使正确,而因为你已付出了全场考试1/4的时间,却只得到了总分的1/10的回报,实在是得不偿失。
这时候,说不定你已急得如热锅上的蚂蚁,方寸大乱了。
高考知识点归纳总结第2篇1. 名词单复数用错,可数与不可数名词的混用。
大多数短文改错都会有此类的错误。
2.动词:时态和语态,常出现在总体时态为过去或现在时,中间杂有不适的另一时态的现象;或是及物动词后无宾语,或是不及物动词后加了宾语;需要接ing形式的接了to,或相反等。
3. 形容词副词:常出现需形容词的地方用了副词或相反;关系副词where, when,why等的缺失或错用。
高三语文知识点总复习

高三语文知识点总复习语文课程在高三阶段是非常重要的一门学科,对于学生们的综合素质提升和高考成绩的影响都非常大。
为了帮助同学们对高三语文知识点进行总复习,本文将从考试大纲出发,系统地梳理并总结高三语文的重要知识点,以期帮助同学们更好地备战高考。
第一部分:阅读理解高三语文考试的一大重点就是阅读理解题型。
阅读理解要求考生能够准确把握文章的主旨,理解作者的观点,并能够从文章中找到相关的细节进行分析和判断。
以下是高考常见的几种阅读理解题型:1.主旨概括题:要求考生能够通过阅读文章准确把握文章的主旨,用精炼的语言进行准确而简洁的概括。
2.细节理解题:要求考生能够在文章中找到与问题相关的细节信息,并进行分析和判断。
3.观点态度题:要求考生能够理解作者的观点,判断作者对待某一问题的态度,并能够找出支持作者观点的相关细节。
4.文段表达题:要求考生能够根据所给的提示,完成对文段的合理补充,使之符合文章的整体逻辑和语言风格。
在备考阶段,同学们应该多做高考真题和模拟题,熟悉不同类型的阅读理解题型,掌握相应的解题技巧,提高自己的分析和判断能力。
第二部分:写作技巧高考语文写作是考察学生综合语言运用能力的重要环节。
以下是几个高考语文写作的必备技巧:1.选题要准:在写作时,要选取与自己熟悉的话题进行创作,结合自己的生活经历和阅读积累,做到有话可说,有料可撰。
2.结构要清:写作时应该注意整体结构的安排,包括开头、主体和结尾三部分,力求逻辑清晰、层次分明,使文章的结构更加紧凑。
3.论点要明:在文章中要明确自己的立场和观点,并通过论述和举例等方式进行支持,增强说服力。
4.用词要准确:写作时应该注意用词准确、得体,力求用简洁、精准的语言表达出自己的意思。
5.修辞要巧妙:适当运用比喻、拟人、夸张等修辞手法,增加文章的表现力和感染力。
通过不断地练习和积累,掌握好写作技巧,同学们就能在高考语文写作中取得更好的成绩。
第三部分:古诗文鉴赏高考语文考试中,对古代文学的鉴赏能力也是一个重要的考察内容。
高考物理电磁学知识点之静电场知识点总复习(1)
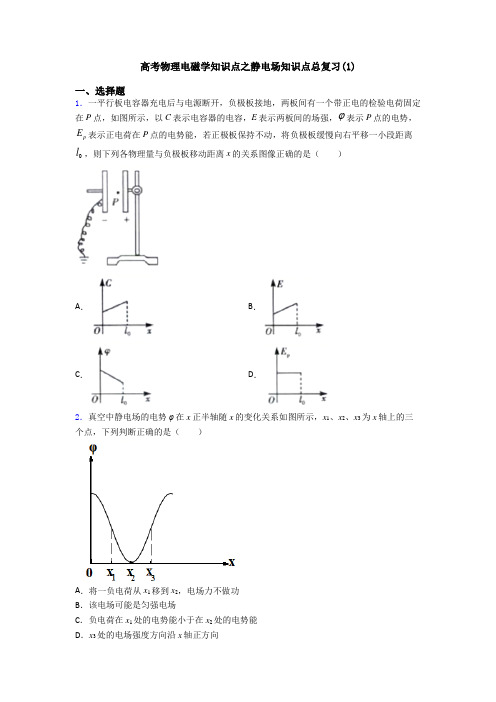
17.如图,一带正电的点电荷固定于O点,两虚线圆均以O为圆心,两实线分别为带电粒子M和N先后在电场中运动的轨迹,a、b、c、d为轨迹和虚线圆的交点,不计重力。则( )
A.a点的场强和c点的场强相同
B.M带正电荷,N带负电荷
C.N在从c点运动到d点的过程中电场力做正功
D.M在b点的电势能等于N在d点的电势能
D.感应起电说明电荷从带电的物体转移到原来不带电的物体上去了
【参考答案】***试卷处理标记,请不要删除
一、选择题
1.C
解析:C
【解析】
【详解】
A.由电容器的决定式:
可知C与两极板间距离d成反比,故C与x不是线性关系,故A错误;
B.电容器充电后与电源断开,电荷量Q不变,由:
可得:
所以可知电场强度E是定值,故B错误;
C.因负极板接地,电势为零,所以P点电势为:
L为P点到负极板的初始距离,因为E不变, 随x增大而线性减小,故C正确;
D.由:
可知 与 成正比,故也随x增大而线性减小,故D错误。
故选C。
2.C
解析:C
【解析】
【分析】
【详解】
A.从 移到 ,电势在降低,将一负电荷从高电势到低电势,其电势能增加,则电场力做负功,故A错误;
7.C
解析:C
【解析】
【分析】
根据电场力功与电势差的关系求解AB和BC各点之间的电势差,然后找到等势面确定场强的方向,根据E=U/d求解场强。
【详解】
将电子由A移动到B点,电场力做功2eV,则 ;同样: ,若设C点的电势为0,则B点的电势为1V,A点的电势为-1V,则AB中点的电势与C点电势相同,可知场强方向沿BA方向斜向上,场强为 ,故选C.
语文高考知识点归纳总结【5篇】

语文高考知识点归纳总结【5篇】语文高考知识点总结1语文基本要素1.小说三要素:人物情节环境2.议论文三要素:论点论据论证3.比喻三要素:本体喻体喻词4.记叙文六要素(五W+H):何时何地何人何因何过何果5.律诗四条件:八句四联偶尾同韵中联对偶平声合调6.五种表达方式:叙述议论抒情说明描写7.六种说明文说明方法:举例子列数字打比方作比较分类别下定义8.三种说明文说明结构:总分总结构总分结构分总结构9.三大说明文说明顺序:按时间顺序按空间顺序按逻辑顺序10.两种基本议论文结构:提出问题---分析问题---解决问题提出观点---论证观点---总结观点11.六种议论文论证方法:举例法对比法喻证法归谬法12.八种主要修辞手法:比喻拟人排比夸张反问设问反复对偶13.四种人物描写方法:外貌描写语言描写动作描写心理描写14.七种短语类型:并列短语偏正短语主谓短语动宾短语动补短语介宾短语的字短语15.六种句子成分:主语谓语宾语补语定语状语16.十二词类:名动形数量代副介连助叹拟17.三种记叙方法:顺叙倒叙插叙18.三种省略号作用:表引文内容省略表列举事项省略表说话中断延长19.四种波折号作用:表解释说明前文表后文跳跃转折表声音中断延长表时地数起止20.四种引号作用:表引用实际内容表讽刺反语表特定谓语语文高考知识点总结2一鉴赏形象1人物形象(1)问:人物形象有什么特征(塑造了什么样的人物形象)答:①概括形象特征:本诗塑造了一位的身份形象。
②结合诗句具体分析(抓关键点手法)③塑造人物形象的意义(作用):寄寓的情感蕴含的哲理。
(2)人物描写手法(怎样塑造刻画描写表现人物形象的,怎样表现人物情绪的) 正面描写:外貌描写动作神态心理语言细节描写(依附于其他描写手法存在)等侧面描写:环境烘托他人正衬对比反衬等借助修辞:比喻象征等2事物形象(咏物诗)(托物言志之物,象征人物品格理想情操)问:描写(刻画)了什么样的形象?答:①概括物象特征②结合诗句分析(点手法)③作用:象征什么样的品格,寄托什么样的情感常见形象:兰花菊花梅花松柏竹蝉马等(分析总结象征内涵)常用手法:比喻拟人借代对比反衬等(描写物)象征借物抒怀托物言志(抒发情)3景物形象:(1)意象:(蕴含诗人情感(意)的景物形象,在诗词中设有几个意象名词。
高考理综物理总复习重要知识点归纳总结

高考理综物理总复习重要知识点归纳总结高中物理复题纲第一章:力一、力F:物体对物体的作用。
力的三要素包括大小、方向和作用点。
物体间力的作用是相互的,即作用力与反作用力,但它们不在同一物体上,不是平衡力。
作用力与反作用力是同性质的力,有同时性。
二、力的分类:1、按性质分:重力G、弹力N、摩擦力f2、按效果分:压力、支持力、动力、阻力、向心力、回复力。
3、按研究对象分:外力、内力。
重力G由于受地球吸引而产生,竖直向下。
重心的位置与物体的质量分布与形状有关。
质量均匀、形状规则的物体重心在几何中心上,不一定在物体上。
弹力由于接触形变而产生,与形变方向相反或垂直接触面。
摩擦力阻碍相对运动的力,方向与相对运动方向相反。
滑动摩擦力与材料有关,与重力、压力无关。
相同条件下,滚动摩擦小于滑动摩擦。
静摩擦力可以用二力平衡来计算。
力的合成与分解遵循平行四边形定则。
以分力F1、F2为邻边作平行四边形,合力F的大小和方向可用这两个邻边之间的对角线表示。
平动平衡是指共点力使物体保持匀速直线运动状态或静止状态。
解题方法是先受力分析,然后根据题意建立坐标系,将不在坐标系上的力分解。
如受力在三个以内,可用力的合成。
利用平衡力来解题。
第二章:直线运动一、运动:1、参考系可以任意选取,但尽量方便解题。
2、质点是研究物体比周围空间小得多时,任何物体都可以作为质点。
只有质量,没有形状与大小。
3、位移s是矢量,方向起点指向终点。
表示位置的改变。
路程是标量,质点初位置与末位置的轨迹的长度,表示质点实际运动的长度。
4、时刻是某一瞬间,用时间轴上的一个点表示。
如4s,第4秒。
时间是起始时刻与终止时刻的间隔,在时间轴上用线段表示。
如4秒内,第4秒内。
ma速度v是一个矢量,表示运动的快慢,可以用公式v=s/t计算,其中s为位移,t为时间。
常用的速度单位是米每秒,也可以用千米每小时表示。
在s-t图中,速度的大小可以用正切tgθ计算。
平均速度是变速运动中位移与对应时间之比,而瞬时速度是质点某一瞬间的速度,大小为速率,标量。
高考必备高三毕业班总复习资料高中地理必背知识点总结大全
【高考必备】高三毕业班总复习资料高中地理必背知识点总结大全【高考必备】高三毕业班总复习资料高中地理知识点总结(必背)第一单元地图专题1.经度的递变:向东度数增大为东经度,向西度数增大为西经度。
2.纬度的递变:向北度数增大为北纬度,向南度数增大为南纬度。
3.纬线的形状和长度:互相平行的圆,赤道是最长的纬线圈,由此往两极逐渐缩短。
4.经线的形状和长度:所有经线都是交於南北极点的半圆,长度都相等。
5.东西经的判断:沿著自转方向增大的是东经,减小的是西经。
6.南北纬的判断:度数向北增大为北纬,向南增大为南纬。
7.东西半球的划分:。
8.太阳活动的影响:黑子--影响气候,耀斑--电离层--无线电通讯,带电粒子流――磁场――磁暴9、太阳辐射的影响:①维持地表温度,促进地球上水、大气、生物活动和变化的主要动力。
②太阳能是我们日常所用能源。
10.自转方向:自西向东,北极上空俯视呈逆时针方向、南极上空俯视呈顺时针方向速度:①线速度(由赤道向两极递减至0)(23h56m4s周期:①恒星日)外,各地相等0除两极为(②角速度.真正周期)②太阳日(24时,昼夜更替周)意义:①昼夜更替②不同经度不同的地方时③水准运动物体的偏移(北右南左)11、晨昏线:沿自转方向,黑夜向白天过渡为晨线,白天向黑夜过渡为昏线(晨昏线上太阳高度角为0度)。
12、晨昏线与经线:晨昏线与经线重合-----春秋分;晨昏线与经线交角最大----夏至、冬至13、时间计算:所求时间=已知时间±区时差+途中时间14、时区=经度/15°(若不整除,则四舍五入)区时差=时区差15、世界时:以本初子午线(0°)时间为标准时,也称为格林尼治时间,也是零时区的区时。
16、日期分割:零点经线往东至日界线(180°)为地球上的“今天”,往西至日界线为“昨天”。
17、日界线:自西向东越过日界线(不完全经过180°经线)日期减一天,自东向西越过日期加一天。
高考理综知识点总结
高考理综知识点总结一、物理部分1. 力学- 运动的描述(速度、加速度)- 力的作用(牛顿运动定律、摩擦力、万有引力)- 动量与能量(动量守恒、机械能守恒、功和功率)- 简单机械(杠杆、滑轮、斜面)- 刚体的平衡与转动(力矩、转动惯量、角动量守恒)2. 热学- 温度与热量(热平衡、比热容、热传递方式)- 理想气体定律(压强、体积、温度的关系)- 热力学第一定律(内能、做功、热量交换)3. 电磁学- 静电场(库仑定律、电场强度、电势能)- 直流电路(欧姆定律、基尔霍夫定律、电功和电功率) - 磁场(安培力、洛伦兹力、磁通量)- 电磁感应(法拉第电磁感应定律、楞次定律、交流电)4. 波动与光学- 机械波(波的传播、波速、波长、频率)- 光的反射和折射(平面镜、凸透镜和凹透镜)- 光的干涉、衍射和偏振(双缝干涉、单缝衍射)二、化学部分1. 基本概念- 物质的组成(元素、化合物、混合物)- 化学反应的类型(合成、分解、置换、还原氧化)- 化学式和化学方程式(书写规则、平衡方程式)2. 无机化学- 元素周期表(周期性、族序性)- 重要元素及其化合物(碱金属、卤素、氧族元素等)3. 有机化学- 有机化合物的分类(烃、醇、酮、酸、酯等)- 有机反应类型(取代反应、加成反应、消除反应、氧化还原反应)4. 化学实验- 实验基本操作(溶解、加热、蒸馏、萃取)- 实验安全与事故处理三、生物部分1. 细胞生物学- 细胞的结构与功能(细胞膜、细胞器、核酸)- 细胞的分裂与增殖(有丝分裂、减数分裂)2. 遗传与进化- 孟德尔遗传定律(分离定律、自由组合定律)- 基因的结构与功能(DNA、RNA、蛋白质合成)- 生物进化的原理(自然选择、遗传多样性)3. 生态与环境- 生态系统的组成与功能(生产者、消费者、分解者)- 人口与环境(资源利用、环境污染、生态平衡)4. 人体健康与疾病- 人体生理系统(循环、呼吸、消化、神经、内分泌)- 常见疾病的预防与治疗(心血管疾病、糖尿病、传染病)附录:- 重要公式汇总- 实验操作步骤与注意事项- 历年高考题型分析与解题技巧请注意,这份总结只是一个框架性的概要,具体的知识点需要根据最新的教学大纲和考试指南进行详细扩展和深入学习。
高考英语新词法固定短语知识点知识点总复习附解析(1)
高考英语新词法固定短语知识点知识点总复习附解析(1)一、选择题1.______of all the staff,I would like to wish you a happy retirement.A.In honour B.In place C.On behalf D.On account2.If Lincoln had lived, it________ be that his postwar policies would have brought criticism upon him that would________ his reputation.A.might as well … have tarnished B.might well … have tarnishedC.might as well … tarnish D.might well … tarnish3.Jack part in the exam because of his cheating in the last exam.A.is banned to take B.is banned from takingC.banned from taking D.banned to take4.______ catch the first bus, he got up very early this morning.A.In order to B.In order that C.So to D.So that5.________, I lost heart in English, but my teacher often said to me, “Keep working hard, and you wil l succeed ________.”A.At a time; in time B.At a time; on timeC.At one time; in time D.At one time; on time6.Don't interrupt;just hear me_______before you start talking.A.on B.off C.out D.over7.You may be an inexperienced candidate, but none of that makes things worse than your walking into that interview room ______in confidence.A.lacked B.lacking C.for lack of D.lacking of 8.The art show was ______ being a failure; it was a great success.A.far from B.along withC.next to D.regardless of9.Doctors always tell us that drinking too much________our health,but some people don’t care.A.is harm to B.does harmful toC.is harmful to D.do harm to10.If you keep on, you’ll succeed _____. Wish you success in the exam.A.in time B.at one time C.for the same time D.sometimes11.I don’t want _______as this.A.as an expensive car B.as a car expensiveC.as expensive a car D.how expensive a car12.Everything _____ doing is worthy of _____ well.A.worthy; being done B.worth; being done C.worthy; doing D.worth; doing 13.Try to discourage him ________ driving too fast, as it’s extremely dangerous.A.from B.into C.to D.for14.The building was named Ford Hall _______ a man named James Ford.A.in need of B.in memory of C.in charge of D.in search of 15.After graduation, Jane_________ her job as a volunteer teacher in the countryside.A.set out B.set up C.took up D.took over16.-------Do you need any help, Lucy?-------Yes. The job is _________ I could do myself.A.less than B.more than C.no more than D.not more than 17.A recent survey shows that only a ________ of the children do some reading every day, while most of them prefer playing games.A.Few B.little C.minority D.majority18.The number of teenagers who commit crimes _________ 20% over the past years. A.have been reduced by B.has been reduced byC.have been reduced to D.has been reduced to19.________ that the small village ________ him. He knows almost everything about it. A.There is no doubt; is familiar with B.There is no doubt; is familiar toC.It is no doubt; is familiar with D.It is no doubt; is familiar to20.In my father’s study there are _____ books about how to keep fit.A.a great many B.large amounts ofC.a great deal of D.a large amount of21.—How’s Jack doing in Britain?—I wrote an email to him last week, but _____ I have had no reply from him.A.from now on B.so far C.just now D.later on 22.everyone here,I wish you a pleasant journey back to your journey.A.By means of B.On behalf of C.In search of D.For fear of 23.My father is lively and____, but he is not very patient_____me.A.energy; with B.energetic; withC.energy; of D.energetic; of24.He said, “Don’t do that again.” He _____ me_______ that again.A.said to me;not to do B.said to me;don’t doC.told me;don’t do D.told me;not to do25.We had lots of good applicants for the job, but one _________ from the rest.A.made out B.stood out C.picked out D.figured out【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】【详解】考查介词短语辨析。
高考物理知识点总结归纳
高考物理知识点总结归纳高考物理知识点总结归纳1一、运动的描述1.物体模型用质点,忽略形状和大小;地球公转当质点,地球自转要大小。
物体位置的变化,准确描述用位移,运动快慢s比t,a用δv与t比。
2.运用一般公式法,平均速度是简法,中间时刻速度法,初速度零比例法,再加几何图像法,求解运动好方法。
自由落体是实例,初速为零a等g.竖直上抛知初速,上升最高心有数,飞行时间上下回,整个过程匀减速。
中心时刻的速度,平均速度相等数;求加速度有好方,δs等at平方。
3.速度决定物体动,速度加速度方向中,同向加速反向减,垂直拐弯莫前冲。
二、力1.解力学题堡垒坚,受力分析是关键;分析受力性质力,根据效果来处理。
2.分析受力要仔细,定量计算七种力;重力有无看提示,根据状态定弹力;先有弹力后摩擦,相对运动是依据;万有引力在万物,电场力存在定无疑;洛仑兹力安培力,二者实质是统一;相互垂直力最大,平行无力要切记。
3.同一直线定方向,计算结果只是“量”,某量方向若未定,计算结果给指明;两力合力小和大,两个力成q角夹,平行四边形定法;合力大小随q变,只在最大最小间,多力合力合另边。
多力问题状态揭,正交分解来解决,三角函数能化解。
4.力学问题方法多,整体隔离和假设;整体只需看外力,求解内力隔离做;状态相同用整体,否则隔离用得多;即使状态不相同,整体牛二也可做;假设某力有或无,根据计算来定夺;极限法抓临界态,程序法按顺序做;正交分解选坐标,轴上矢量尽量多。
三、牛顿运动定律1.f等ma,牛顿二定律,产生加速度,原因就是力。
合力与a同方向,速度变量定a向,a变小则u可大,只要a与u同向。
2.n、t等力是视重,mg乘积是实重;超重失重视视重,其中不变是实重;加速上升是超重,减速下降也超重;失重由加降减升定,完全失重视重零四、曲线运动、万有引力1.运动轨迹为曲线,向心力存在是条件,曲线运动速度变,方向就是该点切线。
2.圆周运动向心力,供需关系在心里,径向合力提供足,需mu平方比r,mrw平方也需,供求平衡不心离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 集1、 常用数集的符号:(1)全体非负整数的集合通常简称非负整数集(或自然数集),记作N (2)非负整数集内排除0的集,也称正整数集,记作N+(或N*) (3)全体整数的集合通常称作整数集,记作Z(4)全体有理数的集合通常简称有理数集,记作Q (5)全体实数的集合通常简称实数集,记作R (6)复数集合计作C(7)属于∈,不属于∉,并集⋃,交集⋂,真包含⊂,被真包含⊃,包含⊆,被包含⊇,不包含⊄,空集∅ 2、 集合部分(1)集合的三个特性:无序性、确定性、互异性(2)集合的分类:按元素的个数分为有限集合无限集;按元素的性质可分为数集和点集等 (3)集合的表示法:举例法、描述法、图示法 (4)集合的运算:①n 元集合共有2n 个子集,其中有2n -1个真子集,2n -1个非空子集;②交集:=⋂B A {x/x A ∈且x B ∈} ③并集:A ∪B={x|x ∈A 或x ∈B}④补集:CuA={x/A x ∉且x ∉}(其中A ⊆ ) (5)集合中常用的运算性质:C B B A ⊆⊆,,则A=B ; C,B B,A ⊆⊆则C A ⊆; A A A =⋂, ∅=∅⋂A ;A A A =⋃ AB B A ⋃=⋃A A =∅⋃; ⋂A CuA=∅ A ⋃CuA=UB A A B A ⊆⇔=⋂ A B A B A ⊆⇔=⋃ A ⊆∅且∅≠A ,则A ⊂∅注意:元素与集合的关系包括:属于与不属于,分别用符号∈与∉表示,注意区分0和∅ 3、 简易逻辑部分(1)命题:可以判断真假的语句叫做命题。
命题分为:简单命题(不含逻辑连接词的命题)和复合命题(由简单命题和逻辑连接词的命题组成的命题)(2)逻辑连接词:且、或、非这些词叫做逻辑连接词。
(3)复合命题的真值表p q ¬pq p ∨ q p ∧ 真 真 假 真 真 真 假 假 真 假 假 真 真 真 假 假假真假假(4)四种命题及其相互之间的关系原命题:若p则q;逆命题:若q则p;否命题:若¬p则¬q;逆否命题:若¬q则¬p注意:原命题与它的逆否命题一定等价,即互为逆否的两个命题是等效的。
(5)充分、必要条件的判断①若p⇒q,但q p,则p是q的充分不必要条件;②若q⇒p,但p q,则p是q的必要不充分条件。
③若p q且q p,则p是q的充要条件;④若p q且q p,则p是q的既不充分也不必要条件.⑤若p⇒q,那么p是q的充分条件,q是p的必要条件第二章函数1、函数的基本概念(1)映射的定义:设A、B是两个集合,如果按照某种法则f,对于集合A中的任何一个元素,在集合B中都有对应的元素和它对应,这样的对应叫集合A到集合B的映射,记作f:A→B(2)函数的定义:设A、B都是非空数集合,f:x→y是从A到B的一个对应法则,那么从A到B的映射f:A→B就叫做集合A到集合B的一个函数,记作y=f(x)其中x∈A,y∈B,集合A叫做函数的定义域,集合C叫做函数的值域,其中C⊆B(3)函数的三要素:定义域、法则、值域(4)函数的表示方法:解析法、列表法、图像法。
注意:判断两个函数是否为同一函数,只需要判断这两个函数的定义域和对应法则是否相同。
(5)函数的定义域:使函数y=f(x)有意义的x的取值范围叫做函数y=f(x)的定义域。
∈}叫做函数的值域,值域由函数的定义域和对应法(6)函数的值域:函数值的集合{f(x)/x A则确定。
2、函数的常见性质(1)函数的单调性①增函数、减函数的定义:如果对于定义域内某个区间上的任意两个自变量x1,x2,当x1<x2时若都有f(x1) <f(x2),则称f(x)在这个区间上是增函数;若都有f(x1)>f(x2),则称f(x)在这个区间上是减函数。
单调区间:如果函数y=f(x)在某个区间是增函数或者减函数,则称函数y=f(x)在这一区间具有单调性,这一区间叫做y=f(x)的单调区间。
②函数单调性的求法方法一:定义法对于定义域内任意x1,x2,且x1<x2,f(x1)-f(x2)=…=…=…≤0(≧0)(判断f(x1)-f(x2)大于零还是小于零),所以f(x1)≤f(x2)(f(x1)≥f(x2) )对于定义域内任意x1,x2,且x1<x2,使得f(x1)≤f(x2)(f(x1)≥f(x2) ),所以函数f(x)是增函数(减函数)。
方法二:导数法(定义域为(X1,X2) ) 对函数f(x)求导→判断f '(x)的符号:A 、 若f '(x)≥0,则函数在定义域内单调递增;若f '(x)≤0,则函数在定义域内单调递减B 、 若定义域内的a ∈(X1,X2)使f '(a)=0,再分开判断区间(X1,a )和(a,X2)的单调性。
方法三:对于复合函数,可分别判断复合函数的内、外层的单调性,再根据“同增异减”的法则判断。
例如:函数y=)12(3-x ,内层为u(x)=2x-1,在定义域内单调递增;外层为f(u)=u 3,在定义域内也单调递增,内外层的单调性相同,根据“同增异减”,函数y=)12(3-x 在定义域内是单调递增的。
方法四:利用函数的奇偶性奇函数在对称的定义域上单调性相同,偶函数在对称的定义域上的单调性相反例如:已知函数f(x)是奇函数,且在区间(-3,0)上单调递减,那么它在区间(0,3)上也单调递减(2) 函数的奇偶性 ① 奇偶函数的定义:如果对于函数f(x)定义域内任何的x ,都有f(x)=f(-x),那么函数f(x)就叫做偶函数。
如果对于函数f(x)定义域内任何的x ,都有f(x)=-f(-x),那么函数f(x)就叫做奇函数。
如果函数是奇函数或者偶函数,我们就称函数具有奇偶性。
注意:判断函数的奇偶性的时候首先判断函数的定义域是否关于原点对称。
若不对称,函数肯定不具有奇偶性,若对称,再进行进一步判断。
有的函数既是奇函数又是偶函数。
具有奇偶性的函数图像的特点:奇函数的图像关于原点对称,反过来,如果一个函数的图像关于原点对称,那么这个函数是奇函数;偶函数的图像关于y 轴对称,反过来,如果一个函数的图像关于y 轴对称,那么这个函数是偶函数。
② 奇、偶函数的判断步骤:判断函数的定义域是否关于原点对称, 如果不是,则函数f(x)是非奇非偶函数如果是,若f(-x)=f(x),则f(x)是偶函数;若f(-x)=-f(x),则f(x)是奇函数 (3) 函数的周期性:对于函数y=f(x),如果存在一个不为零的常数T ,使得当x 取定义域内任意一个值时,使f(x)=f(x+T)都成立,那么f(x)是一个周期函数,T 是它的周期,对于一个周期函数来说,如果在所有周期中存在一个最小正整数,就把这个最小的正数叫最小正周期。
3、 几种常见的函数及其相关知识 (1)二次函数二次函数的三种表示形式: 一般式:f(x)=a 2x +bx+c (a ≠0)顶点式:若二次函数的顶点为(-a b 2,a b ac 442-),则其解析式为f(x)=a(x+ab2)+a b ac 442-两根式:如果二次函数图像与x 轴有交点,交点为(x 1,0),(x 2,0),则其解析式为 f(x)=(x-x 1)(x-x 2). 二次函数的图像和性质: ①函数关于直线x=-ab2对称,定义域为R ②当a>0时,开口向上,值域为(a b ac 442-,+∞),在区间(-∞,-a b 2)单调递减,在区间(a b2,+∞)单调递增;当a <0是,值域为(-∞,a b ac 442-),在区间(-∞,-ab2)单调递增,在区间(ab2,+∞)单调递减 ③∆=ac b 42-,当∆>0是,函数图像与x 轴有两个交点;当∆=0时有一个交点,当∆<0时没有交点。
(2)指数与指数函数指数:n 次方的定义:若a x n=,则称x 为a 的n 次方根,“n”是方根的记号。
在实数范围内,正数的奇次方根是一个正数,负数的奇次方根是负数,0的奇次方根是0;正数的偶次方根是两个绝对值相等符号相反的数,哦的偶次方根是0, 负数没有偶次方根。
当n 为奇数时,nna =a ;a a n n =)(;当n 为偶数时,nna =|a|n mnm a a =,nmn m nm aa a1==--;其中a>0, m 、n 都是正数,n >1。
指数函数:函数y=x a (a>0,且a ≠1)叫作指数函数。
y=x a a>10<a<1 定义域 R 值域(0,+∞) 性质过定点(0,1)当x>0时,y>1;当x<0时,0<y< 当x>0时,0<y<1;当x<0时,y>1 在(-∞,+∞)上是单调增函数在(-∞,+∞)上是单调减函数(3)对数与对数函数对数的定义:如果N a b= (a>0,a ≠1) 那么b 叫作a 为底N 的对数,记作b=log a N. 指数与对数的关系:N a b=⇔b=log a N (a>0,a ≠1,N >0)对数运算性质:log a (MN)=log a M+log a N log a NM=log a M -log a N log a M n =n log a M (M>0,n>0,a>0,a ≠1)对数函数:函数y=log a x (a>0,a ≠1)叫作对数函数,其中x 是自变量,定义域是(0,+∞) y=log a xa>10<a<1性质定义域:(0,+∞)值域:R过点(1,0),即x=1时,y=0当x>1时,y>o,当0<x<1时,y<0 当x>1时,y<0,当0<x<1时,y>o 是(0,+∞)的增函数是(0,+∞)的减函数指数函数与对数函数互为反函数,即y=log a x (a>0,a ≠1)是y=x a (a>0,且a ≠1)的反函数。
(4)复合函数:设y=f(u),u=g(x),当x 在u=g(x)的定义域Dg 中变化时,u=g(x)的值在y=f(u)的定义域Df 内变化,因此变量x 与y 之间通过变量u 形成的一种函数关系,记为 y=f(u)=f[g(x)]称为复合函数其中x 称为自变量,u 为中间变量,y 为因变量(即函数) 比如y=)12(3-x ,其中f(u)=u 3,g(x)=2x-1,Dg 是g(x)=2x-1的定义域,g(x)的值域是f(u)的定义域。
4、 反函数 反函数的定义: 若函数y=f(x)(x ∈A )的值域为C ,由这个函数x ,y 的关系,用y 把x 表示出来,得到x=g(y),x 在A 中都有唯一的值和它对应,那么x=g(y)就表示y 是自变量,x 是自变量的函数。
