粮食产量与化肥施用量回归分析
最新应用回归分析-第6章课后习题参考答案

第6章多重共线性的情形及其处理思考与练习参考答案6.1 试举一个产生多重共线性的经济实例。
答:例如有人建立某地区粮食产量回归模型,以粮食产量为因变量Y,化肥用量为X1,水浇地面积为X2,农业投入资金为X3。
由于农业投入资金X3与化肥用量X1,水浇地面积X2有很强的相关性,所以回归方程效果会很差。
再例如根据某行业企业数据资料拟合此行业的生产函数时,资本投入、劳动力投入、资金投入与能源供应都与企业的生产规模有关,往往出现高度相关情况,大企业二者都大,小企业都小。
6.2多重共线性对回归参数的估计有何影响?答:1、完全共线性下参数估计量不存在;2、近似共线性下OLS估计量非有效;3、参数估计量经济含义不合理;4、变量的显著性检验失去意义;5、模型的预测功能失效。
6.3 具有严重多重共线性的回归方程能不能用来做经济预测?答:虽然参数估计值方差的变大容易使区间预测的“区间”变大,使预测失去意义。
但如果利用模型去做经济预测,只要保证自变量的相关类型在未来期中一直保持不变,即使回归模型中包含严重多重共线性的变量,也可以得到较好预测结果;否则会对经济预测产生严重的影响。
6.4多重共线性的产生于样本容量的个数n、自变量的个数p有无关系?答:有关系,增加样本容量不能消除模型中的多重共线性,但能适当消除多重共线性造成的后果。
当自变量的个数p较大时,一般多重共线性容易发生,所以自变量应选择少而精。
6.5 自己找一个经济问题来建立多元线性回归模型,怎样选择变量和构造设计矩阵X才可能避免多重共线性的出现?答:请参考第三次上机实验题——机场吞吐量的多元线性回归模型,注意利用二手数据很难避免多重共线性的出现,所以一般利用逐步回归和主成分回归消除多重共线性。
如果进行自己进行试验设计如正交试验设计,并收集数据,选择向量使设计矩阵X 的列向量(即X 1,X 2, X p )不相关。
6.6对第5章习题9财政收入的数据分析多重共线性,并根据多重共线性剔除变量。
基于回归分析的粮食产量影响因素分析——以江西省为例

效 灌溉 面积 X 直 接摘 录 自《 中国统计 年鉴 》 ( 1 9 9 5 -2 0 1 2)
p z l n x 2 + p 3 l n X 3 + 4 l n X 4 + B 5 l n X 5 + ( 为随机误差 项 ) ; 模 型 的
对的是江 西省 的粮食播 种面积长久 以来一直维持 在 3 5 0多
万公顷左右 , 加 快 提 高 粮 食 产 能 成 为 提 高 粮 食 产 量 的 重 中 之
( 一) 数 据 收集 本 文 以江 西 省粮 食 产 量为 研 究 对象 , 收 集 了 江 西 省
1 9 9 4 —2 0 1 1 年的农业 生产相关数据 , 数据( 粮食产量 Y、 粮食 播种面积 X , 、 成灾 面积 X 、 化肥施用量 x , 、 农机 总动力 x 、 有
( 青 岛农业大学 经济与管理学院 , 山东 青岛 2 6 6 1 0 9 )
摘
要: 江西 省 作 为 中国 南方 水 稻 主 产 区 , 在 提 高粮 食 产 量 方 面发 挥 着十 分 重 要 的 作 用 , 根 据 江 西省 1 9 9 4 ~2 0 l 1
年 的相 关统计资料 , 选取粮食播种 面积 、 成 灾面积等五个影响 江西省粮食 产量 的指标 , 采 用回 归分析 法 , 解释影响江西
( 中华人民共和 国国家统计局编 ) , 相关数据 ( 见下页表 1 ) 。
( 二) 预 测模 型 的设 计
将 Y作为 因变量 , x均为 自变量 , 参照柯 布一 道格拉斯 生产 函数 , 将 江西 省粮食 生 产模 型设 计 为 : l n Y = C +  ̄ . 1 n X +
我国粮食产量与化肥使用量之间的实证分析

由 于 模 型 研 究 的 是 粮 食 产 量 与 其影 响 因 素 之 间 的 关 系 . 因 此 选 取 C D 生 产 函数 , 一 般 形 式 为 y A 中 : 表 示 - 其 : ‘ 觥 其 Y
件 E i e. vw5 e 0和 S s 1 . 。 PS1 5
量 的 因素之 阍 的 关 系 出发 , 用 c— 生 产 函数 , 用计 量 经 济 利 D 使
学软 件— — E i 50和 S S 1 . 影 响 我 国粮 食 产 量 的主 要 v we . e PS1 5对 因素 进 行 实证 分 析 . 后 得 出农 用 化 肥 的 使 用 是 影 响 我 国粮 食 最
( 2)
量 统 计 分 析 和 经 济 意 义 分 析 . 出 了最 终 的 经济 计 量 模 型 。 得
2 样 本数 据 及 其理 论 模 型
S = 57 6 0 1 5 04 9 0 2 )( .1 ) ( . 0 e ( . )( . 1 )( . )( . 0 0 1 3 0 1 ) 7 4 3 0 t ( 0 5 )( .8 )( .3 )( o5 2 一 . 6 23 0 = 一 . 3 47 8 26 4 - . )( 18 )( . ) 6 4 2 6
R : .5 R2 0 9 7 F 5 . 5 09 4 - _ .3 = 75 9
模型使用时间序列 数据 , 据来源于《 国农村统计年鉴》 数 中
f9 1 2 o) 由 于统 计 数 据 没 有 粮 食 生 产 的 专 用 数 据 , 用 化 18 ~ 0 o。 农
回归分析案例资料

回归分析案例现收集到若干年粮食产量以及受灾面积、农作物总播种面积、乡村从业人员、农用化肥施用折纯量等数据,利用多元线性回归分析,分析影响粮食产量的主要因素。
一、相关分析(相关矩阵)setwd("D:/Rdata")data<-read.csv(file=file.choose(),head=T)colnames(data)<-c("Y","X1","X2","X3","X4")dataX<-cor(data)Xpairs(data)结果显示分析X1与Y的相关系数较小,X2、X3、X4与Y的相关系数较大。
X3、X4可能存在较强的相关性。
二、多重共线性诊断kappa(X,,exact=T)结果显示K值<100说明共线性很小,K值在100到1000之间说明中等强度,K>1000存在严重共线性。
此处K=580.8733,说明存在多重共线性。
三、线性回归attach(data)lm.sol<-lm(Y~X1+X2+X3+X4)summary(lm.sol)结果显示分析F统计量的P-value<0.05,故线性回归显著。
X1、X3的系数显著,其他系数均不显著,2R为0.9023。
这很可能出现多重共线性。
综合kappa检验,确定是多重共线性引起的。
可用逐步回归法修正该模型。
lm.step<-step(lm.sol)summary(lm.step)结果显示分析删掉了X2、X4两个变量,F统计量的P-value<0.05,线性关系同样显著,常数项,X1、X3系数均显著。
2R=0.8966,略微有所降低。
综合来看,模型拟合较合适。
四、异方差检验library(lmtest)bptest(lm.step)结果显示分析p-value=0.1442>0.05 所以可以认为不具有异方差性,即残差是同方差的。
玉米产量与氮肥和钾肥施用量相关性研究

-
-
0 2 3 6 ,说 明玉米施氮量 与产 量 5 g时玉米产 量达 到最高点 ,到最 高点 . 422 3 k
【 考 文 献】 参
之间有显著的回归关系 。 后 随着施 钾量 的提 高 玉米 产量 逐渐 下 通 过 一 元 二 次 方 程 的 拟 合 图 得 出 降 , 最佳施钾量为亩施 K0 . g 4 k。 5
肥试验 , 以确 定 其 最佳 配 比 。 据 禄 丰 县 根
土壤肥力以及气候 特点 , 玉米施肥量为 :
在 亩 施 磷 肥 ( 2 8g 钾 肥 ( : 5 g的 P0 )k 、 KO)k
水平下 ,最佳施氮量 为亩施纯氮 2k ; 0 g 在亩施纯氮 2 k 、 0 g磷肥 ( 8 g的水平 0 )k 下 ,玉米钾 肥 ( 2 K0)的最高施用量 为 5 g 最佳施用量为 45 g k, . 。 k 3 肥 料 在 农 业 生产 中 具 有 举 足 轻 重 ) 教材》对 2 3 6 l 处理进行 回归分析 , 钾 肥 施 用 量 与 产 量 之 间 的 相 关 系 数 为 、 、 、1 得 出在 我 县 中海 拔 地 区玉 米 在 磷 钾 固定 09 2 3说 明 钾 肥 用 量 与 玉 米 产 量 有 高 的作用 。合理施肥能大幅度提高作物产 .7 3 , 降低 生产 成本 。 目前 , 国农村普遍 我 时 玉 米施 氮 肥 与 产 量 的 回归 模 型是 : 度 相 关 关 系 , 测 定 系 数 为 09 5 2 , 量 、 复 .4 4 6 Y= 8 .9 1 .0 X一 . 6 3 4 2 1 + 6 7 3 02 8 X 也 达到较高 的拟合效果 , 差分析 得出 存在盲 目施用 化肥和过量 施肥 的现象 , 方 通过从 回归统计得出 ,在亩施磷肥 F 86 18 , 大 于 F∞ 02 3 15 4说 这不仅造成肥料资源严重浪费 ,农业 生 = .6 8 8 n = .3 6 0 8 , 而且影响农产 品品质 , 污染 ( 2 8 g钾肥( 2 5 g P0 )k 、 K0)k 水平下, 玉米氮 明施钾 量 与产 量之 间有 显著 的 回归 关 产成本增 加 , 环 境 。 而 开 展 测 土 配 方 施肥 有利 于推 进 肥 施 用 量 与 产 量 之 间 的 相 关 系 数 为 系 。 促进耕地质量建设 , 是促 09 5 4 , 明是 高度 相关 关 系, .49 5说 复测 定 通过一元二次方程 的拟合 图得 出在 农业节本增效 ,
河北省粮食产量影响因素多元回归分析

河北省粮食产量影响因素多元回归分析
河北省是中国粮食生产大省之一,其产量受多种因素的影响。
本文将利用多元回归分析方法,探究影响河北省粮食产量的多个因素。
在多元回归分析中,我们需要确定一个依赖变量和多个自变量。
在本文中,依赖变量为河北省粮食产量,而自变量可能包括气候因素(如降雨量、气温等)、土地利用情况、农业技术水平等。
为了进行分析,我们需要收集相关数据。
我们可以收集河北省的粮食产量数据、气象数据、土地利用数据、农业技术数据等。
这些数据可以从相关机构、研究报告、统计年鉴等渠道获取。
获取数据后,我们可以进行多元回归分析。
根据多元回归模型,我们可以得到每个自变量对粮食产量的影响程度和方向。
通过分析回归系数,我们可以确定哪些因素对粮食产量的影响比较大,哪些因素对粮食产量的影响比较小。
在分析中,需要注意的是,多元回归分析只能确定相关关系,并不能确定因果关系。
我们需要谨慎解释结果,不能过于绝对地认为某个因素对粮食产量有直接的因果影响。
除了多元回归分析,我们还可以通过分组分析、趋势分析等方法来进一步研究影响粮食产量的因素。
这些方法可以更全面地了解不同因素对粮食产量的影响。
通过多元回归分析等方法,我们可以揭示影响河北省粮食产量的多个因素。
这对于指导粮食生产、优化农业结构和提高粮食产量具有重要意义。
需要注意的是,多元回归分析只是其中的一种方法,我们还需要综合运用其他分析方法来更全面地研究这一问题。
基于逐步回归分析的粮食产量影响因素研究
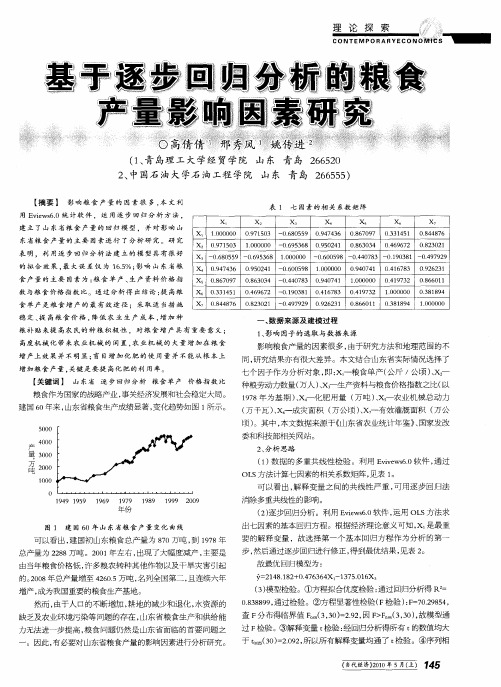
一
、
数 据 来 源 及 建 模 过 程
粮 补 贴来 提 高农 民 的种 粮 积 极 性 .对 粮 食 增 产 具 有 重 要 意 义 :
高度 机 械 化 带 来农 业 机 械 的 闲 置 . 业 机 械 的 大 量增 加 在 粮 食 农 增 产 上 效 果 并 不 明 显 : 目增 加 化 肥 的使 用 量 并 不 能从 根 本 上 盲 增 加 粮 食 产 量 . 键 是 要提 高化 肥 的 利 用 率 。 关
理
—
攘 索
— —
jl _ 曩 一
C NE M P O RA R Y EC ~M℃_●I ■ O T O | 1 ■ l O 誊 c ■■ S s ■
。
—
攮 撼
( 、 岛理工 大学经 贸学院 山 东 青 岛 2 62 1青 6 50 2 中国石油 大学石 油工程 学院 山 东 青 岛 2 6 5 ) 、 6 5 5
1影 响 因子 的 选取 与数 据 来 源 、
影响粮 食产量的因素很 多 , 由于研 究方法和地理 范围的不 同, 研究结果亦 有很大 差异 。本文结 合山东省实际情 况选 择了
七 个因子作为 分析 对象 , : 一粮食单 产( 斤 /公顷 )x厂 即 x 公 、
【 关键词 】 山东省 逐步回归分析 粮食单 产 价格指数比 粮食作 为国家 的战略产业 , 事关经济发展和社会稳定大局 。 建国 6 0年来 , 山东省粮食生产成绩显著 , 变化趋 势如 图 1 所示 。
X2 o 9 1 0 .7 5 3
1 o o o -o 6 5 6 o.5 2 1 oo o 9 3 8 9 0 4
o8 3 3 .6 0 4
o4 9 7 6 6 2
我国粮食生产与相关投入计量经济学模型分析
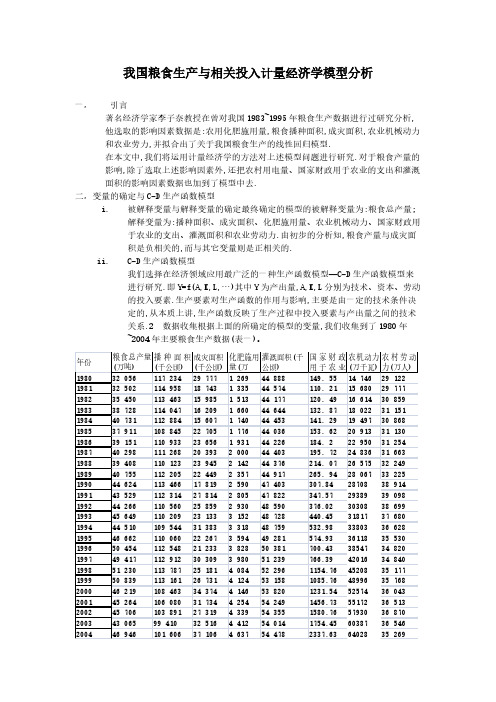
我国粮食生产与相关投入计量经济学模型分析一,引言著名经济学家李子奈教授在曾对我国1983~1995年粮食生产数据进行过研究分析,他选取的影响因素数据是:农用化肥施用量,粮食播种面积,成灾面积,农业机械动力和农业劳力,并拟合出了关于我国粮食生产的线性回归模型.在本文中,我们将运用计量经济学的方法对上述模型问题进行研究.对于粮食产量的影响,除了选取上述影响因素外,还把农村用电量、国家财政用于农业的支出和灌溉面积的影响因素数据也加到了模型中去.二,变量的确定与C-D生产函数模型i.被解释变量与解释变量的确定最终确定的模型的被解释变量为:粮食总产量;解释变量为:播种面积、成灾面积、化肥施用量、农业机械动力、国家财政用于农业的支出、灌溉面积和农业劳动力.由初步的分析知,粮食产量与成灾面积是负相关的,而与其它变量则是正相关的.ii.C-D生产函数模型我们选择在经济领域应用最广泛的一种生产函数模型—C-D生产函数模型来进行研究.即Y=f(A,K,L,…)其中Y为产出量,A,K,L分别为技术、资本、劳动的投入要素.生产要素对生产函数的作用与影响,主要是由一定的技术条件决定的,从本质上讲,生产函数反映了生产过程中投入要素与产出量之间的技术关系.2 数据收集根据上面的所确定的模型的变量,我们收集到了1980年~2004年主要粮食生产数据(表一)。
iii.模型的估计设定:粮食总产量为Y播种面积为X1成灾面积为X2,化肥施用量为X3,灌溉面积为X4,国家财政用于农业资金为X5,农机动力为X6,农村劳动力为X7.由C-D生产函数模型,得模型形式如下:Y t=AX it biεt(i=1,2,…,7)(1)两边取对数并进行变换,得:log Y t =b0+b i logX it+μt (i=1,2,…,7)(2)其中b0=logA,μt=logεt.运用Eviews软件对模型(2)进行OLS估计,我们得到估计结果Dependent Variable: LOG(Y)Method: Least SquaresDate: 06/10/09 Time: 03:55Sample: 1980 2004Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C 3.375895 5.5021110.6135640.5476LOG(X1)0.9587450.279512 3.4300650.0032LOG(X2)-0.1037040.040353-2.5699500.0199LOG(X3)0.4948670.104450 4.7378190.0002LOG(X4)-0.5649730.462026-1.2228180.2381LOG(X5)-0.0143810.074375-0.1933540.8490LOG(X6)0.0183880.1192590.1541820.8793LOG(X7)-0.0694990.137533-0.5053240.6198 R-squared0.963763Mean dependent10.66170varAdjusted R-squared0.948842S.D. dependent var0.127561S.E. of regression0.028852Akaike info criterion-3.998937Sum squared resid0.014151Schwarz criterion-3.608897Log likelihood57.98671F-statistic64.59068Durbin-Watson stat 1.245744Prob(F-statistic)0.000000从表2可以看出,回归估计的判决系数R2很高,方程很显著,但是8个参数的t检验值中,却只有两个略微显著.显然,出现了严重的多重共线性。
