Linear and Nonlinear Supersymmetries
Nonlinear Sigma Models in (1+2)-Dimensions and An Infinite Number of Conserved Currents

Γ is parametrized by σ ∈ [0, 2π ], so we parametrized Σ as follows. We scan Σ with loops passing through x0 and being parametrized by τ ∈ [0, 2π ] such that τ = 0 is the infinitesimal loop around x0 and τ = 2π is Γ. We want to identify a surface Σ in SΓ M with such a parametrization by τ ∈ [0, 2π ]. Here we introduce a gauge field Aµ and an anti-symmetric tensor field Bµν . Then a two-dimensional “holonomy” operator V : SΓ M → G is defined by the differential equation (8) where (9) T (B, A; τ ) ≡
arXiv:hep-th/9802105v1 14 Feb 1998
Nonlinear Sigma Models in (1 + 2)-Dimensions and An Infinite Number of Conserved Currents
Kazuyuki FUJII∗ and Tatsuo SUZUKI†
∂xµ ∂xν λ δx × ∂σ ∂τ (10) where Dλ Bµν ≡ ∂λ Bµν + [Aλ , Bµν ]. If the R.H.S. of (10) vanishes, then δV (2π ) = 0. Namely V becomes surfaceindependent or V becomes a local function on Σ. A comment is in order. The R.H.S. of (10) is identified with the curvature of a principal G-bundle on the loop space ΩG. See the appendix in [3]. Now we can construct conserved charges from V . This is the main story of [3]. Next we must study the vanishing conditions of the R.H.S. of (10). First we restrict a Lie group G. Let g be its Lie algebra. Here we assume g is non-semisimple. If we set p be the radical of g, then g is decomposed into g = h ⊕ p by the Levi’s theorem [4]. Now we assume (11) Aµ ∈ g and B µν ∈ p. dxµ ν δx ] = 0. dσ −[T (B, A; τ ),
自然哲学的数学原理英文

自然哲学的数学原理英文Mathematical Principles of Natural PhilosophyIntroduction:The field of natural philosophy strives to understand the fundamental laws governing the natural world. Mathematics plays a crucial role in this endeavor, providing a formal language to describe and analyze natural phenomena. In this article, we will explore several key mathematical principles that underpin the study of natural philosophy.1. The Principle of Simplicity:One fundamental principle in natural philosophy is the principle of simplicity, also known as Occam's razor. This principle suggests that, when multiple explanations are possible, the simplest explanation is usually the correct one. In mathematical terms, this principle is often applied in the form of parsimony, which favors models with fewer assumptions or variables.2. The Principle of Conservation:Conservation laws are an essential component of mathematical descriptions in natural philosophy. These laws state that certain properties of a system, such as mass, energy, or momentum, remain constant over time, regardless of the changes occurring within the system. Conservation principles provide a mathematical foundation for understanding the behavior of physical systems and are crucial in areas like mechanics and thermodynamics.3. The Principle of Proportionality:The principle of proportionality asserts that certain physicalquantities are directly related to each other in a linear or nonlinear manner. These relationships can be quantitatively expressed using mathematical equations, enabling predictions and explanations of natural phenomena. For example, in Newton's law of universal gravitation, the force between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.4. The Principle of Symmetry:Symmetry is a fundamental concept in both mathematics and natural philosophy. In the context of natural philosophy, symmetry refers to the invariance of certain physical laws under transformations such as rotations, translations, or reflections. Symmetry principles have profound implications, as they often lead to the discovery of fundamental conservation laws. For instance, Noether's theorem connects continuous symmetries with conservation principles in classical mechanics.5. The Principle of Mathematical Modeling:Mathematical modeling is a powerful tool in natural philosophy, allowing scientists to represent complex systems and processes using mathematical equations. By establishing mathematical models, researchers can make predictions, test hypotheses, and gain insights into the underlying mechanisms at work. Mathematical modeling fosters a quantitative understanding of natural phenomena, enabling deeper exploration and discovery. Conclusion:Mathematics provides the language and tools necessary for understanding and studying the laws of nature. The principlesdiscussed in this article highlight the pivotal role of mathematics in natural philosophy. By applying these mathematical principles, scientists can formulate theories, make predictions, and uncover the underlying order and structure of the natural world.。
PACC代码

如何查PACC代码?PACC代码是《Physics Abstracts,Classification and Contents》的缩略。
PACC专业代码是英国科学文摘(INSPEC)用于论文分类的代码。
按照论文的内容将其分为十大类有0000,1000,……5000,……9000表示,例如:凝聚物质由6000及7000表示,其中6000内包括凝聚物质的结构、热学和力学性质,而7000内包括凝聚物质的电子结构、电学、磁学和光学性质。
再仔细分则由6100……6200等表示,例如6100表示液体和固体结构。
而X射线晶体结构测定及精确化技术表示固体结构的测定包含在6100中,而用6110M来表示。
所以要查出某一论文的PACC专业代码,应先确定该论文主要内容属于哪一大类,就在那一大类中找出其代码,其次再找出该论文包括的其它次要内容的代码。
国际物理学分类表PACC(Physics Abstracts, Classification andContents)0000 总论 GENERAL0100 通讯、教育、历史和哲学 communication,education,history,andphilosophy0110 通报、消息和组织活动announcements, news, and organizational activities0110C 通报、消息和颁奖announcements, news, and awards 0110F 会议、演讲和学会conferences, lectures, and institutes 0110H 物理学组织活动physics organizational activities 0130 物理学文献及出版物physics literature and publications0130B 讲稿的出版(进修学院,暑期学校等)publications of lectures (advanced institutes, summer schools, etc.)0130C 会议录 conferenceproceedings 0130E 专著和著作集 monographs,andcollections 0130K 手册和字典handbooks and dictionaries0130L 物理数据、表格汇编collections of physical data, tables0130N 教科书 textbooks0130Q 报告、学位论文、论文reports, dissertations, theses0130R 评论及教学参考论文,资源通讯reviews and tutorial papers, resource letters0130T 书目 bibliographies 0140 教育 education0140D 课程设置与评价course design and evaluation0140E 中小学科学science in elementary and secondary school0140G 课程设置,教学方法,策略和评价curricula, teaching methods, strategies, and evaluation0140J 教师培训 teachertraining0150 教具(包括设备和实验及教学用材料)educational aids(inc.equipment, experiments andteaching approaches to subjects)0150F 视听教具、电影audio and visual aids, films0150H 计算机在教学中的使用instructional computer use0150K 试验理论和技术testing theory and techniques0150M 示范教学的实验和设备demonstration experiments and apparatus 0150P 实验室实验和设备laboratory experiments and apparatus0150Q 实验室课程设置、组织和评价laboratory course design, organization, and evaluation0150T 建筑物和设备 buildingsandfacilities 0155 普通物理 generalphysics 0160 传记、历史和个人笔记biographical, historical, and personal notes 0165 科学史history of science0170 科学哲学 philosophyofscience 0175 科学与社会 scienceandsociety 0190 其他一般论题other topics of general interest0200 物理学中的数学方法mathematical methods in physics0210 代数、集合论和图论algebra, set theory, and graph theory0220 群论(量子力学中的代数方法见0365;基本粒子物理学中的对称见1130)group theory(for algebraic methods in quantummechanics, see 0365; for symmetries inelementary particle physics, see 1130)0230 函数论,分析function theory, analysis0240 几何学、微分几何学和拓扑学(0400相对论与引力)geometry, differential geometry, andtopology(0400 relativity and gravitation)0250 概率论、随机过程和统计学(0500统计物理学)probability theory, stochastic processes, andstatistics(0500 statistical physics)0260 数字近似及分析numerical approximation and analysis0270 计算技术(数据处理与计算见0650)computational techniques(for data handling and computation, see 0650)0290 物理学中数学方法的其它论题other topics in mathematical methods in physics0300 经典及量子物理学;力学与场classical and quantum physics; mechanics and fields0320 离散系统的经典力学:一般数学问题(离散系统的应用经典力学见4610;天体力学见9510)classical mechanics of discrete systems: generalmathematical aspects ( for applied classicalmechanics of discrete systems, see 4610; forcelestial mechanics, see 9510)0330 狭义相对论 specialrelativity0340 连续介质经典力学:一般数学问题classical mechanics of continuous media: general mathematical aspects0340D 弹性力学的数学理论(4620连续介质力学,4630固体力学)mathematical theory of elasticity(4620 continuummechanics, and 4630 mechanics of solids)0340G 流体动力学:一般数学问题(4700流体动力学)fluid dynamics; general mathematicalaspects(4700 fluid dynamics)0340K 波和波传播:一般数学问题(4630M机械波和弹性波;4320一般线性声学)waves and wave propagation; generalmathematical aspects(4630M mechanical andelastic waves, 4320 general linear acoustics)0350 经典场论 classicalfieldtheory0350D 麦克斯韦理论:一般数学问题(应用经典电动力学,见4100)Maxwell theory: general mathematical aspects(forapplied classical electrodynamics, see 4100)0350K 其它具体经典场论other special classical field theories0365 量子论;量子力学(0530量子统计力学;相对论性波动方程,见1110)quantum theory; quantum mechanics(0530quantum statistical mechanics;for relativisticwave equations, see 1110)0365B 基础、测量理论、其它理论foundations, theory of measurement, miscellaneous theories0365C 形式论 formalism 0365D 泛函分析方法functional analytical methods0365F 代数方法(0220群论;3115分子物理学中计算方法)algebraic methods(02 20 group theory; 3115calculation methods in molecular physics)0365G 波动方程解:边界态solutions of wave equations: bound state0365N 非相对论性散射理论 nonrelativisticscatteringtheory 0365S 半经典理论和应用semiclassical theories and applications0367 量子信息 Quantuminformation 0370 量子场论(1110场论) theory of quantized fields(1110 field theory)0380 散射的一般理论(1120 S-矩阵论;1180相对论性散射)general theory of scattering(1120 S-matrix theory,and 1180 relativistic scattering)0400 相对论与引力(狭义相对论,见0330;相对论性天体物理学,见9530; 相对论性宇宙学,见9880)relativity and gravitation(for special relarivity,see0330;for relativistic astrophysics,see 9530;forrelativistic cosmology,see 9880)0420 广义相对论(0240几何学和拓扑学)general relativity (0240 geometry and topology) 0420C 基本问题和普通形式论fundamental problems and general formalism0420F 典型的形式论、拉氏函数和变分原理canonical formalism, Lagrangians, and variationalprinciples0420J 方程解solutions to equations0420M 守恒定律和运动方程conservation laws and equations of motion 0430 引力波和辐射:理论gravitational waves and radiation: theory0440 连续介质;电磁及其它混合引力系统continuous media; electromagnetic and othermixed gravitational systems0450 统一场论及其它引力理论unified field theories and other theories of gravitation0455 引力替代理论alternative theories of gravitation0460 引力的量子论quantum theory of gravitation0465 超引力 supergravity0470 黑洞物理学(参见9760L 黑洞) physics of black holes (see also 9760L black holes)0480 广义相对论的实验检验及引力辐射观测experimental tests of general relativity andobservations of gravitational radiation0485 中程力(包括第五和第六力) intermediate range forces (inc.fifth and sixth forces)0490 相对论和引力的其它论题other topics in relativity and gravitation0500 统计物理学和热力学(0250概率论、随机过程和统计学)statistical physics and thermodynamics(0250probability thory,stochastic processes,andstatistics)0520 统计力学 statisticalmechanics 0520D 分子运动论 kinetictheory0520G 经典系综论classical ensemble theory0530 量子统计力学(6700量子流体;7100凝聚物质的电子态)quantum statistic al mechanics(6700 quantumfluids, and 7100 electron states in condensedmatter)0530C 量子系综论quantum ensemble theory0530F 费米子系统和电子气Fermion systems and electron gas 0530J 玻色子系统 Bosonsystems0530L 任意子和仲统计学(量子统计力学)anyons and parastatistics (quantum statistical mechanics)0540 涨落现象、随机过程和布朗运动fluctuation phenomena, random processes, and Brownian motion0545 混沌系统的理论和模型(流体系统中的混沌,见4752)theory and models of chaotic systems(for chaos inflowing systems,see 4752)0547 非线性动力学系统和分岔(流体系统中的分岔,见4752)nonlinear dynamical systems and bifurcations(bifurcations in flowing systems,see 4752)0550 点阵理论和统计学;伊辛问题(7510H伊辛模型)lattice theory and statistics; Ising problems(7510HIsing models)0555 分形(流体系统中的分形,见4752)fractals (fractals in flowing systems,see 4752) 0560 输运过程:理论 transportprocesses:theory 0565 自组织系统 Self-organizedsystems0570 热力学(4460热力学过程;6400状态方程,相平衡和相变;6500凝聚物质的热性质 ; 化学热力学,见8260)thermodynamics(4460 thermodynamic processes;6400 equation s of state, phase equilibria andphase transitions; 6500 thermal properties ofcondensed matter;for chemical thermodynamics,see 8260)0570C 热力学函数及状态方程thermodynamic functions and equations of state0570F 相变:一般问题phase transitions: general aspects 0570J 临界点现象critical point phenomena0570L 非平衡热力学、不可逆过程(3430势能表面;8200物理化学)nonequilibrium thermodynamics, irreversibleprocesses(3430 potential energy surfaces, 8200physical chemistry)0580 经济物理学 Econophysics0590 统计物理学和热力学的其它论题other topics in statistical physics and thermodynamics0600 测量科学、普通实验室技术及测试设备系统Measurement science, general laboratorytechniques, and instrumentation systems0620 基本度量学 metrology 0620D 测量与误差理论measurement and error theory0620F 单位 units 0620H 测量标准和校正measurement standards and calibration 0620J 基本常数测定determination of fundamental constants 0630 基本变量测量measurement of basic variables0630C 空间变量测量(包括空间延伸的所有变量如:直径、重量、厚度、位移、表面拓扑学、粒子尺寸、弥散系统区)spatial variables measurement(inc.measurementof all variables extending in space e.g. diameter,weight, thickness, displacement , surfacetopography, particle size, area of dispersesystems)0630E 质量与密度的测量mass and density measurement0630F 时间与频率的测量(天文学方面的,见9570)time and frequency measurement(for astronomicalaspects see 9570)0630G 速度、加速度和转动测量(流速测量,见4780)velocity, acceleration and rotationmeasurement(for flow velocity measurement see4780)0630L 基本电磁变量测量(0750电学仪器和技术)measurement of basic electromagneticvariables(0750 electrical instruments andtechniques)0630M 机械变量测量(包括弹性模量,力,冲击,应变,应力,力矩和振动)(压力测量,见0630N;声学变量测量,见4385D;固体力学测量,见4630R;粘度测量,见4780;材料试验,8170)measurement of mechanical variables(inc.elasticmoduli,force,shock ,strain,stress,torque,andvibration)(for pressure measurement,see0630N;for acoustic variables measurement,see4385D;for measurement in the mechanics ofsolids, see 4630R;for viscosity measurement,see4780;for materials testing,see 8170)0630N 压力测量(真空测量,见0730D;高压技术,见0735)pressure measurement(for vacuum measurement,see 0730D;for high-pressure techniques, see0735)0650 数据处理和计算(0270计算技术;2980核信息处理;光学数据处理,存贮及检索, 见423 0;地球物理数据采集和存贮,见9365)data handling and computation(0270computational techniques; 2980 nuclearinformation processing;for optical dataprocessing , storage and retrieval see 4230; forgeophysical data acquisition and storage see9365)0650D 数据搜集、处理、记录、数据显示(含数显技术)data gathering, processing, and recording, datadisplays (including digital techniques)0650M 计算装置与技术computing devices and techniques0660 实验室技术 laboratorytechniques 0660E 样品制备 samplepreparation0660J 高速技术(微秒到微微秒) high speed techniques (microsecond to picosecond)0660S 微检验装置、微定位器和切片机micromanipulators, micropositioners , and microtomes0660V 车间技术(焊接、机械加工、润滑作用和轴承等)workshop techniques ( welding, machining,lubrication, bearings, etc.)0660W 安全(2880辐射监测和防护;8760M辐射剂量测定法;8760P辐射防护)safety( 2880 radiation monitoring and protection,8760M radiation dosimetry, 8760P radiationprotection)0670 普通测试设备 generalinstrumentation 0670D 敏感元件和探测器sensing and detecting devices0670E 试验设备 testingequipment 0670H 显示、记录与指示器display, recording, and indicating instrument s0670M 换能器(电磁辐射换能器见0762;声换能器见4388;液流换能器见4780)transducers(for electromagnetic radiationtransducers see 0762; for acoustic transducers see4388; for flow transducers see 4780)0670T 伺服及控制装置servo and control devices0690 测量科学、普通实验室技术及测试设备系统中的其它论题other topics in measurement science, generallaboratory techniques and instrumentationsystems0700 物理学中普遍使用的专用测试设备与技术(各分支学科的专用测试设备与技术入各自的分支学科)specific instrumentation and techniques of generaluse in physics(within each subdiscipline forspecialized instrumentation and techniques)0710 机械仪器与测量方法(固体力学测量见4630R;材料试验见8170)mechanical instruments and measurementmethods(for measurement in the mechanics of solids, see 4630R; for materials testing, see 8170)0710C 微机械器件和系统(微光学器件和技术,见4283)micromechanical devices and systems (formicrooptical devices and technology,see 4283)0710F 隔振 vibrationisolation0710Y 其他机械仪器和技术(包括摆、陀螺仪、离心器)other mechanical instruments andtechniques(inc.pendulums,gyroscopes,centrifuges)0720 热仪器和技术(4450物质的热性质;4460热力学过程;热辐射的辐射度学和检测, 见 0760D和0762)thermal instruments and techniques(4450 thermalproperties of matter, 4460 thermodynamicprocesses;for radiometry and detection of thermalradiation see 0760D and 0762)0720D 温度测量 thermometry 0720F 量热学 calorimetry 0720H 加热炉 furnaces0720K 高温技术及测试设备;测高温术high temperature techniques and instrumentation; pyrometry0720M 低温实验法 cryogenics 0725 测湿法 hygrometry0730 真空产生与真空技术(包括低于1个大气压的压力;稀薄气体动力学入4745;8115 G 真空淀积)vacuum production and techniques(inc.pressuresbelow 1atmosphere; 4745 rarefied gas dynamics;8115G vacuum deposition)0730B 排空能力、除气、剩余气体evacuating power, degasification, residual gas 0730C 真空泵 vacuumpumps 0730D 真空计 vacuummeters 0730G 真空设备及试验方法vacuum apparatus and testing methods0730K 辅助设备、器件及材料auxiliary apparatus, hardware and materials0735 高压产生与技术(包括大于1个大气压的压力)high pressure production and techniques(inc.pressures above 1 atmosphere)0750 电学仪器及技术electrical instruments and techniques 0755 磁测量仪器及技术magnetic instruments and techniques0758 磁共振谱仪、辅助仪器和技术(6116N电子顺磁共振和核磁共振测定)magnetic resonance spectrometers, auxiliaryinstruments and techniques(6116N EPR and NMRdeterminations)0760 光学仪器和技术(辐射探测见0762;光谱学和光谱计见0765;全息术见4240;光源和标准见4272;光学透镜和反射系统见4278;光学器件、技术和应用见4280;光学试验和加工技术见4285;辐射谱仪和光谱技术见2930;辐射测量、检测和计数见2970)optical instruments and techniques(for radiationdetection, see 0762; for spectroscopy andspectrometers, see 0765; for holography, see4240; for optical sources and standards, see 4272;for optical lens and mirror systems, see 4278; foroptical devices , techniques and applications, see4280; for optical testing and workshop techniques,see 4285; for radiation spectrometers andspectroscopic techniques, see 29 30; for radiationmeasurement, detection and counting, see 2970)0760D 光度学和辐射度学(包括色度学,辐射探测入0762)photometry and radio metry(inc.colorimetry;0762detection of radiation)0760F 偏振测量术与椭园偏振测量术 polarimetryandellipsometry0760H 折射测量术与反射测量术 refractometryandreflectometry 0760L 干涉量度学 interferometry 0760P 光学显微术 opticalmicroscopy0762 辐射探测(测辐射热计、光电管、红外波与亚毫米波探测)detection of radiation (bolometers, photoelectriccells, IR. and submillimetre waves detection)0765 光谱学与光谱计(包括光声谱术) optical spectroscopy and spectrometers(inc.photoacoustic spectroscopy)0765E 紫外和可见光谱学与光谱仪UV and visible spectroscopy and spectrometers 0765G 红外光谱学与光谱仪IR spectroscopy and spectrometers0768 照相术、照相仪器与技术(光敏材料参见4270;照相过程的化学参见8250)photography, photographic instruments andtechniques(for light sensitive materials see also4270 for chemistry of photographic process seealso 8250)0775 质谱仪与质谱测定技术(质谱化学分析见8280)mass spectrometers and m ass spectrometrytechniques(for mass spectroscopic chemicalanalysis, see 8280)0777 粒子束的产生与处理;(2925基本粒子和核物理中的粒子源和靶;4180粒子束和粒子光学)particle beam production and handling;(2925particle sources and targets in elementary particle and nuclear physics, 4180 particle beamsand particle optics)0779 扫描探针显微术及其相关技术(包括扫描隧道显微术,原子力显微术、磁力显微术,摩擦力显微术,和近场扫描光学显微术,(结构测定方面,参见6116P)scanning prob e microscopy and relatedtechniques(inc.scanning tunnellingmicroscopy,atomic force microscopy,magneticforce microscopy,friction force microscopy,andnear field scanning opticalmicroscopy)(structure determination aspects, seealso 6116P)0780 电子与离子显微镜及其技术(6116D凝聚物质中的电子显微术;6116F凝聚物质中的场离子显微术)electron and ion microscopes andtechniques(6116D in condensed matter electronmicroscopy, 6116F field ion microscopy)0781 电子和离子谱仪及其相关技术(参见2930辐射谱仪和光谱技术)electron and ion spectrometers and relatedtechniques(see also 2930 radiation spectrometersan d spectroscopic techniques)0785 X射线与γ射线仪器与技术(包括穆斯堡尔谱仪和技术)X-ray, gamma-ray instruments and techniques(inc.Moessbauer spectrometers and technique s)0788 粒子干涉量度学和中子仪器(粒子束的产生与处理,参见0777;中子谱仪,参见 2930H ,原子干涉量度学,参见3580粒子光学,参见4180)particle interferometry and neutroninstrumentation(for particle beam production andhandling,see 0777;for neutron spectrometers,seealso 2930H;for atomic interferometry,see also3580;for particle optics,see also 4180)0790 专用设备中的其它论题other topics in specialised instrumentation1000 基本粒子物理与场(宇宙线见9440;高能实验技术和设备见 2900)THE PHYSICS OF ELEMENTARY PARTICLESAND FIELDS(for cosmic rays ,see 9440;for highenergy experimental techniques andinstrumentation, see 2900)1100 场和粒子的一般理论(0365量子力学;0370量子场论;0380散射的一般理论)general theory of fields and particles(0365quantum mechanics, 0370 theory of quantizedfields, 0380 general theory of scattering)1110 场论 fieldtheory 1110C 公理法 axiomaticapproach 1110E 拉氏函数和哈密顿函数法Lagrangian and Hamiltonian approach1110G 重正化 renormalization 1110J 渐近问题与特性asymptotic problems and properties1110L 非线性或非局域理论及模型nonlinear or nonlocal theories and models1110M 史文格源理论 Schwingersourcetheory 1110N 规范场论gauge field theories1110Q 相对论性波动方程relativistic wave equations1110S 束缚与非稳定态;贝特-沙耳皮特方程bound and unstable states; Bethe-Salpeterequations1110W 有限温度场论finite temperature field theory1117 弦理论和其他扩展物质理论(包括超弦和膜)theories of strings and other extendedobjects(inc.superstrings and membranes)1120 S-矩阵论 S-matrixtheory 1120D 散射矩阵和微扰论scattering matrix and perturbation theory1120F 色散关系和S矩阵的分析特性dispersion relations and analytic properties of the S-matrix1130 对称和守恒定律(0220群论) symmetry and conservation laws(0220 group theory)1130C 洛伦兹与庞加莱不变性Lorentz and Poincare invariance1130E 电荷共轭、宇称、时间反演和其它分立对称charge conjugation, parity, time reversal and otherdiscrete symmetries1130J SU(2)和SU(3)对称SU(2) and SU(3) symmetries1130K SU(4)对称 SU(4)symmetry 1130L 其他内部对称和高度对称other internal and higher symmetries1130N 非线性对称和动力学对称性(谱生成对称)nonlinear and dynamical symmetries (spectrum generating symmetries)1130P 超对称 supersymmetry1130Q 自发性对称破缺spontaneous symmetry breaking1130R 手征对称 chiralsymmetries 1140 流及其特性currents and their properties1140D 流的一般理论general theory of currents1140F 流代数的拉格朗日算法Lagrangian approach to current algebras1140H 部分守恒轴矢量流partially conserved axial vector currents 1150 色散关系与求和定则dispersion relations and sum rules1150E n/d法 n/dmethod 1150G 靴襻 bootstraps 1150J 交叉对称 crossingsymmetries 1150L 求和定则 sumrules1150N 多变量色散关系(包括曼德尔斯坦表象)multivariable dispersion relations(inc.Mandelstamrepresentation)1160 复合角动量;雷其(理论)体系(0380一般散射理论;1240强相互作用中的复合角动量)complex angular momentum; Reggeformalism(0380 general theory of scattering, 1240in strong interactions)1180 相对论性散射理论(0380一般散射理论)relativistic scattering theory (0380 general theoryof scattering)1180C 运动特性(螺旋性和不变振幅、运动奇异性等)kinematical properties (helicity and invariantamplitudes, kinematic singularities, etc.)1180E 部分波分析 partial wave analysis1180F 近似法(程函近似法,变分原理等) approximations (eikonal approximation, variational principles, etc)1180G 多道散射 multichannelscattering 1180J 多体散射和Faddeev方程Many-body scattering and Faddeev equation 1180L 多次散射 multiplescattering 1190 一般场论和粒子理论的其它论题other topics in general field and particle theory1200 具体理论和相互作用模型;粒子分类系统specific theories and interaction models; particlesystematics1210 统一场论和模型unified field theories and models1210B 电弱理论 electroweaktheories 1210C 统一化标准模型standard model of unification1210D 标准模型以外的统一模型(包括GUTS,颜色模型和SUSY模型)unified models beyond the standardmodel(inc.GUTS,technicolour and SUSY models)1220 电磁相互作用模型models of electromagnetic interactions1220D 量子电动力学的具体计算和极限specific calculations and limits of quantum electrodynamics1220F 量子电动力学的实验检验experimental tests of quantum electrodynamics 1225 引力相互作用模型(0460引力的量models for gravitational interactions(0460子论) quantum theory of gravitation)1230 弱相互作用模型models of weak interactions1230C 中子流 neutralcurrents 1230E 中间玻色子 intermediatebosons 1235 粒子的复合模型composite models of particles1235C 量子色动力学的一般特性(动力学,禁闭等)general properties of quantum chromodynamics(dynamics, confinement, etc.)1235E 量子色动力学在粒子特性和反应中的应用applications of quantum chromodynamics toparticle properties and reactions1235H 粒子的结构和反应的唯象复合模型(部分子模型,口袋模型等)phenomenological composite models of particlestructure and reactions (partons, bags, etc.)1235K 其它复合模型(包括复合夸克模型和轻子模型)other composite models( posite quarksand leptons)1240 强相互作用模型models of strong interactions1240E 统计模型 statisticalmodels1240F 靴襻模型 bootstrapmodels1240H 二重性和双关模型duality and dual models1240K 强子分类方案 hadronclassificationschemes1240M 复合角动量平面;雷其极点和割线(雷其子)(1160复合角动量,雷其体系的一般理论)complex angular momentum plane; Regge polesand cuts (Reggeons)(1160 for general theory)1240P 吸收模型,光学模型和程函模型(衍射和衍射生成模型见1240S)absorptive, optical, and eikonal models(fordiffraction and diffractive production models, see1240S)1240Q 势模型 potentialmodels1240R 边缘碰撞模型(一个或多个粒子交换) peripheral models (one or more particle exchange)1240S 多重边缘碰撞模型和多雷其模型(包括衍射和衍射生成模型)multiperipheral and multi Reggemodels(inc.diffraction and diffractive productionmodels)1240V 矢量介子优势 Vector-mesondominance 1270 强子质量公式hadron mass formulas1290 其它各种理论设想与模型miscellaneous theoretical ideas and models1300 具体基本粒子反应和唯象论specific elementary particle reactions and phenomenology1310 轻子间的弱相互作用和电磁相互作用weak and electromagnetic interactions of leptons1315 中微子相互作用(包括宇宙射线相互作用)neutrino interactions(inc.interactions involvingcosmic rays)1320 介子的轻子与半轻子衰变leptonic and semileptonic decays of mesons1320C π衰变 pidecays1320E K衰变 Kdecays1320G Ψ/J介子、Υ介子、Φ介子psi/J, upsilon, phi mesons1320H B介子轻子/半轻子衰变 Bmesonleptonic/semileptonicdecays 1320I f介子轻子/半轻子衰变 fmesonleptonic/semileptonicdecays 1320J 其它介子衰变other meson decays1325 介子的强子衰变 hadronicdecaysofmesons 1330 重子的衰变 decaysofbaryons1330C 轻子与半轻子衰变leptonic and semileptonic decays1330E 强子衰变 hadronicdecays 1335 轻子的衰变 decaysofleptons1338 中间玻色子和希格斯玻色子的衰变decays of intermediate and Higgs Bosons1340 电磁过程与特性electromagnetic processes and properties1340D 电磁质量差electromagnetic mass differences1340F 电磁形状因子、电矩和磁矩electromagnetic form factors; electric and magnetic moments1340H 电磁衰变 electromagneticdecays1340K 强相互作用和弱相互作用过程的电磁修正electromagnetic corrections to strong and weakinteraction processes1360 光子及带电轻子与强子的相互作用(中微子相互作用见1315)photon and charged lepton interactions withhadrons(for neutrino interactions, see 1315)1360F 弹性散射与康普顿散射elastic and Compton scattering1360H 总截面和单举(反应)截面(包括深度非弹性过程)total and inclusive crosssections(inc.deep-inelastic processes)1360K 介子产生 mesonproduction 1360M 介子共振产生 Meson-resonanceproduction 1360P 重子和重子共振产生baryon and baryon resonance production1365 电子-正电子碰撞产生强子hadron production by electron-positron collisions1375 强子诱发的低能和中能反应及散射(能量≤10GeV见1385)Hadron-induced low energy and intermediate energy reactions and scattering, energy ≤10GeV( for higher energies, see 1385)1375C 核子-核子相互作用,包括反核子和氘核等(能量≤10GeV;核中的核子-核子相互作用见2130)Nucleon-nucleon interactions, includingantinucleon, deuteron, etc. (energy ≤10GeV)(for n-n interactions in nuclei, see 2130)1375E 超子-核子相互作用(能量≤10GeV)Hyperon-nucleon interactions (energy ≤10 GeV)1375G π介子-重子相互作用(能量≤10GeV) Pion-baryon interactions (energy ≤10 GeV)1375J K介子-重子相互作用(能量≤10GeV) Kaon-baryon interactions (energy ≤10 GeV)1375L 介子-介子相互作用(能量≤10GeV)Meson-meson interactions (energy ≤10 GeV) 1380 光子-光子相互作用和散射 Photon-photon interactions and scattering1385 强子诱发的高能和超高能相互作用(能量>10GeV)(低能情况见1375) Hadron-induced high-energy and super-high-energy interactions, energy > 10GeV(for low energies, see 1375)1385D 弹性散射(能量=10GeV) elastic scattering (energy = 10 GeV)1385F非弹性散射、双粒子终态(能量>10GeV) inelastic scattering, two-particle final states(energy > 10 GeV) 1385H 非弹性散射、多粒子终态(能量>10GeV) inelastic scattering, many-particle final states(energy>10GeV)1385K 单举反应,包括总截面(能量>10GeV) inclusive reactions, including total cross sections,(energy > 10 GeV)1385M 宇宙射线相互作用(9440宇宙线) cosmic ray interactions(9440 cosmic rays)1385N 强子诱发的高能相互作用(能量>1TeV) hadron induced very high energy interactions(energy>1 TeV)1387大Q2基本粒子相互作用中的射流jets in large-Q2 elementary particle interactions 1388相互作用和散射中的极化 polarisation in interactions and scattering 1390基本粒子的具体反应及唯象论的其它论题 other topics in specific reactions and phenomenology of elementary particles 1400具体粒子的性质与共振 properties of specific particles and resonances 1420 重子与重子共振(包括反粒子) baryons and baryon resonances(inc.antiparticles)1420C 中子 neutrons1420E 质子 protons1420G s =0时的重子共振baryon resonances with s=0 1420J超子和超子共振 hyperons and hyperon resonances 1420P双重子 dibaryons1440 介子和介子共振 mesons and meson resonances 1440D π介子 pi mesons1440F K 介子 K mesons1440K Ρ介子、Ω介子和η介子rho, omega, and eta mesons 1440L d 介子和F 介子d and F mesons 1440N Ψ/J 介子、Υ介子、Φ介子psi/J, upsilon, phi mesons 1440P其它介子 other mesons 1460 轻子 leptons1460C 电子和正电子 electrons and positrons 1460E μ介子 muons1460G 中微子 neutrinos1460J重轻子 heavy leptons 1480 其它粒子和假设粒子 other and hypothetical particles1480A 光子 photons1480D 夸克和胶子 quarksandgluons 1480F 中间玻色子 intermediateBosons 1480H 磁单极子 magneticmonopoles1480J 超对称粒子(包括标量粒子,超粒子和超离子)Supersymmetric particles(inc.scalarparticles,superparticles and superions)1480K 其它(包括快子) others(inc.tachyons)2000 核物理学 NUCLEARPHYSICS 2100 核结构 nuclearstructure2110 核的一般和平均性质;核能级性质(按质量范围分类的具体核的性质见2700)general and average properties of nuclei;properties of nuclear energy levels(for propertiesof specific nuclei listed by mass ranges, see 2700)2110D 结合能和质量binding energy and masses2110F 形状、电荷、半径和形状因子shape, charge, radius and form factor s2110H 自旋、宇称和同位旋spin, parity, and isobaric spin2110J 谱因子 spectroscopicfactors 2110K 电磁矩 electromagneticmoments 2110M 能级密度和结构level density and structure2110P 单粒子能级结构single particle structure in levels2110R 集团能级结构(包括旋转能带) collective structure in levels(inc.rotational bands) 2110S 库仑效应 Coulombeffects2130 核力(1375C核子-核子相互作用) nuclear forces(1375C nucleon-nucleon interactions)2140 少核子系统 Few-nucleonsystems2160 核结构模型与方法(强子的原子和分子见3610)nuclear structure models and methods(forhadronic atoms and molecules, see 3610)2160C 壳层模型 shellmodel2160E 集体模型 collectivemodels 2160F 群论模型models based on group theory2160G 集团模型 clustermodels 2160J 哈特里-福克和随机-相位近似Hartree-Fock and random-phase approximations 2165 核物质 nuclearmatter 2180 超核 hypernuclei 2190 核结构的其它论题other topics in nuclear structure2300 放射性和电磁跃迁(8255放射化学)radioactivity and electromagnetic transitions(8255 radiochemistry)2320 电磁跃迁 electromagnetictransitions 2320C 寿命和跃迁几率lifetimes and transition probabilities2320E 角分布和校正测量angular distribution and correlation measurements2320G 多极混合比率 multipolemixingratios 2320J 多极矩阵元素 multipolematrixelements 2320L γ跃迁和能级gamma transitions and level energies2320N 内转换和核外效应internal conversion and extranuclear effects 2320Q 核共振荧光nuclear resonance fluorescence2340 β衰变;电子与μ子俘获beta decay; electron and muon capture2340B 弱相互作用和β衰变的轻子特性weak interaction and lepton aspects of beta decay2340H 核矩阵元和从β衰变推断核结构nuclear matrix elements and nuclear structure inferred from beta decay2360 α衰变 alphadecay 2390 核衰变和放射性的其它论题other topics in nuclear decay and radioactivity 2400 核反应和散射:总论nuclear reactions and scattering:general2410 核反应和散射模型与方法nuclear reaction and scattering models and methods2410D 耦合道和多体论方法coupled channel and many body theory methods2410F 平面和扭曲波玻恩近似法Plane- and distorted-wave Born approximations 2410H 光学模型和衍射模型optical and diffraction models2430 共振反应与散射resonance reactions and scattering2430C 巨共振 giantresonances 2430F 同位旋相似共振 isobaricanalogresonances 2450 直接反应 directreactions 2460 统计理论和涨落statistical theory and fluctuations2470 反应和散射中的极化polarization in reactions and scattering2475 裂变的一般性质general properties of fission2485 原子核和核形成过程的夸克模型quark models in nuclei and nuclear processes2490 核反应和散射的其它论题:一般问题other topics in nuclear reactions and scattering:general2500 核反应和散射:具体反应nuclear reactions and scattering:specific reactions2510 少核子系统的核反应与散射nuclear reactions and scattering involving few-nucleon systems2520 光致核反应和光子散射 photonuclearreactions and photon scattering 2530 轻子诱发反应与散射Lepton-induced reactions and scattering 2530C 电子和正电子反应与散射electron and positron reactions and scattering 2530E μ介子反应和散射muon reactions and scattering2530G 中微子反应和散射neutrino reactions and scattering。
Differential equation
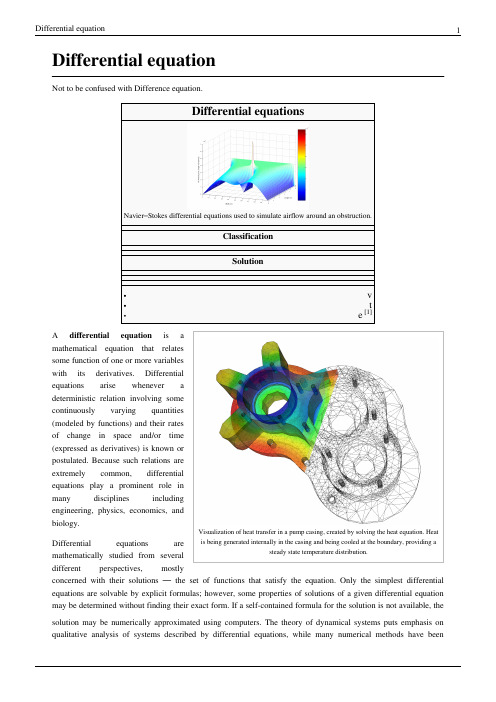
Differential equationNot to be confused with Difference equation.Stokes differential equations used to simulate airflow around an obstruction.ClassificationSolutionVisualization of heat transfer in a pump casing, created by solving the heat equation. Heat is being generated internally in the casing and being cooled at the boundary, providing a steady state temperature distribution.A differential equation is amathematical equation that relatessome function of one or more variableswith its derivatives. Differentialequations arise whenever adeterministic relation involving somecontinuously varying quantities(modeled by functions) and their ratesof change in space and/or time(expressed as derivatives) is known orpostulated. Because such relations areextremely common, differentialequations play a prominent role inmany disciplines includingengineering, physics, economics, andbiology.Differential equations aremathematically studied from severaldifferent perspectives, mostlyconcerned with their solutions — the set of functions that satisfy the equation. Only the simplest differential equations are solvable by explicit formulas; however, some properties of solutions of a given differential equation may be determined without finding their exact form. If a self-contained formula for the solution is not available, the solution may be numerically approximated using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have beendeveloped to determine solutions with a given degree of accuracy.ExampleFor example, in classical mechanics, the motion of a body is described by its position and velocity as the time value varies. Newton's laws allow one (given the position, velocity, acceleration and various forces acting on the body) to express these variables dynamically as a differential equation for the unknown position of the body as a function of time.In some cases, this differential equation (called an equation of motion) may be solved explicitly.An example of modelling a real world problem using differential equations is the determination of the velocity of a ball falling through the air, considering only gravity and air resistance. The ball's acceleration towards the ground is the acceleration due to gravity minus the acceleration due to air resistance. Gravity is considered constant, and air resistance may be modeled as proportional to the ball's velocity. This means that the ball's acceleration, which is a derivative of its velocity, depends on the velocity (and the velocity depends on time). Finding the velocity as a function of time involves solving a differential equation and verifying its validity.Directions of studyThe study of differential equations is a wide field in pure and applied mathematics, physics, and engineering. All of these disciplines are concerned with the properties of differential equations of various types. Pure mathematics focuses on the existence and uniqueness of solutions, while applied mathematics emphasizes the rigorous justification of the methods for approximating solutions. Differential equations play an important role in modelling virtually every physical, technical, or biological process, from celestial motion, to bridge design, to interactions between neurons. Differential equations such as those used to solve real-life problems may not necessarily be directly solvable, i.e. do not have closed form solutions. Instead, solutions can be approximated using numerical methods.Mathematicians also study weak solutions (relying on weak derivatives), which are types of solutions that do not have to be differentiable everywhere. This extension is often necessary for solutions to exist.The study of the stability of solutions of differential equations is known as stability theory.NomenclatureThe theory of differential equations is well developed and the methods used to study them vary significantly with the type of the equation.Ordinary and partial•An ordinary differential equation (ODE) is a differential equation in which the unknown function (also known as the dependent variable) is a function of a single independent variable. In the simplest form, the unknown function is a real or complex valued function, but more generally, it may be vector-valued or matrix-valued: this corresponds to considering a system of ordinary differential equations for a single function.Ordinary differential equations are further classified according to the order of the highest derivative of the dependent variable with respect to the independent variable appearing in the equation. The most important cases for applications are first-order and second-order differential equations. For example, Bessel's differential equation(in which y is the dependent variable) is a second-order differential equation. In the classical literature a distinction is also made between differential equations explicitly solved with respect to the highest derivative and differential equations in an implicit form. Also important is the degree, or (highest) power, of the highest derivative(s) in the equation (cf. : degree of a polynomial). A differential equation is called a nonlinear differential equation if its degree is not one (a sufficient but unnecessary condition).• A partial differential equation (PDE) is a differential equation in which the unknown function is a function of multiple independent variables and the equation involves its partial derivatives. The order is defined similarly to the case of ordinary differential equations, but further classification into elliptic, hyperbolic, and parabolic equations, especially for second-order linear equations, is of utmost importance. Some partial differentialequations do not fall into any of these categories over the whole domain of the independent variables and they are said to be of mixed type.Linear and non-linearBoth ordinary and partial differential equations are broadly classified as linear and nonlinear.• A differential equation is linear if the unknown function and its derivatives appear to the power 1 (products of the unknown function and its derivatives are not allowed) and nonlinear otherwise. The characteristic property of linear equations is that their solutions form an affine subspace of an appropriate function space, which results in much more developed theory of linear differential equations. Homogeneous linear differential equations are a further subclass for which the space of solutions is a linear subspace i.e. the sum of any set of solutions or multiples of solutions is also a solution. The coefficients of the unknown function and its derivatives in a linear differential equation are allowed to be (known) functions of the independent variable or variables; if these coefficients are constants then one speaks of a constant coefficient linear differential equation.•There are very few methods of solving nonlinear differential equations exactly; those that are known typically depend on the equation having particular symmetries. Nonlinear differential equations can exhibit verycomplicated behavior over extended time intervals, characteristic of chaos. Even the fundamental questions of existence, uniqueness, and extendability of solutions for nonlinear differential equations, and well-posedness of initial and boundary value problems for nonlinear PDEs are hard problems and their resolution in special cases is considered to be a significant advance in the mathematical theory (cf. Navier–Stokes existence and smoothness).However, if the differential equation is a correctly formulated representation of a meaningful physical process, then one expects it to have a solution.Linear differential equations frequently appear as approximations to nonlinear equations. These approximations are only valid under restricted conditions. For example, the harmonic oscillator equation is an approximation to the nonlinear pendulum equation that is valid for small amplitude oscillations (see below).ExamplesIn the first group of examples, let u be an unknown function of x, and c and ω are known constants.•Inhomogeneous first-order linear constant coefficient ordinary differential equation:•Homogeneous second-order linear ordinary differential equation:•Homogeneous second-order linear constant coefficient ordinary differential equation describing the harmonic oscillator:•Inhomogeneous first-order nonlinear ordinary differential equation:•Second-order nonlinear (due to sine function) ordinary differential equation describing the motion of a pendulum of length L:In the next group of examples, the unknown function u depends on two variables x and t or x and y.•Homogeneous first-order linear partial differential equation:•Homogeneous second-order linear constant coefficient partial differential equation of elliptic type, the Laplace equation:•Third-order nonlinear partial differential equation, the Korteweg–de Vries equation:Related concepts• A delay differential equation (DDE) is an equation for a function of a single variable, usually called time, in which the derivative of the function at a certain time is given in terms of the values of the function at earlier times.• A stochastic differential equation (SDE) is an equation in which the unknown quantity is a stochastic process and the equation involves some known stochastic processes, for example, the Wiener process in the case of diffusion equations.• A differential algebraic equation (DAE) is a differential equation comprising differential and algebraic terms, given in implicit form.Connection to difference equationsSee also: Time scale calculusThe theory of differential equations is closely related to the theory of difference equations, in which the coordinates assume only discrete values, and the relationship involves values of the unknown function or functions and values at nearby coordinates. Many methods to compute numerical solutions of differential equations or study the properties of differential equations involve approximation of the solution of a differential equation by the solution of a corresponding difference equation.Universality of mathematical descriptionMany fundamental laws of physics and chemistry can be formulated as differential equations. In biology and economics, differential equations are used to model the behavior of complex systems. The mathematical theory of differential equations first developed together with the sciences where the equations had originated and where the results found application. However, diverse problems, sometimes originating in quite distinct scientific fields, may give rise to identical differential equations. Whenever this happens, mathematical theory behind the equations can be viewed as a unifying principle behind diverse phenomena. As an example, consider propagation of light and sound in the atmosphere, and of waves on the surface of a pond. All of them may be described by the same second-order partial differential equation, the wave equation, which allows us to think of light and sound as forms of waves, much like familiar waves in the water. Conduction of heat, the theory of which was developed by Joseph Fourier, is governed by another second-order partial differential equation, the heat equation. It turns out that many diffusion processes, while seemingly different, are described by the same equation; the Black–Scholes equation in finance is, for instance, related to the heat equation.Notable differential equationsPhysics and engineering•Newton's Second Law in dynamics (mechanics)•Euler–Lagrange equation in classical mechanics•Hamilton's equations in classical mechanics•Radioactive decay in nuclear physics•Newton's law of cooling in thermodynamics•The wave equation•Maxwell's equations in electromagnetism•The heat equation in thermodynamics•Laplace's equation, which defines harmonic functions•Poisson's equation•Einstein's field equation in general relativity•The Schrödinger equation in quantum mechanics•The geodesic equation•The Navier–Stokes equations in fluid dynamics•The Diffusion equation in stochastic processes•The Convection–diffusion equation in fluid dynamics•The Cauchy–Riemann equations in complex analysis•The Poisson–Boltzmann equation in molecular dynamics•The shallow water equations•Universal differential equation•The Lorenz equations whose solutions exhibit chaotic flow.Biology•Verhulst equation – biological population growth•von Bertalanffy model – biological individual growth•Lotka–Volterra equations – biological population dynamics•Replicator dynamics – found in theoretical biology•Hodgkin–Huxley model – neural action potentialsEconomics•The Black–Scholes PDE•Exogenous growth model•Malthusian growth model•The Vidale–Wolfe advertising modelReferences•P. Abbott and H. Neill, Teach Yourself Calculus, 2003 pages 266-277•P. Blanchard, R. L. Devaney, G. R. Hall, Differential Equations, Thompson, 2006• E. A. Coddington and N. Levinson, Theory of Ordinary Differential Equations, McGraw-Hill, 1955• E. L. Ince, Ordinary Differential Equations, Dover Publications, 1956•W. Johnson, A Treatise on Ordinary and Partial Differential Equations[2], John Wiley and Sons, 1913, in University of Michigan Historical Math Collection [3]• A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2.•R. I. Porter, Further Elementary Analysis, 1978, chapter XIX Differential Equations•Teschl, Gerald (2012). Ordinary Differential Equations and Dynamical Systems[4]. Providence: American Mathematical Society. ISBN 978-0-8218-8328-0.• D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.[1]/w/index.php?title=Template:Differential_equations&action=edit[2]/cgi/b/bib/bibperm?q1=abv5010.0001.001[3]/u/umhistmath/[4]http://www.mat.univie.ac.at/~gerald/ftp/book-ode/External links•Lectures on Differential Equations (/courses/mathematics/18-03-differential-equations-spring-2010/video-lectures/) MIT Open CourseWare Videos•Online Notes / Differential Equations (/classes/de/de.aspx) Paul Dawkins, Lamar University•Differential Equations (/diffeq/diffeq.html), S.O.S. Mathematics•Differential Equation Solver (/tools/differential_equation_solver/) Java applet tool used to solve differential equations.•Introduction to modeling via differential equations (/mat/u-u/en/ differential_equations_intro.htm) Introduction to modeling by means of differential equations, with critical remarks.•Mathematical Assistant on Web (http://user.mendelu.cz/marik/maw/index.php?lang=en&form=ode) Symbolic ODE tool, using Maxima•Exact Solutions of Ordinary Differential Equations (http://eqworld.ipmnet.ru/en/solutions/ode.htm)•Collection of ODE and DAE models of physical systems (/research/models.htm) MATLAB models•Notes on Diffy Qs: Differential Equations for Engineers (/diffyqs/) An introductory textbook on differential equations by Jiri Lebl of UIUC•Khan Academy Video playlist on differential equations (/math/ differential-equations) Topics covered in a first year course in differential equations.•MathDiscuss Video playlist on differential equations (/category/courses/ solutions-differential-equations/homogeneous-linear-systems/)Article Sources and Contributors8Article Sources and ContributorsDifferential equation Source: /w/index.php?oldid=610771276 Contributors: 17Drew, After Midnight, Ahoerstemeier, Alarius, Alfred Centauri, Amahoney, AndreiPolyanin, Andres, AndrewHowse, Andycjp, Andytalk, AngryPhillip, Anonymous Dissident, Antoni Barau, Antonius Block, Anupam, Apmonitor, Arcfrk, Asdf39, Asyndeton, Attilios,Babayagagypsies, Baccala@, Baccyak4H, Bejohns6, Bento00, Berland, Bidabadi, Bigusbry, BillyPreset, Bob.v.R, Bolatbek, Brandon, Bryanmcdonald, Btyner, Bygeorge2512,Callumds, Charles Matthews, Christian75, Chtito, Cispyre, Cmprince, Coginsys, ConMan, Cxz111, Cybercobra, DAJF, Danski14, Dbroadwell, Ddxc, Delaszk, DerHexer, Dewritech, Difu Wu, Djordjes, DominiqueNC, Donludwig, Dpv, Dr sarah madden, Drmies, DroEsperanto, Duoduoduo, Dysprosia, EconoPhysicist, Elwikipedista, Epicgenius, EricBright, Erin.Annette.Brown,Estudiarme, F=q(E+v^B), Fintor, Fioravante Patrone, Fioravante Patrone en, Flameturtle, Friend of the Facts, FutureTrillionaire, Gabrielleitao, Gandalf61, Gauss, Genedronek, Geni, Giftlite,GoingBatty, Gombang, Grenavitar, Haham hanuka, Hamiltondaniel, Harry, Haruth, Haseeb Jamal, Heikki m, Holmes1900, Ilya Voyager, Iquseruniv, Iulianu, Izodman2012, J arino, J.delanoy, Ja 62, Jak86, JamesBWatson, Jao, Jarble, Jauhienij, Jayden54, Jeancey, Jersey Devil, Jim Sukwutput, Jim.belk, Jim.henderson, JinJian, Jitse Niesen, JohnOwens, Johndoeisnotmyname, JorisvS,Julesd, K-UNIT, Kayvan45622, KeithJonsn, Kensaii, Khalid Mahmood, Klaas van Aarsen, Kr5t, Krushia, LOL, Lambiam, Lavateraguy, Lethe, LibLord, Linas, Lumos3, Madmath789, Mandarax, Mankarse, MarSch, Martastic, Martynas Patasius, Maschen, Math.geek3.1415926, Matqkks, Mattmnelson, Maurice Carbonaro, Maxis ftw, Mazi, McVities, Mduench, Mets501, Mh, MichaelHardy, Mindspillage, MisterSheik, Mohan1986, Mossaiby, Mpatel, MrOllie, Mtness, Mysidia, Nik-renshaw, Nkayesmith, Norm mit, Okopecz, Oleg Alexandrov, Opelio, Pahio, Parusaro, Paul August, Paul Matthews, Paul Richter, PavelSolin, Pgk, Phoebe, Pine, Pinethicket, Pratyya Ghosh, PseudoSudo, Qwerty Binary, Qzd800, R'n'B, Rama's Arrow, Randomguess, Reallybored999, RexNL, Reyk, RichMorin, Robin S, Romansanders, Rosasco, Ruakh, SDC, SFC9394, SakeUPenn, Salix alba, Sam Staton, Sampathsris, Sardanaphalus, Senoreuchrestud, Silly rabbit, Siroxo,Skakkle, Skypher, SmartPatrol, Snowjeep, Spirits in the Material, Starwiz, Suffusion of Yellow, Sverdrup, Symane, TVBZ28, TYelliot, Tannkrem, Tbhotch, Tbsmith, TexasAndroid, Tgeairn, The Hybrid, The Thing That Should Not Be, Timelesseyes, Tranum1234567890, Tsirel, Tuseroni, User A1, Vanished User 0001, Vishwanathnm, Vthiru, Waffleguy4, Waldir, Waltpohl, Wavelength, Wclxlus, Wihenao, Willtron, Winterheart, Wsears, XJaM, Yafujifide, Zepterfd, ﺪﺟﺎﺳ ﺪﺠﻣﺍ ﺪﺟﺎﺳ, 363 anonymous editsImage Sources, Licenses and ContributorsFile:Airflow-Obstructed-Duct.png Source: /w/index.php?title=File:Airflow-Obstructed-Duct.png License: Public Domain Contributors: Original uploader was User A1 at en.wikipediaFile:Elmer-pump-heatequation.png Source: /w/index.php?title=File:Elmer-pump-heatequation.png License: Creative Commons Attribution-Sharealike 3.0Contributors: Christian1985, Crimerob, Kri, User A1, 2 anonymous editsLicenseCreative Commons Attribution-Share Alike 3.0///licenses/by-sa/3.0/。
J-Integral

J-IntegralTrans.TianjinUniv.2009,15:032—036DOI10.1007/s12209—009—0007—4J-IntegralofInterfacialCrackBetweenMetal-BaseCeramicCoatingandSteelxuLianyong(徐连勇)一,JINGHongyang(荆洪阳)一,HEYing(何颖).(1.SchoolofMaterialsScienceandEngineering,TianjinUniversity,Tianjin300072,China;2.TianjinKeyLaboratoryofAdvancedJoiningTechnology,Tianjin300072,China;3.TianjinInternalCombustionEngineResearchInstitute,Tianjin300072,China) Abstract:ThedefinitionofJ-integralofinterfacia1crackwasintroduced.Thethree—pointbendingtestswerecarriedout toobtainthecriticalloadingvalueswhentheinterfacialcrackinitiationoccurredbetweencoat ingsandsubstrates.Thefiniteelementanalysis(FEA)wasadoptedtoanalyzethestressdistributioninthespecimensa ndcomputetheJ-integraloftheinterfacialcrackbetweenLX88AcoatingandChineseQ345stee1.Theresultsshowedtha ttheaveragevalueofcritica1J-integralis0.70N/m.whichcanbetakenasthefractureparametertoevaluatetheinterfacia1fr acturebehaviorforthethree—pointbendingspecimensofLX88Acoating/Q345stee1system.Keywords:interfacialcrack;J-integral;coating;three—pointbendingtest;FEA Debondingofthecoatinglayerfromthesubstrate canleadtofailureoftheentirethermalsprayedcoating systemforthermallysprayedcoatings.Sothebond strengthbetweencoatingandsubstrateisanimportant designparameterusedintheestimationofthecoatinglifetime.Generally,thedebondingofcoatingisresultedfromtheextendingofcracksordefectsintheinterface betweencoatingandsubstrate.Therefore,itisnecessary tomeasurebondstrengthusingtheinterfacialfracture mechanicsapproachandfindthefracturecontrolledpa—rameter.Obviously,itisatypicalbi—materialinterface problem.Atpresent,thebendingtests[-]areusedtomeasure thefracturetoughnessofinterfacebetweencoatingsand substratesbymanyresearchers.Whenthecriticalinterfa—cialstressintensityfactor(Kc)orcriticalinterfacia1en—ergyreleaserate(Gc)areusedasthefractureparameters, thecoatings/substratessystemsareexpectedtobehard elasticcoatings/hardelasticsubstrates.Ifthesubstrates areveryflexiblethelargescaleyielding(LSY)would occurinthesubstratesneartheinterfacialcracktipwhen theinterfacialcrackpropagationinitiates.Soitisre—quiredthatthespecimensbetestedwithintheelastic limitofthesubstrates.Forthehardelasticcoat.ings/flexibleelastic-plasticsubstrates,theJ-integralof interfacialcracktipisstudiedasthefractureparameter fortheevaluationofinterfacialtoughnessintherangeof theelastic-plasticfracturemechanics【12-14]. Inthisstudy,thefracturemechanicsexperiments andtheFEAwereadoptedtocomputetheJ-integralof theinterfacialcrackbetweenLX88AcoatingandChinese Q345steel,andthevalidityoftheJ-integralasinterfacial fractureparametersforthree—pointbendingspecimens wasdiscussed.1J-integraloftheinterfacialcrackTheJ-integraliswidelyusedasafracturemechan—icsparameterforbothlinearandnonlinearmaterialre—sponse,anditisdefinedthroughtheenergyreleaserate associatedwithcrackgrowth【,们.Foravirtualcrackadvance2(s)intheplaneofathree—dimensionalcrackinabody,theenergyreleaserateisgivenby=()nHqdA(1)wheredAisasurfaceelementonavanishinglysmall tubularsurfaceenclosingthecracktip;isoutwardlynormaltodA;gisaunitvectorinthelocalvirtualcrackextentiondirection;Hisgivenby:WI一(2)Accepteddate:2007—11—29. SupportedbyTianjinNaturalScienceFoundation(No08JCYBJC09100),NewTeacherRes earchFundfortheDoctoralProgramofHigherEducationofChinafNo200700560961andNewCenturyOutstandingTalentedPers onPlanofChina.XULianyong,bornin1975,male,DrcorrespondencetoJINGHongyang,E—mail:***************XULianyongetahJ-IntegralofInte咖cialCrackBetweenMetal—BaseCeramicCoatingandSteelForelasticmaterialbehavior,Wistheelasticstrainenergy;forelastic—plasticmaterialbehavior,Wisdefined astheelasticstrainenergyplustheplasticdissipation, thusrepresentsthestrainenergyinanequivalentelasticmateria1.ThisimpliesthattheJ-integralcalculationis suitableonlyformonotonicloadingofelastic—plasticma.ingtheFEAresults,theJ-integralvalueoftheinterfacia1crackcanbeachievedthroughtheintegralof Eq.(1)alongthepathABDBAorEFGFE)inFig.1£Fig.1J-integralpathofinterracialcracktipbetween coatingandsubstrateInaddition.theJ-integralcanbeusedtoanalyzethe fracturebehaviorasthefractureparameterwhentheJ- integralvaluekeepsconservationaccordingtothefrac—turemechanicstheory.WangPtl[171discussedthecon. servationofJ-integralneartheinterfacialcracktip,and confirmedtheconservationusingthenumericalmethod. 2Fracturemechanicsexperiment2.1SpecimenspreparationADZ—-ARC?-400high@tarc??spraysystemwasused toproducethecommercialmetal—baseceramiccoating (LX88A)onthebasemetal(ChineseQ345stee1).The chemica1constitutionsofChineseO345steelandLX88A coatingarepresentedinTab.1andTab.2,respectively. Inthetest,thethree—pointbendingspecimenswere used.Thespecimenconsistsofabi.materialbeam(coat—ingandsubstrate)anditsconfigurationisshowninFig.2.Thecoatingthicknessisabout1.20mm.Thedi—mensionofthesubstrateforthethree—pointbendingtest is100minx9.7mmX9.11Tlnlinlength,widthandthick—ness.respectively.Acentralnotchwhosewidthis0.5 mmwasintroducedacrossthecentralportionofthe specimenusingwireEDM(electricaldischargemachin—ing)technologythroughthethicknessofthecoating.A fatiguecrackalongtheinterfacewasthencreatedfrom thebaseofthenotchonafatigueloadingtestingma-chine.Forthepurposeofanalysis,subscript1indicates thecoating,whereassubscript2denotesthesubstrate. Tab.1ConstitutionofChineseQ345stee1%Tab.2ConstitutionofLX88Acoating%Fig.2Bi—material,notchedthree—pointbendingspecimen withsymmetricalinterfacialcrack2.2Testprocess Threespecimenswerepreparedforthebendingtest. ThespecimenNo.1withthepre—interfacialcrackwas loadedonauniversal—testingmachine(CSS.44100).In theload.onprocess.thevicinityofinterfacialcracktip wasobservedthroughamicro—telescope(Fig.3)inorder toobtainthecriticalloadwhentheinterfacialcrackini—tiationoccurred.Themicro—telescopewasabletotravel inthree—dimensionalorientations.soitcantracethecrack tippositionofthespecimenintheload—onprocess.The imageofcracktipvicinitycanbedisplayedinthecorn—puterscreenthroughaCCDandanimagecollector. Whentheobviouscrackgrowingoccurred,thetestwas ceased.Theloadneededtoberecorded.anditwastaken asthecriticalloadresultingincrackinitiation.Inorderto Fig.3Micro?-telescopeobservingthecracktipofspeci-- menintheload—onprocess一33—TransactionsofTianjinUniversityV o1.15No.2009 observethecrackinitiation.amarking1inehadbeen scratchedaheadofthepre.cracktip.Fig.4isthemicrophotographsofthespecimenNo.1 beforeandaftercrackinitiation.Beforecrackinitiationthedistancebetweencracktipandthemarkinglinewas 0.541mm;aftercrackinitiation,thedistancebecame 0.237mm.ThecracktipmovedtotheleftfromFig.4(a) toFig.4(b).Sotheinterfacialcrackgrewnoticeably.(a)Beforecrackinitiation(b)AtiercrackinitiationFig.4Micr0ph0t0graphsofspecimenNo.1beforeand aftercrackinitiation2.3Testresults Thecriticalloadvaluesofthethreespecimenswhen theinterfacialfractureoccurredarelistedinTab.3. Tab.3Criticalloadofspecimens3Resultsanddiscussion3.1Numericalanalysis Symmetriesaboutthemidsectionsofthebeamde- pictedinFig.2allowtherequisitesolutionstobeOb—tainedbyconsideringaquarterofthecompositebeam (Fig.5(a)).Thefiniteelementsare20一nodequadratic brick,reducedintegrationelements;oneelementhas8 integrationpoints.Themeshofthewholemodelforthis specimenispresentedinFig.5(a).Themeshbecomes denserintheareasurroundingthecracktipandnearthe 一34一interface.Asmallrectangulararea(1mm×1mm) aroundthecracktipwasspeciallyrefined.Thereare threerefinedtipmeshes.Thefinestmeshhas10layers, eachlayerhas32elements;thefinermeshhas8layers, eachlayerhas24elements(aspresentedinFig.5(b)): thecoarsestmeshhas6layers.eachlayerhasl6ele-ments.Thesmallestelementdimensionofthethreere—finedmeshesis0.006mmx0.01mm×0.12mm.0.0lmm×0.016mm×0.12mmand0.015mm×0.02mm×0.12mrn.respectively.TheFEMresultsshowsthestress fieldsnearthecracktipbyusingthethreerefinedmeshesarealmostidentica1.soonlythefinermeshisexhibitedinFig.5.AsshowninFig.5(b),arefinedfocusedmeshis usedintheimmediatevicinityofthecrack.tiDsur—roundedbyarosetteofsingularquarterpointelementsin ordertocapturetheexpectedsquarerootsingularstresses.Arollersupportfixedtheverticaldisplacementatthesupportpoint,whereassymmetrieswereenforcedby inhibitinghorizontaldisplacementsalongthemidsectionofthesubstratelayerinX-directionandbyinhibitingZ- directionaldisplacementalongthemidsectionofthespecimeninZ-direction.Thecracksurfacesweretrac—tion—free.Thethree.dimensionalfiniteelementsolutionswere obtainedwiththegeneralpurposefiniteelementsoftwareABAQUSV ersion6.5一1.1nteInfa1Totalmodelandcracktiptingftrate~(b)ThecracktipregionFig.5Meshusedinthree—dimensionalfiniteelementanalysisXULianyongeta1.J-IntegralofInterfacialCrackBetweenMetal-BaseCeramicCoatingandSteelIntheFEA,theappliedloadvaluewasthecriticaling/Q345steelsystem. Ioadvalueobtainedfrompreviousexperiment.The analysiswaselastic-plastic.Thematerial—propertiesareReferencessh0wninTab.4andFig?6?[1]chara1ambidesPG,LundJ,EvansAG,.Atest Tab.4Materialpropertiesinfracturetest/.1Note:Thecoatingisthelinear-elasticmateria1.IntheFEA,the assumptionthattheyieldstrengthofthecoatingisequaltoavery largevalueismadetoensHrethelinear-elasticdeformbehavior.Fig.6Truestress—straincurveofQ345steel3.2jr-integralofinterfacialcrackAfterthethree.dimensionalfiniteelementanalysis.theJ-integralvaluesofallthespecimenswerecalculated usingthesubroutineintheABAQUSprogram,andthe resultsarelistedinTab.6.Theaveragevalueofis0.70N/m.andtheJ-integralcanbetakenasthefracturepa—rametertoevaluatetheinterfacialfracturebehaviorforthethree-pointbendingspecimensofLX88Acoat.ing/Q345steeIsystem.Tab.6J-integralofinterfacialcracktip4Conclusions Thethree—pointbendingspecimenscontainingthe pre—interfacialcracksintheinterfacebetweentheLX88A coatingandQ345steelwereusedinthefracturemechan. iesexperiments.Thefiniteelementmethodwasadopted toanalyzethestressdistributionofthespecimens.TheJ- integraloftheinterfacecrackwascalculatedbasedonthe FEAresults.Theresultsshowedthattheaveragevalueofis0.70N/mandtheJ-integralcanbetakenasthefrac.tureparametertoevaluatethejnterfacia1fracturebehav—iorforthethree.pointbendingspecimensofLX88Acoat—specimenfordeterminingthefractureresistanceofbimate—rialinterfaces[J].JournalofAppliedMechanics.Transac—tionsoftheASME,1989,56(1):77—82.2JChungHGP,SwainMV,MoriT.Evaluationofthestrain energyreleaserateforthefractureoftitanium..porcelainin.. terfacialbondingEJ].Biomaterials,1997,18(23):1553一l557.13JLiH,KhorKA.CheangP.Y oung'smodulusandfracture toughnessdeterminationofhighvelocityoxy--fuel-?sprayed bioceramiccoatings[J].Su咖ceandCoatingsTechnology, 2002.155(1):21.32.【4jO'DowdNP,ShihCF,StoutMG.Testgeometriesfor measuringinterfacialfracturetoughness[J].International JournalofSolidsandStructures,1992,29(5):571.589.15JBeckerJrTL,McNaneyJM,CannonRMela1. Limitationsontheuseofthemixed.modedelaminating beamtestspecimen:EffectsofthesizeoftheregionofK—dominance[J].MechanicsofMaterials,1997,25(4):291—308.16J0hTaeSung,CannonRMRitchieRO.Subcriticalcrack growthalongceramic—metalinterfaces[J].Journalofthe AmericanCeramicSociety,1987,70(12):C352一C355. 17JCannonRM,DalgleishBJ,DauskardtRHela1.Cyclic fatigue—crackpropagationalongceramic/metalinter. faces.ActaMetallurgicaetMaterialia,1991,39(8): 2145.2156.18JThunG,SchneiderGABahrHAeta1.Toughnessanisot—ropyanddamagebehaviorofplasmasprayedZrO2thermalbarriercoatings[J].SurfaceandCoatingsTechnology. 2000123(2/3):147—158,[9]CaoHC,EvansAG.Anexperimentalstudyoftheffac—tureresistanceofbi—materialinterfaces[J].Mechanicsof Materials,1989,7(4):295—304.【10JHowardSJ,PhillippsAJ,ClyneTW.Theinterpretation ofdatafromthefour—pointbenddelaminationtestto measureinterfacialfracturetoughness[J].Composites, 1993.24(2):103—112.111JMullerD,ChoYR,BergSeta1.Fracturemechanicstests formeasuringtheadhesionofmagnetronsputteredTiN coatingslJj.InternationalJournalofRefractoryMetals andHardMaterials,1996,14:207—211.[12]MoranB,ShihCF.Cracktipandassociateddomaininte—gralsfrommomentumandenergybalance[J].Engineering 一35—TransactionsoJndnJinUniversityV o1.15No.2009 FractureMechanics198727(6):6l5-642.ShihCF,AsaroRJ.Elastic—plasticanalysisofcrackson bi—materialinterfaces(PartI):Smallscaleyielding[J]. JournalofAppliedMechanics,TransactionsoftheASME, 198855(2):299—316.NakamuraT,ParksDM.DeterminationofelasticT—stress alongthree-?dimensionalcrackfrontusinginteractioninte-- grallJj.InternationalJournalofSolidsandStructures, 1992,29(13):1597—1611.ParksDM.Thevirtualcrackextensionmethodfornonlin—earmaterialbehaviour[puterMethodsinAppliedMechanicsandEngineeling,1977,12(3):353—364.一36一ShihCF,MoranB,NakamuraT.Energyreleaseratealong athree—dimensionalcrackfrontinathermallystressed body[J].InternationalJournalofFracture,1986,30(2): 79—1O2.WangLimin,ChenHaoran,XuShilang.Conservationlaw andapplicationofJ-integralinmulti—materials[J].Applied MaematicsandMechanics',2001.22(10):1097一l104. XuLianyong,JingHongyang,HuoLixing.Y oung'S modulusandstressintensityfactordeterminationofhigh velocityelectricarcsprayedmetal-basedceramiccoat?- ing[J].SurfaceandCoatingsTechnology2006,201(6): 2399—2406]J]J]jr.1rlr1]J]J]j345r.1rlrl。
斯普林格数学研究生教材丛书

斯普林格数学研究生教材丛书《斯普林格数学研究生教材丛书》(Graduate Texts in Mathematics)GTM001《Introduction to Axiomatic Set Theory》Gaisi Takeuti, Wilson M.Zaring GTM002《Measure and Category》John C.Oxtoby(测度和范畴)(2ed.)GTM003《T opological Vector Spaces》H.H.Schaefer, M.P.Wolff(2ed.)GTM004《A Course in Homological Algebra》P.J.Hilton, U.Stammbach(2ed.)(同调代数教程)GTM005《Categories for the Working Mathematician》Saunders Mac Lane(2ed.)GTM006《Projective Planes》Daniel R.Hughes, Fred C.Piper(投射平面)GTM007《A Course in Arithmetic》Jean-Pierre Serre(数论教程)GTM008《Axiomatic set theory》Gaisi Takeuti, Wilson M.Zaring(2ed.)GTM009《Introduction to Lie Algebras and Representation Theory》James E.Humphreys(李代数和表示论导论)GTM010《A Course in Simple-Homotopy Theory》M.M CohenGTM011《Functions of One Complex VariableⅠ》John B.ConwayGTM012《Advanced Mathematical Analysis》Richard Beals GTM013《Rings and Categories of Modules》Frank W.Anderson, Kent R.Fuller(环和模的范畴)(2ed.)GTM014《Stable Mappings and Their Singularities》Martin Golubitsky, Victor Guillemin (稳定映射及其奇点)GTM015《Lectures in Functional Analysis and OperatorTheory》Sterling K.Berberian GTM016《The Structure of Fields》David J.Winter(域结构)GTM017《Random Processes》Murray RosenblattGTM018《Measure Theory》Paul R.Halmos(测度论)GTM019《A Hilbert Space Problem Book》Paul R.Halmos (希尔伯特问题集)GTM020《Fibre Bundles》Dale Husemoller(纤维丛)GTM021《Linear Algebraic Groups》James E.Humphreys (线性代数群)GTM022《An Algebraic Introduction to Mathematical Logic》Donald W.Barnes, John M.MackGTM023《Linear Algebra》Werner H.Greub(线性代数)GTM024《Geometric Functional Analysis and Its Applications》Paul R.HolmesGTM025《Real and Abstract Analysis》Edwin Hewitt, Karl StrombergGTM026《Algebraic Theories》Ernest G.ManesGTM027《General Topology》John L.Kelley(一般拓扑学)GTM028《Commutative Algebra》VolumeⅠOscar Zariski, Pierre Samuel(交换代数)GTM029《Commutative Algebra》VolumeⅡOscar Zariski, Pierre Samuel(交换代数)GTM030《Lectures in Abstract AlgebraⅠ.Basic Concepts》Nathan Jacobson(抽象代数讲义Ⅰ基本概念分册)GTM031《Lectures in Abs tract AlgebraⅡ.Linear Algabra》Nathan.Jacobson(抽象代数讲义Ⅱ线性代数分册)GTM032《Lectures in Abstract AlgebraⅢ.Theory of Fields and Galois Theory》Nathan.Jacobson(抽象代数讲义Ⅲ域和伽罗瓦理论)GTM033《Differential Topology》Morris W.Hirsch(微分拓扑)GTM034《Principles of Random Walk》Frank Spitzer(2ed.)(随机游动原理)GTM035《Several Complex Variables and Banach Algebras》Herbert Alexander, John Wermer(多复变和Banach代数)GTM036《Linear Topological Spaces》John L.Kelley, Isaac Namioka(线性拓扑空间)GTM037《Mathematical Logic》J.Donald Monk(数理逻辑)GTM038《Several Complex Variables》H.Grauert, K.Fritzshe GTM039《An Invitation to C*-Algebras》William Arveson (C*-代数引论)GTM040《Denumerable Markov Chains》John G.Kemeny, /doc/e96250642.htmlurie Snell, Anthony W.KnappGTM041《Modular Functions and Dirichlet Series in Number Theory》Tom M.Apostol (数论中的模函数和Dirichlet序列)GTM042《Linear Representations of Finite Groups》Jean-Pierre Serre(有限群的线性表示)GTM043《Rings of Continuous Functions》Leonard Gillman, Meyer JerisonGTM044《Elementary Algebraic Geometry》Keith KendigGTM045《Probabi lity TheoryⅠ》M.Loève(概率论Ⅰ)(4ed.)GTM046《Probability TheoryⅡ》M.Loève(概率论Ⅱ)(4ed.)GTM047《Geometric Topology in Dimensions 2 and 3》Edwin E.MoiseGTM048《General Relativity for Mathematicians》Rainer.K.Sachs, H.Wu伍鸿熙(为数学家写的广义相对论)GTM049《Linear Geometry》K.W.Gruenberg, A.J.Weir(2ed.)GTM050《Fermat's Last Theorem》Harold M.EdwardsGTM051《A Course in Differential Geometry》WilhelmKlingenberg(微分几何教程)GTM052《Algebraic Geometry》Robin Hartshorne(代数几何)GTM053《 A Course in Mathematical Logic for Mathematicians》Yu.I.Manin(2ed.)GTM054《Combinatorics with Emphasis on the Theory of Graphs》Jack E.Graver, Mark E.WatkinsGTM055《Introduction to Operator TheoryⅠ》Arlen Brown, Carl PearcyGTM056《Algebraic Topology:An Introduction》W.S.MasseyGTM057《Introduction to Knot Theory》Richard.H.Crowell, Ralph.H.FoxGTM058《p-adic Numbers, p-adic Analysis, and Zeta-Functions》Neal Koblitz(p-adic 数、p-adic分析和Z函数)GTM059《Cyclotomic Fields》Serge LangGTM060《Mathematical Methods of Classical Mechanics》V.I.Arnold(经典力学的数学方法)(2ed.)GTM061《Elements of Homotopy Theory》George W.Whitehead(同论论基础)GTM062《Fundamentals of the Theory of Groups》M.I.Kargapolov, Ju.I.Merzljakov GTM063《Modern Graph Theory》Béla BollobásGTM064《Fourier Series:A Modern Introduction》VolumeⅠ(2ed.)R.E.Edwards(傅里叶级数)GTM065《Differential Analysis on Complex Manifolds》Raymond O.Wells, Jr.(3ed.)GTM066《Introduction to Affine Group Schemes》William C.Waterhouse(仿射群概型引论)GTM067《Local Fields》Jean-Pierre Serre(局部域)GTM069《Cyclotomic FieldsⅠandⅡ》Serge LangGTM070《Singular Homology Theory》William S.MasseyGTM071《Riemann Surfaces》Herschel M.Farkas, Irwin Kra (黎曼曲面)GTM072《Classical Topology and Combinatorial Group Theory》John Stillwell(经典拓扑和组合群论)GTM073《Algebra》Thomas W.Hungerford(代数)GTM074《Multiplicative Number Theory》Harold Davenport (乘法数论)(3ed.)GTM075《Basic Theory of Algebraic Groups and Lie Algebras》G.P.HochschildGTM076《Algebraic Geometry:An Introduction to Birational Geometry of Algebraic Varieties》Shigeru Iitaka GTM077《Lectures on the Theory of Algebraic Numbers》Erich HeckeGTM078《A Course in Universal Algebra》Stanley Burris, H.P.Sankappanavar(泛代数教程)GTM079《An Introduction to Ergodic Theory》Peter Walters (遍历性理论引论)GTM080《A Course in_the Theory of Groups》Derek J.S.RobinsonGTM081《Lectures on Riemann Surfaces》Otto ForsterGTM082《Differential Forms in Algebraic Topology》Raoul Bott, Loring W.Tu(代数拓扑中的微分形式)GTM083《Introduction to Cyclotomic Fields》Lawrence C.Washington(割圆域引论)GTM084《A Classical Introduction to Modern Number Theory》Kenneth Ireland, Michael Rosen(现代数论经典引论)GTM085《Fourier Series A Modern Introduction》Volume 1(2ed.)R.E.Edwards GTM086《Introduction to Coding Theory》J.H.van Lint(3ed .)GTM087《Cohomology of Groups》Kenneth S.Brown(上同调群)GTM088《Associative Algebras》Richard S.PierceGTM089《Introduction to Algebraic and Abelian Functions》Serge Lang(代数和交换函数引论)GTM090《An Introduction to Convex Polytopes》Ame BrondstedGTM091《The Geometry of Discrete Groups》Alan F.BeardonGTM092《Sequences and Series in BanachSpaces》Joseph DiestelGTM093《Modern Geometry-Methods and Applications》(PartⅠ.The of geometry Surface s Transformation Groups and Fields)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov (现代几何学方法和应用)GTM094《Foundations of Differentiable Manifolds and Lie Groups》Frank W.Warner(可微流形和李群基础)GTM095《Probability》A.N.Shiryaev(2ed.)GTM096《A Course in Functional Analysis》John B.Conway (泛函分析教程)GTM097《Introduction to Elliptic Curves and Modular Forms》Neal Koblitz(椭圆曲线和模形式引论)GTM098《Representations of Compact Lie Groups》Theodor Bre?cker, Tammo tom DieckGTM099《Finite Reflection Groups》L.C.Grove, C.T.Benson (2ed.)GTM100《Harmonic Analysis on Semigroups》Christensen Berg, Jens Peter Reus Christensen, Paul ResselGTM101《Galois Theory》Harold M.Edwards(伽罗瓦理论)GTM102《Lie Groups, Lie Algebras, and Their Representation》V.S.Varadarajan(李群、李代数及其表示)GTM103《Complex Analysis》Serge LangGTM104《Modern Geometry-Methods and Applications》(PartⅡ.Geometry and Topology of Manifolds)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM105《SL? (R)》Serge Lang(SL? (R)群)GTM106《The Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术理论)GTM107《Applications of Lie Groups to Differential Equations》Peter J.Olver(李群在微分方程中的应用)GTM108《Holomorphic Functions and Integral Representations in Several Complex Variables》R.Michael Range GTM109《Univalent Functions and Teichmueller Spaces》Lehto OlliGTM110《Algebraic Number Theory》Serge Lang(代数数论)GTM111《Elliptic Curves》Dale Husemoeller(椭圆曲线)GTM112《Elliptic Functions》Serge Lang(椭圆函数)GTM113《Brownian Motion and Stochastic Calculus》Ioannis Karatzas, Steven E.Shreve (布朗运动和随机计算)GTM114《A Course in Number Theory and Cryptography》Neal Koblitz(数论和密码学教程)GTM115《Differential Geometry:Manifolds, Curves, and Surfaces》M.Berger, B.Gostiaux GTM116《Measure and Integral》Volume1 John L.Kelley, T.P.SrinivasanGTM117《Algebraic Groups and Class Fields》Jean-Pierre Serre(代数群和类域)GTM118《Analysis Now》Gert K.Pedersen (现代分析)GTM119《An introduction to Algebraic Topology》Jossph J.Rotman(代数拓扑导论)GTM120《Weakly Differentiable Functions》William P.Ziemer(弱可微函数)GTM121《Cyclotomic Fields》Serge LangGTM122《Theory of Complex Functions》Reinhold RemmertGTM123《Numbers》H.-D.Ebbinghaus, H.Hermes, F.Hirzebruch, M.Koecher, K.Mainzer, J.Neukirch, A.Prestel, R.Remmert(2ed.)GTM124《Modern Geometry-Methods and Applications》(PartⅢ.Introduction to Homology Theory)B.A.Dubrovin, A.T.Fomenko, S.P.Novikov(现代几何学方法和应用)GTM125《Complex Variables:An introduction》Garlos A.Berenstein, Roger Gay GTM126《Linear Algebraic Groups》Armand Borel (线性代数群)GTM127《A Basic Course in Algebraic Topology》William S.Massey(代数拓扑基础教程)GTM128《Partial Differential Equations》Jeffrey RauchGTM129《Representation Theory:A First Course》William Fulton, Joe HarrisGTM130《T ensor Geometry》C.T.J.Dodson, T.Poston(张量几何)GTM131《A First Course in Noncommutative Rings》/doc/e96250642.htmlm(非交换环初级教程)GTM132《Iteration of Rational Functions:Complex Analytic Dynamical Systems》AlanF.Beardon(有理函数的迭代:复解析动力系统)GTM133《Algebraic Geometry:A First Course》Joe Harris (代数几何)GTM134《Coding and Information Theory》Steven Roman GTM135《Advanced Linear Algebra》Steven RomanGTM136《Algebra:An Approach via Module Theory》William A.Adkins, Steven H.WeintraubGTM137《Harmonic Function Theory》Sheldon Axler, Paul Bourdon, Wade Ramey(调和函数理论)GTM138《A Course in Computational Algebraic NumberTheory》Henri Cohen(计算代数数论教程)GTM139《T opology and Geometry》Glen E.BredonGTM140《Optima and Equilibria:An Introduction to Nonlinear Analysis》Jean-Pierre AubinGTM141《A Computational Approach to Commutative Algebra》Gr?bner Bases, Thomas Becker, Volker Weispfenning, Heinz KredelGTM142《Real and Functional Analysis》Serge Lang(3ed.)GTM143《Measure Theory》J.L.DoobGTM144《Noncommutative Algebra》Benson Farb, R.Keith DennisGTM145《Homology Theory:An Introduction to Algebraic Topology》James W.Vick(同调论:代数拓扑简介)GTM146《Computability:A Mathematical Sketchbook》Douglas S.BridgesGTM147《Algebraic K-Theory and Its Applications》Jonathan Rosenberg(代数K理论及其应用)GTM148《An Introduction to the Theory of Groups》Joseph J.Rotman(群论入门)GTM149《Foundations of Hyperbolic Manifolds》John G.Ratcliffe(双曲流形基础)GTM150《Commutative Algebra with a view toward Algebraic Geometry》David EisenbudGTM151《Advanced Topics in the Arithmetic of Elliptic Curves》Joseph H.Silverman(椭圆曲线的算术高级选题)GTM152《Lectures on Polytopes》Günter M.ZieglerGTM153《Algebraic Topology:A First Course》William Fulton(代数拓扑)GTM154《An introduction to Analysis》Arlen Brown, Carl PearcyGTM155《Quantum Groups》Christian Kassel(量子群)GTM156《Classical Descriptive Set Theory》Alexander S.KechrisGTM157《Integration and Probability》Paul MalliavinGTM158《Field theory》Steven Roman(2ed.)GTM159《Functions of One Complex Variable VolⅡ》John B.ConwayGTM160《Differential and Riemannian Manifolds》Serge Lang(微分流形和黎曼流形)GTM161《Polynomials and Polynomial Inequalities》Peter Borwein, Tamás Erdélyi(多项式和多项式不等式)GTM162《Groups and Representations》J.L.Alperin, Rowen B.Bell(群及其表示)GTM163《Permutation Groups》John D.Dixon, Brian Mortime rGTM164《Additive Number Theory:The Classical Bases》Melvyn B.NathansonGTM165《Additive Number Theory:Inverse Problems and the Geometry of Sumsets》Melvyn B.NathansonGTM166《Differential Geometry:Cartan's Generalization of Klein's Erlangen Program》R.W.SharpeGTM167《Field and Galois Theory》Patrick MorandiGTM168《Combinatorial Convexity and Algebraic Geometry》Günter Ewald(组合凸面体和代数几何)GTM169《Matrix Analysis》Rajendra BhatiaGTM170《Sheaf Theory》Glen E.Bredon(2ed.)GTM171《Riemannian Geometry》Peter Petersen(黎曼几何)GTM172《Classical Topics in Complex Function Theory》Reinhold RemmertGTM173《Graph Theory》Reinhard Diestel(图论)(3ed.)GTM174《Foundations of Real and Abstract Analysis》Douglas S.Bridges(实分析和抽象分析基础)GTM175《An Introduction to Knot Theory》W.B.Raymond LickorishGTM176《Riemannian Manifolds:An Introduction to Curvature》John M.LeeGTM177《Analytic Number Theory》Donald J.Newman(解析数论)GTM178《Nonsmooth Analysis and Control Theory》F.H.clarke, Yu.S.Ledyaev, R.J.Stern, P.R.Wolenski(非光滑分析和控制论)GTM179《Banach Algebra Techniques in Operator Theory》Ronald G.Douglas(2ed.)GTM180《A Course on Borel Sets》S.M.Srivastava(Borel 集教程)GTM181《Numerical Analysis》Rainer KressGTM182《Ordinary Differential Equations》Wolfgang Walter GTM183《An introduction to Banach Spaces》Robert E.MegginsonGTM184《Modern Graph Theory》Béla Bollobás(现代图论)GTM185《Using Algebraic Geomety》David A.Cox, John Little, Donal O’Shea(应用代数几何)GTM186《Fourier Analysis on Number Fields》Dinakar Ramakrishnan, Robert J.Valenza GTM187《Moduli of Curves》Joe Harris, Ian Morrison(曲线模)GTM188《Lectures on the Hyperreals:An Introduction to Nonstandard Analysis》Robert GoldblattGTM189《Lectures on Modules and Rings》/doc/e96250642.htmlm(模和环讲义)GTM190《Problems in Algebraic Number Theory》M.Ram Murty, Jody Esmonde(代数数论中的问题)GTM191《Fundamentals of Differential Geometry》Serge Lang(微分几何基础)GTM192《Elements of Functional Analysis》Francis Hirsch, Gilles LacombeGTM193《Advanced Topics in Computational Number Theory》Henri CohenGTM194《One-Parameter Semigroups for Linear Evolution Equations》Klaus-Jochen Engel, Rainer Nagel(线性发展方程的单参数半群)GTM195《Elementary Methods in Number Theory》Melvyn B.Nathanson(数论中的基本方法)GTM196《Basic Homological Algebra》M.Scott OsborneGTM197《The Geometry of Schemes》David Eisenbud, Joe HarrisGTM198《A Course in p-adic Analysis》Alain M.RobertGTM199《Theory of Bergman Spaces》Hakan Hedenmalm, Boris Korenblum, Kehe Zhu(Bergman空间理论)GTM200《An Introduction to Riemann-Finsler Geometry》D.Bao, S.-S.Chern, Z.Shen GTM201《Diophantine Geometry An Introduction》Marc Hindry, Joseph H.Silverman GTM202《Introduction to T opological Manifolds》John M.Lee GTM203《The Symmetric Group》Bruce E.SaganGTM204《Galois Theory》Jean-Pierre EscofierGTM205《Rational Homotopy Theory》Yves Félix, Stephen Halperin, Jean-Claude Thomas(有理同伦论)GTM206《Problems in Analytic Number Theory》M.Ram MurtyGTM207《Algebraic Graph Theory》Chris Godsil, Gordon Royle(代数图论)GTM208《Analysis for Applied Mathematics》Ward Cheney GTM209《A Short Course on Spectral Theory》William Arveson(谱理论简明教程)GTM210《Number Theory in Function Fields》Michael RosenGTM211《Algebra》Serge Lang(代数)GTM212《Lectures on Discrete Geometry》Jiri Matousek (离散几何讲义)GTM213《From Holomorphic Functions to Complex Manifolds》Klaus Fritzsche, Hans Grauert(从正则函数到复流形)GTM214《Partial Differential Equations》Jüergen Jost(偏微分方程)GTM215《Algebraic Functions and Projective Curves》David M.Goldschmidt(代数函数和投影曲线)GTM216《Matrices:Theory and Applications》Denis Serre (矩阵:理论及应用)GTM217《Model Theory An Introduction》David Marker(模型论引论)GTM218《Introduction to Smooth Manifolds》John M.Lee (光滑流形引论)GTM219《The Arithmetic of Hyperbolic 3-Manifolds》Colin Maclachlan, Alan W.Reid GTM220《Smooth Manifolds and Observables》Jet Nestruev(光滑流形和直观)GTM221《Convex Polytopes》Branko GrüenbaumGTM222《Lie Groups, Lie Algebras, and Representations》Brian C.Hall(李群、李代数和表示)GTM223《Fourier Analysis and its Applications》Anders Vretblad(傅立叶分析及其应用)GTM224《Metric Structures in Differential Geometry》Gerard Walschap(微分几何中的度量结构)GTM225《Lie Groups》Daniel Bump(李群)GTM226《Spaces of Holomorphic Functions in the Unit Ball》Kehe Zhu(单位球内的全纯函数空间)GTM227《Combinatorial Commutative Algebra》Ezra Miller, Bernd Sturmfels(组合交换代数)GTM228《A First Course in Modular Forms》Fred Diamond, Jerry Shurman(模形式初级教程)GTM229《The Geometry of Syzygies》David Eisenbud(合冲几何)GTM230《An Introduction to Markov Processes》Daniel W.Stroock(马尔可夫过程引论)GTM231《Combinatorics of Coxeter Groups》Anders Bjr?ner, Francesco Brenti(Coxeter 群的组合学)GTM232《An Introduction to Number Theory》Graham Everest, Thomas Ward(数论入门)GTM233《T opics in Banach Space Theory》Fenando Albiac, Nigel J.Kalton(Banach空间理论选题)GTM234《Analysis and Probability:Wavelets, Signals, Fractals》Palle E.T.Jorgensen(分析与概率)GTM235《Compact Lie Groups》Mark R.Sepanski(紧致李群)GTM236《Bounded Analytic Functions》John B.Garnett(有界解析函数)GTM237《An Introduction to Operators on the Hardy-Hilbert Space》Rubén A.Martínez-Avendano, Peter Rosenthal (哈代-希尔伯特空间算子引论)GTM238《A Course in Enumeration》Martin Aigner(枚举教程)GTM239《Number Theory:VolumeⅠT ools and Diophantine Equations》Henri Cohen GTM240《Number Theory:VolumeⅡAna lytic and Modern T ools》Henri Cohen GTM241《The Arithmetic of Dynamical Systems》Joseph H.SilvermanGTM242《Abstract Algebra》Pierre Antoine Grillet(抽象代数)GTM243《Topological Methods in Group Theory》Ross GeogheganGTM244《Graph Theory》J.A.Bondy, U.S.R.MurtyGTM245《Complex Analysis:In the Spirit of Lipman Bers》Jane P.Gilman, Irwin Kra, Rubi E.RodriguezGTM246《A Course in Commutative Banach Algebras》Eberhard KaniuthGTM247《Braid Groups》Christian Kassel, Vladimir TuraevGTM248《Buildings Theory and Applications》Peter Abramenko, Kenneth S.Brown GTM249《Classical Fourier Analysis》Loukas Grafakos(经典傅里叶分析)GTM250《Modern Fourier Analysis》Loukas Grafakos(现代傅里叶分析)GTM251《The Finite Simple Groups》Robert A.WilsonGTM252《Distributions and Operators》Gerd GrubbGTM253《Elementary Functional Analysis》Barbara D.MacCluerGTM254《Algebraic Function Fields and Codes》Henning StichtenothGTM255《Symmetry Representations and Invariants》Roe Goodman, Nolan R.Wallach GTM256《A Course in Commutative Algebra》Kemper GregorGTM257《Deformation Theory》Robin HartshorneGTM258《Foundation of Optimization》Osman GülerGTM259《Ergodic Theory:with a view towards Number Theory》Manfred Einsiedler, Thomas WardGTM260《Monomial Ideals》Jurgen Herzog, Takayuki Hibi GTM261《Probability and Stochastics》Erhan CinlarGTM262《Essentials of Integration Theory for Analysis》Daniel W.StroockGTM263《Analysis on Fock Spaces》Kehe ZhuGTM264《Functional Analysis, Calculus of Variations and Optimal Control》Francis ClarkeGTM265《Unbounded Self-adjoint Operatorson Hilbert Space》Konrad Schmüdgen GTM266《Calculus Without Derivatives》Jean-Paul PenotGTM267《Quantum Theory for Mathematicians》Brian C.HallGTM268《Geometric Analysis of the Bergman Kernel and Metric》Steven G.Krantz GTM269《Locally Convex Spaces》M.Scott Osborne。
Supersymmetric Nonlinear Sigma Models on Ricci-flat Kahler Manifolds with O(N) Symmetry

Kiyoshi Higashijima∗ , Tetsuji Kimura† and Muneto Nitta‡
Department of Physics, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan
N −1
AN =
a2 −
Aa Aa .
a=1
(4)
To obtain the Ricci-flat K¨ ahler manifold with O(N ) symmetry, we calculate the Ricci form and solve the Ricci-flat condition. To do this, we first calculate the K¨ ahler metric gab∗ = ∂a ∂b∗ K of the 1
where AN is given by (4). Therefore, we only need the solution of K′ but not K itself, to calculate the Ricci-flat K¨ ahler metric.
2
To solve the nonlinear differential equation (10), we transform it to a linear differential equation: dy (x) x c(N − 1) + (N − 1) 2 y (x) = , 4 dx x −a x2 − a4 The general solution of y (x) is immediately obtained as y (x) = 1 2 x − a4
Linear Robust Control

O ce (626) 395-3371 Home (626) 449-8832
Fax (626) 796-8914
EDUCATION Ph.D. Mathematics
University of California, Berkeley Thesis Title: A Geometric Approach to Modeling and Control
COMPUTER SKILLS Programming in C, Mathematica, Matlab on UNIX platforms.
OTHER INTERESTS AND ACTIVITIES History, Politics and Philosophy Technology trends The Art and Science of Administration and Management Hiking
Stabilization of Relative Equilibria: In this project, we derived feedback laws for asymptotic stabilization of relative equilibria of mechanical systems with symmetry.
CDS 201: Applied Operator Theory
CDS 202: Geometry of Nonlinear Systems
Graduate Student Instructor Department of Mathematics, U.C. Berkeley. Courses taught were: Math 1: Calculus Math 16: Analytic Geometry and Calculus Math 54: Linear Algebra and Di erential Equations
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(6)
i (i = 1, 2) are the supercurrents and Tmn is the stress-energy where the Jαm tensor. Note that Lorentz invariance does not force the right-hand sides of the commutators to be the same. If there were no first supersymmetry, the v 4 term in the second commutator could be absorbed in Tmn ; it would represent the scale of the supersymmetry breaking. Now, however, the first supersymmetry can be said to define the stress-energy tensor, in which case there is an extra term in the second commutator. This discrepancy prevents the current algebra from being integrated into a charge algebra, and the no-go theorem is avoided. The second loophole involves the last step of the theorem. Even if the supercharges were to exist, it is only possible to extract (5) from (4) if the Hilbert space is positive definite. In covariantly-quantized supergravity theories, this is not the case: the gravitino ψmα is a gauge field with negative-norm components. There are, by now, many examples of partial supersymmetry breaking which exploit the first loophole. The first was given by Hughes, Liu and Polchinski
Linear and Nonlinear Supersymmetries
Jonathan Bagger and Alexander Galperin
Department of Physics and Astronomy, Johns Hopkins University 3400 N. Charles Street, Baltimore, MD 21218, USA
arXiv:hep-th/9810109v2 15 Oct 1998
Abstract. In this talk we use nonlinear realizations to study the spontaneous partial breaking of rigid and local supersymmetry.
Because of the supersymmetry algebra, this implies that the Hamiltonian also annihilates the vacuum, H |0 = 0 . (3) Then, according to the supersymmetry algebra, ¯ + SS ¯) |0 = 0 . (SS The final step is to peel apart this relation and conclude that S |0 ¯ |0 = S = 0. (5) (4)
m ¯α { Qα , Q ˙ } = 2 σαα ˙ Pm m ¯ { Sα , Sα ˙ } = 2 σαα ˙ Pm ,
(1)
¯α where Qα and its conjugate Q ˙ denote the first, unbroken supersymmetry, and ¯ Sα , Sα ˙ the second. Suppose that one supersymmetry is not broken, so Q |0 ¯ |0 = Q = 0. (2)
1
Introduction
The winter of 1996 was a hard one for physics, bringing the untimely deaths of Professors Dmitrij Vasilievich Volkov and Victor Isaacovitch Ogievetsky. At this symposium it seems appropriate to celebrate the memories of both men, whose scientific achievements were so closely aligned, and whose inspiring presence is already acutely missed by their many friends and colleagues across the world. In this talk we will discuss a subject close to their hearts: supersymmetry and its nonlinear realizations. In particular, we will consider the partial breaking of extended supersymmetry. For simplicity, we will restrict our attention to the case N = 2 → N = 1, but many of our results can be readily extended to the case of higher supersymmetries, spontaneously broken to N = 1. It is a fitting memorial to see many of the ideas pioneered by Professors Volkov and Ogievetsky come into play. The partial breaking of supersymmetry is of crucial importance to understanding the relation of theory to experiment. As theorists, we know in our bones that there is an ultimate theory, perhaps M theory, that exists at high energies. However, this theory is far removed from the physical world. To connect the two, we must integrate out the degrees of freedom associated with the high energies and construct a nonrenormalizable, effective field theory. This effective field theory should contain only those degrees of freedom that are relevant for physics in the world today. Indeed, it is the point of view that underlies the effective field theory approach to pion dynamics. Below the scale of chiral symmetry breaking, we know that the interactions of pions and hadrons are governed by an effective field theory in which the unbroken isospin symmetry is realized linearly, but the spontaneously broken chiral symmetry is realized nonlinearly. The nonlinear symmetry is all that remains of the chiral symmetry below the scale where it is broken. For the case at hand, we wish to construct a Lagrangian with two supersymmetries. The first supersymmetry, that of N = 1, is realized linearly, so it can be represented in terms of superfields. The second supersymmetry, N = 2, is realized nonlinearly on the superfields. In this way we can construct an effective
From this line of reasoning, one might think that partial breaking is impossible. Fortunately, this argument has two significant loopholes. The first is that, technically-speaking, spontaneously-broken charges do not exist. Indeed, in a spontaneously broken theory, one only has the right to consider the algebra of the currents. For the case at hand, the current algebra can be modified as follows,
