《运筹学》实验素材
运筹学综合实验报告

运筹学综合实验报告本次实验中,我们使用了运筹学的方法来解决了一个经典的优化问题,即整数线性规划问题(Integer Linear Programming,简称ILP)。
一、实验目的本次实验的主要目的是熟悉ILP的求解过程,了解ILP在实际问题中的应用,以及掌握使用现代优化软件Gurobi来求解ILP的方法。
二、实验原理1. 整数线性规划问题整数线性规划问题是在所有线性规划问题中的一个非常重要的子集。
它将优化目标函数的线性组合与整数限制相结合。
一个典型的ILP问题可以被描述为:最大化(或最小化)目标函数:\max(\min) \sum_{j=1}^{n}c_j x_j满足如下的约束条件:\sum_{j=1}^{n}a_{ij} x_j \leq b_i,\ i=1,2,\cdots,mx_j \geq 0,\ j=1,2,\cdots,nx_j \in Z,\ j=1,2,\cdots,nx_j表示自变量,c_j表示目标函数中的系数,a_{ij}表示第i个约束条件中x的系数,b_i表示约束条件的右侧常数,m表示约束条件的数量,n表示变量的数量。
最后两个约束条件要求自变量只能是整数。
2. Gurobi优化软件Gurobi是一个商业优化软件,经过多年的发展,已成为当前最流行的数学优化软件之一。
Gurobi支持多种数学优化方法,包括线性规划、非线性规划、混合整数规划、二次规划等。
Gurobi使用了现代算法来实现高效的求解效果,是工业和学术界备受推崇的优化软件。
三、实验内容1. 利用Gurobi求解整数线性规划问题我们使用Gurobi来求解如下的整数线性规划问题:\max\ \ 2x_1 + 3x_2 + 7x_3满足如下的约束条件:x_1 + x_2 + x_3 \leq 6x_1 - x_2 + x_3 \leq 4x_1, x_2, x_3 \in Z,\ x_1 \geq 0,\ x_2 \geq 0,\ x_3 \geq 0我们使用Python代码来实现该问题的求解过程:```pythonimport gurobipy as gbmodel = gb.Model("integer linear programming")# Create variablesx1 = model.addVar(vtype=gb.GRB.INTEGER, name="x1")x2 = model.addVar(vtype=gb.GRB.INTEGER, name="x2")x3 = model.addVar(vtype=gb.GRB.INTEGER, name="x3")# Set objectivemodel.setObjective(2*x1 + 3*x2 + 7*x3, gb.GRB.MAXIMIZE)# Add constraintsmodel.addConstr(x1 + x2 + x3 <= 6)model.addConstr(x1 - x2 + x3 <= 4)# Optimize modelmodel.optimize()# Print resultsprint(f"Maximum value: {model.objVal}")print(f"x1 = {x1.x}")print(f"x2 = {x2.x}")print(f"x3 = {x3.x}")```运行该代码,得到的输出结果为:```Optimize a model with 2 rows, 3 columns and 6 nonzerosVariable types: 0 continuous, 3 integer (0 binary)Coefficient statistics:Matrix range [1e+00, 1e+00]Objective range [2e+00, 7e+00]Bounds range [0e+00, 0e+00]RHS range [4e+00, 6e+00]Found heuristic solution: objective 9.0000000Presolve time: 0.00sPresolved: 2 rows, 3 columns, 6 nonzerosVariable types: 0 continuous, 3 integer (0 binary)Root relaxation: objective 1.500000e+01, 2 iterations, 0.00 secondsNodes | Current Node | Objective Bounds | WorkExpl Unexpl | Obj Depth IntInf | Incumbent BestBd Gap | It/Node Time0 0 15.00000 0 1 9.00000 15.00000 66.7% - 0sH 0 0 14.0000000 15.00000 7.14% - 0s0 0 15.00000 0 1 14.00000 15.00000 7.14% - 0sExplored 1 nodes (2 simplex iterations) in 0.03 secondsThread count was 4 (of 4 available processors)Solution count 2: 14 9Optimal solution found (tolerance 1.00e-04)Best objective 1.400000000000e+01, best bound 1.400000000000e+01, gap 0.0000%Maximum value: 14.0x1 = 2.0x2 = 4.0x3 = 0.0```经过Gurobi的求解,我们得到了最大值为14,同时x_1=2, x_2=4, x_3=0时取到最优值。
运筹学实验报告

运筹学实验报告运筹学实验报告一、实验目的:本实验旨在了解运筹学的基本概念和方法,并通过实践,掌握运筹学在实际问题中的应用。
二、实验过程:1.确定运筹学的应用领域:本次实验选择了物流配送问题作为运筹学的应用领域。
2.收集数据:我们选择了一个小型企业的物流配送数据进行分析,并将数据录入到计算机中。
3.建立模型:根据所收集的数据,我们建立了一个代表物流配送问题的数学模型。
4.运用运筹学方法进行求解:我们运用了线性规划的方法对物流配送问题进行求解,并得到了最优解。
5.分析结果:通过分析最优解,我们得出了一些有关物流配送问题的结论,并提出了一些优化建议。
三、实验结果:通过运用运筹学方法对物流配送问题进行求解,我们得到了一个最优解,即使得物流成本最低的配送方案。
将最优解与原始的配送方案进行对比,我们发现最优解的物流成本降低了20%,节省了货物运输的时间,减少了仓储成本。
四、实验结论:通过本次实验,我们了解了运筹学的基本概念和方法,并成功应用运筹学方法解决了物流配送问题。
通过分析最优解,我们发现采用最优解可以降低物流成本,提高配送效率。
因此,我们得出结论:运筹学在物流配送问题中的应用具有重要意义,可以帮助企业降低成本、提高效率。
五、实验心得:通过本次实验,我对运筹学有了更深入的了解。
通过实践应用运筹学方法,我明白了运筹学的实用性和价值。
在以后的工作中,我会更加注重运筹学方法的应用,以解决实际问题,提高工作效率。
本次实验不仅增强了我的动手实践能力,也培养了我分析和解决问题的能力。
我将继续学习和探索运筹学的知识,为将来的工作打下坚实的基础。
运筹学实验报告
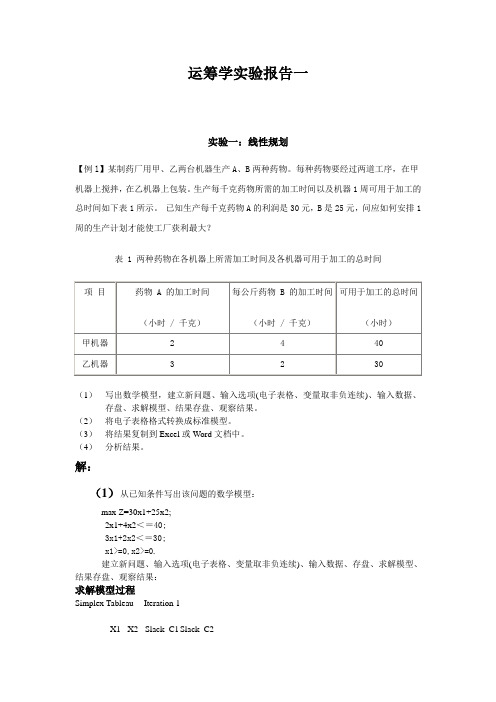
运筹学实验报告一实验一:线性规划【例l】某制药厂用甲、乙两台机器生产A、B两种药物。
每种药物要经过两道工序,在甲机器上搅拌,在乙机器上包装。
生产每千克药物所需的加工时间以及机器1周可用于加工的总时间如下表1所示。
已知生产每千克药物A的利润是30元,B是25元,问应如何安排1周的生产计划才能使工厂获利最大?表 1 两种药物在各机器上所需加工时间及各机器可用于加工的总时间(1)写出数学模型,建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果。
(2)将电子表格格式转换成标准模型。
(3)将结果复制到Excel或Word文档中。
(4)分析结果。
解:(1)从已知条件写出该问题的数学模型:max Z=30x1+25x2;2x1+4x2<=40;3x1+2x2<=30;x1>=0,x2>=0.建立新问题、输入选项(电子表格、变量取非负连续)、输入数据、存盘、求解模型、结果存盘、观察结果:求解模型过程Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 1X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioSlack_C1 0 2.0000 4.0000 1.0000 0 40.0000 20.0000Slack_C2 0 3.0000 2.0000 0 1.0000 30.0000 10.0000C(j)-Z(j) 30.0000 25.0000 0 0 0Simplex Tableau -- Iteration 3X1 X2 Slack_C1 Slack_C2Basis C(j) 30.0000 25.0000 0 0 R. H. S. RatioX2 25.0000 0 1.0000 0.3750 -0.2500 7.5000X1 30.0000 1.0000 0 -0.2500 0.5000 5.0000C(j)-Z(j) 0 0 -1.8750 -8.7500 337.5000(2)将电子表格格式转换成标准模型。
运筹学实验报告

运筹学实验报告导言运筹学是一门研究如何有效地进行决策、规划、控制和优化的学科。
它在不同领域中都有广泛应用,例如物流管理、生产调度、资源分配等。
本实验报告将介绍一个基于运筹学方法的实际案例,展示其在实践中的应用和效果。
问题描述我们选取了一个假设情景作为研究案例:一家电子公司正在考虑如何优化其供应链。
供应链的核心问题是如何在最小的时间和成本内将产品从制造商运送到最终客户手中。
该公司一直面临着供应链效率低下、库存过高等问题,因此需要进行优化。
方法选择为了解决供应链问题,我们选择了线性规划方法进行建模和求解。
线性规划是一种经典的运筹学方法,通过建立目标函数和约束条件来实现优化。
我们将考虑运输成本、库存成本和交货时间等因素,以最小化总成本为目标进行优化。
数据收集与分析首先,我们需要收集与供应链相关的数据,包括产品库存量、制造商的运输能力、客户的需求等信息。
通过对这些数据进行分析,我们可以获得对供应链瓶颈和优化潜力的洞察。
模型建立与求解根据数据分析的结果,我们可以建立数学模型来描述供应链的运作。
假设有n个制造商和m个客户,我们需要决策每个制造商向每个客户运送的产品数量。
我们定义决策变量x_ij表示制造商i 向客户j运送的产品数量。
通过设定合适的约束条件,如制造商的运输能力限制、客户的需求限制等,我们可以建立如下的线性规划模型:minimize ∑(c_ij * x_ij) for all i, jsubject to:∑(x_ij) <= supply_i for all i∑(x_ij) >= demand_j for all jx_ij >= 0 for all i, j其中c_ij表示从制造商i到客户j运输一个产品的成本,supply_i表示制造商i的运输能力,demand_j表示客户j的需求。
接下来,我们可以使用线性规划求解器对模型进行求解。
求解过程将得到最优的运输方案,包括每个制造商向每个客户运输的产品数量。
《运筹学》实验素材

素材1:北方化工厂月生产计划安排一、问题提出根据经营现状和目标,合理制定生产计划并有效组织生产,使一个企业提高效益的核心。
特别是对于一个化工厂而言,由于其原料品种多,生产工艺复杂,原材料和产成品存储费用较高,并有一定的危险性,对其生产计划作出合理安排就显得尤为重要。
现要求对北方化工厂的生产计划作出合理安排。
二、有关数据1、生产概况北方化工厂现有职工120人,其中生产工人105人,该厂主要设备是2套提取生产线,每套生产线容量为800kg,至少需要10人看管,该厂每天24小时连续生产,节假日不停机,从原料投入到成品出线平均需要10小时,成品率约为60%,该厂只有4t卡车1辆,可供原材料运输。
2、产品结构及有关资料该厂目前的产品可分为5类,所用原料15种,根据厂方提供的资料,经整理得表1-1。
3、供销情况(1)根据现有运输条件,原料3从外地购入,每月只能购入1车。
(2)根据前几个月的购销情况,产品1和产品3应占总产量的70%,产品2的产量最好不要超过总产量的5%,产品1的产量不要低于产品3与产品4产量之和。
素材2:石华建设监理公司监理工程师配置问题石华建设监理公司(国家甲级)侧重于国家大中型项目的监理,仅在河北省石家庄市就曾同时监理七项工程,总投资均在5000万元以上。
由于工程开工的时间不同,各工程工期之间相互搭接,具有较长的连续性,1998年监理的工程量与1999年监理的工程量大致相同。
每项工程安排多少监理工程师进驻工地,一般是根据工程的投资、建设规模、使用功能、施工的形象进度、施工阶段来决定的。
监理工程师的配置数量随之变化。
由于监理工程师从事的专业不同,他们每人承担的工作量也是不等的。
有的专业一个工地就需要三人以上,而有的专业一人则可以监管三个以上的工地。
因为从事监理业的专业多达几十个,仅以高层民用建筑为例就涉及到建筑学专业、工民建(结构)专业、给水排水专业、采暖通风专业、强点专业、弱点专业、自动化控制专业、技术经济专业、总图专业、合同和信息管理专业等,这就需要我们合理配置这些人力资源,为了方便计算,我们把所涉及的专业技术人员按总平均人数来计算,工程的施工形象进度按标准施工期和高峰施工期来划分。
运筹学实验报告(题目)

运筹学实验报告(题目)运筹学实验报告指导老师:姓名:学号:班级:目录例题实验一人力资源分配问题实验二配料问题实验三套裁下料问题实验四成本收益平衡问题实验五投资问题例题实验目的:1掌握Excel并熟悉它的使用环境。
2、准备好系统中的Office安装盘,然后选择【工具】|【加载宏】菜单命令,在弹出的【加载宏】对话框中选择【规划求解】3、在Excei中,对已有的问题进行规划求解。
实验内容:1、对下面线性规划问题进行求解;max z =3x1+x2+2x312x1+3x2+6x3+3x4=98x1+x2-4x3+2x5=103x1-x6=0Xj>=0 j=1,2,3,4,5,6一、第一步:打开Excel菜单栏中的工具菜单,出现一个子菜单,单击“规划求解”选项。
第二步:出现规划求解参数的对话框。
该对话框用来输入规划的目标函数,决策变量和约束条件。
第三步:在规划求解参数对话框内填写参数所在的地址如下:在设置目标单元格一栏内,填入表示目标函数值的单元格地址B16,并选择最大值选项;在可变单元格一栏内,填入决策变量的单元格地址B14:C14。
第四步:单击添加按钮,出现添加约束对话框,在单元格引用位置一栏内,填入约束条件左边的值所在的单元格地址B19:B21;选择<=;在约束值一栏内,填入约束条件左边的值的单元格地址D19:D21。
选择确定,得到一个填写完毕的规划求解参数对话框第五步:单击对话框内的选项按钮,出现规划求解选项对话框。
该对话框用来输入规划求解运算中的有关参数,例如是否线性模型、是否假定非负、迭代次数、精度等。
大部分参数已经按一般要求设置好了,只需设置是否采用线性模型,以及是否假定非负。
在本实验中,选择“采用线性模型”;选择“假定非负”。
然后就进行规划求解。
1.2(a)自变量X1 X2 X3 X4 X5 X6约束条件系数12 3 6 3 0 0 9 =8 1 -4 0 2 0 10 =3 0 0 0 0 -1 0 = 目标函数系数 3 1 2 0 0 0 3解0 0 1.5 0 8 0所以该问题有最优解:X=(0,0,1.5,0,8,0)实验(一)人力资源分配问题实验目的:1、根据题目要求,在有限的人力资源约束下进行建模。
运筹学实验报告

运筹学实验报告实验目的:了解及掌握运筹学一些常用软件,如excel,WinQsb:实验步骤1用Excel求解数学规划例:求max=2x1+x2+x34x1+2x2+2x2≥42x1+4x2≤204x1+8x2+2x3≤4步骤:1.输入模型数据制E3的公式到E4-E6:3.从“工具”菜单中选择“规划求解”,将弹出的“规划求解参数”窗口中的目标单元格设为$E$3,可变单元格设为$B$2:$D$2,目标为求最大值: 4.添加约束:由于本例的约束条件类型分别为<=、>=和=,因此要分3次设置,每次设置完毕后都要单击“添加”按钮,如下图。
添加完成后选择“确定”返回。
5.单击“选项”按钮,将“规划求解选项”窗口中的“采用线性模型”和“假定非负”两项选中后点“确定”返回,设置好参数的界面如下图:6.单击“求解”按钮,得到问题的最优解为:x1 =1,x2=0,x3=0,max Z=2。
2.winQSB求解线性规划及整数规划[例]求解线性规划问题:Minz=2x1—x2+2x32x1+2x2+x3=43x1+x2+x4=6第1步:生成表格选择“程序,生成对话框:第2步:输入数据单击“OK”,生成表格并输入数据如下第3步:求解):x1,x2,x3决策变量(Decision Variable最优解:x1=2,x2=0,x3=0目标系数:c1=2,c2= -1,c3=2最优值:4;其中x1贡献4、x2,x3贡献0;检验数(Reduced Cost):0,0,1.75。
目标系数的允许减量(Allowable Min.c[j])和允许增量(Allowable Max.c[j]):目标系数在此范围变量时,最优基不变。
约束条件(Constraint):C1、C2;左端(Left Hand Side):4,6右端(Right Hand Side):4,6松驰变量或剩余变量(Slack or Surplus):该值等于约束左端与约束右端之差。
运筹学实验总结

运筹学实验总结引言:运筹学是一门综合了数学、经济学和工程学等多学科知识的学科,它通过建立数学模型和运用各种优化方法,帮助我们在现实问题中寻找最优解决方案。
在这学期的运筹学课程中,我们进行了一系列实验。
这些实验不仅加深了对运筹学理论的理解,还提供了一种应用运筹学方法解决问题的实践平台。
在本文中,我将总结我参与的运筹学实验,并分享我的体会和收获。
实验一:线性规划问题求解在这个实验中,我们学习了线性规划的基本概念和求解方法。
我选择了一个典型的生产调度问题作为实验题目。
通过建立数学模型,并运用线性规划软件,我成功地解决了这个问题。
通过这个实验,我深刻理解了线性规划问题的本质,以及如何利用线性规划方法找到最优解。
实验二:整数规划问题求解整数规划是线性规划的扩展,它在决策问题中更加实用。
在这个实验中,我选择了货物配送路线问题作为研究对象。
通过构建整数规划模型,并运用求解软件,我得到了最佳的货物配送方案。
这个实验不仅对我的数学建模能力提出了要求,还培养了我的实际问题解决能力。
实验三:动态规划动态规划是一种重要的优化方法,它广泛应用于最优化问题的求解。
在这个实验中,我们学习了动态规划的基本原理和设计思想。
我选择了旅行商问题作为研究对象,通过建立递推关系和寻找最优子结构,我成功地解决了该问题。
这个实验让我意识到了动态规划方法的强大威力,同时也对我的算法设计能力提出了更高的要求。
实验四:模拟退火算法模拟退火算法是一种全局搜索优化算法,具有很强的应用能力。
在这个实验中,我选择了旅行商问题作为研究对象,通过模拟退火算法的迭代和优化,我得到了一个较好的解。
通过这个实验,我掌握了模拟退火算法的基本原理和实现过程,也了解到了算法的优越性。
实验五:遗传算法遗传算法是一种模拟自然选择和遗传机制的优化算法。
在这个实验中,我选择了装箱问题作为研究对象。
通过运用遗传算法的交叉、变异和适应度选择,我得到了一个较好的装箱方案。
这个实验不仅对我的算法设计能力提出了更高的要求,还让我意识到了遗传算法的创新性和解决复杂问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
素材1:北方化工厂月生产计划安排一、问题提出根据经营现状和目标,合理制定生产计划并有效组织生产,使一个企业提高效益的核心。
特别是对于一个化工厂而言,由于其原料品种多,生产工艺复杂,原材料和产成品存储费用较高,并有一定的危险性,对其生产计划作出合理安排就显得尤为重要。
现要求对北方化工厂的生产计划作出合理安排。
二、有关数据1、生产概况北方化工厂现有职工120人,其中生产工人105人,该厂主要设备是2套提取生产线,每套生产线容量为800kg,至少需要10人看管,该厂每天24小时连续生产,节假日不停机,从原料投入到成品出线平均需要10小时,成品率约为60%,该厂只有4t卡车1辆,可供原材料运输。
2、产品结构及有关资料该厂目前的产品可分为5类,所用原料15种,根据厂方提供的资料,经整理得表1-1。
3、供销情况(1)根据现有运输条件,原料3从外地购入,每月只能购入1车。
(2)根据前几个月的购销情况,产品1和产品3应占总产量的70%,产品2的产量最好不要超过总产量的5%,产品1的产量不要低于产品3与产品4产量之和。
素材2:石华建设监理公司监理工程师配置问题石华建设监理公司(国家甲级)侧重于国家大中型项目的监理,仅在河北省石家庄市就曾同时监理七项工程,总投资均在5000万元以上。
由于工程开工的时间不同,各工程工期之间相互搭接,具有较长的连续性,1998年监理的工程量与1999年监理的工程量大致相同。
每项工程安排多少监理工程师进驻工地,一般是根据工程的投资、建设规模、使用功能、施工的形象进度、施工阶段来决定的。
监理工程师的配置数量随之变化。
由于监理工程师从事的专业不同,他们每人承担的工作量也是不等的。
有的专业一个工地就需要三人以上,而有的专业一人则可以监管三个以上的工地。
因为从事监理业的专业多达几十个,仅以高层民用建筑为例就涉及到建筑学专业、工民建(结构)专业、给水排水专业、采暖通风专业、强点专业、弱点专业、自动化控制专业、技术经济专业、总图专业、合同和信息管理专业等,这就需要我们合理配置这些人力资源,为了方便计算,我们把所涉及的专业技术人员按总平均人数来计算,工程的施工形象进度按标准施工期和高峰施工期来划分。
通常标准施工期需求的人数较容易确定。
但高峰期施工期就比较难确定了,原因有两点:(1)高峰施工期各工地不是同时来到,是可以事先预测的,在同一个城市里相距不远的工地,就存在着各工地的监理工程师如何交错使用的运筹问题。
(2)各工地总监在高峰施工期到来的时候要向公司要人,如果每个工地都按高峰施工期配置监理工程师的数量,将造成极大的人力资源浪费,这一点应该说主要是人为因素所造成的。
因此,为了达到高峰施工期监理工程师配置数量最优,人员合理的交错使用,遏制人为因素,根据历年来的经验对高峰施工期的监理工程师数量在合理交错发挥作用的前提下限定了范围。
另经同级测算得知,全年平均标准施工期占7个月,人均成本4万元;高峰施工期占5个月,人均成本7万元。
标准施工期所需监理工程师如表2-1所示。
另外在高峰施工期各工地所需监理工程师的数量要求如下:第1和第2工地的总人数不少于14人;第2和第3工地的总人数不少于13人;第3和第4工地的总人数不少于11人;第4和第5工地的总人数不少于10人;第5和第6工地的总人数不少于9人;第6和第7工地的总人数不少于7人;第7和第1工地的总人数不少于14人;问题:(1)高峰施工期公司最少配置多少监理工程师?(2)监理工程师年耗费的总成本是多少?素材3:北方印染公司应如何合理使用技术培训费为适应现代科学技术的发展,提高工人的技术水平,必须下工夫搞好职工技术培训。
拨出专款进行智力投资,通过提高技术工人的水平,提高产品质量,能获取长期的经济效益。
但是,智力投资的目的是以最小的必要投入换取最大的经济效益,因此要对可利用的有限的资金进行合理的分配和利用,这就需要对智力投资的资金进行规划。
北方印染公司需要的技术工人分为初级、中级、高级三个层次。
统计资料显示:培养出来的每个初级工每年可为公司增加产值1万元,每个中级工每年可为公司增加产值4万元,每个高级工每年可为公司增加产值5.5万元。
公司计划在今后的三年中拨出150万元作为职工培训费,其中,第一年投资55万元,第二年投资45万元,第三年投资50万元。
通过公司过去培养初级工、中级工、高级工的经历并经过咨询,预计培养一名初级工,在高中毕业后需要一年,费用为1000元;培养一名中级工,高中毕业后需要三年时间,第一年和第二年的费用为3000元,第三年的费用为1000元;培养一名高级工,高中毕业后也需要三年时间,其中第一年的费用为3000元,第二年的费用为2000元,第三年的费用为4000元。
目前公司共有初级工226人,中级工560人,高级工496人。
若通过提高目前技术工人的水平来增加中级工和高级工的人数,其培养时间和培训费用分别是:由初级工培养为中级工,需要一年时间,费用为2800元;由中级工培养为高级工需要一年,费用为3600元。
由于公司目前的师资力量不足,教学环境有限,每年可培养的职工人数受到一定限制,根据目前的情况,每年在培的初级工不超过90人,在培的中级工不超过80人。
为了利用有限的职工培训费培养更多的技术工人,并为公司创造更大的经济效益,要确定直接由高中毕业生中培养初、中、高级技术工人各多少人,通过提高目前技术工人的水平来增加中级工和高级工人数的初级工和中级工分别为多少,才能使企业增加的产值最多。
素材4:报刊征订、推广费用的节省问题中华图书进出口总公司的主营业务之一是中文书刊对国外出口业务,由中文书刊出口部及两个分公司负责。
就中文报刊而言,每年10~12月为下一年度报刊订阅的征订期,在此期间,为巩固老订户,发展新订户,要向国外个人、大学图书馆、科研机构等无偿寄发小礼品和征订宣传推广材料。
中华图书进出口总公司在深圳、上海设有分公司,总公司从形成内部竞争机制,提高服务质量的角度考虑,允许这两家分公司也部分经营中文报刊的出口业务。
但为维护公司整体利益,避免内部恶性竞争,公司对征订期间三个部门寄发征订材料的工作作了整体安排(见表4-1所示)。
日本、韩国以及中国香港地区集中了该公司的绝大部分中文报刊订户,根据订户数分布数量的不同,寄发征订材料的数量也不同,对此公司也作了安排(见表4-2)。
表4-1表4-2一般情况下,这些材料无论由三家中哪个部门寄出,征收订户的效益大致相同。
同时,无论读者向那个部门订阅,为总公司创造的利益均是大致一样的。
但由于各部门邮途距离不同,邮寄方式及人工费用不用,导致从各部门寄往各地的费用也不同(见表6-3)。
表4-3由于寄发量大且每份材料的寄发费用较高,导致每年征订期日本、韩国以及中国香港特别行政区三地读者征订费用很高昂,大大加重了经营成本。
为此,如何在服从公司总体安排的前提下合理规划各部门的寄发数量,从而使总费用最省就成为一项有意义,值得研究的课题,根据所学运筹学知识,尝试对以下问题进行探讨。
提示:根据所给出的资料,作出一个公司整体的中文书刊征订材料的邮运方案,使得公司总的邮运费最小。
素材5:华中金刚石锯片厂的销售分配华中金刚石锯片厂是1992年合资建成的股份制企业。
现有员工200多人,主要生产切割石材、钢筋混凝土、陶瓷、玻璃和水泥与沥青路面的金刚石圆锯片的弹簧钢基体。
现有两条生产线,分别生产Φ900~1600mm大锯片基体2000片,Φ350~800mm中小锯片基体40000片。
产品种类有精品锯片、组合锯片、薄型锯片、普通锯片和非标锯片五大系列(如表5-1所示)。
表5-1自建厂以来,企业的经济效益高速增长,1996年实现销售收入4000万元,纯利500万元,产品畅销全国21个省市自治区,并远销东南亚、中东和欧美等多个国家和地区。
由于所研制的钢种刚度高,质量稳定性好,复焊次数多,产品出现了供不应求的局面。
对此情况,一方面,积极通过扩产技术改造和企业兼并扩大生产规模;另一方面,要求各个部门,在产品旺销时不能降低质量水平,不能中断与前期投资辛苦建立的各用户的联系以便为扩产后的销售做准备。
同时,要进一步降低各种成本,以完成董事会提出的年利润指标。
为此,总厂继续贯彻实施和完善从原料采购、下料、热处理、检测、库房和销售公司各部门的逐级买断制,并对销售公司除考核销售收入外,还加强了利润额、汇款率、汇款速度的考核。
销售公司现在全国有25个销售网点,主要销售区域集中在福建、广东、广西、四川、山东5个石材主产区。
为完成总厂的要求,销售公司决定一方面拿出10%的产量稳定与前期各个客户的联系以保证将来的市场区域分额,另一方面,面临如何将剩余的90%的产量分配给五个主要销售区的7个网点,以获取最大的利润,各个网点的最低需求、销售固定费用、每片平均运费、每片从总厂库房的购进价与当地的销售价差贡献等自然情况如表5-1所示。
运费由销售公司承担。
问应如何分配给各个销售区,使得总利润为最大?素材6:北京亚洲公司的存储决策问题北京亚洲科技发展有限公司,涉足多媒体网络应用、数字视频、电子出版和桌面印刷制版等技术领域。
公司提供从产品开发、网络集成、系统销售,直到专业化的影视后期编辑、平面设计、电子出版物制作等多项服务。
非线性视音频编辑系统(简称“非线性”)是公司的主要产品之一。
“非线性”是应用于广播电视领域的专业计算机多媒体设备。
主要用来完成电影、电视节目(如新闻、专题、电视剧……)的编辑制作。
目前该公司的“非线性”产品的核心硬件(Finish qxc/NT,Finish V60 及Finish V80),均从美国进口的,如何订货才能使公司的成本最低是在年初计划时必须解决的问题。
假设该产品的订购折扣是一定的,且在实际销售过程中并不要求必须是现货供应。
具体统计数据如表6-1所示:表6-1素材7:华北加气混凝土厂的钢筋存储问题华北加气混凝土厂1965年从瑞士某公司引进设备和技术。
1989年又改造生产线,从德国某公司引进关键设备进行生产。
装备达到国际20世纪80年代末期水平。
1991年重新投产,产品为加气混凝土砌块及加气混凝土屋面板,主要用于建筑的墙体及屋面,具有良好的保温、防火性能,且质轻易于运输,利于抗震。
从上面的情况可以知道,混凝土厂的产品前途是光明的,效益也是不错的。
但由于种种原因,还有许多不尽如人意的地方,还有许多需要改善的地方。
这需要掌握管理技术的人才细心地管理。
该厂产品优势在加气混凝土板材上,钢筋是供车间生产板材时用的,如果缺货的话,将导致较大的缺货损失,包括板材相应的利润、大批工人停工的损失,顾客买不到相应的产品引起对企业不满造成的损失等等,这些损失远远超过了钢筋的存储成本。
另外,由于现在是买方市场,交通方便,距离较近,价格稳中有降,生产时间可视为非常短。
