第3章习题答案 计算机组成原理课后答案(清华大学出版社 袁春风主编)
计算机组成原理 [袁春风]chap3_1
![计算机组成原理 [袁春风]chap3_1](https://img.taocdn.com/s3/m/6a0eacceaa00b52acfc7cacf.png)
15
南京大学计算机系 多媒体技术研究所 袁春风
3.2.3 先行进位ALU
(1)为什么用先行进位方式 行波进位是串行逐级传递的 整个和的生成受到行波进位的影响 因此 现代计算机采用一种先行进位(Carry look ahead)方式 (2)如何产生先行进位 定义两个辅助函数 Gi=aibi…进位生成 Pi=ai⊕bi…进位传递 通常把实现上述逻辑的电路称为进位生成/传递部件 全加逻辑方程 Si=Pi⊕Ci Ci+1=Gi+PiCi (i=0,1,…n) 设n=4,则 C1=G0+P0C0 C2=G1+P1C1=G1+P1G0+P1P0C0 C3=G2+P2C2=G2+P2G1+P2P1G0+P2P1P0C0 C4=G3+P3C3=G3+P3G2+P3P2G1+P3P2P1G0+P3P2P1P0C0 由上式可知:各进位之间无等待 相互独立并同时产生 通常把实现上述逻辑的电路称为4位CLA部件 由此 根据Si=Pi⊕Ci 可并行求出各位和 通常把实现Si=Pi⊕Ci的电路称为求和部件 CLA加法器由“进位生成/传递部件” “CLA部件”和“求和部件”构成
高位进位逻辑表达式
9
南京大学计算机系 多媒体技术研究所 袁春风
全加和逻辑
10
南京大学计算机系 多媒体技术研究所 袁春风
全加和逻辑 续
11
南京大学计算机系 多媒体技术研究所 袁春风
全加器逻辑图
上述全加器和Sum的延迟为6ty,进位Cout的延迟为 (假定一个与/或门延迟为1ty 异或门的延迟则为
AL BL CL DL CS DS SS ES IP 16位
计算机组成与系统结构课后答案全(清华大学出版社_袁春风主编)

(2)[x]补=10000000 (4)[x]补=11010011 x = –0.0011001B x = –10000000B = –128 x = +0.101001B x = – 101101B = – 45
7.假定一台 32 位字长的机器中带符号整数用补码表示,浮点数用 IEEE 754 标准表示,寄存器 R1 和 R2 的内容分别为 R1:0000108BH,R2:8080108BH。不同指令对寄存器进行不同的操作,因而,不同 指令执行时寄存器内容对应的真值不同。假定执行下列运算指令时,操作数为寄存器 R1 和 R2 的内 容,则 R1 和 R2 中操作数的真值分别为多少? (1) 无符号数加法指令 (2) 带符号整数乘法指令 (3) 单精度浮点数减法指令 参考答案: R1 = 0000108BH = 0000 0000 0000 0000 0001 0000 1000 1011b R2 = 8080108BH = 1000 0000 1000 0000 0001 0000 1000 1011b (1) 对于无符号数加法指令, R1 和 R2 中是操作数的无符号数表示, 因此, 其真值分别为 R1: 108BH, R2:8080108BH。 (2)对于带符号整数乘法指令,R1 和 R2 中是操作数的带符号整数补码表示,由最高位可知, R1 为正数, R2 为负数。R1 的真值为+108BH, R2 的真值为–(0111 1111 0111 1111 1110 1111 0111 0100b + 1b) = –7F7FEF75H。 (3)对于单精度浮点数减法指令,R1 和 R2 中是操作数的 IEEE754 单精度浮点数表示。在 IEEE 754 标准中,单精度浮点数的位数为 32 位,其中包含 1 位符号位,8 位阶码,23 位尾数。 由 R1 中的内容可知, 其符号位为 0, 表示其为正数, 阶码为 0000 0000, 尾数部分为 000 0000 0001 0000 1000 1011,故其为非规格化浮点数,指数为–126,尾数中没有隐藏的 1,用十六进制表示 尾数为+0.002116H,故 R1 表示的真值为+0.002116H × 10-126。 由 R2 中的内容可知, 其符号位为 1, 表示其为负数, 阶码为 0000 0001,尾数部分为 000 0000 0001 0000 1000 1011,故其为规格化浮点数,指数为 1–127 = –126,尾数中有隐藏的 1,用十六进制 表示尾数为–1.002116H,故 R2 表示的真值为–1.002116H × 10-126
计算机组成原理第三章课后习题参考答案
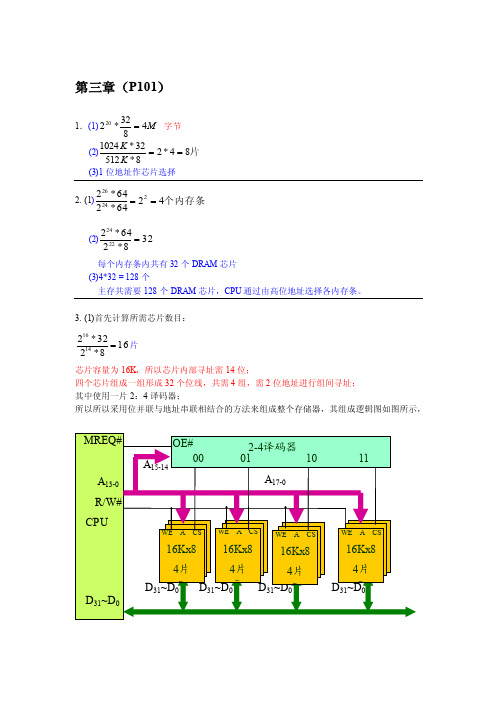
第三章(P101)1.(1)M 4832*220= 字节 (2)片84*28*51232*1024==K K(3)1位地址作芯片选择2. (1)个内存条4264*264*222426==(2)328*264*22242=每个内存条内共有32个DRAM 芯片 (3)4*32 = 128个主存共需要128个DRAM 芯片,CPU 通过由高位地址选择各内存条。
3. (1)首先计算所需芯片数目:168*232*21416=片 芯片容量为16K ,所以芯片内部寻址需14位;四个芯片组成一组形成32个位线,共需4组,需2位地址进行组间寻址; 其中使用一片2:4译码器;所以所以采用位并联与地址串联相结合的方法来组成整个存储器,其组成逻辑图如图所示,(2)根据已知条件,CPU 在1us 内至少访存一次,而整个存储器的平均读/写周期为0.5us ,如果采用集中刷新,有64us 的死时间,肯定不行 如果采用分散刷新,则每1us 只能访存一次,也不行 所以采用异步式刷新方式。
假定16K*8位的DRAM 芯片用128*128矩阵存储元构成,刷新时只对128行进行异步方式刷新,则刷新间隔为2ms/128 = 15.5us ,可取刷新信号周期15us 。
刷新一遍所用时间=15us ×128=1.92ms4. (1)片328*12832*1024 K K ,共分8组,每组4片;地址线共20位,其中组间寻址需3位,组内17位; (2)(3)如果选择一个行地址进行刷新,刷新地址为A 0-A 8,因此这一行上的2048个存储元同时进行刷新,即在8ms 内进行512个周期(即512行)。
采用异步刷新方式,刷新信号周期为:8ms/512 = 15.5us 。
注:存储器由128K*8位的芯片构成,分8组,每组4片,组内芯片并行工作,需17条地址线进行寻址,其中X 行线为9根,Y 位线为8根,29=512行。
5. 用256K*16位的SRAM 芯片设计1024K*32的存储器,需进行字位同时扩展方式继续拧设计,所需芯片数目:片816*25632*1024 K K ,设计的存储器容量为1M ,字长为32,故需20位地址(A0~A19);所用芯片存储容量为256K ,字长为16位,故片内寻址需18位(A0~A17)。
计算机组成与系统结构课后答案版全(清华大学袁春风主编)

(4)(4E.C)16= (78.75)10= (0100 1110.11)2
4.假定机器数为8位(1位符号,7位数值),写出下列各二进制数的原码和补码表示。
+0.1001,–0.1001,+1.0,–1.0,+0.010100,–0.010100,+0,–0
参考答案:
原码补码
+0.1001:0.10010000.1001000
–0.1001:1.10010001.0111000
+1.0:溢出溢出
–1.0:溢出1.0000000
+0.010100:0.01010000.0101000
(1)无符号数加法指令
(2)带符号整数乘法指令
(3)单精度浮点数减法指令
参考答案:
R1=0000108BH= 0000 0000 0000 0000 0001 0000 1000 1011b
R2=8080108BH= 1000 0000 1000 0000 0001 0000 1000 1011b
(1)对于无符号数加法指令,R1和R2中是操作数的无符号数表示,因此,其真值分别为R1:108BH, R2:8080108BH。
(3)[x]补=0.1010010x = +0.101001B
(4)[x]补=11010011x =–101101B =–45
7.假定一台32位字长的机器中带符号整数用补码表示,浮点数用IEEE 754标准表示,寄存器R1和R2的内容分别为R1:0000108BH,R2:8080108BH。不同指令对寄存器进行不同的操作,因而,不同指令执行时寄存器内容对应的真值不同。假定执行下列运算指令时,操作数为寄存器R1和R2的内容,则R1和R2中操作数的真值分别为多少?
计算机组成与系统结构课后答案版全(清华大学袁春风主编)

(3)对于单精度浮点数减法指令,R1和R2中是操作数的IEEE754单精度浮点数表示。在IEEE 754标准中,单精度浮点数的位数为32位,其中包含1位符号位,8位阶码,23位尾数。
S2有8条指令,CPI为(1×1+1×2+1×3+5×4)/8 =3.25,所含的时钟周期数为8×3.25=26,执行时间为26/500M = 52ns。
(注:从上述结果来看,对于同一个高级语言源程序,在同一台机器上所生成的目标程序不同,其执行时间可能不同,而且,并不是指令条数少的目标程序执行时间就一定少。)
7.假设同一套指令集用不同的方法设计了两种机器M1和M2。机器M1的时钟周期为0.8ns,机器M2的时钟周期为1.2ns。某个程序P在机器M1上运行时的CPI为4,在M2上的CPI为2。对于程序P来说,哪台机器的执行速度更快?快多少?
参考答案:
假设程序P的指令条数为N,则在M1和M2上的执行时间分别为:
移码补码
+1001:1000100100001001
–1001:0111011111110111
+1:1000000100000001
–1:01111111111111111
+10100:1001010000010100
–10100:0110110011101100
+0:1000000000000000
M2上可以选择一段A和B类指令组成的程序,其峰值MIPS为1500/2=750MIPS。
计算机组成与系统结构课后答案版全(清华大学袁春风主编)

5.若有两个基准测试程序P1和P2在机器M1和M2上运行,假定M1和M2的价格分别是5000元和8000元,下表给出了P1和P2在M1和M2上所花的时间和指令条数。
程序
M1
M2
指令条数
执行时间(ms)
指令条数
执行时间(ms)
P1
200×106
10000
150×106
5000
P2
300×103
3
420×103
(3)[x]补=0.1010010x = +0.101001B
(4)[x]补=11010011x =–101101B =–45
7.假定一台32位字长的机器中带符号整数用补码表示,浮点数用IEEE 754标准表示,寄存器R1和R2的内容分别为R1:0000108BH,R2:8080108BH。不同指令对寄存器进行不同的操作,因而,不同指令执行时寄存器内容对应的真值不同。假定执行下列运算指令时,操作数为寄存器R1和R2的内容,则R1和R2中操作数的真值分别为多少?
–0:1000000000000000
6.已知[x]补,求x
(1)[x]补=1.1100111(2)[x]补=10000000
(3)[x]补=0.1010010(4)[x]补=11010011
参考答案:
(1)[x]补=1.1100111x =–0.0011001B
(2)[x]补=10000000x =–10000000B =–128
M1:4 N×0.8 = 3.2N (ns)
M2:2 N×1.2 = 2.4 N (ns)
所以,M2执行P的速度更快,每条指令平均快0.8ns,比M1快0.8/3.2×100%=25%。
8.假设某机器M的时钟频率为4GHz,用户程序P在M上的指令条数为8×109,其CPI为1.25,则P在M上的执行时间是多少?若在机器M上从程序P开始启动到执行结束所需的时间是4秒,则P占用的CPU时间的百分比是多少?
计算机组成和系统结构课后答案解析版全(清华大学出版社_袁春风主编)
第 1 章习题答案5.若有两个基准测试程序P1和P2在机器M1和M2上运行,假定M1和M2的价格分别是5000元和8000请回答下列问题:(1)对于P1,哪台机器的速度快?快多少?对于P2呢?(2)在M1上执行P1和P2的速度分别是多少MIPS?在M2上的执行速度又各是多少?从执行速度来看,对于P2,哪台机器的速度快?快多少?(3)假定M1和M2的时钟频率各是800MHz和1.2GHz,则在M1和M2上执行P1时的平均时钟周期数CPI各是多少?(4)如果某个用户需要大量使用程序P1,并且该用户主要关心系统的响应时间而不是吞吐率,那么,该用户需要大批购进机器时,应该选择M1还是M2?为什么?(提示:从性价比上考虑)(5)如果另一个用户也需要购进大批机器,但该用户使用P1和P2一样多,主要关心的也是响应时间,那么,应该选择M1还是M2?为什么?参考答案:(1)对于P1,M2比M1快一倍;对于P2,M1比M2快一倍。
(2)对于M1,P1的速度为:200M/10=20MIPS;P2为300k/0.003=100MIPS。
对于M2,P1的速度为:150M/5=30MIPS;P2为420k/0.006=70MIPS。
从执行速度来看,对于P2,因为100/70=1.43倍,所以M1比M2快0.43倍。
(3)在M1上执行P1时的平均时钟周期数CPI为:10×800M/(200×106)=40。
在M2上执行P1时的平均时钟周期数CPI为:5×1.2G/(150×106)=40。
(4)考虑运行P1时M1和M2的性价比,因为该用户主要关心系统的响应时间,所以性价比中的性能应考虑执行时间,其性能为执行时间的倒数。
故性价比R为:R=1/(执行时间×价格)R越大说明性价比越高,也即,“执行时间×价格”的值越小,则性价比越高。
因为10×5000 > 5×8000,所以,M2的性价比高。
计算机组成与系统结构课后答案版全(清华大学袁春风主编)
5.若有两个基准测试程序P1和P2在机器M1和M2上运行,假定M1和M2的价格分别是5000元和8000元,下表给出了P1和P2在M1和M2上所花的时间和指令条数。
程序
M1
M2
指令条数
执行时间(ms)
指令条数
执行时间(ms)
P1
200×106
10000
150×106
5000
P2
300×103
3
420×103
参考答案:
程序P在M上的执行时间为:1.25×8×109×1/4G = 2.5 s,从启动P执行开始到执行结束的总时间为4秒,其中2.5秒是P在CPU上真正的执行时间,其他时间可能执行操作系统程序或其他用户程序。
程序P占用的CPU时间的百分比为:2.5/4 = 62.5%。
9.假定某编译器对某段高级语言程序编译生成两种不同的指令序列S1和S2,在时钟频率为500MHz的机器M上运行,目标指令序列中用到的指令类型有A、B、C和D四类。四类指令在M上的CPI和两个指令序列所用的各类指令条数如下表所示。
参考答案:
显然,P’的执行时间为10秒,因此,P比P’多花了2秒钟,因此,执行时被换成左移指令的乘法指令的条数为1.2G×2/(5–2) = 800M。
第
3.实现下列各数的转换。
(1)(25.8125)10= (?)2= (?)8= (?)16
(2)(101101.011)2= (?)10= (?)8= (?)16= (?)8421
R=1/(执行时间×价格)
R越大说明性价比越高,也即,“执行时间×价格”的值越小,则性价比越高。
因为10×5000 > 5×8000,所以,M2的性价比高。应选择M2。
计算机组成与系统结构课后答案全(清华大学出版社 袁春风主编)
第 1 章习题答案5.若有两个基准测试程序P1和P2在机器M1和M2上运行,假定M1和M2的价格分别是5000元和8000元,下表给出了P1和P2在M1和M2上所花的时间和指令条数。
请回答下列问题:(1)对于P1,哪台机器的速度快?快多少?对于P2呢?(2)在M1上执行P1和P2的速度分别是多少MIPS?在M2上的执行速度又各是多少?从执行速度来看,对于P2,哪台机器的速度快?快多少?(3)假定M1和M2的时钟频率各是800MHz和1.2GHz,则在M1和M2上执行P1时的平均时钟周期数CPI各是多少?(4)如果某个用户需要大量使用程序P1,并且该用户主要关心系统的响应时间而不是吞吐率,那么,该用户需要大批购进机器时,应该选择M1还是M2?为什么?(提示:从性价比上考虑)(5)如果另一个用户也需要购进大批机器,但该用户使用P1和P2一样多,主要关心的也是响应时间,那么,应该选择M1还是M2?为什么?参考答案:(1)对于P1,M2比M1快一倍;对于P2,M1比M2快一倍。
(2)对于M1,P1的速度为:200M/10=20MIPS;P2为300k/0.003=100MIPS。
对于M2,P1的速度为:150M/5=30MIPS;P2为420k/0.006=70MIPS。
从执行速度来看,对于P2,因为100/70=1.43倍,所以M1比M2快0.43倍。
(3)在M1上执行P1时的平均时钟周期数CPI为:10×800M/(200×106)=40。
在M2上执行P1时的平均时钟周期数CPI为:5×1.2G/(150×106)=40。
(4)考虑运行P1时M1和M2的性价比,因为该用户主要关心系统的响应时间,所以性价比中的性能应考虑执行时间,其性能为执行时间的倒数。
故性价比R为:R=1/(执行时间×价格)R越大说明性价比越高,也即,“执行时间×价格”的值越小,则性价比越高。
计算机组成与系统结构课后答案版全(清华大学出版社-袁春风主编)名师制作优质教学资料
第 1 章习题答案5.若有两个基准测试程序P1和P2在机器M1和M2上运行,假定M1和M2的价格分别是5000元和8000元,下表给出了P1和P2在M1和M2上所花的时间和指令条数。
请回答下列问题:(1)对于P1,哪台机器的速度快?快多少?对于P2呢?(2)在M1上执行P1和P2的速度分别是多少MIPS?在M2上的执行速度又各是多少?从执行速度来看,对于P2,哪台机器的速度快?快多少?(3)假定M1和M2的时钟频率各是800MHz和1.2GHz,则在M1和M2上执行P1时的平均时钟周期数CPI各是多少?(4)如果某个用户需要大量使用程序P1,并且该用户主要关心系统的响应时间而不是吞吐率,那么,该用户需要大批购进机器时,应该选择M1还是M2?为什么?(提示:从性价比上考虑)(5)如果另一个用户也需要购进大批机器,但该用户使用P1和P2一样多,主要关心的也是响应时间,那么,应该选择M1还是M2?为什么?参考答案:(1)对于P1,M2比M1快一倍;对于P2,M1比M2快一倍。
(2)对于M1,P1的速度为:200M/10=20MIPS;P2为300k/0.003=100MIPS。
对于M2,P1的速度为:150M/5=30MIPS;P2为420k/0.006=70MIPS。
从执行速度来看,对于P2,因为100/70=1.43倍,所以M1比M2快0.43倍。
(3)在M1上执行P1时的平均时钟周期数CPI为:10×800M/(200×106)=40。
在M2上执行P1时的平均时钟周期数CPI为:5×1.2G/(150×106)=40。
(4)考虑运行P1时M1和M2的性价比,因为该用户主要关心系统的响应时间,所以性价比中的性能应考虑执行时间,其性能为执行时间的倒数。
故性价比R为:R=1/(执行时间×价格)R越大说明性价比越高,也即,“执行时间×价格”的值越小,则性价比越高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 64 •
10100 10101 +0 0 1 1 0 11010 10101 10101 01011 +00110 11011 01011 10110 10111 +00110 11100 10111 11001 01111 +00110 11111 01111 11110 11111 +00110 00100 11110 +00000 + 1 00100 11111 所以,[X/Y] 补=11111,余数为 00100。
商的数值部分为:00001。所以,[X/Y]原=00001 (最高位为符号位),余数为 0100。 (5) 将 10 和–6 分别表示成补码形式为:[10] 余数寄存器 R 余数/商寄存器 Q 00000 01010 +11010 11010 01010
补 补
先对被除数进行符号扩展,[10] 补=00000 01010,[6] 补 = 0 0110 说 明 开始 R0 = [X] R1=[X] +[Y] R1 与[Y]同号,则 q5 =1
6.设 A4A1 和 B4B1 分别是四位加法器的两组输入,C0 为低位来的进位。当加法器分别采用串行进位和先 行进位时,写出四个进位 C4 C1 的逻辑表达式。 参考答案: 串行进位: C1 = X1C0+Y1C0 + X1 Y1 C2 = X2C1+Y2C1 + X2 Y2 C3 = X3C2+Y3C2 + X3 Y3 C4 = X4C3+Y4C3 + X4 Y4 并行进位: C1 = X1Y1 + (X1+Y1)C0 C2 = X2Y2 + (X2 +Y2) X1Y1 + (X2+Y2) (X1+Y1)C0 C3 = X3Y3 + (X3 + Y3) X2Y2 + (X3 + Y3) (X2 + Y2) X1Y1 + (X3 + Y3) (X2 + Y2)(X1 + Y1)C0 C4=X4Y4+(X4+Y4)X3Y3+(X4+Y4)(X3+Y3)X2Y2+(X4+Y4)(X3+Y3)(X2+Y2)X1Y1+(X4+Y4)(X3+Y3) (X2+Y2)(X1+Y1)C0 7.用 SN74181 和 SN74182 器件设计一个 16 位先行进位补码加/减运算器,画出运算器的逻辑框图,并给出 零标志、进位标志、溢出标志、符号标志的生成电路。 参考答案(图略) :
5.以下是两段 C 语言代码,函数 arith( )是直接用 C 语言写的,而 optarith( )是对 arith( )函数以某个确定的 M 和 N 编译生成的机器代码反编译生成的。 根据 optarith( ), 可以推断函数 arith( ) 中 M 和 N 的值各是 多少?
• 61 •
#define M #define N int arith (int x, int y) { int result = 0 ; result = x*M + y/N; return result; } int optarith ( int x, int y) { int t = x; x << = 4; x - = t; if ( y < 0 ) y += 3; y>>2; return x+y; 参考答案: 可以看出 x*M 和“int t = x; x << = 4; x-=t;”三句对应,这些语句实现了 x 乘 15 的功能(左移 4 位 相当于乘以 16,然后再减 1) ,因此,M 等于 15; y/N 与“if ( y < 0 ) y += 3; y>>2;”两句对应,功能主要由第二句“y 右移 2 位”实现,它实现了 y 除 以 4 的功能,因此 N 是 4。而第一句“if ( y < 0 ) y += 3;”主要用于对 y=–1 时进行调整,若不调整,则 –1>>2=–1 而–1/4=0,两者不等;调整后 –1+3=2,2>>2=0,两者相等。 思考:能否把 if ( y < 0 ) y += 3; 改成 if ( y < 0 ) y += 2; ? 不能!因为 y = - 4 时不正确。
• 62 •
逻辑框图参见教材中的图 3.15 和图 3.16,将两个图结合起来即可,也即只要将图 3.15 中的 B 输入端的每 一位 Bi 取反,得到 Bi,和原码 Bi 一起送到一个二路选择器,由进位 C0 作为选择控制信号。当 C0 为 1 时 做减法,此时,选择将 Bi 作为 SN74181 的 B 输入端;否则,当 C0 为 1 时,做加法。 零标志 ZF、进位标志 CF、溢出标志 OF、符号标志 SF 的逻辑电路根据以下逻辑表达式画出即可。 ZF=F15+F14+F13+F12+F11+F10+F9+F8+F7+F6+F5+F4+F3+F2+F1+F0 CF=C16 OF= C0(A15B15F15 + A15B15F15)+ C0(A15B15F15 + A15B15F15) SF= F15 8. 用 SN74181 和 SN74182 器件设计一个 32 位的 ALU,要求采用两级先行进位结构。 (1) 写出所需的 SN74181 和 SN74182 芯片数。 (2) 画出 32 位 ALU 的逻辑结构图。 参考答案(图略) : 将如图 3.15 所示的两个 16 位 ALU 级联起来即可, 级联时, 低 16 位 ALU 的高位进位 C16 作为高 16 位 ALU 的低位进位 C0,因此,只要用 8 片 SN74181 和 2 片 SN74182。 9.已知 x = 10,y = – 6,采用 6 位机器数表示。请按如下要求计算,并把结果还原成真值。 (1) 求[x+y]补,[x–y]补。 (2) 用原码一位乘法计算[x×y]原。 (3) 用 MBA(基 4 布斯)乘法计算[x×y]补。 (4) 用不恢复余数法计算[x/y]原的商和余数。 (5) 用不恢复余数法计算[x/y]补的商和余数。 参考答案: [10]补 = 001010 [–6]补 = 111010 [6]补 = 000110 [10]原 = 001010 [–6]原 = 100110 (1) [10+(– 6)]补= [10]补+[– 6]补= 001010+111010 = 000100 (+4) [10–(–6)]补= [10]补+[– (–6)]补 = 001010+000110 = 010000 (+16) (2) 先采用无符号数乘法计算 001010× 000110 的乘积,原码一位乘法过程(前面两个 0 省略)如下: C 0 0 0 0 0 0 0 0 0 P 0000 +0000 0000 0000 +1010 1010 0101 +1010 1111 0111 +0000 0111 0011 Y 0110 说明 P0 = 0 y4 = 0,+0 C, P 和 Y 同时右移一位 得 P1 y3 = 1,+X C, P 和 Y 同时右移一位 得 P2 y2 = 1,+X C, P 和 Y 同时右移一位 得 P3 y1 = 0,+0 C, P 和 Y 同时右移一位 得 P4
函数 func1 的功能是把无符号数高 24 位清零 (左移 24 位再逻辑右移 24 位) , 结果一定是正的有符号数; 而函数 func2 的功能是把无符号数的高 24 位都变成和第 25 位一样,因为左移 24 位后进行算术右移,高 24 位补符号位(即第 25 位) 。
4.填写下表,注意对比无符号数和带符号整数的乘法结果,以及截断操作前、后的结果。
0011
0001 0000 1000
1100
若两个 6 位数相乘的话,则还要右移两次,得 000000 111100 符号位为:0 1 = 1,因此,[X×Y]原 = 1000 0011 1100
• 63 •
即 X × Y = –11 1100B = – 60 (3) [–10]补 = 110110,布斯乘法过程如下: P 000000 000000 +110110 110110 111011 +001010 000101 000010 +110110 111000 111100 +000000 111100 111110 +000000 111110 111111 Y 111010 y-1 0 说明 设 y-1 = 0,[P0]补 = 0 y0 y-1 = 00,P、Y 直接右移一位 得[P1]补 y1 y0 =10,+[–X]补 P、Y 同时右移一位 得[P2]补 y2 y1 =01,+[X]补 P、Y 同时右移一位 得[P3]补 y3 y2 = 10,+[–X]补 P、Y 同时右移一位 得[P4]补 y4 y3 = 11,+0 P、Y 同时右移一位 得[P5]补 y5 y4 = 11,+0 P、Y 同时右移一位 得[P6]补
